
Quelle: Wikimedia Commons File:Galileo.arp.300pix.jpg, gemeinfrei
Fassen wir die Ergebnisse des letzten Abschnitts noch einmal zusammen:
Wir haben Transformationen in Raum und Zeit gesucht, bei denen eine geradlinig gleichförmige Bewegung wieder zu einer geradlinig gleichförmigen Bewegung wird.
Um dies mathematisch zu formulieren, haben wir die Zeit \(t\) und den dreidimensionalen Raumvektor \(\boldsymbol{x}\) zu einem vierdimensionalen Raumzeit-Vektor \[ x = \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} \] zusammengefasst und Abbildungen \[ g : \, \mathbb{R}^4 \rightarrow \mathbb{R}^4 \] mit der Eigenschaft \[ g( a + b s ) = a' + b' s \] gesucht. Dabei sollten die 4-dimensionalen Vektoren \(a, b, a', b'\) sowie die Abbildung \(g\) vom reellen Kurvenparameter \(s\) unabhängig sein. Wir konnten zeigen, dass \(g\) von der Form \[ g(x) = A \, x + c \] sein muss mit einer \(4 \times 4\)-Matrix \(A\) und einem 4-dimensionalen Raumzeit-Verschiebe-Vektor \(c\). Es handelt sich also um eine affine Abbildung.
Nun ist diese affine Abbildung noch zu allgemein, um daraus Rückschlüsse auf die Physik zu ziehen. Es zeigt sich, dass die physikalischen Gesetze nicht generell unverändert bleiben, wenn man Raum und Zeit auf diese Weise transformiert. Es ist notwendig, die Abbildung \(g\) durch weitere Zusatzbedingungen weiter einzuschränken.
Machen wir uns noch einmal klar, was eine allgemeine affine Abbildung in der Raumzeit alles bewirken kann.
Zunächst einmal kann sie die zu jeder Zeitangabe eine feste Zeit hinzuaddieren. Das ist so, als würde man das Experiment beispielsweise zwei Stunden später ausführen. Da dies auf das Experiment keinen Einfluss haben sollte, wollen wir hier keine weitere Einschränkung vornehmen.
Dasselbe gilt für Verschiebungen im Raum. Es sollte egal sein, ob wir das Experiment hier oder einige Meter weiter weg durchführen.
Insgesamt wollen wir also Raum- und Zeitverschiebungen weiter zulassen, d.h. der Vektor \(c\) soll keinen weiteren Einschränkungen unterworfen sein.
Bleibt die Matrix \(A\). Sie kann Raumrichtungen verdrehen, Winkel verändern und Raumrichtungen dehnen oder stauchen. Welche dieser Veränderungen würden den Ausgang eines Experimentes wohl beeinflussen?
Drehungen der Raumachsen um einen festen Winkel scheinen in Ordnung zu gehen, denn es sollte egal sein, wie ein Labor im leeren schwerelosen Weltraum orientiert ist. Drehungen sind übrigens nicht mit Rotationen zu verwechseln! Aus der Sicht eines ständig rotierenden Labor fliegt ein Ball nicht mehr geradeaus.
Wie sieht es mit der Vermischung von Raum- und Zeitkoordinaten aus? Hier müssen wir etwas präziser werden und sagen, welche Vermischungen wir genau meinen.
Im folgenden wollen wir Raum- und Zeitverschiebungen nicht ständig mitbetrachten, da wir für sie sowieso keine Einschränkungen machen wollen. Wir setzen also in \(g(x) = A \, x + c\) den Verschiebungsanteil \(c = 0\) und interessieren uns für Bedingungen an die Matrix \(A\).
Betrachten wir eine geradlinig-gleichförmige Bewegung. Zur Vereinfachung wollen wir annehmen, dass der Ort des Teilchens zum Zeitpunkt Null gerade im Ursprung des Koordinatensystems liegt. Dann können wir diese Bewegung im dreidimensionalen Raum darstellen durch \[ \boldsymbol{x} = \boldsymbol{v} t \] Dabei ist \(\boldsymbol{x}\) der Ort des Objektes zur Zeit \(t\) und \(\boldsymbol{v}\) ist die Geschwindigkeit des Objektes.
Welche andere geradlinig-gleichförmige Bewegung können wir wohl mit Hilfe unserer affinen Transformation (mit \(c = 0\)) daraus machen, so dass sich die Naturgesetze nicht ändern?
Da wir momentan keine Informationen haben, die uns hier weiterhelfen, hilft nur raten: wir wollen probehalber fordern, dass die neue Bewegung nach der Transformation durch die Gleichung \[ \boldsymbol{x}' = \boldsymbol{v}' t \] dargestellt wird mit demselben Zeitparameter \(t\) (die Striche dienen nur zur Unterscheidungvon und haben hier nichts mit Ableitungen zu tun). Die Geschwindigkeit darf sich also ändern, so als würden wir die Bewegung nach der Transformation aus einem fahrenden Zug heraus betrachten.
Wir wollen diese Forderung wieder vierdimensional schreiben und fassen dazu die Zeitkoordinate und die drei Raumkoordinaten zu vierdimensionalen Vektoren zusammen. Damit wird \( \boldsymbol{x} = \boldsymbol{v} t \) zu \[ x = b s \] oder genauer \[ x = \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} \, s = b s \] Die Abbildung \(g(x) = A \, x\) soll daraus die Bewegung \[ x' = b's = g(x) = g(bs) = A b s \] machen mit \[ x' = \begin{pmatrix} t \\ \boldsymbol{x}' \end{pmatrix} = \begin{pmatrix} 1 \\ \boldsymbol{v}' \end{pmatrix} \, s = b' s \] erzeugen, d.h. es muss für diese speziellen Vektoren \(b\) und \(b'\) die Gleichung \[ b' = \begin{pmatrix} 1 \\ \boldsymbol{v}' \end{pmatrix} = A b = A \, \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} \] erfüllt sein.
Um diese Bedingung besser auswerten zu können, wollen wir die zeitlichen und räumlichen Komponenten der Matrix \(A\) mit speziellen Buchstaben benennen. Wir schreiben \[ A = \begin{pmatrix} \gamma & \boldsymbol{w} \\ \boldsymbol{u} & R \end{pmatrix} \] d.h. \( \gamma = A_{oo} \) (das Matrixelement links oben in der Ecke), \( w_i = A_{0i} \) (die 3 Matrixelemente in der obersten (nullten) Zeile rechts von \(\gamma\), zusammengefasst zum 3-komponentigen Vektor \(\boldsymbol{w}\)), \( u_i = A_{i0} \) (die 3 Matrixelemente in der linken (nullten) Spalte unterhalb von \(\gamma\), zusammengefasst zum 3-komponentigen Vektor \(\boldsymbol{u}\)) und \(R_{ij} = A_{ij}\) (die \(3 \times 3\)-Matrix \(R\) ist also der Anteil rechts unten in der \(4 \times 4\)-Matrix \(A\), also ohne die nullte Zeile und Spalte). Die Indices \(i\) und \(j\) nehmen also die Werte 1, 2 und 3 an.
Damit haben wir \[ A x = \begin{pmatrix} \gamma & \boldsymbol{w} \\ \boldsymbol{u} & R \end{pmatrix} \, \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} \gamma t + \boldsymbol{w x} \\ \boldsymbol{u} t + R \boldsymbol{x} \end{pmatrix} \] Damit können wir die Bedingung \(b' = A b\) schreiben als \[ b' = \begin{pmatrix} 1 \\ \boldsymbol{v}' \end{pmatrix} = A b = A \, \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma & \boldsymbol{w} \\ \boldsymbol{u} & R \end{pmatrix} \, \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} = \begin{pmatrix} \gamma + \boldsymbol{w v} \\ \boldsymbol{u} + R \boldsymbol{v} \end{pmatrix} \] also insgesamt \[ \begin{pmatrix} 1 \\ \boldsymbol{v}' \end{pmatrix} = \begin{pmatrix} \gamma + \boldsymbol{w v} \\ \boldsymbol{u} + R \boldsymbol{v} \end{pmatrix} \] Die Zeitkomponente (nullte oder oberste Komponente) dieser Gleichung lautet demnach \[ 1 = \gamma + \boldsymbol{w v} \] Das ist eine Bedingung an die Matrixkomponenten \(\gamma\) und \(\boldsymbol{w}\), die für beliebige Geschwindigkeitsvektoren \(\boldsymbol{v}\) gelten soll. Damit folgt sofort, dass \(\gamma = 1\) und \(\boldsymbol{w} = \boldsymbol{0}\) sein muss. Die Matrix \(A\) ist also von der Form \[ A = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} & R \end{pmatrix} \]
Wir wollen Matrizen dieser Form als verallgemeinerte Galilei-Matrizen
bezeichnen – im Unterschied zu den (eigentlichen) Galilei-Matrizen,
bei denen \(R\) noch weiteren Einschränkungen unterliegt – wir kommen weiter
unten nochmal darauf zurück.

Quelle:
Wikimedia Commons File:Galileo.arp.300pix.jpg, gemeinfrei
Wie wirkt sich diese Matrix auf die zeitlichen und räumlichen Komponenten des Vektors \(x\) aus? Probieren wir es aus: \[ x' = A x = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} & R \end{pmatrix} \, \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} t \\ \boldsymbol{u} t + R \boldsymbol{x} \end{pmatrix} \] Die Zeitkomponente wird also überhaupt nicht verändert Das entspricht genau unserer Voraussetzung oben, dass \(t' = t\) sein muss in \(x' = A x\). Es ist jedoch nicht so, als ob es überhaupt keine Vermischung zwischen Raum- und Zeitkoordinaten gäbe, denn in den Ortsanteil nach der Transformation spielt die Zeit mit hinein: \[ \boldsymbol{x}' = \boldsymbol{u} t + R \boldsymbol{x} \] Man kann leicht nachprüfen, dass die obigen Matrizen wieder eine Gruppe bilden, die wir als verallgemeinerte Galilei-Gruppe bezeichnen wollen. So ist die inverse Matrix gegeben durch \[ A^{-1} = \begin{pmatrix} 1 & \boldsymbol{0} \\ -R^{-1} \boldsymbol{u} & R^{-1} \end{pmatrix} \] Rechnen wir es kurz nach: \[ A A^{-1} = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} & R \end{pmatrix} \, \begin{pmatrix} 1 & \boldsymbol{0} \\ -R^{-1} \boldsymbol{u} & R^{-1} \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} - R R^{-1} \boldsymbol{u} & R R^{-1} \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \mathbb{1} \end{pmatrix} \] mit der \(3 \times 3\)-Einheitsmatrix \(\mathbb{1}\).
Wie können wir nun die Abbildungen \(A\) interpretieren? Was bewirken sie in Raum und Zeit? Um das herauszufinden, lassen wir sie wieder auf eine geradlinig-gleichförmige Bewegung wirken.
Aus der Bewegung \[ \boldsymbol{x} = \boldsymbol{v}t \] wird durch die Wirkung von \(A\) die Bewegung \begin{align} \boldsymbol{x}' &= \boldsymbol{u} t + R \boldsymbol{x} = \\ &= \boldsymbol{u} t + R \boldsymbol{v} t = \\ &= (\boldsymbol{u} + R \boldsymbol{v}) \, t \end{align} d.h. die ursprüngliche Geschwindigkeit \(\boldsymbol{v}\) wird zunächst mit \(R\) einer linearen Transformation unterworfen und anschließend wird die Geschwindigkeit \(\boldsymbol{u}\) hinzuaddiert. Der Vektor \(\boldsymbol{u}\) kann also als eine zusätzliche Geschwindigkeit interpretiert werden, der bei allen betrachteten Objekten hinzuaddiert wird. Insbesondere bewegt sich ein vorher ruhendes Objekt ( also \(\boldsymbol{v} = \boldsymbol{0}\)) nach der Galileitransformation mit der Geschwindigkeit \(\boldsymbol{u}\). Man kann sich das so vorstellen, als ob das ganze Experiment in einen fahrenden Zug verlegt wird, der mit der Geschwindigkeit \(\boldsymbol{u}\) dahinfährt. Dabei wird das Experiment vorher zusätzlich durch die lineare Matrix \(R\) gedreht, verzerrt oder Ähnliches.
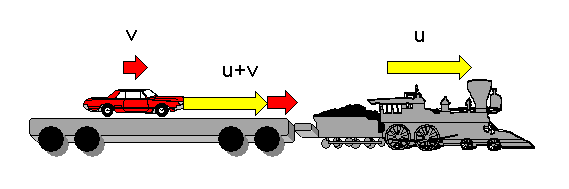
Den Zusammenhang, dass aus einer Geschwindigkeit \(\boldsymbol{v}\)
nach einer Galileitransformation die Geschwindigkeit \(\boldsymbol{u} + R\boldsymbol{v}\)
wird, bezeichnet man auch als das Gesetz für die Addition von Geschwindigkeiten
bei Galileitransformationen. Man stellt sich dabei beispielsweise vor, dass
ein kleines Spielzeugauto in einem stehenden Zug mit der Geschwindigkeit
\(\boldsymbol{v}\) umherfährt. Nun wenden wir eine Galileitransformation an, wobei wir
zur Vereinfachung eine Transformation mit \(R = \mathbb{1}\) betrachten.
Der Zug bewegt sich nun mit der
Geschwindigkeit \(\boldsymbol{u}\) und das Auto mit der Geschwindigkeit \(\boldsymbol{u} + \boldsymbol{v}\).
Die Geschwindigkeit des Autos entsteht also einfach dadurch, dass
man zu seiner Geschwindigkeit im ruhenden Zug die Geschwindigkeit des Zuges
hinzuaddiert.
Die Form der verallgemeinerten Galilei-Matrizen kann man alternativ auch aus einer anderen Forderung ableiten, die zu unserer Forderung von oben gleichwertig ist.
Man fordert, dass die Matrix \(A\) keine zeitlichen Abstände ändern darf.
Oben haben wir gesehen, dass die Matrix \(A\) aus der Zeit \(t\) die Zeit \(t' = \gamma t + \boldsymbol{w x}\) macht. Wenn sich zeitliche Abstände nicht ändern, muss also gelten: \[ t_2' - t_1' = \] \[ = (\gamma t_2 + \boldsymbol{w x}_2) - (\gamma t_1 + \boldsymbol{w x}_1) = \] \[ = t_2 - t_1 \] Man kann diese Bedingung etwas umschreiben: \[ (1 - \gamma) (t_2 - t_1) = \boldsymbol{w} (\boldsymbol{x}_2 - \boldsymbol{x}_1) \] Das gilt für beliebige Zeiten \(t_1, t_2\) und Orte \(\boldsymbol{x}_1, \boldsymbol{x}_2\). Das kann nur erfüllt werden, wenn beide Seiten konstant sind, also unabhängig von den speziellen Werten der Zeiten und Orte. Diese Konstante muss gleich Null sein, da z.B. die linke Seite für \(t_1 = t_2\) Null ist. Daraus folgt \begin{align} \gamma &= 1 \\ \boldsymbol{w} &= \boldsymbol{0} \end{align}
Man kann nun noch einen Schritt weiter gehen und zusätzlich fordern, dass die Matrix \(A\) keine auch keine räumlichen Abstände ändern darf. Dabei müssen die beiden Raumpunkte, zwischen denen der Abstand ermittelt wird, zur gleichen Zeit betrachtet werden, d.h. sie müssen in der gleichen Zeitscheibe der vierdimensionalen Raumzeit liegen. Wir werden muss also gleich \(t_1 = t_2\) verwenden. Wegen \(\boldsymbol{x}' = \boldsymbol{u} t + R \boldsymbol{x}\) ist für gleiche Zeiten also \[ \boldsymbol{x}_2' - \boldsymbol{x}_1' = \] \[ = (\boldsymbol{u} t_2 + R \boldsymbol{x}_2) - (\boldsymbol{u} t_1 + R \boldsymbol{x}_1) = \] \[ = \boldsymbol{u} (t_2 - t_1) + R (\boldsymbol{x}_2 - \boldsymbol{x}_1) = \] \[ = R (\boldsymbol{x}_2 - \boldsymbol{x}_1) \] Wenn sich die räumlichen Abstande bei gleicher Zeitscheibe nicht ändern sollen, muss also gelten: \[ (\boldsymbol{x}_2' - \boldsymbol{x}_1')^2 = \] \[ = (R (\boldsymbol{x}_2 - \boldsymbol{x}_1))^2 = \] \[ = (\boldsymbol{x}_2 - \boldsymbol{x}_1)^2 \] Die Matrix \(R\) muss also eine orthogonale Matrix (also eine Drehmatrix oder eine Raumspiegelung) sein, d.h. sie erfüllt die Bedingung \[ R^T \, R = \mathbb{1} \] mit der transponierten Matrix \(R^T\) und der Einheitsmatrix \(\mathbb{1}\).
Die Gruppe der verallgemeinerten Galilei-Matrizen \(A\), bei denen \(R\) zusätzlich diese Bedingung erfüllt, heißt (eigentliche) Galileigruppe. Die Transformationen dieser Gruppe ändern also räumliche und zeitliche Abstände nicht, so wie man das für Raum-Zeit-Symmetrien bzw. Raum-Zeit-Bezugssystemwechsel intuitiv auch erwartet.
Eine Transformation, die man der Galileigruppe normalerweise noch hinzurechnet, beinhaltet Spiegelungen der Zeit. Man fordert dabei nicht, dass Zeitabstände unverändert bleiben müssen, sondern dass der Absolutbetrag von Zeitabständen unverändert bleiben muss. Neben \(\gamma = 1\) ist dann auch \(\gamma = -1\) ein erlaubter Wert.
Fassen wir am Ende dieses Abschnitts noch einmal zusammen:
Wir haben in diesem Kapitel eine Reihe von plausiblen Forderungen an die Matrix \(A\) der affinen Abbildung \(g\) gestellt und haben so die Matrizen der verallgemeinerten und der eigentlichen Galileigruppe erhalten. Was für Folgen das für den Zusammenhang zwischen Impuls und Geschwindigkeit hat, wollen wir im nächsten Abschnitt untersuchen.
© Jörg Resag, www.joerg-resag.de
last modified on 19 June 2023