Wir hatten im letzten Abschnitt die Darstellung \[ \Lambda = e^X = e^{ \begin{pmatrix} 0 & \boldsymbol{a} \\ \boldsymbol{a} & G \end{pmatrix} } \] mit \(G^T = -G\) für die Matrizen der Lorentztransformationen hergeleitet.
In diesem Abschnitt betrachten wir nun den Spezialfall \(G = 0\). Wir wollen diese speziellen Transformationen als Boosts bezeichnen.
Den Vektor \(\boldsymbol{a}\) schreiben wir in der Form \[ \boldsymbol{a} = \alpha \boldsymbol{e} \] mit der sogenannten Rapidität \(\alpha = |\boldsymbol{a}| \) und dem Einheitsvektor \(\boldsymbol{e}\) mit \(|\boldsymbol{e}| = 1\). Wir können \(\boldsymbol{e}\) fest vorgeben und betrachten \(\alpha\) als Parameter. Dann ist \[ \Lambda_b = e^{ \, \alpha \, \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} } =: e^{\, \alpha X_b} \] mit \[ X_b = \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} \] Der Index \(b\) bei \(\Lambda_b\) und \(X_b\) steht dabei für Boost.
Die Matrix \(X_b\) hängt von dem Einheitsvektor \(\boldsymbol{e}\) ab. Insgesamt können wir also drei linear unabhängige Matrizen \(X_{b,i}\) vorgeben, wobei wir für \(\boldsymbol{e}_i\) den i-ten Einheitsvektor nehmen. Jede Matrix \(X_b\) kann als Linearkombination aus den drei \(X_{b,i}\) gebildet werden. Man bezeichnet die \(X_{b,i}\) auch als die Generatoren der Gruppe der Boosts.
Die Eponential-Funktion war über eine unendliche Reihe definiert. In den einzelnen Termen dieser Reihe muss die Matrix \(X_b\) mehrfach mit sich selbst multipliziert werden. Daher wollen wir sehen, was bei der Multiplikation von \(X_b\) mit sich selbst herauskommt: \[ X_b^2 = \] \[ = \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} \, \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{e} \, \boldsymbol{e}^T \end{pmatrix} = \] \[ =: F \] (so definieren wir also die Matrix \(F\)). Dabei steht \(\boldsymbol{e} \, \boldsymbol{e}^T\) für die Matrix mit den Komponenten \(e_i e_j\), d.h. angewendet auf irgendeinen Dreiervektor \(\boldsymbol{x}\) ergibt diese Matrix \[ (\boldsymbol{e} \, \boldsymbol{e}^T) \, \boldsymbol{x} = \boldsymbol{e} \, (\boldsymbol{e x}) \] mit dem Skalarprodukt \( \boldsymbol{e x} \).
Für \(X_b^3\) ergibt sich damit \[ X_b^3 = X_b^2 \, X_b = F \, X_b = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{e} \, \boldsymbol{e}^T \end{pmatrix} \, \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} = \] \[ = \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} = \] \[ = X_b \] Und für \( X_b^4\) erhalten wir wieder \[ X_b^4 = X_b^3 \, X_b = X_b \, X_b = F \]
Insgesamt haben wir also
für gerade \(n = 2i \) mit \(i \ge 1\):
\[
X_b^n = X_b^{2i} = F
\]
und für ungerade \(n = 2i + 1\):
\[
X_b^n = X_b^{2i+1} = X_b
\]
Damit können wir die unendliche Exponentialreihe in mehrere Teilreihen aufteilen,
eine für gerade \(n\) und eine für ungerade \(n\).
Die geraden \(n\) schreiben wir wie oben als
\(n = 2i\) und die ungeraden \(n\) als \(n = 2i+1\).
In der Reihe für gerade \(n\) schreiben wir den Term für \(n = 0\)
so um, dass sich die Matrix \(F\) auch für diesen Term ausklammern lässt, also
\[
X_b^0 = 1 = F + (1 - F)
\]
Dann ist
\[
\Lambda_b = e^{\, \alpha X_b} =
\sum_{n = 0}^{\infty} \, \frac{\alpha^n}{n!} X_b^n
=
\]
\[
=
\sum_{i = 0}^{\infty} \, \frac{\alpha^{2i}}{(2i)!} X_b^{2i}
+
\sum_{i = 0}^{\infty} \, \frac{\alpha^{2i+1}}{(2i+1)!} X_b^{2i+1}
=
\]
\[
=
\sum_{i = 0}^{\infty} \, \frac{\alpha^{2i}}{(2i)!} F \; + (1 - F) + \,
\sum_{i = 0}^{\infty} \, \frac{\alpha^{2i+1}}{(2i+1)!} X_b
=
\]
\[
= (\cosh{\alpha}) \, F \; + (1 - F) + \, (\sinh{\alpha}) \, X_b =
\]
\[
= (\cosh{\alpha}) \,
\begin{pmatrix}
1 & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{e} \, \boldsymbol{e}^T
\end{pmatrix}
+
\]
\[
+
\begin{pmatrix}
0 & \boldsymbol{0} \\
\boldsymbol{0} & \mathbb{1} - \boldsymbol{e} \, \boldsymbol{e}^T
\end{pmatrix}
+
\]
\[
+
(\sinh{\alpha}) \,
\begin{pmatrix}
0 & \boldsymbol{e} \\
\boldsymbol{e} & 0
\end{pmatrix} =
\]
\[
=
\begin{pmatrix}
(\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\
(\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T)
\end{pmatrix}
\]
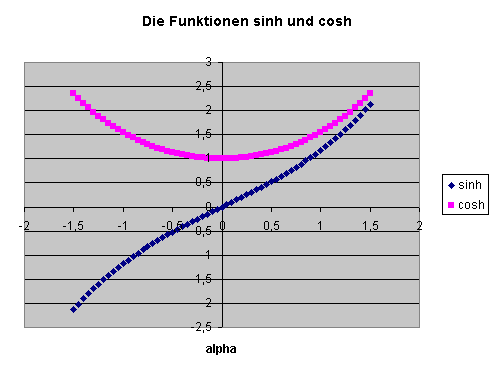
Dabei haben wir die bekannten Reihendarstellung für die Funktionen
Sinus-Hyperbolicus \((\sinh{\alpha})\) und Cosinus-Hyperbolicus \((\cosh{\alpha})\) verwendet.
Zwischen diesen beiden Funktionen gilt
die Beziehung
\[
(\cosh{\alpha})^2 - (\sinh{\alpha})^2 = 1
\]

Ein Beispiel:
für den Spezialfall, dass \(\boldsymbol{e}\) der Einheitsvektor in \(x\)-Richtung ist
(also ein Boost in \(x\)-Richtung mit \(\boldsymbol{e} = (1,0,0)\) ) liefert die obige Formel
\[
\Lambda_b =
\begin{pmatrix}
(\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\
(\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T)
\end{pmatrix}
\]
die recht einfache Matrix
\[
\Lambda_b =
\begin{pmatrix}
\cosh{\alpha} & \sinh{\alpha} & 0 & 0 \\
\sinh{\alpha} & \cosh{\alpha} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\]
(denn in diesem Fall ist \(\boldsymbol{e} \, \boldsymbol{e}^T\)
eine Matrix, die fast nur aus Nullen besteht; lediglich ganz oben links steht eine 1).
Das folgende Bild stellt dar, wie sich diese Abbildung auf die
Einheitsvektoren in Zeitrichtung und in die x-Raumrichtung auswirkt:
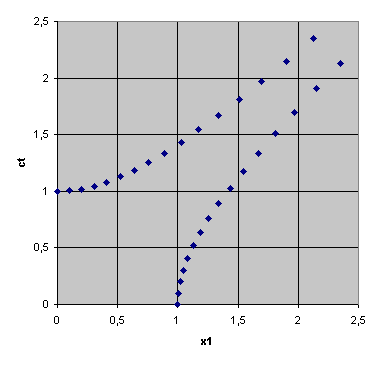
Was bewirken die Boosts nun in Raum und Zeit?
Betrachten wir dazu ein ruhendes Teilchen, dessen Bewegung in Raum und Zeit wir durch die Gerade \[ x = a + bs \] mit \[ b = \begin{pmatrix} 1 \\ \boldsymbol{0} \end{pmatrix} \] darstellen können. Wir hatten bereits früher gesehen, dass die Geschwindigkeit des Teilchens gegeben ist durch \[ \boldsymbol{v} = c \, \frac{\boldsymbol{b}}{b^0} \] Da hier \(\boldsymbol{b} = \boldsymbol{0}\) und damit \(\boldsymbol{v} = \boldsymbol{0}\) ist, ruht das Teilchen, so wie beabsichtigt.
Nun lassen wir den Boost auf Raum und Zeit wirken. Aus dem Vektor \(b\) wird dann der Vektor \[ b' = \Lambda_b \, b = \] \[ = \begin{pmatrix} (\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\ (\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} \, \begin{pmatrix} 1 \\ \boldsymbol{0} \end{pmatrix} = \] \[ = \begin{pmatrix} \cosh{\alpha} \\ (\sinh{\alpha}) \, \boldsymbol{e} \end{pmatrix} \] Also ist die Geschwindigkeit nach dem Boost gleich \[ \boldsymbol{v}' = c \, \frac{\boldsymbol{b}'}{b'^0} = = c \, \frac{\sinh{\alpha}}{\cosh{\alpha}} \, \boldsymbol{e} \] Das ist die Geschwindigkeit, die ein ruhendes Teilchen nach dem Boost aufweist. Ein Boost setzt also Teilchen in Bewegung!
Wie schnell kann ein Teilchen durch einen Boost werden?
Rechnen wir es aus, wobei wir die Beziehung \((\cosh{\alpha})^2 - (\sinh{\alpha})^2 = 1\) verwenden:
\[
(\boldsymbol{v}')^2 =
c^2 \, \frac{(\sinh{\alpha})^2}{(\cosh{\alpha})^2}
=
\]
\[
=
c^2 \, \frac{(\cosh{\alpha})^2 - 1}{(\cosh{\alpha})^2}
=
\]
\[
=
c^2 \, \left( 1 - \frac{1}{(\cosh{\alpha})^2} \right)
\lt c^2
\]
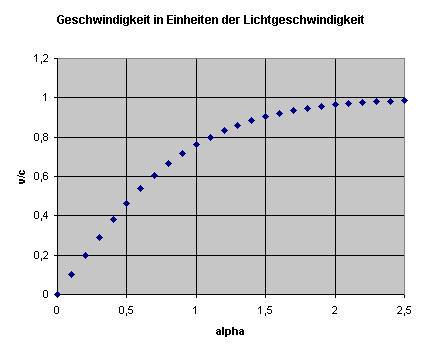
denn \((\cosh{\alpha})\) ist immer größer-gleich 1,
sodass \(\frac{1}{(\cosh{\alpha})^2}\) kleiner-gleich 1 (aber für endliches \(\alpha\) nie Null) ist.
Die Klammer ist also kleiner als 1 (aber größer-gleich Null).
Daher kann das Teilchen
die Lichtgeschwindigkeit nicht überschreiten.
Analog zur üblichen physikalischen Literatur wollen wir die folgende Abkürzung – den Lorentzfaktor – einführen: \[ \gamma := \cosh{\alpha} \] Wegen der Eigenschaften der cosh-Funktion ist \(\gamma \ge 1\).
Wir wollen außerdem die sogenannte Boostgeschwindigkeit \(\boldsymbol{u}\) definieren (das ist die Geschwindigkeit eines zuvor ruhenden Teilchens nach dem Boost, relativ zur Lichtgeschwindigkeit): \[ \boldsymbol{u} = \frac{\sinh{\alpha}}{\cosh{\alpha}} \, \boldsymbol{e} \] Von oben wissen wir bereits, dass \[ \frac{(\sinh{\alpha})^2}{(\cosh{\alpha})^2} = \frac{(\cosh{\alpha})^2 - 1}{(\cosh{\alpha})^2} = \] \[ = \left( 1 - \frac{1}{(\cosh{\alpha})^2} \right) \] ist. Setzen wir hier \(\gamma = \cosh{\alpha}\) ein und ziehen die Wurzel, so ist für \(\alpha \ge 0\) und damit \((\sinh{\alpha}) \ge 0\) (was wir voraussetzen wollen) \[ \frac{\sinh{\alpha}}{\cosh{\alpha}} = \sqrt{ 1 - \frac{1}{\gamma^2} } \] sodass \[ \boldsymbol{u} = \sqrt{ 1 - \frac{1}{\gamma^2} } \, \boldsymbol{e} \] ist. Quadrieren, freistellen nach \(\gamma^2\) und Wurzelziehen ergibt die bekannte Formel für den Lorentzfaktor \[ \gamma = \sqrt{ \frac{1}{1 - \boldsymbol{u}^2} } \] Weiterhin ist \[ \gamma \boldsymbol{u} = \] \[ =\gamma \cdot \sqrt{ 1 - \frac{1}{\gamma^2} } \, \boldsymbol{e} = \] \[ = \sqrt{ \gamma^2 - 1 } \, \boldsymbol{e} = \] \[ = \sqrt{ (\cosh{\alpha})^2 - 1 } \, \boldsymbol{e} = \] \[ = (\sinh{\alpha}) \, \boldsymbol{e} \] Mit diesen Gleichungen können statt der Rapidität \(\alpha\) und \(\boldsymbol{e}\) auch die Boostgeschwindigkeit \(\boldsymbol{u}\) als Parameter für die Boostmatrix verwenden: \[ \Lambda_b = \] \[ = \begin{pmatrix} (\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\ (\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma & \gamma \boldsymbol{u} \\ \gamma \boldsymbol{u} & \mathbb{1} + (\gamma - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} = \] wobei für die Boostgeschwindigkeit \( |\boldsymbol{u}| \lt 1\) gilt, denn man kann ein ruhendes Teilchen niemals auf Überlichtgeschwindigkeit boosten. Die Rapidität \(\alpha\) hatte diese Beschränkung nicht; sie kann beliebig groß werden. Zudem gilt nur für die Rapidität \(\alpha\) wegen der einfachen Exponentialdarstellung \( \Lambda_b = e^{\, \alpha X_b} \) die einfache Beziehung \[ \Lambda_b(\alpha_1) \, \Lambda_b(\alpha_2) = \Lambda_b(\alpha_1 +\alpha_2) \] Für die Boostgeschwindigkeit \(\boldsymbol{u}\) gilt eine solche Beziehung nicht. Wenn wir also ein ruhendes Teilchen zweimal hintereinander einem Boost mit Boostgeschwindigkeit \(\boldsymbol{u}\) unterziehen, so hat es danach nicht die Geschwindigkeit \(2 \boldsymbol{u} c\). Wäre das so, so könnten wir es auf Überlichtgeschwindigkeit boosten, aber das geht nicht. Wir sehen schon: die Addition von Geschwindigkeiten ist hier komplizierter – mehr dazu in einem späteren Abschnitt.
Damit wollen wir die Betrachtung der Boosts beenden und uns den Drehungen zuwenden.
© Jörg Resag, www.joerg-resag.de
last modified on 23 June 2023