Die Poincarégruppe bzw. Lorentzgruppe ist als physikalische Symmetriegruppe offenbar besser geeignet als die Galileigruppe, da sie eine Reihe von physikalischen Phänomenen beschreibt, die die Galileigruppe nicht erfasst. So sagt die Poincarégruppe aus, dass sich kein Teilchen, das auch in Ruhe existieren kann (Geschwindigkeit Null), schneller als mit Lichtgeschwindigkeit bewegen kann. Dies stimmt mit den physikalischen Beobachtungen überein.
Umgekehrt wissen wir, dass die Galileigruppe zumindest für Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit die Physik recht gut beschreibt. Es stellt sich daher die Frage: Auf welche Weise kann man die Poincarégruppe in die Galileigruppe überführen? Welche Näherung oder welchen Grenzwertprozess muss man durchführen, damit aus einer Poincarétransformation eine Galileitransformation wird?
Betrachten wir dazu die Poincaré-Boosts. Wie wir wissen, können wir die Lorentz-Matrix von Boosts schreiben als \[ \Lambda_b = e^{\, \alpha X_b} = e^{ \, \alpha \, \begin{pmatrix} 0 & \boldsymbol{e} \\ \boldsymbol{e} & 0 \end{pmatrix} } = \] \[ = \begin{pmatrix} (\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\ (\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma & \gamma \boldsymbol{u} \\ \gamma \boldsymbol{u} & \mathbb{1} + (\gamma - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} \] mit dem Lorentzfaktor \[ \gamma := \cosh{\alpha} \] und der Boostgeschwindigkeit \[ \boldsymbol{u} = \frac{\sinh{\alpha}}{\cosh{\alpha}} \, \boldsymbol{e} = \] \[ = \sqrt{ 1 - \frac{1}{\gamma^2} } \, \boldsymbol{e} \] mit \(|\boldsymbol{e}| = 1\). Dabei wird \(\alpha\) als Rapidität bezeichnet. Die Boostgeschwindigkeit ist die Geschwindigkeit, die ein ruhendes Objekt nach dem Boost aufweist (gemessen in Anteilen der Lichtgeschwindigkeit, so dass immer \(|\boldsymbol{u}| \lt 1\) gilt).
Die Poincarégruppe sollte für kleine Geschwindigkeiten irgendwie in die Galileigruppe übergehen. Man könnte daher auf die Idee kommen, nur kleine Werte von \(\alpha\) bzw. \(|\boldsymbol{u}| \) zu betrachten und entsprechende Reihenentwicklungen vorzunehmen. Ein Versuch wäre, in der Exponentialdarstellung nur bis zum Term linear in \(\alpha\) zu gehen, also \[ \Lambda_b = = e^{\, \alpha X_b} \approx 1 + \alpha X_b = \] \[ = \alpha \, \begin{pmatrix} 1 & \boldsymbol{e} \\ \boldsymbol{e} & \mathbb{1} \end{pmatrix} \] Ist das eine Galilei-Boostmatrix? Die Galileimatrizen waren gegeben durch \[ A = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v} & R \end{pmatrix} \] (wir verwenden hier den Buchstaben \(\boldsymbol{v}\) statt dem früher verwendeten \(\boldsymbol{u}\), um Verwechselungen mit der relativistischen Boostgeschwindigkeit zu vermeiden) wobei für einen ein Boost \(R = \mathbb{1}\) ist. Wie wir sehen, führt unser naiver Ansatz nicht zu einer Galilei-Boostmatrix!
Doch halt: wir haben einen Fehler gemacht! Die Lorentz-Matrix der Boosts wirkt im Raum der Vierervektoren \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} während die Galileimatrix im Raum der Vektoren \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} wirkt, also ohne die Lichtgeschwindigkeit \(c\) in der Zeitkomponente. Für die Betrachtung der Poincarégruppe hatten wir ja die Zeit mit der Lichtgeschwindigkeit multipliziert, so dass Raum- und Zeitkomponenten des Vierervektors \(x\) die gleiche physikalische Dimension einer Länge erhalten. Bei der Betrachtung der Galileigruppe hatten wir das nicht gemacht, da die Lichtgeschwindigkeit dort keine besondere Rolle spielt. Natürlich könnten wir die Galileimatrix auch so umschreiben, dass sie ebenfalls im Raum der Vektoren \(x = (ct,\boldsymbol{x})\) wirkt. Sie hätte dann die Form \[ A = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v}/c & R \end{pmatrix} \] was uns immer noch nicht weiterhilft.
Machen wir es umgekehrt und schreiben die Lorentz-Boostmatrix so um, dass sie im Raum der Vektoren \(x = (t,\boldsymbol{x})\) wirkt. Dann ist \[ \Lambda_b = \begin{pmatrix} \gamma & \gamma \boldsymbol{u}/c \\ \gamma \boldsymbol{u} c & \mathbb{1} + (\gamma - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} \] Es wird also rechts oben durch die Lichtgeschwindigkeit geteilt, um Längen in Zeiten umzurechnen, links unten wird dagegen mit der Lichtgeschwindigkeit multipliziert, um Zeiten in Längen umzurechnen.
Wie schaffen wir nun den Übergang zur Galileigruppe? Die folgende Idee hilft weiter:
Im Rahmen der Relativitätstheorie spielt die Lichtgeschwindigkeit \(c\) eine zentrale Rolle. Sie ist der zentrale Parameter der Theorie! Sie ist eine neue Naturkonstante, die es in der klassischen Mechanik so nicht gibt. In der klassischen Mechanik ist die Lichtgeschwindigkeit dagegen nichts besonderes. Sie kommt als universelle Naturkonstante dort nicht vor.
Beim Übergang von der Poincarégruppe zur Galileigruppe sollten wir daher versuchen, die Lichtgeschwindigkeit loszuwerden. Das können wir dadurch erreichen, dass wir alle mathematischen Ausdrücke so umschreiben, dass die Lichtgeschwindigkeit nur im Nenner der Ausdrücke vorkommt. Wenn wir nun die Lichtgeschwindigkeit unendlich groß werden lassen, so verschwinden diese Ausdrücke und mit ihnen die Lichtgeschwindigkeit.
Der Grenzübergang Lichtgeschwindigkeit gegen Unendlich (\(c \rightarrow \infty\)) ist nur dann möglich, wenn wir die Zeit-Komponente nicht mehr mit der Lichtgeschwindigkeit multipliziert haben. Ansonsten würden wir ja die Zeitdimension \(x^0 = ct\) unendlich dehnen. Die entsprechende Vorarbeit haben wir oben bereits gemacht. Wir haben die Lorentz-Boostmatrix so umgeschrieben, dass sie im Raum der Vektoren \(x = (t,\boldsymbol{x})\) wirkt. Wie wir sehen, taucht die Lichtgeschwindigkeit in der Lorentz-Boostmatrix allerdings im Term \( \gamma \boldsymbol{u} c\) links unten noch multiplikativ auf.
Das Problem können wir lösen, wenn wir uns daran erinnern, welche Bedeutung die Boostgeschwindigkeit \(\boldsymbol{u}\) hat. Sie ist die Geschwindigkeit, die ein ruhendes Objekt nach dem Boost aufweist, gemessen in Anteilen der Lichtgeschwindigkeit. Die Lichtgeschwindigkeit wird also als Maßeinheit verwendet. Wenn wir die Lichtgeschwindigkeit jedoch unendlich groß machen wollen, so können wir sie nicht mehr als Maßeinheit verwenden. Der Parameter \(\boldsymbol{u}\) muss also durch einen anderen Parameter ersetzt werden. Es bietet sich an, als neuen Parameter die Geschwindigkeit \(\boldsymbol{v}\), gemessen z.B. in Metern pro Sekunde, zu verwenden: \[ \boldsymbol{v} = \boldsymbol{u}c \] Diese Geschwindigkeit werden wir dann beim Grenzübergang als Konstante behandeln.
Nun können wir den Grenzübergang (\(c \rightarrow \infty\)) mit konstantem \(\boldsymbol{v} = \boldsymbol{u}c\) durchführen. Dazu verwenden wir, dass bei diesem Grenzübergang \(\gamma\) gegen 1 geht, denn es war \[ \gamma = \sqrt{ \frac{1}{1 - \boldsymbol{u}^2} } = \] \[ = \sqrt{ \frac{1}{1 - (\boldsymbol{u}/c)^2} } \; \rightarrow \; 1 \] Für die Boostmatrix gilt beim Grenzübergang (\(c \rightarrow \infty\)) also: \[ \Lambda_b = \begin{pmatrix} \gamma & \gamma \boldsymbol{v}/c^2 \\ \gamma \boldsymbol{v} & \mathbb{1} + (\gamma - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} \; \rightarrow \; \] \[ \rightarrow \; \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{1} \end{pmatrix} \] Das ist genau die Boostmatrix \(A_b\) einer Galilei-Transformation (also \(R = \mathbb{1}\)).
Wir haben also gezeigt: Beim Grenzübergang (\(c \rightarrow \infty\)) mit konstantem \(\boldsymbol{v} = \boldsymbol{u}c\) gehen die Lorentz-Boostmatrizen in die Galilei-Boostmatrizen über, wobei wir die Matrizen im Raum der Vektoren \(x = (t,\boldsymbol{x})\) wirken lassen (d.h. die Zeitkomponente enthält nicht die Lichtgeschwindigkeit).
Die Drehungen haben wir dabei bisher nicht betrachtet. Das ist auch nicht nötig, da hier keine Unterschiede zwischen Galileigruppe und Lorentzgruppe bestehen – Drehungen verändern ja keine Geschwindigkeiten und mischen Raum und Zeit nicht.
Es ist ganz interessant, den Grenzübergang auch in der Exponentialdarstellung zu betrachten, da wir dadurch die Exponentialdarstellung für die Galileigruppe herleiten können.
Die allgemeine Darstellung einer Lorentzmatrix (aus der Zusammenhangskomponente der Einheitsmatrix) war im Raum der Vektoren \(x = (ct,\boldsymbol{x})\) gegeben durch \[ \Lambda = e^X = e^{ \begin{pmatrix} 0 & \alpha \boldsymbol{e} \\ \alpha \boldsymbol{e} & G \end{pmatrix} } \] mit \(G^T = -G\) und \(\alpha \boldsymbol{e} = \boldsymbol{a}\)
Zunächst müssen wir die Lichtgeschwindigkeit aus der Zeitkomponente herausnehmen, so dass \(\Lambda\) im Raum der Vektoren \(x = (t,\boldsymbol{x})\) wirkt. Dann hat \(\Lambda\) die Form \[ \Lambda = e^X = e^{ \begin{pmatrix} 0 & (\alpha/c) \, \boldsymbol{e} \\ (\alpha c) \, \boldsymbol{e} & G \end{pmatrix} } \] Begründung: Setze \(x =: Cx'\) mit \(x = (ct,\boldsymbol{x})\) und \(x' = (t,\boldsymbol{x})\), d.h. \[ C = \begin{pmatrix} c & \boldsymbol{0} \\ \boldsymbol{0} & \mathbb{1} \end{pmatrix} \] Es gilt \(e^X x = e^X C x'= C \, e^{C^{-1} X C} x'\), wie man mit der Reihenentwicklung leicht sieht. Die Matrix \(C^{-1} X C\) braucht man nun nur noch auszurechnen.
Um den Grenzübergang korrekt auszuführen, müssen wir noch den Zusammenhang zwischen \(\alpha \boldsymbol{e} = \boldsymbol{a}\) und \(\boldsymbol{v} = \boldsymbol{u}c\) betrachten.
Es war \[ \boldsymbol{u} = \boldsymbol{v}/c = \frac{\sinh{\alpha}}{\cosh{\alpha}} \, \boldsymbol{e} \] Wenn wir \(\boldsymbol{v}\) konstant halten und \(c\) gegen Unendlich gehen lassen, so strebt \(\boldsymbol{u}\) gegen Null. Die einzige Nullstelle der Funktion \(\frac{\sinh{\alpha}}{\cosh{\alpha}}\) liegt bei \(\alpha = 0\), d.h. wir müssen den Grenzübergang \(\alpha \rightarrow 0\) betrachten.
Für die Matrixkomponente mit \(\alpha/c\) rechts oben ist der Fall klar: sie geht gegen Null. Wie aber steht es mit der Matrixkomponente mit \(\alpha c\) linke unten, bei der \(\alpha\) gegen Null und \(c\) gegen Unendlich geht?
Hier brauchen wir wieder unsere Nebenbedingung, dass \[ \boldsymbol{v} = \boldsymbol{u}c = \frac{\sinh{\alpha}}{\cosh{\alpha}} c \, \boldsymbol{e} \] bei \(\alpha\) gegen Null konstant bleiben soll.
Für kleine Werte von \(\alpha\) können wir \(\frac{\sinh{\alpha}}{\cosh{\alpha}} = \alpha + \) Terme mit \(\alpha^2\), \(\alpha^3\) etc. schreiben. Geht \(\alpha\) gegen Null, so brauchen wir nur noch den ersten Term zu berücksichtigen, da die Terme mit höheren Potenzen in \(\alpha\) viel schneller verschwinden. Für den Grenzübergang gilt also die Forderung, dass \[ \boldsymbol{v} \approx \alpha c \, \boldsymbol{e} \] konstant ist.
Aus der Matrix \(\Lambda\) wird in Exponentialdarstellung durch den Grenzübergang also die Matrix \[ \Lambda = e^X = e^{ \begin{pmatrix} 0 & (\alpha/c) \, \boldsymbol{e} \\ (\alpha c) \, \boldsymbol{e} & G \end{pmatrix} } \;\rightarrow \] \[ \rightarrow \; e^{ \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{v} & G \end{pmatrix} } \] mit \(G^T = -G\).
Das ist die Exponentialdarstellung der Galilei-Matrizen!
Als Probe wollen wir die Galilei-Boosts \(A_b\) betrachten, d.h. \(G = \mathbb{0}\) setzen, und die Reihe ausrechnen. Das ist einfach, denn es ist \[ \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{0} \end{pmatrix} \, \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{0} \end{pmatrix} = 0 \] Für Boosts bricht die Reihe also bereits nach den ersten beiden Termen ab. Also ist \[ A_b = e^{ \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{0} \end{pmatrix} } = \] \[ = 1 + \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{0} \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v} & \mathbb{1} \end{pmatrix} \] Die Exponentialdarstellung für Galileimatrizen ist also (zumindest für Boosts) korrekt. Für Drehungen ist das sowieso bereits klar, da wir die Exponentialdarstellung der Drehungen als Untergruppe der Lorentzmatrizen bereits in einem früheren Abschnitt untersucht hatten.
Lorentzmatrizen waren über die Bedingung \(g(\Lambda x, \Lambda y) = g(x,y)\) definiert worden. Mit anderen Worten: Lorentzmatrizen verändern den Ausdruck \[ g(x,y) = x^0 y^0 - \boldsymbol{x y} \] nicht, wenn sie auf die Vektoren \(x = (x^0,\boldsymbol{x}) = (ct_x,\boldsymbol{x})\) und \(y = (y^0,\boldsymbol{y}) = (ct_y,\boldsymbol{y})\) wirken. Was wird aus diesem Raumzeit-Metrik-Ausdruck, wenn wir den Grenzübergang zur Galileigruppe durchführen?
Betrachten wir die Differenz zweier Vierervektoren \(x_2 - x_1\). Falls die Zeitkomponente beider Vierervektoren gleich ist (also \(t_2 - t_1 = 0\)), so ist \[ g(x_2 - x_1,x_2 - x_1) = - (\boldsymbol{x}_2 - \boldsymbol{x}_1)^2 \] Dieser Ausdruck wird durch eine Lorentztransformation nicht verändert, d.h. räumliche Abstände bleiben bei einer Lorentztransformation erhalten, wenn die beiden Vierervektoren, zwischen denen der räumliche Abstand ermittelt wird, zur gleichen Zeit betrachtet werden, also in der gleichen Zeitscheibe der vierdimensionalen Raumzeit liegen. Da in diesem Ausdruck die Lichtgeschwindigkeit nicht vorkommt, ändert sich daran auch im Grenzübergang \(c \rightarrow \infty\) nichts, d.h. auch Galileitransformationen müssen diese Bedingung erfüllen. Damit haben wir eine der beiden Bedingungen für die Galileigruppe hergeleitet: sie ändert räumliche Abstände innerhalb einer Zeitscheibe nicht.
Kommen wir zur Bedingung für die Zeitkomponente. Dazu schreiben wir den Ausdruck zunächst so um, dass die Zeit-Komponente nicht mehr mit der Lichtgeschwindigkeit \(c\) multipliziert sind: \[ g(x,y) = x^0 y^0 - \boldsymbol{x y} = \] \[ = c^2 t_x t_y - \boldsymbol{x y} = \] \[ = c^2 \, \left( t_x t_y - \frac{1}{c^2}\boldsymbol{x y} \right) = \] \[ =: c^2 h(x,y) \]
Wenn \(g(x,y)\) durch eine Lorentztransformation nicht geändert wird, so wird auch \[ h(x,y) = t_x t_y - \frac{1}{c^2}\boldsymbol{x y} \] nicht geändert. Lässt man die Lichtgeschwindigkeit nun gegen Unendlich gehen, so geht \(h(x,y)\) gegen \(t_x t_y\): \[ h(x,y) \rightarrow t_x t_y \] Setzen wir wieder für \(x\) und \(y\) den Abstand zweier Vierervektoren \(x = y = x_2 - x_1\) ein, so folgt im Grenzübergang \(c \rightarrow \infty\) für Galileitransformationen, dass sie den Ausdruck \( (t_2 - t_1) ^2 \) nicht ändern. Galileitransformationen dürfen also Zeitabstände nicht ändern! Damit haben wir die zweite Bedingung für die Galileigruppe hergeleitet.
Zum Schluss dieses Abschnitts wollen wir noch einmal detaillierter auf die Geometrie der relativistischen und der nichtrelativistischen Raumzeit eingehen. Dabei werden wir auch vor vielleicht etwas ungewohnten (abstrakten) Begriffen nicht zurückschrecken, da man so besser erkennt, was man aus mathematischer Sicht eigentlich tut.
Die relativistische Raumzeit ist relativ einfach. Wir können sie als vierdimensionalen reellen Vektorraum mit Metrik auffassen. Die Vektoren in diesem Raum haben eine Zeit- und drei Raumkomponenten: \[ x = \begin{pmatrix} x^0 \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} \] Die Metrik ist durch \[ g(x,y) = x^0 y^0 - \boldsymbol{x y} \] gegeben. Man kann also zwei beliebigen Vektoren aus diesem Raum über diese Metrik eine reelle Zahl zuordnen. Poincaré- und damit auch Lorentz-Transformationen verändern diese Metrik nicht.
Wie sieht die Sache nun für die nichtrelativistische Raumzeit aus? Zunächst scheint alles analog zu sein: Wir können die nichtrelativistische Raumzeit wieder als vierdimensionalen reellen Vektorraum auffassen. Die Vektoren in diesem Raum haben ebenfalls eine Zeit- und drei Raumkomponenten: \[ x = \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} \] Bei der Metrik fängt die Sache allerdings an, komplizierter zu werden. Es macht für die Definition von Galileitransformationen keinen Sinn, zwei beliebigen Vektoren \(x = (t_x,\boldsymbol{x})\) und \(y = (t_y,\boldsymbol{y})\) irgendeinen Abstand oder eine Metrik zuzuordnen.
Die Forderungen für die Galileitransformation unterscheiden nämlich zwischen Zeit und Raum. Sie machen eine Aussage über zeitliche Abstände und – wenn die zeitliche Abstände Null sind – über räumliche Abstände bei gleicher Zeitkoordinate. Die vierdimensionale Raumzeit wird gleichsam in einzelne dreidimensionale Scheiben oder Schichten zerlegt, die sich entlang eines Zeitstrahls zur vierdimensionalen Raumzeit aufstapeln. Auf diesem Zeitstrahl kann man von Abständen reden (nämlich von Zeitabständen), und in jeder dreidimensionale Scheibe, die ja Vektoren mit gleicher Zeitkomponente umfasst, kann man von räumlichen Abständen reden, die durch Galileitransformationen nicht geändert werden. Diese Vorstellung verbirgt sich dahinter, wenn man von einer universellen Zeit spricht.
Man kann versuchen, eine mathematische Struktur aufzubauen, die diese Vorstellung berücksichtigt und präzisiert. Dabei wollen wir zunächst absichtlich keinen Gebrauch von der Komponentendarstellung von Vektoren machen, sondern die mathematische Struktur komponentenfrei definieren.
Bezeichnen wir dazu die nichtrelativistische Raumzeit mit \(V\). Diese Raumzeit \(V\) ist zunächst einmal ein vierdimensionaler reller Vektorraum genauso wie die relativistische Raumzeit. Allerdings macht es hier keinen Sinn, auf dem gesamten Raum eine Metrik zu definieren. Wir müssen diesem Raum eine andere zusätzliche Struktur geben, die die Sonderrolle der Zeit heraushebt. Dazu definieren wir eine Zeitabbildung \(T\), die zu jedem Vektor \(x \in V\) eine zugehörige Zeit ermittelt: \[ T(x) = t \] Diese Abbildung soll linear sein, d.h. \[ T(x - y) = T(x) -T(y) \] \[ T(\lambda x) = \lambda T(x) \] wobei \(\lambda\) eine relle Zahl ist. Man bezeichnet eine solche Abbildung als Linearform.
Diese Abbildung ermöglicht es uns, den Begriff der Zeit und des Zeitabstandes überhaupt erst mathematisch sauber zu fassen. Dazu interpretiert man zunächst Vektoren \(x \in V\) als physikalische Ereignisse, was nichts anderes bedeutet, als dass man Zeit und Ort für irgendein physikalisches Phänomen (z.B. den Zerfall eines Teilchens) angibt. Man interpretiert nun \(T(x) = :t\) als Zeit des Ereignisses \(x\). Bei zwei Ereignissen \(x\) und \(y\) interpretiert man \(T(x - y) = T(x) -T(y) = t_x - t_y\) als Zeitabstand zwischen den Ereignissen.
Wie sieht es nun mit dem räumlichen Abstand zwischen den Ereignissen aus?
Wir hatten es bereits gesagt: Es macht für Galileitransformationen keinen Sinn, den räumlichen Abstand zwischen zwei beliebigen Ereignissen zu definieren, da ein Boost den räumlichen Abstand zwischen zwei Ereignissen, die zu verschiedenen Zeiten stattfinden, ändern würde. Wir suchen aber mathematischen Größen, die durch Galileitransformationen nicht geändert werden!
Die Abbildung \(T\) ermöglicht es uns nun, den räumlichen Abstand für Ereignisse zu gleicher Zeit sauber zu definieren. Man definiert dazu einen neuen Vektorraum \(V_0\) als den sogenannten Kern der Abbildung \(T\). Mit anderen Worten: \(V_0\) besteht aus allen Vektoren \(x \in V\), deren Zeitkomponente gleich Null ist: \[ V_0 := \{ x \in V ; \; T(x) = 0 \} \] \(V_0\) ist ein dreidimensionaler reeller Vektorraum, d.h. man kann drei Basisvektoren \(\boldsymbol{e}_1\), \(\boldsymbol{e}_2\) und \(\boldsymbol{e}_3\) angeben. Auf diesem Raum kann man nun ein euklidisches Skalarprodukt \[ \eta_0(x,y) \] mit \(T(x) = T(y) = 0\) definieren.
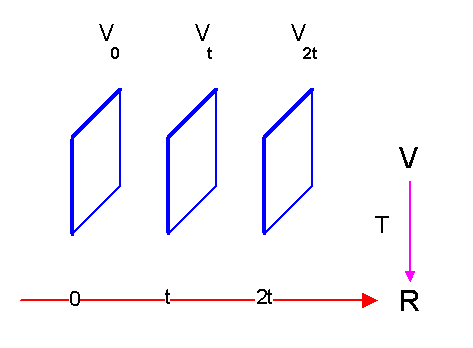
Der Raum \(V_0\) ist eine sogenannte spezielle Faser von \(V\) (also eine spezielle Scheibe oder Schicht des Raumstapels, und zwar die zur Zeit Null). Man kann auch schreiben: \[ V_0 = T^{-1}(0) \] was nichts anderes bedeutet, als dass alle Vektoren aus \(V_0\) durch \(T\) auf Null abgebildet werden.
Analog kann man die Fasern \(V_t\) zur Zeit \(t\) definieren als \[ V_t := \{ x \in V ; \; T(x) = t \} = \] \[ = T^{-1}(t)\] d.h. dieser Raum enthält alle Vektoren oder Ereignisse der Raumzeit, die zur selben Zeit \(t\) gehören.
Wir können nun das euklidisches Skalarprodukt \(\eta_0\) von \(V_0\) nach \(V_t\) übertragen, indem wir das Skalarprodukt \(\eta_t\) in \(V_t\) über die folgende Gleichung definieren: \[ \eta_0(x-y, x-y) =: \eta_t(x,x) - 2 \eta_t(x,y) + \eta_t(y,y) \] mit \(x, y \in V_t\). Das geht, denn \(x-y\) ist wegen \(T(x-y) = T(x) - T(y) = t - t = 0\) aus \(V_0\).
Man kann nun beispielsweise \(y \in V_t\) so wählen, dass
\(\eta_t(x,y) = 0\)
für alle \(x \in V_t\) ist
(das muss gehen, weil \(V_t\) ein Vektorraum und \(\eta_t\) ein Skalarprodukt ist).
Dann ist
\[
\eta_t(x,x) = \eta_0(x-y,x-y)
\]
Das folgende Bild stellt diese Zusammenhänge noch einmal grafisch dar:

Die Galileigruppe könnte man nun abstrakt als affine Abbildung von \(V\) nach \(V\) definieren, so dass \(T(x-y)\) (also Zeitabstände) und \(\eta_0(x-y,x-y)\) (also Raumabstände in derselben Zeitscheibe) sich nicht ändern.
Zugegeben: das ist ziemlich abstrakt. Man kann sich die Zusammenhänge in der Koordinatendarstellung noch einmal klar machen: Mit \(x = (t,\boldsymbol{x})\) ist \(T(x) = t\) und \(\eta_0(x-y,x-y) = (\boldsymbol{x} - \boldsymbol{y})^2\). Man nennt diese Koordinatendarstellung ein sogenanntes Modell der obigen mathematischen Struktur.
Die abstrakte Struktur hilft, zu verstehen, was man begrifflich genau tut. Ähnliche Vorgehensweisen haben sich in der Mathematik sehr oft bewährt, beispielsweise bei der Definition des Begriffs Vektorraum oder des Begriffs Gruppe. Durch die abstrakte Formulierung treten oft Ähnlichkeiten zwischen bereits bekannten mathematischen Strukturen zutage. So bilden auch Polynome einen Vektorraum. Und wer schon einmal eine Vorlesung über Quantenmechanik gehört hat, wird sich daran erinnern, wie die Wellenformulierung von Schrödinger und die Matrizenformulierung von Heisenberg sich als Modelle derselben mathematischen Struktur herausstellten (es handelt sich im Wesentlichen um einen Hilbertraum mit gewissen linearen Operatoren, die darauf wirken – wir kommen darauf noch zurück).
Die Präzision der Begrifflichkeit kann bei Verwendung von Koordinatendarstellungen mitunter verlorengehen, so dass man gelegentlich gezwungen ist, zu der abstrakten Darstellungsweise zurückzukehren, um keinen Irrtümern zu unterliegen und Zusammenhänge besser zu erkennen. Wie schnell man Ungenauigkeiten begeht, sieht man beispielsweise, wenn man die Zeit vergisst und nur nach Transformationen des dreidimensionalen Raums sucht, die räumliche Abstände unverändert lassen: man erhält lediglich die Drehungen und übersieht die Möglichkeit von Boosts!
Die abstrakte Darstellung macht etwas deutlich: Obwohl die physikalische Interpretation der mathematischen Objekte in der relativistischen Theorie schwieriger ist als in der nichtrelativistischen Theorie, ist dennoch die mathematische Struktur der nichtrelativistischen Raumzeit und der zugehörigen Galileigruppe komplizierter als die Struktur der relativistischen Raumzeit und der zugehörigen Poincarégruppe. Im relativistischen Fall genügt eine einfache Metrik, um dem vierdimensionalen reellen Vektorraum die notwendige Struktur zu geben.
Im nichtrelativistischen Fall dagegen benötigt man eine Linearform \(T\), über die sich der vierdimensionale Raum in dreidimensionale Fasern aufteilen lässt, und man benötigt ein euklididsches Skalarprodukt in diesen Fasern. Diese höhere Komplexität wird in der Quantentheorie noch Folgen haben: Die Darstellungen der Galileigruppe erfordern dort weitergehende mathematische Werkzeuge als die Darstellungen der Poincarégruppe. Wir werden in späteren Kapiteln noch darauf zurückkommen.
© Jörg Resag, www.joerg-resag.de
last modified on 28 June 2023