Wie im letzten Teilkapitel bereits vorweggenommen, wollen wir die Quantentheorie auf dem Begriff der Wahrscheinlichkeitsamplitude aufbauen.
Warum reden wir überhaupt über Wahrscheinlichkeiten? Muss denn die Physik als Inbegriff einer exakten Naturwissenschaft nicht beschreiben, was wirklich geschieht, anstatt sich mit dem zu begnügen, was geschehen könnte?
Die Antwort, die man auf diese Frage nach heutigem Wissen geben muss, ist ernüchternd: Es gibt physikalische Phänomene, bei denen es nicht möglich ist, zu sagen, was wirklich geschieht. Es ist beispielsweise unmöglich, zu sagen, wo sich die einzelnen Photonen (also die Teilchen des Lichts) in einem Lichtstrahl befinden, denn diese Information existiert in der Natur überhaupt nicht. Das Photon weiß gewissermaßen selbst nicht, wo es sich aufhält. Ein Photon in einem Lichtstrahl hat keinen Ort! Dasselbe gilt auch für Elektronen in einem Teilchenstrahl, wenn sie sich mit einer bestimmten Geschwindigkeit gleichförmig bewegen.
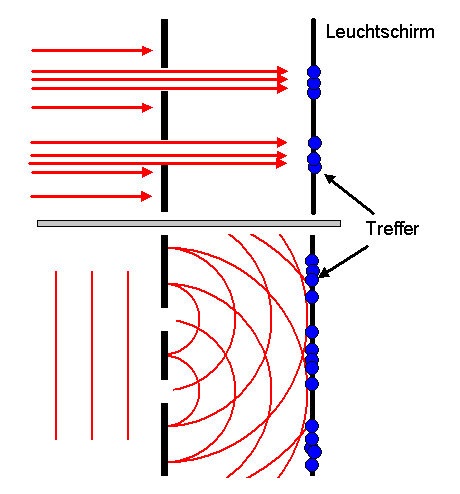
Andererseits kann man im Experiment nachsehen, wo sich das Elektron befindet. Es kann z.B. auf einem Leuchtschirm auftreffen und einen Lichtblitz auslösen. Die einzige Möglichkeit, hier eine physikalische Beschreibung zu gewinnen, besteht in der Angabe der Wahrscheinlichkeit, mit der das Elektron an diesem Ort eintrifft. Den Ort selber vorauszuberechnen geht nicht, und es scheint in der Natur selbst keine Information vorhanden zu sein, die das möglich machen könnte.
Um es noch einmal klar zu sagen: nicht unser Unwissen macht gewisse Vorhersagen unmöglich, sondern das Fehlen einer entsprechenden Information in der Natur selbst (so zumindest die heute vorherrschende Sichtweise). Das ist wirklich sehr merkwürdig und widerspricht dem, was wir uns unter einer quantitativen Beschreibung der Wirklichkeit vorstellen. Aber dennoch ist es so, nach allem was wir heute wissen. Jeder Versuch, verborgene lokale Informationen in der Natur anzunehmen, ist bisher gescheitert und führt zu Widersprüchen mit den experimentellen Ergebnissen (Beispiel: die Bellschen Ungleichungen; auf spezielle Konstrukte wie die De-Broglie-Bohm-Theorie gehen wir hier nicht weiter ein).
Die Hauptschwierigkeit mit der Quantentheorie liegt darin, zu akzeptieren, dass man nicht über das reden kann, was wirklich geschieht, sondern nur sagen kann, welche Ergebnisse ein Experiment mit welchen Wahrscheinlichkeiten haben kann. Hat man das erst einmal akzeptiert, so ist der grundlegende begriffliche Rahmen relativ einfach. Probleme bekommt man immer dann, wenn man daraus eine Vorstellung darüber ableiten will, was in der Natur wirklich passiert, denn offenbar gibt es eine absolute, grundlegende, objektiv existierende Wirklichkeit mit lokal in Raum und Zeit existierenden Objekten, wie wir sie uns normalerweise vorstellen, in der Natur gar nicht (eine gewisse Quantenwirklichkeit kann es allerdings dennoch geben).
Wie sieht der begriffliche Rahmen der Quantentheorie nun im Detail aus?
Zunächst einmal beobachtet man Interferenzeffekte, beispielsweise beim
Durchgang von Elektronen durch einen feinen Doppelspalt.

Man beobachtet auf dem Leuchtschirm hinter dem Doppelspalt ein Streifenmuster. Streifen mit vielen Elektronentreffern wechseln mit Streifen mit wenigen Treffern ab. Es gibt sogar Orte auf dem Leuchtschirm hinter dem Doppelspalt, an denen überhaupt keine Elektronen auftreffen, obwohl sie zwei verschiedene Möglichkeiten haben, dahin zu gelangen: durch den ersten oder durch den zweiten Spalt. Nimmt man ihnen eine dieser Möglichkeiten weg (verschließt also einen Spalt), so kommen auf einmal Elektronen an diesem Ort an (das Streifenmuster verschwindet)! Weniger kann hier also mehr sein.
Das gleiche Phänomen kennt man von der Interferenz von Wellen: zwei Wellenzüge können sich gegenseitig auslöschen, wenn die Amplituden der beiden Wellen einander entgegengesetzt sind.
Die Idee ist also die folgende:
Man ordnet jeder Möglichkeit, mit der ein physikalisches Ereignis eintreten kann, eine bestimmte Amplitude zu, ähnlich einer Amplitude bei einer Welle. Beim Doppelspalt gibt es also zwei Amplituden, mit denen ein Elektron an einem bestimmten Ort eintreffen kann: durch den ersten oder den zweiten Spalt. Die Wahrscheinlichkeit, mit der das Ereignis eintritt, wird durch die Überlagerung der verschiedenen Amplituden bestimmt. Dabei können sich die Amplituden auch gegenseitig auslöschen.
Nun müssen wir diese Idee weiter präzisieren:
Zur ersten Frage:
Es gibt hier im Prinzip viele mathematische Objekte, die sich zu Null überlagern (also addieren) und somit gegenseitig auslöschen können. Beispiele dafür sind reelle Zahlen, dreidimensionale Vektoren und vieles mehr. Man muss also weitere Informationen haben, um das geeignete Objekt zu finden. Das soll an dieser Stelle nicht weiter vertieft werden, und wir wollen gleich das Ergebnis angeben:
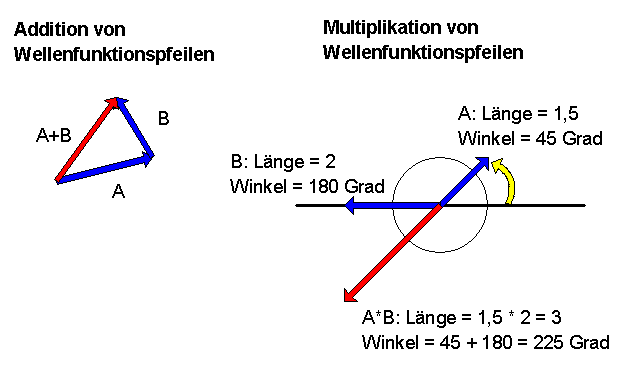
Reelle Zahlen reichen nicht. Quantenmechanische Amplituden müssen durch komplexe Zahlen beschrieben werden. Eine komplexe Zahl ist dabei nichts anderes als ein zweidimensionaler Vektor mit einer bestimmten Zusatzregel für die Multiplikation dieser Vektoren. Diese Multiplikation eines solchen Vektors mit einem zweiten Vektor entspricht einer Drehstreckung, wobei der zweite Vektor angibt, wie stark gedreht und gestreckt wird. Wozu diese Multiplikation gebraucht wird, werden wir erst etwas später betrachten.
Die Überlagerung von Amplituden entspricht nun der Addition der komplexen Zahlen,
also dem Hintereinanderhängen der zweidimensionalen Vektoren.
Zur zweiten Frage (Wie hängt eine Amplitude mit der Wahrscheinlichkeit für ein Ereignis zusammen?):
Eine Wahrscheinlichkeit wird immer durch eine reelle Zahl zwischen Null und Eins angegeben. Eine komplexe Zahl ist dagegen ein zweidimensionaler Vektor. Man könnte nun vermuten, dass die Länge dieses Vektors etwas mit der Wahrscheinlichkeit zu zun hat. Eine genauere Betrachtung zeigt, dass man das Quadrat dieser Länge nehmen muss, also das Quadrat des Betrages der komplexen Zahl. Wegen dieses Zusammenhangs zwischen Amplitude und Wahrscheinlichkeit nennt man quantenmechanische Amplituden auch Wahrscheinlichkeitsamplituden.
Wie müssen wir nun das Doppelspaltexperiment in der Quantentheorie beschreiben?
Zunächst einmal können wir nicht sagen, was alles genau passiert ist, wenn das Elektron an einem Ort (nennen wir ihn \(\boldsymbol{x}\)) auf dem Leuchtschirm auftrifft. Wir können lediglich fragen, mit welcher Wahrscheinlichkeit das Elektron dort ankommt. Dabei können wir verschiedene Fälle untersuchen: beide Spalte (nennen wir sie \(a\) und b) sind offen, nur Spalt \(a\) ist offen oder nur Spalt \(b\) ist offen.
Betrachten wir den Fall, dass nur Spalt \(a\) offen ist. Dann gibt es für das Elektron nur eine Möglichkeit, dorthin zu gelangen, nämlich durch diesen Spalt. Dieser Möglichkeit müssen wir eine komplexe Zahl \(A\) zuordnen, deren Betragsquadrat die Wahrscheinlichkeit für das Elektron angibt, am Ort \(\boldsymbol{x}\) anzukommen, wenn nur Spalt a offen ist. Was für eine komplexe Zahl \(A\) ist, braucht uns zunächst noch nicht zu interessieren: wir wollen erst mal den begrifflichen Rahmen klären.
Für den Fall, dass nur Spalt \(b\) offen ist, gibt es analog eine Amplitude \(B\) und eine entsprechende Wahrscheinlichkeit.
Nun zum eigentlich interessanten Fall: beide Spalte \(a\) und \(b\) sind offen. Wieder muss es eine Amplitude (wir nennen sie \(C\)) geben, deren Betragsquadrat die Wahrscheinlichkeit dafür angibt, am Ort \(\boldsymbol{x}\) anzukommen, wenn beide Spalte offen sind.
Diese Amplitude \(C\) hängt mit den Amplituden \(A\) und \(B\) zusammen, denn das
Elektron hat nun zwei Möglichkeiten, am Ort \(\boldsymbol{x}\) anzukommen:
es kann Spalt \(a\) oder \(b\) benutzen. Diesen beiden Möglichkeiten hatten wir die
Amplituden \(A\) und \(B\) zugeordnet. Nach der obigen Regel müssen wir diese beiden
Amplituden addieren, um die Gesamtamplitude \(C\) für das Ereignis zu konstruieren.
Es gilt also:
\[
C = A + B
\]
Die Wahrscheinlichkeit dafür, dass das Elektron am Ort \(\boldsymbol{x}\) ankommt, ist also
gleich
\[
|C|^2 = |A + B|^2
\]
Wir sehen nun, wie die Interferenz zustandekommt:
Es gibt offenbar Orte, an denen beide Amplituden entgegengesetzt gleich sind,
also \(A = -B\). Dann ist die Wahrscheinlichkeit
\( |A + B|^2 = |A - A|^2 = 0\), d.h. das
Elektron kommt an diesem Ort überhaupt nicht an. Verschließt man jedoch beispielsweise
Spalt \(b\), so kommen auf einmal Elektronen bei \(\boldsymbol{x}\) an, denn nun ist die Wahrscheinlichkeit
dafür gleich \(|A|^2\), und \(A\) ist an diesem Ort offenbar nicht Null.
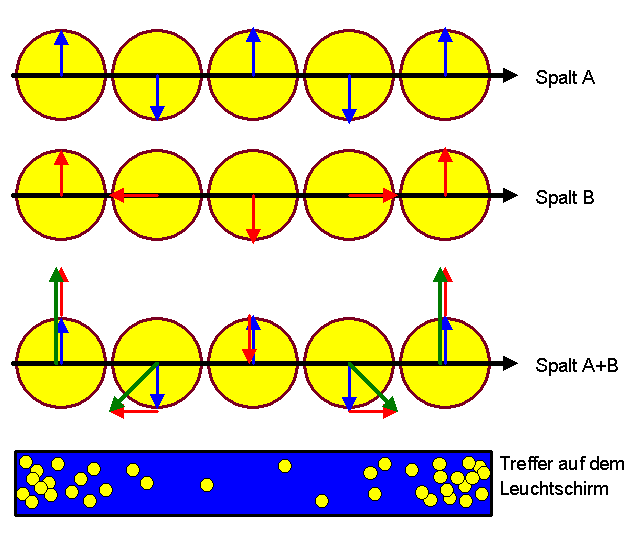
Welchen Weg hat das Elektron denn genommen, wenn beide Spalte offen sind? Setzen wir voraus, dass das Elektron beim Durchgang durch die Spalte keine irgendwie gearteten Spuren hinterlassen hat, so kann diese Frage prinzipiell nicht beantwortet werden, ohne das Experiment zu verändern. Man kann in dem vorliegenden Experiment nur sagen, dass das Elektron zwei Möglichkeiten hat (Spalt \(a\) und b), und dass beide Amplituden addiert werden müssen. Die beiden Möglichkeiten sind in diesem Experiment ununterscheidbar, und genau deshalb darf man auch die entsprechenden Wahrscheinlichkeitsamplituden addieren, so dass Interferenz entstehen kann.
Versucht man, die Frage experimentell zu klären, welcher Spalt genommen wurde, so muss das Experiment entsprechend verändert werden. Man könnte beispielsweise an jedem der Spalte einen Ladungsdetektor anbringen, der so empfindlich ist, dass er den Durchgang des Elektrons registriert. Nun muss man aber sehr aufpassen, was man als Ereignis in diesem Experiment betrachtet, denn ein Ereignis muss alles beinhalten, was in dem Experiment prinzipiell beobachtbar ist.
Als Ereignis kann nun nicht mehr gelten, dass das Elektron am Ort \(\boldsymbol{x}\) ankommt. Stattdessen gibt es ein Ereignis "das Elektron hat den Detektor am Spalt \(a\) ausgelöst und ist am Ort \(\boldsymbol{x}\) angekommen" und ein Ereignis "das Elektron hat den Detektor am Spalt \(b\) ausgelöst und ist am Ort \(\boldsymbol{x}\) angekommen". Für jedes dieser Ereignisse kann man eine Wahrscheinlichkeitsamplitude angeben. Man darf diese Amplituden aber nicht addieren, wenn man nach der Wahrscheinlichkeit für das Auftreffen am Ort \(\boldsymbol{x}\) sucht, denn die Amplituden gehören zu zwei unterscheidbaren Ereignissen. Stattdessen gelten die Regeln der normalen Wahrscheinlichkeitsrechnung: Man muss die Wahrscheinlichkeiten (also nicht die Amplituden) für die beiden Ereignisse addieren! Als Folge davon verschwindet das Interferenzmuster.
Fassen wir die bisherigen Ergebnisse (nach dem Vorbild Feynmans) noch einmal zusammen:
Wir können noch eine weitere Eigenschaft der Quantentheorie am Doppelspaltexperiment lernen:
Stellen wir einen Ladungsdetektor an Spalt \(a\) auf und fragen wir uns: Wie groß ist die Wahrscheinlichkeit, dass das Elektron Spalt \(a\) durchquert und dabei den Ladungsdetektor auslöst? Nennen wir die entsprechende Amplitude \(A_1\), so ist diese Wahrscheinlichkeit gleich \( |A_1|^2 \).
Betrachten wir nun ausschließlich die Fälle, bei denen wir bereits wissen, dass das Elektron Spalt \(a\) genommen hat, weil der dortige Ladungsdetektor ausgelöst wurde. Wir können nun fragen: Wie groß ist die Wahrscheinlichkeit, dass anschließend das Elektron am Ort \(\boldsymbol{x}\) ankommt? Nennen wir diese Amplitude \(A_2\), so ist diese Wahrscheinlichkeit gleich \( |A_2|^2 \).
Nun können wir die beiden Betrachtungen kombinieren und fragen: Wie groß ist die Wahrscheinlichkeit, dass das Elektron Spalt \(a\) durchquert (und dabei den Ladungsdetektor auslöst) und dann am Ort \(\boldsymbol{x}\) auf den Schirm trifft? Die Antwort kennen wir bereits: die zugehörige Amplitude ist \(A\) (denn wir wissen, dass Spalt \(a\) genommen wurde) und die entsprechende Wahrscheinlichkeit ist \( |A|^2 \).
Aber wie hängt \(A\) mit den beiden Amplituden \(A_1\) und \(A_2\) zusammen? Die Antwort lautet: \(A\) ist das Produkt dieser Amplituden, also \[ A = A_2 \cdot A_1 \] (es wird sich später als günstig erweisen, die Amplituden in dieser Reihenfolge zu schreiben, also gleichsam umgekehrt zu der Reihenfolge der zugehörigen Teilschritte).
Halten wir diesen Punkt als weitere Regel der Quantentheorie fest:
Damit haben wir bereits den allgemeinen Rahmen der Quantentheorie kennengelernt. Man könnte die Regeln auch wie folgt zusammenfassen:
Konkret berechnen können wir damit noch nicht viel, denn dafür müssen wir mehr über die Amplituden wissen, die zu den verschiedenen physikalischen Phänomenen gehören. Das wird unser Thema in den nächsten Kapiteln sein.
Vielleicht werden Sie nun fragen: Warum ist das alles so? Was bringt die Natur dazu, sich ausgerechnet so zu verhalten? Die Antwort, die man heute geben muss, ist ernüchternd: Wir wissen es nicht! Niemand kann diese Regeln heute tiefer begründen. Und dennoch sieht es so aus, als sei ausgerechnet dies die grundlegende Methode, mit der die Natur beschrieben werden muss. Selbst die modernsten Theorien, die sich mit den tiefsten Strukturen von Materie und Wechselwirkungen befassen, basieren auf diesen Regeln!
Das schränkt unsere Möglichkeiten, die Natur wirklich zu verstehen, stark ein! Wir wissen nicht, wie man exakt vorhersagen kann, was unter vorgegebenen Umständen passieren würde, und man glaubt heute, dass dies prinzipiell unmöglich ist – so hat es Feynman sinngemäß ausgedrückt. Es ist nicht einfach, sich damit abzufinden, aber niemand hat einen Weg gefunden, diese Art der Naturbeschreibung zu vermeiden.
© Jörg Resag, www.joerg-resag.de
last modified on 06 July 2023