Bei unseren bisherigen Überlegungen haben wir uns auf Experimente beschränkt, in denen ein physikalisches Ereignis durch das Verhalten eines einzigen Teilchens bestimmt wurde. So hatten wir uns für die Wahrscheinlichkeit interessiert, dass ein Elektron nach dem Durchfliegen des Doppelspaltes an einem bestimmten Ort auf dem Leuchtschirm auftrifft.
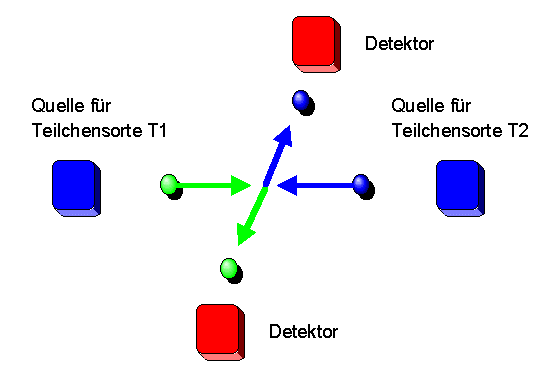
Ein physikalisches Ereignis kann aber auch durch das Verhalten mehrerer Teilchen festgelegt werden. Betrachten wir als Beispiel die Streuung zweier Teilchen, die wir als T1 und T2 bezeichnen wollen. Ein Strahl aus Teilchen der Sorte T1 soll mit einem Strahl aus Teilchen der Sorte T2 kollidieren. Zur Vereinfachung wollen wir annehmen, dass die Teilchen alle einen festen Impuls haben. Weiter wollen wir annehmen, dass nur elastische Stöße stattfinden, d.h. es geht keine Bewegungsenergie verloren.
Wir wollen uns dafür interessieren, wieviele Teilchen im Durchschnitt um welchen Winkel von ihrer ursprünglichen Flugrichtung abgelenkt werden. Dazu wollen wir die folgende Konvention treffen: Wir wollen die Flugrichtung der Teilchen durch einen Winkel \(\theta\) kennzeichnen, der relativ zur ursprünglichen Flugrichtung der Teilchensorte T1 angegeben wird, wobei \(0 \le \theta \le \pi\) sein soll (Winkel geben wir hier im Bogenmaß an). Zusätzlich wollen wir davon ausgehen, dass beide Teilchen entgegengesetzt zueinander abgelenkt werden (also oben versus unten oder links versuch rechts).
Da auch in der Quantenmechanik Energie und Impuls erhalten sind, sind die Impulse von zwei Teilchen T1 und T2 nach der Wechselwirkung abhängig voneinander. Ihre Summe muss gleich der Impulssumme vor der Wechselwirkung sein, und dasselbe gilt für die Energien. Betrachten wir beispielsweise Teilchen der Sorte T1, die um einen bestimmten Winkel \(\theta_1\) abgelenkt werden, so liegt der Winkel \(\theta_2\), der die Flugrichtung für die Teilchen T2 angibt, fest. Der Teilchendetektor für Teilchensorte T2 muss also an der richtigen Stelle aufgebaut werden, je nachdem, wo man den Detektor für Teilchensorte T1 hinstellt.
Ein Beispiel:
Angenommen, wir lassen die Teilchenstrahlen T1 und T2 mit entgegengesetzt gleichem Impuls
frontal aufeinanderprallen. Dann müssen die Teilchen
nach der Wechselwirkung genau entgegengesetzt zueinander wieder auseinanderfliegen.
Wenn also beispielsweise ein Teilchen T1 um den Winkel \(\theta_1\) nach oben abgelenkt wird
(d.h. seine neue Flugbahn wird durch diesen Winkel charakterisiert),
so muss Teilchen T2 nach unten in Richtung \(\theta_2 = \pi - \theta_1\) fliegen.

Wir könnten nun nach der Wahrscheinlichkeit fragen, mit der die Teilchen T1 um den Winkel \(\theta_1\) abgelenkt werden. Damit ist der Winkel \(\theta_2\) für die Teilchen T2 automatisch festgelegt. Das Ereignis, für das wir uns interessieren, lautet also:
Das ist ein Ereignis, dass das gemeinsame Verhalten zweier Teilchen umfasst. Dabei ist zu beachten: Wir dürfen dies nur dann als vollständiges physikalisches Ereignis betrachten, wenn die Teilchen keine weiteren Eigenschaften haben, die noch zusätzlich zumindest im Prinzip ermittelt werden könnten und die zu einer feineren Unterscheidung einzelner Fälle führen.
Betrachten wir einen Fall, bei dem es tatsächlich keine weiteren möglichen Messwerte gibt, die berücksichtigt werden müssten: die Streuung von Teilchen mit Spin Null, z.B. von Alphateilchen (also Heliumkerne) an Sauerstoffkernen bei nicht zu hohen Energien (so dass die innere Strukur der Teilchen keine Rolle spielt). Was der Spin eines Teilchens bedeutet, werden wir erst später genauer verstehen können. Teilchen mit Spin Null nennt man auch Bosonen.
Da wir hier also ein vollständiges Ereignis betrachten, können wir eine Wahrscheinlichkeitsamplitude dafür angeben, dass ein Alphateilchen (T1) in Richtung \(\theta_1\) abgelenkt wird und der zugehörige Sauerstoffkern (T2) in Richtung \(\theta_2\). Wir wollen diese Amplitude \[ A(\theta_1, \theta_2) \] nennen. Die Wahrscheinlichkeit für dieses Ereignis beträgt also \[ |A(\theta_1, \theta_2)|^2 \] Zur Schreibweise: Im Prinzip hätte es genügt, die Amplitude als \(A(\theta_1)\) zu bezeichnen, da der Winkel \(\theta_2\) für Teilchen T2 ja durch den von Teilchen T1 vollständig festgelegt wird. Die Amplitude hängt also nur von einer freien Variablen ab. Richard Feynman geht in seiner Vorlesung Feynmans Vorlesungen über Physik Band III: Quantenmechanik, Kapitel 3-4, an der ich mich hier lose orientiere, auch genauso vor.
Für die spätere Diskussion der Vertauschung von Teilchen ist es jedoch bequem, die Winkel beider Teilchen T1 und T2 in die Schreibweise für die Amplitude mit aufzunehmen. Ganz allgemein bedeutet also \(A(\theta_1, \theta_2)\) die Wahrscheinlichkeitsamplitude dafür, dass ein Teilchen T1 nach der Wechselwirkung in Richtung des Winkels \(\theta_1\) und ein Teilchen T2 in Richtung des Winkels \(\theta_2\) fliegt, wobei beide Winkel relativ zur ursprünglichen Flugrichtung von Teilchen T1 angegeben werden. Dabei treffen wir die Konvention, dass der Winkel für Teilchen T1 an erster Stelle, der für Teilchen T2 an zweiter Stelle in den Argumenten der Amplituden-Funktion \(A()\) steht.
Betrachten wir nun die Situation, in der die Rollen der beiden Teilchen nach der Streuung vertauscht sind. Wir interessieren und also für die Wahrscheinlichkeitsamplitude, dass ein Alphateilchen (T1) in Richtung \(\theta_2\) abgelenkt wird und der zugehörige Sauerstoffkern (T2) in Richtung \(\theta_1\). Der Ablenkwinkel \(\theta_2\) gehört also jetzt zu Teilchen T1 und umgekehrt, d.h. der Index des Winkels gibt nicht automatisch die Zuordnung zur Teilchensorte an. Unsere Konvention war ja, dass der erste Winkel in \(A()\) zu Teilchen T1 gehört und der zweite zu Teilchen T2. Die Amplitude für dieses Ereignis ist also \[ A(\theta_2, \theta_1) \] und die Wahrscheinlichkeit demnach \[ |A(\theta_2, \theta_1)|^2 \] Nehmen wir nun an, dass wir nicht daran interessiert sind, ob das Alphateilchen oder der Sauerstoffkern in Richtung \(\theta_1\) fliegt. Wir wollen wissen: wie groß ist die Wahrscheinlichkeit, dass eines der beiden Teilchen in Richtung \(\theta_1\) und das andere Teilchen in Richtung \(\theta_2\) abgelenkt wird. Es handelt sich hier um zwei unterscheidbare Ereignisse, bei denen wir uns für den Unterschied einfach nicht interessieren, obwohl wir das könnten.
In diesem Fall wissen wir, dass wir nicht die Amplituden, sondern die Wahrscheinlichkeiten für die beiden Ereignisse addieren müssen. Die Gesamtwahrscheinlichkeit (nennen wir sie \(P(\theta_1, \theta_2)\) ) ist also gleich \[ P(\theta_1, \theta_2) = |A(\theta_1, \theta_2)|^2 + |A(\theta_2, \theta_1)|^2 \] Es ist interessant, dass diese Wahrscheinlichkeit nicht von der Reihenfolge abhängt, in der die beiden Winkel angegeben werden: \[ P(\theta_1, \theta_2) = P(\theta_2,\theta_1) \] d.h. die Wahrscheinlichkeit ist symmetrisch in den beiden Winkeln. Das liegt daran, dass wir die beiden Teilchensorten hier nicht unterscheiden wollen. Die Wahrscheinlichkeit, eines der beiden Teilchen in Richtung \(\theta_1\) und das andere in Richtung \(\theta_2\) nachzuweisen, ist eben genauso groß wie die Wahrscheinlichkeit, eines der beiden Teilchen in Richtung \(\theta_2\) und das andere in Richtung \(\theta_1\) nachzuweisen, denn beide Aussagen bedeuten dasselbe.
Dagegen ist die Wahrscheinlichkeit, ein Teilchen der Sorte T1 in Richtung \(\theta_1\) und ein Teilchen der Sorte T2 in Richtung \(\theta_2\) nachzuweisen, meist nicht genauso groß wie die Wahrscheinlichkeit, ein Teilchen der Sorte T1 in Richtung \(\theta_2\) und ein Teilchen der Sorte T2 in Richtung \(\theta_1\) nachzuweisen.
Was passiert nun aber, wenn wir die Steuung von Alphateilchen mit Alphateilchen betrachten? Kann man nach der Streuung noch sehen, welches der beiden Alphateilchen ursprünglich aus welcher Richtung gekommen war? Lässt sich unterscheiden, ob ein Alphateilchen, welches nach der Streuung in Richtung \(\theta_1\) unterwegs ist, aus dem einen oder dem anderen ursprünglichen Strahl stammt? Die Antwort lautet: Nein, man kann diese Fälle nicht unterscheiden. Man kann prinzipiell nicht entscheiden, ob das Alphateilchen T1 oder das Alphateilchen T2 in Richtung \(\theta_1\) fliegt. Die beiden Teilchen sind ununterscheidbar.
Das ist anders als in der klassichen Mechanik. Dort kann man die Flugbahnen der Teilchen verfolgen und weiß daher genau, welches der beiden Teilchen man vor sich hat. Die Flugbahnen ermöglichen es einem im Prinzip, ein bestimmtes Teilchen zu verfolgen und zu identifizieren. In der Quantentheorie gibt es aber keine Flugbahnen mehr.
Das vollständige physikalische Ereignis, für das wir die Wahrscheinlichkeitsamplitude angeben wollen, lautet also:
Dieses Ereignis kann auf zwei nicht unterscheidbare Arten eintreten:
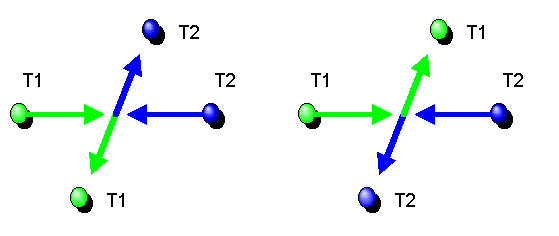
Nach unserer bisherigen Regel für Wahrscheinlichkeitsamplituden müssen wir also die Amplituden für diese beiden ununterscheidbaren Alternativen addieren, um die Gesamtamplitude zu erhalten. Nennen wir diese Gesamtamplitude \(B\). Es ist also \[ B(\theta_1, \theta_2) \] die Amplitude dafür, dass nach der Streuung eines der beiden Alphateilchen in Richtung \(\theta_1\) und das andere Alphateilchen in Richtung \(\theta_2\) fliegt. Die Addition der einzelnen Amplituden ergibt \[ B(\theta_1, \theta_2) = A(\theta_1, \theta_2) + A(\theta_2, \theta_1) \] Die Gesamtamplitude B hat wieder eine bemerkenswerte Eigenschaft, wie die obige Formel zeigt: sie ist symmetrisch, wenn wir die Argumente vertauschen: \[ B(\theta_1, \theta_2) = B(\theta_2,\theta_1) \] Die Wahrscheinlichkeit \(P(\theta_1, \theta_2)\) für das Eintreffen unseres Ereignisses ergibt sich als Betragsquadrat dieser Amplitude: \[ P(\theta_1,\theta_2) = |B(\theta_1, \theta_2)|^2 \] Die Wahrscheinlichkeit hängt also nicht von der Reihenfolge ab, in der wir die beiden Winkel angeben; sie ist symmetrisch. Und das muss auch so sein, denn damit können wir keinen der beiden Winkel mehr einem der beiden Teilchen zuordnen. Beide Teilchen sind gleichberechtigt; sie sind identisch.
Betrachten wir den Spezialfall eines frontalen Zusammenstoßes zweier Alphateilchen mit gleich großem, aber entgegengesetzt gerichtetem Impuls, bei dem die Teilchen um 90 Grad abgelenkt werden. Dann ist \(\theta_1 = \theta_2 = \pi/2\) und somit die Wahrscheinlichkeit gleich \[ P(\pi/2, \pi/2) = |B(\pi/2, \pi/2)|^2 = \] \[ = |2 \cdot A(\pi/2, \pi/2)|^2 = 4 \cdot |A(\pi/2, \pi/2)|^2 \] Wären die beiden Alternativen dagegen unterscheidbar (d.h. wir müssten die Quadrate der Amplituden addieren) und der Unterschied wäre uns lediglich egal, so wäre diese Wahrscheinlichkeit nur halb so groß gewesen! Man sieht: Bosonen (also Spin 0) bevorzugen es, sich gleich zu verhalten, in diesem Fall also um den gleichen Winkel abgelenkt zu werden.
Betrachten wir nun die Streuung einer anderen Teilchensorte: Elektronen. Elektronen haben Spin 1/2. Auch hier können wir erst später genauer verstehen, was das bedeutet. Im Moment brauchen wir nur folgendes zu wissen:
Bei Teilchen mit Spin 1/2 (man nennt sie auch Fermionen)
kann man messen, ob die Spinkomponente +1/2 oder -1/2 bezüglich einer
beliebig vorgegebenen Richtung beträgt.
Wenn es sich um elektrisch neutrale Teilchen handelt,
kann diese Messung einfach durch ein inhomogenes Magnetfeld erfolgen.
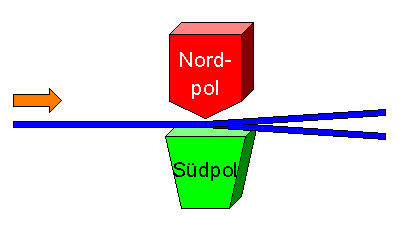
Nehmen wir ein Magnetfeld, das im Wesentlichen in z-Richtung (also nach oben)
orientiert ist und das in z-Richtung
stärker wird. Ein in x-Richtung durch dieses Magnetfeld fliegender Teilchenstrahl spaltet
sich dann auf in einen Teilchenstrahl, der nach oben abgelenkt wird, und einen zweiten
Teilchenstrahl, der nach unten abgelenkt wird. Die Teilchen des einen Teilstrahls
haben dann Spinkomponente +1/2, die des anderen -1/2. Auf diese Art kann man auch Teilchenstrahlen
mit definierter Spinkomponente erzeugen. Bei Bosonen (d.h. Spin 0) gibt es dagegen keine
solche Aufspaltung in Teilstrahlen.
Bei elektrisch geladenen Fermionen (also Spin 1/2) wird dieser Effekt durch die Lorentzkraft überlagert, denn elektrisch geladene Teilchen werden generell in einem Magnetfeld abgelenkt. Die Messung kann aber auch über andere Mechanismen erfolgen, beispielsweise mit Hilfe polarisierter Photonen. Solche Details wollen wir aber hier nicht weiter betrachten, da sie uns vom Kern der Diskussion ablenken.
Ein vollständiges Ereignis bei der Streuung von Elektronen aneinander muss den Spin mit umfassen. Wir wollen unsere Überlegungen daher vereinfachen und voraußetzen, dass alle ankommenden Elektronen Spinkomponente +1/2 in z-Richtung besitzen. Bei neutralen Teilchen könnten wir einen solchen Strahl z.B. mit Hilfe des obigen Magnetfeldes herstellen.
Es zeigt sich im Experiment, dass die Elektronen auch nach der Streuung immer noch dieselbe Spinkomponente +1/2 besitzen. Wir brauchen daher nicht zwischen verschiedenen Spinkomponenten zu unterscheiden.
Das vollständige physikalische Ereignis, für das wir die Wahrscheinlichkeitsamplitude angeben wollen, lautet dann:
Auch hier kann dieses Ereignis wieder auf zwei nicht unterscheidbare Arten eintreten:
Nach unseren bisherigen Regeln müssten wir die Amplituden für diese beiden ununterscheidbaren Alternativen wieder addieren, um die Gesamtamplitude zu erhalten. Es zeigt sich jedoch, dass die Berechnungen dann nicht mit den experimentellen Resultaten übereinstimmen!
Im Gegenteil: Wenn wir bei frontalem Zusammenstoß mit gleichem Impulsbetrag die Ablenkung um 90 Grad (also \(\theta_1 = \theta_2 = \pi/2\) im Bogenmaß) betrachten, so sinkt die Wahrscheinlichkeit im Experiment auf Null!
Wir können dieses Ergebnis erklären, wenn wir die beiden Amplituden nicht addieren, sondern subtrahieren. Die Wahrscheinlichkeit \(P(\theta_1, \theta_2)\) für das Ereignis ist dann \[ P(\theta_1, \theta_2) = |A(\theta_1, \theta_2) - A(\theta_2, \theta_1)|^2 \] Auch hier interferieren die beiden Amplituden miteinander, allerdings mit verschiedenem Vorzeichen. Für die Ablenkung um 90 Grad bei frontalem Zusammenstoß (also \(\theta_1 = \theta_2 = \pi/2\) ) ergibt das die Wahrscheinlichkeit Null. Man kann bildlich sagen, dass Fermionen es vermeiden, sich gleich zu verhalten.
Es zeigt sich, dass die Regel, für Fermionen die Amplituden zu subtrahieren statt zu addieren, überall in der Quantentheorie korrekte Ergebnisse liefert.
Nennen wir die Gesamtamplitude wieder \(B\), so ist für Fermionen \[ B(\theta_1, \theta_2) = A(\theta_1, \theta_2) - A(\theta_2, \theta_1) \] Die Gesamtamplitude B ist antisymmetrisch, wenn wir die Argumente vertauschen: \[ B(\theta_1, \theta_2) = - B(\theta_2, \theta_1) \] Da sich die Wahrscheinlichkeit für das Eintreffen unseres Ereignisses als Betragsquadrat dieser Amplitude ergibt, hängt sie wieder nicht von der Reihenfolge ab, in der wir die beiden Winkel angeben. Beide Teilchen sind erneut vollkommen gleichberechtigt, analog zur Wahrscheinlichkeit bei Bosonen. Allerdings hat eine antisymmetrische Amplitude eine ganz andere Abhängigkeit von den Streuwinkeln als eine symmetrische Amplitude. Bosonen verhalten sich gerne gleich, Fermionen dagegen überhaupt nicht. Das negative Vorzeichen hat also einen großen Einfluss auf das Verhalten der Teilchen, auch wenn die Gesamtwahrscheinlichkeit symmetrisch beim Vertauschen der Streuwinkel bleibt!
Fassen wir die Regeln für identische Teilchen noch einmal in allgemeiner Form zusammen:
Man bezeichnet dieses Ergebnis auch als Spin-Statistik-Theorem oder für den Fermionen-Fall auch als Pauli-Prinzip.
Das Ergebnis lässt sich auf beliebig viele Teilchen verallgemeinern. Die Gesamtamplitude für identische Bosonen ist symmetrisch unter Vertauschung zweier Messwertsätze, und die Amplitude für identische Fermionen antisymmetrisch bei einer solchen Vertauschung.
Man kann eine solchen Gesamtamplitude durch Interferenz der Einzelamplituden für die einzelnen nicht unterscheidbaren Alternativen aufbauen, analog zu unserem Zwei-Teilchen-Fall. Im symmetrischen Fall muss man dazu einfach die Amplituden für alle möglichen Permutationen (d.h. Umsortierungen) der Messwertsätze aufsummieren. Im antisymmetrischen Fall dagegen haben die einzelnen Amplituden in der Summe mal ein positives und mal ein negatives Vorzeichen, je nach Charakter der in der Amplitude vorkommenden Umsortierung. Das Vorzeichen ist positiv, wenn man die Umsortierung der Messwerte durch eine gerade Zahl von Vertauschungen erreichen kann, und negativ bei einer ungeraden Zahl von Vertauschungen (wer in der Mathematik schon sogenannte Determinanten kennengelernt hat, der erkennt das Prinzip wieder). Auf diese Weise erreicht man vollkommen symmetrische bzw. antisymmetrische Amplituden. Auf die Angabe der konkreten Formeln möchte ich hier verzichten. Wir kommen darauf zurück, wenn wir sie benötigen.
Wir könnten uns umgekehrt die Frage stellen: welche Symmetrie-Möglichkeiten gibt es allgemein für die Amplitude zweier identischer Teilchen?
Zunächst einmal muss die Wahrscheinlichkeit symmetrisch in den Messwerten der beiden Teilchen sein, also in unserem Fall \[ P(\theta_1, \theta_2) = P(\theta_2, \theta_1) \] Der Grund dafür war, dass die Aussage "eines der beiden Teilchen tut dies und das andere der Teilchen tut das" gleichwertig ist zu der Aussage "eines der beiden Teilchen tut das und das andere der Teilchen tut dies". Das ist schon in der klassischen Wahrscheinlichkeitsrechnung so, wenn man die beiden Teilchen nicht unterscheiden will.
Wenn wir es nun mit der Wahrscheinlichkeit für ein vollständiges Ereignis im Sinne der Quantentheorie zu tun haben (d.h. die beiden Teilchen sind wirklich ununterscheidbar, und wir sind nicht einfach nur zu faul, uns für den Unterschied zu interessieren), dann gehört zu diesem Ereignis eine Wahrscheinlichkeitsamplitude \(B\) und es gilt \[ P(\theta_1, \theta_2) = |B(\theta_1, \theta_2)|^2 \] Die Symmetrie der Wahrscheinlichkeit \(P\) ist also gewährleistet, wenn die Amplitude die Bedingung \[ B(\theta_1, \theta_2) = e^{i \varphi} B(\theta_2, \theta_1) \] erfüllt. Beim Vertauschen der Argumente ändert sich also der Betrag der Amplitude nicht, aber sie kann um einen beliebigen Winkel \(\varphi\) gedreht werden. Warum die Natur gerade die beiden Fälle \( \varphi = 0 \) (Bosonen) und \( \varphi = \pi \) (Fermionen) realisiert hat, erscheint für uns hier wie ein Zufall zu sein.
Bisweilen hört man in diesem Zusammenhang das Argument, dass ein zweimaliges Vertauschen ja zur alten Situation zurückführt, und dass daher nach zweimaligem Vertauschen auch wieder die gleiche Amplitude wie vorher entstehen müsse. Die Folge ist, dass die Amplitude symmetrisch oder antisymmetrisch sein muss. Das Argument ist jedoch nicht schlüssig, denn beobachtbar ist alleine die Wahrscheinlichkeit, nicht die einzelne Amplitude. Es zeigt sich sogar, dass bei einem zweidimensionalen Raum tatsächlich alle möglichen Werte von \(\varphi\) physikalisch möglich sind. Man kann dies experimentell in der Oberflächenphysik z.B. mit Hilfe sogenannten Magnetflussschläuche nachweisen. Analog zu Bosonen und Fermionen spricht man hier von Anyonen.
Woran also liegt es, dass wir zur Beschreibung von Ereignissen mit identischen Bosonen eine symmetrische Amplitude, bei identischen Fermionen dagegen eine antisymmetrische Amplitude verwenden müssen?
Wir haben hier den Fall vor uns, dass eine einfache Regel keine einfache Begründung hat. Es gibt schon eine Begründung. Sie wurde zuerst von Wolfgang Pauli ausgearbeitet. Aber diese Begründung greift auf nicht-elementare Methoden der relativistischen Quantenfeldtheorie zurück. Erst die Kombination von Quantentheorie und spezieler Relativitätstheorie reicht also aus, um das Spin-Statistik-Theorem zu beweisen und seinen inneren Grund zu verstehen.
Ich möchte hier nicht versuchen, diesen Beweis im Detail wiederzugeben. Stattdessen möchte ich einige anschauliche Argumente geben und einige Kernideen des Beweises kurz vorstellen. Dabei lasse ich mich u.a. von Feynmans Dirac-Memorial-Lecture aus dem Jahr 1986 leiten (siehe Richard Feynman und Steven Weinberg: Elementary Particles and the Laws of Physics, Cambridge University Press 1987).
Zunächst ein anschauliches Argument. Betrachten wir zwei identische punktförmige Teilchen an den Orten x und y. Nun vertauschen wir die Positionen der beiden Teilchen. Sieht diese vertauschte Situation genauso aus wie die ursprüngliche Situation? Da wir die Teilchen nicht unterscheiden können, und da sie punktförmig sind, würden wir sagen: ja! Nun wollen wir die Situation etwas verändern: wir befestigen ein Band zwischen den beiden Teilchen, wobei das Band ruhig durchhängen darf. Das Band soll nicht verdreht sein (also keinen dünnen Faden nehmen, bei dem man so eine Verdrehung nicht sieht, sondern wirklich ein Band mit einer gewissen Breite). Sie sollten diese Überlegung unbedingt praktisch nachvollziehen: nehmen sie z.B. einen dünnen Streifen Papier und halten sie ihn mit beiden Händen fest.
Nun vertauschen wir die beiden Teilchen (bzw. die Hände, wobei wir das Band festhalten,
ohne die Bandenden dabei zu drehen).
Sieht die Situation noch genauso aus wie die ursprüngliche Lage? Nein! Das Band ist verdreht!
Wir müssen eines der beiden Teilchen (also eines der Band-Enden) um 360 Grad drehen,
um die Verdrehung vollständig zu beseitigen!
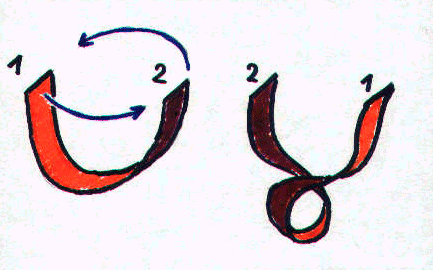
In unserem Beispiel mit dem Band, das die Teilchen verbindet, führt also erst eine Vertauschung zusammen mit einer vollen Umdrehung eines der beiden Teilchen zu einer Situation, die wie die Anfangssituation außieht.
Man könnte auch sagen: eine Vertauschung der Teilchen führt zu einer Verdrehung des Bandes. Diese Verdrehung kann man alternativ auch durch Drehung eines der Enden des Bandes um 360 Grad erreichen. In diesem Sinne wären also Teilchenvertauschung und volle Umdrehung eines der beiden Teilchen gleichwertig zueinander.
Nun ist natürlich nicht klar, ob sich die Natur für solche Details interessiert. Die Mathematik der Quantenfeldtheorie aber zeigt: sie tut es! Man kann tatsächlich die folgende Regel aufstellen:
Wie wir später noch sehen werden, führt eine volle Umdrehung bei einem Fermion zu einem Vorzeichenwechsel der Amplitude. Genau dieser Vorzeichenwechsel ist es, den wir im Spin-Statistik-Theorem für Fermionen sehen!
Damit haben wir zumindest schon einmal eine anschauliche Vorstellung davon bekommen, was hinter dem merkwürdigen Vorzeichen bei Fermionen steckt. Ein Beweis war das natürlich noch lange nicht.
Einen solchen Beweis kann man in Feynmans Dirac-Memorial-Lecture (siehe oben) finden. Für den interessierten Leser möchte ich hier kurz Feynmans eigene Zusammenfassung dieses Beweises übersetzen bzw. erläutern:
Wenn wir darauf bestehen, dass Teilchen nur positive Energien haben dürfen, dann lassen sich Amplituden nicht vermeiden, die der Propagation (also der Bewegung) von Teilchen außerhalb des Lichtkegels entsprechen (Anmerkung: das entspricht formal einer Bewegung mit Überlichtgeschwindigkeit; die Argumentation basiert hier generell auf dem Rahmen der speziellen Relativitätstheorie). Wenn wir uns eine solche Propagation ansehen, so hängt es vom Betrachter ab, ob er sie als die Propagation eines Teilchens oder eines Antiteilchens interpretiert: "One man's virtual particle is another man's virtual antiparticle." Nun verwenden wir zusätzlich, dass die Wahrscheinlichkeit dafür, dass irgendetwas mit einem Teilchen passieren muss (d.h. dass es nicht einfach im Nichts verschwinden kann), gleich Eins ist. Dies hat Folgen für die Vorzeichen, mit der die Amplituden, die zu diesem Prozess beitragen (u.a. Paarproduktion und die Beteiligung von Antiteilchen), in die Gesamtamplitude eingehen müssen. Diese Vorzeichen sind unterschiedlich für Bosonen und Fermionen.
Zugegeben, unmittelbar verstehen kann man das nicht. Aber immerhin erhält man eine Idee, welche Zutaten notwendig sind. Im Zentrum steht dabei die spezielle Relativitätstheorie und die Folgen, die sie für die Quantentheorie hat (u.a. die Existenz von Antiteilchen). Und außerdem erkennt man: eine einfache Regel (symmetrische Amplituden bei Bosonen, antisymmetrische Amplituden bei Fermionen) hat nicht unbedingt eine einfache Begründung. In diesem Fall muss man tief in die Strukturen der relativistischen Quantenfeldtheorie abtauchen!
Mehr zu dem Thema gibt es auch auf der interessanten Webseite von John Baez: Spin, Statistics, CPT and All That Jazz.
© Jörg Resag, www.joerg-resag.de
last modified on 15 July 2023