Zufallszahlen
Die meisten sehr großen Zahlen sind zufällig
Zufallszahlen kann man nicht allgemein erkennen
Zufälligkeit und das Halteproblem
Die Komplexität von Zahlen
Die Beweiskraft formaler Systeme
Die Zufälligkeit unendlich langer Zeichenketten
Zu Beginn dieses Kapitels möchte ich den Leser bitten, sich die folgende Zahl anzusehen
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337...
und nun die Frage zu beantworten: Ist diese Zahl zufällig?
Wenn man sich die Zahl so ansieht, hat man tatsächlich den Eindruck, dass sie zufällig ist. Die einzelnen Ziffern scheinen vollkommen unregelmäßig aufeinander zu folgen, und es ist kein Muster erkennbar. Insofern besitzt diese Zahl tatsächlich viele Eigenschaften, die man bei einer zufälligen Zahl erwarten würde.
Um die obige Frage klar zu beantworten, müssen wir jedoch genauer spezifizieren, was wir unter einer zufälligen Zahl (oder kurz Zufallszahl) verstehen wollen.
Dazu legen wir fest:
Zufallszahl ist damit gleichbedeutend mit nicht komprimierbarer Zahl. Was dabei die Formulierung "deutlich kürzer" bedeuten soll, muss man strenggenommen noch genau festlegen. Man kann z.B. fordern, dass es bei Zufallszahlen kein Computerprogramm gibt, dass um mindestens 10 Bit kürzer ist als die Zahl. Außerdem gilt diese Definition nur für Zahlen, die sich durch einen endlichen Binärstring darstellen lassen. Wir gehen weiter unten noch genauer darauf ein.
Der Grund für diese Festlegung von Zufälligkeit einer Zahl liegt darin, dass wir bei einer Zufallszahl keine Muster oder Regelmäßigkeiten erwarten, die sich zum Komprimieren der Zahl nutzen lassen. Beispielsweise lässt sich die Zahl \(1212121212\) komprimieren durch die Anweisung "Drucke fünfmal die Ziffernfolge \(12\)". Bei größeren Ziffernfolgen kann man sich so leicht vorstellen, dass das entsprechende Computerprogramm deutlich kürzer als die Zahl selbst ist.
Die obige Definition wirft die Frage auf, ob es überhaupt Zahlen gibt, die in diesem Sinn nicht komprimierbar und damit zufällig sind. Vielleicht lässt sich ja jede Zahl wenigstens um einige Prozent komprimieren?
Man kann diese Frage durch Abzählen klären. Dazu zählt man einerseits, wieviele Zahlen es bis maximal \(n\) Bit Speicherplatz für diese Zahlen gibt, und vergleicht diese Zahl mit der Zahl der Programme mit maximal \(n\) Bit Speicherplatz. Gibt es deutlich mehr Zahlen als Programme, so bleiben Zahlen übrig, zu denen es kein kürzeres Programm geben kann. Diese Zahlen sind dann nicht-komprimierbar und damit zufällig.
Beginnen wir mit den Zahlen, die maximal \(n\) Bit lang sind (die sich also als Binärstring mit höchstens \(n\) Stellen schreiben lassen; z.B. wird die Zahl 19 durch den Binärstring 10011 dargestellt, was soviel bedeutet wie \( 1 \cdot 16 + 0 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1\cdot 1 \). Es gibt \(2^n\) solche Zahlen mit maximal \(n\) Bit Länge, denn jeder Binärstring mit höchstens \(n\) Stellen ist eine solche Zahl.
Betrachten wir nun zum Vergleich alle Programme, die als Binärstring kodiert maximal \(n\) Bit lang sind (letztlich werden auf einem üblichen Computer ja alle Programme als Binärstring abgelegt). Dazu müssen wir natürlich vorher irgendeine Programmiersprache auswählen. Programme müssen entsprechend der gewählten Programmiersprache eine gewisse Struktur haben, d.h. ein Compiler wird nicht jeden beliebigen Binärstring als Programm generieren können. Eine genauere Analyse zeigt, dass Binärstrings, die Programme kodieren sollen, eine wichtige Eigenschaft besitzen müssen (Gregory Chaitin, der sich viel mit diesen Fragestellungen beschäftigt hat, benötigte nach eigenen Angaben etwa 10 Jahre, um dieses wichtige technische Detail zu erkennen und sauber auszuarbeiten):
Man sagt auch, die Programmiersprache muss Präfix-frei sein, d.h. ausbalancierte Klammersymbole und BEGIN-END-Kommandos haben. Wenn man also einmal in der Liste aller Binärstrings auf einen Binärstring stößt, der einem Programm entspricht, so kann man alle durch Verlängerung daraus erzeugten Binärstrings aus der Liste wegstreichen, denn sie sind keine als Programm zulässigen Binärstrings. Damit ist klar, dass viele Binärstrings mit \(n\) Bit Länge keine zulässigen Programme repräsentieren.
Wie groß ist nun die Zahl der Programm-Binärstrings im Vergleich zu der Gesamtzahl der Binärstrings gleicher Länge? Das kann man beispielsweise mit dem folgenden kleinen Modell grob abschätzen:
Angenommen, nur solche Binärstrings kommen grundsätzlich als Programme in Frage, deren Länge ein Vielfaches einer natürlichen Zahl (nennen wir sie \(N\)) ist. Wenn beispielsweise \( N = 2 \) ist, so müssen Programm-Binärstrings die Länge 2 Bit oder 4 Bit oder 6 Bit usw. aufweisen. Natürlich kann man auch \( N = 1 \) wählen; dann ist jede Bitlänge für Programme erlaubt.
Nun nehmen wir weiter an, dass unter den Binärstrings, die Programme repräsentieren dürfen (deren Länge also ein Vielfaches von \(N\) ist und die keine Verlängerung eines kürzeren Programm-Binärstrings sind), nur jeder \( 2^N \)-te Binärstring tatsächlich ein Programm darstellt. Für \( N = 2 \) bedeutet das, dass jeder vierte noch erlaubte Binärstring mit geradzahliger Bitlänge ein Programm ist.
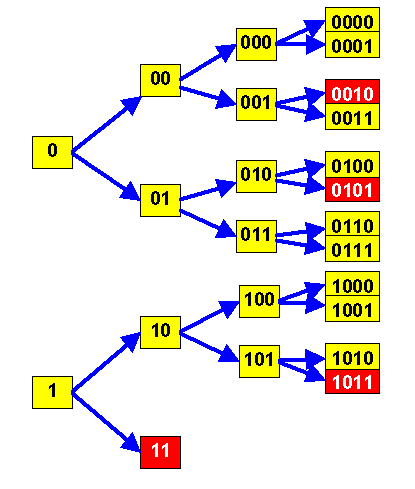
Betrachten wir den Fall \( N = 1 \). Jeder Binärstring könnte also von der Länge her ein Programm sein Beginnen wir mit Binärstrings der Länge Eins, also den beiden Strings "0" und "1". Da jeder \( 2^N \)-te erlaubte Binärstring ein Programm sein soll, muss einer dieser beiden Stringe ein Programm sein. Sagen wir also, der String "0" ist das Programm. Ab sofort sind damit alle längeren Binärstrings, die mit "0" beginnen, keine möglichen Programm-Binärstrings mehr, denn Verlängerungen von Programmstrings sind keine Programmstrings.
Gehen wir nun zu den Binärstrings der Länge Zwei. Nur die beiden Strings "10" und "11" sind möglich, denn Strings, die mit "0" beginnen, sind ausgeschlossen. Nun ist wieder einer dieser beiden Strings ein Programm (sagen wir "10").
Gehen wir zu den Strings der Länge Drei über. Strings, die mit "0" oder "10" beginnen, fallen raus, sodass wieder nur zwei Kandidaten bleiben: "110" und "111".
Und so geht es immer weiter. Wir sehen, wie jeder Programmstring einen ganzen Baum von Möglichkeiten abschneidet, nämlich alle längeren Strings, die mit dem Programmstring beginnen. Im Fall \( N = 1 \) gibt es deshalb für jede Bitlänge nur einen einzigen Programmstring, während die Zahl der als Zahlen geeigneten Binärstrings exponentiell mit der Bitlänge wächst (denn jeder Binärstring stellt eine Zahl dar).
Wir sehen: eine hohe Wahrscheinlichkeit (also kleines \(N\) ), dass ein erlaubter Binärstring ein Programm ist, führt dazu, dass sehr viele Äste des Baums abgeschnitten werden, so dass bei \( N = 1 \) pro Bitlänge nur ein Programmstring übrig bleibt.
Betrachten wir daher den Fall \(N = 2\). Nur Binärstrings mit gerader Bitlänge können jetzt
noch Programmstrings sein.
Unter den 4 Binärstrings der Länge 2 befindet sich 1 Programmstring
(denn nur jeder vierte erlaubte String ist jetzt noch ein Programm).
Damit fallen von den 16 Binärstrings der Länge 4 die 4 Binärstrings weg, die
mit diesem Programmstring anfangen. Es bleiben 12 Strings übrig, von denen drei
Programmstrings sind. Und so geht es weiter.

Man kann unser kleines Modell natürlich noch weiter untersuchen und verschiedene andere \(N\) ausprobieren. Dabei kommt immer herauss:
Das Abschneiden der Äste im Baum bewirkt, dass nur relativ wenige Binärstrings Programme darstellen können, egal welches \(N\) wir wählen. Daher kann es nicht zu jeder Zahl mit höchstens \(n\) Bit ein Programm mit weniger als \(n\) Bit geben (das diese Zahl auch noch ausgibt), denn es sind nicht genug Programme da! Also muss es Zahlen geben, die nicht durch ein kürzeres Programm ausgegeben werden können, d.h. es muss zufällige Zahlen geben.
Der Unterschied zwischen der Zahl der Programme mit maximal \(n\) Bit und der \(2^n\) Zahlen mit maximal \(n\) Bit vergrößert sich, je größer die Bitzahl \(n\) ist. Je größer \(n\) wird, umso größer ist die Wahrscheinlichkeit, dass irgendeine willkürlich herausgegriffene Zahl eine Zufallszahl ist. Lässt man beliebig große Zahlen und Programme zu (d.h. die Bitzahl \(n\) darf beliebig groß werden), so wird fast jede Zahl zufällig ist. Wir werden weiter unten noch eine präzise Version dieser Aussage kennenlernen.
Was passiert nun, wenn man die einzelen Bits einer \(n\)-Bit langen Zahl würfelt, die Bits also zufällig bestimmt? Ist die so erhaltene Zahl im Sinne unserer Definition zufällig, also nicht komprimierbar?
Es könnte natürlich sein, dass man nur Einsen würfelt. Die so erhaltene Zahl lässt sich sicher komprimieren, ist also in diesem Sinne nicht zufällig. Je mehr Bits jedoch die Zahl enthält, d.h. je öfter gewürfelt wird, umso größer ist die Wahrscheinlichkeit, auf diese Weise eine nicht komprimierbare Zahl zu erzeugen. Im Grenzfall, dass unendlich viele Bits zu würfeln sind, ist die Wahrscheinlichkeit sogar gleich Eins, dass eine Zufallszahl dabei entsteht.
Nun ist es keineswegs immer offensichtlich, ob in einer vorgegebenen Zahl ein Muster vorhanden ist oder nicht. So konnten wir in der Zahl am Anfang dieses Textes kein Muster erkennen. Aber dennoch gibt es eines, denn es gibt relativ einfache und kurze Computerprogramme, die die obige Zahl berechnen können. Vermutlich wissen Sie bereits, warum: es handelt sich um die Kreiszahl \( \pi \). Eine der vielen Möglichkeiten, \( \pi \) zu berechnen, ist die folgende: \begin{equation} \pi = 4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + ... \end{equation}
Dieser Algorithmus lässt sich leicht in einem kleinen Computerprogramm codieren. Auf diese Weise kann man beliebig viele Stellen der Zahl \( \pi \) berechnen, wenn nur der Computer und sein Speicher groß genug sind.
Wäre es möglich, ein Computerprogramm zu entwickeln, das dieses Muster in der Zahl \( \pi \) oben entdecken würde und damit die Zahl deutlich komprimieren könnte? Natürlich wäre das möglich, denn dieses Programm würde jede Zahl daraufhin untersuchen, ob \( \pi \) darin vorkommt, und dann das Wissen über \( \pi \) anwenden.
Interessanter wäre es, ein Programm zu besitzen, das beliebige versteckte Muster in irgendeiner vorgegebenen Zahl entdecken könnte und damit bei jeder Zahl angeben könnte, ob sie komprimierbar (und damit nicht-zufällig) ist oder nicht. Dass ein solches Programm wohl nicht einfach zu schreiben ist, hat uns das Beispiel der Zahl \( \pi \) bereits gezeigt, denn ihre Ziffernfolge sieht absolut zufällig aus, obwohl die Zahl nicht zufällig ist. Gregory Chaitin hat schließlich gezeigt, dass es unmöglich ist, ein solches Programm zu schreiben:
Warum ist das so?
Nehmen wir einmal an, es gäbe doch einen solchen Algorithmus, den wir dann z.B. als Unterprogramm für andere Programme zur Verfügung stellen könnten. Nun schreiben wir ein Programm, das eine interne Zählervariable \(N\) schrittweise von 1 an hochzählt. Das Programm besitzt also eine Schleife, in der \(N\) nacheinander die Werte 0, 1, 2, 3 usw. annimmt.
Innerhalb der Schleife wird nun das obige Zufallsprüf-Unterprogramm aufgerufen. Es überprüft, ob die Zählervariable \(N\) zufällig ist oder nicht. Wenn sie zufällig ist, so druckt das Programm die Zahl \(N\) aus und hält an. Ist die Zahl \(N\) jedoch nicht zufällig, so läuft die Schleife einfach weiter, d.h. das Programm überprüft für das nächste \(N\), ob es zufällig ist, und so weiter.
Auf diese Weise wird die Schleifenvariable \(N\) schrittweise solange hochgezählt, bis sie irgendwann vom Unterprogramm als zufällig angesehen wird, woraufhin das Programm sie ausdruckt anhält. Damit würde das Programm die kleinste natürliche Zahl ausdrucken, die zufällig ist.
Wir können dieses Programm nun leicht so modifizieren, dass es eine zufällige Zahl ausdruckt, die (als Binärstring) sehr viel größer ist als das Programm selbst (auch kodiert als Binärstring). Nehmen wir an, die Größe des Programms sei \(L\) Bit. Dann lassen wir die obige Schleife nicht mit dem Wert \(N = 1\) beginnen , sondern beispielsweise mit der Zahl \(N_{\mathrm{start}} = 2^{2 L} \). Damit ist gewährleistet, dass diese Startzahl \(N_{\mathrm{start}}\) mindestens doppelt so viel Speicherplatz benötigt wie das Programm (und damit mehr als \(L\) Bit).
Das Programm beginnt nun, die Zahlen ab der Zahl \(N_{\mathrm{start}}\) schrittweise auf Zufälligkeit hin zu untersuchen. Die erste gefundene Zufallszahl wird ausgedruckt, und das Programm hält an. Wir wissen, dass es eine Zufallszahl oberhalb von \(N_{\mathrm{start}}\) geben muss, denn es gibt sehr viel mehr Zahlen oberhalb von \(N_{\mathrm{start}}\) als Programme mit maximal gleicher Bitlänge (siehe oben). Die Existenz von Zufallszahlen oberhalb von \(N_{\mathrm{start}}\) erscheint uns auch plausibel, denn schließlich können wir ja unbegrenzt viele Stellen einer Zahl zufällig würfeln. Das Programm wird also irgendwann eine Zufallszahl ausdrucken, die mehr als \(2 L\) Bit Speicherplatz benötigt und dann anhalten. Andererseits benötigt das Programm selbst nur \(L\) Bit Speicherplatz.
Unsere Überlegung zeigt: Wenn es einen Algorithmus gibt, mit dem man jede beliebige Zahl auf Zufälligkeit hin überprüfen kann, so kann man damit ein Programm schreiben, das eine Zufallszahl ausgibt, die deutlich mehr Speicherplatz benötigt als das Programm, welches sie ausgibt. Das aber bedeutet, dass sich die ausgegebene Zahl komprimieren lässt, denn wir haben gerade ein Programm angegeben, das deutlich kürzer ist als die Zahl und das dennoch die Zahl ausgeben kann. Nach unserer Definition kann damit die ausgegebene Zahl nicht zufällig sein. Wir haben einen Widerspruch! Daher muss unsere Annahme falsch sein – es kann also keinen Algorithmus geben, der beliebige Zahlen auf Zufälligkeit überprüfen kann. Chaitins Theorem ist damit bewiesen.
Noch eine kurze Randbemerkung: In Einzelfällen mag es durchaus möglich sein, zu beweisen, dass eine Zahl zufällig ist. Es ist jedoch unmöglich, dies mit Hilfe eines einzigen Algorithmus bei beliebigen Zahlen zu tun.
Es gibt einen engen Zusammenhang zwischen Chaitins Theorem und Turings Halteproblem. Angenommen, Turings Halteproblem wäre lösbar, d.h. wir können bei jedem Programm mechanisch bestimmen, ob es irgendwann anhält oder nicht. Dann könnten wir folgenden Algorithmus aufbauen:
Wenn ein solches Programm dabei ist, so wissen wir, dass \(x\) nicht zufällig ist, denn wir haben gerade in der Liste ein Programm gefunden, das kürzer als "PRINT \(x\)" ist und das die Zahl \(x\) ausgibt. Andernfalls wissen wir, dass \(x\) zufällig ist, denn kein kürzeres Programm kann sie ausgeben. Damit hätten wir einen Algorithmus gefunden, der jede Zahl auf Zufälligkeit hin untersuchen kann – im Widerspruch zu Chaitins Theorem, das wir gerade bewiesen haben. Einer der Schritte in diesem Algorithmus muss also undurchführbar sein. Der einzige Schritt, der dafür in Frage kommt, ist der Vorletzte (Lösche alle Programme aus der Liste, die nicht anhalten). Aus Chaitins Theorem folgt also unmittelbar, dass Turings Halteproblem unlösbar ist.
Im Folgenden möchte ich die obigen Aussagen etwas erweitern und präzisieren (siehe z.B. Wikipedia: Algorithmic information theory). Man kann den oben definierten Begriff der Zufälligkeit erweitern und den Begriff der Komplexität einer Zahl (oder allgemeiner: einer Zeichenkette) einführen:
(statt von Zahlen kann man auch allgemeiner von Zeichenketten (Strings) reden). Je kürzer das kürzeste Programm ist, das eine bestimmte Zahl ausgeben kann, umso weniger komplex ist die Zahl, d.h. umso weniger Information enthält sie. Eine zufällige Zahl lässt sich dagegen praktisch gar nicht komprimieren, d.h. das kürzeste Programm, das sie ausgibt, hat ungefähr dieselbe Länge wie die Zahl selbst (z.B. das Programm "PRINT Ziffernfolge der Zahl" ).
Um die Definition der Komplexität einer Zahl formell sauber zu fassen, muss man strenggenommen genau festlegen, welcher Typ von Programmen erlaubt ist, d.h. welche Programmiersprache, welcher Compiler und welcher Computer verwendet wird. Man könnte z.B. Turingmaschinen verwenden, oder eine Programmiersprache wie C oder LISP sowie einen bestimmten Compiler und einen bestimmten PC-Prozessor.
Glücklicherweise spielt es letztlich keine Rolle, für welchen Computer und für welche Programmiersprache man sich entscheidet, solange sich verschiedene Computer und Programmiersprachen gegenseitig simulieren können. So wissen wir ja, dass eine Turingmaschine alles das tun kann, was ein gewöhnlicher Digitalcomputer tut. Ein Programm in der einen Programmiersprache lässt sich in ein Programm in einer anderen Programmiersprache umwandeln, indem man einen Interpreter für die umzuwandelnde Programmiersprache dem vorgegebenen Programm hinzufügt sowie in der neuen Sprache eine Art Container für das Programm baut. Wechselt man also die Programmiersprache, so verändert sich die Komplexität einer Zahl maximal um einen konstanten Faktor \(C\) (die den Speicher-Overhead beschreibt, um das umzuwandelnde Programm zu erfassen) und eine additive Konstante \(D\) (entsprechend der Länge des hinzugefügten Interpreters), die beide nur von den verwendeten Programmiersprachen abhängen, nicht aber von der untersuchten Zahl.
Im Folgenden wollen wir einfach irgendeine Programmiersprache und einen Computertyp wählen (z.B. Turingmaschinen). Damit ist eindeutig festgelegt, was die Komplexität einer Zahl bedeutet. Es stellt sich nun die Frage, ob und wie man die Komplexität einer beliebigen Zahl berechnen kann.
Wir hatten oben nachgewiesen, dass man die Zufälligkeit einer beliebigen Zahl nicht allgemein ermitteln kann. Vollkommen analog lässt sich auch zeigen, dass man die Komplexität einer beliebigen Zahl nicht mit einem einzigen Algorithmus berechnen kann (d.h. die Komplexität ist eine nicht-berechenbare Eigenschaft oder Funktion natürlicher Zahlen).
Nehmen wir beispielsweise an, es gäbe einen solchen Algorithmus, mit dem man die Komplexität jeder Zahl berechnen kann. Wieder stellen wir diesen Algorithmus als Unterprogramm zur Verfügung. Nun schreiben wir ein Programm, das eine interne Variable \(N\) schrittweise von 1 an hochzählt. Innerhalb der Schleife rufen wir das obige Unterprogramm auf und bestimmen die Komplexität der Schleifenvariablen \(N\). Wenn die Komplexität von \(N\) größer als eine gewisse Zahl \(L\) (über die wir gleich etwas sagen) ist, so druckt das Programm die Zahl \(N\) aus und hält an. Andernfalls läuft die Schleife weiter.
Auf diese Weise wird die Schleifenvariable \(N\) schrittweise solange um 1 vergrößert, bis eine Zahl ausgegeben wird, deren Komplexität größer als die im Programm vorgegebene Konstante \(L\) ist. Solche Zahlen muss es geben, denn es gibt oberhalb von \(L\) unendlich viele Zufallszahlen, und Zufallszahlen haben eine Komplexität, die ungefähr gleich ihrer eigenen Bitlänge ist (denn sonst ließen sie sich komprimieren).
Nun müssen wir den Programmparameter \(L\) noch festlegen. Wir wählen ihn so, dass er deutlich größer als die Bitgröße des Programms selbst ist (z.B. doppelt so groß). Das Programm würde dann eine Zahl ausgeben, deren Komplexität deutlich größer als \(L\) ist. Aber die Komplexität dieser Zahl kann nicht deutlich größer als \(L\) sein, denn wir haben gerade ein Programm der Länge \(L\) geschrieben, das diese Zahl ausgibt. Dieser Widerspruch zeigt, dass es keinen allgemeinen Algorithmus zur Berechnung der Komplexität einer beliebigen Zahl geben kann.
Halten wir das Ergebnis noch einmal fest:
Auch hier gilt natürlich wieder, dass in Ausnahmefällen die Komplexität bestimmter Zahlen berechnet werden kann. Aber sie kann nicht allgemein in jedem Fall auf dieselbe Weise berechnet werden.
Der obige Beweis ist eng verwandt mit dem bekannten Berry-Paradoxon: "Es sei \(N\) die kleinste Zahl, die sich nicht in weniger als zwanzig Worten definieren lässt." Dieser Satz besitzt 16 Worte und damit weniger als 20 Worte. Damit konnten wir \(N\) in weniger als 20 Worten definieren, obwohl \(N\) so definiert war, dass genau dies unmöglich sein sollte. Wir haben einen Widerspruch!
Die Analogie zwischen Berrys Paradoxon und unserem Beweis ergibt sich folgendermaßen. Der Satz "Es sei \(N\) die kleinste Zahl, die sich nicht in weniger als zwanzig Worten definieren lässt." wird ersetzt durch das obige Programm, das die kleinste Zahl ausdruckt, die eine Komplexität von mindestens \(L\) aufweist. \(L\) war aber gerade die Größe des Programms, d.h. das Programm gibt eine Zahl \(N\) aus, die wegen ihrer Komplexität sich nicht durch ein Programm von \(L\) Bit Größe ausdrucken lässt. Genau das tut aber das Programm – ein Widerspruch, der zeigt, dass es dieses Programm nicht geben kann.
Es ist interessant, wie sich verschiedene Paradoxa als mathematische Sätze widerspiegeln. Berrys Paradoxon führt zur Nicht-Berechenbarkeit der Komplexität einer Zahl, und das Paradoxon "Ich bin nicht wahr" führt zur Nicht-Beweisbarkeit von Gödels Satz (wobei wahr durch beweisbar zu ersetzen ist). Paradoxien sind also weit mehr als nur merkwürdige, nicht ernst zu nehmende Konstrukte. Sie zeigen die prinzipiellen Grenzen von Sprachen und von formalen Systemen auf.
Nun ist die Komplexität einer beliebigen Zahl zwar nicht allgemein berechenbar, aber es ist leicht möglich, obere Grenzen für diese Komplexität anzugeben. Dazu komprimiert man die Zahl einfach mit irgend einem Kompressionsalgorithmus, wie er in Packprogrammen auf Computern zur Verfügung steht (z.B. das bekannte ZIP-Programm). Wie nahe man damit allerdings an die Komplexität (und damit an die maximal mögliche Kompression der Zahl) herankommt, kann man höchstens im Einzelfall ermitteln, nicht aber allgemein für beliebige Zahlen.
Wir hatten oben den Zusammenhang zwischen der Komplexität und der Zufälligkeit einer Zahl bereits erwähnt: die Komplexität (in Bit) einer zufälligen Zahl entspricht ungefähr der Länge des Binärstrings der Zahl. Dabei hatte wir weiterhin gesagt, dass bei größeren Zahlen die meisten dieser Zahlen zufällig sind, also eine hohe Komplexität aufweisen. Diese Aussage können wir nun präzisieren:
Die Wahrscheinlichkeit, dass die Kompexität einer Zahl \(x\) um \(n\) Bit kleiner als ihre Bitlänge ist, nimmt also exponentiell mit \(n\) ab. Mit sehr großer Wahrscheinlichkeit hat \(x\) also eine Komplexität, die nur wenig unter ihrer Bitlänge liegt. Das ist damit gemeint, wenn man sagt, die meisten Zahlen sind zufällig.
Der Beweis dieser Aussage erfolgt ähnlich zu unserem obigen Modell, mit dem wir abgeschätzt haben, wieviele Binärstrings als Programme in Frage kommen.
Obwohl die meisten Zahlen zufällig sind, können wir die Zufälligkeit bei beliebig herausgegriffenen Zahlen weder beweisen noch wiederlegen, sobald ihre Komplexität eine gewisse kritische Grenze überschreitet. Präzise ausgedrückt, lautet diese Aussage so:
Es gibt also eine obere Grenze für beweisbare Komplexität in einem formalen System, die ungefähr gleich der Größe des formalen Systems ist (Details kommen gleich). Eine Komplexität oberhalb dieser Grenze kann in dem formalen System nicht mehr erfasst werden, d.h. sie kann bei den entsprechenden Zahlen nicht mehr erkannt werden. Es muss Zahlen mit entsprechend großer Komplexität geben, doch die Aussage "Die Zahl \(x\) hat eine Komplexität größer als \(L\)" ist bei den meisten Zahlen \(x\) nicht entscheidbar. Dies ist ein weiteres Beispiel für Gödels Unvollständigkeitssatz. Gregory Chaitin hat es einmal sinngemäß so ausgedrückt: "Man kann eine 10-Kilo-Aussage nicht mit einem 5-Kilo-Axiomensystem beweisen".
Warum ist das so?
Der Beweis verläuft wieder ähnlich zu den obigen Beweisen (siehe z.B. J. P. Lewis: Formally Unsolvable Problems in Software Engineering): Zur Abkürzung bezeichnen im Folgenden wir mit \(H(x)\) die Komplexität der Zahl \(x\).
Nehmen wir an, wir könnten die Aussage \( H(x) > L \) für irgendeine Zahl \(x\) in unserem formalen System beweisen. Wir können das formale System als ein Programm betrachten, dass wohlgeformte Zeichenketten erzeugen und manipulieren kann. Das Programm verfügt dabei über Unterprogramme, die alle Regeln des formalen Systems repräsentieren. Die Axiome entsprechen gewissen Start-Zeichenketten, die dem Programm (z.B. in Form interner Konstanten) bekannt sind. Das Programm ist nun in der Lage, beliebig viele Beweise des formalen Systems in alphabetischer Reihenfolge, der Größe nach sortiert, zu erzeugen, denn in jedem formalen System gibt es nach Definition eine vollständige, unendlich lange Liste aller Beweise (siehe Kapitel 2.2). Wir können das Programm daher als Unterprogramm dazu verwenden, den Beweis zur Aussage \( H(x) > L \) zu suchen, und \(x\) anschließend auszugeben. Wenn es diesen Beweis gibt, so muss das Programm ihn nach endlich vielen Schritten in der Beweisliste finden können.
Nehmen wir an, das Unterprogramm, welches unser formales System repräsentiert, ist \(N\) Bit lang. Wir haben dieses Unterprogramm in ein etwas größeres Programm eingebunden, das die Aussage \( H(x) > L \) in der Beweisliste sucht, die vom Unterprogramm erzeugt wird, und das dann \(x\) ausgibt. Sagen wir, dieses Programm ist um \(k\) Bit länger als das Unterprogramm, d.h. das Programm hat eine Länge von \(N + k\) Bit. Man kann sich leicht vorstellen, dass bei umfangreichen formalen Systemen \(N\) sehr viel größer als \(k\) sein wird, denn der Überbau zum Durchsuchen der Beweisliste und Ausgeben von \(x\) wird gegenüber der Programmierung des kompletten formalen Systems kaum noch ins Gewicht fallen.
Wir setzen nun \( L \) gleich der Programmgröße \(N + k\), also \( L = N + k \). Dann würde unser Programm eine Zahl \(x\) ausgeben, deren Komplexität laut Beweis größer als \(N + k\) ist, obwohl das Programm nur \(N + k\) Bit lang ist (d.h. die Komplexität der Zahl \(x\) kann höchstens \(N + k\) Bit betragen). Wir haben einen Widerspruch, der zeigt, dass es ein solches Programm nicht geben kann, und das bedeutet, dass das formale System die Aussage \( H(x) > L \) (mit \( L = N + k \) ) für keine Zahl \(x\) beweisen kann. Das Durchsuchen der Beweisliste verläuft also erfolglos, und die Zahl \(x\) wird nicht ausgegeben.
Die obige Definition der Komplexität ist in dieser Form zunächst nur für Zahlen mit endlicher Binärdarstellung (oder analog für endliche Zeichenketten) anwendbar. Man kann den daraus abgeleiteten Begriff Zufälligkeit, den wir bisher nur für endliche natürliche Zahlen definiert haben, auf reelle Zahlen übertragen, die eine unendliche Anzahl von Dezimalstellen hinter dem Komma besitzen können.
Zunächst einmal ist klar, dass sich der Begriff unmittelbar auf reelle Zahlen übertragen lässt, die nur endlich viele Dezimalstellen hinter dem Komma haben. Das Dezimalkomma spielt keine Rolle - wichtig ist, dass sich die Zahl als endliche Zeichenkette darstellen lässt, die von Programmen ggf. ausgegeben werden kann.
Wie sieht es nun aus, wenn unendlich viele Dezimalstellen möglich sind, so wie bei unserem Eingangsbeispiel, der Zahl \( \pi \) ?
Zunächst einmal spielt das Dezimalkomma wieder keine Rolle, d.h. wir lassen es einfach weg und betrachten die Zahl einfach als unendlich lange Zeichenkette, wobei wir die Zahl als Binärstring schreiben wollen (d.h. in der Form "1001101..."). Bei dieser Zeichenkette (nennen wir sie \(Z\)) können wir nun vorne anfangen, die ersten \(n\) Zeichen betrachten und untersuchen, welche Komplexität diese Zeichenkette (nennen wir sie \(Z_n\) ) besitzt.
Nun wird die Komplexität der einzelnen Zeichenketten \(Z_n\) mit wachsender Länge der Zeichenkette sicher schwanken. Wenn die gesamte unendlich lange Zeichenkette \(Z\) jedoch zufällig genannt werden soll, so erwarten wir, dass die Komplexität der Binär-Zeichenkette aus den ersten \(n\) Zeichen ungefähr gleich der Länge dieser Zeichenkette (also gleich \(n\)) ist.
Wir wollen die Komplexität der Binär-Zeichenketten \(Z_n\) mit \( H(Z_n) \) bezeichnen. Für eine zufällige unendlich lange Zeichenkette \(Z\) erwarten wir also, dass \( H(Z_n) \) ungefähr gleich \(n\) ist: \( H(Z_n) \approx n \).
Dieses ungefähr kann man präzisieren. Sicher wird aufgrund der Schwankung in der Komplexität der einzelnen Teilzeichenketten \(Z_n\) bei mancher Zeichenkette auch mal eine deutliche Abweichung der Komplexität von \(n\) vorkommen – die Komplexität kann gelegentlich deutlich kleiner als \(n\) sein, d.h. die Teilzeichenkette ist etwas weniger zufällig. Wir verlangen nun aber, dass diese Abweichung nicht beliebig groß werden darf. Es muss eine obere Grenze für die Abweichung der Komplexität von \(n\) geben. Präzise ausgedrückt bedeutet das:
Es ist interessant, dass bei den unendlich langen Zeichenketten der Begriff Zufälligkeit durch diese Festlegung ohne jede Unschärfe definiert ist. Bei den endlichen Zeichenketten gab es noch eine gewisse Unschärfe, denn man musste sagen, wie weit die Komplexität denn unterhalb der Bitlänge der Zeichenkette liegen darf, damit die Zeichenkette noch als zufällig angesehen werden kann. Bei den unendlich langen Zeichenketten fällt dagegen die maximale Abweichung \(c\) nicht mehr ins Gewicht, da \(n\) gegen Unendlich geht. Deshalb ist es im Grenzfall unendlich langer Zeichenketten egal, wie groß die maximale Abweichung \(c\) ist. Sie muss nur endlich sein und darf nicht mit der Zeichenkettenlänge \(n\) anwachsen.
Wir sind nun gerüstet, um uns im folgenden Kapitel einer naheliegenden Frage zuzuwenden: Ist es möglich, eine Zufallszahl mathematisch zu konstruieren, ohne dass diese Konstruktionsvorschrift eine Komprimierung der Zahl zulässt? Wir dürfen gespannt sein, ob das möglich ist.
© Jörg Resag, www.joerg-resag.de
last modified on 01 March 2023