Kapitel 5
Ungelöste Rätsel

1    Die Komplexität von Problemen (ist P = NP ?)

Millennium Prize Problems
Entscheidungsprobleme, Problemklassen und Instanzen
Die Laufzeit von Algorithmen
Unentscheidbare Probleme
Das schwierigste entscheidbare Problem
Das Beweisbarkeitsproblem der Presburger-Arithmetik
Die Problemklasse EXPTIME
Die Problemklasse P
Die Problemklasse NP
Nicht-deterministische Algorithmen
Die Problemklasse co-NP
NP-vollständige Probleme: ist P = NP ?
Wie könnte man die P = NP -Frage lösen?
Orakelmaschinen
Die Suche nach brauchbaren Beweistechniken

Millennium Prize Problems

Gödels Satz zeigt, dass es in jedem hinreichend mächtigen formalen System Aussagen gibt, die sich aus den Axiomen des Systems weder beweisen noch widerlegen lassen. Wir wollen uns daher in Kapitel 5 einige der bekanntesten Aussagen der Mathematik ansehen, bei denen bisher weder ein Beweis noch eine Widerlegung gelungen ist. Dies könnte natürlich daran liegen, dass bisher einfach noch niemand die richtige Beweisidee hatte. Jedes der offenen Rätsel könnte aber auch ein Beispiel für die Gültigkeit von Gödels Unvollständigkeitssatz sein. Alle Beweis- und Widerlegungsversuche wären bei einem solchen Problem vergeblich – allerdings sollte man dann wenigstens beweisen können, dass das Problem tatsächlich unabhängig von den üblichen Axiomen der Mathematik (z.B. den Zermelo-Fränkel-Axiomen ZFC der Mengenlehre) ist. Die Kontinuumshypothese hat gezeigt, dass das möglich ist. Dann müsste man im nächsten Schritt darüber nachdenken, was eine solche Unabhängigkeit für die mathematische Begriffswelt bedeutet.

Im vorliegenden Unterkapitel 5.1 wollen wir uns die Komplexität von mathematischen Problemen ansehen. Unter Komplexität verstehen wir dabei den Rechenaufwand, der zur Lösung des Problems notwendig ist. Einfache Probleme lassen sich mit geeigneten Algorithmen auf Computern sehr schnell lösen. Schwierige Probleme werden dagegen mehr Rechenaufwand erfordern. Dabei werden wir auf eine große Klasse von Problemen stoßen, bei denen unklar ist, ob sie schwierig sind oder nicht. Klar ist nur, dass sich ein Lösungsvorschlag (ein sogenanntes Zertifikat) bei dieser Problemklasse leicht überprüfen lässt. Aber lässt sich ein solcher Vorschlag auch leicht errechnen, oder muss man ihn mit viel Glück erraten? Ist Rateglück bei diesen Problemen entbehrlich? Dies ist eines der großen ungelösten Rätsel der Mathematik und Informatik. Die Kurzform für dieses Rätsel lautet:

• P = NP ?

Der erste, der dieses Rätsel löst, hat Anspruch auf ein ausgesetztes Preisgeld von einer Millionen US-Dollar, denn das P=NP -Problem ist eines der sieben Millennium Prize Problems, auf deren Lösung im Jahr 2000 in Gedenken an Hilberts berühmten Vortrag ein Jahrhundert zuvor insgesamt sieben Millionen US-Dollar ausgesetzt wurden (siehe The Millennium Prize Problems und P vs NP Problem).

Entscheidungsprobleme, Problemklassen und Instanzen

Motiviert durch die Aussicht auf eine Million Dollar wollen wir versuchen, zu verstehen, was mit P=NP gemeint ist. Dabei müssen wir zunächst genauer festlegen, was wir unter einem Problem verstehen wollen und wie die Komplexität eines solchen Problems definiert ist.

Als ersten Schritt wollen wir eine Vereinfachung vornehmen, um Probleme gut miteinander vergleichen zu können: Wir wollen uns auf sogenannte Entscheidungsprobleme beschränken. Hier sind einige Beispiele für Entscheidungsprobleme:

1. Ist eine vorgegebene natürliche Zahl die Summe von zwei Quadratzahlen?

2. Kann man eine vorgegebene natürliche Zahl ohne Rest durch irgendeine andere natürliche Zahl teilen?

3. Gibt es in einer vorgegebenen endlichen Menge ganzer (positiver sowie negativer) Zahlen eine Teilmenge, deren Zahlen sich zu Null addieren? (das Teilsummenproblem)

4. Gibt es in einer vorgegebenen Schachstellung eine Gewinnzug?

5. Ist eine vorgegebene wohlgeformte Aussage der Peano-Arithmetik aus den Peano-Axiomen ableitbar?

Entscheidungsprobleme sind also derart, dass als Antwort nur JA und NEIN möglich sind.

Weiter sehen wir, dass jedes dieser Probleme eigentlich eine ganze Problemklasse darstellt, zu der es viele verschiedene Probleminstanzen gibt. So wird durch die Frage "Ist eine vorgegebene natürliche Zahl die Summe von zwei Quadratzahlen?" die Problemklasse festgelegt, und durch die Vorgabe einer bestimmten natürlichen Zahl erhält man eine bestimmte Instanz dieser Problemklasse. Eine solche Instanz wäre beispielsweise die Frage "Ist 25 die Summe von zwei Quadratzahlen?" Die Antwort wäre in diesem Fall JA, denn \( 25 = 3^2 + 4^2 \).

Die Instanzen eines Problems kann man allgemein durch einen String (Zeichenkette) darstellen, nachdem man irgendeine Notation festgelegt hat. So ist dieser Probleminstanz-String im ersten und zweiten obigen Beispiel einfach die vorgegebene natürliche Zahl. Im dritten Beispiel gibt der String die vorgegebene Menge ganzer Zahlen an. Im vierten Beispiel enthält der String die Positionen der einzelnen Schachfiguren auf dem Schachbrett, und im fünften Beispiel ist der String gleich der vorgegebenen wohlgeformten Aussage.

In der Mathematik kann man den recht abstrakten Standpunkt einnehmen, dass ein Entscheidungsproblem vollständig durch eine Menge von Probleminstanz-Strings definiert wird, die man auch als eine formale Sprache ansehen kann (die Strings der Menge werden auch oft als Wörter dieser Sprache bezeichnet). Für alle Strings, die sich in der Menge befinden, besitzt das Entscheidungsproblem eine positive Antwort (so ist diese Menge definiert). So ist im zweiten Beispiel diese Menge gegeben durch alle Strings, die teilbaren natürlichen Zahlen entsprechen. In vielen praxisnahen Fällen sind die String jedoch recht groß (sie könnten z.B. den Flugplan einer Fluggesellschaft enthalten), und man stellt sie sich daher oft besser als Datei und nicht als Wort vor.

Man kann sich nun die Frage stellen, ob man aufgrund der Beschränkung auf Entscheidungsprobleme nicht sehr viele andere interessante Probleme vernachlässigt. Betrachten wir als Beispiel das folgende Problem:

• Finde den kleinsten Teiler einer Zahl. Genauer: finde die kleinste natürliche Zahl, durch die sich eine vorgegebene natürlichen Zahl ohne Rest teilen lässt.

Die Antwort auf dieses Problem ist nicht JA oder NEIN, sondern ein String, der die gesuchte Zahl darstellt, bzw. ein leerer String, wenn es keine solche Zahl gibt.

Wir können nun dieses Problem etwas umformulieren. Dazu legen wir fest, dass wie Zahlen hier als Binärstring darstellen wollen. Der String "1101" entspricht also der Zahl 8 + 4 + 1 = 13. Das umformulierte Problem lautet nun:

• Vorgegeben sei eine natürliche Zahl \(n\) und eine weitere natürliche Zahl \(k\). Ist das \(k\)-te Bit des kleinsten Teilers von \(n\) gleich 1?

Wenn wir nun \(k\) von 1 an bis zur Bitlänge des gesuchten Teilers durchlaufen lassen, so können wir alle Binärstellen der gesuchten Zahl ermitteln. Statt einem Problem, in dem ein Ausgabestring gesucht wird, haben wir nun mehrere Entscheidungsprobleme zu lösen, und zwar für jedes Bit des Ausgabestrings eines. Die Suche nach einem Ausgabestring lässt sich also auf mehrere Entscheidungsprobleme zurückführen. Analog könnte man auch die Suche nach dem besten Zug in einer Schachpartie auf mehrere Entscheidungsprobleme zurückführen: Gewinnt dieser Zug, oder dieser, oder dieser, oder .... ? Die Einschränkung auf Entscheidungsprobleme ist also nicht so gravierend, wie man zunächst vielleicht annehmen könnte.

Die Laufzeit von Algorithmen

Nun wissen wir also, was ein Entscheidungsproblem ist. Was uns noch fehlt, ist ein Maß für seine Komplexität, also für den Lösungsaufwand. Wie aufwendig ist es, bei einer gegebenen Probleminstanz herauszufinden, ob die Antwort JA oder NEIN lautet, ob also der Probleminstanz-String zur JA-Menge dazugehört oder nicht?

Um die Antwort JA oder NEIN für eine Probleminstanz zu ermitteln, benötigen wir irgendein Verfahren, d.h. einen Algorithmus, der auf irgendeinem Computer laufen soll. Beispielsweise könnten wir als Computer eine Turingmaschine wählen (siehe Kapitel 2.3). Aber auch ein gewöhnlicher PC und ein Algorithmus, z.B. geschrieben in der Programmiersprache C, erfüllen den Zweck, solange der Arbeitsspeicher (RAM) nur groß genug ist (wir erinnern uns: der Arbeitsspeicher einer Turingmaschine, also das Band, ist per Definition unendlich groß). Wir legen uns also auf irgendeinen Computer und eine Programmiersprache fest. Ein Algorithmus zur Lösung einer bestimmten Problemklasse ist dann ein entsprechendes Computerprogramm, das einen zur Problemklasse passenden Probleminstanz-String einliest (z.B. eine natürliche Zahl oder eine Schachstellung) und irgendwann JA oder NEIN ausgibt. Als Maß für den Rechenaufwand zur Problemlösung wählen wir die Zahl der elementaren Rechenschritte, die das Computerprogramm dazu benötigt. Wir wollen diese Anzahl Rechenschritte auch als Laufzeit bezeichnen, wobei die wirkliche Zeit bis zur Problemlösung natürlich davon abhängt, wie lange der Computer für einen elementaren Rechenschritt benötigt.

Natürlich hängt die Laufzeit einerseits von der Problemklasse und dem gewählten Algorithmus ab (es gibt sicher effiziente und weniger effiziente Algorithmen). Andererseits wird die Laufzeit auch von der Größe der jeweiligen Probleminstanz abhängen, also von der Bitlänge des jeweiligen Probleminstanz-Strings, den der Algorithmus als Vorgabe einliest. Bei einer großen Zahl wird die Frage, ob diese ohne Rest teilbar ist, sicher schwieriger zu beantworten sein als bei einer kleinen Zahl.

Nun interessieren wir uns nicht für die spezielle Laufzeit eines Algorithmus bei einer bestimmten Probleminstanz. Wir wollen uns vielmehr für den schlimmsten Fall interessieren: Wie lang ist die längste Laufzeit, die ein gegebener Problemlösungs-Algorithmus braucht, wenn wir alle möglichen Probleminstanz-Strings mit \(n\) Bit Länge ausprobieren? Wie lang braucht also ein Algorithmus zu einer bestimmten Problemklasse, um die schwierigste Probleminstanz einer vorgegebenen Problemgröße zu knacken? Halten wir fest:

• Laufzeit:
  Die Laufzeit \(l_A(n)\) eines Algorithmus \(A\) auf Inputs der Bitlänge \(n\) ist die maximale Anzahl elementarer Rechenoperationen, die der Algorithmus \(A\) ausführt, wenn er mit Probleminstanz-Strings der Maximallänge \(n\) Bit als Input aufgerufen wird.

Es geht also um ein Worst-Case-Szenario: wie lange braucht der Algorithmus bei Probleminstanzen bis zu einer bestimmten Größe im schlimmsten Fall? Dabei wollen wir uns im Folgenden anschauen, wie schnell diese maximale Laufzeit anwächst, wenn wir zu immer größeren Probleminstanzen übergehen. Steigt diese Laufzeit sehr schnell an, so werden bereits relativ kleine Probleminstanzen nicht mehr in der Praxis entscheidbar sein. Der Computer wird uns dann beispielsweise die Frage, ob eine Zahl teilbar ist, dann schon bei etwas größeren Zahlen möglicherweise nicht mehr beantworten können.

Unentscheidbare Probleme

In den vorherigen Kapiteln dieses Buches haben wir die Frage nach der praktischen Berechenbarkeit von Problemen vollkommen ignoriert. Wir haben uns lediglich die Frage gestellt, wann ein Problem überhaupt prinzipiell durch Algorithmen lösbar ist. Auf diese Weise haben wir versucht, die Probleme, bei denen wenigstens im Prinzip Hoffnung auf Berechenbarkeit besteht, von den absolut hoffnungslosen Fällen zu trennen. Tatsächlich gibt es diese absolut hoffnungslosen Fälle! Es gibt Problemklassen, die auch in beliebig vielen Rechenschritten mit keinem noch so raffinierten Algorithmus für alle Probleminstanzen zu knacken sind. Das berühmteste Beispiel dafür ist Turings Halteproblem (siehe Kapitel 2.3). Wir haben solche Entscheidungsprobleme als nicht-entscheidbaren Probleme bezeichnet. Sie bilden sicher die schwierigste Problemklasse.

Das schwierigste entscheidbare Problem

Wenden wir uns nun den entscheidbaren Problemen zu. Welches sind die schwierigsten entscheidbaren Probleme?

In Kapitel 3.4 ist uns ein solches Problem bereits begegnet. Erinnern wir uns: Wir haben zunächst einen Computer und eine Programmiersprache festgelegt und dann einen immer länger werdenden Zufalls-Binärstring erzeugt in der Hoffnung, auf diese Weise ein anhaltendes Programm zu generieren. Zunächst würfeln wir dabei ein erstes Bit und fragen, ob dieser 1-Bit-String ein anhaltendes Programm ist. Falls nicht, würfeln wir ein zweites Bit dazu und fragen erneut, ob dieser 2-Bit-String ein anhaltendes Programm ist. Und so machen wir ggf. immer weiter, bis wir auf ein anhaltendes Programm stoßen. Dabei kann es natürlich auch passieren, dass nie ein anhaltendes Programm ensteht, selbst wenn wir immer weitere Bits hinzufügen. Es gibt also eine gewisse Wahrscheinlichkeit dafür, ein anhaltendes Programm auf diese Weise zufällig zu generieren. Diese Wahrscheinlichkeit haben wir als \(\Omega\) bezeichnet und ihr den Namen Chaitins Zahl gegeben. Diese Zahl hängt natürlich vom gewählten Computer und von der gewählten Programmiersprache ab.

Chaitins Zahl hat nun eine interessante Eigenschaft:
Man kann aus den ersten \(n\) Bit von \(\Omega\) (geschrieben als Binärzahl) das Halteproblem für alle Programme mit maximal \(n\) Bit Länge lösen.

Den Algorithmus dazu kann man in Kapitel 3.4 im Detail nachlesen. Der Kern des Algorithmus besteht darin, die maximale Anzahl elementarer Rechenschritte \(s\) zu ermitteln, innerhalb derer jedes Programm mit maximal \(n\) Bit Programmlänge anhält. Dazu muss man für ein gegebenes Versuchs-\(s\) alle Programme mit maximal \(s\) Bit Programmlänge bis zu \(s\) Schritten laufen lassen, die bis dahin anhaltenden Programme ermitteln und mit dieser Information eine bestimmte Bedingung überprüfen, die einen Vergleich mit den ersten \(n\) Bit von Ω beinhaltet. Man vergrößert nun \(s\) schrittweise so lange, bis die Bedingung erfüllt ist – damit ist das gesuchte \(s\) gefunden. Der Rechenaufwand, um dies zu tun, wächst mit anwachsendem \(n\) schneller als jede berechenbare Funktion von \(n\) an! Das ist kaum noch zu überbieten.

Das Beweisbarkeitsproblem der Presburger-Arithmetik

Ein etwas einfacheres, aber immer noch sehr schwieriges entscheidbares Problem haben wir am Ende von Kapitel 2.4 kennengelernt: Ist ein vorgegebener wohlgeformter Ausdruck der Presburger-Arithmetik beweisbar?

Zur Erinnerung: Die Presburger-Arithmetik entspricht der Peano-Arithmetik mit einer wichtigen Einschränkung: die beiden Axiome zur Festlegung der Multiplikation wurden weggelassen. Die Presburger-Arithmetik beschäftigt sich also mit natürlichen Zahlen und deren Addition, nicht aber mit deren Multiplikation. Daher ist z.B. der Begriff Primzahl in der Presburger Arithmetik nicht definierbar.

Die Presburger-Arithmetik ist nicht in der Lage, alle berechenbaren Funktionen der natürlichen Zahlen darzustellen, d.h. das Representation Theorem ist in ihr nicht gültig. Daher ist Gödels Unvollständigkeitssatz hier nicht anwendbar, und es gelang im Jahr 1929 dem Mathematiker Mojzesz Presburger tatsächlich, zu beweisen, dass die Presburger-Arithmetik vollständig und widerspruchsfrei ist. Jede wohlgeformte Aussage der Presburger-Arithmetik lässt sich in endlich vielen Schritten entweder beweisen oder widerlegen. Die Frage nach der Beweisbarkeit eines vorgegebenen Ausdrucks ist in diesem formalen System also entscheidbar.

Allerdings kann es extrem schwierig sein, die Lösung für etwas längere Ausdrücke allgemein zu finden, denn im Jahr 1974 gelang es Michael J.Fischer und Michael O.Rabin, folgendes zu beweisen:

• Jeder allgemeine Algorithmus, der für einen beliebigen geschlossenen (d.h. ohne freie Variable) Ausdruck \(A\) der Länge \(n\) entscheiden kann, ob er aus den Axiomen der Presburger-Arithmetik ableitbar ist oder nicht, benötigt dafür mindestens \( 2^{2^{C \cdot n}} \) Schritte (dabei ist \(C\) ist eine Konstante).

Der Rechenaufwand steigt also mindestens doppelt exponentiell mit der Länge des zu untersuchenden Ausdrucks. Bereits für etwas längere Ausdrücke kann dies zu astronomisch langen Laufzeiten führen. Das Beweisbarkeitsproblem der Presburger-Arithmetik ist also zumindest für bestimmte Worst-Case-Ausdrücke extrem schwierig, wenn man einen allgemeinen Entscheidungsalgorithmus einsetzen will!

Die Problemklasse EXPTIME

In den obigen Beispielen gab es jeweils eine untere Grenze für die Laufzeit, die sehr schnell mit \(n\) anwuchs. Bei der Ermittelung der anhaltenden Programme mit maximal \(n\) Bit Länge aus den ersten \(n\) Bit von \(\Omega\) wuchs die Laufzeit schneller als jede berechenbare Funktion mit \(n\) an. Im Fall der Presburger-Arithmetik wuchs die Laufzeit eines allgemeinen Algorithmus, der die Beweisbarkeit eines beliebigen wohlgeformten Ausdrucks mit \(n\) Bit Länge entscheidet, mindestens doppelt exponentiell mit \(n\) an.

Es wäre sicher wünschenswert, statt einer unteren eine obere Grenze für die Laufzeit angeben zu können – dann weiß man wenigstens: schlimmer kann es nicht mehr kommen. Eine sehr allgemeine Problemklasse, bei der das möglich ist, ist die Problemklasse EXPTIME. Für jede Problemklasse aus EXPTIME kann man einen Algorithmus \(A\) finden, so dass die Laufzeit \(l_A(n)\) kleiner als \(2^{p(n)}\) ist. Dabei ist \(p(n)\) irgendein Polynom, z.B. \(p(n) = 5 \cdot n \) oder \( p(n) = 2 \cdot n^2 \). Die Laufzeit wächst also nicht schneller als exponentiell mit wachsender Probleminstanzgröße \(n\) an! Damit sind extreme Katastrophen wie im Fall der Presburger-Arithmetik ausgeschlossen.

Ein Beispiel für ein EXPTIME-Entscheidungsproblem ist das folgende:

• Kann in einem Go-Spiel (oder Schachspiel), das auf einem \(n \times n\) -Brett gespielt wird, der erste Spieler einen Gewinn erzwingen?

Dabei stellt man sich vor, dass man diese Frage für verschiedene Brettgrößen stellt. Dies ist erforderlich, da man ja den Anstieg des Rechenaufwands mit wachsender Problemgrößen untersuchen muss.

In dem dargestellten Beispiel wächst die Laufzeit zur Problemlösung tatsächlich etwa exponentiell mit der Brettgröße. Der Grund dafür ist, dass ein Spiel zwischen zwei perfekten Spielern sehr lang sein kann, und dass die Spieldauer und die Zahl der möglichen Spielabläufe mit steigender Brettgröße sehr schnell anwachsen.

Die Problemklasse P

Nun ist ein exponentielles Wachstum der Laufzeit mit steigender Problemgröße \(n\) immer noch sehr ungünstig. Allerdings kann man auch Glück haben, denn das exponentielle Wachstum ist ja nur der schlimmste Fall in der Problemklasse EXPTIME. Vielleicht enthält diese Problemklasse eine Untermenge von Problemen, bei denen die Laufzeit wesentlich langsamer als exponentiell wächst?

Tatsächlich gibt es solche Probleme. Man kann beispielsweise die Klasse aller Probleme definieren, bei denen man einen Algorithmus \(A\) finden kann, so dass die Laufzeit \(l_A(n)\) kleiner als \(p(n)\) ist. Dabei ist \(p(n)\) wieder irgendein Polynom. Die Laufzeit wächst also nicht schneller als polynomial mit wachsender Probleminstanzgröße \(n\) an! Wir bezeichnen diese Problemklasse mit dem Buchstaben P.

Hier sind einige Beispiel für Probleme in \(P\):

• Suchproblem:
  Gegeben ist eine Datei, die \(n+1\) Zahlen enthält. Ist die erste Zahl gleich einer der anderen \(n\) Zahlen?

• Matrix-Invertierbarkeit:
  Ist eine gegebene \(n \times n\) -Matrix invertierbar?

• Sortierproblem:
  Ist eine gegebene Liste aus \(n\) Zahlen der Größe nach sortiert?

• Primzahlproblem:
  Ist eine vorgegebene Zahl eine Primzahl? Dass dieses Problem tatsächlich in P ist, wurde im Jahr 2002 von Manindra Agarwal, Nitin Saxena und Neeraj Kayal bewiesen (siehe AKS-Primzahltest).

Die ersten drei Probleme haben Laufzeiten, die nur relativ langsam (z.B. linear oder quadratisch) mit der Probleminstanzgröße \(n\) wachsen. Sie lassen sich deshalb auch für große Probleminstanzen auf Computern gut lösen. Beim Primzahlproblem dagegen weiß man noch nicht, wie effektiv der polynomiale Algorithmus in der Praxis ist. Es gibt aber sehr effektive andere Algorithmen für das Primzahlproblem, bei denen eine polynomielle Laufzeit allerdings nicht für jede beliebige Zahl garantiert werden kann. Man sieht also: In der Praxis reicht das Kriterium Problem ist in P nicht aus, um die Brauchbarkeit von Algorithmen zu beurteilen. Auch statistische Überlegungen und praktische Erfahrungen sind notwendig.

Die Problemklasse NP

Betrachten wir nun eine scheinbar ganz andere Problemklasse von Entscheidungsproblemen. Hier sind einige Beispiele daraus:

• Subset Sum Problem (Teilmengen-Summenproblem):
  Gibt es in einer vorgegebenen endlichen Menge ganzer Zahlen eine Teilmenge, deren Zahlen sich zu Null addieren? Für die Menge \( \{ -7, -3, -2, 5, 8 \} \) lautet die Antwort beispielsweise JA, denn die Zahlen der Teilmenge \( \{ -3, -2, 5 \} \) summieren sich zu Null auf.

• Knapsack Problem (Rucksackproblem):
  Wir betrachten eine Menge von Gegenständen, denen jeweils ein bestimmtes Gewicht und ein bestimmter Wert zugeordnet ist. Nun wollen wir mehrere dieser Gegenstände in einen Rucksack packen, und zwar so, dass das Gesamtgewicht eine bestimmte vorgegebene Maximalgrenze nicht übersteigt (damit wir den Rucksack noch tragen können). Die Frage lautet nun: Schaffen wir es, Gegenstände im Wert von mindestens – sagen wir 1000 – Euro einzupacken, ohne dass der Rucksack zu schwer wird?

• Boolean satisfiability problem (Boolsches Erfüllbarkeitsproblem):
  Wir betrachten einen Boolschen Ausdruck, der nur die logischen Zeichen \( \land \) (und), \( \lor \) (oder) und \( \neg \) (nicht) sowie Variablen und Klammern enthalten darf (siehe auch Kapitel 4.4). Die Variablen können nur die Werte wahr und falsch annehmen. Ein Beispiel wäre der Ausdruck \[ (a \land (b \lor c)) \land \neg ((d \lor e) \land f) \] Die Frage lautet nun: Kann man die Variablenwerte so wählen, dass der gesamte Boolsche Ausdruck den Wert wahr annimmt?

• Teilerproblem:
  Kann man eine vorgegebene natürliche Zahl ohne Rest durch irgendeine andere natürliche Zahl teilen?

Diese Probleme weisen eine interessante Gemeinsamkeit auf: Angenommen, jemand behauptet, die Antwort auf die Entscheidungsfrage bei einer bestimmten Probleminstanz sei JA, und er liefert gleich auch noch eine Begründung mit. Beispielsweise könnte er beim Teilmengen-Summenproblem behaupten:
Für die Menge \( \{ -7, -3, -2, 5, 8 \} \) lautet die Antwort JA, denn die Zahlen der Teilmenge \( \{-3, -2, 5 \} \) summieren sich zu Null auf. Dann ist es kein Problem, die Begründung für seine Antwort zu überprüfen.

Dies war anders beim Go-Spiel (siehe weiter oben). Die Frage dort lautete:
Kann in einem Go-Spiel (oder Schachspiel), das auf einem \(n \times n\) -Brett gespielt wird, der erste Spieler einen Gewinn erzwingen?
Wenn jemand hier seine JA-Antwort begründen will, so muss er eine gigantische Liste aller möglichen Spielabläufe als Begründung hinzufügen. Diese Liste zu überprüfen wäre extrem aufwendig, besonders wenn das Go-Brett groß ist.

Wir wollen nun etwas präziser formulieren, was es bedeutet, dass sich eine Begründung für eine JA-Antwort leicht überprüfen lässt:

• Lautet für eine gegebene Probleminstanz (charakterisiert durch einen Probleminstanz-String \(w\) ) die Antwort auf die Entscheidungsfrage JA, so gibt es eine Begründung (auch Zertifikat genannt, dargestellt durch einen Begründungsstring \(C\) ), mit deren Hilfe sich die Korrektheit der JA-Antwort überprüfen lässt. Die Umkehrung gilt ebenfalls.

• Es gibt einen Prüfalgorithmus \(A(w,C)\), der jeden Probleminstanz-String \(w\) und jeden potentiellen Begründungsstring \(C\) als Input akzeptiert und der in einer Laufzeit, die höchstens polynomial mit der Bitlänge des Probleminstanz-Strings \(w\) anwächst, überprüft, ob der Begründungsstring \(C\) ein Beweis für die Korrektheit der JA-Antwort ist. Es gibt also ein Polynom \(p(n)\) (z.B. \(p(n) = n^2\), wobei \(n\) die Bitlänge des Probleminstanzstrings \(w\) ist), so dass in höchstens \(p(n)\) Schritten der Algorithmus \(A(w,C)\) eine JA/NEIN-Antwort liefert.

• Die beiden obigen Punkte zusammen bedeuten:
  \(w\) ist eine JA-Probleminstanz (d.h. die Antwort auf die Entscheidungsfrage für die Probleminstanz \(w\) lautet JA) genau dann, wenn es einen Begründungsstring \(C\) gibt, so dass der Prüfalgorithmus \(A(w,C)\) in polynomialer Zeit mit Ja antwortet.

Ein Beispiel: Beim Teilerproblem ist \(w\) die natürliche Zahl, von der man wissen möchte, ob sie ohne Rest durch irgendeine andere natürliche Zahl teilbar ist. Schlägt jemand einen solchen Teiler \(C\) vor, so lässt sich sehr leicht überprüfen, ob dieser Teiler auch ein Teiler ist. Der Prüfalgorithmus \(A(w,C)\) lautet nämlich einfach: Teile \(w\) durch \(C\) und sieh nach, ob ein Rest übrig bleibt. Den Teiler \(C\) zu finden ist dabei das eigentliche Problem. Hat man ihn erst einmal, so ist der Rest einfach.

Begründungen lassen sich also für diese Problemklasse leicht verifizieren, aber nicht unbedingt leicht finden. Ob sie leicht zu finden sind, ist das zentrale Thema dieses Kapitels. Wer die Antwort kennt und sie beweisen kann, erhält die oben versprochene Million US-Dollar.

Die Problemklasse aller Entscheidungsprobleme, die die obigen Eigenschaften haben, bezeichnet man als die Klasse der nichtdeterministisch-polynomialen Entscheidungsprobleme. Man kürzt die Menge dieser Probleme mit NP ab. Dabei steht NP für Nichtdeterministisch Polynomiell (und nicht etwa für nicht-polynomial). Woher diese Bezeichnung kommt, schauen wir uns im Folgenden nun genauer an.

Nicht-deterministische Algorithmen

Man kann die Problemklasse NP auch etwas anders als oben definieren, wobei die beiden Definitionen gleichwertig zueinander sind. Dazu benötigt man den Begriff der nicht-deterministischen Turingmaschine.

Deterministische (also normale) Turingmaschinen haben wir bereits kennengelernt (z.B. in Kapitel 1 und Kapitel 2.3). Sie entsprechen heutigen Computern, die ein festes Programm ausführen. Eine Turingmaschine weiß in jedem Arbeitsschritt genau, was sie zu tun hat. Das Turing-Programm gibt den nächsten Schritt in Abhängigkeit vom inneren Zustand und dem gerade gelesenen Zeichen eindeutig vor.

Bei einer nicht-deterministischen Turingmaschine ist das anders. Hier kann das Programm mehrere Möglichkeiten vorsehen, was bei einem gegebenen inneren Zustand und einem gegebenen eingelesenen Zeichen als nächstes gemacht werden soll, z.B. gehe nach rechts, oder schreibe eine 1 auf das Band, oder schreibe ein Blank auf das Band. Die Maschine entscheidet zufällig, welche der Möglichkeiten sie wählt. Auf diese Weise gibt es für ein Programm sehr viele mögliche Programmabläufe, je nachdem, für welche Möglichkeit sich die Maschine jeweils entscheidet. Eine nicht-deterministische Turingmaschine entspricht damit einem Computer, der während des Programmlaufs immer wieder Zufallszahlen abfragt und abhängig davon den weiteren Programmlauf wählt. Diese Zufallszahlen können ihm z.B. von einem eingebauten radioaktiven Zufallsgenerator vorgegeben werden, oder er kann sie auch von einem externen Bediener als Eingaben abfragen.

Betrachten wir nun den folgenden nicht-deterministischen Algorithmus zur Lösung eines NP-Problems:

1. Lese die zu untersuchende Probleminstanz \(w\) (z.B. im Binärformat) ein.

2. Setze für den Begründungsstring \(C\) einen leeren String ein: \(C = ""\)

3. Schleifenbeginn

4. Wähle eine der folgenden Möglichkeiten (dies ist der Rateschritt):
   • Füge den String \(0\) rechts an \(C\) an: \( C \rightarrow C0 \)
   • Füge den String \(1\) rechts an \(C\) an: \( C \rightarrow C1 \)

5. Lasse den Prüfalgorithmus \(A(w,C)\) laufen, bis er JA oder NEIN ausgibt.
   Falls er JA ausgibt, gib ebenfalls JA aus und halte an.
   Falls er NEIN ausgibt, gehe wieder zum Schleifenbeginn.

Was tut dieser Algorithmus? Er erzeugt schrittweise (Bit für Bit) einen Begründungsstring \(C\) (in Binärdarstellung) und testet in jedem Schritt, ob der so erratene String \(C\) ein Begründungsstring für eine JA-Antwort auf das Entscheidungsproblem zur Instanz \(w\) ist. Dabei gibt es für jeden möglichen Begründungsstring \(C\) einen möglichen Programmlauf. Die einzelnen Programmläufe kann man sich dabei wie in einem Baum angeordnet vorstellen:
Zuerst beginnt ein Programmlauf mit einem leeren String. Im nächsten Schleifendurchlauf entstehen aus dem einen Programmlauf zwei parallele Läufe, die auf zwei verschiedenen Rechnern mit gleicher Geschwindigkeit ablaufen. Ein Programmlauf untersucht den Fall \(C = 0\), der andere den Fall \(C = 1\). Im nächsten Schleifendurchlauf erfolgt eine analoge Verzweigung auf vier parallele Programmläufe usw.. Man sagt auch, eine nicht-deterministische Turingmaschine arbeitet parallel einen ganzen Berechnungs-Baum ab, während eine deterministische Turingmaschine nur einen einzigen Berechnungspfad verfolgt.

Wenn die Antwort auf das Entscheidungsproblem JA ist, so wird der nichtdeterministische Algorithmus (d.h. einer der möglichen Programmläufe im Baum) irgendwann anhalten und JA ausgeben, denn irgendein Programmlauf muss zu einem gültigen Begründungsstring C gehören. In diesem Moment stoppen wir sofort alle anderen parallel laufenden Programmläufe und halten die Zahl der Schritte fest, die der erfolgreiche Programmlauf benötigt hat. Diese Anzahl Schritte bezeichnen wir als Laufzeit des nichtdeterministischen Algorithmus zur Lösung des Entscheidungsproblems. Man kann zeigen, dass diese Laufzeit polynomial mit der Problemgröße \(n\) zunimmt genau dann, wenn das Problem zur Klasse NP gehört. Fassen wir zusammen:

• Ein Entscheidungsproblem gehört genau dann zur Klasse NP, wenn es einen nicht-deterministischen Algorithmus gibt, bei dem mindestens einer der möglichen Programmläufe in einer Zeit JA ausgibt, die polynomial mit der Problemgröße \(n\) (also der Bitlänge des Probleminstanzstrings \(w\)) anwächst, vorausgesetzt, die Antwort auf die Probleminstanz des Entscheidungsproblems lautet JA. Lautet die Antwort NEIN, so wird über die Laufzeit eines nicht-deterministischen Algorithmus keine Aussage gemacht (er kann also z.B. ewig weiterlaufen).

Nichtdeterministische Algorithmen überprüfen in deterministischer Weise, ob eine gegebene Begründung korrekt ist. Diese Begründung (der String \(C\)) wird dabei gleichsam erraten.

Die Problemklasse co-NP

Was geschieht nun, wenn die Antwort auf ein NP-Problem NEIN ist? In diesem Fall gibt nie ein möglicher Programmlauf JA aus. Die einzige Chance, die man hat, besteht darin, dass man das Polynom kennt und damit weiß, nach wieviel Rechenschritten wenigstens ein möglicher Programmlauf JA hätte ausgeben müssen. Ist diese JA-Antwort in der Zeit bei keinem möglichen Programmlauf erfolgt, so muss die Antwort offenbar NEIN sein.

Generell weisen NP-Probleme eine merkwürdige Asymmetrie zwischen JA und NEIN auf. Die Klasse NP wird nur über das Verhalten der Algorithmen im JA-Fall definiert: Es gibt einen Begründungsstring (Zertifikat), der sich mit einem polynomialen Prüfalgorithmus testen lässt, oder gleichwerig dazu: einer der möglichen Programmabläufe des nicht-deterministischen Algorithmus gibt in polynomialer Zeit JA aus (weil er einen passenden Begründungsstring erraten hat).

Man kann nun z.B. das Teilerproblem (Kann man eine vorgegebene natürliche Zahl ohne Rest durch irgendeine andere natürliche Zahl teilen?) durch Ja-Nein-Vertauschung in das dazu spiegelbildliche (komplementäre) Primzahlproblem umwandeln (Kann man eine vorgegebene natürliche Zahl nicht ohne Rest durch irgendeine andere natürliche Zahl teilen, d.h. ist die vorgegebene Zahl eine Primzahl?). Man bezeichnet die Klasse aller Probleme, die in diesem Sinne komplementär zu NP-Problemen sind, als co-NP.

Das Teilerproblem ist in NP. Ist das Primzahlproblem, das ja nach Definition in co-NP ist, womöglich ebenfalls in NP? Man konnte im Jahr 1975 zeigen, dass das tatsächlich der Fall ist: Das Primzahlproblem und das Teilerproblem sind beide zugleich in NP und in co-NP. Sie befinden sich also in der Schnittmenge von NP und co-NP. Dabei ist es keineswegs einfach, für das Primzahlproblem zu zeigen, dass es in NP ist, denn wie soll ein Begründungsstring (Zertifikat) und der zugehörige Prüfalgorithmus aussehen? Dennoch gelang der entsprechende Beweis mit Hilfe der Zahlentheorie im Jahr 1975 (siehe V.R.Pratt: Every prime has a succinct certificate, SIAM Journal on Computing, 4(3): 214-220, 1975 sowie Wikipedia: Primality certificate). Seit 2002 weiß man sogar, dass das Primzahlproblem und damit auch das Teilerproblem nicht nur in NP, sondern zugleich in P sind (siehe oben).

Ist womöglich sogar NP = co-NP ? Gehört zu jedem NP-Problem ein komplementäres Problem, das ebenfalls in NP ist?

Schauen wir uns dazu ein weiteres NP-Beispiel an:

• Problem des Hamiltonschen Weges in einem Graphen:
  Stellen wir uns eine einfache Karte vor, auf der mehrere Städte durch Punkte dargestellt sind. Zwischen den Städten sind Straßen als gerade Linien eingezeichnet, die verschiedene Städte miteinander verbinden. Jede Stadt liegt dabei an mindestens einer Straße oder ist Endpunkt einer Straße. Nicht jede Stadt ist unbedingt mit jeder anderen durch eine Straße direkt verbunden, aber je zwei Städte sind höchstens durch eine Straße direkt miteinander verbunden. Die Straßen besitzen keine Straßenkreuzungen, d.h. man kann nur in einer Stadt die Straße wechseln.
  Wir fragen nun, ob es eine Fahrroute gibt, die in irgendeiner beliebigen Stadt beginnt, in irgendeiner anderen beliebigen Stadt endet, durch alle anderen Städte genau einmal hindurchführt und nur die eingezeichneten Straßen zwischen den Städten verwendet. Ein Handlungsreisender, der alle Städte genau einmal besuchen will, würde sich beispielsweise für einen solchen Weg interessieren. Man bezeichnet eine solche Fahrroute auch als Hamiltonschen Weg, die Karte als Graph, die Städte als Knoten und die Straßen als Kanten des Graphen.

Ein Begründungsstring (also ein Zertifikat) wäre hier einfach die Angabe einer passenden Fahrroute für den Handlungsreisenden.

Das dazu Ja-Nein-vertauschte Problem aus co-NP würde nun stattdessen danach fragen, ob die Existenz einer entsprechenden Fahrroute ausgeschlossen werden kann. Ist dieses Problem auch in NP?

Keiner kennt heute die Antwort auf diese Frage, denn niemand weiß derzeit, wie man hierfür einen Begründungsstring (also ein Zertifikat) angeben kann, das in polynomialer Zeit überprüfbar ist. Das ist bei Positivfragen einfacher: Gibt es einen Hamiltonschen Weg? Klar, hier ist einer. Aber bei Negativfragen: Gibt es keinen Hamiltonschen Weg? Keine Ahnung, ich habe zwar noch keinen gefunden, aber ....

Es ist also bis heute eine offene Frage, ob NP = co-NP ist. Es sieht eher so aus, als wäre das nicht der Fall.

Eine kleine Randbemerkung dazu (ohne Begründung, siehe auch Stephen Cook: The P versus NP Problem, Official Problem Description):

Die Aussage NP ≠ co-NP ist gleichwertig zu der Aussage, dass es keinen Beweisalgorithmus gibt, der für alle logisch richtigen Aussagen kurze (d.h. polynomial begrenzte) Beweise ermitteln kann. Zur Erinnerung (siehe Kapitel 4.4): Eine logisch richtige Aussage ist eine Aussage, die immer wahr unter allen Interpretationen ist. Man spricht auch von universell wahren Aussagen oder auch von Tautologie. Ein Beispiel ist die Aussage \( B \Rightarrow (C \Rightarrow (B \land C)) \), denn unabhängig vom Wahrheitswert von \(B\) und \(C\) hat der Gesamtausdruck nach den Wahrheitstabellen immer den Wahrheitswert wahr.

NP-vollständige Probleme: ist P = NP ?

Wir hatten etwas weiter oben die Klasse P aller Probleme definiert, bei denen man einen Lösungsalgorithmus \(A\) finden kann, so dass die Laufzeit \(l_A(n)\) kleiner als ein Polynom \(p(n)\) ist, wobei \(n\) die Bitlänge des Probleminstanz-Strings ist. P enthält also alle Entscheidungsprobleme, die in polynomialer Laufzeit durch einen deterministischen Algorithmus lösbar sind. Nun ist ein deterministischer Algorithmus einfach ein Spezialfall eines nicht-deterministischen Algorithmus, bei dem man sich eben Null mal zufällig entscheiden muss (so zumindest definiert man diese Begriffe). Alternativ kann man auch sagen, dass der Prüfalgorithmus \(A(w,C)\) eines P-Problems einfach den Begründungsstring \(C\) ignoriert, den Lösungsalgorithmus für das Problem aufruft und entsprechend JA oder NEIN ausgibt. Daher sind alle Probleme aus P auch gleichzeitig in NP, und analog auch in co-NP. Als Beispiele für solche Probleme hatten wir oben das Teilerproblem und das dazu komplementäre Primzahlproblem kennengelernt.

P ist also in der Schnittmenge von NP und co-NP enthalten. Ist P vielleicht gleich dieser Schnittmenge? Oder ist vielleicht sogar P = NP ?

Niemand kennt heute die Antwort auf diese Fragen. Insbesondere weiß niemand, ob P = NP ist:

• P = NP - Problem:
  Ist P = NP ? Das bedeutet: Kann man für jede NP-Entscheidungsprobleminstanz \(w\), bei der sich eine (erratene) Begründung \(C\) für eine JA-Antwort leicht überprüfen lässt (indem man den polynomial laufenden Prüfalgorithmus \(A(w,C)\) verwendet), auch die JA/NEIN-Antwort selber leicht (d.h. durch einen polynomial laufenden Algorithmus) finden? Lässt sich also eine Begründung \(C\) für eine JA-Antwort nicht nur polynomial testen, sondern auch polynomial finden?

Wie bereits oben erwähnt, ist die Antwort auf diese Frage eine Millionen US-Dollar wert. Es handelt sich also offenbar um eine sehr wichtige Fragestellung.

Der Grund für die Relevanz dieser Frage liegt darin, dass viele Probleme, denen man in der Praxis begegnet, zumindest verwandt mit NP-Entscheidungsproblemen sind. Beispiele dafür sind die Ermittlung optimaler Produktionspläne, günstiger Stundenpläne oder optimaler Reiserouten. Ein anderes wichtiges Beispiel ist die Zerlegung von großen natürlichen Zahlen in Primfaktoren. Die Annahme, dass diese Zerlegung schwierig, die Überprüfung einer Lösung dagegen einfach ist, liegt vielen Verschlüsselungsalgorithmen zugrunde. Sollte nun P = NP sein, so gäbe es möglicherweise einen polynomialen Algorithmus für diese Zerlegung. Die Sicherheit von Verschlüsselungsalgorithmen wäre in Frage gestellt, sollte sich ein solcher Algorithmus als praktikabel erweisen. Allerdings muss man aufpassen: Beispielsweise führt die Tatsache, dass das Primzahlproblem und damit auch das Teilerproblem in P liegen, nicht zu einem polynomiellen Algorithmus für die Primfaktorzerlegung von Zahlen.

Neben praktischen Fragestellungen ist das Problem aber auch aus theoretischer Sicht sehr interessant. Es gibt nämlich innerhalb von NP eine Unterklasse von Problemen, die man als NP-vollständige Probleme bezeichnet, und die eine wichtige Eigenschaft besitzen:

• NP-vollständige Probleme:
  Falls es für irgendein NP-vollständiges Problem einen polynomialen Lösungsalgorithmus gibt, so ist P = NP, d.h. dann gibt es für alle Probleme aus NP einen solchen Algorithmus.

Wenn man also daran glaubt, dass NP größer als P ist, dann müssen alle NP-vollständigem Probleme auf jeden Fall außerhalb von P sein. Beispielsweise kann das Primzahlproblem kein NP-vollständiges Problem sein, denn es ist in \(P\). In diesem Sinne bezeichnet man auch die NP-vollständigen Probleme als die vermutlich schwierigsten Probleme aus NP.

Man kann NP-vollständige Probleme auch noch etwas anders charakterisieren:

• NP-vollständige Probleme:
  Ein Problem U aus NP ist NP-vollständig, wenn man jedes andere Problem aus NP auf U reduzieren kann. Das bedeutet, dass es für jedes Problem L aus NP einen polynomialen Umwandlungsalgorithmus gibt, der Probleminstanzen von L in Probleminstanzen von U umwandelt, so dass beide Probleminstanzen die gleiche Lösungsantwort (JA oder NEIN) besitzen.

Alle Probleme aus NP lassen sich also in polynomialer Zeit in ein beliebiges gleichwertiges NP-vollständiges Problem umwandeln und damit auf dieses zurückführen (nicht aber umgekehrt!). Man kann sich also irgendein NP-vollständiges Problem gleichsam als Referenzproblem aussuchen. Es genügt, nur für dieses Referenzproblem nach einem polynomialen Lösungsalgorithmus zu suchen, um das P = NP-Problem zu lösen. Das hört sich zunächst einmal nicht sonderlich schwierig an.

Gibt es Beispiele für NP-vollständige Probleme? Ja, es gibt sogar sehr viele davon. Beispielsweise sind das Teilmengen-Summenproblem, das Rucksackproblem, das Boolsches Erfüllbarkeitsproblem und das Problem des Hamiltonschen Weges in einem Graphen NP-vollständig, also im Prinzip ineinander übersetzbar. Als Referenzproblem verwendet man wegen seiner Verbindung zur Logik häufig das Boolsche Erfüllbarkeitsproblem. Dieses war auch das erste Problem, dessen NP-Vollständigkeit im Jahr 1971 von Stephen Cook bewiesen wurde – ein Meilenstein der Mathematik!

Wie könnte man die P = NP -Frage lösen?

Was muss man tun, wenn man die P = NP -Frage lösen möchte? Nach dem oben gesagten genügt es, sich ein NP-vollständiges Referenzproblem auszusuchen und nach einem polynomialen Lösungsalgorithmus zu suchen bzw. zu zeigen, dass es keinen solchen Algorithmus gibt. Obwohl sich das relativ einfach anhört, ist weder das eine noch das andere bis heute gelungen. Woran kann das liegen?

Man geht heute von der Vermutung aus, dass NP größer als P ist, denn es erscheint unglaubwürdig, dass ein deterministischer Algorithmus in polynomialer Zeit ebensoviel erreichen kann wie ein nichtdeterministischer Algorithmus, den man durch extrem mächtige Raterei gleichsam aufpeppt. Also versucht man, ein Entscheidungsproblem zu finden, das nachweislich nicht in polynomialer Zeit gelöst werden kann. Man versucht, durch einen Beweis die Existenz eines entsprechenden Algorithmus auszuschließen, so wie das auch beispielsweise bei Turings Halteproblem gelungen ist (siehe Kapitel 2.3).

Leider sieht es so aus, als ob uns dafür zur Zeit wirksame Beweistechniken fehlen. Man hat es analog zu Turings Halteproblem z.B. mit Diagonalisierung versucht. Es konnte jedoch nachgewiesen werden, dass P ≠ NP damit nicht bewiesen werden kann (siehe T. Baker, J. Gill, R. Solovay: Relativizations of the P =? NP question, SIAM Journal on Computing, 4 (1975) S.431-442). Anderen Beweistechniken ist es ähnlich ergangen (z.B. Boolean circuit lower bounds). Es könnte daher sein, dass ganz neue mathematische Methoden notwendig sind, um das Problem zu knacken. Wir gehen am Schluss des Kapitels noch einmal darauf ein.

Nach Gödels Unvollständigkeitssatz wäre es sogar denkbar, dass sich die P = NP -Frage als unabhängig von den Axiomen der Mengenlehre erweist, ähnlich wie die Kontinuumshypothese (siehe Kapitel 4.3). Die heute übliche Mathematik, die ja auf diesen Axiomen beruht, wäre dann gar nicht in der Lage, das Problem zu lösen. Was das für die Mathematik und ihre Grundlagen bedeuten würde, ist aus heutiger Sicht schwer abzuschätzen. Und was würde das für die Praxis bedeuten?

Umgekehrt ist es auch interessant, sich zu überlegen, was ein Beweis für P = NP (oder für das Gegenteil) bedeuten würde:

• Beweis für P ≠ NP gelingt:
  Wenn man P ≠ NP beweisen könnte, so wäre die Situation für die Praxis ähnlich wie heute: Die in der Praxis überall auftretenden NP-vollständigen Probleme müssten im Einzelfall untersucht werden und man würde weiterhin versuchen, z.B. mit maßgeschneiderten Näherungsalgorithmen (sogenannten Heuristiken) für die Praxis brauchbare Lösungen zu finden. Außerdem ist es teilweise möglich, polynomiale Algorithmen zu finden, die für viele Probleminstanzen einer gewissen Problemsorte funktionieren, aber eben nicht bei allen.

• Nicht-konstruktiver Beweis für P = NP gelingt:
  Es könnte sein, dass man P = NP durch nicht-konstruktive Argumente beweist. Widerspruchsbeweise sind typische Beispiele für solche nicht-konstruktiven Beweise. So könnte es sein, dass man zeigt: Wenn es keinen polynomialen Algorithmus für mindestens ein NP-vollständiges Problem gibt, so entsteht ein logischer Widerspruch. Will man diesen nicht zulassen, so muss man von der Existenz eines polynomialen Algorithmus ausgehen. Den Algorithmus selber kann man allerdings nicht angeben.
  Ein solches Ergebnis würde sicher eine gewisse Ratlosigkeit hervorrufen: Was soll man damit nur anfangen? Ähnliche Erlebnisse kennt man aus der Mengenlehre (siehe Kapitel 4.2): Das Auswahlaxiom führt dazu, dass man beweisen kann, dass jede Menge (also auch die reellen Zahlen) wohlgeordnet werden kann. Das bedeutet, dass es für die reellen Zahlen so etwas wie eine spezielle "kleiner-gleich"-Beziehung (oder "früher oder gleich-früh"-Beziehung) geben muss, so dass jede Teilmenge reeller Zahlen ein kleinstes (oder frühestes) Element bezüglich dieser Beziehung besitzt. Nur ist es bis heute nicht gelungen, eine solche Beziehung auch anzugeben (die normale kleiner-gleich-Beziehung scheidet aus, denn nicht jede Teilmenge reeller Zahlen muss ein kleinstes Element in diesem Sinn haben).
  Vielleicht würde ein nicht-konstruktiver Beweis für P = NP sogar interessante Einsichten über die Fundamente der Mathematik ermöglichen. Welche Axiome der Mengenlehre sind erforderlich, um P = NP nicht-konstruktiv zu beweisen? Ähnlichkeiten zur Kontinuumshypothese drängen sich auf (siehe Kapitel 4.3).

• Konstruktiver Beweis für P = NP gelingt:
  In diesem Fall kann man (zumindest im Prinzip) für jedes NP-Problem einen polynomialen Algorithmus zu dessen Lösung konstruieren. Nun basiert beispielsweise die moderne Kryptographie, mit der z.B. Internet-Banking verschlüsselt wird, auf der Annahme, dass das Primfaktor-Zerlegungsproblem für große Zahlen schwierig zu lösen ist. Wäre P = NP, so gäbe es möglicherweise einen polynomialen Algorithmus, um dieses Problem zu lösen und damit Internet-Codes zu knacken. Die Sicherheit von Verschlüsselungen wäre plötzlich in Frage gestellt.
  Doch ein polynomialer Algorithmus ist noch keine Garantie für die praktische Lösbarkeit der zugehörigen Probleme, denn auch ein solcher Algorithmus kann bei großen Problemen sehr langsam werden, wenn z.B. die Rechenzeit mit der tausendsten Potenz der Problemgröße (also mit \(n^{1000}\) anwächst. Oder aber das Polynom besitzt sehr große Koeffizienten (z.B. \(p(n) = 10000000000 \cdot n\) ), so dass der Algorithmus deswegen sehr langsam ist. Aus Erfahrung weiß man auch, dass z.B. Kürzeste-Wege-Probleme viel einfacher zu lösen sind als Hamiltonsche-Wege-Probleme, obwohl beide in derselben Problemklasse NP liegen. Wäre P = NP, so müsste man die Struktur der Problemklasse P im Detail untersuchen, um solche Unterschiede theoretisch erfassbar zu machen. Erste Ansätze dazu gibt es (Stichwort endliche Modelltheorie).

Orakelmaschinen

Das P = NP-Problem hat sich bisher als sehr hartnäckig erwiesen. Daher hat man versucht, einen anderen Weg zu beschreiten, um neue Einsichten in die Ursachen für diese Schwierigkeiten zu gewinnen:

Wenn Du ein Problem nicht lösen kannst, versuche, es unter anderen Voraussetzungen zu betrachten.

Die Idee ist also, die Voraussetzungen so zu ändern, dass das Problem lösbar wird. Man hofft, dadurch Hinweise auf Lösungsansätze für das ursprüngliche Problem zu erhalten.

Wie kann man nun beim P = NP-Problem die Voraussetzungen entsprechend erweitern, so dass sich P = NP (oder das Gegenteil) beweisen lässt?

Die Idee ist sehr einfach: Wir erlauben jedem Algorithmus, bestimmtes Zusatzwissen zu verwenden, das er nicht errechnen, sondern einfach nur abfragen muss, wobei jeder Algorithmus dasselbe Zusatzwissen zur Verfügung gestellt bekommt. Dadurch wird es sicher möglich sein, die Effizienz der verschiedenen Algorithmen zu steigern, wobei diese Effizienzsteigerung von der Art des Zusatzwissens abhängen wird, das wir zur Verfügung stellen.

Bei den Problemen aus NP gibt es nun einen polynomialen Prüfalgorithmus für gegebene Begründungsstrings. Das Problem aber lag darin, einen effizienten Algorithmus zu finden, der in polynomialer Zeit einen geeigneten Begründungsstring findet. Vielleicht ist es ja möglich, bei erlaubter Verwendung von Zusatzwissen einen solchen Algorithmus zu finden. In diesem Universum (d.h. für Algorithmen mit Zusatzwissen) wäre dann P = NP.

Präzisieren wir zunächst, was es bedeuten soll, Zusatzwissen zu verwenden. Dazu muss man den Begriff der Turingmaschine erweitern und sogenannte Orakelmaschinen definieren. Eine Orakelmaschine besitzt ein zusätzliches Frageband, auf dem sie Input-Strings (also Fragen) für ein sogenanntes Orakel hinterlegen kann. Das Orakel antwortet dann in einem Verarbeitungsschritt mit JA oder NEIN. Diese Antwort kann man durch separate Zustände der Turingmaschine darstellen.

Anschaulich kann man sich Orakelmaschinen als Computer vorstellen, die jederzeit eine gigantische Datenbank abfragen können, wobei diese Abfrage praktisch keine Zeit benötigt. Abgefragt wird dabei, ob ein bestimmter String in der Datenbank vorhanden ist oder nicht. Die Datenbank ist dabei in ihrer Größe nicht beschränkt – insofern hinkt der Vergleich mit der Datenbank. Genauer müsste man sagen, die Orakelmaschine fragt ein Orakel, ob ein bestimmtes Objekt (dargestellt als String) in einer beliebigen, aber fest vorgegebene Menge vorhanden ist oder nicht. Das Orakel wird gleichsam durch die vorgegebene Menge definiert.

Die vorgegebene Menge bestimmt nun, wie mächtig das Orakel ist. Da wir an die Menge keinerlei Bedingungen gestellt haben, muss es sehr mächtige Orakel geben. So könnte die Menge beispielweise alle anhaltenden Turingprogramme enthalten. Ein solches Orakel würde mit einem Schlag Turings Halteproblem lösen. Wie wir sehen, muss die Menge also nicht per Computer auflistbar (also rekursiv aufzählbar) sein. Damit sind sogar Algorithmen für normalerweise nicht-berechenbare Funktionen möglich.

Die Suche nach brauchbaren Beweistechniken

Gibt es nun Orakel, die so mächtig sind, dass man mit ihrer Hilfe NP-Probleme in polynomialer Zeit lösen kann? Tatsächlich ist es im Jahr 1975 gelungen, solche Orakel anzugeben (T. Baker, J. Gill, R. Solovay: Relativizations of the P =? NP question, SIAM Journal on Computing, 4 (1975)). Man konnte zeigen, dass das Orakel dazu lediglich eine Menge abfragen muss, die alle JA-Probleminstanzstrings eines bestimmten Problemtyps enthält, der sich mit polynomial wachsenden Speicherplatzbedarf (aber unbegrenzter Rechenzeit) lösen lässt. Genauer: es muss sich um ein PSPACE-vollständiges Problem handeln:

• Entscheidungsprobleme der Problemklasse :
  Dazu gehören alle Entscheidungsprobleme, die sich auf einer Turingmaschine in unbegrenzter Zeit lösen lassen, wobei der dazu benötigte Speicherplatz höchstens polynomial mit der Problemgröße (Bitlänge des Probleminstanzstrings) anwächst.

• PSPACE-vollständige Probleme:
  Analog zu NP-vollständig: Ein Problem U aus PSPACE ist PSPACE-vollständig, wenn man jedes andere Problem aus PSPACE auf U reduzieren kann.

Zum Vergleich: bei der Problemklasse P war der Speicherplatz unbeschränkt, aber die Laufzeit durfte nur polynomial mit der Problemgröße anwachsen.

Was für einen Charakter haben PSPACE-vollständige Probleme? Sie entsprechen Problemen wie in einem Spiel: Gibt es irgendeinen Zug für mich, so dass für alle möglichen Züge meines Gegners ein Zug für mich existiert, mit dem ich gewinne? Diese Frage kann noch um viele Stufen weitergeführt werden. 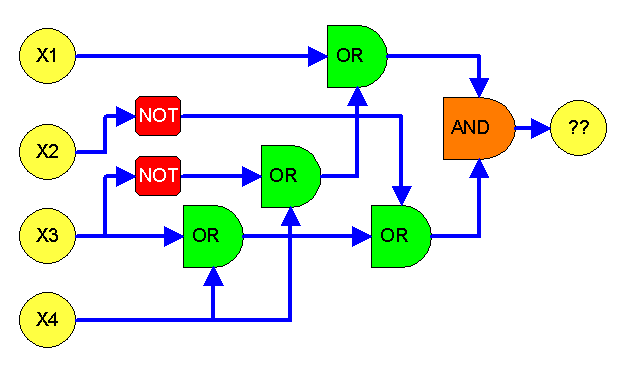Daher ist es nicht verwunderlich, dass das bekannteste PSPACE-vollständige Problem darin besteht, den Wahrheitswert von logischen Ausdrücken der folgenden Form anzugeben (Beispiel): \[ \exists x_1 : \forall x_2 : \exists x_3 : \forall x_4 : \] \[ ((x_1 \lor \neg x_3 \lor x_4) \land (\neg x_2 \lor x_3 \lor x_4)) \] Wichtig dabei ist, dass dabei \( \exists \) (es gibt) und \( \forall \) (für alle ... gilt) abwechselnd vorkommen. Zum Vergleich das analoge Problem aus NP (Boolsches Erfüllbarkeitsproblem): \[ \exists x_1 : \exists x_2 : \exists x_3 : \exists x_4 : \] \[ ((x_1 \lor \neg x_3 \lor x_4) \land (\neg x_2 \lor x_3 \lor x_4)) \] Hier sind alle \( \forall \) -Ausdrücke durch \( \exists \) -Ausdrücke ersetzt worden. Dieses Problem entspricht eher einem Puzzle, bei dem passende Variablenwerte gesucht werden. Entsprechend haben NP-Probleme meist den Charakter eines Puzzles. PSPACE-Probleme dagegen suchen eher nach dem richtigen Zug in einem Spiel, so dass der Erfolg bei allen denkbaren Spielabläufen gewährleistet ist. Das Damespiel, gespielt auf einem \(n \times n\) -Brett, ist beispielsweise PSPACE-vollständig. Man nimmt daher an, dass PSPACE-vollständige Probleme sehr viel schwerer zu lösen sind als NP-Probleme, auch wenn dies bisher nicht bewiesen wurde (bewiesen ist lediglich, dass NP eine Teilmenge von PSPACE ist). Schach und Go sind übrigens noch schwieriger: sie sind wegen der möglichen sehr langen Spielabläufe sogar EXPTIME-vollständig (siehe oben).

Fassen wir noch einmal zusammen: Verwendet man die Menge aller JA-Probleminstanzstrings eines PSPACE-vollständigen Problems als Orakel-Abfragemenge, so kann man zur Lösung aller NP-Probleme einen zugehörigen Algorithmus mit eingebauten Orakel-Abfragen erstellen, der das NP-Problem in einer Zeit löst, die höchstens polynomial mit der Bitlänge des Probleminstanzstrings anwächst. Bezeichnen wir die Orakel-Abfragemenge mit A, so schreibt man dafür auch

• P^A = NP^A

Natürlich ist klar, dass man eine solche Menge A nicht wirklich vollständig angeben kann, denn sie entspricht ja einem Orakel, das über ein ungeheures (unendlich großes) Wissen verfügt. Ein solches Orakel wäre z.B. ein perfekter Dame-Spieler auf beliebig großem Spielbrett, wobei jeder Spielzug ohne Nachdenken ausgeführt wird.

Es ist interessant, dass man andererseits auch eine Orakel-Abfragemenge B konstruieren kann, so dass sich garantiert nicht alle NP-Probleme in polynomialer Zeit lösen lassen (das Orakel mit Menge B ist also garantiert schwächer als das mit Menge A):

• P^B ≠ NP^B

Es hängt also von der Mächtigkeit des Orakels bzw. seiner Abfragemenge ab, ob für die zugehörigen Algorithmen P = NP gilt oder nicht. Aber was sollen wir mit diesem Ergebnis anfangen, um das ursprüngliche Problem P =? NP ohne Orakel zu lösen?

Der entscheidende Punkt dabei ist, dass sich verschiedene Beweistechniken zur Lösung des P =? NP -Problems komplett ausschließen lassen. Warum ist das so?

Nehmen wir an, wir verwenden eine bestimmte Beweistechnik wie z.B. die Diagonalisierung (analog zum Beweis von Turings Halteproblem). Wir könnten nun die Beobachtung machen, dass diese Beweistechnik unabhängig davon arbeitet, ob die untersuchten Algorithmen Orakel verwenden oder nicht. Solche Beweistechniken nennt man auch relativierend. Entsprechende Beweise müssen also ohne Orakel genauso gelten wie für die Verwendung beliebiger Orakel in den Algorithmen. Ein einfaches Beispiel für ein Ergebnis, das sich mit solchen Beweistechniken beweisen lässt, ist P ⊆ NP (P ist Teilmenge von NP), denn es gilt P^C ⊆ NP^C für beliebige Orakel C. Ein anderes Beispiel ist die Identität PSPACE = NPSPACE.

Wenn eine solche relativierende Beweistechnik nun P = NP beweisen soll, so würde sie gleichzeitig für beliebige Orakel (nennen wir sie C) P^C = NP^C beweisen (und analog für den Fall P ≠ NP). Nun haben wir aber gesehen, dass es Orakel \(A\) gibt, so dass P^A = NP^A ist, und Orakel B, so dass P^B ≠ NP^B ist. Daher kann eine Beweistechnik, die ohne oder mit beliebigem Orakel gleich funktioniert, P = NP (oder das Gegenteil) nicht beweisen, denn dann würde dieses Ergebnis auch für alle Orakel gelten, was falsch wäre. Daher gilt:

• Relativierende Beweistechniken (die also unabhängig davon funktionieren, ob Orakel in den Algorithmen verwendet werden oder nicht) können P = NP weder beweisen noch widerlegen.

Damit fallen die meisten bewährten Beweistechniken der theoretischen Informatik für den Beweis von P = NP oder dem Gegenteil weg.

Gibt es überhaupt Beweistechniken, die übrig bleiben, die also nicht-relativierend sind? Es gibt tatsächlich einige Kandidaten, z.B. algebraische Ansätze, endliche Modelltheorie oder interaktive Beweise (dabei kommunizieren Turingmaschinen über ein Protokoll miteinander). Mit Hilfe der interaktiven Beweise ist es im Jahr 1999 tatsächlich gelungen, ein Problem zu lösen, bei dem relativierende Beweistechniken nicht funktionieren können (bewiesen wurde IP = PSPACE, wobei wir hier die Problemklasse IP nicht genauer erklären wollen). Damit wurde zum ersten Mal eine nicht-relativierende Beweismethode angewendet, die ein Orakel schlug.

Die Entwicklung neuer Beweistechniken zeigt, warum das P =? NP -Problem so interessant ist: Es ist einfach zu verstehen, schwierig zu beweisen und es entstehen interessante neue mathematische Ideen bei dem Versuch, es zu lösen. Nicht allein die Lösung, sondern auch der Weg dorthin sind ein lohnendes Ziel. In diesem Sinne ist das P =? NP -Problem ein sehr gutes mathematisches Problem, das wert ist, in den exklusiven Club der sieben Millenium-Probleme aufgenommen worden zu sein.

Literatur:

• Martin Grötschel: P = NP?, Elem. Math. 57 (2002) 1-6, Birkhäuser Verlag, Basel 2002 (Elemente der Mathematik),

• Clay Mathematics Institute: The Millennium Prize Problems und P vs NP Problem sowie Stephen Cook: The P versus NP Problem, Official Problem Description

• Ian Steward: Million-Dollar Minesweeper

• Erhard Behrends: Probleme vom Typ P und NP, oder: Ist Glück in der Mathematik entbehrlich?, erschienen in der Wochenzeitschrift DIE ZEIT am 4.3.1999

• Christian Soltenborn: Zur Beweisbarkeit von P = NP