Im letzten Kapitel haben wir gesehen, wie man eine Quantentheorie zur Elektrodynamik konstruieren kann. Dabei haben wir das Kochrezept der kanonischen Quantisierung angewendet, d.h. wir haben die Maxwellgleichungen mit Hilfe der Potentiale umformuliert und die Zeitentwicklung der Potentiale und der dazu kanonisch konjugierten Felder mit Hilfe von Poissonklammern geschrieben. Diese Poissonklammern haben wir nun durch Kommutatoren der Feldoperatoren ersetzt und so eine Quantentheorie konstruiert.
Dabei mussten wir allerdings feststellen, dass diese Vorgehensweise nicht so geradlinig durchführbar war, wie dies noch bei der Quantisierung der klassischen Mechanik möglich gewesen ist. Hauptproblem war, dass es zu den vier Potentialen \(A^\mu\) nur drei konjugierte Variablen \(\pi^\mu\) gab, denn es war \(\pi^0 = 0\). Grund dafür war, dass nicht alle Potentiale \(A^\mu\) als voneinander unabhängige Freiheitsgrade angesehen werden können. Potentiale, die man durch Eichtransformationen ineinander überführen kann, sind gleichwertig zueinander, denn sie ergeben dieselben elektromagnetischen Felder. Man muss also Wege finden, um die überflüssigen Freiheitsgrade in den Potentialen loszuwerden. Dies kann man entweder vor der Quantisierung durchführen, was zu geänderten Poissonklammern führt, oder nach der Quantisierung, was zu Zusatzbedingungen in den Hilberträumen führt, um unphysikalische Quantenzustände loszuwerden. In jedem Fall ist die Vorgehensweise trickreich, und es stellt sich heraus, dass sie sich nur sehr mühevoll auf komplexere Eichtheorien übertragen lässt. Der Formalismus wird unübersichtlich, da er weder manifest kovariant noch eichinvariant ist.
Wie wir wissen, gibt es eine alternative Möglichkeit zur Quantisierung: die Pfadintegralmethode von Feynman. Diese Methode kommt sehr viel besser mit Symmetrien wie Poincaretransformationen und Eichtransformationen zurecht. Man zahlt allerdings auch einen Preis: Die mathematischen Grundlagen dieser Methode sind teilweise noch wenig fundiert, da über mehrfach unendlichdimensionale Räume integriert werden muss. Man muss daher immer auf Überraschungen gefasst sein, wenn man zu unbefangen mit diesen Integralen umgeht, und hoffen, dass sich alles mathematisch rechtfertigen lässt (z.B. als Grenzwert einer entsprechenden Gittertheorie). Andererseits muss man sich eine gewisse Furchtlosigkeit bewahren, da man sonst nicht weiterkommt. Das Ganze hat also manchmal einen gewissen Kochrezept-Charakter, und es wird sicher noch eine Weile dauern, bis die mathematischen Grundlagen gefestigt werden können. Vermutlich befanden sich Newton und Leibnitz in einer ähnlichen Situation, als sie vor mehr als 300 Jahren mit unendlich kleinen (infinitesimalen) Ausdrücken hantierten. Heute gehört so etwas zum mathematischen Standard und ist wohlfundiert.
Es erschien mir unmöglich, in diesem Kapitel im Detail den Formalismus zur Pfadintegralquantisierung der Elektrodynamik darzustellen. Daher werde ich in diesem Kapitel nicht so genau auf die Details eingehen, sondern stattdessen versuchen, die wesentlichen Ideen darzustellen, auch im Hinblick auf kompliziertere Eichtheorien. Fangen wir also an!
Zur Erinnerung:
Im vorletzten Kapitel haben wir die Pfadintegraldarstellung für den freien Einteilchenpropagator der nichtrelativistischen Quantenmechanik im eindimensionalen Raum kennengelernt: \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \int_{\mathrm{Wege} \; \boldsymbol{x}} \, \mathcal{D}\boldsymbol{x} \; e^{ \frac{i}{\hbar} \, S[\boldsymbol{x}] } \] Dabei definierte der Propagator die Zeitentwicklung der Zustände: \[ \psi(t,\boldsymbol{x}) = \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] mit \(t > t'\). Das Maß \( \mathcal{D}\boldsymbol{x} \) im Raum der möglichen Wege war definiert als \[ \lim_{n \rightarrow \infty} \, \int d^3x_1 \, ... \, d^3x_{n-1} \, \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \, ... \, = \] \[ =: \int_{\mathrm{Wege} \; \boldsymbol{x}} \, \mathcal{D}\boldsymbol{x} \, ... \] wobei jeder Weg als Grenzwert eines Polygonzuges angesehen wird, der vom Punkt \(\boldsymbol{x}'\) zur Zeit \(t'\) zum Punkt \(\boldsymbol{x}\) zur Zeit \(t\) (mit \(t > t'\)) über die Zwischenpunkte \(\boldsymbol{x}_1, \boldsymbol{x}_2, ... \boldsymbol{x}_{n-1}\) führt. Dabei ist \( \Delta t = (t - t')/n \), und der Zwischenpunkt \(\boldsymbol{x}_m\) wird zur Zeit \( t_m := t' + m \, \Delta t \) erreicht.
Ob der obige Grenzwert \(n \rightarrow \infty\) existiert, ist eine schwierige Frage, da der Intergrand \( e^{ \frac{i}{\hbar} \, S[\boldsymbol{x}] } \) eine sehr heftig oszillierende Funktion sein kann. Man versucht daher oft, das Integral durch analytische Fortsetzung in der Zeitvariablen durch ein Integral ohne die imaginäre Einheit \(i\) im Exponenten zu definieren, da in diesem Integral der dämpfende Integrand \( e^{ - \frac{S[\boldsymbol{x}]}{\hbar}} \) vorkommt. Auf Details wollen wir hier nicht eingehen.
Versuchen wir, in Analogie zu dem obigen Pfadintegral einen Ausdruck für das Pfadintegral der Quantenelektrodynamik aufzustellen. Dazu müssen wir zunächst die Anzahl der Freiheitsgrade kräftig erhöhen: Statt drei Koordinaten-Freiheitsgraden \(\boldsymbol{x}(t)\) brauchen wir unendlich viele Freiheitsgrade \(A^\mu(ct, \boldsymbol{x})\), wobei \(\mu\) und \(\boldsymbol{x}\) als Doppelindex zu sehen ist, der die unendlich vielen Freiheitsgrade gleichsam durchnummeriert. Für jedes \(\mu\) und jedes \(\boldsymbol{x}\) ist also \(A^\mu(ct, \boldsymbol{x})\) ein Freiheitsgrad der klassischen Theorie, dessen Zeitabhängigkeit man untersucht.
Im Pfadintegral oben muss man also jede Zwischenebene \(\boldsymbol{x}_m\), über die integriert wird, durch eine Integration über alle Zwischen-Feldkonfigurationen \( A^\mu_m(\boldsymbol{x})\) ersetzen, wobei der Index \(m\) andeutet, dass die Feldkonfiguration zur Zwischenzeit \( t_m = t' + m \, \Delta t \) betrachtet wird. Um das zu konkretisieren, kann man beispielsweise ein Gitter mit Gitterpunkten \( \boldsymbol{x}_j \) betrachten, das man im Grenzfall immer feiner werden lässt. Jede der unendlich vielen eindimensionalen Integrationen über die Zwischenebenen \(\boldsymbol{x}_m\) in unserem Teilchen-Pfadintegral wird also durch ein unendlichdimensionales Integral über alle Feldkonfigurationen \( A^\mu_m(\boldsymbol{x}_j)\) über alle Gitterpunkte \( \boldsymbol{x}_j \) ersetzt. Insofern enthält das Pfadintegral unendlich viele unendlich-dimensionale Integrationen – wer hier an ein mathematisches Monster denkt, liegt vielleicht nicht ganz falsch. Aber wie oben gesagt: bloß keine Angst, einfach weitermachen!
Im Grenzübergang erhalten wir schließlich ein Integral, das den Integranden \( e^{ \frac{i}{\hbar} \, S[A] } \) integriert, und zwar über alle Möglichkeiten \(A^\mu(ct, \boldsymbol{x})\), über die sich eine Feldkonfiguration gegeben zur Zeit \(t'\) in eine andere Feldkonfiguration gegeben zur Zeit \(t\) entwickeln kann. Integriert wird dabei über alle möglichen Zwischen-Feldkonfigurationen: \[ \int_{\mathrm{Feldkonfig.} \; A} \, \mathcal{D}A \; e^{ \frac{i}{\hbar} \, S[A] } \] Über die genaue Definiton des Maßes \(\mathcal{D}A\) wollen wir uns hier keine Gedanken machen (so müssten wir beispielsweise überlegen, was aus dem Faktor \( \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \) wird, der eine Rolle bei der Normierung des Pfadintegrals spielt und der seine Herkunft im freien Propagator hat, siehe vorletztes Kapitel).
Die obige Amplitude beschreibt das Ereignis, dass man zur Zeit \(t'\) mit einer Anfangskonfiguration \(A^\mu(ct', \boldsymbol{x})\) im gesamten Raum startet und zur Zeit \(t\) mit einer Endkonfiguration \(A^\mu(ct, \boldsymbol{x})\) im gesamten Raum endet. Dabei wird im Pfadintegral über alle möglichen (in gewissem Sinn hinreichend glatten) Funktionsverläufe \(A^\mu(ct'', \boldsymbol{x})\) (mit \(t''\) zwischen \(t'\) und \(t\)) integriert, die die beiden räumlichen Feld-Konfigurationen über die Zeit hinweg miteinander verbinden. Nun ist dieses Ereignis normalerweise nicht wohlbestimmt, denn man kann die Anfangs- und Endkonfiguration gar nicht messen. Wir erinnern uns an den Schluss des letzten Kapitels, der aufzeigt, wann wir überhaupt von elektromagnetischen Feldern und damit Potentialen sprechen können.
Man kann versuchen, andere (besser messbare) Amplituden zu finden und diese durch Pfadintegrale analog zu oben auszudrücken. Interessant ist beispielsweise der Photonpropagator, der die Amplitude dafür ist, dass sich ein Photon von einem Orts-Zeitpunkt zu einem anderen Orts-Zeitpunkt bewegt. Auch dieser Propagator ist nicht direkt messbar, ist jedoch Bestandteil vieler Berechnungen und deshalb interessant. Wirklich messbar sind dagegen Übergangsamplituden von einem in einen Streuprozess einlaufenden freien Zustand zu einem aus dem Prozess auslaufenden freien Zustand. Man bezeichnet diese Amplituden auch als Streuamplituden oder auch als Matrixelemente der S-Matrix. Die freie Quantenelektrodynamik, auf die wir uns hier beschränken, ist jedoch eine Theorie freier Quantenzustände, d.h. die Photonen wechselwirken nicht miteinander. Daher treten auch keine Streuprozesse auf. Dies wird bei komplexeren Eichtheorien anders sein!
Stellt man die Pfadintegralformeln für solche Amplituden (z.B. Propagatoren oder komplexere Objekte) auf, so enthalten diese Formeln im Wesentlichen diverse Funktionalableitungen (siehe vorheriges Kapitel) des folgenden Pfadintegrals
| \[ W[J] = \int \, \mathcal{D}A \; e^{ \frac{i}{\hbar} \, \left( S[A] + \int d^4x \, J_\mu(x) \, A^\mu(x) \right) } \] |
nach den sogenannten Quellen \( J_\mu(x) \). Man bezeichnet \(W[J]\) auch als erzeugendes Funktional. Es besitzt große Ähnlichkeit mit der Zustandssumme aus der statistischen Physik (Thermodynamik) – auch dort bilden Ableitungen der Zustandssumme ein zentrales Element der Theorie. Das erzeugende Funktional kann man interpretieren als die Vakuum-zu-Vakuum-Amplitude in der Gegenwart einer externen Quelle \(J\) (wir wollen hier nicht genauer darauf eingehen).
Genau genommen ist \(W[J]\) erst über die analytische Fortsetzung der Zeitvariable definiert. Man müsste also die Zeit \(t\) als komplexe Variable ansehen. Für rein imaginäres \( t = i \tau \) (mit reellem \(\tau\)) kann man \( i \, dt = - d\tau\) verwenden und erhält \( W[J] = \int \, \mathcal{D}A \; e^{ - \int d\tau \, ... } \) Aus einer oszillierenden Funktion wird so eine nicht-oszillierende Exponentialfunktion, die zur Konvergenz des Pfadintegrals beiträgt.
Wir wollen im Folgenden nicht so genau unterscheiden, welches Pfadintegral wir nun genau betrachten, da wir uns eher für die allgemeine Struktur und allgemeine Probleme interessieren wollen – diese treten dann überall in ähnlicher Form auf! Halten wir einfach nur allgemein fest:
Vielleicht hat sich der eine oder andere Leser an dieser Stelle bereits die folgende Frage gestellt:
Die Frage ist in der Tat berechtigt, und wir wollen uns das Pfadintegral (ohne Quellterm) genauer ansehen, um eine Antwort zu geben. Dazu schreiben wir den Exponenten im Pfadintegral zunächst ein wenig um: \[ S[A] = - \frac{1}{4} \int d^4x \, F_{\mu\nu} F^{\mu\nu} = \] \[ = - \frac{1}{4} \int d^4x \, (\partial_\mu A_\nu - \partial_\nu A_\mu) \cdot \] \[ \qquad \qquad \qquad \quad \cdot (\partial^\mu A^\nu - \partial^\nu A^\mu) = \, ... \] ... ausmultiplizieren und Indices ggf. umbenennen: \[ = - \frac{1}{2} \int d^4x \, ( (\partial_\mu A_\nu) (\partial^\mu A^\nu) + \] \[ \qquad \qquad \qquad \quad - (\partial_\mu A_\nu) (\partial^\nu A^\mu) ) = \, ... \] ... es ist \( (\partial_\mu A_\nu) (\partial^\mu A^\nu) = \partial_\mu (A_\nu \, \partial^\mu A^\nu) - A_\nu (\partial_\mu \partial^\mu A^\nu) \) und analog für den zweiten Term. Nach einigen kleineren Umformungen und Zusammenfassungen erhalten wir: \[ = - \frac{1}{2} \int d^4x \, [ \partial_\mu (A_\nu F^{\mu\nu}) + \] \[ - A_\nu \, \left( g^{\mu\nu} \partial_\rho \partial^\rho - \partial^\nu \partial^\mu \right) A_\mu ] = \, ... \] ... das Integral über den ersten Term können wir nach dem Gauß'schen Satz in ein Integral über den Fluss von \( A_\nu F^{\mu\nu} \) über den unendlich fernen Rand der vierdimensionalen Raumzeit überführen. Wieder verwenden wir die Randbedingung, dass die Felder im Unendlichen hinreichend schnell abfallen, so dass dieses Integral verschwindet: \[ = \frac{1}{2} \int d^4x \, A_\nu \, \left( g^{\mu\nu} \partial_\rho \partial^\rho - \partial^\nu \partial^\mu \right) A_\mu = \] \[ =: \frac{1}{2} \int d^4x \, A_\nu \, K^{\mu\nu} A_\mu \] Der Operator \[ K^{\nu\mu} := g^{\mu\nu} \partial_\rho \partial^\rho - \partial^\nu \partial^\mu \] hat große Ähnlichkeit mit dem transversalen Projektionsoperator \( P_T \) aus dem letzten Kapitel. So gilt: \[ \partial_\nu \, K^{\nu\mu} A_\mu = 0 \] d.h. der Operator \(K^{\nu\mu}\) macht aus jedem Vierervektorfeld \(A_\mu\) ein vierer-divergenzfreies Vektorfeld. Mit anderen Worten: Das Vierer-Vektorfeld \( K^{\nu\mu} A_\mu \) erfüllt die Stromerhaltungsgleichung. Der Operator \(K^{\nu\mu}\) vergisst also die Anteile von \(A_\mu\), die nicht vierer-divergenzfrei sind, d.h. er verhält sich wie ein Projektionsoperator.
Was geschieht, wenn man \(A_\mu\) umeicht, also durch ein eichtransformiertes Potential \(A'_\mu = A_\mu + \partial_\mu \chi \) ersetzt? Man rechnet leicht nach, dass \( K^{\nu\mu} \partial_\mu \chi = 0 \) ist, also \[ K^{\nu\mu} A'_\mu = K^{\nu\mu} (A_\mu + \partial_\mu \chi) = K^{\nu\mu} A_\mu \] Für den Operator \(K^{\nu\mu}\) spielen also Eichtransformationen keine Rolle, d.h. der Term \( K^{\nu\mu} A_\mu \) ist eichinvariant. Das wundert uns nicht, denn schließlich haben wir den Operator oben aus einem eichinvarianten Ausdruck abgeleitet. Der Operator projeziert Eichtransformationen also gleichsam weg.
Die Folge davon ist, dass \(K^{\nu\mu}\) nicht invertierbar ist. Die präzise Version dieser Aussage lautet: \(K^{\nu\mu}\) besitzt keine Greensfunktion (genauer: Distribution), d.h. die Gleichung \[ K^{\nu\mu} G_{\mu\rho}(x-y) = g^\nu_{\; \rho} \, \delta(x-y) \] besitzt keine Lösung \(G_{\mu\rho}(x-y)\), wie man durch vierdimensionale Fouriertransformation sehen kann.
Warum stört uns die Tatsache, dass \(K^{\nu\mu}\) nicht invertierbar ist? Hier ist ein Argument dafür, das wir aber nur grob anreißen wollen: Das Pfadintegral \[ W[J] = \int \, \mathcal{D}A \; e^{ \frac{i}{\hbar} \, \int d^4x \, \left( \frac{1}{2} \, A_\nu \, K^{\mu\nu} A_\mu + J_\mu \, A^\mu \right) } \] hat große Ähnlichkeit mit einem unendlich-dimensionalen Gauß-Integral (wobei wir wieder die analytische Fortsetzung in der Zeit vornehmen, so dass die imaginäre Einheit \(i\) verschwindet und durch ein Minuszeichen ersetzt wird). Schauen wir uns zum Vergleich ein \(n\)-dimensionales Gaußintegral mit einer symmetrischen \(n \times n\)-Matrix \(K\) und \(n\)-dimensionalen Vektoren \(a\) und \(j\) an. Es gilt: \[ \int d^n a \, e^{- a^T \, K \, a - 2 j^T a} = \sqrt{ \frac{\pi^n}{\det{K}}} \, e^{j^T K^{-1} j} \] Wobei das hochgestellte \(T\) das Transponieren bedeutet.
Voraussetzung für die Existenz dieses Integrals ist also, dass die Matrix \(K\) invertierbar ist, denn in der Formel taucht der inverse Operator \(K^{-1}\) auf und es wird durch die Matrix-Determinante dividiert. Ist \(K\) nicht invertierbar, so divergiert das Integral. Dies kann man auch anschaulich verstehen: Diagonalisiert man \(K\) durch eine entsprechende unitäre Transformation der Variablen \(a\), so ist bei einem nicht-invertierbaren \(K\) eines der Diagonalelemente (Eigenwerte) gleich Null. In Richtung des entsprechenden Eigenvektors \(a_0\) ist dann \( e^{- a_0^T \, K \, a_0} = e^0 = 1 \), d.h. das Integral in \(a_0\)- Richtung liefert einen unendlichen Beitrag.
Analog ist die Nichtinvertierbarkein des Differenzialoperators \(K^{\nu\mu}\) ein Zeichen dafür, dass das Pfadintegral so gar nicht definiert ist. Ursache für die Nichtinvertierbarkeit war aber, dass sich \(K^{\nu\mu}\) nicht für Eichtransformationen von \(A_\mu\) interessiert und diese wegprojeziert. Die Integration in Eichrichtung liefert deshalb einen unendlichen Beitrag. Und damit sind wir beim Kern des Problems angelangt:
Dann müsste auch das Invertierungsproblem mit \(K^{\nu\mu}\) in den Griff zu bekommen sein, denn auf den Eichklassen sollte sich eine solche Inversion sicher definieren lassen.
Wie aber kann man die Integration im Pfadintegral so einschränken, dass jede Eichklasse nur einmal vorkommt?
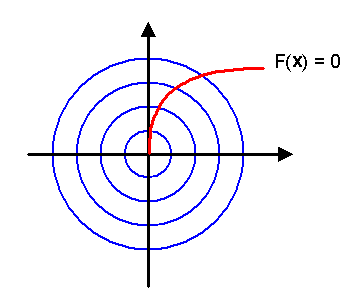
Zunächst einmal wird es sicher nötig sein, jede dieser Eichklassen eindeutig durch eines ihrer Elemente zu kennzeichnen. Aus jeder Klasse ineinander eichtranstransformierbarer Potentiale wollen wir also genau ein Potential herausfiltern. Wir nehmen an, dass wir dies durch eine Funktionalgleichung der Form \[ F[A] = 0 \] erreichen können, also durch eine Nebenbedingung, die in jeder Klasse genau von einem Repräsentanten erfüllt wird (Anmerkung: wir haben hier die Bezeichnungsweise \(F[A]\) statt \(g[A]\) (siehe letztes Kapitel) gewählt, um den Buchstaben \(g\) weiter unten für Elemente der Eichgruppe verwenden zu können). Dies könnte beispielsweise die Lorentz-Eichbedingung \( F[A] = \partial_\mu A^\mu = 0 \) sein (siehe letztes Kapitel). Diese Bedingung würde allerdings noch nicht ausreichen, um genau ein Element aus jeder Klasse auszuwählen, denn die Lorentz-Eichbedingung fixiert die Eichung ja noch nicht vollständig.
Das Beispiel der Lorentz-Eichbedingung zeigt, dass der Wert von \(F[A]\) keine reelle Zahl sein muss (so wie noch im letzten Kapitel). Der Wert von \(F[A]\) kann hier allgemeiner eine Funktion sein, d.h. \(F\) ist ein Operator, der in Funktionenräumen wirkt. Die Bedingung \( F[A] = 0 \) bedeutet, dass \(F[A]\) die Nullfunktion ist, die für jedes Argument \(x\) den Wert Null ergibt.
Bei komplexeren Eichtheorien ist die Frage, wie man ein geeignetes \(F[A]\) finden kann, tatsächlich sehr komplex und meines Wissens noch nicht zufriedenstellend gelöst. Die Fläche mit \( F[A] = 0 \) tendiert im Raum der Potentiale dazu, jede Eichklasse mehrfach zu schneiden, d.h. in jeder Klasse zueinander eichtransformierbarer Potentiale gibt es immer mehrere, die \( F[A] = 0 \) erfüllen. Man spricht vom Gribov-Problem.
Man könnte nun auf die Idee kommen, im Pfadintegral einfach eine Art Delta-Funktion der Form \( \delta(F[A]) \) hinter dem Integrationsmaß \( \mathcal{D}A \) einzufügen und so eine Eichfixierung zu erzwingen. Das funktioniert jedoch nicht, denn es zeigt sich, dass das ursprüngliche Pfadintegral nicht einfach derart willkürlich verfälscht werden darf. Das ursprüngliche Pfadintegral ist schon der korrekte Ausgangspunkt, aber man muss die Ursache der Divergenz sorgfältig aus diesem Integral isolieren und dann beseitigen.
Versuchen wir, anhand von einfachen zweidimensionalen Integralen ein Gefühl dafür zu bekommen, wie man das Problem angehen könnte (siehe z.B. Cheng, Li: Gauge theory of elementary particle physics, Oxford University Press 1984, Kapitel 9 Quantum gauge theories). Statt einem Integral über den unendlich dimensionalen Funktionenraum der Potentiale betrachten wir also ein Integral über die zweidimensionale reelle Ebene. Aus dem Integrationsmaß \( \mathcal{D}A \) wird also das Flächenelement \(d^2x\) (in karthesischen Koordinaten \(x\) und \(y\) ist dann \( d^2x = dx dy \)). Aus dem Wirkungsfunktional \(S[A]\) wird die Funktion \(S(\boldsymbol{x})\) mit \( \boldsymbol{x} = (x, y) \) in karthesischen Koordinaten.
Nun ist das Wirkungsfunktional \(S[A]\) eichinvariant, ändert sich also unter Eichtransformationen von \(A\) nicht. Analog nehmen wir an, dass \(S(\boldsymbol{x})\) rotationsinvariant ist, also nur von \(|\boldsymbol{x}|\) abhängt und nicht vom Drehwinkel, also der Richtung von \(\boldsymbol{x}\).
Wie können wir nun das Integral \[ W = \int d^2x \, e^{i \, S(\boldsymbol{x})} \] geeignet umschreiben, so dass nicht mehr über den überflüssigen Freiheitsgrad (den Drehwinkel) integriert werden muss? Dazu schreiben wir \( \boldsymbol{x} \) in Polarkoordinaten: \begin{align} \boldsymbol{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} r \, \cos{\varphi} \\ r \, \sin{\varphi} \end{pmatrix} \end{align} mit der Vektorlänge \( r = |\boldsymbol{x}| \) und dem Drehwinkel \(\varphi\).
Natürlich könnte man einfach die obigen Polarkoordinaten einführen und die Integration
über \(\varphi\) ausführen. Wir wollen aber nach einer Methode suchen, die sich auf
Pfadintegrale übertragen lässt. Dazu verwenden wir analog zur Eichbedingung
\( F[A] = 0 \) eine Nebenbedingung der Form \( F(\boldsymbol{x}) = 0 \).
Diese Nebenbedingung muss aus jeder Klasse zueinander gleichwertiger Vektoren \(\boldsymbol{x}\)
genau einen auszeichnen. Wegen der Rotationsinvarianz von \(S(\boldsymbol{x})\)
wollen wir zwei Vektoren als gleichwertig ansehen, wenn sie sich durch Rotation ineinander
transformieren lassen, oder anders gesagt: wenn sie denselben Betrag haben.
Die Bedingung \( F(\boldsymbol{x}) = 0 \) soll also aus jeder Menge von Vektoren
\(\boldsymbol{x}\), die denselben Betrag haben, genau einen herausfiltern, d.h. nur einer dieser Vektoren
soll \( F(\boldsymbol{x}) = 0 \) erfüllen.
Anschaulich muss die Linie der Vektoren mit \( F(\boldsymbol{x}) = 0 \)
jeden Kreis um den Ursprung in genau einem Punkt schneiden.
In Polarkoordinaten lassen sich solche
Bedingungen leicht formulieren, z.B.
\[
F(\boldsymbol{x}) = F(x,y) = F(r \, \cos{\varphi}, r \, \sin{\varphi}) =
\]
\[ = \varphi - \varphi_0 = 0
\]
mit fest vorgegebenem Winkel
\( \varphi_0 \) (allgemein könnte \( \varphi_0 \)
sogar von \(r = |\boldsymbol{x}|\) abhängen, also \( \varphi_0(r) \).

Für die folgende Diskussion ist es nützlich, die Drehung eines Vektors durch die Wirkung eines Operators (einer Drehmatrix) \( R_\Phi \) auszudrücken, d.h. \( R_\Phi \) führt eine Drehung um den Winkel \( \Phi \) gegen den Uhrzeigersinn durch.
Betrachten wir nun das Integral \[ \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) \] mit der uns bereits bekannten Deltafunktion \(\delta\) und einem vorgegebenem Vektor \(\boldsymbol{x}\). Integriert wird dabei über den Drehwinkel \(\Phi\) der Drehmatrix, und zwar von \(0\) bis \(2\pi\), also über alle möglichen Winkelwerte.
Die Deltafunktion filtert nun im Integral über alle Winkel \(\Phi\) genau denjenigen Winkel heraus, der \(F(R_\Phi \boldsymbol{x}) = 0\) erfüllt. Deshalb kann zu jedem vorgegebenem \(\boldsymbol{x}\) nur ein einziger Winkel \(\Phi\) einen Beitrag zum Integral ergeben, nämlich genau dann, wenn der gedrehte Vektor \(R_\Phi \boldsymbol{x}\) die Nebenbedingung \(F(R_\Phi \boldsymbol{x}) = 0\) erfüllt.
Wie groß dieser Beitrag und wie groß damit das Integral ist, hängt von der Funktion \(F\) ab. Insgesamt berechnet also das Integral zu jedem Vektor \(\boldsymbol{x}\) eine reelle Zahl, deren Wert von der Funktion \(F\) abhängt. Das gesamte Integral definiert also eine reellwertige Funktion des Vektors \(\boldsymbol{x}\), die von der Funktion \(F\) abhängt. Es erweist sich später als günstig, diese Funktion als Kehrwert einer anderen Funktion namens \(\Delta_F(\boldsymbol{x})\) zu schreiben, d.h. wir definieren: \[ \frac{1}{\Delta_F(\boldsymbol{x})} := \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) \] Der Name \(\Delta_F(\boldsymbol{x})\) für die Funktion ist üblich in der Literatur und hat nichts mit irgendwelchen Intervallen etc. zu tun. Der Vorteil, den Kehrwert zu verwenden, liegt darin, dass man später den Term \[ 1 = \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) \] in das Pfadintegral einfügen kann (Achtung: Der großgeschrieben Drehwinkel \(\Phi\) ist nicht der kleingeschriebene Winkel \(\varphi\) des Vektors \(\boldsymbol{x}\), d.h. \(\boldsymbol{x}\) ist für das Integral über \(\Phi\) eine Konstante).
Zur Veranschaulichung schauen wir uns das folgende Beispiele an: \[ F(\boldsymbol{x}) = \varphi \] mit \( \boldsymbol{x} = (x,y) = \) \((r \, \cos{\varphi}, r \, \sin{\varphi}) \) und \( r = |\boldsymbol{x}| \). Die Bedingung \( F(\boldsymbol{x}) = 0 \) läuft also auf \( \varphi = 0 \) heraus, d.h. von allen Vektoren mit gleichem Betrag erfüllt derjenige in Richtung der \(x\)-Achse gerade die Bedingung.
Was bedeutet dann die Bedingung \( F(R_\Phi \boldsymbol{x}) = 0 \) ? Sie sagt, dass der um \(\Phi\) gedrehte Vektor \(R_\Phi \boldsymbol{x}\) in Richtung der \(x\)-Achse zeigen muss. Das bedeutet, dass \( F(R_\Phi \boldsymbol{x}) = \Phi + \varphi = 0 \) sein muss, also \( \Phi = - \varphi \). Wir müssen also den Vektor \(\boldsymbol{x}\), der im Winkel \(\varphi\) zur waagerechten \(x\)-Achse steht, mit \(R_\Phi\) um den Winkel \( \Phi = - \varphi \) drehen, sodass anschließend \(R_\Phi \boldsymbol{x}\) in Richtung der \(x\)-Achse zeigt und somit \( F(R_\Phi \boldsymbol{x}) = 0 \) wird. Für das Integral folgt: \[ \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) = \int d\Phi \; \delta(\Phi + \varphi) = 1 \] so dass \( \Delta_F(\boldsymbol{x}) = 1 \) ist. In diesem sehr einfachen Fall hätten wir uns also die Definition der Funktion \( \Delta_F(\boldsymbol{x}) \) sparen können.
Sobald die Bedingungsfunktion \(F\) jedoch etwas komplizierter ist, sieht die Sache anders aus. In Polarkoordinaten \(r\) und \(\varphi\) können wir \(F(\boldsymbol{x})\) in der Form \( F(r, \varphi) \) schreiben (wir verzichten der Einfachheit halber auf ein neues Funktionssymbol). Analog ist \( F(R_\Phi \boldsymbol{x}) = F(r, \Phi + \varphi) \). Die Funktion \(F\) muss nun bei jedem gegebenem \(r\) genau für einen Winkel (nennen wir ihn \( \varphi_r \) ) eine Nullstelle haben – so ist gewährleistet, dass von allen Vektoren gleichen Betrags nur einer die Bedingung erfüllt. Es ist also \( F(r, \varphi_r) = 0 \). Anders ausgedrückt legt die Bedingung \( F(r, \varphi_r) = 0 \) den Wert von \( \varphi_r \) als Funktion von \(r\) eindeutig fest (man spricht hier von impliziten Funktionen).
Schauen wir uns nun wieder das Integral an: \[ \frac{1}{\Delta_F(\boldsymbol{x})} = \] \[ = \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) = \] \[ = \int d\Phi \; \delta(F(r, \Phi + \varphi)) = \] \[ = \frac{1}{|\partial_\varphi F(r, \varphi_r)|} \] mit der partiellen Ableitung \( \partial_\varphi F = \frac{\partial}{\partial \varphi}F \) ausgewertet an der Stelle \(\varphi_r\). Die letzte Zeile gilt aufgrund einer allgemeinen Rechenregeln für die Delta-Funktion: Wenn \(g\) nur die Nullstelle \(x_0\) hat, dann ist \(\delta(g(x)) = \frac{\delta(x-x_0)}{|g'(x_0)|}\) mit der abgeleiteten Funktion \(g'\) (siehe Wikipedia: Delta-Distribution).
Insgesamt haben wir also: \[ \Delta_F(\boldsymbol{x}) = |\partial_\varphi F(r, \varphi_r)| \] Genau diesen Faktor würden wir unterschlagen, wenn wir einfach nur einen Faktor \( \delta(F(\boldsymbol{x})) \) in das Wirkungsintegral \[ W = \int d^2x \, e^{i \, S(\boldsymbol{x})} \] eingefügt hätten. Stattdessen müssen wir den Faktor \[ 1 = \int d\Phi \; \delta(F(R_\Phi \boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) \] im Integranden einfügen und können dabei die Winkel-Integration vorziehen: \[ W = \int d^2x \, e^{i \, S(\boldsymbol{x})} = \] \[ = \int d\Phi \int d^2x \, e^{i \, S(\boldsymbol{x})} \, \delta(F(R_\Phi \boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) = \] \[ =: \int d\Phi \, W_\Phi \] mit \[ W_\Phi := \int d^2x \, e^{i \, S(\boldsymbol{x})} \, \delta(F(R_\Phi \boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) \] Wir sehen, dass neben der Deltafunktion \( \delta(F(R_\Phi \boldsymbol{x})) \) auch noch die Funktion \(\Delta_F(\boldsymbol{x})\) in \(W_\Phi\) auftritt.
Hängt \(W_\Phi\) überhaupt von \(\Phi\) ab? Ist die Drehung \(R_\Phi\) überhaupt relevant, oder können wir \(\Phi\) gleich Null setzen und damit \(R_\Phi\) weglassen, so dass wir unsere ursprünglich angedachte Deltafunktion \( \delta(F(\boldsymbol{x})) \) erhalten?
Um das herauszufinden, setzen wir \( R_\Phi \boldsymbol{x} =: \boldsymbol{x}' \), d.h. \(\boldsymbol{x}'\) ist gegenüber \(\boldsymbol{x}\) um den Winkel \(\Phi\) nach links gedreht. Das Flächenmaß \(d^2x\) ist rotationsinvariant, d.h. \(d^2x = d^2x'\). Dasselbe hatten wir für die Wirkung vorausgesetzt (da sie nur vom Betrag des Vektors abhängen soll): \( S(\boldsymbol{x}) = S(\boldsymbol{x}') \). Bleibt die Frage, was mit \( \Delta_F(\boldsymbol{x}) \) los ist. Schauen wir es uns an: \[ \frac{1}{\Delta_F(\boldsymbol{x}')} = \] \[ = \int d\Phi' \; \delta(F(R_{\Phi'} \, \boldsymbol{x}')) = \] \[ = \int d\Phi' \; \delta(F(R_{\Phi'} \, R_\Phi \, \boldsymbol{x})) = \] \[ = \int d\Phi' \; \delta(F(R_{(\Phi'+\Phi)} \, \boldsymbol{x})) = \] ... setze \(\Phi'+\Phi =: \Phi''\), d.h. \(d\Phi' = d\Phi''\) für jedes vorgegebene \(\Phi\): \[ = \int d\Phi'' \; \delta(F(R_{\Phi''} \, \boldsymbol{x})) = \] \[ = \frac{1}{\Delta_F(\boldsymbol{x})} \] denn es ist egal, ob der Integrationswinkel nun \(\Phi'\) oder \(\Phi''\) heißt. Also ist \[ \Delta_F(\boldsymbol{x}') = \Delta_F(R_\Phi \boldsymbol{x}) = \Delta_F(\boldsymbol{x}) \] und wir können \( W_\Phi\) wie folgt umschreiben: \[ W_\Phi = \] \[ = \int d^2x \, e^{i \, S(\boldsymbol{x})} \, \delta(F(R_\Phi \boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) = \] ... setze wieder \( R_\Phi \boldsymbol{x} =: \boldsymbol{x}' \) : \[ = \int d^2x \, e^{i \, S(\boldsymbol{x})} \, \delta(F(\boldsymbol{x}')) \; \Delta_F(\boldsymbol{x}) = \] ... und verwende wieder \(d^2x = d^2x'\) sowie \( S(\boldsymbol{x}) = S(\boldsymbol{x}') \) und \(\Delta_F(\boldsymbol{x}') = \Delta_F(\boldsymbol{x})\) : \[ = \int d^2x' \, e^{i \, S(\boldsymbol{x}')} \, \delta(F(\boldsymbol{x}')) \; \Delta_F(\boldsymbol{x}') = \] \[ =: W_0 \] Unsere Vermutung hat sich bestätigt: \(W_\Phi\) hängt nicht vom Drehwinkel \(\Phi\) ab, so dass wir es immer durch \(W_0\) ersetzen können. Für das Gesamtintegral \(W\) bedeutet das: \[ W = \int d\Phi \, W_0 \] mit \[ W_0 = \int d^2x \, e^{i \, S(\boldsymbol{x})} \, \delta(F(\boldsymbol{x})) \; \Delta_F(\boldsymbol{x}) = \] (wir haben den Strich in der Integrationsvariablen wieder weggelassen, diese also umbenannt).
Da \(W_0\) nicht von \(\Phi\) abhängt, ist der Term \(\int d\Phi\) ein unabhängiger Volumenfaktor, der gleichsam das Volumen der Invarianzgruppe misst. In unserem Beispiel ist einfach \[ \int d\Phi = 2 \pi \] denn es wird ja über den gesamten Vollkreis integriert.
Analog geht man nun beim unendlich-dimensionalen Pfadintegral vor. An die Stelle des zweidimensionalen Vektors \(\boldsymbol{x}\) tritt die Funktion \( A_\mu(x)\), bei der \(\mu\) und \(x\) als Doppelindex gesehen werden, und an die Stelle der Drehung des Vektors \(R_\Phi \boldsymbol{x}\) tritt die Eichtransformation des Potentials, also die Transformation \(A'^\mu = A^\mu +\partial^\mu \chi\).
Diese Eichtransformation wollen wir noch etwas umschreiben, und zwar in eine Form, die auch bei komplexeren Eichgruppen gültig ist. Ausgangspunkt ist eine sogenannte Eichgruppe \(G\), wobei \(G\) normalerweise eine der Gruppen \(SU(n)\) mit vorgegebenem \(n > 1\) ist. Im Fall der Elektrodynamik ist \(G = U(1)\), also die unitären \(1 \times 1\)-Matrizen. Ein Element \(g\) der Gruppe \(U(1)\) lässt sich also als komplexe Zahl der Form \( g = e^{i \chi} \) schreiben. Die reelle Zahl \(\chi\) ist dabei der Parameter der Gruppe, d.h. sein Wert legt das Gruppenelement \(g\) eindeutig fest. Bei komplexeren Gruppen treten auch mehrere reelle Parameter auf, die man gleichsam als Koordinaten im Raum der Gruppenelemente ansehen kann.
Bei Eichtheorien geht man nun davon aus, dass die Gruppenelemente differenzierbare Funktionen von Raum und Zeit sind – man spricht von lokalen Eichtransformationen. Gleichwertig dazu kann man auch sagen, dass die Gruppenparameter differenzierbare Funktionen von Raum und Zeit sind. In userem Fall ist also \( g = e^{i \chi(x)} \). Warum man so vorgeht, werden wir uns erst im nächsten Kapitel genauer ansehen – hier wollen wir einfach die Vorgehensweise akzeptieren, ohne sie weiter zu hinterfragen.
Man definiert nun auf den Potentialen \(A^\mu(x)\) eine Darstellung der Gruppe \(G\). Wir hatten diesen Begriff bereits früher kennengelernt. Er bedeutet, dass wir eine Umrechnungsvorschrift (einen Operator) \(T_g\) definieren, die aus einer gegebenen Potentialfunktion \(A\) eine neue Potentialfunktion \( A' = T_g A \) errechnet, wobei die Umrechnung durch Angabe eines Gruppenelementes \(g\) aus der Gruppe \(G\) gesteuert wird. Dabei soll sich die Gruppenstruktur auf die Umrechnungsvorschrift übertragen, d.h. wir fordern für zwei beliebige Gruppenelemente \(g\) und \(h\), dass die Beziehung \( T_{g h} = T_g T_h \) gilt.
Wie diese Darstellung nun aussehen muss, werden wir erst im nächsten Kapitel genauer verstehen. Hier wollen wir einfach das Ergebnis zur Kenntnis nehmen: \[ A'^\mu = (T_g A)^\mu = (\partial^\mu g) g^{-1} + g A^\mu g^{-1} \] Für die Eichgruppe \(U(1)\) führt \( g(x) = e^{i \chi(x)} \) zu unserer bekannten Eichtransformation \(A'^\mu = A^\mu +\partial^\mu \chi\).
Wichtig ist dabei, dass bei lokalen Eichtransformationen neben den Potentialfeldern \(A\) auch die Gruppenelemente \(g\) Funktionen von Raum und Zeit sind! Genau genommen hat man daher nicht nur eine Darstellung der Gruppe \(G\), sondern eine Darstellung eines unendlichen Produktes dieser Gruppe mit sich selbst, nämlich je eine pro Raum-Zeitpunkt. Man könnte sagen, dass jeder Funktion \(g\) (mit Werten in \(G\)) einen Operator \(T_g\) zuordnet, der auf den Funktionen \(A\) wirkt (mit Werten in diesem Funktionenraum).
Wir müssen nun die Rotation
\(R_\Phi \boldsymbol{x}\)
durch die Eichtransformation \(T_g A\) ersetzen.
Die Integration über \(\Phi\) wird analog ersetzt durch die Integration
über die Eichgruppe, wobei an jedem Raumpunkt \(\boldsymbol{x}\) zu jeder Zwischenzeit \(t\)
über die Eichgruppe integriert werden muss.
Die genauen Details sollen uns hier nicht interessieren.
Als Ergebnis erwarten wir ein unendlich-dimensionales Integral
über ein Maß \(\mathcal{D}g \),
von dem wir annehmen wollen, dass es invariant
unter Eichtransformationen ist, so wie oben auch das Flächenmaß \(d^2x\)
invariant bei Rotationen war. Auch dür das Maß \(\mathcal{D}A \) nehmen wir diese Eichinvarianz an.
Auf diese Weise ziehen wir gleichsam alle die
Zwischen-Feldkonfigurationen aus dem Pfadintegral heraus, die sich nur
durch Umeichungen voneinander unterscheiden. Das Ergebnis ist
(wir lassen den Term mit \(J\) der Einfachheit halber weg):
\[
W =
\int
\, \mathcal{D}A \; e^{ \frac{i}{\hbar} \, S[A] } =
\]
\[
=
\int \mathcal{D}g
\int
\, \mathcal{D}A \; \delta(F[A]) \; \Delta_F[A] \; e^{ \frac{i}{\hbar} \, S[A] }
\]

Der (unendliche) Faktor \( \int \mathcal{D}g \) entspricht dem Volumen der Eichgruppe \(G\), unendlich oft mit sich selbst multipliziert (nämlich für jeden Raum-Zeitpunkt einmal). Man kann versuchen, \( \int \mathcal{D}g \) als Grenzwert eines unendlich-fachen Integrals über \( dg_1 \, dg_2 \, dg_3 \, ... \) zu definieren, wobei \( dg_i \) jeweils das sogenannte Haar'sche Maß der Gruppe \(G\) ist. Der Faktor \( \int \mathcal{D}g \) drückt die Tatsache aus, dass im ursprünglichen Pfadintegral über viele zueinander gleichwertige (d.h. ineinander eichtransformierbare) Feldkonfigurationen \(A\) integriert wird, und führt zur Divergenz des Pfadintegrals (diese Divergenz drückte sich weiter oben in der Nichtinvertierbarkeit von \(K^{\nu\mu}\) aus). Wir lassen diesen Faktor nun weg (d.h. wir definieren \(W\) neu; der Rest hängt ja nicht von \(g\) ab) und sorgen damit dafür, dass in \(W\) jede Klasse zueinander eichtransformierbarer Potentiale nur einmal berücksichtigt wird:
|
Neudefinition:
\[
W :=
\int
\, \mathcal{D}A \; \delta(F[A]) \; \Delta_F[A] \; e^{ \frac{i}{\hbar} \, S[A] }
\]
mit
\[
\frac{1}{\Delta_F[A]} =
\int \mathcal{D}g
\; \delta(F[T_g A])
\]
|
Das naive Einfügen des Terms \( \delta( F[A] ) \) zur Eichfixierung hätte demnach zu falschen Ergebnissen geführt. Erst zusammen mit dem Funktional \( \Delta_F[A] \) erhält man die korrekte Quantisierung. Dabei spielt \( \Delta_F[A] \) gleichsam die Rolle eines Gewichtsfaktors, mit dem die durch ein bestimmtes \(A\) (das \(F[A] = 0\) erfüllt) repräsentierte Klasse ineinander eichtransformierbarer Felder in das Pfadintegral eingeht.
Das Funktional \( \delta( F[A] ) \) lässt sich als unendlich-dimensionale Verallgemeinerung einer Determinante interpretieren und wird auch als Faddeev-Popov-Determinante bezeichnet (was das bedeutet, sehen wir etwas weiter unten). Um den Grund dafür zu erkennen, schauen wir uns noch einmal die Definition an: \[ \frac{1}{\Delta_F[A]} = \int \mathcal{D}g \; \delta(F[T_g A]) \] Wir betrachten nun \(F[T_g A]\) für festes \(A\) als Funktion von \(g(x)\) (wobei wir \(g(x)\) wieder als unendlich-dimensionalen Vektor mit Index \(x\) betrachten). Nun führen wir die neuen Variablen \(y\) ein durch \[ y := F[T_g A] \] wobei wir \(A\) festhalten. Wir wechseln also von dem Vektor \(g\) zum Vektor \(y\) als Integrations-Variable, d.h. \(y\) ist wie \(g\) zuvor eine Funktion von \(x\). Auf diese Weise erreichen wir, dass in der Delta-Funktion nur noch die Variable \(y\) steht. Dazu muss \(F\) entsprechende Eigenschaften haben (Invertierbarkeit an bestimmten Stellen usw.).
Für den Variablenwechsel gilt nun in Verallgemeinerung des endlich-dimensionalen Falls: \[ \mathcal{D}g = \frac{\mathcal{D}y}{\det{\left(\frac{\delta y}{\delta g}\right)}} \] (was das genau bedeutet, klären wir gleich). Dies setzen wir nun oben ein: \[ \frac{1}{\Delta_F[A]} = \] \[ = \int \mathcal{D}g \; \delta(F[T_g A]) = \] \[ = \int \frac{\mathcal{D}y}{\det{\left(\frac{\delta y}{\delta g}\right)}} \; \delta(y) = \] \[ = \frac{1}{\det{\left(\frac{\delta y}{\delta g}\right)}\bigg|_{y=0}} \] d.h. wir erhalten \[ \Delta_F[A] = \det{\left(\frac{\delta y}{\delta g}\right)}\bigg|_{y=0} \] Schauen wir uns für die Elektrodynamik die Determinante genauer an. Die zentrale Formel bei der Definition einer solchen unendlichdimensionalen Determinante ist \[ \det{B} = e^{\mathrm{Spur} \, (\log{B})} \] Hier ist eine kurze Skizze, wie man mit solchen Determinanten umgeht (siehe z.B. Eduardo Fradkin: Path Integrals in Quantum Mechanics and Quantum Field Theory:
Betrachten wir zunächst im endlichdimensionalen Fall eine diagonalisierbare Matrix \(B\) mit Eigenwerten \(b_i\). Dann ist die Determinante gegeben durch das Produkt dieser Eigenwerte: \[ \det{B} = b_1 \, b_2 \, ... \, b_n \] Um zum unendlichdimensionalen (kontinuierlichen) Fall übergehen zu können, ist es nützlich, statt des Produktes eine Summe zu verwenden, denn diese würde dann in ein Integral übergehen. Dies erreichen wir durch Bilden des (natürlichen) Logarithmus der obigen Formel: \[ \log{(\det{B})} = \] \[ = \log{b_1} + \log{b_2} + \, ... \, + \log{b_n} = \] \[ =: \mathrm{Spur} \, (\log{B}) \] was uns nach Exponentieren zur obigen Formel \[ \det{B} = e^{\mathrm{Spur} \, (\log{B})} \] führt.
Wie sieht \( B = \frac{\delta y}{\delta g} \) nun in der Elektrodynamik aus? Das hängt wegen \(y := F[T_g A]\) natürlich von der Eichbedingung \(F\) ab. Schauen wir uns als Beispiel die Lorentzeichbedingung \( F[A] = \partial_\mu A^\mu \) an. Außerdem ist \(G\) gleich der Gruppe \(U(1)\), d.h. \( g(x) = e^{i \chi(x)} \) und \( A'^\mu(x) = (T_g A)^\mu(x) = A^\mu(x) + \partial^\mu \chi(x)\), so dass wir \[ y = F[T_g A] = \partial_\mu A^\mu + \partial_\mu \partial^\mu \chi \] erhalten.
Um die Funktionalableitung (siehe letztes Kapitel) auszurechnen, verwenden wir \[ g_\epsilon := e^{i (\chi + \epsilon \eta)} \] mit einem reellen Parameter \(\epsilon\) und einer beliebigen differentierbaren reellwertigen Funktion \(\eta(x)\). Die Definition der Funktionalableitung lautet in Verallgemeinerung der Definition aus dem letzten Kapitel: \[ \frac{\delta y}{\delta g}[\eta] = \] \[ = \frac{\delta F[T_g A]}{\delta g}[\eta] = \] \[ = \frac{d}{d \epsilon} F[T_{g_\epsilon} A] |_{\epsilon = 0} = \] \[ = \frac{d}{d \epsilon} \left( \partial_\mu A^\mu + \partial_\mu \partial^\mu (\chi + \epsilon \eta) \right) = \] \[= \partial_\mu \partial^\mu \eta \] d.h. \(\frac{\delta y}{\delta g}\) ist ein linearer Operator (so muss es auch sein), und zwar hier der Wellenoperator \(\partial_\mu \partial^\mu\).
Wie sieht nun die Determinante dieses Operators aus? Nach dem oben gesagten brauchen wir dazu die Eigenwerte \(b_n\) des Operators. Die Logarithmen dieser Eigenwerte müssen wir aufsummieren bzw. aufintegrieren, und das Ergebnis als Argument der Exponentialfunktion verwenden. Dies führt jedoch häufig zu divergenten Ausdrücken und ist als Hinweis darauf zu werten, dass wir bei der Definition der Determinante linearer Operatoren noch nicht genug Sorgfalt angewendet haben (der endlich-dimensionale Fall lässt sich eben doch nicht ohne Weiteres auf den unendlich-dimensionalen Fall übertragen).
Man kann mathematische Methoden finden, um dennoch eine sinnvolle Definition einer Determinante eines Operators \(B\) aufzustellen. Man verfährt dabei ähnlich zu der Methode, mit der man die unendlichen Reihe \[ \zeta(s) := 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ... \] (ja, das ist die berühmte Zetafunktion) die zunächst nur für komplexe \(s\) mit Realteil größer als \(1\) definiert ist, auch auf andere \(s\)-Werte analytisch fortzusetzen kann (siehe Kapitel 5.2 Die Riemannsche Vermutung ).
Statt den Summanden \(\frac{1}{n^s}\) mit \(n = 1, 2, 3, \, ... \) verwendet man aber hier \(\frac{1}{b_n^s}\), wobei \(b_n\) die Eigenwerte des Operators \(B\) sind: \[ \zeta_B(s) := \frac{1}{b_1^s} + \frac{1}{b_2^s} + \frac{1}{b_3^s} + \, ... \] bzw. statt der Summe ein Integral bei kontinuierlichen Eigenwerten. Diese spezielle Zetafunktion des Operators \(B\) konvergiert zunächst wieder nur für komplexe \(s\) mit hinreichend großem Realteil, lässt sich aber zumeist auf andere \(s\) analytisch fortsetzen und so dort definieren (insbesondere bei \(s = 0\)).
Wir leiten nun formal die Reihe nach \(s\) an der Stelle \(s = 0\) ab. Wegen \[ \frac{d}{ds} \frac{1}{b_n^s} = \frac{d}{ds} e^{-s \, \log{b_n}} = - (\log{b_n}) \, e^{-s \, \log{b_n}} \] gilt (der Exponentialterm wird an der Stelle \(s = 0\) gleich Eins): \[ \frac{d}{ds} \zeta_B(s)|_{s=0} = \] \[ = - \left( \log{b_1} + \log{b_2} + \log{b_3} + \, ... \right) = \] \[ = = -\log{(\det{B})} \] Diese Formeln sind jedoch keine präzise Herleitung, sondern eher eine Motivation, denn die Reihe konvergiert normalerweise für \(s = 0\) nicht. Genauer macht man folgendes: Man ermittelt die analytische Fortsetzung der Reihe, so dass man eine Funktion \(\zeta_B(s)\) erhält, die auch bei \(s = 0\) definiert ist, und definiert nun die Determinante des Operators \(B\) durch die Gleichung \[ \det{B} := e^{- \frac{d}{ds} \zeta_B(s)|_{s=0}} \] Die Erfahrung und der Vergleich mit anderen Berechnungen zeigt, dass diese Methode zu sinnvollen Ergebnissen führt.
Wir wollen hier die Details nicht weiter verfolgen, sondern nur erwähnen, dass die Determinante des Wellenoperators physikalisch etwas mit der Energie des Grundzustandes zu tun hat und in gewissem Sinn gleichsam die Vakuumfluktuationen wiederspiegelt. Weiter haben wir oben gesehen, dass für die Elektrodynamik die Funktion \( \Delta_F[A] \) von \(A\) unabhängig ist. Bei allgemeineren Eichtheorien ist das leider nicht so einfach. Man geht hier sehr trickreich vor und schreibt \( \Delta_F[A] \) als ein Gauß-Integral über sogenannte Geistfelder. Diese Geistfelder sind Elemente sogenannter Grassmann-Algebren, d.h. eine Vertauschung zweier solcher Felder ergibt ein Minuszeichen. Geistfelder sind unphysikalische Hilfsfelder, die man benötigt, um den Formalismus konsistent zu halten. Auch hier wollen wir nicht weiter ins Detail gehen.
Mit Hilfe des Pfadintegrals lassen sich nun alle Amplituden der Quantenelektrodynamik berechnen, die man auch im Rahmen der kanonischen Quantisierung mit Hilfe von Operatoren und Hilberträumen berechnen kann – mit demselben Ergebnis. Die Pfadintegralmethode hat damit ihre erste Bewährungsprobe bestanden. Für komplexere Eichtheorien und auch für andere Theorien wie beispielsweise die Stringtheorie ist sie sowieso die einzige praktikable Methode, um von einer klassischen Theorie zu einer Quantentheorie zu gelangen – die kanonische Quantisierung aus dem letzten Kapitel führt hier zu großen Problemen. Richard Feynman hatte also wohl den richtigen Riecher, als er die Pfadintegralmethode zu einer Zeit ersann, als fast jeder andere noch ausschließlich an Poissonklammern, Hilberträume, Operatoren und Kommutatoren dachte, wenn das Wort Quantisierung fiel. Im nächsten Kapitel wollen wir uns nun genauer anschauen, wie die erwähnten komplexeren Eichtheorien aussehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 04 June 2023