
Rechts: Gottfried Leibniz (1646-1716), gemalt von Christoph Bernhard Francke um 1700.
Quellen: Wikimedia Commons File:GodfreyKneller-IsaacNewton-1689.jpg, Wikimedia Commons File:Gottfried Wilhelm von Leibniz.jpg, beide dort public domain.
Die Definition der Zeit
Die Zeit in der Speziellen Relativitätstheorie
Die Zeit im Gravitationsfeld (Allgemeine Relativitätstheorie)
Entropie und das Rätsel des Zeitpfeils
Der quantenmechanische Messprozess und die zeitlose Welt der Quantengravitation
"Es gibt ein großes und doch ganz alltägliches Geheimnis. Alle Menschen haben daran teil, jeder kennt es, aber die wenigsten denken je darüber nach. Die meisten Leute nehmen es einfach so hin und wundern sich kein bisschen darüber. Dieses Geheimnis ist die Zeit."
aus Michael Ende: Momo (1973)
Was ist Zeit? Wir spüren sie unmitttelbar und haben ein intuitives Zeitempfinden. Zeit scheint zu fließen und sich unaufhaltsam von der Vergangenheit in die Zukunft zu entwickeln, wobei es immer einen ausgezeichneten Zeitpunkt zu geben scheint: die Gegenwart. Vergangene Zeit ist unwiederbringlich verloren und kann nicht zurückgeholt werden. Reisen durch die Zeit scheinen unmöglich zu sein, und doch hat die Zeit auch viele Ähnlichkeiten mit einer räumlichen Dimension, denn sowohl Zeit- als auch Raumpunkte werden durch ein Kontinuum reeller Zahlen beschrieben – nur dass man die Raumdimensionen ungehindert bereisen kann, die Zeitdimension aber nicht.
Für viele dieser Eigenschaften der Zeit bietet die moderne Physik heute Erklärungen an, die unserer menschlichen Vorstellungskraft einiges abverlangen, denn es stellt sich heraus: Die Zeit ist einer der rätselhaftesten Begriffe in der Physik, und sie lässt sich erst in einem tiefgehenden und umfassenden Bild unseres Universums verstehen. Was also ist Zeit? Wie ist der Begriff der Zeit eigentlich definiert?
Eine der bekanntesten Definitionen stammt von Isaac Newton, der im Jahr 1687 – also vor über 300 Jahren – schrieb:
"Die absolute, wahre und mathematische Zeit verfließt an sich und vermöge ihrer Natur gleichförmig und ohne Beziehung auf irgendeinen äußeren Gegenstand."
Diese Definition entspricht unserem intuitiven Zeitempfinden.
Mathematisch bedeutet sie, dass die Zeit in den physikalischen Bewegungsgleichungen
als äußerer Parameter auftritt, der die zeitliche Entwicklung
eines physikalischen Systems kennzeichnet, ohne selbst vom System beeinflusst zu werden.
Beispielsweise wird die Bahnkurve eines Teilchens durch eine Funktion
\( \boldsymbol{x}(t) \)
dargestellt, die der Newtonschen Bewegungsgleichung
\begin{equation}
m \, \frac{d^2\boldsymbol{x}}{dt^2} = \boldsymbol{F}(\boldsymbol{x})
\end{equation}
gehorcht.
Dabei ist das äußere Kraftfeld \(\boldsymbol{F}\) vorgegeben und man sucht die Bahnkurve
\( \boldsymbol{x}(t) \) als Lösung dieser Gleichung.
Die Zeit \(t\) wird durch die Gleichung in keiner Weise eingeschränkt.
Die einzige Nebenbedingung, die man an die Parametrisierung der Bahnkurve durch die Zeit \(t\) dabei
stellt, liegt darin, dass die äußere Kraft \(\boldsymbol{F}\) möglichst einfach sein soll.
Anschaulich bedeutet das, dass die Zeit \(t\) gleichmäßig verstreichen soll,
sodass keine Scheinkräfte notwendig sind, wie sie bei einer ungleichmäßigen Zeitparametrisierung
auftreten würden (ähnlich der Scheinkräfte in einem beschleunigten Bezugssystem).
Anders ausgedrückt: Gibt es keine erkennbaren äußeren Einflüsse (Kräfte),
so soll die Bewegung geradlinig-gleichförmig sein.
Wer es mathematisch exakt haben möchte:
Scheinkräfte würden auf der rechten Seite der obigen Gleichung auftreten,
wenn man eine Umparametrisierung
\( \boldsymbol{y}(t) := \boldsymbol{x}(f(t)) \)
der Bahnkurve mit einer nichtlinearen Funktion \(f\) vornehmen würde (z.B. eine Exponentialfunktion).
Anschaulich betrachtet vergeht die Zeit dann nicht mehr gleichförmig, wie es Newton in seiner
Definition vorausgesetzt hatte.
Offenbar kommt also auch Newtons Zeitdefinition nicht so ganz ohne ein physikalisches Objekt aus, dessen zeitliche Veränderung wir betrachten können, und sei es nur die Bahnkurve eines Teilchens. Wir brauchen also irgendetwas, das sich zeitlich verändert, um dem Zeitbegriff überhaupt einen praktischen Sinn zu geben. Newtons Zeitgenosse und zeitweiliger Konkurrent Gottfried Wilhelm Leibniz betrachtete sogar die Zeit – und ebenso den Raum – lediglich als gedankliches Konstrukt, das keine eigene Existenz besitzt:
"Die Zeit ist die Ordnung des nicht zugleich Existierenden. Sie ist somit die allgemeine Ordnung der Veränderungen, in der nämlich nicht auf die bestimmte Art der Veränderungen gesehen wird."
Gottfried Wilhelm Leibniz: Die metaphysischen Anfängen der Mathematik in Handschriften zur Grundlage der Philosophie II, S. 35 ff.

Rechts:
Gottfried Leibniz (1646-1716), gemalt von Christoph Bernhard Francke um 1700.
Quellen:
Wikimedia Commons File:GodfreyKneller-IsaacNewton-1689.jpg,
Wikimedia Commons File:Gottfried Wilhelm von Leibniz.jpg,
beide dort public domain.
Wer mehr darüber erfahren möchte, wie Newton und Leibniz vor dem Hintergrund ihrer Epoche über den Zeitbegriff stritten, dem möchte ich das Buch von Thomas de Padova: Leibniz, Newton und die Erfindung der Zeit (Piper 2013, Buchseite des Verlags) ans Herz legen.
Auch viele andere Philosophen haben über die Zeit nachgedacht und sind zu den unterschiedlichsten Definitionen gekommen. Wir merken also: Mit der abstrakten Definition physikalischer Begriffe ist das so eine Sache. Meist ist es gar nicht möglich, physikalische Begriffe absolut exakt zu definieren. So schrieb Richard Feynman in seinen Feynman Lectures Band I, 8-1:
"We cannot define anything precisely! If we attempt to, we get into that paralysis of thought that comes to philosophers, who sit opposite each other, one saying to the other, "You don't know what you are talking about!" The second one says, "What do you mean by know? What do you mean by talking? What do you mean by you?," and so on. In order to be able to talk constructively, we just have to agree that we are talking about roughly the same thing."
Und auch Albert Einstein machte zusammen mit L. Infeld in Die Evolution der Physik klar, dass physikalische Begriffe wie die Zeit keineswegs eindeutig durch die Natur vorgegeben sind, sondern eher intuitiv erfasst werden:
"Physikalische Begriffe sind freie Schöpfungen des Geistes und ergeben sich nicht etwa, wie man sehr leicht zu glauben geneigt ist, zwangsläufig aus den Verhältnissen in der Außenwelt."
(siehe z.B. Claus Kiefer: Der Quantenkosmos, S. 307). Mehr noch als auf die Zeit trifft dies beispielsweise auf die Begriffe Energie, Kraft und Impuls zu. So hat erst Isaac Newton dem Begriff der Kraft eine klare physikalische Bedeutung gegeben, während man davor oft suchend im Nebel möglicher physikalischer Begriffsbildungen herumstocherte, um die wahre Natur der Bewegungsgesetze zu ergründen.
Zurück zum Zeitbegriff: Was bleibt ohne eine abstrakte Definition der Zeit zu tun? Glücklicherweise stellt sich heraus, dass wir in der Physik gar keine abstrakte Definition der Zeit brauchen, sondern nur wissen müssen, wie wir sie messen können.
"Zeit ist das, was man an der Uhr abliest"
sagte Albert Einstein pragmatisch. Wir brauchen also irgendeinen physikalischen Vorgang, den wir als Zeitmaßstab – also als Uhr – für andere Vorgänge verwenden können. Genau das haben Menschen schon seit Jahrtausenden getan. In der Frühzeit diente beispielsweise der Lauf der Sonne und der Gestirne als Zeitmaßstab; man denke an Sonnenuhren. Eine andere Möglichkeit waren Wasseruhren, bei denen Wasser langsam aus einem Gefäß auslief und der abnehmende Wasserstand als Zeitmaßstab diente; sie waren in der Antike sehr beliebt. Problematisch ist dabei allerdings, dass das Wasser immer langsamer ausläuft, je niedriger der Wasserstand bereits ist, sodass man eine nichtlineare Skala benötigt, um aus dem Wasserstand eine gleichmäßig fließende Zeit abzuleiten.
Besser eignen sich daher periodische Vorgänge, die immer wieder in gleicher Weise ablaufen,
beispielsweise das Hin- und Herschwingen eines Pendels.
Bei solchen Vorgängen können wir davon ausgehen, dass sie immer ungefähr gleich lang dauern, sodass
sie uns einen gleichmäßig ablaufenden Zeitstandard liefern können.
Irgendein genialer Erfinder kam dabei eines Tages auf die Idee, ein schwingendes Pendel
zur Hemmung eines Uhrgetriebes einzusetzen, sodass jede Pendelschwingung ein Zahnrad
des Getriebes um einen Zahn weiterlaufen ließ.
Damit ließen sich erstmals präzise laufende mechanische Uhren entwickeln, die schnell eine weite
Verbreitung fanden.


Rechts:
Eine der Cäsium-Atomuhren der PTB in Braunschweig.
Quellen:
Wikimedia Commons File:Riefler Uhr 01.jpg (public domain),
Wikimedia Commons File:Atomuhr-CS2.jpg,
Urheber: Jörg Behrens, unter der
Creative Commons-Lizenz Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported lizenziert.
Auch andere Schwingungen lassen sich zur Steuerung einer Uhr verwenden, beispielsweise ein schwingender Quarzkristall. Da dessen Schwingungsfrequenz sehr viel höher ist als die eines mechanischen Pendels, kann man mit ihm viel präzisere Uhren bauen als mit einem Pendel. Seit den siebziger Jahren hat sich die Quarzuhr fast überall durchgesetzt und mechanische Uhren weitgehend verdrängt.
Noch genauer als Quarzuhren sind die sogenannten Atomuhren, bei denen der Strahlungsübergang zwischen zwei Energieniveaus in bestimmten Atomen ausgenutzt wird. Die elektromagnetische Strahlung, die ein Atom bei einem solchen Übergang aussendet oder absorbiert, hat dabei eine sehr genau messbare Frequenz, sodass man die Zahl der Schwingungen dieser Strahlung als Zeitmaßstab verwenden kann. Moderne Atomuhren schaffen es heute, mithilfe eines bestimmten Strahlungsübergangs von Caesiumatomen die Maßeinheit Sekunde mit einer Genauigkeit von 10−15 festzulegen – eine Atomuhr geht in 20 Millionen Jahren also höchstens eine Sekunde vor oder nach. Dabei umfasst eine Sekunde per Definition genau 9.192.631.770 Schwingungen.
Es gibt in der Natur sogar einen noch genaueren periodischen Vorgang, den man im Prinzip als Zeitmaßstab verwenden kann: die Rotation von schnell rotierenden Neutronensternen – sogenannten Pulsaren. Ein solcher Pulsar kann bis zu Tausend Mal pro Sekunde rotieren und dabei wie ein Leuchtturm bei jeder Umdrehung ein elektromagnetisches Signal zur Erde senden, das sich beispielsweise mit Radioteleskopen empfangen lässt. Da ein Pulsar mehr als eine Sonnenmasse in einer Kugel von nur rund 10 bis 20 km Radius beherbergt, ist seine Rotation extrem stabil und unempfindlich gegen äußere Störungen, sodass er sein Signal wie eine kosmische Hochpräzisionsuhr in das Weltall hinaussendet. Dabei nimmt seine Rotationsgeschwindigkeit aufgrund der abgestrahlten Energie im Lauf der Zeit sehr langsam und gleichmäßig ab.
Wir sind also in der Lage, die Zeit zu messen und ihr damit eine physikalische Bedeutung zu geben. Ist damit das Rätsel der Zeit bereits umfassend gelöst? Keineswegs, denn die so definierte Zeit erweist sich als komplexe physikalische Größe.
So machte Albert Einstein im frühen zwanzigsten Jahrhundert im Rahmen seiner
Speziellen Relativitätstheorie eine erstaunliche Entdeckung:
Es gibt gar keine absolute Zeit! Die Zeit, die ein Beobachter auf einer schnell
vorbeifliegenden Uhr abliest,
läuft umso langsamer, je schneller sich die Uhr bewegt – man spricht von Zeitdilatation.

Quelle:
Wikimedia Commons,
Urheber: Ferdinand Schmutzer (1870-1928), Copyright abgelaufen.
Man kann sich diesen Effekt leicht erklären, wenn man das grundlegende Prinzip der Speziellen Relativitätstheorie berücksichtigt:
Der Prototyp eines solchen Inertialsystems ist dabei ein Raumschiff, das ohne jeden Antrieb gleichmäßig durch den leeren Weltraum gleitet. In dem Raumschiff muss also Schwerelosigkeit herrschen, sodass ein einmal angestoßener Gegenstand darin geradlinig-gleichförmig weiterfliegt, wenn man Reibungskräfte vermeidet. Misst ein mitfliegender Astronaut nun die Lichtgeschwindigkeit relativ zu den Wänden des Raumschiffs, so findet er immer denselben Wert: knapp 300000 Kilometer pro Sekunde. Dabei ist es egal, wie schnell sich das Raumschiff selbst bewegt. Ohne einen Blick nach draußen kann der Astronaut mit keinem einzigen Experiment die Geschwindigkeit des Raumschiffs bestimmen, auch nicht durch eine Messung der Lichtgeschwindigkeit innerhalb des Raumschiffs.
Das ist sehr überaschend, denn ein ruhender außenstehender Beobachter könnte beispielsweise beobachten, dass sich das Raumschiff bereits mit 90 % der Lichtgeschwindigkeit bewegt, sodass in Flugrichtung nur noch 10 % der Lichtgeschwindigkeit fehlen, um mit einem Lichtstrahl mitfliegen zu können. Man würde daher eigentlich erwarten, dass für einen Astronauten im Raumschiff sich ein Lichtstrahl in Flugrichtung nur noch mit 10 % der Lichtgeschwindigkeit bewegt. Würde sich das Raumschiff gar mit Lichtgeschwindigkeit bewegen, so müsste für den Astronauten das Licht in Flugrichtung sogar stillstehen. Das kann aber nicht sein, wie Albert Einstein bemerkte, denn einen stillstehenden Lichtstrahl kann es für keinen Beobachter geben – er ist beispielsweise keine Lösung der Maxwellgleichungen, die das Verhalten von Licht beschreiben. Nach den Maxwellgleichungen muss Licht immer mit Lichtgeschwindigkeit fliegen, so wie Einstein es schließlich als Grundprinzip seiner Theorie gefordert hat.
Was aber müssen wir dann an unserem anschaulichen Bild ändern? Es stellt sich heraus, dass der außenstehende Beobachter und der Astronaut im fliegenden Raumschiff räumliche und zeitliche Abstände sowie die Gleichzeitigkeit von Ereignissen unterschiedlich beurteilen. Beide verwenden ein unterschiedliches Koordinatensystem für Raum und Zeit, oder kurz: für die Raumzeit. Nur so ergibt sich insgesamt wieder ein konsistentes Bild.
Schauen wir uns das für die Zeit genauer an:
Dazu bauen wir eine spezielle Lichtuhr, in der ein Lichtblitz zwischen zwei parallelen
Spiegeln hin- und herpendelt. Dieses Pendeln des Lichtblitzes ist nun gleichsam das Ticken
der Uhr. Unser ruhender außenstehender Beobachter erhält nun eine solche Lichtuhr,
und unser Astronaut im Raumschiff erhält ebenfalls eine solche Lichtuhr.
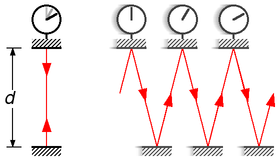
Der außenstehende Beobachter sieht nun, wie der Lichtblitz auf der bewegten Uhr des Astronauten
auf einer schrägen Bahn zwischen den beiden Spiegeln pendelt. Da diese schräge Bahn
länger ist als die Bahn zwischen den Spiegeln seiner ruhenden Uhr, und da das Licht
immer dieselbe Geschwindigkeit hat, benötigt es aus Sicht des ruhenden Beobachters
für einen Pendelvorgang im Raumschiff länger
als auf seiner ruhenden Uhr. Er kommt zu dem Schluss, dass die bewegte Lichtuhr im Raumschiff
langsamer tickt als seine eigene ruhende Uhr.
Quelle:
Wikimedia Commons File:Light-clock.png, Urheber: Michael Schmid,
dort u.a. lizensiert unter der
Creative Commons-Lizenz
Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported.
Ganz anders sieht dieselbe Situation für den mitfliegenden Astronauten aus: Für ihn ruht seine Lichtuhr, und das Licht bewegt sich mit Lichtgeschwindigkeit auf geradem Weg zwischen den beiden Spiegeln hin und her. Die aus seiner Sicht bewegte Uhr des äußeren Beobachters geht dagegen offenbar langsamer.
Eine Lichtuhr ist nun nichts besonderes. Man könnte ja beispielsweise dem äußeren Beobachter und dem Astronauten noch je eine mechanische Pendeluhr mitgeben. Beide würden schwören, dass ihre Pendeluhr synchron mit ihrer jeweiligen Lichtuhr mitläuft. Also muss für den äußeren ruhenden Beobachter die Pendeluhr des Astronauten ebenfalls langsamer laufen und umgekehrt.
Die Tatsache, dass für den ruhenden Beobachter die bewegte Uhr des Astronauten langsamer läuft, ist dabei kein Scheineffekt oder irgendeine Art von Einbildung. Es handelt sich um einen ganz realen physikalischer Effekt. Beispielsweise müssten Myonen (instabile schwere Verwandte des Elektrons), die aufgrund der kosmischen Strahlung in der oberen Atmosphäre entstehen, eigentlich bereits zerfallen sein, bevor sie den Erdboden erreichen. Aufgrund ihrer großen Geschwindigkeit (vom Erdboden aus gesehen) zerfallen sie aber wesentlich langsamer als ruhende Myonen, sodass sie den Erdboden dennoch erreichen können.
Dass der Effekt der Zeitdilatation ganz real ist, zeigt auch das Zwillingsparadoxon. Dazu schicken wir den Astronauten mit seinem Raumschiff auf eine Rundreise. Beim Start synchronisiert er seine Uhr mit der des zurückbleibenden ruhenden Beobachters und beschleunigt anschließend, um in der Ferne zu entschwinden. Irgendwann kehrt er um und landet schließlich wieder am Ort des ruhenden Beobachters. Beide vergleichen nun ihre Uhren: Auf der Uhr des Astronauten ist weniger Zeit vergangen als auf der Uhr des ruhenden Beobachters.
Klar – er war ja auch zwischendurch mit hoher Geschwindigkeit unterwegs, sodass seine Uhr aus Sicht des ruhenden Beobachters langsamer lief. Außerdem sind beide Uhren nicht mehr gleichwertig, anders als wenn sich der Astronaut ständig gleichförmig bewegt wie weiter oben. Der Astronaut hat zwischendurch beschleunigt und gebremst, während der ruhende Beobachter keine Beschleunigung erlebt hat. Auf einer Uhr, die beschleunigt und abgebremst wird, vergeht also weniger Zeit (Eigenzeit genannt) als auf einer ruhenden Uhr, wenn beide Uhren am selben Punkt in Raum und Zeit starten und an einem anderen Raum-Zeit-Punkt wieder zusammenfinden. Übrigens muss die Uhr mit der größeren Eigenzeit nicht unbedingt ruhen, denn wir können uns dieselbe Situation auch aus einem gleichmäßig dahindriftenden Raumschiff heraus ansehen: dann bewegt sich die zuvor ruhende Uhr nun gleichmäßig mit konstanter Geschwindigkeit. Wichtig ist dabei, dass beide Uhren zwei gemeinsame Raum-Zeit-Punkte – also Zusammentreffen – haben, nämlich beim Start und bei der Landung. Halten wir dieses wichtige Ergebnis noch einmal fest:
Das bedeutet, dass der Zeitbegriff (genauer: die Eigenzeit, also die auf einer Uhr vergehende Zeit) vom Weg durch Raum und Zeit abhängt – ein wegabhängiger Zeitbegriff also! Man spricht in diesem Zusammenhang auch von der vielfingrigen Zeit (siehe z.B. H. Dieter Zeh: Physik ohne Realität, S. 146).
Man kann das auch geometrisch ausdrücken: So wie im dreidimensionalen Raum die Wegstrecke zwischen zwei Raumpunkten vom eingeschlagenen Weg abhängt, so hängt in der vierdimensionalen Raumzeit (drei Raum- und eine Zeitdimension) die Eigenzeit zwischen zwei Raum-Zeit-Punkten vom eingeschlagenen Weg zwischen diesen Punkten ab. Im dreidimensionalen Raum hat der gerade Weg dabei die kürzeste Wegstrecke, in der vierdimensionalen Raumzeit hat er dagegen die längste Eigenzeit. Dabei hängt die Eigenzeit nicht vom Beobachter ab – alle Beobachter sind sich einig über die Zeit, die auf einer Uhr auf ihrem Weg zwischen zwei Raum-Zeit-Punkten verstreicht! Außerdem hängt die Eigenzeit nicht von der Anwesenheit anderer materieller Objekte in der Raumzeit ab, d.h. sie ist in diesem Sinne absolut gegeben, wenn auch wegabhängig. Das wird sich bei Einbeziehung der Gravitation ändern!
Für Interessierte hier noch etwas Mathematik – wen das weniger interessiert, der kann diesen Abschnitt auch gerne ohne Probleme überspringen und direkt mit der Zeit im Gravitationsfeld fortfahren.
Mathematisch kann man die Wegabhängigkeit der Eigenzeit eines Objektes durch eine entsprechende fest vorgegebene Metrik in der Raumzeit ausdrücken. Das bedeutet: Wenn ein gleichförmig bewegter oder ruhender Beobachter sieht, dass in seinem Bezugssystem eine Uhr ein sehr kurzes nahezu gerades Wegstück der Länge \(ds\) in der Zeit \(dt\) zurücklegt, so vergeht auf dieser Uhr die quadrierte Eigenzeit \begin{equation} d\tau^2 = dt^2 - (ds/c)^2 \end{equation} mit der Lichtgeschwindigkeit \(c\). Man spricht hier deswegen von Metrik, weil diese Formel analog aussieht wie die Formel \( ds^2 = dx^2 + dy^2 \) , mit der man beispielsweise in einer Ebene die Länge eines Wegstücks \(ds\) aus den Koordinatendifferenzen \(dx\) und \(dy\) der zugehörigen Endpunkte ermittelt (man denke an ein rechtwinkliges Dreieck und den Satz von Pythagoras). Allerdings wird in der Raumzeit nicht addiert, sondern zwischen quadriertem Zeit und Raumabstand subtrahiert. Die Metrik der Raumzeit ist also nicht euklidisch – man nennt sie auch Minkowskimetrik zu Ehren des deutschen Mathematikers Hermann Minkowski, der als erster um 1907 die Spezielle Relativitätstheorie mit dieser Metrik in die elegante mathematische Formulierung brachte, die heute überall verwendet wird. Albert Einstein hatte dagegen alles noch gleichsam zu Fuß gerechnet, also ohne die Vorteile dieser metrischen Formulierung.
Wenn nun ein anderer relativ dazu gleichförmig bewegter Beobachter diese kurze Bewegung der Uhr beobachtet, während der auf der Uhr die Eigenzeit \(d\tau\) abläuft, so wird er das Wegintervall, das die Uhr relativ zu ihm zurücklegt, anders sehen, denn die Uhr bewegt sich ja aus seiner Sicht normalerweise mit einer anderen Geschwindigkeit – nennen wir dieses Wegintervall \(ds'\). Außerdem wird er auch das Zeitintervall, in dem die Uhr diese Bewegung ausführt, mit seiner Uhr anders beurteilen (das hätte Newton noch anders gesehen!): Die Uhr legt für ihn also die Wegstrecke \(ds'\) in der Zeit \(dt'\) zurück, während auf ihr die Eigenzeit \(dτ\) abläuft. Es gilt also: \begin{equation} d\tau^2 = dt^2 - (ds/c)^2 = (dt')^2 - (ds'/c)^2 \end{equation} Nimmt man noch die Forderung hinzu, dass beide Beobachter eine geradlinig-gleichförmige Bewegung sehen, so ergibt sich daraus das Umrechnungsgesetz für die Orts- und Zeitkoordinaten der beiden Beobachter – man bezeichnet es als Lorentz-Transformation. Die obige Formel sagt dabei, dass die Minkowskimetrik durch eine Lorentz-Transformation nicht verändert wird, auch wenn sich die Orts- und Zeitkoordinaten der Raumzeit dabei ändern. Ganz anlog ändert eine Drehung im zweidimensionalen Raum zwar die x- und y-Koordinaten der Punkte in der Ebene, nicht aber die euklidische Metrik, also die Länge von Wegstücken.
Dabei zeigt der vordere Teil \( d\tau^2 = dt^2 - (ds/c)^2 \) der Formel: Ruht eine Uhr relativ zum Beobachter (d.h. \(ds = 0\) ), so ist \( d\tau = dt \) , d.h. die betrachtete Uhr läuft synchron mit der Uhr des Beobachters. Bewegt sich die Uhr dagegen relativ zum Beobachter, d.h. ist \( ds > 0 \) , so muss \( dt > d\tau \) sein, wie die Gleichung zeigt. Die Zeit \(dt\) die für den Beobachter verstreicht, ist also größer als die Zeit \(d\tau\), die auf der bewegten Uhr verstreicht – die bewegte Uhr geht also langsamer. Das ist genau die Zeitdilatation, die wir oben kennengelernt haben.
Bewegt sich das Objekt sogar mit Lichtgeschwindigkeit (d.h. \( ds = c \, dt \) ), dann ist \( d\tau = 0 \) , d.h. für das Objekt vergeht überhaupt keine Zeit. Anders gesagt: ein Photon (Lichtteilchen) altert nicht. Dabei zeigt die obige Formel, dass das Photon auch für den zweiten Beobachter mit Lichtgeschwindigkeit fliegt, denn aus \( d\tau = 0 \) folgt \( ds' = c \, dt' \) . Man sieht, wie insbesondere die unterschiedlich beurteilten Zeitintervalle es möglich machen, dass für beide Beobachter das Photon mit Lichtgeschwindigkeit fliegt, selbst wenn sich die Beobachter relativ zueinander geradlinig-gleichförmig bewegen. Und zugleich wird klar, dass eine reale Uhr, auf der noch Zeit verstreicht, niemals die Lichtgeschwindigkeit erreichen kann.
Für krummlinige Wege muss man übrigens einfach sehr viele solche kurzen Wegstücke aufsummieren (genauer: aufintegrieren).
So kann man beispielsweise auch ausrechnen, welche Zeit für den Astronauten auf seiner Rundreise vergeht.
Betrachten verschiedene zueinander geradlinig-gleichförmig bewegte Beobachter eine Uhr,
so bewegt sich für diese Beobachter die Uhr mit unterschiedlichen Geschwindigkeiten.
Wenn auf der Uhr nun eine Zeitspanne \(d\tau\) verstreicht (die sogenannte Eigenzeit der Uhr),
so legt die Uhr in dieser Zeit relativ zu den einzelnen Beobachtern eine unterschiedliche Wegstrecke \(ds\) zurück,
je nachdem, wie schnell sich die Uhr relativ zum Beobachter bewegt.
Diese Wegstrecke \(ds\) ist in der Grafik entlang der x-Achse aufgetragen.
Nur für einen Beobachter, der relativ zur Uhr ruht (sodass für ihn die Uhr die Wegstrecke \( ds = 0 \) zurücklegt),
ist die auf der Uhr ablaufende Zeitspanne \(d\tau\) identisch mit der Zeitspanne \(dt\), die er selber empfindet
(siehe den Punkt links auf der y-Achse).
Wenn sich die Uhr dagegen relativ zum Beobachter bewegt, sodass \( ds > 0 \) wird, dann
dauert es für den Beobachter länger, bis auf der bewegten Uhr die Zeitspanne \(d\tau\) vergangen ist,
d.h. \( dt > d\tau \) . Die bewegte Uhr geht also aus seiner Sicht langsamer – das nennt man Zeitdilatation.
Diese Zeitdilatation wird umso größer, je schneller sich die Uhr bewegt, d.h. je größer die
zurückgelegte Wegstrecke \(ds\) wird, wie die Punkte weiter rechts oben zeigen.
Dabei nähern sich diese Punkte immer mehr der Diagonalen an, erreichen sie jedoch nie.
Diese Diagonale kennzeichnet Weg-Zeit-Intervalle, die Objekte mit Lichtgeschwindigkeit aufweisen,
sodass \( ds = c \, dt \) und \( d\tau = 0 \) ist.
Da die Punkte die Diagonale nie erreichen, kann ein Objekt, für das eine endliche Eigenzeit \(d\tau\) vergeht,
die Lichtgeschwindigkeit nie erreichen, denn für diese Punkte ist immer \( ds < c \, dt \).
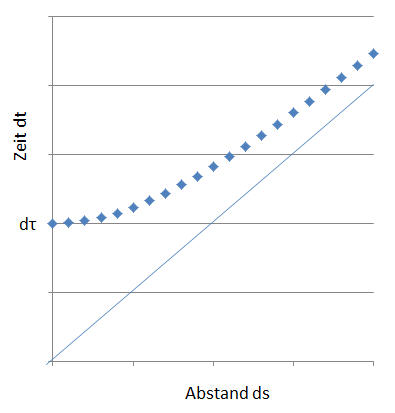
Zugleich vergeht für die verschiedenen Beobachter auch eine unterschiedliche Zeitspanne \(dt\),
die entlang der y-Achse eingetragen ist.
Die blauen Punkte zeigen dabei, welche Kombination aus Wegstrecke \(ds\) und Zeitspanne \(dt\) die
unterschiedlichen Beobachter wahrnehmen, wenn auf der Uhr die feste Zeitspanne \(d\tau\) vergeht.
Sie liegen auf der Hyperbel
\( d\tau^2 = dt^2 - (ds/c)^2 \) .
Albert Einstein fand noch mehr heraus: Die Zeit, die an einem Ort vergeht, hängt vom Gravitationsfeld ab, das die umliegenden Massen erzeugen. Wie kann das sein?
Tatsächlich kann man dieses Verhalten der Zeit gut verstehen, wenn man das grundlegende Prinzip berücksichtigt, auf dem Albert Einstein seine relativistisch korrekte Beschreibung der Gravitation – die Allgemeine Relativitätstheorie – aufbaute. Dieses Prinzip lautet:
Das bedeutet: Wenn sich ein Astronaut in einem fensterlosen Raumschiff befindet,
so kann er ohne einen Blick nach draußen
nicht unterscheiden, ob sich das Raumschiff bewegungslos auf der Startrampe befindet,
oder ob es im leeren Weltraum mit laufendem Antrieb beschleunigt wird.
Die Gravitationskraft ist lokal (also in einem kleinen Raumschiff)
nicht von der Scheinkraft zu unterscheiden, die in einer beschleunigten Rakete alle Gegenstände
nach unten bzw. hinten fallen lässt. Und das bedeutet sofort, dass die Schwere eines Objekts
aus seiner Trägheit resultiert: Schwere und träge Masse sind gleich!
Warum das so ist, konnte erst Einstein mit seinem Äquivalenzprinzip beantworten.
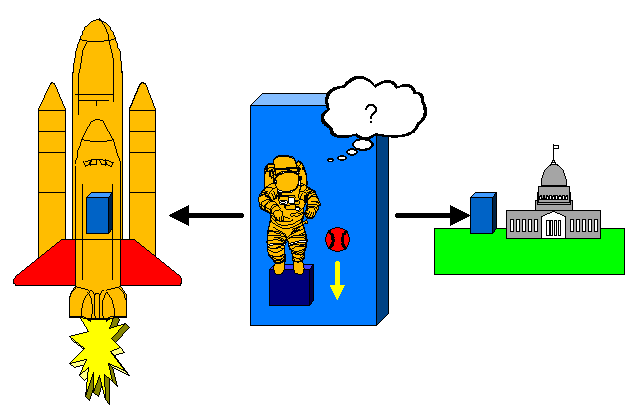
Umgekehrt bedeutet das:
Genau deshalb schweben die Astronauten schwerelos in einer antriebslosen Raumkapsel, denn diese befindet sich im freien Fall um die Erde herum. Freier Fall bedeutet dabei nicht unbedingt, dass man nach unten fällt, sondern es bedeutet, dass man sich ohne jeden Antrieb der Gravitation überlässt, so wie dies auch eine antriebslose Raumkapsel in einer Umlaufbahn tut. In dieser Raumkapsel gelten wieder die Gesetze der Speziellen Relativitätstheorie wie für einen sich gleichmäßig bewegenden Beobachter in einem Raum ohne Schwerkraft.
Auch in einer beschleunigten Raumkapsel gelten ohne Gravitation die Gesetze der Speziellen Relativitätstheorie, aber diesmal gesehen von einem beschleunigten Beobachter aus. Um herauszufinden, was das für die Zeit bedeutet, befestigen wir am Boden der beschleunigten Raumkapsel eine Uhr, die bei jedem Ticken einen Lichtblitz nach oben aussendet. Während der Lichtblitz nach oben wandert, eilt der obere Teil der Raumkapsel mit zunehmender Geschwindigkeit vor ihm davon. Insgesamt führt das dazu, dass die Lichtblitze oben mit größeren Zeitabständen eintreffen, als sie unten ausgesendet wurden. Von oben betrachtet scheint die Uhr am Boden also langsamer zu ticken, als wenn sie oben in der Raumkapsel befestigt wäre. Eine Uhr läuft in der beschleunigten Raumkapsel also unten langsamer als oben, wenn man sie von der beschleunigten Raumkapsel aus betrachtet. Und da nun eine beschleunigte Raumkapsel ohne Gravitation gleichwertig ist zu einer ruhenden Raumkapsel in einem Gravitationsfeld, muss auch im Gravitationsfeld eine Uhr unten langsamer ticken als oben!
Halten wir also fest:
Isaac Newton wäre das wohl vollkommen verrückt erschienen, und doch lässt es sich mit den modernen Atomuhren präzise nachweisen. Für das korrekte Funktionieren des GPS-Systems muss dieser Effekt sogar unbedingt berücksichtigt werden, damit Ihr Navigationsgerät seine Position genau bestimmen kann. Im Extremfall eines Schwarzen Lochs bleibt von außen betrachtet die Zeit am Ereignishorizont sogar stehen!
Was hat es aber nun mit der berühmten Krümmung der Raumzeit auf sich? Bisher war davon ja gar nicht die Rede! Ein erster Hinweis ergibt sich aus dem unterschiedlichen Verhalten von Uhren oben und unten in einer beschleunigten Rakete: Die Zeitkoordinate ist in dem zugehörigen Koordinatensystem krummlinig, um dieses Verhalten der Uhren darstellen zu können. Analog ist auch für einen Beobachter auf dem Erdboden im Gravitationsfeld der Erde die Zeitkoordinate krummlinig. Dieses unterschiedliche Verhalten der Zeit weiter oben und unten ist sogar der Hauptgrund für die Gravitationswirkung, die wir am Erdboden spüren!
Die Raumzeit selbst ist aber in der beschleunigten Rakete nicht krummlinig, denn wir können dort jederzeit zu einem anderen Beobachter wechseln, der nicht selbst beschleunigt, sodass dessen Zeitkoordinate geradlinig ist. Analog können wir auch in einem Gravitationsfeld lokal immer zu so einem Beobachter wechseln – einfach indem wir uns frei fallen lassen. Lokal ist also auch die Raumzeit in einem Gravitationsfeld flach.
Die Krümmung der Raumzeit macht sich – wie auch die Krümmung der Erdoberfläche – erst dann bemerkbar, wenn wir größere Bereiche betrachten. Ein viele tausend Kilometer großes Raumschiff kann sich zwar im Schwerefeld der Erde frei fallen lassen, aber es kann dadurch die Schwerkraft nicht mehr überall in seinem Inneren neutralisiseren, da sich das Schwerefeld der Erde über die vielen Kilometer hinweg ändert. Das führt dazu, dass man nicht überall zugleich im gesamten Inneren des Raumschiffs geradlinige Koordinaten in Raum und Zeit definieren kann, sondern immer nur lokal in kleinen Teilbereichen. Genau das meint man mit der Krümmung der Raumzeit! Sie bewirkt beispielsweise, dass man zwar zwei Körper anfangs auf parallelen Bahnen im Schwerefeld der Erde starten kann, aber im Lauf der Zeit werden diese Bahnen auseinanderlaufen, da die Schwerkraft nicht exakt gleich auf beide Körper einwirkt.
Die Gravitation wird also durch die Krümmung der Raumzeit beschrieben. Andererseits wird die Gravitation von Massen hervorgerufen, wie Newton gezeigt hat. Albert Einstein fand nun heraus, dass man dieses Gesetz verallgemeinern muss, damit es mit der Beschreibung der Gravitation als Raumkrümmung zusammenpasst:
Wenn also starker negativer Druck vorliegt, so kann es auch abstoßende Gravitation geben. Genau solche abstoßenden Gravitationskräfte haben sehr wahrscheinlich den Urknall hervorgerufen (Stichwort inflationäre Expansion), und sie scheinen auch im heutigen Universum den Raum zunehmend expandieren zu lassen (Stichwort dunkle Energie).
Einsteins Gravitationsgesetz führt nun zu einer deutlichen Veränderung in unserem Verständnis von Raum und Zeit: Bisher bildeten Raum und Zeit lediglich die Bühne, auf der sich das physikalische Geschehen abspielte, wobei diese Bühne durch das Geschehen nicht verändert wurde. Nun werden Raum und Zeit plötzlich selber zu physikalischen Akteuren, die sich verbiegen und krümmen lassen, ähnlich wie sich ein Trampolin unter dem Gewicht von Objekten verbiegt. Die Krümmung der Raumzeit legt die Gravitation fest und bestimmt so die Bewegung der Materie darin, und umgekehrt wird diese Krümmung von der Materie im Raum beeinflusst. Die Raumzeit kann sogar in Schwingungen versetzt werden – man denke an Gravitationswellen.
Außerdem gibt es in dieser gekrümmten Raumzeit in allgemeinen Fall keinen globalen Zeitstandard mehr, auf den sich alle lokalen Beobachter einigen können, denn der Verlauf der Zeit hängt davon ab, wo man sich im Gravitationsfeld befindet und wie man sich darin bewegt. Materie und Raumzeit wirken gegenseitig aufeinander ein, sodass die Raumzeit nun keine unabhängige Bühne für das physikalische Geschehen mehr ist, sondern selbst am physikalischen Geschehen teilnimmt. Damit hat sich Newtons Idee von einer absoluten mathematischen Zeit endgültig erledigt.
Wie bewegt sich nun ein frei fallender Körper in einer gekrümmten Raumzeit? Das können wir aus unseren obigen Überlegungen zum Äquivalenzprinzip und zum Zwillingsparadoxon ableiten, und es hat wieder etwas mit der Zeit zu tun, die auf einer mitgeführten Uhr verstreicht. Schauen wir uns dazu wieder eine frei fallende kleine Raumkapsel im Schwerefeld der Erde an. Da sie frei fällt (z.B. in einer Umlaufbahn um die Erde), herrscht in ihr Schwerelosigkeit, d.h. ein Astronaut schwebt in ihr scheinbar schwerelos, bewegt sich also auf aus Sicht der Raumkapsel geradlinig-gleichförmig. Nun gelten in der Raumkapsel die Gesetze der Speziellen Relativitätstheorie, denn die Gravitation wird ja in ihrem Inneren durch den freien Fall neutralisiert. Das Zwillingsparadoxon sagt uns nun, dass auf der Uhr des Astronauten die maximale Zeitspanne vergeht, verglichen mit jeder anderen Uhr, die vom Astronauten aus auf eine andere Bahn gestartet wird und die später zu ihm zurückkehrt. Diese Uhr muss nämlich zwischendurch aus Sicht des schwebenden Astronauten beschleunigt und abgebremst werden, befindet sich also anders als der Astronaut und die Raumkapsel nicht im freien Fall. Das bedeutet:
Dieses einfache Prinzip legt die Bewegung von Körpern in der gekrümmten Raumzeit eindeutig fest.
Man bezeichnet solche Bahnen mit maximaler Eigenzeit auch als Geodäten
in Analogie zu Bahnen auf gekrümmten Flächen, die eine minimale Weglänge zwischen zwei Punkten
aufweisen.
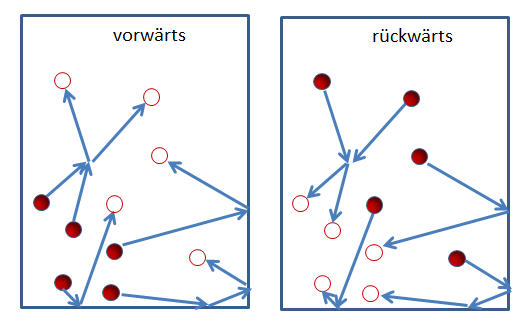
Links oben:
Soll eine Uhr nach einer gewissen Zeit in einem Inertialssystem
(z.B. einer frei fallenden Raumkapsel) wieder an ihrem Ausgangspunkt
ankommen, so ist die Eigenzeit maximal, wenn sich die Uhr in der frei
fallenden Raumkapsel gar nicht bewegt.
Jede andere Bewegung (dargestellt durch die gelben Pfeile)
führt zu einer kürzeren Eigenzeit.
Rechts oben:
Betrachtet man dieselbe Uhr von einem anderen, ebenfalls frei fallenden Inertialsystem aus,
so führt sie eine geradlinig-gleichförmige Bewegung aus (in Blau dargestellt).
Diese Bewegung ist wie im anderen Bezugssystem
zuvor die Bewegung mit der längsten Eigenzeit.
Unten:
Für einen auf dem Erdboden fest stehenden Beobachter sieht die Bewegung mit der längsten Eigenzeit
krummlinig aus – die Uhr fällt zusammen mit der Raumkapsel.

Damit haben wir bereits viel über das Wesen der Zeit herausgefunden: Sie ist eng mit dem Raum verknüpft und muss zusammen mit ihm als Raumzeit betrachtet werden, die wiederum durch die darin enthaltene Materie gekrümmt wird, was wir als Gravitation interpretieren.
Doch immer noch bleiben Rätsel: Nichts erzwingt in dieser Raumzeit, dass die Zeit von der Vergangenheit in die Zukunft voranschreitet. Die grundlegenden physikalischen Gesetze zeichnen keine Zeitrichtung aus (bis auf eine sehr seltene Ausnahme, die bestimmte Teilchenzerfälle betrifft). Betrachtet man einen physikalischen Prozess zeitlich rückwärts, so erhält man wieder einen physikalisch möglichen Prozess. Das gilt sowohl in der klassischen Mechanik als auch in der Physik des elektromagnetischen Feldes (Elektrodynamik) und in der Allgemeinen Relativitätstheorie der Gravitation. Sogar in der Quantenmechanik gibt es keine Zeitrichtung, solange wir den Messprozess außen vor lassen und nur die zeitliche Entwicklung der Wellenfunktion verfolgen (mehr dazu gleich).
In der klassischen Mechanik scheint der Fall klar: Wenn wir uns beispielsweise die Bewegung eines Planeten um die Sonne zeitlich rückwärts ansehen, so sehen wir wieder eine physikalisch mögliche Planetenbewegung.
In der Elektrodynamik ist die Situation schon komplexer. So reagiert das elektrische Feld einer Ladung erst mit einer zeitlichen Verzögerung auf eine Positionsänderung der Ladung, denn die Information über die neue Position kann sich nur mit Lichtgeschwindigkeit ausbreiten, und zwar in die Zukunft – nicht in die Vergangenheit. Analog sendet eine schwingende Ladung elektromagnetische Wellen aus, die sich mit fortschreitender Zeit in den Raum hinein ausbreiten – also nicht mit rückschreitender Zeit. Physiker drücken dies oft dadurch aus, dass sie die retardierte Greensfunktion zur Lösung der Maxwellgleichungen verwenden und nicht die avancierte Greensfunktion.
Gibt es in der Elektrodynamik also einen Zeitpfeil, der Zukunft und Vergangenheit unterscheidet? Nein, den gibt es nicht, denn wir können diese Vorgänge auch zeitlich rückwärts betrachten und sehen wieder einen physikalisch möglichen Prozess, bei dem eine elektische Ladung die elektromagnetische Welle nicht aussendet, sondern absorbiert. Statt mit einer Sendeantenne haben wir es dann mit einer Empfängerantenne zu tun. Ursache und Wirkung tauschen hier ihre Plätze: Im einen Fall verursacht die schwingende Ladung eine nach außen wandernde Welle, im anderen Fall verursacht die zur Ladung laufende Welle die Schwingung der Ladung. Wir sehen also, dass die zeitliche Asymmetrie nur durch die konkrete physikalische Situation vorgetäuscht wurde, die wir betrachtet haben.
Dennoch kommt der Fall, dass schwingende Ladungen elektromagnetische Wellen aussenden, viel häufiger vor als der umgekehrte Fall. Sterne strahlen Licht normalerweise ab und absorbieren es nicht. Der Grund dafür ist klar: Sterne sind viel heißer als der dunkle Weltraum. Es ist also der Zustand unseres Universums, der hier eine Zeitrichtung vorgibt, nicht aber die Gesetze der Elektrodynamik.
Ähnlich liegt der Fall in der Allgemeinen Relativitätstheorie. Besonders deutlich sieht man das bei Schwarzen Löchern: Materie fällt in Schwarze Löcher hinein und kommt niemals wieder aus ihnen heraus. Doch es gibt auch die zeitlich umgekehrte Lösung: Weiße Löcher! Sie spucken ständig Materie hinaus, und nie fällt etwas in sie hinein. Auch hier ist es wieder der Zustand unseres Universums, der die Entstehung Schwarzer Löcher erlaubt, während man Weiße Löcher nie beobachtet – offenbar können sie in unserem Universum nicht entstehen. Hierfür gibt es einen tieferen Grund, den die Allgemeine Relativitätstheorie nicht erfassen kann: Schwarze Löcher besitzen die maximale Entropie, die Materie in einem Raumgebiet annehmen kann. Und damit sind wir bei der eigentlichen Ursache für den Unterschied zwischen Zukunft und Vergangenheit: der Entropie!
Die Entropie kommt ins Spiel, wenn man makroskopische Systeme betrachtet, also Systeme mit sehr vielen Freiheitsgraden (beispielsweise viele Atome oder Moleküle), und dabei die mikroskopische Detailinformation über diese Freiheitsgrade verliert oder zumindest ignoriert. Genauer werden wir das im Kapitel "Was ist Entropie?" kennenlernen.
Schauen wir uns als Beispiel ein Zimmer an, in dem sich sehr viele Gasteilchen bewegen. Wenn wir mit allen Gasmolekülen in einer Zimmerecke starten, so werden diese sich nach und nach gleichmäßig im Zimmer verteilen. Sie stoßen dabei immer wieder mit den Wänden und untereinander zusammen und ändern ständig ihre Richtung. Daher ist es extrem unwahrscheinlich, dass sie sich alle von selbst wieder in einer Zimmerecke versammeln. Streng verboten ist es aber nicht!
Da die Gesetze, nach denen sich die Gasmoleküle im Zimmer bewegen, keine Zeitrichtung
auszeichnen, muss auch der zeitlich umgekehrte Vorgang physikalisch möglich sein.
Würden wir also die Bewegung der Gasteilchen aus der Zimmerecke in das Zimmer hinaus
im Detail zeitlich umgekehrt betrachten, so wäre dieser Vorgang im Prinzip physikalisch möglich!
Dennoch käme er uns extrem künstlich vor, denn normalerweise tun die
Gasteilchen so etwas nicht.
Das liegt daran, dass die Bahnen der Gasteilchen sehr exakt
zusammenpassen müssen, damit sie sich nachher in einer Zimmerecke wiederfinden.
Die Teilchenorte und Geschwindigkeiten müssten extrem fein aufeinander abgestimmt sein.
Würden wir nur die Bahn eines einzigen Gasteilchens
ein klein wenig ändern, so würde sich diese Ungenauigkeit durch die vielen
Zusammenstöße nach und nach auf alle anderen Gasteilchen übertragen und
sie würden sich nicht mehr in der Ecke einfinden, sondern weiter wie zufällig
den ganzen Raum durchfliegen. Die Ungenauigkeit würde sich exponentiell verstärken,
wie man aus der Chaostheorie weiß, und das exakte Zusammenspiel der Teilchen
zerstören, das man bräuchte, um sie zurück in die Ecke zu zwingen.
Hinzu kommt, dass wir makroskopische Objekte wie das Zimmer mit den Gasteilchen nie als vollkommen isolierte Objekte betrachten können. Es kommt immer zu kleinen Wechselwirkungen mit der Umgebung, beispielsweise durch abgestrahlte oder absorbierte Wärme-Photonen. Diese Wechselwirkungen würden jede Feinabstimmung in den Bahnen der Gasteilchen sehr schnell durcheinander bringen und so normalerweise verhindern, dass sich diese in einer Zimmerecke versammeln.
Es ist also sehr unwahrscheinlich, dass sich alle Gasteilchen in einem kleinen Bereich des Zimmers versammeln, denn nur ein verschwindend geringer Anteil aller möglichen Bahnen der Teilchen (in Summe kurz Mikrozustand genannt) führt zu diesem makroskopischen Zustand (Makrozustand), während der weitaus größte Anteil der möglichen Teilchenbahnen eine gleichmäßige Verteilung im Zimmer zur Folge hat. Die Anzahl \( \Omega \) der möglichen Mikrozustände (hier Bahnen), die zu einem bestimmten Makrozustand (hier: mittlere Teilchenverteilung) gehört, bestimmt also, wie wahrscheinlich dieser Makrozustand ist. In der statistischen Physik verwendet man statt der Anzahl \( \Omega \) der Mikrozustände den natürlichen Logarithmus dieser Zahl – das macht Sinn, da die Zahl \( \Omega \) sehr groß ist und man deshalb besser nur mit ihrer Größenordnung arbeitet, also mit der ungefähren Anzahl ihrer Dezimalstellen, die man über den Logarithmus bestimmen kann. Außerdem hat der Logarithmus den Vorteil, dass er beim Zusammensetzen zweier makroskopischer Systeme additiv ist, während die Wahrscheinlichkeit multiplikativ ist. Aus historischen Gründen multipliziert man den Logarithmus noch mit der Boltzmannkonstanten \( k \), die Energieeinheiten in Temperatureinheiten (Kelvin) umrechnet, und bezeichnet das Ergebnis als Entropie \( S \) des makroskopischen Zustandes:
Entropie: \begin{equation} S = k \ln \Omega \end{equation}
mit der Boltzmannkonstanten \(k\) = 1,38... × 10−23 J/K = 8,617... × 10−5 eV/K und der Zahl \( \Omega \) der Mikrozustände, die zum Makrozustand gehören. Mehr zum Thema Entropie folgt in Kapitel 7: Was sind Entropie und Temperatur?.
Die Entropie beschreibt also die Größenordnung der Wahrscheinlichkeit eines makroskopischen Zustandes. Sie wächst normalerweise mit der Zeit an – die gleichmäßig im Zimmer verteilten Gasmoleküle haben mehr Entropie als die Gasmoleküle in der Zimmerecke. Dieses statistische Verhalten makroskopischer Systeme definiert damit letztlich erst den Zeitpfeil, den wir in unserer Welt sehen! Genau das drückt der zweite Hauptsatz der Thermodynamik aus:
Man kann es auch kurz so ausdrücken:
Erst wenn man die makroskopischen Zustände unserer Welt betrachtet, dann entsteht eine Zeitrichtung – also ein Zeitpfeil. So sind die Bewegungen aller Gasteilchen in einem Zimmer mikroskopisch zwar prinzipiell umkehrbar, aber wenn man mit allen Gasmolekülen in einer Zimmerecke startet, dann werden sie sich mit allergrößter Wahrscheinlichkeit nach und nach gleichmäßig im Zimmer verteilen und nicht mehr dahin zurückkehren.
Man muss sich immer wieder klar machen, dass der zweite Hauptsatz der Thermodynamik nur eine Wahrscheinlichkeitsaussage für makroskopische Systeme ist, auch wenn die Wahrscheinlichkeit für ein zufälliges Absinken der Entropie verschwindend gering ist. So bewies Ende des neunzehnten Jahrhunderts der französische Mathematiker und Physiker Henri Poincaré seinen berühmten poincaréschen Wiederkehrsatz, nach dem ein mechanisches System mit beschränkten Teilchenbahnen im Lauf der Zeit den ursprünglichen Anfangsbedingungen unendlich oft beliebig nahekommt. Das bedeutet, dass die Gasteilchen in unserem Zimmer grundsätzlich immer wieder in eine Zimmerecke zurückkehren, wenn sie einmal in der Zimmerecke gestartet sind. Doch wie das oft mit grundsätzlichen mathematischen Aussagen so ist: Die Zeit, bis dies geschieht, ist um ein Vielfaches größer als das Alter der Universums, so dass es in jedem praktischen Sinne niemals geschieht. Zudem kann man das Zimmer ja nicht absolut vom Rest des Universums isolieren, sodass letztlich das gesamte Universum mit einbezogen und mit betrachtet werden muss – und dessen theoretische Wiederkehrzeit sprengt jede Größenordnung. Wenn man allerdings unendlich viel Zeit zur Verfügung hat, so geschieht auch das extrem Unwahrscheinliche irgendwann einmal.
Der zweite Hauptsatz ist oft missverstanden worden, denn eine wichtige Voraussetzung wird oft übersehen: Er gilt nur für nahezu abgeschlossene Systeme, wobei der Zusatz nahezu berücksichtigt, dass man ein makroskopisches System nie absolut isolieren kann – genau deshalb kann man seinen Mikrozustand auch nie genau angeben, sondern es fluktuiert zwischen vielen Mikrozuständen hin- und her. Die Zahl der so erreichbaren Mikrozustände hatten wir oben Ω genannt und zur Grundlage der Entropiedefinition gemacht.
In einem offenen System, das mit seiner Umgebung makroskopische Energiemengen austauschen kann, kann die Entropie sehr wohl abnehmen! Das beweist unsere eigene Existenz, denn jedes Lebewesen ist ein solches offenes System. Doch wenn man ein Lebewesen von seiner Umgebung abschottet, sodass es weder Energie aufnehmen noch Wärme abgeben kann, dann erlöschen seine Lebensvorgänge sehr schnell und es stirbt, da es seine niedrige Entropie nicht mehr aufrecht erhalten kann. Wie schnell das gehen kann, zeigt ein Gift wie Zyankali: Weniger als ein Gramm Zyankali genügen, um einen Menschen innerhalb von Sekunden bis Minuten umzubringen. Dabei blockiert Zyankali ein wichtiges Enzym in der Atmungskette der Zellen, sodass deren Energieversorgung zusammenbricht. Das Leben unterliegt also sehr wohl dem zweiten Hauptsatz, und viele molekulare Nanomaschinen in den Zellen müssen unermüdlich daran arbeiten, den Zerfall und das Anwachsen der Entropie zu verhindern.
Unser subjektives Gefühl, dass die Zeit fließt, hängt dabei entscheidend damit zusammen, dass wir das Wirken des zweiten Hauptsatzes in unserer Umwelt ständig hautnah zu spüren bekommen und dass er auch für uns selber gilt. Ständig muss beispielsweise Energie in konzentrierter Form verfügbar gemacht werden, um Prozesse in unserer Umwelt und in uns selbst in Gang zu halten, und ständig geht diese Energie letzten Endes als nutzlose Wärme in unserer Umgebung verloren und erhöht deren Entropie. Dabei dürfte wohl auch der Eindruck einer existierenden Gegenwart subjektiver Natur sein und mit der Funktionsweise unseres Gehirns zusammenhängen, denn jeder Zeitpunkt in unserem Leben ist mit einer einmaligen Struktur unserer Gedanken und Erinnerung verbunden. Als physikalischen Begriff gibt es die Gegenwart jedenfalls nicht.
Unser Universum besitzt also einen Zeitpfeil, da seine Entropie anwächst. Doch damit stellt sich eine ganz neue fundamentale Frage: Warum besitzt unser Universum überhaupt eine Entropie, die noch ansteigen kann? Viel wahrscheinlicher wäre es doch, wenn sich das Universum schon immer in einem Zustand maximaler Entropie befunden hätte, also im thermischen Gleichgewicht. Die Zeit hätte dann ihre Richtung verloren und es gäbe in diesem Universum nichts, das ein Fließen der Zeit von der Vergangenheit in die Zukunft erkennen ließe – keine Uhren, kein Leben, nichts, nur einen strukturlosen Nebel aus Materie oder ein einziges schwarzes Loch. Es ist gut möglich, dass unser Universum langfristig auf so einen zeitlosen Makrozustand hinsteuert – man nennt das den Wärmetod des Universums. Alle Sterne wären dann schon lange erloschen, sämtliche Materie wäre zerfallen und hätte sich in den Weiten des expandierenden Universums verloren – ein trostloser Ausblick! Glücklicherweise dürfte es wohl noch sehr lange dauern, bis es soweit ist.
Die Ursache für die steigende Entropie des Universums muss also einen kosmologischen Ursprung haben. Das Universum muss seine Existenz in einem Zustand mit niedriger Entropie begonnen haben – zumindest in dem für uns sichtbaren Bereich. Wie das genau geschehen konnte, ist noch nicht wirklich geklärt. Vermutlich kann dies erst im Rahmen einer umfassenden Theorie geklärt werden, die insbesondere die Gesetze der Allgemeinen Relativitätstheorie mit denen der Quantenmechanik verbindet, also im Rahmen einer Theorie der Quantengravitation – mehr dazu weiter unten.
Eines scheint aber schon heute recht sicher zu sein: Irgendwie muss beim Anbeginn unseres sichtbaren Universums ein winziger Bereich entstanden sein, der vielleicht zufällig eine niedrige Entropie besaß und der von einem sehr hochenergetischen Feld (oft Inflatonfeld genannt, es könnte aber auch eine Art Vakuumenergie sein) durchdrungen war, das einen extrem starken negativen Druck aufwies, sich also zusammenziehen möchte wie ein gespanntes Gummi. Solche Felder treten in den modernen – noch spekulativen – Theoriegebäuden der Teilchenphysik häufig auf, sodass dieses Szenario durchaus plausibel erscheint. Einsteins Gravitationsgesetz sagt dann, dass dieser extreme negative Druck eine stark abstoßende Gravitation zur Folge hatte, die den winzigen Bereich innerhalb von Sekundenbruchteilen um viele (vielleicht 30 bis 50) Zehnerpotenzen exponentiell expandieren ließ – unser sichtbares Universum umfasst vermutlich nur einen winzigen Teil dieses extrem aufgeblähten Raumbereichs.
Diese inflationäre Expansion ist der eigentliche Urknall. Das Energiefeld wird dabei durch die Expansion des Raums nicht etwa ausgedünnt, denn der negative Druck zapft gleichsam die Gravitationsenergie des Feldes an und transformiert sie in neue Feldenergie im expandierenden Raum. In Summe heben sich dabei die positive Feldenergie und die negative Gravitationsenergie gegenseitig auf, d.h. die Gesamtenergie der so entstehenden Raumblase ist Null oder zumindest nahezu Null. Beobachtungen der letzten Jahrzehnte zeigen, dass dies auf unser sichtbares Universum tatsächlich zutrifft – genau genommen kann man dies aus der beobachteten Flachheit des Universums ableiten. Die Energie, die die Materie im sichtbaren Universum enthält, entspricht also betragsmäßig gerade ihrer negativen Gravitationsenergie. Das ist ein Zeichen dafür, dass zumindest energiemäßig unser Universum durchaus aus Nichts oder fast Nichts entstanden sein kann.
Nach wenigen Sekundenbruchteilen inflationärer Expansion zerfällt das Energiefeld schließlich in ein sehr dichtes und heißes Teilchenplasma, das sich anschließend zusammen mit dem Raum weiter ausdehnt und dabei abkühlt. Dabei ist dieses Teilchenplasma recht gleichmäßig im Raum verteilt und besitzt überall nahezu dieselbe Temperatur. Nun könnte man nach unseren Überlegungen von oben über das Gas in einem Zimmer meinen, ein solches gleichmäßig verteiltes Teilchenplasma hätte eine besonders große Entropie, sodass unser Universum bereits mit großer Entropie begonnen hätte. Ein Zeitpfeil hätte sich dann nie ausbilden können, denn unser Universum wäre bereits im thermischen Gleichgewicht gestartet. Wie sollte auch in einem solchen strukturlosen Teilchennebel je irgendeine Art von Uhr entstehen, geschweige denn ein Lebewesen.
Das stimmt jedoch nur, wenn wir die Gravitation nicht beachten. In dem Teilchenplasma gibt es keinen negativen Druck mehr wie noch zuvor im Inflaton-Energiefeld, sodass die Gravitation nun anziehend wirkt. Die Gravitation versucht nun, die winzigen Unregelmäßigkeiten in der Plasmadichte zu verstärken und immer dichtere Materieklumpen hervorzubringen, also letztlich Sterne, Galaxien und Planeten. Und das bedeutet, dass das gleichmäßige Teilchenplasma bei anziehender Gravitation eine sehr viel geringere Entropie besitzt als das Universum, das wir heute sehen. Gravitation ist somit die Hauptquelle für anwachsende Entropie im Universum. Mit Gravitation ist der Materiezustand mit der größten Entropie letztlich ein schwarzes Loch, also die maximal mögliche Zusammenballung der Materie.
Unser sichtbares Universum befand sich also nach der inflationären Expansion in einem Zustand sehr niedriger Entropie, auch wenn man zunächst den gegenteiligen Eindruck hat. Im Lauf der Jahrmilliarden erhöhte die Gravitation diese Entropie nach und nach, indem sie Materie zu Sternen kollabieren ließ, in denen schließlich die Kernfusion zünden konnte. Diese Sterne und mit ihnen unsere Sonne sind dadurch sehr viel heißer als der inzwischen durch die Expansion stark abgekühlte Weltraum. Erst durch diesen Temperaturgegensatz war die Entstehung von Leben auf unserer Erde möglich. Würde die Sonne dagegen erlöschen, so würde der zweite Hauptsatz erbarmungslos zuschlagen und das Leben auf der Erde würde schnell erlöschen.
Noch ist unser Universum weit vom thermischen Gleichgewicht, also der maximalen Entropie, entfernt. Doch irgendwann werden alle Sterne erloschen sein. Die Materie wird nach vielen Tausend Jahrmilliarden entweder zerfallen (Stichwort Protonzerfall) oder sich in Schwarzen Löchern zusammenfinden, die im weiter expandierenden Universum nach Ewigkeiten schließlich aufgrund der Hawking-Strahlung zerstrahlen. Zu guter Letzt bleibt nach heutigem Wissen vermutlich nur der Hauch eines dünnen Teilchennebels übrig, verloren in den endlosen Weiten des Raums. Das wäre dann der Wärmetod des Universums, in dem auch die Zeit, wie wir sie kennen, ihr Ende gefunden hätte.
Damit haben wir bereits viel über das erstaunliche Wesen der Zeit erfahren. Sie hat sich als viel komplexer erwiesen, als es Newton oder Leibniz geahnt haben können. Und doch sind wir noch nicht am Ende, denn ganz merkwürdig wird es, wenn wir uns an die Front der Forschung begeben und physikalische Theorien betrachten, die neben der Gravitation auch die Quantenmechanik berücksichtigen.
In der üblichen Quantenmechanik – also ohne Gravitation – tritt die Zeit noch als äußerer Parameter auf, ganz ähnlich wie es sich Newton vorgestellt hatte. Die Wellenfunktion, die die quantenmechanischen Wahrscheinlichkeiten beschreibt, entwickelt sich vollkommen deterministisch, so wie es die sogenannte Schrödingergleichung festlegt. Nimmt man die Spezielle Relativitätstheorie hinzu, so wird die Sache etwas komplizierter, da man nun das gemeinsame Verhalten von Raum und Zeit beachten muss – aber immer noch bleiben die Wellengleichungen deterministisch und zeichnen keine Zeitrichtung aus.
Wie oben bereits erwähnt, gibt es allerdings bestimmte sehr seltene quantenmechanische Teilchenzerfälle, bei denen die Zeitumkehrinvarianz nicht exakt gilt – man spricht von der T-Verletzung. Diese T-Verletzung konnte im Jahr 2012 nachgewiesen werden, nachdem sie bereits lange zuvor indirekt aufgrund der bereits nachgewiesenen CP-Verletzung vermutet wurde. Hintergrund für die Vermutung ist das berühmte CPT-Theorem, das tief in der Synthese von Spezieller Relativitätstheorie und Quantenmechanik begründet ist und das besagt: Ersetzt man alle Teilchen durch die entsprechenden Antiteilchen (C = change conjugation = Ladungsumkehr) und spiegelt zudem Raum (P = Paritätstransformation = Raumspiegelung) und Zeit (T = T-Transformation = Zeitumkehr, d.h. man betrachtet den zeitlich umgekehrten Prozess), so erhält man wieder einen physikalisch möglichen Prozess, der mit denselben Übergangswahrscheinlichkeiten (genauer: Amplituden) abläuft. Wenn man dagegen die Zeitumkehr weglässt – also nur CP betrachtet – so gilt die analoge Aussage nicht immer. Daher kann auch die Zeitumkehrinvarianz T nicht immer gelten, denn wenn CP verletzt ist, so muss auch T verletzt sein, damit CPT wieder unverletzt bleibt. Genau diese T-Verletzung konnte nun also auch direkt nachgewiesen werden, wobei man tief in den quantenmechanischen Mechanismus der entsprechenden Zerfälle einsteigen muss, um zu verstehen, wie sich die T-Verletzung bei ihnen äußert. Wir wollen hier nicht genauer darauf eingehen – siehe z.B. pro-physik: Zeitasymmetrie erstmals direkt nachgewiesen.
Insgesamt kann die seltene T-Verletzung bei bestimmten Zerfällen aber kaum den globalen Zeitpfeil erklären, den wir im Universum beobachten, auch wenn sie durchaus ein bemerkenswertes Phänomen ist, denn sie zeigt, dass nicht alle Naturgesetze zeitumkehrinvariant sind. Allerdings ist nur die sogenannte schwache Wechselwirkung, die für diese Zerfälle verantwortlich ist, von der Verletzung der Zeitumkehrinvarianz betroffen. Alle anderen Wechselwirkungen – also Gravitation sowie Elektromagnetismus und die starke Kernkraft – sind zeitumkehrinvariant, zeichnen also keine Zeitrichtung aus.
Abgesehen von der beschriebenen seltenen T-Verletzung der schwachen Wechselwirkung tritt eine ausgezeichnete Zeitrichtung in der Quantenmechanik normalerweise erst auf, wenn man den quantenmechanischen Messprozess betrachtet, der aus den vielen quantenmechanischen Möglichkeiten, die in einer Wellenfunktion stecken, genau eine klassische makroskopische Realität zu machen scheint, wobei die Auswahl anscheinend rein zufällig erfolgt. Was soll man davon halten?
Um es gleich zu sagen: So ganz genau weiß man heute noch nicht, was das zu bedeuten hat, denn der quantenmechanische Messprozess und seine Interpretation wird auch heute noch heiß diskutiert. Dennoch scheint sich ein gewisses Bild herauszukristallisieren, wenn man davon ausgeht, dass es keine prinzipielle Gültigkeitsgrenze für die Quantenmechanik gibt, so dass sie letztlich auch das Messgerät, uns selbst als Beobachter und letztlich das ganze Universum beschreibt. Zumindest konnte bis heute kein Experiment eine solche Grenze finden – im Gegenteil: alle Experimente sprechen für die universelle Gültigkeit der Quantenmechanik. Außerdem wollen wir davon ausgehen, dass die Dynamik der Quantenmechanik für den Messprozess nicht modifiziert werden muss, sodass es bei der Messung keinen Kollaps der Wellenfunktion gibt, und dass die Wellenfunktion eine gewisse Quantenrealität repräsentiert, also kein reines Werkzeug zur Verwaltung unseres Wissens über ein physikalisches System ist. Auch diese Annahmen sind heute noch alle durchaus umstritten.
Das sich aus diesen Annahmen ergebende Bild ist komplex und widerspricht unserem gesunden Menschenverstand – wobei dieser in der modernen Physik ja sowieso schnell an seine evolutionär vorgeprägten Grenzen kommt. Ich kann die Grundidee daher an dieser Stelle leider nur recht unvollständig skizzieren, will es aber dennoch versuchen (mehr dazu findet man in den Kapiteln Was ist ein Quant? und Was ist Realität? sowie beispielsweise bei Claus Kiefer: Der Quantenkosmos: Von der zeitlosen Welt zum expandierenden Universum, S. Fischer Verlag (2009)):
Die Wellenfunktion eines quantenmechanischen Objektes umfasst eine wohldefinierte Quanten-Überlagerung vieler Möglichkeiten. So ist der Spin eines Teilchens im Allgemeinen nicht festgelegt, sondern es gibt beispielsweise bei einem Elektron oder Proton zwei mögliche Einstellungen bezüglich jeder gegebenen Raumrichtung. Eine Messung des Spins bedeutet nun, dass das Teilchen in Wechselwirkung mit seiner makroskopischen Umgebung tritt, beispielsweise mit einem Magneten. Diese Wechselwirkung muss auf den Spin empfindlich sein, so wie das bei einem Magneten der Fall ist. Durch die Wechselwirkung entsteht nun eine Verschränkung des Spins mit der Umgebung, sodas sich Umgebung und Spin quantenmechanisch nur noch gemeinsam beschreiben lassen. Spin und Umgebung sind nun miteinander korreliert, und die Umgebung sieht für die beiden Spineinstellungen im Magnetfeld jeweils anders aus. So muss es ja auch sein, wenn wir die Spineinstellung makroskopisch erkennen wollen, also messen wollen. Es gibt also nun nur noch eine gemeinsame Wellenfunktion des Spins zusammen mit seiner Umgebung (Messgerät inclusive Beobachter), die beide Spinmöglichkeiten und die zugehörige Konfiguration der Umgebung umfasst.
Dabei muss die Umgebung sehr viele Freiheitsgrade aufweisen – sie darf also nicht einfach nur aus einem anderen Atom bestehen. Eine solche Umgebung lässt sich aber nicht vom Rest des Universums isolieren, sodass letztlich der Spin eine Verschränkung mit dem Universum selbst eingeht. Die Wellenfunktion des Universums besteht also nun aus zwei Anteilen, die den beiden Spinmöglichkeiten entsprechen. Da aber nun diese Wellenfunktion extrem komplex ist, kommt es zur Dekohärenz der beiden Möglichkeiten. Das bedeutet, dass sich für einen lokalen Beobachter am Magneten keinerlei quantenmechanische Interferenz dieser Möglichkeiten mehr feststellen lässt. Die dazu notwendige Quanteninformation ist nämlich vollkommen delokalisiert worden und ist für ihn unzugänglich in der Komplexität der Universums-Wellenfunktion verborgen. Letztlich umfasst die Wellenfunktion des Universums damit nun zwei Anteile, die nichts mehr voneinander spüren – zumindest aus der klassischen Froschperspektive eines lokalen Beobachters, für den die subtilen und extrem komplexen globalen Zusammenhänge zwischen den beiden Anteilen der globalen Wellenfunktion sich gleichsam wegmitteln und damit unmessbar werden. In jedem dieser Wellenfunktionszweige würde ein lokaler Beobachter am Magneten nur die eine zugehörige Spinmöglichkeit feststellen – in dem einen Zweig in Magnetfeldrichtung, in dem anderen Zweig entgegen der Magnetfeldrichtung.
Damit umfasst die globale Wellenfunktion nach der Wechselwirkung des Spins mit seiner Umgebung nun zwei Zweige, die jeweils als eigenständige makroskopische Realität interpretiert werden können, wobei sich sogar der lokale Beobachter am Magneten gleich mit verdoppelt hat – ein geradezu bizarrer Gedanke, aber dennoch eine logische Konsequenz, wenn man von der universellen Gültigkeit der Quantenmechanik ausgeht. Es entsteht das Bild einer globalen Wellenfunktion, die sich ständig in einzelne makroskopische Zweige aufteilt – nämlich immer dann, wenn eine lokale quantenmechanische Überlagerung durch Wechselwirkung mit vielen anderen Freiheitsgraden zerstört wird und sich dadurch auf den Rest der globalen Wellenfunktion überträgt. Hugh Everett war der erste, der dieses Szenario im Jahr 1957 vorschlug, auch wenn ihm der entscheidende Baustein der Dekohärenz damals noch fehlte. Es wird meist etwas unglücklich als Viele-Welten-Interpretation bezeichnet, obwohl es deutlich über eine reine Interpretation hinausgeht, denn es ist die logische Konsequenz unserer Annahmen von oben: universelle Gültigkeit der Quantenmechanik ohne Modifikation der Quantendynamik (Schrödingergleichung) sowie der Anspruch, dass die Wellenfunktion eine physikalische Realität wiederspiegelt.
Der Gedanke, dass sich in diesem Bild auch unser eigenes Ich ständig verzweigt, erscheint vielen von uns grotesk, und auch mir wird mulmig dabei. Lange wurde dieses Szenario von der Fachwelt daher also zu barock abgelehnt, doch in den letzten Jahren rückte es zunehmend in den Fokus, da Messergebnisse immer deutlicher zeigen, dass die Quantenmechanik keine Gültigkeitsgrenze zu haben scheint, und da man den Prozess der Dekohärenz mittlerweile gut experimentell untersuchen kann. Wenn wir also die Quantenmechanik mit all ihren Konsequenzen ernst nehmen – und das wollen wir hier tun – dann müssen wir uns wohl irgendwie mit diesem bizarren Bild arrangieren. Nur so ist es konsistent möglich, die Quantenmechanik auf unseren gesamten Kosmos zu übertragen und das Wesen der Zeit noch einen Schritt tiefer zu ergründen. Ehrlicherweise muss dabei allerdings auch hinzugefügt werden, dass gegenwärtig noch kein Konsens in der Wissenschaft darüber besteht, ob dieses Bild wirklich korrekt ist, auch wenn einiges dafür spricht. Das Messproblem der Quantenmechanik wird nach wie vor heiß diskutiert.
Warum entsteht nun bei einer quantenmechanischen Messung in diesem Bild ein Zeitpfeil? Weil aus der Froschperspektive eines lokalen Beobachters die Information, die in einer lokalen Wellenfunktion wie der des Spins enthalten ist, teilweise verloren geht, indem sie durch Dekohärenz blitzschnell in die Umgebung abwandert und dort für ihn im praktischen Sinne nicht mehr zugänglich ist – er sieht nur noch ein einziges Messergebnis, das seiner jeweiligen makroskopischen Realität entspricht, und verliert die Interferenz der quantenmechanischen Möglichkeiten (diese würden sich beispielsweise bemerkbar machen, wenn man den Spin in einer anderen Raumrichtung misst). Es ist wie bei der Entropie: Nichts verbietet es grundsätzlich, den Messvorgang zeitlich umzukehren, denn der Messprozess entspricht einer zeitlich umkehrbaren Entwicklung der globalen Wellenfunktion. Es ist einfach nur extrem unwahrscheinlich, dass die global verteilte Information wieder lokal zusammenfindet und das Quantenobjekt, so wie es vor der Messung war, wiederauferstehen lässt – was zugleich bedeuten würde, dass auch die makroskopischen Realitäten wieder miteinander verschmelzen würden.
Wenn man es genau betrachtet, so ist der Informationsverlust durch Dekohärenz für einen lokalen Beobachter identisch mit der Zunahme der Entropie, die er lokal beobachtet. Entropie hatten wir oben als die Zahl der Mikrozustände definiert, die bei einem lokalisierbaren physikalischen Objekt (z.B. das Zimmer mit den Gasmolekülen) makroskopisch gleich aussehen. Wenn die Entropie anwächst, sehen also mehr Mikrozustände gleich aus, und man hat makroskopisch weniger Information darüber, in welchem Bereich der Mikrozustände sich das System denn nun befindet. Durch die Wechselwirkung (Verschränkung) mit der Umgebung wird dabei das System ständig zwischen den gleichwertig aussehenden Mikrozuständen hin- und hergeworfen, sodass die Information, in welchem Mikrozustand sich das System kurzzeitig befindet, nur durch Einbeziehung der Umgebung zu ermitteln wäre. Etwas präziser drückt es Claus Kiefer in seinem Buch Der Quantenkosmos aus (S. 156 dort):
"Da Beobachter von lokaler Natur sind, also nur einen kleinen Teil der nichtlokalen Quantenwelt erfahren, fehlt ihnen Information – was sich in einer nichtverschwindenden Entropie äußert. Diese Entropie ist also ein Maß für die fehlende Information über den verschränkten Zustand."
Ein Anstieg der Entropie entspricht also der Delokalisierung von Information durch Wechselwirkung mit der Umgebung – und genau das geschieht auch bei der Messung eines Quantensystems. Letztlich hat also der thermodynamische Zeitpfeil durch Antieg der Entropie und der Zeitpfeil bei einer Quantenmessung in diesem Bild dieselbe Ursache.
So – das war jetzt nicht einfach, und es ist in dieser Kürze sicher unmöglich, diese verrückte Quantenwelt tiefer zu verstehen. Wir kommen daher in Kapitel 6: Was ist ein Quant? noch einmal genauer darauf zurück. Aber vielleicht konnte ich wenigstens eine grobe Idee davon vermitteln, wie der Zeitpfeil in der Quantenwelt für einen makroskopischen lokalen Beobachter entstehen könnte.
Gehen wir nun noch einen Schritt weiter und nehmen die Gravitation mit hinzu, so wie sie Einstein in seiner Allgemeinen Relativitätstheorie durch die Krümmung der Raumzeit beschrieben hat. Was geschieht dann?
Ganz genau wissen wir es nicht, denn es gibt bis heute keine klar etablierte Theorie, die Quantenmechanik und Allgemeinen Relativitätstheorie beide konsistent umfasst. Dennoch hat man bereits viel über das Zusammenspiel dieser beiden Grundpfeiler der Physik herausgefunden, und es gibt mehrere theoretische Ansätze, denen der Vorstoß in dieses noch unbekannte physikalische Gebiet zumindest teilweise gelingt.
Ein Ergebnis ist, dass sich die Kontinuität des Raums auf unterster mikroskopischer Ebene aufzulösen scheint und er eine diskrete, körnige oder blasige Struktur bekommt. Diese Struktur entsteht durch ein Zusammenspiel des Quanten-Wellencharakters der Materie mit der Gravitation: Hohe Ortsauflösung bedeutet in der Quantenwelt kurze Wellenlängen und damit hohe Energie. Hohe Energie bedeutet aber zugleich auch starke Gravitation, sodass sich ab einer bestimmten Energie schwarze Mikrolöcher zu bilden beginnen, die eine weitere Steigerung der Ortsauflösung verhindern. Wir das genau geschieht werden uns das im nächsten Kapitel 2: Was ist Raum? ansehen.
Die Grenze für die maximale Ortsauflösung findet man, indem man die drei Naturkonstanten der Quantenmechanik (Planck'sches Wirkungsquantum \( \hbar = h/(2\pi) \) ), Relativitätstheorie (Lichtgeschwindigkeit \(c\)) und Gravitation (Gravitationskonstante \(G\)) zu einer Länge kombiniert, die man Plancklänge nennt:
Die Plancklänge bildet eine natürliche Maßeinheit für Längen, die von der Natur selbst zur Verfügung gestellt wird – anders als der willkürliche menschliche Längenmaßstab Meter. Zugleich ist die Plancklänge eine unvorstellbar winzige Länge: Sie ist um rund zwanzig Zehnerpotenzen kleiner als die Ausdehnung eines Atomkerns. Längen unterhalb dieser Plancklänge sind physikalisch bedeutungslos, da sie sich mit keiner Messvorschrift mehr erfassen lassen.
Nun braucht ein Lichtstrahl eine bestimmte – wenn auch winzige – Zeit, um eine Plancklänge zurückzulegen. Die entsprechende Zeit ist die Planckzeit:
Könnte man physikalisch eine noch kleineren Zeitspanne messen, so könnte man über die Strecke, die ein Lichtstrahl in dieser kürzeren Zeit zurücklegt, auch eine Länge unterhalb der Plancklänge messen. Das geht aber nicht, wenn die Plancklänge die maximale Ortsauflösung ist. Also können auch Zeitintervalle unterhalb der Planckzeit keine physikalische Bedeutung haben. Es gibt keine Uhr mehr, die sie messen könnte. Damit erhält neben dem Raum auch die Zeit eine körnige, diskrete Struktur.
Doch nicht nur das: Der Zeitbegriff selbst scheint sich aufzulösen, wenn Gravitation und Quantenmechanik intensiv zusammenwirken und wenn die klassischen makroskopischen Welten, die in der sich ständig verzweigenden globalen Wellenfunktion des Universums auftreten, ihr eigenständige Identität verlieren. Genau das geschieht nämlich im Urknall – also am Beginn von Raum und Zeit – und womöglich auch am Ende der Zeit, wenn die Entropie der Welt ihr Maximum erreicht. Es gibt dann keine klassischen Welten mehr, wie wir sie kennen.
Um genauer herauszufinden, was das bedeutet, brauchen wir eine Theorie der Quantengravitation, in der sich die globale Wellenfunktion des Universums aufstellen lässt. So eine Theorie gibt es heute noch nicht, wie wir wissen, aber es gibt vielversprechende Ansätze in diese Richtung. Ein solcher Ansatz ist die Wheeler-DeWitt-Gleichung. Sie entsteht, wenn man Einsteins Allgemeine Relativitätstheorie so umformuliert, dass sie in Analogie zur hamiltonschen Formulierung der klassischen Mechanik mit ihren Orts- und Impulsvariablen steht. An die Stelle des Teilchenorts tritt dabei die räumliche innere Geometrie (Metrik) des Raums. Man kann es auch etwas anders ausdrücken: Die Rolle der kinetischen Energie übernimmt die äußere Raumkrümmung (die von der Einbettung des gekrümmten Raums in einen höherdimensionalen Raum abhängt), während die Rolle der potentiellen Energie von der inneren Raumkrümmung übernommen wird (diese ist unabhängig von solchen Einbettungen).
Ein Beispiel: Rollt man ein Blatt Papier zu einem Zylinder zusammen, so ist seine innere Krümmung immer noch Null, denn beispielsweise ist die Winkelsumme eines Dreiecks auf der Zylinderoberfläche immer noch 180 Grad wie auf dem ursprünglichen Blatt Papier. Bei einer Kugeloberfläche ist die innere Krümmung dagegen positiv, denn ein Dreieck hat dort eine Winkelsumme oberhalb von 180 Grad. Die äußere Krümmung der Zylinderoberfläche ist dagegen ungleich Null, denn man hat das Blatt Papier ja zusammengerollt, was aber ein zweidimensionales Wesen, das nur auf dem Papier lebt, nicht erkennen kann. Erst ein dreidimensionales Wesen, das die Einbettung der Zylinderoberfläche im dreidimensionalen Raum sehen kann, erkennt seine äußere Krümmung.
Bei der klassischen Mechanik gibt es nun ein Standardrezept, mit dem man aus der hamiltonschen Formulierung eine dazu passende Quantentheorie erzeugen kann. Wendet man dieses Rezept nun analog auf die umformulierte Allgemeine Relativitätstheorie an, so entsteht – vereinfacht ausgedrückt – die Wheeler-DeWitt-Gleichung. Sie hat die folgende Form:
Dabei ist \( \psi \) die Wellenfunktion des Universums, die aber hier nicht vom Ort abhängt, sondern von der Geometrie und dem Materieinhalt der gesamten Raumzeit.
Formal sieht die Wheeler-DeWitt-Gleichung genauso aus wie die zeitunabhängige Schrödingergleichung, mit der sich beispielsweise die statische Wellenfunktion von Elektronen in den Atomhüllen berechnen lässt. Und das ist genau der entscheidende Punkt: Die Wheeler-DeWitt-Gleichung ist statisch, enthält also gar keine Zeit mehr! Die Wellenfunktion des Universums ist damit zeitunabhängig. Das kann auch gar nicht anders sein, denn die Allgemeine Relativitätstheorie, von der wir ja ausgegangen sind, enthält auch keinen separaten Zeitparameter, sondern beschreibt die gesamte Raumzeit.
Außerdem entspricht die Wheeler-DeWitt-Gleichung der Schrödingergleichung zur Energie Null. Auch das passt gut zu unseren obigen Überlegungen, nach denen sich in unserem Universum die positive Energie der Materie und die negative Energie der Gravitation gerade gegenseitig aufheben.
Aus einer hypothetischen Vogelperspektive heraus, in der wir die gesamte Wellenfunktion des Universums überblicken könnten, gibt es also gar keine Zeit, sondern nur eine einzige, unglaublich komplexe statische Quantenwelt mit Gesamtenergie Null, die alle möglichen Zustände des Universums umfasst. Die Zeit ist demnach gar kein fundamentales physikalisches Konzept, sondern erst die Wellenfunktion könnte ein solches Fundament darstellen.
Umgekehrt lässt sich aus der statischen Wellenfunktion des Universums die Zeit als Näherung zurückgewinnen, sobald sich Zweige in der Wellenfunktion herausbilden, die man als separate klassische Welten interpretieren kann – man spricht von der quasiklassischen oder Born-Oppenheimer-Näherung. Die klassische Zeit entsteht also zusammen mit den klassischen Welten erst durch eine Art Mittelungsprozess über die Quantenwelt. Dazu braucht man allerdings das Mitwirken vieler Freiheitsgrade, sodass die oben besprochene Dekohärenz zum Zuge kommt, sowie lokale Beobachter innerhalb dieser Quantenwelt, die die Zeit messen können. Die Zeit stellt sich also als emergentes Phänomen heraus, das sich unter bestimmten Bedingungen aus der Quantenwelt herausbilden kann, um gewisse Zusammenhänge innerhalb der statischen Wellenfunktion des Universums näherungsweise zu parametrisieren.
Damit stellt sich auch die Frage nach dem Anfang und dem Ende der Zeit und des ganzen Universums in neuem Licht: Was gab es vor dem Anfang, und was kommt nach dem Ende? Nichts, würden wir antworten, denn am Anfang und am Ende des Universums bricht die quasiklassische Näherung zusammen, die den Zeitbegriff erst hervorbringt, und wir haben es nur noch mit dem entsprechenden zeitlosen Teil der globalen Wellenfunktion zu tun.
Die Wheeler-DeWitt-Gleichung ist nun eine extrem komplizierte Gleichung, die in ihrer vollen Schönheit wohl noch nicht einmal mathematisch sauber definiert ist. Hier zeigt sich wieder das noch ungelöste Problem, Gravitation und Quantenmechanik konsistent zu vereinen. Wenn man jedoch bestimmte Näherungen für unser Universum macht, so entsteht eine Gleichung, die sich handhaben und analysieren lässt. Eine solche Näherung ist beispielsweise, dass man von einem nahezu homogenen und isotropen Universum ausgeht, das weitgehend durch seinen Skalenparameter (also seine "Ausdehnung" relativ zu heute) beschrieben wird. Im Urknall ist dieser Skalenparameter Null, während sein heutiger Wert bei Eins liegt. Damit hat man ein durchaus brauchbares Modell für unser sichtbares Universum formuliert.
In diesem Modell stellt sich nun heraus, dass der Skalenparameter selbst den fundamentalen Zeitstandard des Universums liefert. Das Universum dehnt sich demnach nicht in der Zeit aus, sondern seine Ausdehnung definiert erst den Zeitbegriff. Dabei erweist sich die Wheeler-DeWitt-Gleichung als asymmetrisch im Skalenparameter, sodass automatisch ein Zeitpfeil entsteht. Letztlich folgt dieser Zeitpfeil dabei daraus, dass bei kleinem Skalenparameter die Wellenfunktion des Universums weniger verschränkt ist als bei größerem Skalenparameter, sodass für lokale klassische Beobachter in ihrem klassischen Zweig des Universums die Entropie ansteigt.
Was sagt so ein Modell über den Urknall selbst aus?
Welche Raumzeit-Geometrien liefern den wichtigsten Beitrag in der Wellenfunktion?
Auch hierzu gibt es verschiedene Ansätze. Eine der bekanntesten Ideen stammt
von James Hartle und Stephen Hawking. Sie gehen davon aus, dass in der Nähe des Urknalls
die Zeit sich wie eine vierte Raumdimension verhält. Lässt man zur Veranschaulichung
zwei Raumdimensionen weg, so formen die beiden übrig gebliebenen Raumzeitdimensionen
beim Urknall beispielsweise eine Art Trichter mit abgerundeter Spitze.
Wegen dieser abgerundeten Spitze hat demnach eine solche Raumzeit gar keinen Rand, und die Zeit somit
keinen festen Anfang.
An der Rundung der Spitze verhalten sich Raum und Zeit wie Längen- und Breitengrade auf einer Kugeloberfläche.
Die Frage nach dem Anfang der Zeit erübrigt sich damit, genauso wie es sinnlos ist, nach einem Ort
südlich vom Südpol zu fragen.
Hartle und Hawking stellen nun die Keine-Ränder-Bedingung auf, nach der nur solche Raumzeiten
in der Wellenfunktion auftreten können, die wie der Trichter mit der abgerundeten Spitze keinen Rand haben.
Anders ausgedrückt: Die Randbedingung des Universums besteht darin, dass es keinen Rand hat,
weder im Raum noch in der Zeit!
Weit genug weg von der abgerundeten Spitze, wenn sich das Universum stark genug ausgedehnt hat,
beginnt die vierte Raumdimension dann, sich nach und nach wie eine Zeitdimension zu verhalten
– die quaiklassische Näherung beginnt zu greifen und die Zeit erhebt sich aus dem Quantensumpf.
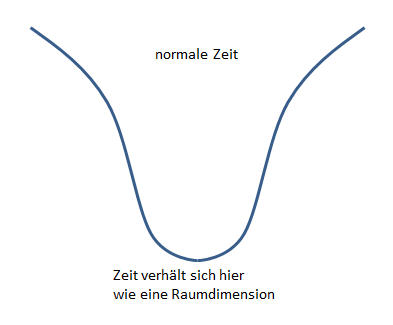
Neben der Idee von Hartle und Hawking gibt es auch noch weitere Lösungsideen, in denen sich ebenfalls Raum und Zeit als Quantenfluktuation gleichsam aus dem Nichts erheben. So hat Alexander Vilenkin eine Wellenfunktion des Universums vorgeschlagen, die sich beim Urknall so ähnlich wie die Wellenfunktion eines Teilchens verhält, das beim radioaktiven Zerfall eines Atoms die Energiebarriere des Atomkerns durchtunnelt und so den Zerfall erst ermöglicht. Genauer tat Vilenkin folgendes:
Er betrachtete ein mikroskopisch kleines sphärisches Universum, dessen dreidimensionaler Raum sich analog zu einer Kugeloberfläche verhält, sodass man vom Radius des Mikro-Universums sprechen kann. Dieses Universum enthält nun in Vilenkins Modell ein Energiefeld (Inflatonfeld) mit stark negativem Druck, das eine abstoßende Gravitation hervorruft, sowie normale Materie ohne negativen Druck, die gravitativ anziehend wirkt. Bei einer Expansion dieses Mini-Universums verdünnt sich die normale Materie, nicht aber das Energiefeld, das konstant bleibt (bis es irgendwann in normale Materie zerfällt). Ist das Universum sehr klein, so gewinnt daher die anziehende Gravitation der dichten normalen Materie und das Mikro-Universum kollabiert. Ist es dagegen groß genug, so ist die normale Materie so verdünnt, dass die abstoßende Gravitation gewinnt und die inflationäre Expansion ein neues makroskopisches Universum entstehen lässt.
Die Quantenmechanik bewirkt nun, dass mit einer gewissen Wahrscheinlichkeit ein zu kleines Universum (das kollabieren müsste) zu einem Universum werden kann, das groß genug ist, um zu expandieren – analog zu dem oben angesprochenen Tunnelprozess, bei dem ein geladenes Kernteilchen, das den Atomkern klassisch nicht verlassen kann, dennoch quantenmechanisch sich so weit von ihm entfernen kann, dass es dem Anziehungsfeld der starken Kernkraft entkommt und von der elektrischen Abstoßung nach außen getrieben wird. Nun untersuchte Vilenkin, was geschieht, wenn das anfängliche Universum immer kleiner wird und gegen Null schrumpft: Bleibt dennoch eine endliche Tunnelwahrscheinlichkeit für die Entstehung eines Universums erhalten, das groß genug ist, um inflationär zu expandieren? Tatsächlich – genau so war es! Es gab eine endliche Wahrscheinlichkeit, dass so ein inflationär expandierendes Universum spontan entsteht, selbst wenn das Vorgängeruniversum unendlich klein wird und verschwindet. Das Universum mitsamt Raum, Zeit und Materie tunnelt gleichsam aus dem Nichts in seine Existenz!
Woher allerdings die Naturgesetze kommen, die dieses Tunneln ermöglichen, bleibt mysteriös. Ob womöglich alle mathematisch konsistenten Strukturen zugleich ein existierendes Universum darstellen, wie es beispielsweise Max Tegmark in seiner Mathematical universe hypothesis vermutet und wie es Brian Greene in seinem Buch Die verborgene Wirklichkeit: Paralleluniversen und die Gesetze des Kosmos als Ultimatives (letztmögliches) Multiversum beschreibt? Ein faszinierender Gedanke, der allerdings nach heutigem Wissensstand noch reine Spekulation bleibt.
Auch wenn es in diesem Zusammenhang sicher noch viele Unklarheiten gibt, so finde ich es faszinierend, wie die moderne Physik Möglichkeiten eröffnet, mit denen sich der Anfang der Zeit und mit ihr der Beginn unseres Universums womöglich erklären lassen. Wir sind damit auf einem guten Weg, in die tiefsten Geheimnisse der Zeit vorzudringen, und wir sehen, dass diese Geheimnisse eng mit der grundlegenden Struktur unseres Universums verknüpft sind. Erst wenn es uns gelingt, diese innere Struktur der Welt zu begreifen, werden wir auch wirklich verstehen, was Zeit eigentlich ist.
Zum Schluss darf natürlich die unvermeidliche Frage nicht fehlen: Gibt es in einem solchen Universum noch Platz für den lieben Gott? Alexander Vilenkin sagte dazu in einem Zeit-Interview von 2008: "Der Spielraum Gottes in der Kosmologie schrumpft." Tatsächlich wird der Standpunkt, die Wissenschaft könne den Anfang der Welt prinzipiell nicht erklären und es bliebe nur Gott als letzte Erklärung, durch die moderne Physik zunehmend in Frage gestellt. Die Wissenschaft schreitet mit Riesenschritten voran und kann mittlerweile Erklärungen für Dinge anbieten, die vor hundert Jahren noch weit jenseits aller Wissenschaft zu liegen schienen. Aber genau dafür ist Naturwissenschaft ja auch gemacht: Um die Natur unserer Welt mit wissenschaftlichen Methoden zu ergründen. Wünschen wir ihr viel Glück, dass ihr das auch weiterhin so gut gelingt, denn ich finde nichts spannender, als herauszufinden, was unsere Welt "im Innersten zusammenhält".
Natürlich gibt es Menschen, die ihren Glauben an Gott durch den Fortschritt der Wissenschaft bedroht sehen, und die Kirche hat in der Vergangenheit ja auch manche Abwehrschlacht geführt – und meist langfristig verloren. Es gibt aber auch durchaus gläubige Menschen, die gelassen mit den Fortschritten der modernen Naturwissenschaft umgehen und sich sogar aktiv daran beteiligen. So sagte der Leiter der Vatikanischen Sternwarte in Castel Gandolfo, Pater José Gabriel, in einem Interview mit Welt Online):
"[...] ich bin Priester und Astronom zur gleichen Zeit. [...] Es ist unsere bleibende Sehnsucht, unseren Kollegen, der Suche nach Wahrheit, dem Menschen und dem täglichen Beweis zu dienen, dass Religion und Wissenschaft keine Gegensätze, sondern fruchtbare Ergänzungen sind."
So entspannt und kann man es also auch sehen!
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 09 February 2023