
Quelle: Wikimedia Commons File:Aristotle Altemps Inv8575.jpg, dort public domain; Foto: Jastrow (2006)
Der lange Weg zum Kraftbegriff
Newtons Trägheitsprinzip und Aktionsprinzip
Die Bedeutung des Aktionsprinzips
Wechselwirkungsprinzip und Impulserhaltung
Quantenmechanik: der Kraftbegriff verschwindet
Nachdem wir in den letzten beiden Kapiteln Raum und Zeit näher kennen gelernt haben, wollen wir uns nun einer fundamentalen physikalischen Größe zuwenden, die der gesamten Mechanik zugrunde liegt: der Kraft. Was ist eigentlich eine Kraft?
Wie bei Raum und Zeit haben wir auch für die Kraft ein gewisses intuitives Verständnis. Wir spüren es unmittelbar, wenn unsere Muskeln eine Kraft aufwenden müssen, um beispielsweise einen schweren Gegenstand hochzuheben. Doch was genau bedeutet es physikalisch, wenn eine Kraft auf einen Gegenstand wirkt? Was macht sie mit dem Gegenstand? Und wie entstehen Kräfte eigentlich?
Diese Fragen sind keineswegs leicht zu beantworten, und es hat viele Jahrhunderte lang gedauert, bis es uns Menschen gelang, die richtige Antwort herauszufinden. Daher ist es sehr lehrreich, sich bei einem kurzen Gang durch die Geschichte einmal anzusehen, welche Schlussfolgerungen die Menschen der jeweiligen Zeit aus ihren Beobachtungen gezogen haben.
Einer der einflussreichsten antiken Denker war Aristoteles, der 384 bis 322 vor Christus in Griechenland lebte. Neben unzähligen anderen Gebieten machte er sich auch Gedanken zu den Gesetzen der Natur und stellte einige erste Bewegungsprinzipien auf. So muss es nach Aristoteles für eine Bewegung immer eine Ursache geben. Dabei kann es sich entweder um einen äußeren Antrieb handeln, oder es kann auch in dem eigenen Bestreben des Gegenstandes liegen, möglichst geradlinig seinen natürlichen Ort zu erreichen. Dabei stellte sich Aristoteles vor, dass jedes Objekt aus den Elementen Wasser, Erde, Feuer und Luft besteht, wobei das jeweils vorherrschende Element den natürlichen Ort bestimmt. Wasser und Erde streben dabei nach unten zum Erdmittelpunkt, Feuer und Luft dagegen nach oben.

Quelle:
Wikimedia Commons File:Aristotle Altemps Inv8575.jpg,
dort public domain; Foto: Jastrow (2006)
Für Aristoteles gibt es also so etwas wie eine absolute Schwere und absolute Leichtigkeit, und jede Bewegung kommt für ihn zum Stillstand, wenn kein äußerer Antrieb mehr da ist und wenn schließlich der natürliche Ort erreicht ist. So ein Antrieb muss dabei durch ein Medium vermittelt werden, das auf den Körper einwirkt und ihn nach vorne treibt oder an der Bewegung hindert. Einen Raum ohne ein Medium – also ein Vakuum – schloss Aristoteles kategorisch aus.
Wenn man sich die Bewegungslehre von Aristoteles so ansieht, dann scheint sie zunächst recht gut auf unsere Welt zu passen, und sie galt über lange Zeit hinweg als ernst zu nehmende Basis für die Beschreibung von Bewegungen. Beispielsweise fährt ein Auto mit kräftigem Antrieb schneller als ein Auto mit nur schwachem Antrieb, und ganz ohne Antrieb bleibt es stehen. Kraft ist also für Aristoteles die Ursache jeder Bewegung, und je mehr Kraft wirkt, umso schneller verläuft die Bewegung. Für Aristoteles gild: Alles was in Bewegung ist, wird von etwas anderem bewegt.
Dennoch waren einige Probleme unübersehbar: Was ist beispielsweise mit der Bewegung eines Pfeils, der von einer Bogensehne abgeschossen wird? Die antreibende Kraft – also die Bogensehne – wirkt hier nur kurz zu Beginn der Bewegung, während anschließend keinerlei Antrieb mehr zu wirken scheint. Dennoch fliegt der Pfeil ohne Antrieb weiter, wobei er nach und nach langsamer wird und schließlich zu Boden fällt.
Offenbar ist auch eine Bewegung ohne äußeren Antrieb (oder natürlichen Ort) möglich. Um diesem Umstand Rechnung zu tragen, kam im Mittelalter die Idee auf, dass es neben äußeren Kräften auch innere Kräfte geben müsse. Beim Abschuss wird demnach dem Pfeil eine solche innere Kraft – auch Impetus genannt – eingepflanzt, die sich während des Fluges nach und nach verbraucht, sodass der Pfeil schließlich zu Boden fällt und zur Ruhe kommt.
Doch auch diese Idee hatte ihre Schwierigkeiten. Was legt beispielsweise fest, wie schnell der eingeprägte Impetus eines Körpers verloren geht? Besteht vielleicht sogar die Möglichkeit, dass der Impetus in bestimmten Fällen sogar komplett erhalten bleibt und das Objekt gar nicht mehr zur Ruhe kommt? Ein Blick hinauf zu den Planeten, die sich anscheinend ungebremst auf ihren Kreisbahnen zu bewegen schienen, legte auch diese Möglichkeit nahe – allerdings ging man meist davon aus, dass im Himmel andere Gesetze herrschen als auf der Erde.
Offenbar war es Galileo Galilei, der als erster im Jahr 1638 auf die Idee kam, dass es Reibungskräfte sind, die den Impetus schwinden lassen. Ohne Reibung müsste sich ein Körper demnach ungebremst immer weiter bewegen, wobei Galilei allerdings noch annahm, dass diese ungebremste Bewegung auf Kreisen um die Himmelskörper erfolgt, so wie dies für die Bewegung der Planeten um die Sonne gilt. Aber immerhin: Galilei hatte als erster das Trägheitsprinzip erkannt, das allen Gesetzen der Mechanik zugrunde liegt – auch wenn er die kräftefreie Bewegung noch nicht ganz korrekt ermittelt hatte.
Johannes Kepler, der ein deutscher Zeitgenosse des Italieners Galilei war,
fand schließlich im Jahr 1609 in mühevoller Kleinarbeit heraus, dass sich die Planeten
nur angenähert auf Kreisbahnen bewegen: Genau genommen sind es Ellipsen,
in deren einem Brennpunkt sich die Sonne befindet.
Dabei erfolgt die Bewegung im Ellipsenbereich nahe an der Sonne
etwas schneller als im sonnenfernen Bereich.
Galileis Idee von der gleichförmigen Kreisbewegung als kräftefreie Grundform der Bewegung
kann also nicht ganz richtig sein.
Kepler selbst nahm dabei noch ganz in der Tradition von Aristoteles an, dass irgendeine
Kraft die Planeten auf ihren Bahnen vorantreibe. Die Sonne sollte dabei wie ein
Schaufelrad wirken, dessen Antriebswirkung mit wachsendem Abstand
immer schwächer würde. Auf diese Weise konnte er den langsameren Lauf der Planeten
mit zunehmendem Sonnenabstand erklären.


Wikimedia Commons File:Galileo.arp.300pix.jpg,
Gemälde von Justus Susterman (1636),
Foto von Adrian Pingstone (2003), dort gemeinfrei;
Wikimedia Commons File:Johannes Kepler 1610.jpg, dort gemeinfrei
Erst im Jahr 1687, also fast 80 Jahre später, gelang es schließlich
dem englischen Physiker
Isaac Newton, alles zu einem konsistenten Gesamtbild zusammenzufügen.
Dabei erzielte Newton einen entscheidenden Durchbruch: Er erkannte
die korrekte kräftefreie Grundbewegung von Körpern.
Anders als Aristoteles dachte, kommt ein kräftefreier Körper nicht zur Ruhe,
und anders als Galilei annahm, bewegt er sich auch nicht auf Kreisbahnen
um Himmelskörper, sondern er bewegt sich einfach mit unveränderter Geschwindigkeit
immer weiter geradeaus! Die kräftefreie Grundform der
Bewegung ist geradlinig-gleichförmig!

Quelle:
Wikimedia Commons File:GodfreyKneller-IsaacNewton-1689.jpg, dort public domain.
Diese für uns heute so selbstverständliche Erkenntnis blieb den Menschen über viele Jahrhunderte hinweg verborgen, denn die geradlinig-gleichförmige Grundform der Bewegung kommt in unserer Umgebung praktisch nicht vor. Auf der Erde unterliegt jede Bewegung vielerlei Einflüssen, insbesondere der Schwerkraft und verschiedenen Reibungskräften, die die wahre Natur der Bewegungsgesetze verschleiern. Würden wir im luftleeren Weltraum weitab aller Sterne und Planeten leben, so wäre uns dagegen die geradlinig-gleichförmige Bewegung vollkommen geläufig. Wir wüssten von Kindesbeinen an, dass ein Gegenstand immer weiter geradeaus fliegt, solange wir ihn nicht aufhalten. Es gehört schon eine enorme Vorstellungskraft dazu, auch auf der Erde diese Einsicht zu gewinnen. Galileo Galilei und insbesondere Isaac Newton ist dies schließlich gelungen!
Newton formulierte die kräftefreie Grundform der Bewegung als erstes Bewegungsgesetz in seinem 1687 erschienenen Werk Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie):
Kräfte sind also nicht mehr die Ursache für eine Bewegung, sondern sie bewirken die Änderung einer Bewegung! Den Zusammenhang zwischen der Kraft und der durch sie hervorgerufenen Änderung der Bewegung legte Newton in seinem zweiten Bewegungsgesetz genauer dar:
Genau genommen hätte Newton sein erstes Gesetz – das Trägheitsprinzip – auch weglassen können, denn es ist im Aktionsprinzip mit enthalten: Ohne eine Kraft ändert sich die Bewegung nicht. Da es jedoch so wichtig ist, die kräftefreie Bewegung als geradlinig-gleichförmig zu erkennen, lohnte es sich, das Trägheitsprinzip noch einmal extra aufzuführen und es sogar an den Anfang aller Überlegungen zu stellen.
Schauen wir uns das zweite Gesetz – also das Aktionsprinzip – genauer an:
Ganz präzise ist dieses Gesetz so nicht, denn wir müssen noch
genauer angeben, was wir mit der Änderung einer Bewegung meinen.
Normalerweise versteht man darunter die Änderung der Geschwindigkeit,
also die Beschleunigung
\(
\boldsymbol{a} = d\boldsymbol{v}/dt
\)
, und
führt als Proportionalitätsfaktor zwischen der Kraft \( \boldsymbol{F} \)
und der Beschleunigung \( \boldsymbol{a} \)
die konstante träge Masse \( m \) des jeweiligen Körpers ein,
die die Trägheit des Körpers kennzeichnet:
\begin{equation}
\boldsymbol{F} = m \boldsymbol{a}
\end{equation}
Dabei sind die Kraft \( \boldsymbol{F} \) und die Beschleunigung \( \boldsymbol{a} \)
Vektoren, die man sich als Pfeile im Raum vorstellen kann:
Sie haben neben einem Betrag (einer Länge) auch eine Richtung.
Wir wollen vektorielle Größen hier wie immer durch Fettdruck kennzeichnen,
während wir ihre Beträge ohne Fettdruck schreiben.
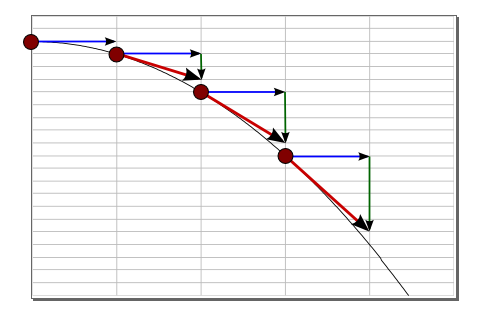
Für Geschwindigkeiten, die klein gegenüber der Lichtgeschwindigkeit sind, ist diese Formulierung des Aktionsprinzips vollkommen ausreichend. Für größere Geschwindigkeiten kann sie jedoch nicht mehr korrekt sein, denn eine konstante Kraft würde eine konstante Beschleunigung bewirken, die nach einiger Zeit dazu führt, dass die Geschwindigkeit eines Körpers die Lichtgeschwindigkeit überschreitet. Das stünde jedoch im Widerspruch zu Einsteins spezieller Relativitätstheorie, nach der sich nichts schneller als das Licht fortbewegen kann.
Wenn man die Änderung einer Bewegung etwas anders versteht, dann wird Newtons Gesetz auch für große Geschwindigkeiten anwendbar. Erinnern wir uns an den Impetus, also die eingeprägte innere Kraft oder besser den inneren Schwung, der einen abgeschossenen Pfeil weiterfliegen lässt, wenn er die Bogensehne bereits verlassen hat. Statt Impetus wollen wir ab sofort einen moderneren Begriff verwenden: den Impuls \( \boldsymbol{p} \) , den wir im nächsten Kapitel noch genauer kennenlernen werden. Wie der Fettdruck andeutet, handelt es sich beim Impuls um einen Vektor, der analog zur Geschwindigkeit \( \boldsymbol{v} \) in Bewegungsrichtung zeigt. Reibungskräfte bewirken, dass bei einem fliegenden Pfeil dessen Impuls langsam abnimmt – ohne Reibung und andere Kräfte wäre er konstant und der Pfeil würde seinen Schwung nicht verlieren. Die Änderung einer Bewegung können wir also auch als zeitliche Änderung des Impulses \( d\boldsymbol{p}/dt \) interpretieren, wobei wir bei passendem Impulsbegriff sogar auf eine Proportionalitätskonstante verzichten können, denn die Trägheit des Objektes steckt dann bereits im Impuls mit drin – je träger ein Körper ist, umso größer ist dann bei gleicher Geschwindigkeit sein mitgeführter Schwung und damit sein Impuls: \begin{equation} \boldsymbol{F} = \frac {d \boldsymbol{p} }{dt} \end{equation} In dieser Form ist Newtons zweites Gesetz tatsächlich allgemeingültig. Insbesondere kann der Impuls eines Objekts – anders als seine Geschwindigkeit – beliebig groß werden, denn es gilt ganz allgemein der folgende Zusammenhang zwischen dem Impuls \( \boldsymbol{p} \) und der Geschwindigkeit \( \boldsymbol{v} \) (mehr dazu im nächsten Kapitel): \begin{equation} \boldsymbol{p} = m \gamma \boldsymbol{v} \end{equation}
mit dem geschwindigkeits-abhängigen Lorentzfaktor
\begin{equation}
\gamma = \sqrt {\frac{1}{1 - (v/c)^2} }
\end{equation}
und der weiterhin konstanten Masse \( m \).
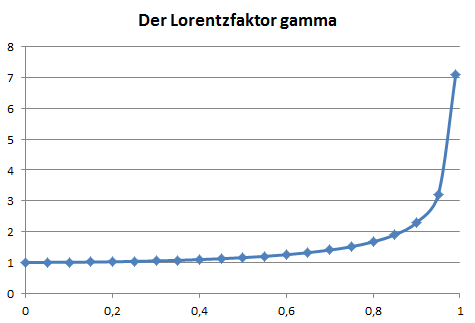
Dieser Lorentzfaktor startet für Geschwindigkeit Null bei 1 und wächst immer weiter an, je näher
die Geschwindigkeit \( v \) der Lichtgeschwindigkeit \( c \) kommt.
Man kann sich das so vorstellen, dass das Produkt \( m \gamma \) die
Trägheit eines Objektes kennzeichnet.
Diese Trägheit wird mit wachsender Geschwindigkeit immer
größer, sodass das Objekt immer schwieriger weiter zu beschleunigen ist – daher
kann die Lichtgeschwindigkeit nie überschritten werden, obwohl der Impuls immer weiter anwächst.
Die wachsende Trägheit bewirkt auch, dass fast lichtschnelle Teilchen nur sehr schwer
aus ihrer Bahn abgelenkt werden können.
An den modernen Teilchen-Ringbeschleunigern wie dem Large Hadron Collider LHC
sind daher sehr starke Magnetfelder notwendig,
um die hochenergetischen Teilchen auf eine Kreisbahn zu zwingen.
Wir sehen also, dass die Trägheit eines Objektes von seiner Geschwindigkeit abhängt – Newton wusste das noch nicht! Warum das so ist, werden wir erst im nächsten Kapitel verstehen können.
Für kleine Geschwindigkeiten (relativ zur Lichtgeschwindigkeit, die ja immerhin knapp 300000 km/s beträgt) ist die Trägheit nahezu konstant, da der Lorentzfaktor γ hier kaum größer als 1 ist und erst sehr langsam ansteigt, wie die Grafik oben zeigt. Wir können daher für Geschwindigkeiten, wie sie typischerweise in unserem Alltag auftreten, den Lorentzfaktor \( \gamma \) in guter Näherung weglassen: \begin{equation} \boldsymbol{p} = m \boldsymbol{v} \quad \mathrm{wenn} \quad v \ll c \end{equation} Damit ergibt sich für normale Geschwindigkeiten \begin{equation} \boldsymbol{F} = \frac {d \boldsymbol{p} }{dt} = m \frac {d \boldsymbol{v} }{dt} = m \boldsymbol{a} \end{equation} also unser Gesetz etwas weiter oben.
Es ist gar nicht so einfach, sich die physikalische Bedeutung des Aktionsprinzips und des damit verbundenen Kraftbegriffs genau klar zu machen. Richard Feynman hat dies in seinen Feynman-Vorlesungen über Physik (Band I) im Kapitel 12.1 Was is eine Kraft? in unvergleichlicher Weise getan, und wir folgen hier einigen seiner Gedankengängen:
Wenn wir uns das Aktionsprinzip in seiner allgemeinen Form
\begin{equation} \boldsymbol{F} = \frac {d \boldsymbol{p} }{dt} \end{equation}
bzw. in seiner nichtrelativistischen Variante \begin{equation} \boldsymbol{F} = m \boldsymbol{a} \end{equation} ansehen, so könnten wir es leicht für eine Definition der Kraft halten. Wir könnten sagen: Wir definieren das Produkt von Masse und Beschleunigung bzw. allgemeiner die zeitliche Änderung des Impulses als Kraft. Entsprechend ist ja auch die Maßeinheit Newton für die Kraft definiert: Ein Newton ist gleich einem Kilogramm mal einem Meter pro Sekunde zum Quadrat, d.h. die Kraft von einem Newton führt bei einem ruhenden oder nur langsam bewegten Körper pro Sekunde zu einem Geschwindigkeitszunahme von einem Meter pro Sekunde. Nur warum hat es dann viele hundert Jahre gedauert, bis die Menschen auf diese Definition gekommen sind?
Die Bewegungslehre von Aristoteles hätte es nahegelegt, den Kraftbegriff ganz anders zu definieren – Feynman nannte den entsprechenden Begriff scherzhaft Schmaft (im englischen Original gorce). Es muss eine Schmaft wirken, um einen Körper in Bewegung zu halten. Ohne Schmaft bewegt er sich nicht, und je mehr Schmaft wirkt, umso schneller ist er. Man könnte also folgende Definition aufstellen: \begin{equation} \mathrm{Schmaft} = k \boldsymbol{v} \end{equation} mit irgendeiner Proportionalitätskonstanten \( k \). Keiner kann es uns verbieten, einen solchen Begriff zu definieren. Leider wäre damit gar nichts gewonnen, wie man im Lauf der Jahrhunderte zunehmend herausfand, als man versuchte, aus der Bewegungslehre von Aristoteles heraus handfeste Berechnungen und Vorhersagen zu gewinnen. Wann immer man irgendwelche Annahmen über die Schmaft machte, so fanden sich Ausnahmen davon, wie der Flug eines Pfeils oben gezeigt hat. Nehmen wir beispielsweise an, dass nur beim Abschuss eine Schmaft auf den Pfeil wirkt, so kann er anschließend nach dem obigen Schmaftgesetz nicht weiterfliegen: keine Schmaft – keine Bewegung! Also müsste auch nach dem Abschuss noch eine Schmaft auf den Pfeil wirken, nur wo soll die herkommen, wenn der Bogen doch bereits verlassen wurde?
Interessanterweise kam man mit der Impetustheorie langsam dahinter, dass der Schmaftbegriff so keinen Sinn macht: Schmaft war nun nicht mehr nur die Abschusskraft, sondern sie wurde um eine innere Kraft – den Impetus – erweitert, der dem Impulsbegriff nahekommt. Für den Impuls – also den Schwung eines Objekts – macht die obige Beziehung durchaus Sinn, denn der Impuls ist tatsächlich (zumindest für kleine Geschwindigkeiten) proportional zur Geschwindigkeit. Das Problem ist nur, dass die Impetustheorie nicht mehr sauber zwischen verschiedenen Kraftbegriffen wie innerer und äußerer Kraft unterscheiden konnte, denn für die äußere Kraft oder Schmaft – also den Abschuss – ist die obige Beziehung unbrauchbar. Man weiß hier nicht mehr so genau, welche Größen einem äußeren Einfluss entsprechen und welche Größen dem Objekt und seiner Bewegung zugeordnet werden müssen.
Ganz anders bei Newton: Sein Gesetz sagt nicht mehr, dass man von außen einen Einfluss ausüben muss, um eine Bewegung aufrecht zu erhalten, sondern es sagt, dass man ohne Einfluss von außen eine geradlinig-gleichförmige Bewegung erhält, während ein äußerer Einfluss diese Bewegung ändert. Die Kraft repräsentiert gerade diesen äußeren Einfluss – sie gehört also eindeutig zur Außenwelt, die auf das bewegte Objekt einwirkt, und nicht mehr zum Objekt selbst. Mit Newtons Gesetz als Grundlage kann man sich nun auf die Suche nach solchen äußeren Einflüssen – also Kräften – begeben. Man kann sich beispielsweise fragen, welchen Einfluss Sonne und Planeten aufeinander ausüben. Newton tat genau dies und konnte so zeigen, dass eine Anziehungskraft, die quadratisch mit zunehmendem Abstand zwischen den Himmelskörpern abnimmt, genau die elliptischen Planetenbahnen hervorbringt, die Johannes Kepler mehrere Jahrzehnte zuvor gefunden hatte. Man kann sich heute kaum noch vorstellen, welchen ungeheuren Eindruck diese Leistung auf die damaligen Zeitgenossen Newtons ausgeübt hat – man kann ihn vermutlich nur noch mit dem Einfluss Albert Einsteins vergleichen, als dieser rund 220 Jahre nach Newton unsere Vorstellung von Raum und Zeit revolutionierte.
Wie wir wissen, ist es meist sehr schwierig, physikalische Begriffe sauber zu definieren. Sie entsprechen zunächst anschaulichen Vorstellungen, die man schrittweise zu präzisieren versucht. Genauso ist das auch bei den Begriffen in Newtons Gesetzen.
Am saubersten ist darin noch die Beschleunigung \( \boldsymbol{a} \) definiert, wenn wir ein klares Verständnis von Raum und Zeit voraussetzen – was auch seine Schwierigkeiten hat, wie wir in den letzten beiden Kapiteln gesehen haben. Die Masse \( m \) steht wiederum für die Trägheit des Körpers, also für sein Vermögen, sich trotz Krafteinwirkung einer Beschleunigung zu widersetzen. Newton nahm noch an, dass diese Trägheit eine feststehende Eigenschaft des bewegten Körpers ist. Dass das so nicht stimmt, fand knapp 220 Jahre später Albert Einstein heraus – der Lorentzfaktor war die Folge, wie wir gesehen haben. Diese Erkenntnis zeigt, dass \( \boldsymbol{F} = m \boldsymbol{a} \) nicht alleine eine Definition sein kann, denn wäre sie eine, so müssten wir sie nicht ändern. Wenn aber die Kraft \( \boldsymbol{F} \) nur äußere Einflüsse beinhalten soll, dann muss die Trägheit des Körpers in den Größen auf der rechten Seite der Gleichung enthalten sein. Die mit der Geschwindigkeit anwachsende Trägheit erzwingt dann eine Veränderung der Gleichung auf der rechten Seite. Nur so passt die Gleichung noch zu den Interpretationen, die wir für die physikalischen Größen darin beabsichtigen.
Die Kraft steht also nach Newton für einen äußeren Einfluss, der die Bewegung eines Körpers ändert. Um weiterzukommen, müssen wir mehr über solche äußeren Einflüsse herausfinden. Woher kommen solche Einflüsse? Was erzeugt Kräfte?
Unsere Erfahrung zeigt, dass Kräfte auf einen Körper von anderen Körpern ausgehen. Zwei Körper können sich also gegenseitig beeinflussen! Das kann beispielsweise durch direkte Berührung erfolgen, und man nahm über sehr lange Zeiten hinweg an, dass dies die einzige Möglichkeit für eine gegenseitige Beeinflussung sei. Auch der offensichtliche Einfluss, den die Sonne auf die Planeten ausübt, stellte man sich vermittelt durch eine Art von Medium vor – auch Äther genannt. Erst Newton verzichtete auf diesen Äther, der immer wieder zu Problemen und Widersprüchen führte, und formulierte sein Gravitationsgesetz als unmittelbare Fernwirkung zwischen den Himmelskörpern. Damit ließ er offen, wie es denn die Gravitation schaffte, über den leeren Raum hinweg ihren Einfluss auszuüben. Newton selbst empfand dies als Makel an seiner Theorie, der noch zu beseitigen sei, aber erst Albert Einstein gelang es mit seiner allgemeinen Relativitätstheorie, den vermittelnden Mechanismus zu entschlüsseln, nämlich die Krümmung von Raum und Zeit.
Unabhängig von dem genauen Mechanismus der gegenseitigen Beeinflussung fiel Newton eine allgemeine Eigenschaft der beteiligten Kräfte auf:
Das passt sehr gut zu unserer Anschauung, nach der nur ein äußerer Einfluss
eine Bewegung ändern kann.
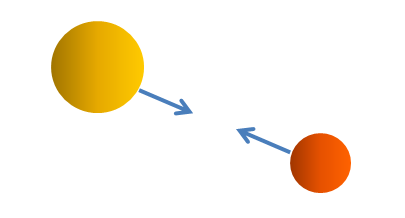
Schauen wir uns als Beispiel ein Doppelsternsystem an, also zwei Sonnen, die sich
gegenseitig gravitativ anziehen und umkreisen.
Dabei wird Sonne A genauso stark zu Sonne B hingezogen wie umgekehrt Sonne B zu Sonne A.
Aus der Entfernung betrachtet handelt es sich dabei um innere Kräfte innerhalb des
Doppelsternsystems. Sie heben sich gegenseitig auf, d.h.
auf das Doppelsternsystem als Ganzes wirkt von innen heraus
keine Kraft mehr ein, die das gesamte System
in irgendeine Richtung beschleunigen würde.
Eine solche Kraft müsste also von außen kommen, beispielsweise von den anderen Sternen
innerhalb der Milchstraße.
Diese Überlegung können wir auch auf die Milchstraße als Ganzes ausdehnen, also auf die gegenseitige Beeinflussung zwischen sehr vielen Sternen: Die gegenseitigen Anziehungskräfte zwischen den Sternen der Milchstraße heben sich in Summe auf, sodass die Milchstraße als Ganzes unbeirrt ihre Bahn zieht, solange keine Gravitationskräfte von außen auf sie einwirken – dies wäre dann eine auf viele Objekte erweiterte Fassung des Wechselwirkungsprinzips. Erst der Einfluss anderer Galaxien kann die Bahn der Milchstraße verändern.
Manchmal erscheint es uns so, als ob es doch einzelne Kräfte ohne Gegenkraft gäbe. So wird unser eigener Körper offensichtlich von der Masse der Erde angezogen. Wo ist hier die zugehörige Gegenkraft? Tatsächlich wird auch die Erde von unserem Körper angezogen, und zwar mit genau derselben Stärke. Wenn wir also hochspringen, so werden nicht nur wir selbst hoch und wieder herunterfallen, sondern auch die gesamte Erde wird spiegelbildlich eine entsprechende Gegenbewegung ausführen, nur mit sehr viel geringerer Auslenkung, da sie eine viel größere Massenträgheit als wir selbst besitzt. Die Bewegung der Erde ist bei einem solchen Sprung also gegenüber unserer eigenen Bewegung praktisch nicht wahrnehmbar, aber sie existiert!
Aus dem Wechselwirkungsprinzip folgt eine sehr interessante Eigenschaft für den Gesamtimpuls. Schauen wir uns dazu noch einmal das Doppelsternsystem ohne äußere Kräfte an, das aus den Sternen A und B besteht. Für die Impulssumme von Stern A und Stern B gilt: \begin{equation} \frac{ d ( \boldsymbol{p}_{\mathrm{A}} + \boldsymbol{p}_{\mathrm{B}} ) }{dt} = \frac{ d \boldsymbol{p}_{\mathrm{A}} }{dt} + \frac{ d \boldsymbol{p}_{\mathrm{B}} }{dt} = \boldsymbol{F}_{\mathrm{A}} + \boldsymbol{F}_{\mathrm{B}} = 0 \end{equation}
denn nach dem Wechselwirkungsprinzip (actio gleich reactio) ist \( \boldsymbol{F}_{\mathrm{B}} = - \boldsymbol{F}_{\mathrm{A}} \) . Der Gesamtimpuls des Doppelsternsystem ändert sich aufgrund innerer Kräfte also nicht, da diese sich gegenseitig aufheben. Dieses Gesetz von der Impulserhaltung spiegelt genau das Fehlen äußerer Kräfte wider, denn nur diese sollten in der Lage sein, den Gesamtimpuls des Sternensystems zu ändern. Aus dem Wechselwirkungsprinzip folgt also die Gesamtimpulserhaltung, die wir uns als Erhaltung des Gesamtschwungs des zusammengesetzten Systems veranschaulichen können.
Genau genommen ist das Gesetz von der Impulserhaltung sogar allgemeiner als das Wechselwirkungsprinzip, denn letzteres gilt nur näherungsweise unter der Voraussetzung, dass die verschiedenen Körper so nahe beieinander und so langsam sind, dass sich die Lichtgeschwindigkeit nicht bemerkbar macht. Das Wechselwirkungsprinzip setzt nämlich voraus, dass sich der gegenseitige Einfluss der Körper unmittelbar auswirkt. Nach Einsteins Relativitätstheorie kann sich aber jeder Einfluss – also auch beispielsweise die Wirkung der Gravitation oder elektromagnetische Kräfte – höchstens mit Lichtgeschwindigkeit auswirken.
Schauen wir uns als Beispiel eine ruhende elektrische Ladung an, die innerhalb eines kurzen Zeitintervalls ihre Position verändert und dann wieder ruht. Diese Positionsänderung kann sich erst mit zeitlicher Verzögerung auf andere Ladungen auswirken. Dennoch kann die Ladung bei ihrer Positionsänderung Energie und Impuls (also Schwung) verlieren, auch wenn die anderen Ladungen diese Energie und diesen Impuls erst später aufnehmen können, da sie von der Bewegung zunächst gar nichts mitbekommen. Wo steckt der fehlende Impuls in der Zwischenzeit während seiner Reise zu den anderen Ladungen?
Um dieses Rätsel lösen zu können, müssen wir die Kraftübertragung
zwischen den Ladungen in zwei Einzelschritte aufteilen.
Wir müssen uns von Newtons unmittelbarer Fernwirkung verabschieden und
wieder so etwas wie ein vermittelndes Medium einführen, das aber diesmal
kein konkretes Material zu sein braucht, sondern zunächst nur ein mathematisches
Hilfsmittel ist.
Nennen wir dieses Hilfsmittel ein Feld, und im Fall von elektrischen Ladungen
konkret ein elektromagnetisches Feld.
Dieser begriffliche Schritt, den der englische Naturforscher Michael Faraday
um das Jahr 1852 (also rund 165 Jahre nach Newtons bahnbrechenden Arbeiten) vollzog,
bildete einen Meilenstein im Verständnis
von Kräften und ihrer Ausbreitung im Raum, ohne den eine effiziente
Beschreibung insbesondere der elektromagnetischen Kräfte nicht möglich gewesen wäre.
Quelle:
Wikimedia Commons File:M Faraday Th Phillips oil 1842.jpg,
dort gemeinfrei.
Nun können wir sagen: Ladungen erzeugen im sie umgebenden Raum ein
elektromagnetisches Feld, und umgekehrt bestimmt das Feld an jedem Ort,
welche Kraft dort auf eine Ladung wirkt.
Dieses Feld kann nun mit Verzögerung auf eine Positionsänderung
der felderzeugenden Ladungen reagieren:
Das Wissen um die Positionsänderung breitet sich wie eine Welle
mit Lichtgeschwindigkeit im Feld aus und verändert dieses Feld.
Dabei kann diese Welle Energie und Impuls transportieren.
Das Gesetz der Impulserhaltung ist also nur dann gültig, wenn
wir die Energie und den Impuls mit berücksichtigen, den ein elektromagnetisches
Feld tragen kann. Damit wird das Feld tatsächlich mehr als ein rein mathematisches
Werkzeug zur Beschreibung von Kräften: es kann selber physikalische Eigenschaften
aufweisen, die man normalerweise nur von einem massiven Objekt gewohnt ist.
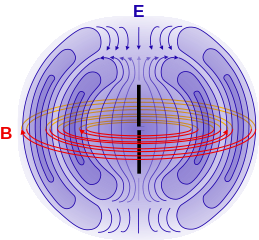
Quelle:
Wikimedia Commons File:Felder um Dipol.svg,
dort
Creative Commons CC0 1.0 Universal Public Domain Dedication.
Mithilfe des Feldbegriffs gelang es tatsächlich, die elektromagnetischen Kräfte umfassend zu beschreiben. Newtons Gesetze erwiesen sich dabei als voller Erfolg, wenn man zusätzlich berücksichtigte, dass sich die Kraftfelder nur mit Lichtgeschwindigkeit ausbreiten können und dass sie dabei Energie und Impuls transportieren.
Bei den Gravitationskräften musste man allerdings nach Newton weiterhin von einer unmittelbaren Fernwirkung ohne Zeitverzug ausgehen, wie ihn Newtons Gravitationsgesetz vorsah. Der Feldbegriff reichte hier nicht aus, um eine konsistente Gesamtbeschreibung zu erreichen, die sich mit der endlichen Ausbreitungsgeschwindigkeit von Kraftwirkungen vertrug. Erst Albert Einstein gelang es im Jahr 1916, den richtigen mathematischen Rahmen zu finden. Und mit eben diesem Rahmen verließ er erstmals das Gebäude, das Newton auf dem Kraftbegriff begründet hatte. Wie ist ihm das gelungen?
Betrachten wir als Beispiel zwei Himmelskörper, die sich zunächst parallel mit gleicher Geschwindigkeit in konstantem Abstand zueinander bewegen. Ohne eine gegenseitige Anziehungskraft werden sie diese Bewegung nach Newton ewig beibehalten. Erst die Anziehungskraft zwischen ihnen lässt sie sich aufeinander zu bewegen. Anders bei Einstein: Für ihn gibt es keine Anziehungskraft zwischen den Himmelskörpern, sondern beide Körper krümmen die sie umgebende Raumzeit. In dieser Raumzeit bewegen sie sich so geradeaus wie möglich (genauer: sie bewegen sich so, dass mitgeführte Uhren so schnell wie möglich laufen). Es ist die Raumzeitkrümmung, die für die Annäherung der Himmelskörper sorgt. Die Himmelskörper empfinden dabei keinerlei Kraftwirkung – sie befinden sich im freien Fall und empfinden die Welt als schwerelos.
Man kann sich das Prinzip gut mithilfe der gekrümmten Erdoberfläche veranschaulichen.
Nehmen wir an, wir lassen am Äquator zwei Flugzeuge in einem Kilometer Abstand
genau in Richtung Norden starten. Dabei sollen sie nie von diesem Kurs abweichen:
ihr Weg führt sie immer genau geradeaus nach Norden.
Zunächst verläuft ihr Flug parallel, doch nach einigen Stunden stellen die
beiden Piloten erstaunt fest, dass sich die Flugzeuge näher kommen.
Für jemanden, der ihren Flug auf einem Globus verfolgen kann, ist
die Sache klar: Sie habe beide denselben Punkt als Ziel: den Nordpol.
Dort treffen sich alle Großkreise mit festem Längengrad, und jedes der Flugzeuge
folgt einem solchen Großkreis.
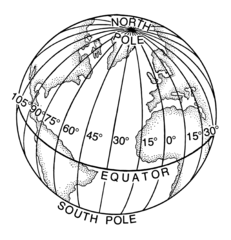
Quelle:
Wikimedia Commons File:Longitude (PSF).png
von Pearson Scott Foresman, dort public domain.
Wir sehen also, wie sich Newtons Kraftbegriff in Einsteins allgemeiner Relativitätstheorie der Gravitation auflöst – er wird für die Beschreibung der Gravitation nicht mehr benötigt, da in einer gekrümmten Raumzeit die geradlinig-gleichförmige Bewegung nicht mehr die Grundform jeder Bewegung darstellt. Der freie Fall liefert nun diese Grundform der Bewegung, und die erfolgt innerhalb der gekrümmten Raumzeit in einem gewissem Sinn so geradeaus wie möglich. Physikalisch bedeutet das, dass man innerhalb einer frei fallenden Raumkapsel keine Schwerkraft spürt. Erst wenn man sich dem freien Fall entgegenstemmt – beispielsweise indem man die Raumkapsel auf die feste Erdoberfläche stellt – so empfindet man eine Kraftwirkung, wie sie als Scheinkraft in einem beschleunigten Bezugssystem auftritt. Wir kennen das bereits aus den vorherigen Kapiteln und wollen daher hier nicht mehr genauer darauf eingehen.
Besonders deutlich wird der Unterschied zwischen Newtons Kraftbeschreibung und Einsteins geometrischer Beschreibung der Gravitation, wenn wir uns das expandierende Universum als Ganzes ansehen. Nach Newton ist es die abstoßende Gravitationskraft aufgrund der dunklen Energie des Raums, welche die Galaxien immer schneller auseinander treibt. Nach Einstein ist es die Expansion des Raums selbst, die den Abstand zwischen den Galaxien immer schneller vergrößert. Diese Expansion ist wiederum eine Folge der gekrümmten Zeit in der Raumzeit des Universums. Die Galaxien selbst bewegen sich dabei kaum im Raum, wenn wir die Lichtgeschwindigkeit als Maßstab nehmen. Jede Galaxie empfindet sich also weitgehend als ruhend im Raum und kann das auch nachweisen, indem sie ihre Bewegung relativ zur kosmischen Hintergrundstrahlung misst (siehe das vorherige Kapitel). Das lässt sich nur mit Einsteins allgemeiner Relativitätstheorie der Gravitation verstehen – Newtons Kraftbegriff ist hier machtlos.
Der Kraftbegriff beruht darauf, dass man ein wohldefiniertes materielles Objekt vor sich hat, dessen Bewegung sich exakt verfolgen lässt. Immer wenn dieses Objekt von seiner geradlinig-gleichförmigen Bewegung abweicht, so muss nach Newton eine Kraft auf dieses Objekt einwirken und die Ablenkung verursachen.
In der Quantenmechanik, die auf mikroskopischer Ebene die Materie beschreibt, gibt es aber keine klar definierten Bahnkurven mehr. Die Bewegung von Teilchen wird vielmehr durch Wahrscheinlichkeitswellen beschrieben, wobei die Intensität der Welle an einem Ort angibt, mit welcher Wahrscheinlichkeit man dort ein Teilchen antreffen kann, wenn man nachsieht.
Es verwundert daher nicht, dass mit der Bahnkurve auch der Kraftbegriff verschwindet – er kommt in der Quantenmechanik einfach nicht mehr vor. Aber was tritt an seine Stelle?
An Stelle der Bewegung eines Objekts entlang einer Bahnkurve
muss man nun die zeitliche Entwicklung
einer Welle im gesamten Raum betrachten. Das geschieht mithilfe einer passenden Wellengleichung,
also einer Differentialgleichung in Ort und Zeit, beispielsweise der Schrödingergleichung.
Aber wie macht sich darin ein äußerer Einfluss wie beispielsweise
ein elektromagnetisches Feld bemerkbar? Eine Kraftwirkung kann es ja nicht mehr sein,
denn es gibt kein direkt greifbares Objekt mehr, auf dessen Bewegung die Kraft einwirken könnte.
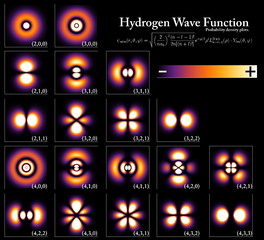
Quelle:
Wikimedia Commons File:Hydrogen Density Plots.png
von PoorLeno, dort public domain.
Um das herauszufinden, müssen wir uns ansehen, wie die Welle mit den Eigenschaften des zugehörigen Teilchens – beispielsweise eines Elektrons – zusammenhängt. Dieses Teilchen hat zwar keine Bahnkurve mehr, aber man kann dennoch seinen momentanen Impuls und seine momentane Energie bestimmen (eine gleichzeitige Bestimmung seines Ortes ist dabei nicht möglich – daher gibt es auch keine Bahnkurve mehr). Allerdings haben Impuls und Energie des Teilchens nur bei einer ebenen Welle – also einem weit ausgedehnten gleichförmigen Wellenfeld mit fester Wellenlänge und Frequenz – eindeutig festgelegte Werte: Die Teilchenenergie wächst proportional zur Frequenz, während der Teilchenimpuls sich umgekehrt proportional zur Wellenlänge verhält; der Umrechnungsfaktor ist das berühmte Planck'sche Wirkungsquantum.
Zum Glück lässt sich jede beliebige Welle als Überlagerung vieler ebener Wellen verstehen, sodass eine allgemeine Welle meist eine gewisse Bandbreite verschiedener Wellenlängen und Frequenzen umfasst. Das zugehörige Teilchen weist entsprechend einen ganzen Wertebereich für mögliche Impuls- und Energiewerte auf, die bei einer Messung mit gewissen Wahrscheinlichkeiten zufällig auftreten können. Hier macht sich wieder der physikalische Charakter der Welle bemerkbar: es handelt sich um eine Wahrscheinlichkeitswelle.
In der Quantenmechanik spielen also Energien und Impulse die entscheidende Rolle, da sie direkt mit Frequenzen und Wellenlängen verknüpft sind. Nun kann man auch die klassische Mechanik so umformulieren, dass sie ebenfalls mit Energien und Impulsen arbeitet – man nennt das die Hamilton'sche Formulierung der Mechanik. In dieser Formulierung tritt der Kraftbegriff nicht mehr direkt auf – er versteckt sich gewissermaßen hinter dem Begriff des Potentials (genauer des skalaren Potentials, das für die potentielle Energie steht, sowie des Vektorpotentials, das man als Ersatzbegriff für Magnetfelder braucht – wir schauen uns den Potentialbegriff im nächsten Kapitel noch genauer an). Ganz analog tritt auch in der Quantenmechanik das Potential an die Stelle der Kraft.
Nimmt man zur Quantenmechanik noch die spezielle Relativitätstheorie hinzu, so wird auch der Potentialbegriff hinfällig – er wird ersetzt durch den Austausch von Teilchen wie dem Photon. In dieser sogenannten relativistischen Quantenfeldtheorie gibt es nur noch Teilchen, die durch Wahrscheinlichkeitswellen beschrieben werden, wobei ständig neue Teilchen entstehen und wieder eingefangen werden können. Energien und Impulse bleiben dabei immer erhalten, aber von einer Kraft oder einem Potential ist hier nichts mehr zu sehen. Es sieht fast so aus, als seien Energie und Impuls die fundamentaleren Begriffe in der Natur, und deshalb wollen wir uns diese physikalischen Größen in den beiden nächsten Kapiteln genauer ansehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 09 February 2023