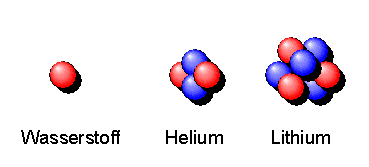
Zusammenfassung des Buchkapitels:
Atomkerne besitzen eine Ausdehnung von wenigen Fermi (fm) und sind damit etwa Zehntausend mal kleiner als die Atome. Sie bestehen aus positiv geladenen Protonen und elektrisch neutralen Neutronen, die wir uns zunächst als etwa ein Fermi große, relativ kompakte Kugeln vorstellen können und die sich dicht an dicht zum Atomkern zusammenlagern. Oft fasst man Protonen und Neutronen unter dem Begriff Nukleonen zusammen.
In elektrisch neutralen Atomen ist die Zahl der Protonen gerade gleich der Zahl der Elektronen in der Atomhülle. Neutronen und Protonen sind ebenso wie das Elektron Teilchen mit Spin 1/2. Wie für alle Fermionen (Teilchen mit Spin 1/2) gilt auch für Protonen und Neutronen das Pauliprinzip, so dass sich die vielen Nukleonen im Atomkern nicht beliebig dicht zusammenballen können.
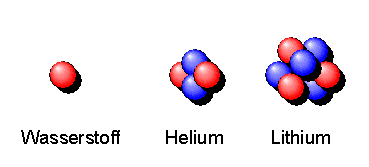
Da die Protonen des Atomkerns elektrisch positiv geladen sind,
stoßen sie sich gegenseitig ab.
Was also hält eigentlich Protonen und Neutronen im Atomkern
zusammen? Die Gravitation ist viel zu schwach, um das leisten zu können.
Zwischen den Bausteinen der Atomkerne wirkt eine neuartige anziehende Kraft, die bei den sehr kleinen Abständen im Bereich weniger Fermi etwa einhundert mal stärker ist als die elektrische Abstoßungskraft. Diese Kraft nennen wir starke Kernkraft oder auch starke Kern-Wechselwirkung. Sie macht zwischen Protonen und Neutronen keinen Unterschied.
Sobald sich Nukleonen mehr als einige Fermi voneinander entfernen, erlischt die starke Kernkraft zwischen ihnen sehr schnell. Eine einfache Abschätzung (Yukawa 1935) ergibt für die Abstandsabhängigkeit der starken Kernkraft die Formel \[ F \sim \left( \frac{1}{br} + \frac{1}{r^{2}} \right) \, e^{- r/b} \] mit \(b = 1,4\) fm und \( e = 2,71828... \). Man bezeichnet \(b\) auch als Reichweite der starken Kernkraft.
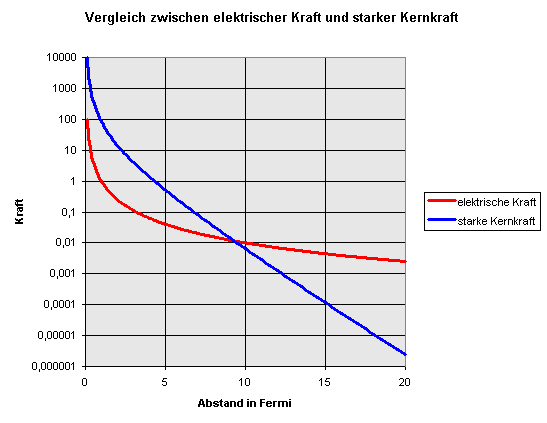
Vergleich zwischen starker Kernkraft und elektrischer Kraft.
Für die Erstellung der beiden Kurven wurde einfach
näherungsweise angenommen, dass bei sehr kleinen
Abständen die starke Kernkraft zwischen Protonen etwa 100-mal
stärker ist als die elektrische Kraft.
Die obigen Kurven machen nur oberhalb von etwa 1 bis 2 Fermi Sinn,
da sich darunter die Nukleonen bereits gegenseitig
überlappen können und es zu Abstoßungseffekten kommt.
Protonen und Neutronen sind fast gleich schwer
und besitzen etwa das Zweitausendfache der Elektronenmasse,
wobei das Neutron etwas schwerer als das Proton ist.
Die Masse des Protons beträgt 938,272 MeV,
die des Neutrons 939,566 MeV (zur Erinnerung: die
Elektronmasse liegt bei 0,511 MeV).
Man macht nun in den Experimenten eine sehr interessante
Beobachtung:
Ein Heliumkern, der aus zwei Protonen und zwei Neutronen zusammengesetzt ist, besitzt eine Masse von 3727,4 MeV. Addiert man die Massen von zwei Protonen und zwei Neutronen, so ergibt sich ein Wert von 3755,7 MeV. Dies sind 28,3 MeV mehr als die im Experiment gemessene Masse des Heliumkerns, d.h. es sind 28,3 MeV (0,7 Prozent) an Masse verloren gegangen. Genau 28,3 MeV an Energie werden zugleich beim Zusammenschluss freigesetzt. Die verlorengegangene Masse hat sich also nach der Formel \[ E = m c^{2} \] vollständig in Energie umgewandelt. Dieser sogenannte Massendefekt ist nicht auf Atomkerne beschränkt, sondern er gilt allgemein bei jeder Energiefreisetzung (auch bei einer Kerzenflamme).
Die Ursache für dieses Phänomen wurde im Jahre 1905 von Albert Einstein gefunden, als er seine spezielle Relativitätstheorie formulierte. Mehr dazu im nächsten Kapitel.
a) die starke Kraftformel nach Yukawa
Die Formel \[ F \sim \left( \frac{1}{br} + \frac{1}{r^{2}} \right) \, e^{- r/b} \] wurde aus dem sogenannten Yukawa-Potential \[ V(r) = - A \, \frac{e^{- r/b}}{r} \] (siehe Wikipedia: Yukawa-Potential) abgeleitet, das die Abstandsabhängigkeit des Nukleon-Nukleon-Potentials bei Abständen ab etwa 1 bis 2 Fermi recht gut beschreibt: \[ \boldsymbol{F} = - \mathrm{grad} \, V(r) = \] \[ = - \frac{dV(r)}{dr} \, \boldsymbol{e}_{r} = \] \[ = - (- A) \left( - \frac{1}{br} - \frac{1}{r^{2}} \right) \, e^{- r/b} \, \boldsymbol{e}_{r} = \] \[ = - A \, \left( \frac{1}{br} + \frac{1}{r^{2}} \right) \, e^{- r/b} \, \boldsymbol{e}_{r} \] Das negative Vorzeichen besagt dabei, dass die Kraft anziehen wirkt. Man kann das Yukawa-Potential in der Quantenfeldtheorie durch den Austausch virtueller Teilchen zwischen Nukleonen erklären. Die Reichweite \(b\) ist dabei antiproportional zur Masse \(m\) des virtuellen Teilchens: \[ b = \frac{\hbar}{mc} \] Dass das so ist, kann man sich auch mit der Energie-Zeit-Unschärferelation veranschaulichen. Der Wert \(b = 1,4\) fm entspricht demnach einer Teilchenmasse \[ mc^{2} = \frac{\hbar c}{b} = \] \[ = \frac{200 \, \mathrm{MeV} \, \mathrm{fm}}{1,4 \, \mathrm{fm}} = \] \[ = 143 \, \mathrm{MeV} \] Das ist ungefähr der Masse der leichtesten Mesonen: der Pionen. Entsprechend kann man sich annähernd vorstellen, dass die starken Kernkräfte zwischen Nukleonen durch den Austausch virtueller Mesonen entstehen, wobei die leichtesten Pionen für etwas größere Abstände den Hauptanteil liefern.
In der Elektrodynamik werden keine Mesonen, sondern virtuelle Photonen ausgetauscht. Sie haben die Masse Null, so dass \(b\) unendlich groß wird. In diesem Fall erhält man \[ F \sim \frac{1}{r^{2} } \] also genau das Kraftgesetz zwischen statischen bzw. langsamen elektrischen Ladungen.
Die Herleitung des Yukawa-Potentials aus einer Feldgleichung für massive Teilchen (Klein-Gordon-Gleichung mit äußerer Quelle) ist in den Zusatzinfos zu Kapitel 5.2 dargestellt.
© Jörg Resag, www.joerg-resag.de
last modified on 31 December 2023