Die Darstellung der Drehgruppe im Hilbertraum ist fester Bestandteil der Quantenmechanik-Vorlesungen. Daher werde ich in diesem Kapitel diese Standard-Anteile relativ kurz darstellen – man findet sie in jedem Vorlesungsskript zur Quantenmechanik. Es gibt aber auch wichtige Aspekte der Drehgruppe, die meist nur knapp dargestellt werden können. Auf diese Aspekte möchte ich hier genauer eingehen.
Versuchen wir, möglichst analog zu den Translationen im vorherigen Kapitel vorzugehen. Wir beginnen also mit der Darstellung der Drehungen im dreidimensionalen Raum. In Kapitel 3.4 haben wir bereits gesehen, wie das geht. Hier eine kurze Wiederholung:
|
Drehungen im dreidimensionalen Raum: Eine Drehung im dreidimensionalen Raum ist eine lineare Abbildung \(R(\boldsymbol{w})\), die die Länge von Vektoren nicht ändert und die sich stetig mit der Eins verbinden lässt (wir schließen also Spiegelungen aus). Dabei hängt \(R\) von drei reellen Parametern \[ \boldsymbol{w} = \begin{pmatrix} w_1 \\ w_2 \\ w_3 \end{pmatrix} \] ab, die die Drehwinkel um die drei Raumachsen repräsentieren. Wir können jede Drehung durch folgende Matrix aus \(SO(3)\) (die speziell orthogonalen Matrizen) darstellen: \[ R(\boldsymbol{w}) \, \boldsymbol{x} := e^{G(\boldsymbol{w})} \, \boldsymbol{x} \] mit \[ G(\boldsymbol{w}) \, \boldsymbol{x} = \boldsymbol{w} \times \boldsymbol{x} \] In Komponenten bedeutet das: \[ G(\boldsymbol{w})_{ik} \, x_k = \epsilon_{ijk} \, w_j \, x_k \] (mit Summierung über doppelte Indices und dem total antisymmetrischen Levi-Civita-Symbol \( \epsilon_{ijk} \) aus dem vorherigen Kapitel). Die Matrix \(G(\boldsymbol{w})\) ist also gegeben durch \[ G(\boldsymbol{w})_{ik} = \epsilon_{ijk} \, w_j \] oder ausgeschrieben \[ G = \begin{pmatrix} 0 & -w_3 & w_2 \\ w_3 & 0 & -w_1 \\ -w_2 & w_1 & 0 \end{pmatrix} \] Man kann die Exponentialreihe komplett aufsummieren (siehe Kapitel 3.4) und erhält als allgemeine Darstellung für eine Drehung: \[ e^{G(\boldsymbol{w})} \boldsymbol{x} = \] \[ = - ( \cos{\omega}) \, [(\boldsymbol{e} \boldsymbol{x}) \boldsymbol{e} - \boldsymbol{x}] + (\boldsymbol{e} \boldsymbol{x}) \boldsymbol{e} + \] \[ + (\sin{\omega}) \, (\boldsymbol{e} \times \boldsymbol{x}) \] mit \[ \boldsymbol{w} = \omega \boldsymbol{e} \] d.h. \( \omega = |\boldsymbol{w}| \) und dem Einheitsvektor \( \boldsymbol{e} = \boldsymbol{w} / |\boldsymbol{w}| \). In Kapitel 3.4 hatten wir gesehen, dass wir \(\boldsymbol{e}\) als Drehachse und \(\omega\) als Drehwinkel um diese Achse interpretieren können. Der Vektor \(\boldsymbol{w}\) ist also in Richtung der Drehachse orientiert, und sein Betrag gibt den Drehwinkel entgegen dem Uhrzeigersinn an, wenn wir die Drehung von der Spitze von \(\boldsymbol{w}\) aus betrachten.
|
Wie sieht die Lie-Algebra der Drehgruppe aus? Das können wir sofort an der Exponentialdarstellung ablesen. Dazu schreiben wir \(G(\boldsymbol{w})\) als \[ G(\boldsymbol{w}) =: i w_j A_j \] (das heranmultiplizierte \(i\) ist die imaginäre Einheit, also kein Index), d.h. \[ R(\boldsymbol{w}) = e^{i w_j A_j} \] (mit Summe über \(j\)). Aus \[ G(\boldsymbol{w})_{ik} = \epsilon_{ijk} w_j = \] \[ =: i w_j (A_j)_{ik} \] lesen wir ab: \[ i (A_j)_{ik} = \epsilon_{ijk} \] Wenn man die Matrizen \( i (A_j)_{ik} \) explizit hinschreiben will, so nimmt man am Besten einfach die Matrix \(G(\boldsymbol{w})\) von oben und verwendet \[ G(\boldsymbol{e}_i) = i A_i \] Rechnen wir den Kommutator der \(A_i\) -Matrizen aus. Das kann man explizit machen, oder aber man rechnet über \( G(\boldsymbol{w}) \, \boldsymbol{x} = \boldsymbol{w} \times \boldsymbol{x} \) und den bekannten Formeln für das doppelte Kreuzprodukt nach, dass gilt: \[ [G(\boldsymbol{v}), G(\boldsymbol{w})] = G(\boldsymbol{v} \times \boldsymbol{w}) \] In diese Formel können wir \( G(\boldsymbol{e}_i) = i A_i \) einsetzen: \[ [G(\boldsymbol{e}_i), G(\boldsymbol{e}_j)] = G(\boldsymbol{e}_i \times \boldsymbol{e}_j) = \] \[ = G(\epsilon_{ijk}\boldsymbol{e}_k) = \epsilon_{ijk} G(\boldsymbol{e}_k) \] und somit \[ [i A_i , i A_j] = \epsilon_{ijk} \, i A_k \] (das \(i\) vor den \(A\)'s ist wieder die imaginäre Einheit), also
| \[ [A_i , A_j] = - \epsilon_{ijk} \, i A_k \] |
(das negative Vorzeichen bekommt man weg, wenn man die \(A_i\) mit umgekehrtem Vorzeichen definiert – so werden wir es weiter unten bei den Drehimpulsen machen).
Im Gegensatz zur Translationsgruppe bilden die Drehungen keine abelsche Gruppe. Zwei verschiedene Drehungen vetauschen i.a. nicht miteinander. Dafür ist die Drehgruppe aber (anders als die Translationsgruppe) kompakt. Man kann nämlich den Drehvektor \(\boldsymbol{w}\) auf alle Vektoren mit Betrag kleiner-gleich \(\pi\) einschränken. Damit erfasst man tatsächlich alle Drehungen, denn eine Drehung um \(3/2 \, \pi\) mit Drehachse \(\boldsymbol{e}\) entspricht einer Drehung um \(1/2 \, \pi\) mit Drehachse \(-\boldsymbol{e}\). Aus der Kompaktheit der Drehgruppe folgt, dass sich jede Drehung als Exponentialreihe schreiben lässt, so wie wir es oben getan haben (siehe dazu Kapitel 4.6 )
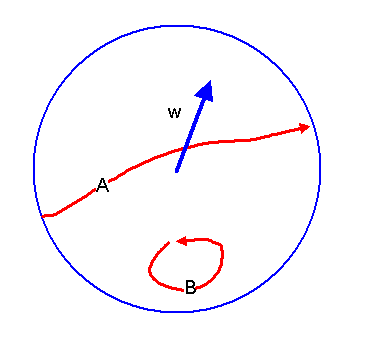
Man kann sich den Raum der Drehungen daher durch den Raum der Drehvektoren \(\boldsymbol{w}\) veranschaulichen, also durch eine Kugel mit Radius \(\pi\). Jeder Punkt in dieser Kugel entspricht einem Drehvektor \(\boldsymbol{w}\) und damit einer Drehung. Es gibt allerdings eine wichtige Besonderheit: Ein Punkt auf der Oberfläche mit Drehvektor \( \boldsymbol{w} = \pi \boldsymbol{e} \) und sein gegenüberliegender Punkt mit Drehvektor \( -\boldsymbol{w} = -\pi \boldsymbol{e} \) stellen dieselbe Drehung dar, denn es ist egal, ob man eine halbe Drehung rechts oder links herum durchführt.
Insofern hat die Mannigfaltigkeit der Drehgruppe auch keinen Rand!
Es gibt nun geschlossene Wege in dieser Kugel, die sich nicht stetig auf einen Punkt zusammenziehen lassen.
So kann man vom Ursprung aus radial nach außen gehen. Sobald man den Kugelrand erreicht (halbe Drehung),
taucht man auf der gegenüberliegenden Seite wieder in die Kugel ein und kann radial wieder nach innen bis
zum Ursprung laufen. Dies entspricht dem Durchlaufen aller Drehungen um eine feste Drehachse mit
Drehwinkeln von 0 bis 360 Grad (also \(0\) bis \(2\pi\)).
Am Schluss hat man eine Umdrehung geschafft, die gleichwertig mit gar keiner Umdrehung ist.
Dieser geschlossene Weg lässt sich nicht stetig zu einem Punkt zusammenziehen.
Daher ist die Drehgruppe zwar zusammenhängend, aber nicht einfach zusammenhängend.
Siehe dazu auch Kapitel 3.5.

Nun zu Strahl-Darstellungen der Drehgruppe durch Operatoren auf einem Hilbertraum. Zunächst zu den Zentralladungen: Lassen sich diese immer wegdefinieren? Schauen wir uns dazu den allgemeinen Fall aus Kapitel 4.6 an: \[ [T(A_i), T(A_j)] = i \, f^k_{\,ij} \, T(A_k) + i \, C_{ij} \, 1 \] Die Strukturkonstanten \( f^k_{\,ij} \) sind über \[ [A_i, A_j] = i \, f^k_{\, ij} \, A_k \] definiert. In unserem Fall ist also \( f^k_{\,ij} = -\epsilon_{ijk} \).
Wie bei den Translationen im vorherigen Kapitel gilt wieder: Da der Kommutator antisymmetrisch in \(i\) und \(j\) ist, gilt dies auch für \(C_{ij}\) , d.h. nur 3 der 9 Zahlen \(C_{ij}\) sind unabhängig und ungleich Null. Wir können daher allgemein schreiben: \[ C_{ij} = \epsilon_{ijk} \, C_k \] mit geeigneten drei Zahlen \(C_k\) (und Summe über \(k\)). Setzen wir beides oben ein, so haben wir \[ [T(A_i), T(A_j)] = -i \epsilon_{ijk} \, ( T(A_k) - C_k \,1 ) \] Jetzt brauchen wir nur noch neue Operatoren zu definieren: \[ T'(A_i) := T(A_k) - C_k \, 1 \] (man beachte den kleinen Strich in \(T'(A_i)\) links). Da der additive Term \( C_k \, 1 \) im Kommutator wegfällt, kann man leicht nachrechnen, dass im Kommutator der neuen Operatoren keine Zentralladung mehr auftritt: \[ [T'(A_i), T'(A_j)] = -i \epsilon_{ijk} \, T'(A_k) \] Aus einer beliebigen Strahldarstellung der Lie-Algebra der Drehgruppe kann man also immer eine echte Darstellung der Lie-Algebra machen. Man kann also die Zentralladungen wegdefinieren.
Bei einer einfach zusammenhängenden Gruppe würde das bedeuten, dass man die Phase in der Strahldarstellung weglassen kann und eine unitäre Darstellung ausreicht, um alle Strahldarstellungen zu erfassen. Leider ist die Drehgruppe nicht einfach zusammenhängend, d.h. nicht jede projektive Darstellung der Drehgruppe ist eine unitäre Darstellung der Drehgruppe. Erst wenn wir zur universellen Überlagerungsgruppe der Drehgruppe übergehen, decken deren unitäre Darstellungen alle projektiven Darstellungen der Drehgruppe ab. Was also ist die universelle Überlagerungsgruppe der Drehgruppe?
Überlegen wir uns, wie die Mannigfaltigkeit dieser Überlagerungsgruppe aussehen könnte. Sie muss einfach zusammenhängend sein – sodass sich jede geschlossene Kurve stetig auf einen Punkt zusammenziehen lässt – und sie muss lokal so aussehen wie die Mannigfaltigkeit der Drehgruppe. Das kann man leicht durch einen einfachen Trick erreichen:
Wir starten mit der Mannigfaltigkeit der Drehgruppe, also mit der Kugel mit Radius \(\pi\), bei der die gegenüberliegenden Punkte der Kugeloberfläche miteinander identifiziert werden. Da es gerade diese Identifikation der Punkte ist, die zu den nicht-kontrahierbaren geschlossenen Kurven führt, wollen wir sie loswerden, ohne dass dabei die Mannigfaltigkeit einen Rand bekommt. Man kann also die Identifikation nicht einfach weglassen, da man sonst beim Durchstoßen der Kugeloberfläche nicht wieder in die Kugel hineinkäme – muss man aber, da Drehungen keinen Rand (also keine größte Drehung) haben.
Die Lösung ist:
Wir verdoppeln die Kugel und wandern einfach beim Durchstoßen der Oberfläche in die
zweite Kugel hinein, und zwar am genau gegenüberliegenden Punkt!
Wenn wir also am Nordpol die erste Kugeloberfläche durchstoßen, so tauchen wir augenblicklich
am Südpol in die zweite Kugel ein. Die folgende Grafik stellt dies dar
(siehe dazu im Internet auch beispielsweise
Visualizing the N-Sphere ):
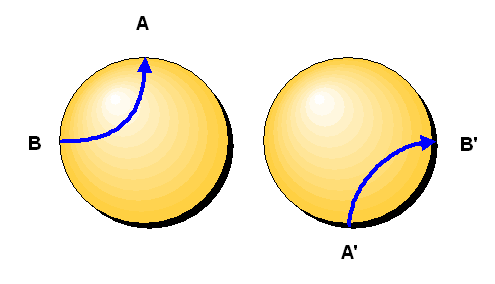
Der Punkt A auf der linken Kugeloberfläche entspricht dem Punkt A' auf der rechten Kugeloberfläche usw.. Die dargestellte Kurve ist daher tatsächlich eine geschlossene Kurve! Man kann sich anhand von Beispielen nun davon überzeugen, dass man jede geschlossene Kurve nun tatsächlich auf einen Punkt zusammenziehen kann, d.h. die Mannigfaltigkeit dieser Doppel-Kugeln ist einfach zusammenhängend. Zudem sieht jede der beiden Kugeln lokal wie eine Kugel aus – so wie gefordert.
Das obige Bild macht auch unmittelbar den Überlagerungsbegriff anschaulich: Die Mannigfaltigkeit der beiden Kugeln mit identifizierten Oberflächenpunkten kann man surjektiv auf die eine Kugel mit identifizierten gegenüberliegenden Oberflächenpunkten abbilden, indem man einfach vergisst, von welcher Kugel ein Punkt herkommt. Man legt die beiden Kugeln einfach übereinander (besser: ineinander), als ob sie aus Luft wären, wobei wir dafür sorgen, dass ein Punkt A' der rechten Kugel genau gegenüber dem damit identifizierten Punkt A der linken Kugel zu liegen kommt.
Sie kennen das obige Bild vielleicht bereits aus
Die Grenzen der Berechenbarkeit, Kapitel 5.3.
Dort erfahren wir, dass es sich bei der obigen Mannigfaltigkeit
um die 3-Sphäre handelt, also um das 3-dimensionale
Analogon zur 2-dimensionalen Kugeloberfläche. Auch die 2-dimensionalen
Kugeloberfläche ist ja einfach zusammenhängend.
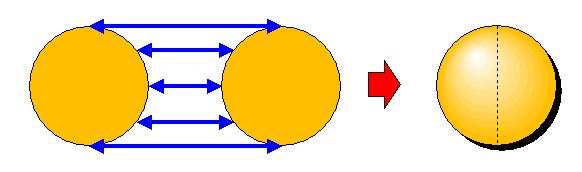
Die Topologie der 2-dimensionalen Kugeloberfläche kann man analog durch 2 Vollkreise darstellen, deren
Randpunkte man miteinander identifiziert. Der eine Vollkreis ist die
plattgedrückte Oberfläche der linken Halbkugel,
der andere die plattgedrückte Oberfläche der rechten
Halbkugel und der Kreisrand entspricht der Schnittlinie
zwischen den beiden Halbkugeloberflächen.
Mehr dazu siehe Die Grenzen der Berechenbarkeit, Kapitel 5.3
und unter der externen
Webseite Visualizing the N-Sphere.
Nun wissen wir also, dass die Mannigfaltigkeit der universellen Überlagerungsgruppe der Drehgruppe topologisch so wie die 3-Sphäre aussehen sollte. Schön wäre es, wenn wir ein Konstruktionsverfahren hätten, um die Überlagerungsgruppe explizit herzuleiten. So etwas gibt es, und wir werden es im Kapitel 4.11 über Clifford-Algebren und Spingruppen) noch kennenlernen.
Alternativ kann man auch über die Lie-Algebra gehen, die ja bei der Überlagerungsgruppe genauso aussehen muss wie bei der Drehgruppe. Eine der Darstellungen der Lie-Algebra sollte dann über die Exponentialreihe die Überlagerungsgruppe ergeben. Genau so geht man in den Quantenmechanik-Vorlesungen auch vor – meist ohne den Begriff der Überlagerungsgruppe explizit zu erwähnen. Wir werden diese Vorgehensweise etwas weiter unten noch kennenlernen.
Das oben erwähnte Konstruktionsverfahren (ohne den üblichen Weg über die Lie-Algebra) liefert das folgende Ergebnis, das an dieser Stelle gleichsam vom Himmel fällt und das wir nur nachträglich überprüfen können (siehe auch Kapitel 6.1 ): Die Überlagerungsgruppe der Drehgruppe ist die Gruppe \(SU(2)\), also die komplexen unitären 2-mal-2-Matrizen mit Determinante Eins. Hier die Details:
|
Ausgeschrieben lautet die Matrix \(\sigma(\boldsymbol{x})\) also \[ \sigma(\boldsymbol{x}) = \begin{pmatrix} x_3 & x_1 - i x_2 \\ x_1 + i x_2 & - x_3 \end{pmatrix} \]
Man rechnet leicht nach, dass wegen \( \det{u} = 1 \) die so definierte Matrix \(R\) die euklidische Norm eines Vektors nicht ändert: \[ (R \boldsymbol{x})^2 = \] \[ = - \det{\sigma(R \boldsymbol{x})} = \] \[ = - \det{(u \, \sigma(\boldsymbol{x}) \, u^+)} = \] \[ = - (\det{u}) \, (\det{\sigma(\boldsymbol{x})}) \, (\det{u^+}) = \] \[ = - \det{\sigma(\boldsymbol{x})} = \] \[ = \boldsymbol{x}^2 \] Also ist \(R\) eine orthogonale Matrix. Dass Spiegelungen ausgeschlossen sind, weist man nach, indem man \(u\) und damit \(R\) über einen stetigen Weg mit der Einheitsmatrix verbindet. Man kann auch beweisen, dass man tatsächlich jede Drehmatrix \(R\) durch ein passendes \(u\) so erreichen kann. Außerdem ist gesichert, dass dem Produkt zweier Gruppenelemente \(u\) und \(u'\) aus \(SU(2)\) auch das Produkt der entsprechenden Drehmatrizen zugeordnet wird, d.h. die Gruppenstruktur wird berücksichtigt. Details dazu siehe z.B. D. Schütte: Darstellungstheorie der Drehgruppe, speziell Kapitel 10.
Allerdings ist die Zuordnung von \(SU(2)\) zu den Drehmatrizen nicht eindeutig: Den beiden \(SU(2)\)-Matrizen \( u \) und \( - u \) wird dieselbe Drehmatrix zugeordnet! Daher ist \(SU(2)\) eine Überlagerungsgruppe der Drehgruppe. Wir haben das am Beispiel der Drehungen um die z-Achse bereits in Kapitel 4.6 gesehen.
Die Gleichung \( u \, \sigma(\boldsymbol{x}) \, u^+ = \sigma(R \boldsymbol{x}) \) definiert also eine surjektive Projektion \[ \rho: \, SU(2) \rightarrow SO(3) \] die mit der Gruppenstruktur verträglich ist – so wie es in Kapitel 4.6 für eine Überlagerungsgruppe verlangt wird.
Bleibt die Frage: Hat \(SU(2)\) als Mannigfaltigkeit auch die gewünschte Topologie, ist also einfach zusammenhängend wie die 3-Sphäre? Das sieht man tatsächlich sehr einfach, denn man kann jede Matrix \(u\) aus \(SU(2)\) so schreiben: \[ u = \begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix} \] Dabei sind \(a\) und \(b\) komplexe Zahlen, deren Real- und Imaginärteile wir als karthesische Koordinaten des \(\mathbb{R}^4\) auffassen können, in den die Gruppenmannigfaltigkeit eingebettet ist. Wir schreiben also \[ a = y_1 + i y_2 \] \[ b = y_3 + i y_4 \] mit reellen Koordinaten \(y_i\). Die Bedingung \( \det{u} = 1 \) bedeutet dann: \[ \det{u} = \] \[ = a a^* - (-b b^*) = \] \[ = |a|^2 + |b|^2 = \] \[ = y_1^2 + y_2^2 + y_3^2 + y_4^2 = \] \[ = 1 \] Die Koordinaten erfüllen also die Bedingung einer 3-Sphäre im vierdimensionalen Raum. Man kann \(SU(2)\) also als 3-Sphäre auffassen – genau so wollten wir es ja haben!
Man kann auch einen expliziten Zusammenhang der \(SU(2)\)-Matrizen mit den beiden Vollkugeln oben herstellen. Ich will es aber nicht übertreiben, daher hier nur ein kleines Beispiel:
Wir laufen vom Mittelpunkt der linken Kugel (Drehung um Null Grad, \(u = 1\)) radial nach Norden (Drehung links herum um die z-Achse mit wachsendem Drehwinkel), erreichen die Kugeloberfläche am Nordpol (halbe Drehung nach links um die z-Achse), tauchen auf der rechten Kugeloberfläche am Südpol ein (mehr als eine halbe Drehung nach links um die z-Achse) und erreichen schließlich den Mittelpunkt der rechten Kugel (ganze Drehung nach links um die z-Achse, \(u = -1\)).
Im Raum der \(SU(2)\)-Matrizen ist also eine ganze Drehung nach links um die z-Achse nicht identisch
mit einer Drehung um 0 Grad. Die linke Kugel gibt die Drehungen mit Drehwinkel kleiner als \(\pi\) an,
während die rechte Kugel die Drehungen mit Drehwinkel von \(\pi\) bis \(2\pi\) darstellt
(die Drehachse zeigt dabei bei der rechten Kugel radial nach innen).
Der Drehwinkel \(2\pi\) liegt im Mittelpunkt der rechten Kugel.
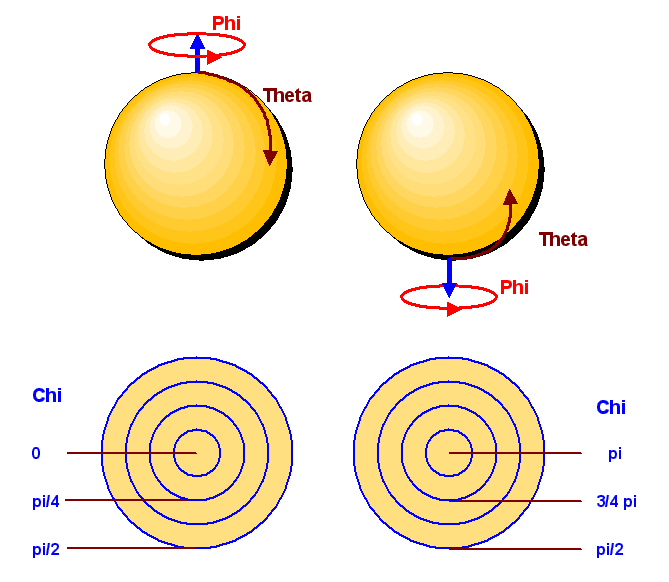
Die folgende Grafik aus Die Grenzen der Berechenbarkeit, Kapitel 5.3
stellt dies dar,
wobei allerdings der halbe Drehwinkel angegeben wird
(Grund: der halbe Drehwinkel entspricht gerade der Kugelkoordinate \(\chi\),
die hier radial nach außen
dargestellt ist – Details
siehe Die Grenzen der Berechenbarkeit, Kapitel 5.3):
Die Tatsache, dass sich jede Kurve in der Überlagerungsgruppe der Drehgruppe stetig auf einen Punkt
zusammenziehen kann, lässt sich sehr anschaulich demonstrieren, beispielsweise mit einem Gürtel
(Dirac belt trick).
Wir nehmen also einen Gürtel und legen ihn schön gerade von links nach rechts vor uns hin.
Auf den Gürtel können wir nun Pfeile senkrecht zur Gürtelausrichtung mit einer kleinen Pfeilspitze
zur entfernteren Gürtelkante malen, so dass
der Gürtel aussieht wie eine Strickleiter.
Diese Pfeile zeigen alle in dieselbe Richtung.
Nun nehmen wir das rechte Ende und drehen es zweimal um die Ausrichtungsachse des Gürtels.
Der Gürtel ist also nun doppelt verdreht.
Entsprechend sind nun auch die aufgemalten Pfeile nicht mehr parallel zueinander, sondern sie drehen sich
zweimal um die Gürtelachse, wenn wir den Gürtel von links nach rechts durchlaufen.
Die Pfeile am linken Ende, in der Mitte und am rechten Ende liegen aber noch parallel zueinander:
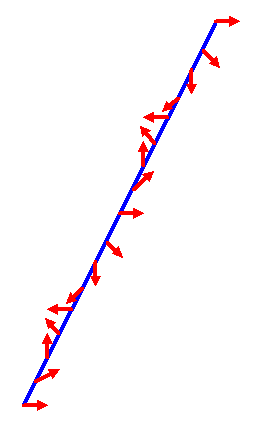
Jeder einzelne Pfeil auf dem verdrehten Gürtel repräsentiert nun eine Drehung im dreidimensionalen Raum, nämlich die Drehung, die beim Verdrehen des Gürtels auf diesen Pfeil wirkt und ihn in die neue räumliche Ausrichtung bringt. Dabei repräsentieren benachbarte Pfeile auch benachbarte Drehungen, denn die Pfeilausrichtung und damit die zugehörige Drehung ändert sich stetig, wenn wir den Gürtel entlanglaufen. Die Pfeile auf dem verdrehten Gürtel repräsentieren insgesamt eine doppelt geschlossene Kurve im Raum der Drehungen: Man startet mit dem unverdrehten Pfeil am linken Gürtelende (also mit der Drehung um 0 Grad), läuft dann nach rechts auf dem Gürtel entlang und durchläuft zugleich die entsprechenden Drehungen, bis man am rechten Gürtelende bei einem Pfeil ankommt, der um 720 Grad gedreht wurde, was identisch mit einer Drehung um Null Grad ist. Auch in der Gürtelmitte trifft man auf einen dazu parallel ausgerichteten Pfeil, der um 360 Grad gedreht wurde (entsprechend einer Drehung um Null Grad). Man durchläuft also bei den Drehungen eine geschlossene Kurve, die zweimal durch die Identität geht. Anders gesagt: Der doppelt verdrehte Gürtel entspricht einer stetigen Kurve, die alle Drehungen um die Gürtelachse von 0 Grad bis 720 Grad (eine Doppeldrehung) durchläuft.
Dieser Kurve im Raum der Drehungen entspricht auch in der Überlagerungsgruppe \(SU(2)\) eine geschlossene Kurve, die allerdings nur einmal durch die Identität geht, denn in der Überlagerungsgruppe können wir ja eine Drehung um Null Grad und eine um 360 Grad voneinander unterscheiden – genau wie auf dem Gürtel, wenn wir den Verlauf der Drehung von links nach rechts berücksichtigen. Jedem Pfeil auf dem Gürtel können wir also einem Element der Überlagerungsgruppe \(SU(2)\) umkehrbar eindeutig zuordnen – anhand der Verdrehung des Gürtels erkennen wir ja, ob ein Pfeil einmal oder zweimal verdreht wurde. Der Gürtel mit seinen Pfeilen erlaubt es also, anschaulich eine geschlossene Kurve in der Überlagerungsgruppe \(SU(2)\) darzustellen.
Und nun kommt Diracs Trick: Wir dürfen das rechte Gürtelende im Raum bewegen, ohne dabei
die Ausrichtung des Gürtelendes zu verändern. Der Pfeil am Gürtelende (und am Gürtelanfang)
darf also nicht räumlich verdreht werden und repräsentiert weiter die Drehung um Null Grad.
Beim Bewegen des Gürtelendes ändert sich aber die Orientierung der Pfeile zwischen
Gürtelanfang und Gürtelende, denn der Gürtel verändert seine Lage im Raum.
Insgesamt verändern wir also die geschlossene Kurve
in der Überlagerungsgruppe. Das Erstaunliche ist nun:
Man kann die Doppelverdrehung des Gürtels komplett zurücknehmen, alleine durch Bewegung
des rechten Gürtelendes und ohne jede weitere Verdrehung des Gürtels!
Probieren Sie es mit einem realen Gürtel einmal aus!
Man muss das rechte Gürtelende nur geschickt um die ursprüngliche Gürtelachse herumbewegen.
Hier ist ein Versuch von mir, die Vorgehensweise einigermaßen darzustellen:
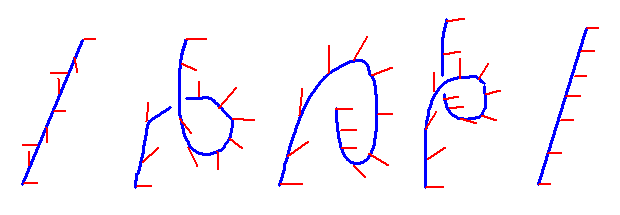
Den Schritt von Bild 1 nach Bild 2 macht der Gürtel fast automatisch aufgrund seiner inneren Spannung durch die Verdrehung, wenn man die beiden Enden einander annähert. Der Gürtel merkt gleichsam schon selbst, dass er sich ent-drehen kann und bildet eine Schlaufe. Nun muss man nur noch das hintere Ende nach vorne bringen (Bild 3) und es dann unter statt über dem Gürtel wieder nach hinten ziehen. Man merkt, wie dabei die Spannung im Gürtel nachlässt und wie er sich schließlich in Bild 5 vollkommen glatt strecken lässt. Natürlich kann man die Schritte auch von rechts nach links ausführen und so aus einem unverdrehten einen doppelt verdrehten Gürtel machen, ganz ohne ein Gürtel-Ende drehen zu müssen.
Statt eines Gürtels kann man übrigens auch gut einen Papierstreifen nehmen, auf den man sogar kleine Pfeile aufmalen kann (so habe ich es gemacht, um die Bilder oben zeichnen zu können). Im Internet findet man übrigens viele schöne Animationen zu dem Thema (einfach nach den Worten belt trick oder Dirac belt trick suchen oder auch direkt unter diesem Link).
Der doppelt verdrehte Gürtel lässt sich also stetig in den unverdrehten Gürtel umwandeln, ohne dabei die Pfeile an den Gürtelenden verdrehen zu müssen. Bei der Bewegung des rechten Gürtelendes verändert sich die zugehörige Kurve in der Überlagerungsgruppe stetig, bleibt aber ständig eine geschlossene Kurve durch die Identität, denn die Pfeile auf den Gürtelenden werden ja nicht verdreht. Am Schluss hat man einen unverdrehten Gürtel, bei dem sich von Pfeil zu Pfeil die Ausrichtung nicht ändert, d.h. jeder Pfeil repräsentiert dort die Drehung um Null Grad. Damit hat man die geschlossene Kurve in der Überlagerungsgruppe stetig auf einen Punkt (die Drehung um Null Grad) zusammengezogen.
Wenn man den Gürtel nur einfach verdreht, dann geht das nicht! Diesen Gürtel kann man nicht wie oben in einen unverdrehten Gürtel umwandeln. Der einfach verdrehte Gürtel entspricht einer geschlossenen Kurve im Raum der Drehungen, die sich nicht stetig auf einen Punkt zusammenziehen lässt. In der Überlagerungsgruppe stellt diese Gürtel aber noch keine geschlossene Kurve dar. Erst der doppelt verdrehte Gürtel entspricht hier einer geschlossenen Kurve, und die lässt sich stetig auf einen Punkt zusammenziehen. Da sich nun jede geschlossene Kurve in der Überlagerungsgruppe durch einen irgendwie im Raum liegenden Gürtel mit doppelt gegeneinander verdrehten Enden darstellen lässt, und da sich diese Doppelverdrehung immer wie oben auflösen lässt, deshalb kann man jede geschlossene Kurve in der Überlagerungsgruppe \(SU(2)\) stetig auf einen Punkt zusammenziehen, d.h. \(SU(2)\) ist einfach zusammenhängend. Erstaunlich, dass sich eine scheinbar abstrakte topologische Eigenschaft so anschaulich demonstrieren lässt! So hat man doch gleich das Gefühl, es mit einer realen Tatsache zu tun zu haben, und das hat man ja auch!
Um zur Überlagerungsgruppe der Drehgruppe und all ihrer Darstellungen zu gelangen, geht man oft den Weg über die Lie-Algebra und deren Darstellungen durch hermitesche Operatoren auf dem Hilbertraum. Zentralladungen brauchen wir ja nicht mehr zu befürchten, denn oben hatten wir gesehen, dass wir diese wegdefinieren können. Es muss also für die Darstellungsoperatoren der Generatoren gelten: \[ [T(A_i), T(A_j)] = -i \epsilon_{ijk} \, T(A_k) \] (die Striche lassen wir jetzt weg). Wir wollen diese Operatoren wie üblich als \[ \hat{J}_i := - T(A_i) \] schreiben (den Faktor \(\hbar\) lassen wir in natürlichen Einheiten wieder weg) – so werden wir auch das lästige Vorzeichen los:
|
\[ [\hat{J}_i, \hat{J}_j] = i \epsilon_{ijk} \, \hat{J}_k \] |
also beispielsweise \[ [\hat{J}_1, \hat{J}_2] = i \, \hat{J}_3 \] Man bezeichnet die Operatoren \(\hat{J}_i\) als Drehimpulsoperatoren und spricht von der Drehimpulsalgebra. Warum, werden wir noch sehen. Analog zum Impulsvektor schreibt man auch für den Operator \[ \hat{\boldsymbol{J}} = \begin{pmatrix} \hat{J}_1 \\ \hat{J}_2 \\ \hat{J}_3 \end{pmatrix} \] Tatsächlich ist es nun so, dass die Drehimpulsalgebra \( [\hat{J}_i, \hat{J}_j] = i \epsilon_{ijk} \, \hat{J}_k \) die Eigenschaften der Operatoren \(\hat{J}_i\) bereits eindeutig (bis auf Phasenfaktoren) festlegt. Wie das im Einzelnen geht, findet man in jedem Text zur Quantenmechanik, beispielsweise in Darstellungstheorie der Drehgruppe von Prof. Schütte (ITKP Bonn), Kapitel 6, S.28 oder auch in Wikipedia: Drehimpuls (Quantenmechanik). Daher hier nur das Wichtigste in Kürze:
Da unitäre Darstellungen der Überlagerungsgruppe ausreichen, um alle projektiven Darstellungen der Drehgruppe zu konstruieren, sind analog zu den Impulsen auch die Drehimpuls-Operatoren \(\hat{J}_i\) hermitesch. Sie haben also reelle Eigenwerte, die als Observable in Betracht kommen. Daher suchen wir die Eigenwerte und Eigenvektoren der \(\hat{J}_i\) im Hilbertraum. Andere Zustände können wir dann als Superposition dieser Eigenvektoren schreiben.
Allerdings gibt es (bis auf eine Ausnahme) keine Vektoren, die zugleich Eigenvektoren zu allen drei \(\hat{J}_i\) sein können, denn die \(\hat{J}_i\) vertauschen nicht miteinander. Ein Beispiel: Angenommen, es gäbe einen Vektor \( |j_1 j_2 j_3 \rangle \), der \[ \hat{J}_i \, |j_1 j_2 j_3 \rangle = j_i \, |j_1 j_2 j_3 \rangle \] erfüllt. Dann wäre \[ [\hat{J}_i, \hat{J}_j] \, |j_1 j_2 j_3 \rangle = \] \[ = (j_i j_j - j_j j_i) \, |j_1 j_2 j_3 \rangle = \] \[ = 0 = i \epsilon_{ijk} \, \hat{J}_k \, |j_1 j_2 j_3 \rangle \] d.h. \( \hat{J}_k \, |j_1 j_2 j_3 \rangle = 0 \). Damit ist Null der einzige Eigenwert, der simultaner Eigenwert der drei \(\hat{J}_k\) zum selben Eigenvektor sein kann. Das war bei den Impulsoperatoren \(\hat{P}_i\) anders, denn diese kommutieren miteinander (wenn man von Zentralladungen absieht).
Man kann nun aus den drei \(\hat{J}_k\) neue Operatoren zusammenbauen, die sich gut zur Ermittlung der Eigenwerte und Eigenvektoren eignen: \[ \hat{\boldsymbol{J}}^2 := \hat{J}_1^2 + \hat{J}_2^2 + \hat{J}_3^2 \] \[ \hat{J}^+ := \hat{J}_1 + i \hat{J}_2 \] \[ \hat{J}^- := \hat{J}_1 - i \hat{J}_2 \] \[ \hat{J}_3 \; \; \mathrm{unverändert} \] \(\hat{\boldsymbol{J}}^2\) und jedes einzelne der drei \(\hat{J}_i\) kommutieren und haben deshalb simultane Eigenwerte und Eigenvektoren – daher nennt man \(\hat{\boldsymbol{J}}^2\) auch den Casimiroperator der Drehimpulsalgebra. Da aber die drei \(\hat{J}_i\) nicht kommutieren, müssen wir einen davon auswählen: Wir haben uns für \(\hat{J}_3\) entschieden. Eine genauere Analyse mit Hilfe der sogenannten Leiteroperatoren \(\hat{J}^+\) und \(\hat{J}^-\) zeigt:
Die Quantenzahl \(j\) (im Folgenden Drehimpuls genannt) kann also von Null aufwärts ganz- und halbzahlige Werte annehmen, und die sogenannte magnetische Quantenzahl \(m\) (auch Drehimpulskomponente entlang der 3-Achse genannt) kann dann für jedes \(j\) in ganzzahligen Schritten die Werte von \(-j\) bis \(j\) annehmen. Hier explizit die Fälle \(j = 0, \frac{1}{2}\) und \(1\):
Die Wirkung der Operatoren \(\hat{\boldsymbol{J}}^2, \hat{J}_3, \hat{J}^+, \hat{J}^-\) auf die Basisvektoren \( |j \, m \rangle \) sind durch die obigen Formeln komplett festgelegt. Dabei fällt auf, dass sich \(j\) nie ändert. Man kann daher die Wirkung der Operatoren in den einzelnen Unterräumen zu den verschiedenen \(j\) getrennt voneinander betrachten und die Operatoren dort als \((2j+1)\)-dimensionale komplexe Matrizen auf den zugehörigen \(m\)-Werten darstellen. Man sagt auch, die Darstellung der Operatoren zerfällt in irreduzible Darstellungen, die jeweils durch einen Wert von \(j\) gekennzeichnet sind.
Auch die beiden Operatoren \(\hat{J}_1\) und \(\hat{J}_2\) kann man in dieser Basis als Matrizen darstellen, indem man \[ \hat{J}_1 = \; \frac{1}{2} \, (\hat{J}^+ + \hat{J}^-) \] \[ \hat{J}_2 = - \frac{i}{2} (\hat{J}^+ - \hat{J}^-) \] verwendet. Diese Matrizen sind in dieser Basis nicht diagonal, da sie nicht mit \(\hat{J}_3\) vertauschen. Man kann aber jederzeit zu einer neuen Basis übergehen, in der dann beispielsweise \(\hat{J}_1\) diagonal ist (nicht aber \(\hat{J}_2\) und \(\hat{J}_3\)). Es ist in diesem Sinne willkürlich, welches der \(\hat{J}_i\) wir diagonal wählen.
Zur Übung schauen wir uns die Matrizen für \(j = 0, \frac{1}{2}, 1\) an.
Der Fall \(j = 0\):
Bei \(j = 0\) ist die Sache ganz einfach: \(m\) muss auch gleich 0 sein, d.h. der Darstellungsraum ist eindimensional und die Matrizen sind einfach gleich der Zahl Null. Wir haben also eine triviale Darstellung der Lie-Algebra vor uns.
Der Fall \(j = \frac{1}{2}\):
Hier ist die Sache schon interessanter, denn \(m\) kann die beiden Werte \(\frac{1}{2}\) und \(-\frac{1}{2}\) annehmen. Der Darstellungsraum ist also zweidimensional mit den beiden Basisvektoren \[ \bigg|\frac{1}{2}, \frac{1}{2} \bigg\rangle \] \[ \bigg|\frac{1}{2}, - \frac{1}{2} \bigg\rangle \] In dieser Basis erhalten wir für die \(\hat{J}_i\)-Matrizen, die wir mit \( D^{\frac{1}{2}}(\hat{J}_i ) \) bezeichnen wollen: \[ D^{\frac{1}{2}}(\hat{J}_i ) = \frac{1}{2} \, \sigma_i \] mit den drei Paulimatrizen \[ \sigma_1 = \begin{pmatrix} 0 & \; 1 \\ 1 & \; 0 \end{pmatrix} \] \[ \sigma_2 = \begin{pmatrix} 0 & -i \\ i & \; 0 \end{pmatrix} \] \[ \sigma_3 = \begin{pmatrix} 1 & \; 0 \\ 0 & -1 \end{pmatrix} \]
Der Fall \(j = 1\):
Der Darstellungsraum ist jetzt dreidimensional, denn \(m\) kann die Werte \(1, 0, -1\) annehmen und wir haben die drei Basisvektoren \[ |1, 1 \rangle \] \[ |1, 0 \rangle \] \[ |1, -1 \rangle \] In dieser Basis erhalten wir für die \(\hat{J}_i\)-Matrizen \( D^1(\hat{J}_i) \): \[ D^1(\hat{J}_1) = \frac{1}{\sqrt{2}} \, \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \] \[ D^1(\hat{J}_2) = \frac{-i}{\sqrt{2}} \, \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} \] \[ D^1(\hat{J}_3) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \] Man kann diese Darstellung zu \(j = 1\) mit der definierenden Darstellung \( i (A_j)_{ik} = \epsilon_{ijk} \) von oben in Beziehung setzen, indem man die Matrix \(A_3\) diagonalisiert. Die Basisvektoren \(\boldsymbol{e}_i\) des \(\mathbb{R}^3\) lassen sich so in die neue Basis der \( |1, m \rangle \) umrechnen. Man findet: \[ |1, 0 \rangle = \boldsymbol{e}_3 \] \[ |1, 1 \rangle = - \frac{1}{\sqrt{2}} \, ( \boldsymbol{e}_1 + i \boldsymbol{e}_2 ) \] \[ |1, -1 \rangle = \frac{1}{\sqrt{2}} \, ( \boldsymbol{e}_1 - i \boldsymbol{e}_2 ) \] Die Darstellung der Lie-Algebra zu \(j=1\) lässt sich also durch einen Basiswechsel in die definierende Ausgangs-Darstellung der Lie-Algebra umrechnen, die wir aus der Drehgruppe ganz oben erhalten haben.
Da \(SU(2)\) kompakt und einfach zusammenhängend ist, lässt sich jede ihrer Darstellungen als Exponentialreihe schreiben, wobei im Exponenten eine Darstellung der Lie-Algebra steht. Die hermiteschen Darstellungen der Lie-Algebra ergeben also über die Exponentialreihe sofort alle unitären Darstellungen von \(SU(2)\).
Tatsächlich ist es so, dass man mit den unitären Darstellungen sogar alle Darstellungen der Gruppe \(SU(2)\) erfasst, denn man kann zeigen:
| Jede Darstellung einer kompakten Gruppe durch endlich-dimensionale komplexe (bzw. reelle) Matrizen lässt sich durch Basiswechsel in eine Darstellung durch unitäre (bzw. orthogonale) Matrizen umrechnen. |
Das wird später bei Hinzunahme der Boosts anders werden, denn dann wird die entsprechende Gruppe (Galileigruppe oder Poincaregruppe) nicht-kompakt sein.
Die unitären Darstellungen von \(SU(2)\) bilden für festes \(j\) jeweils selbst eine Matrixgruppe mit derselben Lie-Algebra wie \(SU(2)\). Daher befinden sich unter ihnen auch alle Gruppen (mit ihren Darstellungen), zu denen \(SU(2)\) die Überlagerungsgruppe ist, denn alle Gruppen mit derselben Lie-Algebra wie \(SU(2)\) haben \(SU(2)\) als universelle Überlagerungsgruppe. Dazu gehört die Drehgruppe mit ihren Darstellungen.
Schreiben wir die Darstellungen explizit auf:
|
Darstellungen von SU(2): Jede Darstellung \( D^j(\hat{J}_i ) \) der Lie-Algebra der Drehgruppe ergibt über die Exponentialreihe eine Darstellung \( D^j(u) \) der Überlagerungsgruppe \(SU(2)\): \[ D^j(u) := e^{-i \, w_k \, D^j(\hat{J}_k )} \] mit \(u\) aus \(SU(2)\) und Summe über \(k\) im Exponenten. Die Matrixelemente von \( D^j(u) \) sind \[ D^j_{m m'}(u) = \] \[ = \langle j m | e^{-i \boldsymbol{w \hat{J}}} | j m' \rangle = \] \[ = \langle j m | T_u | j m' \rangle \] mit \[ T_u \, | j m' \rangle = \] \[ = \sum_m \, | j m \rangle \, \langle j m | T_u | j m' \rangle = \] \[ = \sum_m \, | j m \rangle \, D^j_{m m'}(u) \] mit \( \boldsymbol{w \hat{J}} = w_k \hat{J}_k \) (Summe über \(k\)) und \( T_u = e^{-i \boldsymbol{w \hat{J}}} \). In der Summe läuft \(m\) von \(-j\) bis \(j\). Dabei werden alle Darstellungen von \(SU(2)\) und somit alle Darstellungen der Drehgruppe erfasst. Die Darstellungen sind irreduzibel, d.h. sie enthalten keine invarianten Unterräume (die Matrizen zerfallen also nicht in kleinere Unter-Blöcke) – jeder Vektor zu einem festen \(j\) lässt sich aus jedem anderen Vektor zu diesem \(j\) durch eine passende Matrix \( D^j(u) \) erreichen. Die Dimension der Darstellungsräume ist wie bei den Matrizen der Lie-Algebra gleich \(2j+1\), d.h. \( D^j(u) \) ist eine \(2j+1\) mal \(2j+1\) -Matrix.
|
Der Fall \( j = 0 \):
Der Fall \(j = 0\) ist wieder trivial, denn aus \( D^j(\hat{J}_k ) = 0 \) folgt \( D^j(u) = 1\).
Der Fall \( j = \frac{1}{2} \):
Für \( j = \frac{1}{2} \) spricht man auch vom Spin eines Zustandes. Die \( D^{\frac{1}{2}}(u) \) sind speziell-unitäre 2-mal-2-Matrizen, d.h. die Darstellung von \(SU(2)\) ergibt für \( j = \frac{1}{2} \) gerade \(SU(2)\) selbst: \[ D^{\frac{1}{2}}(u) = u \] Man kann die Exponentialreihe explizit aufsummieren und erhält:
| \[ u = e^{-\frac{i}{2} \, \sigma(\boldsymbol{w})} = \] \[ = 1 \, \cos{\frac{\omega}{2}} - i \, \sigma(\boldsymbol{e}) \, \sin{\frac{\omega}{2}} \] |
mit \( \boldsymbol{w} = \omega \, \boldsymbol{e} \), d.h. \( \omega = |\boldsymbol{w}| \) und \( \boldsymbol{e} = \boldsymbol{w} / |\boldsymbol{w}| \) sowie \( \sigma(\boldsymbol{x}) = x_i \sigma_i \) mit Summe über \(i\) (siehe oben). Die Rechnung findet man z.B. in D. Schütte: Darstellungstheorie der Drehgruppe, Kapitel 10, Seite 51.
Diese Darstellung zeigt sofort, dass bei einer 360-Grad-Drehung (also \( \omega' = \omega + 2\pi \) ) sich \(u\) in \(-u\) verwandelt. Erst nach einer zweiten 360-Grad-Drehung erreicht man wieder das alte \(u\). Das hatte bereits die Formel \[ u \, \sigma(\boldsymbol{x}) \, u^+ = \sigma(R \boldsymbol{x}) \] gezeigt, die wir weiter oben kennengelernt haben. Diese Formel, die den Zusammenhang zwischen \(SU(2)\) und der Drehgruppe herstellt, können wir natürlich mit den expliziten Formeln für \(u\) und \(R\) nun auch nachrechnen. Wir verzichten hier darauf. Übrigens: Die Formeln für die Drehung um die z-Achse in Kapitel 4.6 erhält man, indem man oben \(\boldsymbol{e}_3\) für \(\boldsymbol{e}\) einsetzt (vielleicht bis auf ein irrelevantes Vorzeichen).
Der Fall \( j = 1 \):
Für \( j = 1 \) kann man durch den Basiswechsel, den wir bei der Lie-Algebra-Darstellung zu \( j = 1 \) gesehen haben, die Matrix \( D^1(u) \) in die Drehmatrix \(R\) von ganz oben umrechnen. Die Darstellung zu \( j = 1 \) entspricht also der Drehgruppe selbst.
Der allgemeine Fall:
Man kann zeigen, dass nur die Darstellungen zu ganzzahligem \(j\) eine unitäre Darstellung der Drehgruppe bilden. Die Darstellungen zu halbzahligem \(j\) bilden dagegen eine unitäre Darstellung der Überlagerungsgruppe \(SU(2)\) und damit eine Strahldarstellung der Drehgruppe, aber keine unitäre Darstellung der Drehgruppe. Den Grund kennen wir bereits: erst zwei Drehungen um 360 Grad ergeben bei halbzahligem \(j\) wieder den Ausgangszustand, eine Drehung um 360 Grad führt dagegen zu einem Vorzeichenwechsel.
In der klassischen Physik spielen nur Drehungen und deren Darstellungen eine Rolle, nicht aber Darstellungen der Überlagerungsgruppe. Bei einer Bahnkurve oder einem elektrischen Feld darf eine 360-Grad-Drehung keinen Vorzeichenwechsel hervorrufen. Das bedeutet aber auch: Für Zustände mit halbzahligem Spin gibt es keinen klassischen Grenzfall. Der halbzahlige Spin eines Teilchens ist ein rein quantenmechanisches Phänomen, während man bei ganzzahligem \(j\) den Grenzübergang zum Drehimpuls hinbekommt (siehe unten). Daher hat auch die Veranschaulichung des Spins als innerer Drehimpuls seine Tücken – wie soll sich ein punktförmiges strukturloses Teilchen um seine Achse drehen?
Ein interessanter Punkt, auf den ich in Steven Weinbergs Standardwerk The Quantum Theory of Fields Vol. 1 gestoßen bin, sind die Superauswahlregeln. Wenn man voraussetzt, dass \(SU(2)\) eine quantenmechanische Symmetriegruppe ist, so darf man Zustände mit halbzahligem und mit ganzzahligem Spin nicht überlagern, denn eine 360-Grad-Drehung würde das relative Vorzeichen zwischen ihnen ändern, und das wäre über Interferenzexperimente messbar. Eine 360-Grad-Drehung würde damit die Situation messbar beeinflussen und dann wäre die Drehgruppe keine Symmetriegruppe mehr. Man muss also fordern, dass es nicht möglich ist, Zustände mit halb- und mit ganzzahligem Spin im Experiment zu überlagern (man nennt dies eine Superauswahlregel). Das entspricht tatsächlich den experimentellen Tatsachen.
Falls nun aber doch solche Zustände gefunden werden, was dann? Dann darf man unitäre Darstellungen von \(SU(2)\) nicht mehr als Symmetriegruppe auf dem Hilbertraum verwenden, sondern man muss projektive Darstellungen der Drehgruppe betrachten, bei denen die Phase nur noch von den miteinander kombinierten Drehungen abhängt, nicht aber von der Halbzahligkeit des Spins. Eine 360-Grad-Drehung muss für die überlagerten Zustände zur selben Phase führen, damit diese Phase nicht messbar ist. Wir sind in Kapitel 4.6 bereits kurz darauf eingegangen.
Es kommt in der Physik häufig vor, dass man ein quantenmechanisches System betrachtet, dass aus mehreren Subsystemen besteht. Ein Beispiel sind quantenmechanische Zustände aus mehreren Teilchen. Dabei spielen Produktzustände eine Rolle. Für Drehungen werden z.B. Zustände wichtig, die sich als \[ | j m \rangle \otimes | j' m' \rangle \] oder alternativ als \[ | j m , j' m' \rangle \] schreiben lassen. Man spricht von einem Tensorprodukt. Man kann dieses Tensorprodukt mathematisch sauber definieren (siehe z.B. Wikipedia: Tensorprodukt). Die wichtigste Eigenschaften sind:
Ein Beispiel: Das Tensorprodukt zwischen Funktionen kann man so definieren: \[ ( \psi \otimes \phi ) (x,y) := \psi(x) \, \phi(y) \] Dabei ist \( \psi \otimes \phi \) eine Funktion, die von zwei Variablen abhängt.
Zurück zu den Drehimpuls-Produktzuständen \( | j m \rangle \otimes | j' m' \rangle \). Die Schreibweise bedeutet, dass bei einer Drehung beide Zustände zugleich mit dem entsprechenden Drehoperator gedreht werden: \[ T_u \, ( | j m \rangle \otimes | j' m' \rangle ) = \] \[ = | j n \rangle \otimes | j' n' \rangle \, D^j_{nm}(u) \, D^{j'}_{n'm'}(u) \] mit Summe über \(n\) und \(n'\). Man kann die Zahlenpaare \((j,j')\), \((n,n')\) und \((m,m')\) wieder als Doppelindizes ansehen, denn sie indizieren ja die Basiszustände im Produktraum. Oben wird gleichsam über den Doppelindex \((n,n')\) summiert. Entsprechend kann man das Produkt \[ D^j_{nm}(u) \, D^{j'}_{n'm'}(u) \] auch als Matrixelement einer Matrix \[ D^{(j,j')}_{(n,n') \, (m, m')}(u) \] ansehen. Diese Matrix stellt die Überlagerungsgruppe \(SU(2)\) im Produktraum dar, der auch ein Vektorraum (Hilbertraum) ist.
Nun haben wir oben gezeigt, dass man jede Darstellung von \(SU(2)\) auf einem Hilbertraum durch Matrizen \(D^J(u)\) auf Unterräumen des Hilbertraums darstellen kann, wobei diese Unterräume Eigenräume zum Operator \(\hat{\boldsymbol{J}}^2\) mit Eigenwert \(J(J+1)\) sind (wir schreiben die Zahl \(J\) hier groß). Entsprechend muss man auch den Produktraum in solche Unterräume zerlegen können (man spricht von der Ausreduktion der Darstellung). Man muss also einen Basiswechsel \[ | J M \rangle := \] \[ = | j m, j' m' \rangle \, \langle j m, j' m' | J M \rangle \] (mit Summe über doppelte Indizes) im Produktraum finden können, so dass die Matrix mit Matrixelementen \( D^{(j,j')}_{(n,n') \, (m, m')}(u) \) in dieser neuen Basis in einzelne Blöcke zerfällt, die jeweils innerhalb der Unterräume zu festem \(J\) wirken und die den Matrizen \( D^J(u) \) entsprechen.
Die komplexen Zahlen \( \langle j m, j' m' | J M \rangle \) bezeichnet man als Clebsch-Gordan-Koeffizienten. Sie sind die Komponenten der neuen Basisvektoren in der alten Produktbasis.
Physiker verwenden hier eine praktische Schreibweise, die auch den Bezug zur Lie-Algebra klar macht. Man nimmt einfach den Drehimpulsoperator aus dem Raum der \( | j m \rangle \) (nennen wir ihn \(\hat{\boldsymbol{J}}^{(1)}\)) und den aus dem Raum der \( | j' m' \rangle \) (nennen wir ihn \(\hat{\boldsymbol{J}}^{(2)}\)) und definiert im Produktraum den Operator \[ \hat{\boldsymbol{J}} := \hat{\boldsymbol{J}}^{(1)} + \hat{\boldsymbol{J}}^{(2)} \] mit \[ \hat{\boldsymbol{J}} \, (| j m \rangle \otimes | j' m' \rangle) := \] \[ = (\hat{\boldsymbol{J}}^{(1)} \, | j m \rangle) \otimes | j' m' \rangle + \] \[ + | j m \rangle \otimes (\hat{\boldsymbol{J}}^{(2)} \, | j' m' \rangle) \] \(\hat{\boldsymbol{J}}^{(1)}\) wirkt also nur auf den ersten Zustand, \(\hat{\boldsymbol{J}}^{(2)}\) nur auf den zweiten. So ist beispielsweise \[ \hat{J}_3 \, (| j m \rangle \otimes | j' m' \rangle) = \] \[ = (\hat{J}_3^{(1)} \, | j m \rangle ) \otimes | j' m' \rangle + | j m \rangle \otimes (\hat{J}_3^{(2)} \, | j' m' \rangle) = \] \[ = (m \, | j m \rangle) \otimes | j' m' \rangle + | j m \rangle \otimes (m' \, | j' m' \rangle) = \] \[ = (m + m') \, | j m \rangle \otimes | j' m' \rangle \] d.h. \( | j m \rangle \otimes | j' m' \rangle \) ist ein Eigenzustand von \( \hat{J}_3 \) zum Eigenwert \( M = m + m' \).
Da die Operatoren \(\hat{\boldsymbol{J}}^{(1)}\) und \(\hat{\boldsymbol{J}}^{(2)}\) miteinander vertauschen, kann man leicht überprüfen, dass die Komponenten von \(\hat{\boldsymbol{J}} := \hat{\boldsymbol{J}}^{(1)} + \hat{\boldsymbol{J}}^{(2)}\) eine Darstellung der Lie-Algebra von \(SU(2)\) auf dem Produktraum sind. Daher muss \( T_u = e^{-i \boldsymbol{w \hat{J}}} \) eine Darstellung von \(u\) auf dem Produktraum sein und es ist \[ D^{(j,j')}_{(n,n') \, (m, m')}(u) = \] \[ = \langle j n, j' n' | \, e^{-i \boldsymbol{w \hat{J}}} \, | j m, j' m' \rangle = \] \[ = \langle j n, j' n' | \, e^{-i \boldsymbol{w} (\hat{\boldsymbol{J}}^{(1)} + \hat{\boldsymbol{J}}^{(2)})} \, | j m, j' m' \rangle = \] \[ = \langle j n | e^{-i \boldsymbol{w} \hat{\boldsymbol{J}}^{(1)}} | j m \rangle \, \langle j' n' | e^{-i \boldsymbol{w} \hat{\boldsymbol{J}}^{(2)}} | j' m' \rangle = \] \[ = D^j_{nm}(u) \, D^{j'}_{n'm'}(u) \] d.h. die Schreibweise reproduziert genau das gewünschte Verhalten für die Matrixelemente. Damit die Matrix in Blöcke zerfällt, muss jeder neue Basisvektor \[ | J M \rangle := \] \[ = | j m, j' m' \rangle \, \langle j m, j' m' | J M \rangle \] ein Eigenvektor zu \(\hat{\boldsymbol{J}}^2\) und \(\hat{J}_3\) sein, denn dann haben wir wie gewünscht \[ D^\hat{J}_{MM'}(u) = \langle J M | \, e^{-i \boldsymbol{w \hat{J}}} \, | J' M' \rangle \, \delta_{J J'} \] Bezüglich \(\hat{J}_3\) ist aber bereits \( | j m, j' m' \rangle \) Eigenvektor mit Eigenwert \( M = m + m' \), wie wir oben gesehen haben, d.h. das ist problemlos. Anders sieht das bei \(\hat{\boldsymbol{J}}^2\) aus – die entsprechende Matrix muss man also diagonalisieren, um die Eigenwerte und Eigenvektoren zu berechnen. Auf diese Weise erhält man die Clebsch-Gordan-Koeffizienten des Basiswechsels.
Ein letzter Punkt dazu: Welche \(J\) können sich dabei aus \(j\) und \(j'\) ergeben? Da \( M = m + m' \) ist, muss als maximales \(J\) der Wert \( J = j + j' \) vorkommen. Man kann zeigen, dass alle \(J\) von \( j + j' \) bis \( |j - j'| \) vorkommen.
Über die Drehgruppe und ihre projektiven Darstellungen wäre damit alles gesagt. Oft findet man in der Literatur aber konkrete Darstellungen der Drehgruppe auf ortsabhängigen Funktionen, beispielsweise Kugelflächenfunktionen. Eine weitere bekannte Formel ist die Darstellung des Drehimpulsoperators \[ \hat{\boldsymbol{L}} = \hat{\boldsymbol{x}} \times \hat{\boldsymbol{p}} \] mit der man in der Quantenmechanik oft startet (um dann später festzustellen, dass dieser Operator nur für ganzzahlige Drehimpulse greift).
Um auf systematischem Weg dorthin zu gelangen, muss man Drehungen und Translationen als gemeinsame Symmetriegruppen betrachten. Im vorherigen Kapitel 4.7 haben wir gesehen, dass man bei den Translationen ganz von alleine auf Impulsamplituden \(f(\boldsymbol{p})\) und deren Fouriertransformierte \(\psi(\boldsymbol{x})\) stößt. Wenn wir nun die Drehungen hinzunehmen, werden wir untersuchen können, wie sich diese auf \(f(\boldsymbol{p})\) und \(\psi(\boldsymbol{x})\) auswirken und damit (Strahl)-Darstellungen der Drehgruppe auf diesen Funktionen erhalten. Die Vorgehensweise ist dabei vollkommen allgemein, gilt also auch in der relativistischen Quantenfeldtheorie.
Schauen wir uns an, ob Drehungen und Translationen vertauschen. Dazu betrachten wir eine Drehung \(R(\boldsymbol{w})\) aus \(SO(3)\) und eine Translation \(g(\boldsymbol{a})\) mit \[ g(\boldsymbol{a}) \, \boldsymbol{x} = \boldsymbol{x} + \boldsymbol{a} \] Dann ist \[ R(\boldsymbol{w}) \, g(\boldsymbol{a}) \, \boldsymbol{x} = \] \[ = R(\boldsymbol{w}) \, (\boldsymbol{x} + \boldsymbol{a}) = \] \[ = R(\boldsymbol{w}) \, \boldsymbol{x} + R(\boldsymbol{w}) \, \boldsymbol{a} = \] \[ = g(R(\boldsymbol{w}) \, \boldsymbol{a}) \, R(\boldsymbol{w}) \, \boldsymbol{x} \] Translationen und Drehungen vertauschen also nicht miteinander. Um den Kommutator auszurechnen, schreiben wir diese Gleichung noch etwas um: \[ R(\boldsymbol{w}) \, g(\boldsymbol{a}) \, R(\boldsymbol{w})^{-1} = \] \[ = g(R(\boldsymbol{w}) \, \boldsymbol{a}) \] Aus Kapitel 4.6 wissen wir, dass für den Kommutator von beliebigen Generatoren einer Gruppe ganz allgemein gilt: \[ [A_i, A_j] = \frac{d}{ds} e^{i s A_j} \, (i A_i) \, e^{- i s A_j} \, \bigg|_{s=0} = \] \[ = \frac{d}{ds} \frac{d}{dt} e^{i s A_j} \, e^{i t A_i} \, e^{- i s A_j} \, \bigg|_{s=0, \, t=0} \] Insgesamt haben wir nun 6 verschiedene Generatoren \(A_i\), nämlich 3 für die Translationen und 3 für die Drehungen. Um Verwirrung zu vermeiden, wollen wir für die Generatoren der Translationen hier \(B_i\) schreiben. Also ist \[ [B_i, A_j] = \] \[ = \frac{d}{ds} \frac{d}{dt} \, e^{i s A_j} \, e^{i t B_i} \, e^{- i s A_j} \, \bigg|_{s=0, \, t=0} = \] \[ = \frac{d}{ds} \frac{d}{dt} \, R(s \boldsymbol{e}_j) \, g(t \boldsymbol{e}_i) \, R(s \boldsymbol{e}_j)^{-1} \, \bigg|_{s=0, \, t=0} = \] ... wir verwenden die Gleichung \( R(\boldsymbol{w}) \, g(\boldsymbol{a}) \, R(\boldsymbol{w})^{-1} = \) \( g(R(\boldsymbol{w}) \, \boldsymbol{a}) \) von oben: \[ = \frac{d}{ds} \frac{d}{dt} \, g(R(s \boldsymbol{e}_j) \, t \boldsymbol{e}_i) \, \bigg|_{s=0, \, t=0} = \] \[ = \frac{d}{ds} g(R(s \boldsymbol{e}_j) \, \boldsymbol{e}_i) \, \bigg|_{s=0} = \] wir verwenden \( R(\boldsymbol{w}) = e^{G(\boldsymbol{w})} \) und somit \( R(s \boldsymbol{e}_j) = e^{G(s \boldsymbol{e}_j)} \) sodass \( \frac{d}{ds} \, R(s \boldsymbol{e}_j) \, \bigg|_{s=0} = G(\boldsymbol{e}_j) \) ist: \[ = g(G(\boldsymbol{e}_j) \, \boldsymbol{e}_i) = \] hier verwenden wir \( G(\boldsymbol{w}) \, \boldsymbol{x} = \boldsymbol{w} \times \boldsymbol{x} \), d.h. \[ = g(\boldsymbol{e}_j \times \boldsymbol{e}_i) = \] \[ = - \epsilon_{ijk} \, g(\boldsymbol{e}_k) = \] wir verwenden \( g(\boldsymbol{e}_k) = \) \( \frac{d}{dt} g(t \boldsymbol{e}_k) \, \bigg|_{t=0} = \) \( \frac{d}{dt} e^{i t B_k} \, \bigg|_{t=0} = i B_k \) \[ = - \epsilon_{ijk} \, i B_k \] Wir haben also insgesamt \[ [B_i, A_j] = - \epsilon_{ijk} \, i B_k \] wobei \( B_k \) die Generatoren der Translationen und \( A_i \) die Generatoren der Drehungen sind.
Natürlich kann man alternativ diese Gleichung auch mit Hilfe der Matrixdarstellung der Gruppen und damit der Generatoren auf direktem Weg ausrechnen. Für eine Strahldarstellung muss also gelten: \[ [T(B_i), T(A_j)] = - \epsilon_{ijk} \, i T(B_k) + i C_{ij} \, 1 \] wobei die Zentralladungen \(C_{ij}\) wieder zur Phase in der projektiven Darstellung der Dreh-Translations-Gruppe führen. Man könnte nun meinen, dass man diese Zentralladungen ganz analog zu oben loswerden kann. Ganz so einfach ist es aber nicht, denn \( [T(B_i), T(A_j)] \) muss nicht antisymmetrisch in den Indices \(i\) und \(j\) sein, anders als \( [T(A_i), T(A_j)] \) bei den reinen Drehungen. Schließlich ist \(B_i\) nicht gleich \(A_i\).
Schauen wir uns das insgesamt etwas genauer an.
Wie bisher schreiben wir dazu wieder
\[
\hat{J}_i = - T(A_i)
\]
\[
\hat{P}_i := - T(B_i)
\]
(siehe Kapitel 4.7) und haben damit für die Strahl-Darstellung der Lie-Algebra:
\[
[\hat{J}_i, \hat{J}_j] = i \epsilon_{ijk} \hat{J}_k
\]
\[
[\hat{P}_i, \hat{P}_j] = i \epsilon_{ijk} C_k \, 1
\]
\[
[\hat{P}_i, \hat{J}_j] = i \epsilon_{ijk} \hat{P}_k + i C_{ij} 1
\]
Dass die Zentralladungen in der ersten Gleichung wegdefiniert werden können,
das hatten wir bereits weiter oben gesehen (unter der Überschrift: keine Zentralladungen).
Die zweite Gleichung kennen wir aus Kapitel 4.7.
Die dritte Gleichung haben wir gerade eben neu kennengelernt.
Wir werten nun die sogenannten Jacobi-Identitäten aus, die jeder Kommutator erfüllt. Beginnen wir mit \[ [\hat{P}_i, [\hat{P}_j, \hat{J}_k]] + \] \[ + [\hat{J}_k, [\hat{P}_i, \hat{P}_j]] + \] \[ + [\hat{P}_j, [\hat{J}_k, \hat{P}_i]] = 0 \] Zentralladungen in den inneren Kommutatoren können wir weglassen, denn sie fallen in den äußeren Kommutatoren sowieso weg. Damit fällt der zweite Term komplett weg und wir erhalten (mit Summe über doppelte Indices): \[ [\hat{P}_i, i \epsilon_{jkl} \hat{P}_l] + [\hat{P}_j, -i \epsilon_{ikl} \hat{P}_l] = 0 \] und mit \( [\hat{P}_i, \hat{P}_j] = i \epsilon_{ijk} C_k 1 \) dann \[ i \epsilon_{jkl} (-i) \epsilon_{ilm} C_m - i \epsilon_{ikl} (-i) \epsilon_{jlm} C_m = 0 \] was wir vereinfachen können zu \[ (\epsilon_{jkl} \epsilon_{ilm} - \epsilon_{ikl} \epsilon_{jlm}) \, C_m = 0 \] Wir können nun die Terme mit \(i = k\) aufsummieren (man sagt auch, man kontrahiert mit \(\delta_{ik}\)). Dabei fällt der zweite Tem weg und wir erhalten \[ \epsilon_{jil} \epsilon_{ilm} \, C_m = 0 \] Umsortieren ergibt \[ \epsilon_{ilj} \epsilon_{ilm} \, C_m = 0 \] Für vorgegebene \(i\) und \(l\) wählen wir \(j\) so, dass \( \epsilon_{ilj} = 1\) ist und erhalten \[ \epsilon_{ilm} \, C_m = 0 \] Das ist eine schiefsymmetrische Matrix analog zu \(G(\boldsymbol{w})\) von oben. Sie muss wegen der Jacobi-Identität Null sein, und das geht nur wenn \( C_m = 0 \) ist.
Bei zusätzlicher Drehsymmetrie verschwinden also die Zentralladungen in den Kommutatoren der Impulse, d.h. die Translationen werden durch eine unitäre Darstellung auf dem Hilbertraum ohne projektive Phase wiedergegeben.
Genau das hatten wir im letzten Kapitel bereits verwendet (aus der Lie-Algebra der Translations-Generatoren alleine folgt das nicht, wie wir in Kapitel 4.7 gesehen haben). Erst die Hinzunahme der Drehungen bewirkt, dass die Phase in der Darstellung der Translationen generell unnötig wird. Entsprechend kann auch kein äußeres Magnetfeld mehr beschrieben werden, das ja die Drehsymmetrie zerstören würde.
Für die \(C_{ij}\) schauen wir uns die folgende Jacobi-Identität an: \[ [\hat{P}_i, [\hat{J}_j, \hat{J}_k]] + \] \[ + [\hat{J}_k, [\hat{P}_i, \hat{J}_j]] + \] \[ + [\hat{J}_j, [\hat{J}_k, \hat{P}_i]] = 0 \] Wieder fallen Zentralladungen in den inneren Kommutatoren weg und wir erhalten (mit Summe über doppelte Indices): \[ [\hat{P}_i, i \epsilon_{jkl} \hat{J}_l] + \] \[ + [\hat{J}_k, i \epsilon_{ijl} \hat{P}_l] + \] \[ + [\hat{J}_j, -i \epsilon_{ikl} \hat{P}_l] = 0 \] Wenn wir hier die Terme mit \(k = j\) aufsummieren, würde der erste Term wegfallen und es bliebe \[ [\hat{J}_j, i \epsilon_{ijl} \hat{P}_l] + [\hat{J}_j, -i \epsilon_{ijl} \hat{P}_l] = 0 \] übrig. Da diese Gleichung immer stimmt, hilft sie uns nicht weiter. Also versuchen wir es mit Summation über \(k = i\) (hier fällt der dritte Term weg): \[ [\hat{P}_i, i \epsilon_{jil} \hat{J}_l] + [\hat{J}_i, i \epsilon_{ijl} \hat{P}_l] = 0 \] oder etwas anders geschrieben: \[ i \epsilon_{jil} \, ( [\hat{P}_i, \hat{J}_l] + [\hat{P}_l, \hat{J}_i] ) = 0 \] Der Term in der Klammer ist symmetrisch in \(i\) und \(l\). Dagegen ist \(\epsilon_{jil}\) antisymmetrisch in \(i\) und \(l\). Die Summe über \(i\) und \(l\) für gegebenes \(j\) ist also immer Null, d.h. auch diese Gleichung ist trivial erfüllt.
Ich habe zwar in der Literatur bisher dazu nichts gefunden, aber es sieht so aus, als ob die bisherigen Informationen nicht ausreichen, um die Zentralladungen \(C_{ij}\) in wegzudiskutieren. Betrachtet man ausschließlich Translationen und Drehungen als Symmetrien, so kann es offenbar zu projektiven Phasen kommen, wenn man eine Drehung und eine Translation nacheinander ausführt (bei zwei Drehungen oder zwei Translationen nacheinander kann man dagegen projektive Phasen wegdefinieren, wie wir gesehen haben). Ob es physikalische Anwendungen dieser Möglichkeit gibt (analog zum Magnetfeld bei Translationen wie im vorhergehenden Kapitel) ist mir leider nicht bekannt. Es müsste sich um ein System handeln, bei dem Boosts keine Symmetrie darstellen, bei dem es also ein ausgezeichnetes Inertialsystem gibt.
Nimmt man Boosts hinzu, so kann man nachrechnen, dass man die Zentralladungen in \( [\hat{P}_i, \hat{J}_j] \) loswerden kann, so dass man eine echte Darstellung der obigen Lie-Algebra erreichen kann. Die konkrete Rechnung findet man (in relativistischer Notation) in Steven Weinbergs Buch The Quantum Theory of Fields, Vol. 1, Kapitel 2.7.. In diesem Sinn ignorieren wir im Folgenden Zentralladungen in \( [\hat{P}_i, \hat{J}_j] \) und betrachten nur die Darstellung \[ [\hat{J}_i, \hat{J}_j] = i \epsilon_{ijk} \hat{J}_k \] \[ [\hat{P}_i, \hat{P}_j] = 0 \] \[ [\hat{P}_i, \hat{J}_j] = i \epsilon_{ijk} \hat{P}_k \] Für die unitäre Darstellung der Gruppenelemente folgt aus \( R(\boldsymbol{w}) \, g(\boldsymbol{a}) = g(R(\boldsymbol{w}) \, \boldsymbol{a}) \, R(\boldsymbol{w}) \) die Gleichung \[ e^{-i \boldsymbol{w \hat{J}}} \, e^{-i \boldsymbol{a \hat{P}}} = \] \[ = e^{-i (R(\boldsymbol{w}) \boldsymbol{a}) \boldsymbol{\hat{P}}} \, e^{-i \boldsymbol{w \hat{J}}} \] die wir natürlich auch mit Hilfe der Lie-Algebra etwas mühsam nachrechnen können. Da \(R(\boldsymbol{w})\) eine Drehmatrix ist, gilt \[ (R(\boldsymbol{w}) \, \boldsymbol{a}) \, \boldsymbol{\hat{P}} = \boldsymbol{a} (R(\boldsymbol{w})^{-1} \boldsymbol{\hat{P}}) \] und somit \[ e^{-i \boldsymbol{w \hat{J}}} \, e^{-i \boldsymbol{a \hat{P}}} = e^{-i \boldsymbol{a} (R(\boldsymbol{w})^{-1} \boldsymbol{\hat{P}})} \, e^{-i \boldsymbol{w \hat{J}}} \] Abgeleitet nach den einzelnen \(a_i\) ergibt das \[ e^{-i \boldsymbol{w \hat{J}}} \, \boldsymbol{\hat{P}} = \] \[ = (R(\boldsymbol{w})^{-1} \, \boldsymbol{\hat{P}} ) \, e^{-i \boldsymbol{w \hat{J}}} \] und multipliziert mit \(R(\boldsymbol{w})\) dann \[ e^{-i \boldsymbol{w \hat{J}}} \, (R(\boldsymbol{w}) \boldsymbol{\hat{P}}) = \boldsymbol{\hat{P}} \, e^{-i \boldsymbol{w \hat{J}}} \] Damit können wir nun angeben, wie sich eine Drehung auf einen Eigenvektor \( |\boldsymbol{p} \rangle \) des Impulsoperators auswirkt: \[ \boldsymbol{\hat{P}}\, e^{-i \boldsymbol{w \hat{J}}} \, |\boldsymbol{p} \rangle = \] \[ = e^{-i \boldsymbol{w \hat{J}}} \, (R(\boldsymbol{w}) \, \boldsymbol{\hat{P}}) \, |\boldsymbol{p} \rangle = \] \[ = e^{-i \boldsymbol{w \hat{J}}} \, (R(\boldsymbol{w}) \, \boldsymbol{p}) \, |\boldsymbol{p} \rangle = \] \[ = (R(\boldsymbol{w}) \boldsymbol{p}) \, e^{-i \boldsymbol{w \hat{J}}} \, |\boldsymbol{p} \rangle \] d.h. der gedrehte Zustand \( e^{-i \boldsymbol{w \hat{J}}} \, |\boldsymbol{p} \rangle \) ist ein Eigenzustand zum Impulsoperator \(\boldsymbol{\hat{P}}\) zum Eigenwert \( R(\boldsymbol{w}) \, \boldsymbol{p} \). Der Impuls des Zustandes wurde also gedreht – genau das entspricht unserer Anschauung aus der klassischen Mechanik! Man könnte nun versucht sein, deshalb \( e^{-i \boldsymbol{w \hat{J}}} \, |\boldsymbol{p} \rangle = |R(\boldsymbol{w}) \, \boldsymbol{p} \rangle \) zu schreiben. Doch Vorsicht: Wir wissen, dass eine 360-Grad-Drehung zu einem Vorzeichenwechsel führen kann.
Was also ist zu tun? Wir müssen die Möglichkeit berücksichtigen, dass es neben dem Impuls weitere Freiheitsgrade des Systems gibt, die sich bei einer Drehung verändern. Man könnte also allgemein \( | \boldsymbol{p}, \sigma \rangle \) mit einem Sammelindex \( \sigma \) schreiben, der diese zusätzlichen Freiheitsgrade berücksichtigt (das \( \sigma \) hat hier nichts mit den Paulimatrizen von oben zu tun). Allgemein könnte \( \sigma \) sogar kontinuierlich sein (beispielsweise wenn \( \sigma \) den Relativimpuls zweier freier Teilchen darstellt – dann wäre \( \boldsymbol{p} \) der Gesamtimpuls der beiden Teilchen).
Wir wollen nun an dieser Stelle davon ausgehen, dass für einen Einteilchen-Zustand ein diskretes \(\sigma\) ausreicht (das definiert den Begriff Einteilchen-Zustand letztlich). Achtung: Wir haben nicht von einem Elementarteilchen gesprochen! Auch ein gebundenes System wie ein Wasserstoffatom kann als ein Teilchen angesehen werden, zumindest in der relativistischen Quantentheorie. Siehe dazu auch Steven Weinberg: The Quantum Theory of Fields Vol. 1, Kapitel 2.5 .
Wenn wir von einem bestimmten Einteilchenzustand \( | \boldsymbol{p}, \sigma \rangle \) ausgehen, so sollten sich alle dazu gedrehten Einteilchenzustände desselben Teilchens durch Anwendung des Drehoperators \( e^{-i \boldsymbol{w \hat{J}}} \) daraus gewinnen lassen. Zustände mit gedrehtem Impuls, die sich so nicht erreichen lassen, gehören zu einem anderen Teilchen bzw. Teilchentyp. Die Zustände zu einem Teilchen bilden also bei Drehungen einen irreduziblen Raum.
All diese Forderungen können wir einhalten, indem wir den Drehimpulsoperator \( \hat{\boldsymbol{J}} \) folgendermaßen aufspalten:
| \[ \hat{\boldsymbol{J}} = \hat{\boldsymbol{L}} + \hat{\boldsymbol{S}} \] wobei \(\hat{\boldsymbol{L}}\) mit \(\hat{\boldsymbol{S}}\) kommutiert und die \(\hat{L}_i\) und \(\hat{S}_i\) jeweils unabhängig voneinander die Drehimpulsalgebra erfüllen. Wichtig: \(\hat{\boldsymbol{S}}\) soll mit \(\boldsymbol{\hat{P}}\) kommutieren, d.h. alleine \(\hat{\boldsymbol{L}}\) besitzt noch nicht-triviale Kommutatoren mit \(\boldsymbol{\hat{P}}\): \[ [\hat{P}_i, \hat{L}_j] = i \epsilon_{ijk} \, \hat{P}_k \] \[ [\hat{P}_i, \hat{S}_j] = 0 \] |
Wir nennen \(\hat{\boldsymbol{S}}\) den Spinoperator und \(\hat{\boldsymbol{L}}\) den Bahndrehimpuls-Operator (warum, wird noch klar werden). Insgesamt ergibt sich so wieder \[ [\hat{P}_i, \hat{J}_j] = i \epsilon_{ijk} \hat{P}_k \] Dabei soll \(\hat{\boldsymbol{L}}\) für die Drehung des Impulses zuständig sein, während sich \(\hat{\boldsymbol{S}}\) um den zweiten Freiheitsgrad \(\sigma\) kümmern soll.
Vielleicht fällt die Ähnlichkeit zum Operator \[ \hat{\boldsymbol{J}} := \hat{\boldsymbol{J}}^{(1)} + \hat{\boldsymbol{J}}^{(2)} \] auf, den wir oben im Tensorproduktraum zweier Darstellungsräume definiert haben. Genauso ist es auch hier: Wir suchen eine Darstellung der Drehungen auf einem Tensorproduktraum, bei dem nur einer der beiden Räume mit den Translationen und dem Impulsoperator zusammenhängt.
Da \(\hat{\boldsymbol{S}}\) die Drehimpulsalgebra erfüllt, kann man wieder Eigenzustände zu \(\hat{\boldsymbol{S}}^2\) und \(\hat{S}_3\) angeben – nennen wir die Eigenwerte \(s\) und \(m_s\) und bezeichnen \(s\) als Spin. Außerdem kommutiert \(\hat{\boldsymbol{S}}\) mit \(\boldsymbol{\hat{P}}\), d.h. auch \(\boldsymbol{p}\) kann zugleich Eigenwert sein. Wir nennen diese Zustände also \[ | \boldsymbol{p}, s \, m_s \rangle \] Der Index \(\sigma\) entspricht also dem Indexpaar \(s\) und \(m_s\). Schauen wir uns die Drehung dieses Zustandes an: \[ e^{-i \boldsymbol{w \hat{J}}} \, | \boldsymbol{p}, s \, m_s \rangle = \] \[ = e^{-i \boldsymbol{w \hat{L}}} \, e^{-i \boldsymbol{w \hat{S}}} \, | \boldsymbol{p}, s \, m_s \rangle = \] \[ = e^{-i \boldsymbol{w \hat{L}}} \, \sum_{m_s'} \, | \boldsymbol{p}, s \, m_s' \rangle \, D^s_{m_s' m_s}(u) \] Analog zu oben können wir wieder zeigen, dass \( e^{-i \boldsymbol{w \hat{L}}} \; | \boldsymbol{p}, s \, m_s' \rangle \) ein Eigenvektor von \(\boldsymbol{\hat{P}}\) zum gedrehten Eigenwert \( (R(\boldsymbol{w}) \, \boldsymbol{p}) \) ist (wir brauchen dazu nur \(\hat{\boldsymbol{L}}\) statt \(\hat{\boldsymbol{J}}\) in der Rechnung zu schreiben, denn \(\hat{\boldsymbol{L}}\) bestreitet den Kommutator mit \(\boldsymbol{\hat{P}}\) ja alleine; \(\hat{\boldsymbol{S}}\) spielt im Kommutator mit \(\boldsymbol{\hat{P}}\) schließlich keine Rolle). Wir definieren nun: \[ e^{-i \boldsymbol{w \hat{L}}} \, | \boldsymbol{p}, s \, m_s' \rangle =: \] \[ =: | R(\boldsymbol{w}) \, \boldsymbol{p}, s \, m_s' \rangle \] Auf diese Weise werden die Vektoren zu gleichem \(s\) und \(m_s'\), aber verschieden gedrehten Impulsen miteinander in Beziehung gesetzt. Diese Definition entspricht unserer Absicht, zwei voneinander unabhängige Freiheitsgrade (Impuls und Spin) zu beschreiben, die sich beide bei Drehungen verändern, wobei \(\hat{\boldsymbol{L}}\) für die Impulsdrehung und \(\hat{\boldsymbol{S}}\) für die Spindrehung zuständig ist. Setzen wir dies oben ein, so erhalten wir:
|
\[
e^{-i \boldsymbol{w \hat{J}}}
\, | \boldsymbol{p}, s \, m_s \rangle
=
\]
\[ =
\sum_{m_s'} \,
| R(\boldsymbol{w}) \, \boldsymbol{p}, s \, m_s' \rangle \,
D^s_{m_s' m_s}(u)
\]
|
Für den Spinindex haben wir damit die gewünschte irreduzible Darstellung.
Ein Beispiel: Für \(s = \frac{1}{2}\) führt eine 360-Grad-Drehung (also \( u = - 1 \) und \( R(2\pi\boldsymbol{e}) = 1 \) ) zu \( D^{\frac{1}{2}}_{m_s' m_s} (-1) = - \delta_{m_s' m_s} \) und somit zu \[ e^{-i 2\pi \boldsymbol{e \hat{J}}} \,| \boldsymbol{p}, \frac{1}{2} \, m_s \rangle = \] \[ = \sum_{m_s'} \, | R(2\pi\boldsymbol{e}) \, \boldsymbol{p}, \frac{1}{2} \, m_s' \rangle D^{\frac{1}{2}}_{m_s' m_s} (-1) = \] \[ = - | \boldsymbol{p}, \frac{1}{2} m_s \rangle \] d.h. der Spin garantiert, dass eine 360-Grad-Drehung zu einem Vorzeichenwechsel führen kann.
Wir wollen nun wie im vorherigen Kapitel wieder Impulsamplituden einführen und deren Fouriertransformation betrachten. Diesmal müssen wir allerdings nicht nur verschiedene Impulse überlagern, sondern auch verschiedene Werte von \(m_s\), um einen allgemeinen Zustand (mit festem \(s\)) zu konstruieren. Verschiedene Spinwerte \(s\) wollen wir hier nicht überlagern. Die Überlagerung von halb- und ganzzahligen \(s\) ist nach der Super-Auswahlregel sowieso verboten (siehe oben). \[ |\psi_s \rangle = \sum_{m_s} \int d^3p \, f_{s m_s}(\boldsymbol{p}) \, | \boldsymbol{p}, s \, m_s \rangle \] (die Summe schreiben wir hier ausnahmsweise einmal explizit hin). Wir gehen nun vollkommen analog zu Kapitel 4.7 vor, um Drehungen \( T_u = e^{-i \boldsymbol{w \hat{J}}} \) auf den Impulsamplituden darzustellen: \[ T_u \, |\psi_s \rangle = \] \[ = \sum_{m_s} \int d^3p \, f_{s m_s}(\boldsymbol{p}) \, T_u \, | \boldsymbol{p}, s \, m_s \rangle = \] \[ = \sum_{m_s m_s'} \int d^3p \, f_{s m_s} (\boldsymbol{p}) \, \cdot \] \[ \quad \cdot | R(\boldsymbol{w}) \, \boldsymbol{p}, s m_s' \rangle \, D^s_{m_s' m_s}(u) = \] Wir substituieren nun die Integrationsvariable \( \boldsymbol{p}' := R(\boldsymbol{w}) \, \boldsymbol{p} \) und lassen den Strich wieder weg. Außerdem vertauschen wir die Bezeichnungen für \(m_s'\) und \(m_s\): \[ = \sum_{m_s' m_s} \int d^3p \, f_{s m_s'}(R(\boldsymbol{w})^{-1} \boldsymbol{p}) \, \cdot \] \[ \quad \cdot | \boldsymbol{p}, s \, m_s \rangle \, D^s_{m_s m_s'}(u) = \] \[ =: \sum_{m_s} \int d^3p \, [T_u f ]_{s m_s}(\boldsymbol{p}) \, | \boldsymbol{p}, s \, m_s \rangle \] mit
| \[ [T_u f ]_{s m_s}(\boldsymbol{p}) := \sum_{m_s'} \, D^s_{m_s m_s'}(u) \, f_{s m_s'}(R(\boldsymbol{w})^{-1} \, \boldsymbol{p}) \] |
Wir können die Schreibweise noch etwas vereinfachen, indem wir den Spaltenvektor \( f_s(\boldsymbol{p}) \) mit Komponenten \( f_{s m_s}(\boldsymbol{p}) \) einführen und die obige Gleichung als Matrixgleichung auffassen:
| \[ [T_u f ]_s (\boldsymbol{p}) := D^s(u) \, f_s(R(\boldsymbol{w})^{-1} \, \boldsymbol{p}) \] |
mit fest vorgegebenem Spin \(s\). Einen Vektor, der sich bei Drehungen so verhält, bezeichnet man als Spinor. Man spricht auch von der Spinordarstellung der Drehgruppe. Anschaulich besagt die Gleichung, dass der gedrehte Spinor für den gedrehten Impuls gleich dem alten Spinor für den ungedrehten Impuls ist, zusätzlich multipliziert mit der \(SU(2)\)-Darstellungsmatrix \( D^s(u) \), die für die Drehung des Spins zuständig ist.
Natürlich können wir durch Fouriertransformation analog zu Kapitel 4.7 von der Impulsvariable \(\boldsymbol{p}\) zu einer Ortsvariable \(\boldsymbol{x}\) übergehen. \[ \psi_s(\boldsymbol{x}) := N \int d^3p \, f_s(\boldsymbol{p}) \, e^{i \boldsymbol{p x}} \] Dabei sind \(f_s\) und \(\psi_s\) jetzt Spinoren mit \(2s+1\) Komponenten. Analog zu Kapitel 4.7 definieren wir die gedrehte Fouriertransformierte als: \[ [T_u \psi]_s(\boldsymbol{x}) := \] \[ = N \int d^3p \, [T_u f]_s(\boldsymbol{p}) \, e^{i \boldsymbol{p x}} = \] \[ = N \int d^3p \, D^s(u) \, f_s(R(\boldsymbol{w})^{-1} \boldsymbol{p}) \, e^{i \boldsymbol{p x}} = \] Wir substituieren die Integrationsvariable \( \boldsymbol{p}' := R(\boldsymbol{w})^{-1} \boldsymbol{p} \) und lassen den Strich wieder weg. \[ = N \int d^3p \, D^s(u) \, f_s(\boldsymbol{p}) \, e^{i (R(\boldsymbol{w}) \, \boldsymbol{p}) \boldsymbol{x}} = \] \[ = N \int d^3p \, D^s(u) \, f_s(\boldsymbol{p}) \, e^{i \boldsymbol{p} \, (R(\boldsymbol{w})^{-1} \boldsymbol{x})} = \] \[ = D^s(u) \, \psi_s(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \] Der Spinor \(\psi_s\) transformiert sich bei Drehungen also vollkommen analog zu \(f_s\). Das entspricht der Anschauung, dass sich bei Drehungen Ort und Impuls vollkommen gleich verhalten, nämlich wie ein Vektor. Halten wir fest:
| \[ [T_u \psi]_s (\boldsymbol{x}) = D^s(u) \, \psi_s(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \] |
Häufig beginnt man in der Literatur sogar mit dieser Darstellung als definierende Darstellung von \(SU(2)\) auf Funktionen. Bei uns ist diese Darstellung ganz natürlich so nebenbei herausgekommen, wenn wir Translationen und Drehungen als gemeinsame Symmetriegruppen in der Quantentheorie betrachten (und mögliche projektive Phasen ignorieren, da sie bei der Poincaregruppe später sowieso nicht auftreten können).
In Kapitel 4.7 sind wir nun in einem nächsten Schritt hingegangen und haben eine Darstellung des Impulsoperators auf diesen Funktionen berechnet. Das können wir hier analog für den Drehimpulsoperator machen. Für den Spinoperator können wir uns das allerdings schenken, denn das Ergebnis wissen wir bereits von der Darstellung der Lie-Algebra von oben: Er wird durch \(2s+1\) -dimensionale Matrizen dargestellt.
Kommen wir also zum Drehimpulsoperator \(\hat{\boldsymbol{L}}\), der nach unserer Formel \[ e^{-i \boldsymbol{w \hat{L}}} \, | \boldsymbol{p}, s \, m_s' \rangle = | R(\boldsymbol{w}) \boldsymbol{p}, s \, m_s' \rangle \] für die Drehung des Impulses bzw. nach Fouriertransformation für die Drehung des Ortsvektors zuständig ist. Entsprechend definieren wir \[ [\hat{\boldsymbol{L}} \psi] (\boldsymbol{x}) := \] \[ = i \frac{d}{d\boldsymbol{w}} [e^{-i \boldsymbol{w \hat{L}}} \psi] (\boldsymbol{x}) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \frac{d}{d\boldsymbol{w}} \psi(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \frac{d}{d\boldsymbol{w}} \psi(e^{-G(\boldsymbol{w})} \boldsymbol{x}) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \frac{d}{d\boldsymbol{w}} \psi(\boldsymbol{x} - (\boldsymbol{w} \times \boldsymbol{x}) + \, ... ) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \frac{d}{d\boldsymbol{w}} \psi(\boldsymbol{x} \times \boldsymbol{w}) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \frac{d}{d\boldsymbol{w}} \psi(G(\boldsymbol{x}) \boldsymbol{w}) \, \bigg|_{\boldsymbol{w} = 0} = \] \[ = i \left( \, \frac{d}{dw_i} \psi(G(\boldsymbol{x}) \boldsymbol{w}) \, \right) = \] \[ = i \left( \, \frac{d\psi(\boldsymbol{x})}{dx^j} \, \frac{d [G(\boldsymbol{x}) \boldsymbol{w}]^j}{dw_i} \, \right) = \] \[ = i \left( \, \frac{d\psi(\boldsymbol{x})}{dx^j} \, G(\boldsymbol{x})^j_{\,i} \right) = \] \[ = i \left( \, \frac{d\psi(\boldsymbol{x})}{dx^j} \, \epsilon_{jki} \, x_k \right) = \] \[ = -i \left( \epsilon_{ikj} \, x_k \, \frac{d}{dx^j} \psi(\boldsymbol{x}) \right) = \] \[ = -i \, \boldsymbol{x} \times \frac{d}{d\boldsymbol{x}} \psi(\boldsymbol{x}) = \] \[ = \boldsymbol{x} \times \boldsymbol{\hat{P}} \, \psi(\boldsymbol{x}) \] mit Summation über doppelte Indices, wobei die große äußere Klammer beim Übergang zur Indexschreibweise den Spaltenvektor mit den Komponenten in der Klammer bedeuten soll. In der letzten Zeile haben wir die Darstellung des Impulsoperators \[ [\boldsymbol{\hat{P}} \psi] (\boldsymbol{x}) = -i \frac{d}{d\boldsymbol{x}} \psi(\boldsymbol{x}) \] aus Kapitel 4.7 verwendet (in natürlichen Einheiten, also \(\hbar = 1\)). Fassen wir zusammen:
| Darstellung des Bahn-Drehimpulsoperators auf ortsabhängigen Funktionen: \[ [\hat{\boldsymbol{L}} \psi] (\boldsymbol{x}) = -i \, \boldsymbol{x} \times \frac{d}{d\boldsymbol{x}} \psi(\boldsymbol{x}) = \boldsymbol{x} \times \boldsymbol{\hat{P}} \, \psi(\boldsymbol{x}) \] |
Das entspricht genau der Definition des klassischen Drehimpulses \( \boldsymbol{L} = \boldsymbol{x} \times \boldsymbol{p} \). Wenn also Erwartungswerte von \(\boldsymbol{\hat{P}}\) im klassischen Grenzfall den klassischen Impuls ergeben, so werden Erwartungswerte von \(\hat{\boldsymbol{L}}\) im klassischen Grenzfall den klassischen Drehimpuls ergeben. Das ist der Grund dafür, warum wir \(\hat{\boldsymbol{L}}\) als Bahn-Drehimpulsoperator bezeichnet haben. Der Zusatz Bahn- dient dabei zur Unterscheidung vom Spin-Drehimpulsoperator \(\hat{\boldsymbol{S}}\), zu dem es kein klassisches Gegenstück gibt.
In der Quantenmechanik-Vorlesung geht man meist umgekehrt vor und führt den Drehimpulsoperator einfach in formaler Analogie zum klassischen Drehimpuls als \( \hat{\boldsymbol{L}} = \boldsymbol{x} \times \boldsymbol{\hat{P}} \) ein. Erst bei der Analyse der Lie-Algebra seiner Komponenten stößt man dann zufällig auf die Möglichkeit, dass es auch Spin-Operatoren geben könnte. Das vorliegende Kapitel hat gezeigt, dass man die Form von \(\hat{\boldsymbol{L}}\) gar nicht erraten muss, sondern dass sie automatisch aus der Analyse der Strahldarstellungen der Drehgruppe (zusammen mit der Translationsgruppe) herauskommt.
Wir haben damit also nun eine Darstellung des Bahn-Drehimpulsoperators \(\hat{\boldsymbol{L}}\) auf Funktionen.
Nun bilden Funktionen (mit gewissen Zusatzbedingungen) einen Hilbertraum.
Weiter oben haben wir gesehen, dass die allgemeine Darstellung eines
Drehimpulsoperators \(\hat{\boldsymbol{L}}\) auf einem
Hilbertraum durch Basisvektoren
\( | l \, m_l\rangle \)
festgelegt wird (die Bezeichnungen haben wir entsprechend angepasst, also \(l\) statt \(j\)
und \(m_l\) statt \(m\) geschrieben).
Dabei gilt:
\[
\hat{\boldsymbol{L}}^2 \, | l \, m_l \rangle =
l (l + 1) \, | l \, m_l \rangle
\]
\[
\hat{L}_3 \, | l \, m_l \rangle = m_l \, | l \, m_l \rangle
\]
\[
\hat{L}^+ \, | l \, m_l \rangle =
N \, | l m_l+1 \rangle
\]
\[
\hat{L}^- \, | l \, m_l \rangle =
N' \, | l m_l-1 \rangle
\]
mit \(l = 0, 1, 2, \, ... \)
und \(m_l = -l, -l+1, \, ... \, , l-1, l \)
und \(N = \sqrt{l(l+1) - m_l(m_l+1)} \)
und \(N' = \sqrt{l(l+1) - m_l(m_l-1)} \)
In der Basis der \( | l \, m_l \rangle \) kann man damit die Wirkung der \( \hat{L}_k \) durch Matrizen beschreiben: \[ \hat{L}_k \, | l \, m_l \rangle = \] \[ = \sum_{m_l'} \, | l m_l' \rangle \, \langle l m_l' | \hat{L}_k | l \, m_l \rangle = \] \[ = \sum_{m_l'} \, | l m_l' \rangle \, D^l_{m_l' \, m_l}(\hat{L}_k) \] Die Matrizen \( D^l(\hat{L}_k) \) mit den Matrixelementen \( D^l_{m_l' \, m_l}(\hat{L}_k) \) kann man mit Hilfe der obigen Formeln ausrechnen, was wir weiter oben in einigen Beispielen bereits getan haben. Über die Exponentialfunktion ergibt sich für Drehungen: \[ D^l(u) = e^{-i w_k D^l(\hat{L}_k )} \] mit \[ D^l_{m_l' \, m_l}(u) = \] \[ = \langle l \, m_l' | e^{-i \boldsymbol{w \hat{L}}} | l \, m_l \rangle = \] \[ = \langle l \, m_l' | \, T_u \, | l \, m_l \rangle \] mit \[ T_u \, | l \, m_l \rangle = \] \[ = \sum_{m_l'} \, | l \, m_l' \rangle \, \langle l \, m_l | \, T_u \, | l \, m_l \rangle = \] \[ = \sum_{m_l'} \, | l \, m_l' \rangle \, D^l_{m_l' \, m_l} (u) \] Wenn Funktionen nun einen Hilbertraum bilden, dann muss sich all dies eins-zu-eins auf diese Funktionen übertragen lassen. Es muss also Funktionen \( \psi_{l \, m_l}(\boldsymbol{x}) \) geben, so dass gilt:
|
Eigenfunktionen des Bahn-Drehimpulsoperators: \[ [\hat{\boldsymbol{L}}^2 \psi_{l \, m_l} ] (\boldsymbol{x}) = l (l + 1) \, \psi_{l \, m_l}(\boldsymbol{x}) \] \[ [\hat{L}_3 \psi_{l \, m_l} ] (\boldsymbol{x}) = m_l \, \psi_{l \, m_l}(\boldsymbol{x}) \] \[ [\hat{L}^+ \psi_{l \, m_l} ] (\boldsymbol{x}) = N \, \psi_{l \, m_l+1}(\boldsymbol{x}) \] \[ [\hat{L}^- \psi_{l \, m_l} ] (\boldsymbol{x}) = N' \, \psi_{l \, m_l-1}(\boldsymbol{x}) \] mit der Folge \[ [\hat{L}_k \psi_{l \, m_l} ] (\boldsymbol{x}) = \] \[ = \sum_{m_l'} \, \psi_{l \, m_l'}(\boldsymbol{x}) \, D^l_{m_l' \, m_l}(\hat{L}_k) \] und \[ [e^{-i \boldsymbol{w \hat{L}}} \psi_{l \, m_l} ](\boldsymbol{x}) = \] \[ = \sum_{m_l'} \, \psi_{l \, m_l'}(\boldsymbol{x}) \, D^l_{m_l' m_l}(u) = \] \[ = \psi_{l \, m_l}(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \] |
In der letzten Gleichung haben wir dabei am Schluss verwendet, dass für beliebigen Funktionen \(\psi\) die Gleichung \[ [e^{-i \boldsymbol{w \hat{L}}} \psi](\boldsymbol{x}) = \psi(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \] gilt, wie wir weiter oben gesehen haben.
Die Funktionen \( \psi_{l \, m_l}(\boldsymbol{x}) \) sind Eigenfunktionen von \(\hat{\boldsymbol{L}}^2\) und \(\hat{L}_3\) (siehe die ersten beiden Gleichungen). Die ersten 4 Gleichungen ergeben zusammen ein System von Differentialgleichungen, mit dessen Hilfe man die Funktionen \( \psi_{l \, m_l}(\boldsymbol{x}) \) explizit ausrechnen kann. Die entsprechende Rechung findet man in jedem Buch zur Quantenmechanik. Ich möchte diese Rechnungen hier nicht wiederholen, sondern nur einige allgemeine Bemerkungen machen:
Zunächst einmal zeigt die unterste Gleichung \[ [e^{-i \boldsymbol{w \hat{L}}} \psi_{l \, m_l} ](\boldsymbol{x}) = \] \[ = \psi_{l \, m_l}(R(\boldsymbol{w})^{-1} \boldsymbol{x}) \] dass der Betrag von \(\boldsymbol{x}\) keine Rolle spielt, denn \(R(\boldsymbol{w})^{-1}\) dreht den Vektor ja nur. Um das besser sichtbar zu machen, schreiben wir \[ \psi_{l \, m_l}(\boldsymbol{x}) = \psi_{l \, m_l}(r, \boldsymbol{\Omega}) \] mit \[ r = |\boldsymbol{x}| \] \[ \boldsymbol{\Omega} = \frac{\boldsymbol{x}}{r} \] In Kugelkoordinaten hängt \(\boldsymbol{\Omega}\) nur von den Winkeln \(\theta\) und \(\varphi\) ab, weshalb man auch \( \psi_{l \, m_l}(r, \theta, \varphi)\) schreiben kann. In der Schreibweise mit \(r\) und \(\boldsymbol{\Omega}\) haben wir dann \[ [e^{-i \boldsymbol{w \hat{L}}} \psi_{l \, m_l} ](r, \boldsymbol{\Omega}) = \] \[ = \psi_{l \, m_l}(r, R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}) \] und damit auch \[ [\hat{\boldsymbol{L}} \psi_{l \, m_l}](r, \boldsymbol{\Omega}) = \] \[ = i \frac{d}{d\boldsymbol{w}} \, \psi_{l \, m_l}(r, R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}) \, \bigg|_{\boldsymbol{w} = 0} \] d.h. der Drehimpulsoperator \(\hat{\boldsymbol{L}}\) erfasst nur Änderungen in \(\theta\) und \(\varphi\), nicht aber in \(r\). Daher kommt es, dass in Kugelkoordinaten \(\hat{\boldsymbol{L}}\) nur Ableitungen nach \(\theta\) und \(\varphi\) enthält, aber keine Ableitungen nach \(r\). Die obigen Gleichungen werden also die \(r\)-Abhängigkeit in den Funktionen \( \psi_{l \, m_l}(r, \boldsymbol{\Omega}) \) nicht festlegen.
Wie sieht es mit der Abhängigkeit von \(\theta\) und \(\varphi\) aus, also mit der Abhängigkeit von \(\boldsymbol{\Omega}\)? Als Ausgangspunkt wählen wir dazu ein festes \(\boldsymbol{\Omega}_0\) , beispielsweise die z-Richtung. Die Gleichungen \[ \sum_{m_l'} \, \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \, D^l_{m_l' m_l} (u) = \] \[ = \psi_{l \, m_l}(r, R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}_0) \] erlauben es nun, ausgehend von den Funktionswerten \( \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \) die Funktionswerte \( \psi_{l \, m_l}(r, R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}_0) \) für beliebige andere Richtungen \( \boldsymbol{\Omega} := R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}_0 \) zu bestimmen. Etwas umgestellt lauten die Gleichung dann \[ \psi_{l \, m_l}(r, \boldsymbol{\Omega}) = \] \[ = \sum_{m_l'} \, \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \, D^l_{m_l' m_l} (u) \] Die \(\boldsymbol{\Omega}\)-Abhängigkeit von \(\psi_{l \, m_l}(r, \boldsymbol{\Omega}) \) ist damit alleine durch die \(\boldsymbol{\Omega}\)-Abhängigkeit von \( D^l_{m_l' m_l} (u) \) festgelegt und hängt nicht von \(r\) ab. Dabei gehört \(u\) zur Drehung \(R\), die \( \boldsymbol{\Omega} = R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}_0 \) erfüllt. Für ganzzahlige \(l\) ist \(u\) durch \(R\) eindeutig festgelegt. Nur diese ganzzahligen \(l\) sind hier erlaubt – das hatten wir weiter oben bereits durch die Forderung \[ e^{-i \boldsymbol{w \hat{L}}} \, | \boldsymbol{p}, s \, m_s' \rangle = | R(\boldsymbol{w}) \, \boldsymbol{p}, s \, m_s' \rangle \] festgeschrieben.
Da \( r \) für die \(\boldsymbol{\Omega}\)-Abhängigkeit keine Rolle spielt, definiert man sogenannte Kugelflächenfunktionen \( Y_{l \, m_l} \), die nur von \(\boldsymbol{\Omega}\) abhängen:
|
Kugelflächenfunktionen:
(graphische Darstellungen siehe Wikipedia: Kugelflächenfunktionen) \[ Y_{l \, m_l}(\boldsymbol{\Omega}) = \psi_{l \, m_l}(1, \boldsymbol{\Omega}) \] |
(ggf. noch multipliziert mit einem Normierungsfaktor). Für sie gilt dann ebenfalls \[ Y_{l \, m_l}(\boldsymbol{\Omega}) = \] \[ = \sum_{m_l'} \, Y_{l \, m_l'}(\boldsymbol{\Omega}_0) \, D^l_{m_l' m_l} (u) \] Um den Zusammenhang zwischen \( Y_{l \, m_l} \) und \( \psi_{l \, m_l}\) zu ermitteln, definieren wir die Funktion \[ R_{l \, m_l}(r, \boldsymbol{\Omega}) := \frac{ \psi_{l \, m_l}(r, \boldsymbol{\Omega}) }{ Y_{l \, m_l}(\boldsymbol{\Omega})} \] oder umgestellt \[ \psi_{l \, m_l}(r, \boldsymbol{\Omega}) = R_{l \, m_l}(r, \boldsymbol{\Omega}) \, Y_{l \, m_l}(\boldsymbol{\Omega}) \] (die Funktionsbezeichnung \(R\) nicht mit der Drehmatrix verwechseln!). Sowohl für \( \psi_{l \, m_l}(r, \boldsymbol{\Omega}) \) als auch für \( Y_{l \, m_l}(\boldsymbol{\Omega}) \) ist die \(\boldsymbol{\Omega}\)-Abhängigkeit durch die Drehmatrizen gegeben. Das können wir nun in die obige Gleichung einsetzen: \[ \sum_{m_l'} \, \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \, D^l_{m_l' m_l}(u) = \] \[ = R_{l \, m_l}(r, \boldsymbol{\Omega}) \, \sum_{m_l'} \, Y_{l \, m_l'} (\boldsymbol{\Omega}_0) \, D^l_{m_l' m_l} (u) \] Diese Matrixgleichung können wir von rechts mit der inversen Matrix \(D^l(u^{-1})\) multiplizieren mit dem Ergebnis: \[ \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) = R_{l \, m_l}(r, \boldsymbol{\Omega}) \, Y_{l \, m_l'} (\boldsymbol{\Omega}_0) \] Zugleich haben wir aus der Definition von \( R_{l \, m_l}(r, \boldsymbol{\Omega}) \) die Gleichung (mit \(m_l'\) statt \(m_l\) und \(\boldsymbol{\Omega}_0\) statt \(\boldsymbol{\Omega})\): \[ \psi_{l \, m_l'} (r, \boldsymbol{\Omega}_0) = R_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \, Y_{l \, m_l'} (\boldsymbol{\Omega}_0) \] Vergleichen wir diese beiden Gleichungen, so folgt: \[ R_{l \, m_l}(r, \boldsymbol{\Omega}) = R_{l \, m_l'} (r, \boldsymbol{\Omega}_0) \] Diese Gleichung gilt für beliebige Werte von \(\boldsymbol{\Omega}\) und \(\boldsymbol{\Omega}_0\), also auch für \(\boldsymbol{\Omega} = \boldsymbol{\Omega}_0\). Dann ist \[ R_{l \, m_l}(r, \boldsymbol{\Omega}) = R_{l \, m_l'} (r, \boldsymbol{\Omega}) \] d.h. die Funktion hängt gar nicht von \(m_l\) oder \(m_l'\) ab. Wir lassen daher den Index \(m_l\) ab sofort weg und schreiben: \[ R_l (r, \boldsymbol{\Omega}) = R_l (r, \boldsymbol{\Omega}_0) \] Da diese Gleichung für beliebige Werte von \(\boldsymbol{\Omega}\) und \(\boldsymbol{\Omega}_0\) gilt, kann die Funktion nicht von \(\boldsymbol{\Omega}\) oder \(\boldsymbol{\Omega}_0\) abhängen. Wir haben also: \[ R_{l \, m_l} (r, \boldsymbol{\Omega}) = R_l (r) \] Halten wir das Ergebnis noch einmal fest:
|
Eigenfunktionen des Drehimpulses und Kugelflächenfunktionen \(Y_{l \, m_l}\): \[ \psi_{l \, m_l}(r, \boldsymbol{\Omega}) = R_l(r) Y_{l \, m_l}(\boldsymbol{\Omega}) \] |
Eine zentrale Eigenschaft der Kugelflächenfunktionen ist, dass sie eine vollständige Basis für (zivilisierte) Funktionen von \(\boldsymbol{\Omega}\) darstellen (auf den Beweis verzichten wir hier). Jede Funktion von \(\boldsymbol{\Omega}\) lässt sich also als unendliche Linearkombination von Kugelflächenfunktionen schreiben (mit einem bestimmten Konvergenzbegriff). Allgemein lässt sich sogar jede gutartige Funktion \(\psi(\boldsymbol{x})\) schreiben als
|
Entwicklung nach Kugelflächenfunktionen: \[ \psi(\boldsymbol{x}) = \psi(r, \boldsymbol{\Omega}) = \] \[ = \sum_{l \, m_l} \, R_{l \, m_l}(r) Y_{l \, m_l}(\boldsymbol{\Omega}) \] |
mit geeigneten Radial-Funktionen \( R_{l \, m_l}(r) \), die natürlich von \( \psi(\boldsymbol{x}) \) abhängen. Wichtig: Die Radial-Funktionen hängen hier auch von \(m_l\) ab!
Ein Beispiel: Für die ebene Welle \( \psi(\boldsymbol{x}) = e^{i \boldsymbol{kx}} \) ist \[ R_{l \, m_l}(r) = \frac{4\pi}{kr} \, j_l(kr) \, i^l \, Y_{l \, m_l} (\boldsymbol{\Omega}_k) \] mit \( k = |\boldsymbol{k}| \) und \(\boldsymbol{\Omega}_k = \frac{\boldsymbol{k}}{k} \) und den Riccati-Bessel-Funktionen \( j_l \). Durch geeignete Integrale über \(\boldsymbol{k}\) kann man daraus auch quadratintegrable Funktionen bauen.
Auch Funktionen von \(\boldsymbol{p}\) lassen sich analog nach Kugelflächenfunktionen entwickeln. Auf diese Weise können wir \( |\psi_s \rangle \) so umschreiben, dass die Tensorprodukt-Struktur von Bahndrehimpuls und Spin besonders gut sichtbar wird: \[ |\psi_s \rangle = \] \[ = \sum_{m_s} \, \int d^3p \, f_{s m_s}(\boldsymbol{p}) \, | \boldsymbol{p}, s \, m_s \rangle = \] \[ = \sum_{m_s} \, \sum_{l \, m_l} \, \int p^2 \, dp \, d\Omega_p \] \[ \quad \quad R_{s m_s \, l m_l}(p) \, Y_{l \, m_l}(\boldsymbol{\Omega}_p) \, | \boldsymbol{p}, s \, m_s \rangle =: \] \[ =: \sum_{m_s} \, \sum_{l \, m_l} \, \int p^2 dp \, R_{s m_s \, l m_l}(p) \] \[ \quad \quad \, | p , l m_l , s m_s \rangle \] mit \( p = |\boldsymbol{p}|\), \(\boldsymbol{\Omega}_p = \frac{\boldsymbol{p}}{p}\), \( d^3p = p^2 \, dp \, d\Omega_p \) \( = p^2 \, dp \, \sin{\theta} \, d\theta \, d\varphi \) und
\[ | p , l m_l , s m_s \rangle := \int d\Omega_p \, Y_{l \, m_l}(\boldsymbol{\Omega}_p) \, | \boldsymbol{p}, s \, m_s \rangle \] Diese Schreibweise ist dadurch motiviert, dass für eine Drehung gilt: \[ T_u \, | p , l m_l , s m_s \rangle = \] \[ = \int d\Omega_p \, Y_{l \, m_l}(\boldsymbol{\Omega}_p) \, T_u \, | \boldsymbol{p}, s \, m_s \rangle = \] \[ = \int d\Omega_p \, Y_{l \, m_l}(\boldsymbol{\Omega}_p) \] \[ \quad \quad \sum_{m_s'} \, | R(\boldsymbol{w}) \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s} (u) = \] \[ = \int d\Omega_p \, Y_{l \, m_l} (R(\boldsymbol{w})^{-1} \boldsymbol{\Omega}_p) \] \[ \quad \quad \sum_{m_s'} \, | \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s} (u) = \] \[ = \sum_{m_l' m_s'} \, \int d\Omega_p \, Y_{l \, m_l'} (\boldsymbol{\Omega}_p) \, | \boldsymbol{p} , s m_s' \rangle \] \[ \quad \quad D^l_{m_l' m_l} (u) \, D^s_{m_s' m_s} (u) = \] \[ = \sum_{m_l' m_s'} \, | p , l m_l' , s m_s' \rangle \] \[ \quad \quad D^l_{m_l' m_l} (u) \, D^s_{m_s' m_s} (u) \] Zusammengefasst:
|
Tensorproduktdarstellung von Bahndrehimpuls und Spin: \[ |\psi_s \rangle = \sum_{m_s} \, \sum_{l \, m_l} \, \int p^2 \, dp \] \[ \quad \quad R_{s m_s l m_l}(p) \, | p , l m_l , s m_s \rangle \] mit \[ | p , l m_l , s m_s \rangle := \] \[ = \int d\Omega_p \, Y_{l \, m_l}(\boldsymbol{\Omega}_p) \, | \boldsymbol{p}, s \, m_s \rangle \] und der Dreheigenschaft \[ T_u \, | p , l m_l , s m_s \rangle = \] \[ = \sum_{m_l' m_s'} \, | p , l m_l' , s m_s' \rangle \] \[ \quad \quad D^l_{m_l' m_l} (u) D^s_{m_s' m_s} (u) \] |
Soviel zur Drehgruppe und ihrer Strahldarstellung in der Quantentheorie. Wenden wir uns im nächsten Kapitel einem weiteren interessanten Thema zu: den nichtrelativistischen Boosts.
© Jörg Resag, www.joerg-resag.de
last modified on 30 July 2023