
Das Supersymmetrie ist nicht ganz einfach zu verstehen. Wir wollen daher hier nicht in aller Tiefe in das Thema einsteigen, sondern versuchen, einen Weg zum Verständnis der Supersymmetrie zu finden, der auch von Nicht-Experten auf diesem Gebiet ebenfalls nachvollzogen werden kann.
Die Supersymmetrie gehört (anders als Relativitätstheorie, Quantentheorie oder Standardmodell) keineswegs bereits zu den experimentell abgesicherten physikalischen Theorien, sondern sie gehört zu den aktuellen Forschungsgebieten ganz vorne an der Front der Forschung. Es deutet aber sehr viel darauf hin, dass die Supersymmetrie in modernen physikalischen Theorien jenseits des Standardmodells eine wichtige Rolle spielen kann.
Natürlich braucht man ein solides physikalisches Vorwissen, wenn man sich einem so modernen Thema zuwenden möchte. Ich werde versuchen, die notwendigen Grundlagen hier und da kurz zu erläutern oder zumindest anzugeben, wo man die Details findet. Mehr würde den Rahmen des Kapitels sprengen.
Über Supersymmetrie wurden ganze Bücher und Skripte geschrieben und es wäre sinnlos, das hier alles zu wiederholen. In diesem Kapitel wollen wir also sehen, um was es geht und nicht, wie es im Detail geht. Für die Details werde ich dann auf entsprechende andere Texte verweisen.
Zunächst einmal müssen wir uns an die Grundlagen der Quantentheorie erinnern (Kapitel 4), insbesondere an Kapitel 4.4: Identische Teilchen. Dort hatten wir gesehen, dass in der Quantentheorie zwei identische Teilchen, die an einem Ereignis beteiligt sind, prinzipiell ununterscheidbar sind. Die entsprechenden Wahrscheinlichkeiten sind deshalb unverändert, wenn wir die Rollen der beiden Teilchen vertauschen. Zu den Wahrscheinlichkeiten gehören komplexe Wahrscheinlichkeitsamplituden, deren Betragsquadrat die Wahrscheinlichkeit ergibt, dass das Ereignis eintritt.
Es gibt nun zwei Möglichkeiten: die Wahrscheinlichkeitsamplitude ist entweder symmetrisch oder antisymmetrisch beim Vertauschen der beiden identischen Teilchen. Den symmetrischen Fall haben wir bei Teilchen mit ganzzahligem Spin (z.B. Null; Bosonen), den antisymmetrischen Fall haben wir bei Teilchen mit halbzahligem Spin (z.B. 1/2, Fermionen). Man bezeichnet dieses Ergebnis als Spin-Statistik-Theorem oder für den Fermionen-Fall auch als Pauli-Prinzip.
Wir haben hier den Fall vor uns, dass eine einfache Regel keine einfache Begründung hat. Die Begründung wurde zuerst von Wolfgang Pauli ausgearbeitet und greift auf nicht-elementare Methoden der relativistischen Quantenfeldtheorie zurück. Mehr dazu siehe Kapitel 4.4: Identische Teilchen.
In Kapitel 4.5 haben wir dann gesehen, wie quantenmechanische Zustände durch Vektoren in einem unendlichdimensionalen Hilbertraum dargestellt werden können. Die Wahrscheinlichkeitsamplituden sind dann Skalarprodukte zwischen dem Zustand, der vorliegt (der also präpariert wurde), und dem Zustand, der die gemessenen physikalischen Größen darstellt. Die Symmetrie der Wahrscheinlichkeitsamplituden überträgt sich dann auf die Symmetrie der Hilbertraumvektoren, die die quantenmechanischen Zustände darstellen. Man braucht für die Beschreibung identischer Bosonen symmetrische Hilbertraumvektoren, für die Beschreibung identischer Fermionen antisymmetrische Hilbertraumvektoren.
Nehmen wir als Beispiel zwei identische Teilchen, bei denen eines davon den Messwertsatz \(a\) und das andere den Messwertsatz \(b\) tragen soll (z.B. hat ein Teilchen den Impuls \(\boldsymbol{p}\), das andere den Impuls \( - \boldsymbol{p}\)). Die beiden Teilchen werden zusammen durch einen gemeinsamen Hilbertraumvektor dargestellt, den wir mit \[ |a,b \rangle \] bezeichnen wollen. Dann gilt:
Bosonen: \[ |a,b \rangle = |b,a \rangle \] Fermionen: \[ |a,b \rangle = - |b,a \rangle \] Bei freien Teilchen kann man diese Zweiteilchenzustände als Tensorprodukt von Einteilchenzuständen schreiben. Dieses Produkt muss man dann für Bosonen symmetrisieren, für Fermionen antisymmetrisieren. Bei Fermionen schreibt man für dieses Produkt auch \[ |a,b \rangle = |a \rangle \wedge |b \rangle \] mit \[ |a \rangle \wedge |b \rangle = - |b \rangle \wedge |a \rangle \] In der nichtrelativistischen Quantenmechanik stellt man Zustände oft durch Wellenfunktionen dar. In diesem Fall ist das Tensorprodukt einfach das Produkt der beiden Funktionen, und die antisymmetrische Wellenfunktion zweier Fermionen wäre gegeben durch \[ (\psi \wedge \varphi)(x,y) = \psi(x) \, \varphi(y) - \varphi(x) \, \psi(y) \] (evtl. mal einem Normierungsfaktor). Weitere Details dazu siehe Quantenfeldtheorie und Eichfelder, Kapitel 2.
Bei Bosonen müsste man rechts statt dem Minuszeichen ein Pluszeichen schreiben.
Die Supersymmetrie schafft nun eine Verbindung zwischen Fermionen und Bosonen, d.h. sie setzt symmetrische und antisymmetrische Vektoren zueinander in Beziehung.
Symmetrien werden in der Physik sehr oft durch Lie-Gruppen dargestellt. Beispiele dafür sind die Drehgruppe, die Galileigruppe oder die Poincarégruppe. Diese Gruppen sind zugleich Mannigfaltigkeiten (mit den Gruppenparametern als Koordinaten, beispielsweise den Drehwinkeln), und sie hängen über die Exponentialdarstellung der Gruppenelemente zugleich mit Algebren zusammen (den Lie-Algebren der Generatoren, siehe Kapitel 3.3 und 3.4). Wenn wir also Symmetrien zu Supersymmetrien erweitern, so werden zugleich die Superstrukturen von Gruppen, Mannigfaltigkeiten und Algebren eine Rolle spielen.
Damit es nicht zu theoretisch wird, wollen wir uns gleich den Fall ansehen, der für die Physik am wichtigsten ist: die Poincarégruppe. Diese Gruppe beschreibt die Transformationen in Raum und Zeit im Rahmen der speziellen Relativitätstheorie, also Translationen, Boosts und Drehungen. Wenn wir einen experimentellen Aufbau räumlich verschieben oder um einen festen Winkel drehen oder den Aufbau in ein schwerelos dahingleitendes Raumschiff setzen oder das Experiment zu einer anderen Zeit ausführen – die physikalischen Grundgesetze dürfen davon nicht beeinträchtigt werden.
Mit anderen Worten: Man betrachtet einen physikalischen Prozess und stellt sich anschließend vor, dass derselbe Prozess beispielsweise in einem dahingleitenden Raumschiff stattfindet (alternativ kann man auch den ursprünglichen Prozess aus einem dahingleitenden Raumschiff betrachten). Man führt also mathematisch eine Poincarétransformation (hier einen Boost) der physikalischen Größen durch. Dann muss auch dieser Prozess mit den transformierten Größen physikalisch möglich sein. In Kapitel 3 sind wir ausführlich darauf eingegangen.
Wie muss man nun physikalische Größen wie beispielsweise Teilchenimpulse bei einer Poincarétransformation umrechnen, also transformieren?
Das hängt von der physikalischen Größe ab: gerade das Transformationsverhalten prägt entscheidend den Charakter der physikalischen Größe. In jedem Fall muss sich aber die Gruppenstruktur der Poincarétransformationen auf die Umrechnungsvorschrift übertragen. Führt man zwei Poincarétransformationen nacheinander durch, so kann man diese immer durch eine einzige Poincarétransformationen ersetzen. Entsprechend muss man auch die zweifache Transformation der physikalischen Größen durch diejenige Transformation ersetzen können, die zur Ersatz-Poincarétransformation gehört. Man spricht von einer Darstellung der Poincarégruppe. Mehr dazu siehe Quantenfeldtheorie und Eichfelder, Kapitel 2.
In der Quantentheorie braucht man ebenfalls eine Art Darstellung der Poincarégruppe auf den quantenmechanischen Zustandsvektoren, d.h. eine Umrechnungsvorschrift für die Zustandsvektoren bei Boosts, Drehungen oder Translationen.
Da beim Bilden von Wahrscheinlichkeiten das Betragsquadrat der Wahrscheinlichkeitsamplitude gebildet wird, überträgt sich die Gruppenstruktur nicht eins-zu eins, sondern es dürfen bei der Umrechnung der Zustandsvektoren zusätzlich komplexe Zahlen mit Betrag Eins auftreten (sogenannte Phasen). So darf z.B. eine 360-Grad-Drehung zu einem Vorzeichenwechsel des Zustandsvektors führen.
Man nennt so etwas eine Strahldarstellung der Poincarégruppe. Man hat heute einen vollständigen Überblick über die möglichen Strahldarstellungen der Poincarégruppe. Das Hauptergebnis ist:
Man muss also beispielsweise nicht die elektrische Ladung eines Teilchens kennen, um zu wissen, wie man den Zustandsvektor bei einer Poincarétransformation umrechnen muss (denn die Ladung ist immer gleich groß, egal ob sich das Objekt bewegt oder nicht).
Neben den Raum-Zeit-Symmetrien, wie sie durch die Poincarégruppe ausgedrückt werden, gibt es auch innere Symmetrien, beispielsweise Eichsymmetrien. So tragen beispielsweise die Zustandsvektoren von Quarks neben Masse, Impuls und Spin noch eine starke Farbladung. Die Farbladungen kann man nun teilweise verändern, ohne dass sich am Gesamtzustand etwas ändert. Man kann beispielsweise in einem Proton die Farbladungen der drei Quarks untereinander vertauschen.
Es gibt nun das sogenannte Coleman-Mandula-Theorem aus dem Jahr 1967. Es besagt im Wesentlichen, dass innere Symmetrien und Raum-Zeit-Symmetrien, wie sie die Poincarégruppe ausdrückt, nicht gemischt als Symmetrien der Quantentheorie vorkommen können. Es macht also keinen Sinn, eine Eichtransformation der starken Farbladungen mit einer räumlichen Drehung so zu vermischen, dass die Eichtransformation vom Drehwinkel abhängt. Ein Boost oder eine Drehung ist nicht mit einer inneren Symmetrietransformation untrennbar verknüpft, sondern Poincarétransformationen und innere Symmetrietransformationen müssen unabhängig voneinander ausführbar sein, wenn sie Symmetrien der Quantentheorie sein sollen.
Eine wichtige Voraussetzung des Coleman-Mandula-Theorems ist dabei, dass die Raum-Zeit-Symmetrien und die inneren Symmetrien beide durch Lie-Gruppen dargestellt werden, bei denen die Generatoren Elemente einer Lie-Algebra sind. Das ist sowohl bei der Poincarégruppe als auch bei den Eichsymmetrien der Fall. Schauen wir uns das für die Poincarégruppe genauer an:
Bei einer Poincarétransformation wird aus einem Zeit-Orts-Vektor \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} \] (mit der Lichtgeschwindigkeit \(c\)) der neue Zeit-Orts-Vektor \[ x' = \Lambda \, x + d \] Die Lorentzmatrix \( \Lambda \) lässt sich dabei schreiben als (siehe Kapitel 3.2) \[ \Lambda = e^X \] mit \[ X = \begin{pmatrix} 0 & \boldsymbol{a} \\ \boldsymbol{a} & G \end{pmatrix} \] und der schiefsymmetrischen Matrix \[ G^T = -G \] (Raum- und Zeitspiegelungen lassen wir dabei erst einmal weg).
Das ist genau die Exponentialdarstellung, die das Gruppenelement \( \Lambda \) mit den Generatoren im Exponenten verknüpft.
In den Kapiteln 3.3 und 3.4 hatten wir gesehen, wie der Vektor \( \boldsymbol{a} \) zu Boosts führt, während die schiefsymmetrische Matrix \(G\) Drehungen bewirkt.
Der Vektor \[ \boldsymbol{a} = \alpha \, \boldsymbol{e}_1 \] ergibt mit \(G = 0\) beispielsweise einen Boost in 1-Richtung (x-Richtung). Man sagt, er ist der Generator dieses Boosts. Analog kann man bei \( \boldsymbol{a} = 0 \) die Matrix \(G\) so wählen, dass z.B. eine Drehung um die z-Achse entsteht. Dann ist dieses \(G\) der Generator dieser Drehung.
Insgesamt gibt es 3 Boostgeneratoren und drei Drehgeneratoren, aus denen man jede Matrix \(X\) im Exponenten von \(\Lambda\) zusammensetzen kann, indem man die Generatoren mit reellen Parametern (Drehwinkeln und Boostparameter) multipliziert und dann addiert. Bezeichnen wir alle 6 Generatormatrizen mit \( A_{i} \) (\(i = 1, 2, \, ... \, , 6\)) und die reellen Parameter mit \( \lambda_{i} \), so ist \[ X = \sum_{i=1}^{6} \, \lambda_{i} \, A_{i} \] und somit \[ \Lambda = e^{\sum_{i=1}^{6} \, \lambda_{i} \, A_{i} } \] Hinzu kommen noch 4 Generatoren für Raum- und Zeittranslationen (Verschiebungen), die wir mit \(P^{\mu}\) bezeichnen (\(\mu\) von 0 bis 3), da sie etwas mit dem Viererimpuls zu tun haben.
Die 6 Generatormatrizen \(A_{i}\) und die vier \(P^{\mu}\) vertauschen nun im Allgemeinen nicht. Das Matrixprodukt \( A_{i} \, A_{j} \) ist nicht unbedingt dasselbe wie \( A_{j} \, A_{i} \). Es ist sogar so, dass diese Nicht-Vertauschbarkeit entscheidend für die Gruppenstruktur der Poincarégruppe ist. Die Kommutatoren \[ [A_{i}, A_{j}] := A_{i} \, A_{j} - A_{j} \, A_{i} \] sowie die weiteren Kommutatoren mit \( P^{\mu} \) legen sogar die lokale Gruppenstruktur der Poincarégruppe in der Nähe der Einheitsmatrix fest.
Grund dafür ist die Baker-Campbell-Hausdorff formula: \[ e^{\lambda_{i} \, A_{i}} \, e^{\lambda_{j} \, A_{j}} = \] \[ = e^{\lambda_{i} \, A_{i} + \lambda_{j} \, A_{j} + \frac{1}{2} \, \lambda_{i} \, \lambda_{j} \, [A_{i}, A_{i}] + \, ... } \] für festes \(i\) und \(j\) (also keine Summen), wobei die Punkte höhere Kommutatorterme mit höheren Potenzen in den Parametern \(\lambda_{i}\) und \(\lambda_{j}\) andeuten.
Bei kleinen Parametern (also z.B. kleinen Drehwinkeln oder kleinen Boostparametern) spielen diese höheren Terme keine Rolle und nur der Kommutator \( [A_{i}, A_{i}] \) bleibt wichtig. Damit legt der Kommutator der Generatoren bei kleinen Gruppenparametern fest, wie aus der Multiplikation zweier Gruppenelemente (Lorentzmatrizen) ein neues Gruppenelement (eine neue Lorentzmatrix) entsteht. Genau das ist die Verknüpfung zwischen Lie-Algebra (das ist der Vektorraum der Generatormatrizen zusammen mit dem Kommutator als multiplikative Struktur) und Lie-Gruppe (die Lorentztransformationen).
Die Lie-Algebra (also die Kommutatoren der Generatoren) legen allerdings nicht die gesamte Struktur der Lie-Gruppe fest. Es gibt verschiedene Lie-Gruppen, die dieselbe Lie-Algebra haben (d.h. die Kommutatoren zweier Generatoren ergeben dieselben Generator-Linearkombinationen).
Man kann aber zeigen, dass in der Quantentheorie diese Gruppen gleichwertig sind, denn es wird nur eine Strahldarstellung gesucht. Insofern spielt in der Quantentheorie weniger die Gruppe eine Rolle, sondern das, was die Lie-Algebra über die Gruppe aussagt.
Genau so geht man beispielsweise vor, wenn man sich in der Quantenmechanik mit Drehungen befasst: Man schaut sich die Generatoren der Drehgruppe an, deren Darstellung im Hilbertraum die Drehimpulsoperatoren sind. Diese Operatoren sind dann aber nicht mehr Generatoren der Drehgruppe, sondern Generatoren der Gruppe \(SU(2)\). So kommt es, dass eine Drehung um 360 Grad auch einen Faktor \( (-1) \) bei einem Zustandsvektor bewirken kann.
Halten wir also fest:
In der Quantentheorie ist die Lie-Algebra entscheidend.
Man muss also die Generatoren und ihre Kommutatoren kennen.
Zurück zum Coleman-Mandula-Theorem:
Übersetzt in die Sprache der Lie-Algebren besagt es,
dass die Generatoren der Raum-Zeit-Symmetrie (Poincarégruppe) und der inneren Symmetrien
immer brav getrennt bleiben. Nie ergibt der Kommutator zweier Poincaré-Generatoren
einen Generator einer inneren Symmetrie.
Nach der Baker-Campbell-Hausdorff Formel von oben zerfällt daher jede Symmetrietransformation
in ein Produkt aus innerer und Raum-Zeit-Transformation. Ein räumlicher Drehwinkel
bestimmt nie die Stärke einer inneren Symmetrietransformation.
Das ändert sich jedoch, wenn man die Voraussetzung fallen lässt, dass die Symmetriegruppen Liegruppen sein müssen. Statt nur antisymmetrische Kommutatoren zuzulassen, kann man auch symmetrische Antikommutatoren zulassen.
Eigentlich ist das naheliegend, denn wenn man Quantenfeldtheorie betreibt, so braucht man dort neben den Kommutatoren für Quantenfelder bosonischer Teilchen auch Antikommutatoren für Quantenfelder fermionischer Teilchen. Warum sollte man also darauf verzichten, sie auch bei Symmetrie-Generatoren in Betracht zu ziehen?
Im Jahr 1975 bewiesen Haag, Lopuszanski und Sohnius, dass die Verwendung von Symmetrie-Antikommutatoren dazu führt, dass die Poincarégruppe zu einer supersymmetrischen Super-Poincarégruppe erweitert werden kann und dass diese erweiterte Gruppe eine mögliche Symmetrie der Quantentheorie ist.
Man kann diese Super-Poincarégruppe als eine Erweiterung der Raum-Zeit-Symmetrie ansehen. Sie operiert in einem größeren Raum als die Poincarégruppe, geht also über die Veränderung von Raum und Zeit hinaus. Man kann sich den Raum, in dem die Super-Poincarégrupe operiert, so vorstellen, dass zur Raumzeit weitere neuartige Dimensionen hinzukommen. Diese zusätzlichen Dimensionen haben aber eine besondere mathematische Struktur, d.h. sie werden nicht durch reelle Parameter dargestellt, sondern durch sogenannte antikommutierende Grassmann-Variablen. Man spricht auch von Grassmann-Dimensionen. Mehr dazu unten im Anhang.
Die Analyse von Haag, Lopuszanski und Sohnius zeigt, dass die neue Super-Lie-Algebra der Super-Poincarégruppe folgendermaßen aussehen muss (die \(P^{\mu}\) schreiben wir hier einfach auch als zusätzliche \(A_{i}\)):
Man spricht auch von einer graduierten Algebra (siehe auch John Baez: Week 212 ).
Für eine genaue Herleitung der Kommutatoren und Antikommutatoren ist nun eine umfangreiche und präzise Analyse der Poincarégruppe und ihrer Strahldarstellungen erforderlich, insbesondere der Spinordarstellungen. Man kann aber auch stattdessen erst einmal ein einfaches Modell betrachten.
Eine gute Darstellung findet man z.B. in Stephen P. Martin: A Supersymmetry Primer, http://arxiv.org/pdf/hep-ph/9709356|. Dort wird in Kapitel 3 die einfachste mögliche supersymmetrische Quantenfeldtheorie betrachtet: das masselose wechselwirkungsfreie Wess-Zumino-Modell. Mit Hilfe dieses Modells kann man die Kommutatoren und Antikommutatoren explizit ableiten. Wenn Sie Supersymmetrie etwas detaillierter verstehen möchten, können Sie sich dieses Modell genauer anschauen – wir wollen das hier nur ansatzweise tun (die Details stehen beispielsweise im obigen Supersymmetry Primer).
Im Wesentlichen kommt dabei heraus, dass die \(Q\)-Generatoren etwas mit Fermionen und ihrem Transformationsverhalten bei Drehungen zu tun haben. In einer Quantentheorie werden die Generatoren durch entsprechende Operatoren im Hilbertraum dargestellt. Zu den \(Q\)-Operatoren gibt es dann die adjungierten Operatoren \(Q^{+}\). Schematisch (ohne Spinorindices etc.) sehen die wichtigsten Regeln für die \(Q\)-Operatoren dann so aus:
\(Q\) macht aus einem quantenmechanischen Bosonzustand einen Fermionzustand und umgekehrt. Schematisch heißt das: \[ Q \, | \mathrm{Boson} \rangle = | \mathrm{Fermion} \rangle \] \[ Q \, | \mathrm{Fermion} \rangle = | \mathrm{Boson} \rangle \] Da Bosonen meist Spin Null haben, verhalten sie sich bei Drehungen sehr einfach. Fermionen verhalten sich wegen ihres hablzahligen Spins bei Drehungen komplizierter. Genau das ist ja der Unterschied zwischen Fermionen und Bosonen.
Damit beide Seiten in der ersten Gleichung gleich sein können, muss dieses Verhalten bei Drehungen durch den \(Q\)-Operator reproduziert werden, d.h. \(Q\) verhält sich bei Drehungen wie ein Fermion.
Dadurch wird deutlich, dass \(Q\) hier nicht eine innere Symmetrie erzeugt, die abgekoppelt von den Raum-Zeit-Symmetrien ist. Eine Symmetrie zwischen Fermionen und Bosonen muss mit den Raum-Zeit-Symmetrien verkoppelt sein, denn Fermionen und Bosonen verhalten sich bei Poincarétransformationen (speziell Drehungen) unterschiedlich.
Es ist \[ \{ Q, Q \} = \{ Q^{+}, Q^{+} \} = 0 \] (Genau genommen muss man hier zwei verschiedene Spinorindices dranschreiben, d.h. es handelt sich um den Antikommutator zweier verschiedener Komponenten).
Weiter ist \[ [P^{\mu}, Q] = [P^{\mu}, Q^{+}] = 0 \] Die Gleichung besagt, dass wenn man aus einem Bosonzustand mit gegebenem Viererimpuls \(p = (p^{\mu})\) (klein geschrieben im Gegensatz zum groß geschriebenen Impulsoperator) per \(Q\)-Anwendung ein Fermion macht oder umgekehrt, dass dieser neue Zustand dann denselben Viererimpuls \(p\) hat: \[ [P^{\mu}, Q] \, | \mathrm{Boson}, p \rangle = \] \[ = P^{\mu} \, Q \, | \mathrm{Boson}, p \rangle - Q \, P^{\mu} \, | \mathrm{Boson}, p \rangle = \] \[ = P^{\mu} \, | \mathrm{Fermion}, p' \rangle - p^{\mu} \, Q \, | \mathrm{Boson}, p\rangle = \] \[ = p'^{\mu} \, | \mathrm{Fermion}, p' \rangle - p^{\mu} \, | \mathrm{Fermion}, p' \rangle = \] \[ =0 \] \[ \Rightarrow \; p = p' \] Da \(p^{2} = m^{2}\) ist (Faktoren wie \(c\) lassen wir weg), haben also Boson und Fermion dieselbe Masse, wenn sie durch \(Q\) ineinander überführt werden können! Sie sind massegleiche Superpartner.
Und schließlich haben wir noch \[ \{ Q, Q^{+} \} \sim P^{\mu} \] (auch hier fehlen Spinorindizes bei \(Q\) sowie ein Objekt, das die Spinorindizes mit dem Lorentzindex \(\mu\) verbindet (das leisten die Paulimatrizen) – wir haben es zur Vereinfachung weggelassen).
Diese Gleichung berücksichtigt, dass sich \(Q\) und \(Q^{+}\) bei Drehungen wie Fermionen verhalten, die man zu einem Spin-1-Objekt verkoppeln kann. Ein Spin-1-Objekt hat aber etwas mit einem Vektor zu tun, und so einer steht rechts. Umgekehrt folgt aus der Gleichung auch, dass sich \(Q\) und \(Q^{+}\) wie Fermionen bei Drehungen verhalten müssen. Und daraus folgt, dass sich der Ausdruck \( Q \, | \mathrm{Boson} \rangle \) wie ein Fermion bei Drehungen verhält – genau das rechtfertigt die Gleichung \[ Q \, | \mathrm{Boson} \rangle = | \mathrm{Fermion} \rangle \] Die Gleichung \( \{ Q, Q^{+} \} \sim P^{\mu} \) besagt auch, dass Supersymmetrieoperationen (genauer: Supertranslationen) zu einer Translation in der Raumzeit führen. Siehe auch den Anhang ganz unten.
Um das alles im Detail zu verstehen, muss man sich den Zusammenhang zwischen der Poincarégruppe (so transformiert sich die rechte Seite von \( \{ Q, Q^{+} \} \sim P^{\mu} \) ) und der Überlagerungsgruppe der Poincarégruppe (die Gruppe \( SL(2,\mathbb{C}) \), so transformieren sich Spinoren bzw. Fermionen) ansehen. Mehr dazu im Anhang unten.
Anmerkung:
In der Natur haben Superpartner offenbar NICHT dieselbe Masse – sie müssen deutlich schwerer sein
als die bekannten Teilchen, denn sonst hätte man sie bereits gefunden.
Man nimmt daher an, dass die Supersymmetrie spontan gebrochen ist, d.h. dass der Vakuumzustand
nicht supersymmetrisch ist. Eine detaillierte Erklärung würde hier den Rahmen sprengen.
So weit, so gut! Um tiefer einzutauchen wäre es nun an der Zeit, das Wess-Zumino-Modell noch genauer nachzuvollziehen. Das würde hier zu weit führen, daher hier nur die wichtigsten Zutaten und Ergebnisse dieses Modells:
Man startet in dem Modell mit einem komplexen skalaren masselosen Feld \(\phi\) (einem masselosen Boson) und einem masselosen Weyl-Spinorfeld \(\psi\) (einem masselosen linkshändigen Fermion, mehr dazu im Anhang unten).
Die Lagrangedichte dieser Felder enthält dann keine Massenterme, sondern nur die kinetischen Terme der beiden Felder, so dass sich als Lösungen der klassischen Feldgleichungen ebene Wellen der beiden Felder ergeben, die sich mit Lichtgeschwindigkeit fortbewegen. In einer Quantentheorie entsprechen diese Wellen masselosen Teilchen (Bosonen und linkshändigen Fermionen) mit festem Impuls. Eine Wechselwirkung zwischen Teilchen gibt es nicht. Einfacher kann man es nicht angehen!
Wenn Sie Eichtheorien kennen, dann wissen Sie vielleicht, wie es dort beim Einbau der Symmetrie in die Lagrangedichte weitergeht: Man definiert eine Symmerietransformation der Felder und fordert, dass sich das Wirkungsintegral der Lagrangedichte (kurz: die Wirkung) durch diese sogenannten Eichtransformation der Felder nicht ändert (denn dann ist es wirklich eine Symmetrietransformation, die die physikalischen Grundgesetze nicht ändert). Die Transformation darf dabei sogar lokal sein, also vom Raumzeitpunkt \(x\) abhängen.
Das erzwingt die Einführung von Eichpotentiale \( A^{\mu} \) in den Raumzeit-Ableitungstermen der Lagrangedichte, die der Einführung von Wechselwirkungsteilchen wie Photonen oder Gluonen entsprechen. Mehr zu Eichtheorien siehe Quantenfeldtheorie und Eichfelder, Kapitel 6 .
Analog wollen wir hier eine Supersymmetrie einführen, die Bosonen und Fermionen miteinander verbindet. Das machen wir so: Bei einer Symmetrietransformation verändern wir das skalare Bosonenfeld \( \phi \), wobei diese Veränderung durch einen Parameter \( \theta \) gesteuert wird. Dabei ist \( \theta \) analog zu einem Drehwinkel oder einem Boostparameter zu verstehen, allerdings mit einem Unterschied:
Es handelt sich um eine sogenannte antikommutierende Superzahl (Grassmann-Variable), d.h. wenn man in einem Produkt zwei solche Superzahlen vertauscht, so gibt es einen Vorzeichenwechsel. Genau genommen sind es sogar zwei Parameter, denn \( \theta \) ist ein antikommutierender Weyl-Spinor (siehe auch den Anhang unten).
Die Symmetrie-Transformation \( \delta \phi \) hängt linear vom fermionischen Spinorfeld \( \psi \) ab. Die Kurzschreibweise lautet: \[ \delta \phi = \theta \, \psi \] mit einer geeigneten Summation über die Spinorindices. Die Supersymmetrietransformation mischt also zum Bosonenfeld \( \phi \) fermionische Anteile hinzu.
Parallel dazu verändern wir auch das Spinorfeld \( \psi \) mit demselben Parameter \( \theta \), wobei wir bosonische Anteile hinzumischen wollen. Wie genau das geschehen muss, das müssen wir am Wirkungsintegral der Lagrangedichte ablesen, denn dieses Integral soll sich durch diese parallele Symmetrie-Veränderung der Felder \( \phi \) und \( \psi \) nicht ändern, d.h. die Zusatzterme, die durch das veränderte \( \phi \) entstehen, müssen durch die Zusatzterme, die durch das parallel dazu veränderte \( \psi \) entstehen, genau aufgehoben werden.
Es zeigt sich, dass die Veränderung des Fermionfeldes \( \psi \) nicht einfach multiplikativ vom skalaren Feld \( \phi \) abhängen kann. Stattdessen muss sie von der raum-zeitlichen Änderung \[ \frac{\partial \phi}{\partial x^{\mu}} \] abhängen (siehe Stephen P. Martin: A Supersymmetry Primer, http://arxiv.org/pdf/hep-ph/9709356|, Seite 16). Schematisch lautet die Formel: \[ \delta \psi \sim (W \, \phi) \, \theta^{*} \] mit dem Weyl-Operator \(W\), der die Raum-Zeit-Ableitungen \( \frac{\partial}{\partial x^{\mu}} \) enthält (siehe Anhang unten).
Das ist genau der Grund dafür, dass Supersymmetrie nicht einfach eine innere Symmetrie unabhängig von Raum und Zeit ist!
Wichtig ist dabei, dass \( \theta \) nicht vom Raumzeitpunkt \(x\) abhängt, d.h. wir betrachten globale Supersymmetrietransformationen. Obwohl also \( \theta \) unabhängig von Raum und Zeit ist, ist dennoch eine Supersymmetrietransformation zwangsläufig mit Raum-Zeit-Transformationen vermischt.
Mathematisch kann man sich das dadurch erklären, dass fermionische Spinoren eine Differentialgleichung mit ersten Ableitungen nach Raum und Zeit erfüllen (die Diracgleichung bzw. die Weyl-Gleichung, siehe Anhang unten), die bosonischen Felder dagegen eine Differentialgleichung mit zweiten Ableitungen nach Raum und Zeit (die Klein-Gordon-Gleichung). Vermischt man diese Felder, so ist es naheliegend, dass man dabei Ableitungen der Felder nach Raum und Zeit bilden muss.
Man kann auch anders argumentieren: Die Felder \( \phi \) und \( \psi \) unterscheiden sich im Wesentlichen durch ihr Transformationsverhalten bei räumlichen Drehungen. Bei einer Supersymmetrie-Transformation, die beide Feldsorten vermischt, muss also das Dreh-Transformationsverhalten der einen Feldsorte in die der anderen Feldsorte umgewandelt werden und umgekehrt. Das sorgt für das Ineinandergreifen von Supersymmetrie-Transformation und Raum-Zeit-Transformation (Poincarétransformation).
Die Symmetrietransformationen (also die entsprechende Super-Lie-Algebra) sind aber im obigen naiven Ansatz nicht geschlossen, bilden also keine wohldefinierte Gruppenstruktur bzw. Algebra. Sie tun dies nur für die Felder, für die die Wirkung minimal ist (also für die Lösungen der Feldgleichungen). Man sagt, die Supersymmetrie-Algebra ist nur auf der Massenschale geschlosen (da die Lösungen der Feldgleichungen einer bestimmten Masse – nämlich Null – entsprechen).
Um das Problem zu lösen, muss man die Lagrangedichte etwas erweitern: Man braucht ein zusätzliches komplexes skalares Hilfsfeld \(F\) (ein sogenanntes Geistfeld), das einen Term \[ F^{*} \, F \] zur Lagrangedichte beisteuert, also einen Potentialterm. Da kein kinetischer Term für \(F\) hinzukommt, lautet die Lösung der Feldgleichungen für \(F\) einfach \(F = 0\). In einer Quantentheorie würde \(F\) nur virtuelle Teilchen besitzen, aber keine reellen Teilchen. \(F\) spielt also nur die Rolle eines Buchhalters und kann keine \(F\)-Wellen oder freie \(F\)-Teilchen erzeugen. Letztlich braucht man \(F\), um den zwei komplexen Komponenten von \( \psi \) auch zwei komplexe skalare Felder \( \phi \) und \(F\) entgegensetzen zu können. Nur dann kann man alles so zusammensetzen, dass es passt.
Mit Hilfe des Geistfeldes \(F\) kann man die Symmetrietransformationen etwas abändern, so dass sie nun eine geschlossene Struktur bilden. Das Noether-Theorem ermöglicht es anschließend, aufgrund der Invarianz der Wirkung Erhaltungsgrößen zu konstruieren: Superströme und Superladungen.
Die Superladungen sind nun die obigen Generatoren der Supersymmetrie. Man kann nun Kommutatoren und Antikommutatoren explizit ausrechnen und so die präzise Version der oben nur angedeuteten Beziehungen zwischen \(Q, Q^{+}\) und \(P^{\mu}\) konstruieren. All das findet man im Detail in Kapitel 3 von Stephen P. Martin: A Supersymmetry Primer, http://arxiv.org/pdf/hep-ph/9709356|.
Das Ganze kann man nun immer weiter treiben und beispielsweise versuchen, die Lagrangedichte von Eichtheorien oder gar die Lagrangedichte des Standardmodells supersymmetrisch zu machen. Schließlich braucht man dann noch einen Mechanismus, um die Supersymmetrie spontan zu brechen, so dass Teilchen und ihre Superpartner verschiedene Massen bekommen (so ist es ja in der Natur, falls die schweren Superpartner existieren).
Es stellt sich in den Rechnungen heraus, dass aufgrund der erhalten bleibenden Superladung das leichteste Superteilchen stabil sein muss, also nicht weiter in leichtere normale Teilchen zerfallen kann. Dieses Teilchen ist der wichtigste Kandidat für die dunkle Materie, von der es im Universum sechs mal mehr gibt als von der uns bekannten normalen Materie.
Daneben hat die Supersymmetrie viele weitere Aspekte, die für sie sprechen: Sie lindert ganz wesentlich die Divergenzen in der Quantenfeldtheorie, sie ist die maximal mögliche Erweiterung der Raum-Zeit-Symmetrie in der Quantentheorie (siehe oben), und sie deutet eine Vereinheitlichung aller Naturkräfte bei hohen Energien an, wenn man die Stärken (Kopplungskonstanten) der Naturkräfte zu hohen Energien hin extrapoliert und dabei die Supersymmetrie berücksichtigt.
Die Gleichung \[ \{ Q, Q^{+} \} \sim P^{\mu} \] von oben sagt aus, dass Supersymmetrietransformationen zu einer Translation in der Raumzeit führen können. Bisher war der Parameter \( \theta \) der Supersymmetrietransformation global, also unabhängig vom Raumzeitpunkt \(x\). Man kann sich nun fragen, was geschieht, wenn man analog zu lokalen Eichtransformationen auch zu lokalen Supersymmetrie-Transformationen übergeht, also zulässt, dass \( \theta \) vom Raumzeitpunkt \(x\) abhängt.
Es ist naheliegend, dass dann lokale Supersymmetrie-Transformationen nicht mehr nur zu einer Translation in der Raumzeit führen, sondern dass der Begriff der Parallelverschiebung aus der allgemeinen Relativitätstheorie ins Spiel kommt. Aus dem Operator \( P^{\mu} \), der in der Quantenmechanik Ableitungen nach den Raumzeitkoordinaten entspricht, wird dann eine Art kovariante Ableitung werden.
Lokale Supersymmetrie bringt über diesen Weg letztlich die Gravitation mit ins Spiel! Das ist ein deutlicher Hinweis darauf, dass man Supersymmetrie braucht, wenn man die Naturkräfte inklusive Gravitation gemeinsam in einer Theorie erfassen möchte. Als Ergebnis erhält man Supergravitationstheorien. Diese Theorien hat man mittlerweile als Grenzfall der hypothetischen M-Theorie erkannt, die möglicherweise ein Kandidat für die universelle physikalische Theorie aller Naturkräfte sein könnte.
Bleibt zu hoffen, dass auch irgendwann die experimentelle Suche nach den Superteilchen Erfolg hat, so dass die Supersymmetrie zu einer etablierten Theorie im Gebäude der Physik wird. Verdient hätte sie es, und die theoretischen Physiker wären ziemlich ratlos, wenn es anders kommt.
Im Folgenden habe ich einfach in loser Folge einige mathematische Bausteine zusammengetragen,
die im Zusammenhang mit Supersymmetrie nützlich sind.
Die Details kann man ggf. in den angegebenen Quellen nachlesen.
Als Basis braucht man unbedingt die Spinordarstellung der Poincarégruppe bzw. der Lorentzgruppe. Das ist ganz analog zur Darstellung von Drehungen bei Spin-1/2-Wellenfunktionen in der gewöhnlichen Quantenmechanik. Mehr dazu in Kapitel 4.10 und Kapitel 4.11. Hier das Wichtigste:
In der Quantentheorie ist die Lie-Algebra entscheidend, nicht die Lie-Gruppe. Das liegt daran, dass wir nur eine Strahldarstellung der Gruppe auf den Zuständen brauchen, d.h. komplexe Zusatzfaktoren mit Betrag Eins sind erlaubt.
Nun gibt es zu jeder Lie-Algebra \(L\) eine eindeutige einfach zusammenhängende Gruppe \(G_{0}\), die \(L\) als Lie-Algebra besitzt. Jede andere Gruppe \(G\), die dieselbe Lie-Algebra hat, hat \(G_{0}\) als Überlagerungsgruppe, d.h. in der Quantentheorie braucht man nicht nach einer Darstellung von \(G\) auf den Zuständen zu suchen, sondern es reicht eine Darstellung der Überlagerungsgruppe \(G_{0}\), um eine Strahldarstellung von \(G\) zu erreichen (Feinheiten wie die Zentrale Erweiterung etc. lassen wir hier weg, da sie bei der Poincarégruppe bzw. Lorentzgruppe keine Rolle spielen).
Wie sieht das bei der Lorentzgruppe aus? Die Überlagerungsgruppe ist die Gruppe \(SL(2,\mathbb{C})\), also die komplexen 2-mal-2-Matrizen mit Determinante Eins. Man kann jeder Matrix \(g \in SL(2,\mathbb{C})\) über die folgende Gleichung eindeutig eine Lorentzmatrix \( \Lambda \) zuordnen:
|
Zusammenhang zwischen der Lorentzgruppe und der Überlagerungsgruppe SL(2,\mathbb{C}):
\[ g \, \sigma(x) \, g^{+} = \sigma(\Lambda x) \] Dabei ist \(g \in SL(2,\mathbb{C})\), also eine komplexe 2-mal-2-Matrix mit Determinante Eins, \(g^{+}\) ist die dazu transponierte und komplex konjugierte Matrix, \( \Lambda \) ist die zugeordnete Lorentzmatrix, \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \] ist ein reeller Vierervektor (z.B. ein Ereignis in der Raumzeit) und \[ \sigma(x) = \sum_{\mu = 0}^{3} \, x^{\mu} \, \sigma_{\mu} \] ist eine hermitesche 2-mal-2-Matrix, die mit Hilfe der drei Paulimatrizen \( \sigma_1, \sigma_2, \sigma_3 \) und der 2-mal-2-Einheitsmatrix \( \sigma_{0} = 1 \) gebildet wird. Insbesondere ist \[ \det{ \sigma(x) } = (x^{0})^{2} - \boldsymbol{x}^{2} \] die Lorentz-Metrik. |
Hier sind noch einmal die Paulimatrizen:

Ausgeschrieben lautet die Matrix \(\sigma(x)\) also:
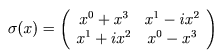
Die Gleichung \[ g \, \sigma(x) \, g^{+} = \sigma(\Lambda x) \] ist die entscheidende Gleichung!. Man rechnet leicht nach, dass die so definierte Matrix \(\Lambda\) die Lorentz-Metrik eines Vektors nicht ändert. Außerdem ist gesichert, dass dem Produkt zweier Gruppenelemente \(g\) und \(g'\) aus \(SL(2,\mathbb{C})\) auch das Produkt der entsprechenden Lorentzmatrizen zugeordnet wird, d.h. die Gruppenstruktur wird berücksichtigt. Allerdings ist die Zuordnung von \(SL(2,\mathbb{C})\) zu den Lorentzmatrizen nicht eindeutig: Den beiden \(SL(2,\mathbb{C})\)-Matrizen \( g \) und \( - g \) wird dieselbe Lorentzmatrix zugeordnet! Das ist mit dem Begriff Überlagerungsgruppe gemeint.
Nützlich ist auch die folgende Definition für komplexe 2-mal-2-Matrizen: \[ \tilde{A} := \epsilon A^{T} \, \epsilon^{- 1} \] mit

denn mit dieser Definition gilt \[ A \, \tilde{A} = \tilde{A} \, A = 1 \, \det {A} \] und daher auch \[ \sigma(x) \, \tilde{\sigma}(x) = \tilde{\sigma}(x) \, \sigma(x) = \] \[ = 1 \, \det {\sigma(x)} = (x^{0})^{2} - \boldsymbol{x}^{2} \] sowie \[ g \, \tilde{g} = \tilde{g} \, g = 1 \, \det {g} = 1 \] Quantenzustände versucht man nun durch mehrdimensionale komplexwertige Funktionen in der Raumzeit darzustellen, analog zu Wellenfunktionen. Allerdings haben diese Funktionen selbst zumeist keine direkte physikalische Interpretation. Erst ein passendes Skalarprodukt auf diesen Funktionen ergibt eine solche Interpretation, denn nur so können wir Wahrscheinlichkeitsamplituden aufbauen. Um so ein Skalarprodukt zu definieren, geht man oft von einem erhaltenen Strom aus und integriert die Null-Komponente über den Raum.
Man muss festlegen, wie die Funktionen bei Poincarétransformationen umgerechnet werden müssen, d.h. man braucht eine Darstellung der Poincarégruppe auf diesen Funktionen. Eine Spinordarstellung kann man nun auf zweikomponentigen Funktionen \(\xi(x)\) folgendermaßen definieren (\(x\) ist dabei ein Raum-Zeit-Vierervektor, \(a\) ist ein Raum-Zeit-Translationsvektor und \(\xi(x)\) ist ein Vektor (Spinor) mit zwei komplexen Zahlen):
| \[ (T_{g,a} \, \xi)(x) := g \, \xi(\Lambda^{- 1} (x - a)) \] |
Rechts wird dabei die komplexe 2-mal-2-Matrix \(g\) auf den zweikomponentigen komplexen Vektor
\( \xi(\Lambda^{- 1} (x - a)) \) angewendet.
Weiter ist \(T_{g,a}\) eine Abbildung, die aus einer Funktion \(\xi\) eine neue Funktion
\( T_{g,a} \, \xi \) macht, und zwar definiert über die obige Gleichung.
Man sagt, die Poincarégruppe (genauer: ihre Überlagerungsgruppe) wird auf diesen Funktionen
durch die Abbildung \( T_{g,a} \) dargestellt.
Die neue Funktion an der neuen Stelle \(x\) ist also gleich der alten Funktion an der Ursprungsstelle \( \Lambda^{- 1} (x - a) \), multipliziert mit der Matrix \(g\).
Eine Funktion, die sich so verhält, nennt man auch einen Weyl-Spinor.
Zum Vergleich: Eine skalare (bosonische) Funktion \( \phi \) ist durch folgendes Transformationsverhalten gekennzeichnet: \[ (T_{g,a} \, \phi)(x) := \phi(\Lambda^{- 1} (x - a)) \] d.h. hier braucht man die Überlagerungsgruppe (also die Matrix \(g\)) gar nicht erst, sondern man hat direkt eine Darstellung der Poincarégruppe. Während eine Drehung um 360 Grad bei \(\xi\) zu einem Vorzeichenwechsel führt, ist das bei \(\phi\) nicht der Fall.
Eine andere Darstellungsmöglichkeit der Überlagerungsgruppe auf zweikomponentigen komplexwertigen Funktionen (hier \(\eta\) genannt) ist folgende:
| \[ (T '_{g,a} \, \eta)(x) := (g^{+})^{- 1} \, \eta(\Lambda^{- 1} (x - a)) \] |
Hier wird mit der transponierten, komplex konjugierten und dann invertierten \(g\)-Matrix multipliziert.
Man spricht von einem konjugierten Weyl-Spinor \(\eta\). Wichtig ist dabei die Gleichung
\[
(g^{+})^{- 1} \, \tilde{\sigma}(x) \, g^{- 1} = \tilde{\sigma}(\Lambda x)
\]
Häufig arbeitet man hier auch mit Indexschreibweisen
(ungepunktete und gepunktete Indizes, die normale und konjugierte
Weyl-Spinoren kennzeichnen). Die Matrix \( \epsilon \) dient dabei zum Hoch- und Runterziehen von Indices.
Dabei wird \( \epsilon \) bzw. \( \epsilon^{- 1} = - \epsilon \)
analog zur metrischen Matrix eingesetzt. Begründung:
\[
\tilde{g} \, g = 1
\]
\[
\Rightarrow
\;
\epsilon \, g^{T} \, \epsilon^{- 1} \, g = 1
\]
\[
\Rightarrow
\;
g^{T} \, \epsilon^{- 1} \, g = \epsilon^{- 1}
\]
\[
\Rightarrow
\;
\xi^{T} \, g^{T} \, \epsilon^{- 1} \, g \, \xi =
\xi^{T} \, \epsilon^{- 1} \, \xi
\]
\[
\Rightarrow
\;
(g \, \xi)^{T} \, \epsilon^{- 1} \, (g \, \xi) =
\xi^{T} \, \epsilon^{- 1} \, \xi
\]
d.h. der rechte Ausdruck
\[
\xi^{T} \epsilon^{- 1} \xi
\]
ändert sich nicht, wenn man \( \xi \) durch \( g \, \xi \) ersetzt.
Er ist in diesem Sinn \( SL(2,\mathbb{C})\)-invariant, verhält sich also bei Poincarétransformationen
wie eine skalare Funktion \(\phi\).
Analog kann man zeigen, dass sich der Ausdruck \[ \eta^{T} \, \epsilon \, \eta \] nicht ändert, wenn man \(\eta\) durch \( (g^{+})^{- 1} \, \eta \) ersetzt. Persönlich finde ich diese Matrixschreibweise übersichtlicher als die Indexschreibweise mit hoch- und tiefgestellten sowie gepunkteten und ungepunkteten Indices.
Hier noch eine andere interessante Formel in diesem Zusammenhang: Aus \[ \tilde{g} \, g = 1 \] folgt direkt \[ \tilde{g} = g^{- 1} \] oder ausgeschrieben \[ \epsilon \, g^{T} \, \epsilon^{- 1} = g^{- 1} \] Transponieren und komplexes Konjugieren ergibt \[ \epsilon \, g^{*} \, \epsilon^{- 1} = (g^{+})^{- 1} \] oder umgeschrieben \[ \epsilon \, g^{*} = (g^{+})^{- 1} \, \epsilon \] Angewendet auf \( \xi^{*} \) erhält man \[ \epsilon \, (g \, \xi)^{*} = (g^{+})^{- 1} \, \epsilon \, \xi^{*} \] Das bedeutet: Wenn sich im Ausdruck \( \epsilon \, \xi^{*} \) der Spinor \( \xi \) wie ein Weyl-Spinor verhält (also mit \(g\) multipliziert wird, was die linke Seite ergibt), so verhält sich der Gesamtausdruck \( \epsilon \, \xi^{*} \) wie ein konjugierter Weyl-Spinor (wird also mit \((g^{+})^{- 1}\) multipliziert, was die rechte Seite ergibt). In diesem Sinn macht die Matrix \( \epsilon \) zusammen mit dem komplexen Konjugieren aus einem Weyl-Spinor einen konjugierten Weyl-Spinor.
Um die Weyl-Spinoren irgendwie mit quantenmechanischen Zuständen identifizieren zu können, braucht man eine sogenannte Ausreduktion der Darstellung. Man braucht Unterräume von Weyl-Spinoren, die sich bei Poincarétransformationen nur innerhalb der Unterräume ineinander umwandeln. Insbesondere möchte man diese Unterräume durch eine Masse kennzeichnen können.
Um das zu erreichen, betrachtet man Differentialgleichungen, deren Lösungsräume gerade solche Unterräume ergeben sollen. Dazu definieren wir den Weyl-Operator \(W\) und den konjugierte Weyl-Operator \(W'\) wie folgt: \[ W := \sum_{\mu=0}^{3} \, \sigma_{\mu} \, \frac{\partial}{\partial x_{\mu}} \] \[ W' := - \sum_{\mu=0}^{3} \, \tilde{\sigma}_{\mu} \, \frac{\partial}{\partial x_{\mu}} \] mit den den Paulimatrizen \(\sigma_{\mu}\) (inclusive der Einheitsmatrix \(\sigma_{0} = 1\)) und den Ableitungen nach den Raum-Zeit-Koordinaten \[ \frac{\partial}{\partial x_{0}} = \frac{\partial}{\partial x^{0}} \] \[ \frac{\partial}{\partial x_{i}} = - \frac{\partial}{\partial x^{i}} \] mit \(i = 1, 2, 3\).
Die Definition von \( \tilde{\sigma}_{\mu}\) mit Hilfe der Matrix \( \epsilon \) von oben bewirkt, dass \[ \tilde{\sigma}_{\mu} = \sigma^{\mu} \] ist, also \[ \tilde{\sigma}_{0} = \sigma_{0} \] \[ \tilde{\sigma}_{i} = - \sigma_{i} \] mit \(i = 1, 2, 3\).
Man kann nun folgendes nachrechnen: \[ W \, W' = W' \, W = \] \[ = - \sum_{\mu=0}^{3} \, \frac{\partial}{\partial x_{\mu}} \, \frac{\partial}{\partial x^{\mu}} =: - \partial^{2} \] Das ist bis auf das Vorzeichen der relativitstische Wellenoperator. Außerdem gilt
Intertwining Relation 1: \[ W \, T '_{g,a} = T_{g,a} \, W \] Intertwining Relation 2: \[ W' \, T_{g,a} = T '_{g,a} \, W' \] Man sieht, wie die beiden Darstellungen und die beiden Weyl-Operatoren miteinander verflochten sind.
Die Operatoren \(W\) und \(W'\) benutzen wir nun, um bestimmte Teilräume der Weyl- und konjugierten Weyl-Spinoren herauszugreifen. Wir fordern nämlich die Gleichungen
| Weyl-Gleichung: \[ W \, \eta(x) = 0 \] konjugierte Weyl-Gleichung: \[ W' \, \xi(x) = 0 \] |
Das macht Sinn, denn wenn \( \eta \) eine Lösung der Weyl-Gleichung ist,
dann ist auch die Poincaré-transformierte
Funktion \( T '_{g,a} \, \eta \) eine Lösung der Weyl-Gleichung:
\[
W \, \eta(x) = 0
\]
\[
\Rightarrow
\]
\[
(W \, T '_{g,a} \, \eta)(x) =
(T_{g,a} \, W \, \eta)(x) = 0
\]
Analog gilt: Wenn \(\xi\) eine Lösung der konjugierten Weyl-Gleichung ist,
dann ist auch die Poincaré-transformierte
Funktion \( T_{g,a} \, \xi \) eine Lösung der konjugierten Weyl-Gleichung.
Die Darstellungen der Poincarégruppe wirken also innerhalb der Lösungsräume der beiden Gleichungen.
Die Lösungen der beiden Gleichungen erfüllen automatisch die relativistische Wellengleichung: \[ W \, \eta(x) = 0 \] \[ \Rightarrow \] \[ W' \, W \, \eta(x) = - \partial^{2} \, \eta(x) = 0 \] (analog für \(\xi\)). Es handelt sich also um Wellen, die sich wie Lichtwellen mit Lichtgeschwindigkeit fortbewegen. Der in der Quantenmechanik zugeordnete Teilchenimpuls ist also der eines masselosen Teilchens. Die Lösungen der beiden Weyl-Gleichungen beschreiben masselose Teilchen.
Für Spinoren, die zur Beschreibung von Zuständen für Teilchen mit Masse geeignet sind, muss man die obigen Gleichungen abwandeln und geeignet kombinieren, denn man kann nicht einfach beispielsweise die Gleichung \( (W + m) \, \eta(x) = 0 \) mit Masse \(m\) fordern. Eine Poincaré-transformierte Lösung wäre keine Lösung der Gleichung mehr.
Die Ursache dafür liegt darin, dass wegen der obigen Intertwining Relationen sich die Größe \( W \, \eta \) bei Poincaré-Transformationen nicht wie ein konjugierter Weyl-Spinor (also wie \(\eta\)) transformiert, sondern wie ein normaler Weyl-Spinor (also wie \(\xi\)):
d.h. in der Gleichung \( (W + m) \, \eta(x) = 0 \) transformiert sich \( W \, \eta \) anders als \( m \, \eta \). Analog ist es für \( W' \, \xi \) und \( m \, \xi \).
Damit ist aber auch schon klar, was man machen muss: statt \( (W + m) \, \eta(x) = 0 \) und \( (W' + m) \, \xi(x) = 0 \) muss man die folgenden kombinerten Gleichungen verwenden:
| \[ W \, \eta(x) + m \, \xi(x) = 0 \] \[ W' \, \xi(x) + m \, \eta(x) = 0 \] |
Das ist ein Gleichungssystem für die Funktionen \(\xi\) und \(\eta\). Es führt dazu, dass die beiden Funktionen miteinander verkoppelt werden, so dass sie nicht mehr unabhängig voneinander sind. So kann man Lösungen \(\eta\) durch Lösungen \(\xi\) ausdrücken und umgekehrt.
Meist fasst man die beiden 2-komponentigen Gleichungen zu einer vierkomponentigen Gleichung zusammen, die Diracgleichung genannt wird.
Wendet man \(W'\) auf die erste und \(W\) auf die zweite Gleichung an, so erhält man \[ W' \, W \, \eta(x) + m \, W' \, \xi(x) = 0 \] \[ W \, W' \, \xi(x) + m \, W \, \eta(x) = 0 \] Im Massenterm (zweiten Term) können wir nun jeweils die beiden Teilgleichungen der Diracgleichung im Kästchen oben verwenden und so beispielsweise \( W' \, \xi \) durch \( - m \, \eta \) ersetzen. Außerdem verwenden wir von oben \( W W' = W' W = - \partial^{2} \) und erhalten: \[ - \partial^{2} \, \eta(x) - m^{2} \, \eta(x) = 0 \] \[ - \partial^{2} \, \xi(x) - m^{2} \, \xi(x) = 0 \] Die beiden Spinoren erfüllen also die Klein-Gordon-Gleichung, d.h. die Lösungen lassen sich aus ebenen Wellen zusammensetzen, die in der Quantentheorie Teilchen mit bestimmtem Viererimpuls und Masse \(m\) beschreiben.
Bei der supersymmetrischen Erweiterung der Poincarégruppe werden die 4 Raumzeit-Dimensionen um 4 Grassmann-Dimensionen erweitert. Eine supersymmetrische Transformation verändert im Superfeld-Formalismus (siehe unten) nicht nur die Raumzeitkoordinaten, sondern auch die Grassmann-Koordinaten. Über Grassmann-Zahlen erfährt man oft nur, dass es sich bei ihnen um geheimnisvolle Größen handelt, die beim Vertauschen einen Vorzeichenwechsel hervorrufen. Versuchen wir, genauer herauszufinden, was dahinter steckt.
Einen Hinweis findet man in Wikipedia: Grassmann number. Grassmann-Zahlen bilden eine Algebra, die von Generatoren erzeugt wird und die man durch Matrizen darstellen kann.
Ein Beispiel ist eine Grassmann-Algebra, die von 2 Generatoren erzeugt wird. Nennen wir diese Generatoren \( \theta_{1} \) und \( \theta_{2}\) . Die Eigenschaft, Generator zu sein, drückt sich darin aus, dass \(\theta_{1}\) und \(\theta_{2}\) linear unabhängig sind, d.h. es gibt keine reelle Zahl \(x\), so dass \( \theta_{1} = x \, \theta_{2} \) wäre (mit komplexen Zahlen \(x\) befassen wir uns weiter unten; Achtung: \(x\) hat hier noch nichts mit den Vierervektoren der Raumzeit zu tun).
Auf den Grassmann-Zahlen ist nun eine antisymmetrische Multiplikation definiert, so dass \[ \theta \, \theta' = - \theta' \, \theta \] ist.
Das gilt natürlich auch für die beiden Generatoren, d.h. \[ \theta_{i} \, \theta_{j} = - \theta_{j} \, \theta_{i} \] und somit \[ \theta_{i} \, \theta_{i} = 0 \] Daraus folgt, dass man jede Grassmann-Zahl \( \theta \) in dieser Algebra schreiben kann als \[ \theta = x_{1} \, \theta_{1} + x_{2} \, \theta_{2} + x_{3} \, \theta_{1} \, \theta_{2} \] mit reellen Koeffinzienten \(x_{i}\) (diese \(x_{i}\) haben hier nichts mit den Vierervektoren der Raumzeit zu tun). Die beiden Generatoren und ihr Produkt bilden also eine Basis der Algebra.
Probieren wir aus, ob diese Grassmann-Zahlen tatsächlich antikommutieren. Dabei verwenden wir, dass wegen der Antisymmetrie jeder Term Null ist, der einen Generator doppelt enthält: \[ \theta \, \theta' = \] \[ = \left( x_{1} \, \theta_{1} + x_{2} \, \theta_{2} + x_{3} \, \theta_{1} \, \theta_{2} \right) \cdot \] \[ \cdot \left( x_{1}' \, \theta_{1} + x_{2}' \, \theta_{2} + x_{3}' \, \theta_{1} \, \theta_{2} \right) = \] \[ = x_{1} \, \theta_{1} \, x_{2}' \, \theta_{2} + x_{2} \, \theta_{2} \, x_{1}' \theta_{1} = \] \[ = \left( x_{1} \, x_{2}' - x_{2} \, x_{1}' \right) \, \theta_{1} \, \theta_{2} \] Dieser Ausdruck ist offensichtlich antisymmetrisch beim Vertauschen von \(\theta\) und \(\theta'\).
Man kann leicht eine Matrixdarstellung für die Grassmann-Zahlen mit zwei Generatoren angeben (siehe Wikipedia: Grassmann number):

\[ \theta = \begin{pmatrix} 0 & 0 & 0 & 0 \\ x_1 & 0 & 0 & 0 \\ x_2 & 0 & 0 & 0 \\ x_3 & -x_2 & x_1 & 0 \end{pmatrix} \] Auch bei mehr Generatoren geht das.
Wie kommt man auf die obigen Matrizen?
Nun, man muss \( \theta_{i} \) als Heranmultiplizieren von links ansehen. \( \theta_{i} \) macht also aus einer Zahl \(x\) die Zahl \( \theta_{i} \, x \) sowie aus der Grassmann-Zahl \( \theta_{j} \) die Grassmann-Zahl \( \theta_{i} \, \theta_{j} \).
Die Matrizen oben sind nun die Matrixdarstellung dieses Heranmultiplizierens in der Basis \[ 1, \, \theta_{1}, \, \theta_{2}, \, \theta_{1} \, \theta_{2} \] Die i-te Spalte gibt dabei in dieser Basis an, was durch das Heranmultiplizieren von links aus dem i-ten Basisvektor wird. So macht \( \theta_{1} \) durch Heranmultiplizieren von links aus dem ersten Basisvektor (der \(1\)) den zweiten Basisvektor (nämlich \(\theta_{1}\)), und aus dem dritten Basisvektor (also \(\theta_{2}\)) den vierten Basisvektor (nämlich \(\theta_{1} \, \theta_{2} \)). Genau das sagt die Matrixdarstellung aus!
Analog ist es mit der Matrix von \( \theta_{2} \). Aus dem ersten Basisvektor (der \(1\)) wird der dritte Basisvektor \( \theta_{2} \), und aus dem zweiten Basisvektor \( \theta_{1} \) wird \( \theta_{2} \, \theta_{1} = - \theta_{1} \, \theta_{2} \).
Wer es kennt, der sieht vielleicht die Parallele zu den Fermion-Erzeugungsoperatoren in der Quantenfeldtheorie. So definiert man dort \[ a^{+}(v) \, w := v \wedge w \] mit dem antisymmetrischen Tensorprodukt \( \wedge \) im Hilbertraum der Fermionen, d.h. \(a^{+}(v)\) bewirkt ein antisymmetrisches Heranmultiplizieren mit \(v\) von links. Wenn man nun ein quantenmechanisches System mit zwei möglichen Basis-Einteilchenzuständen \(e_{1}\) und \(e_{2}\) hat, so sind die möglichen fermionischen Zustände für 0, 1 oder 2 Fermionen gegeben durch die 4 Basisvektoren \[ 1, \, e_{1}, \, e_{2}, \, e_{1} \wedge e_{2} \] (die \( 1 \) steht hier für das leere Vakuum) und man hat die zwei Erzeuger \( a^{+}(e_{1}) \) und \( a^{+}(e_{2}) \). Die obigen Matrizen sind dann genau die Matrixdarstellungen für die Erzeuger in dieser Basis aus möglichen fermionischen Basiszuständen.
Damit ist klar, wie man bei mehr als 2 Generatoren vorgehen muss. Man kann immer eine entsprechende Matrixdarstellung für die Grassmann-Zahlen finden.
Anmerkung:
Auch bei der Matrixdarstellung komplexer Zahlen kann man analog vorgehen. Die Basisvektoren sind dabei \[ 1, \, i \] und man kann eine Matrixdarstellung in dieser Basis für \(1\) und \(i\) finden, indem man sie zugleich als Multiplikationsoperatoren sieht. So lässt die \(1\) die beiden Basisvektoren unverändert, während \(i\) aus dem ersten Basisvektor (der \(1\)) den zweiten Basisvektor (also \(i\)) macht, und aus dem zweiten Basisvektor (dem \(i\)) dann minus den ersten Basisvektor (also \(- 1\)) macht. Die Matrixdarstellung für das Heranmultiplizieren einer komplexen Zahl \(x + iy\) in der Basis aus \(1\) und \(i\) sieht also so aus: \[ x + iy = \begin{pmatrix} x & -y \\ y & x \end{pmatrix} \] Die Multiplikationswirkung einer komplexen Zahl besteht also in einer Drehstreckung. Mehr dazu siehe Die Grenzen der Berechenbarkeit, Kapitel 5.2.
Die Grassmannzahlen in unserem obigen Beispiel kann man analog als lineare Abbildungen im vierdimensionalen
Raum auffassen. Man erkennt, dass die beiden Generatoren Projektionen vornehmen.
So projeziert \(\theta_{1}\) die 1- und die 3-Komponente heraus (wirft also die 2- und die 4-Komponente weg)
und macht daraus die 2- und die 4-Komponente des neuen Vektors (wenn man von einem reellen Vektorraum ausgeht).
Das ist allerdings nicht mehr so anschaulich wie die Drehstreckung bei komplexen Zahlen.
Man versucht nun, möglichst viele Teile der Mathematik (speziell der Analysis) auf Grassmann-Zahlen zu übertragen, so wie man das auch beim Übergang von reellen zu komplexen Zahlen gemacht hat. So möchte man gerne Funktionen von Grassmann-Zahlen untersuchen. Dazu muss man aber erst einmal festlegen, was man darunter verstehen will.
In unserem obigen Beispiel mit 2 Generatoren hängen die Grassmann-Zahlen von 3 reellen Parametern \(x_{i}\) ab. In diesem Sinne wäre eine Funktion der Grassmann-Zahlen einfach eine Funktion der drei Parameter. Das ist aber nicht unser Ziel, denn dadurch hätten wir nichts gewonnen. Insbesondere würde an keiner Stelle die besondere Multiplikationsstruktur der Grassmann-Zahlen eingehen.
Auch Funktionen einer komplexen Zahl \(z\) (mit Werten in den komplexen Zahlen) kann man als Funktionen zweier reeller Zahlen auffassen. Auch hier hätte man aber so nichts gewonnen und die besondere Multiplikationsstruktur der komplexen Zahlen wäre nutzlos. Daher macht man in der Funktionentheorie die Einschränkung, dass man holomorphe Funktionen betrachten möchte, also Funktionen, die sich in der Nähe eines Punktes \(z\) schreiben lassen als \[ f(z+h) = f(z) + h \cdot f '(z) + \, ... \] Für kleine \(h\) ist dann die Abweichung \( f(z+h) - f(z) \) durch die Drehstreckung von \(h\) mit \(f '(z)\) gegeben (siehe Die Grenzen der Berechenbarkeit, Kapitel 5.2). Man bezeichnet die Drehstreckung \(f '(z)\) als Ableitung von \(f\) an der Stelle \(z\) und schreibt auch \[ f'(z) = \frac{\partial f(z)}{\partial z} \] Im Term \( h \cdot f '(z) \) geht dabei die multiplikative Struktur der komplexen Zahlen entscheidend ein.
Analog kann man es für Grassmann-Zahlen versuchen. Wir wollen also nur Funktionen betrachten, deren Funktionswerte Grassmann-Zahlen sind und die sich für kleine Grassmann-Zahlen \( \phi \) schreiben lassen als \[ f(\theta + \phi) = f(\theta) + \phi \cdot f '(\theta) + \, ... \] (man könnte auch \( \wedge \) statt \( \cdot \) schreiben, d.h. die antisymmetrische Grassmann-Multiplikation ist gemeint – d.h. die Reihenfolge ist in der obigen Definition von \(f '(\theta)\) wichtig und entspricht einer bestimmten Vorzeichenkonvention).
Dabei müsste man noch genauer festlegen, was denn eine kleine Grassmannzahl sein soll. Wir wollen hier nicht auf mögliche Schwierigkeiten eingehen, sondern uns einfach vorstellen, dass in unserem Beispiel die drei Parameter \(x_{i}\) klein werden. Die Grassmannzahl \( f '(\theta) \) schreiben wir auch als \[ f '(\theta) = \frac{\partial f(\theta)}{\partial \theta} \] und bezeichnen sie als Ableitung.
Schauen wir uns als Beispiel den Spezialfall \[ f(\theta) = \theta \cdot \rho \] an (dabei ist \(\rho\) irgendeine konstante Grassmann-Zahl). Dann ist \[ f(\theta + \phi) = \] \[ = \theta \cdot \rho + \phi \cdot \rho = \] \[ = f(\theta) + \phi \cdot f '(\theta) \] und somit \[ f '(\theta) = \rho \] Das ist die gewohnte Ableitungsregel.
In der Funktionentheorie holomorpher Funktionen stellt man fest, dass man immer lokal eine Reihenentwicklung für diese Funktionen angeben kann. Über diese Reihenentwicklung kann man aus einer reellen Funktion auch leicht (zumindest lokal) eine komplexe Funktion machen. Man spricht von analytischer Fortsetzung.
Wie das bei den Funktionen in den Grassmann-Zahlen ist, wollen wir uns hier nicht genauer ansehen, aber die Analogie ist klar: Wie soll man eine solche Funktion anders definieren als über eine Reihenentwicklung?! Nur so kann die multiplikative Struktur der Grassmannzahlen auch eingehen.
Genauso findet man es auch in den Büchern: Funktionen in den Grassmann-Zahlen sind Reihenentwicklungen, wobei die Reihe nach endlich vielen Termen abbricht, denn höhere Potenzen der Grassmannvariablen sind wegen der Antisymmetrie gleich Null. Deshalb ist jede (Grassmann-ableitbare = superholomorphe) Funktion einer einzigen Grassmann-Variable \(\theta\) immer linear, denn \( \theta^{2} = 0 \) wegen der Antisymmetrie: \[ f(\theta) = a + b \, \theta \] Eine Grassmann-ableitbare Funktion von zwei Grassmannvariablen \( \theta \) und \( \theta' \) kann dagegen auch quadratische Terme enthalten: \[ f(\theta, \theta') = a + b \, \theta + b' \, \theta' + c \, \theta \, \theta' \] Der letzte (quadratische) Term ist allerdings nur dann ungleich Null, wenn die betrachtete Grassmann-Algebra auch mindestens zwei Generatoren \(\theta_{1}\) und \(\theta_{2}\) besitzt. Gäbe es nur einen Generator, so wäre \( \theta' = x \, \theta \) mit einem reellen \(x\) , und damit \( \theta \, \theta' = x \, \theta \, \theta = 0 \).
Anders ausgedrückt: Eine Funktion von zwei Grassmann-Variablen macht nur dann Sinn, wenn es auch zwei (oder mehr) Generatoren in der entsprechenden Grassmann-Algebra gibt.
Gäbe es nur einen Generator, so wäre \( f(\theta, \theta') \) nur eine Funktion einer Grassmann-Variable sowie einer reellen Zahl \(x\). Man kann sich also als Regel merken:
Die Zahl der benötigten Generatoren in der Grassmann-Algebra entspricht (mindestens) der Anzahl der Argumente in den betrachteten Funktionen.
Bisher haben wir immer von reellen Zahlen \(x_{i}\) gesprochen. Analog zu Vektorräumen können wir aber auch komplexe Zahlen zulassen. Man spricht dann von einer Grassmann-Algebra über den komplexen Zahlen. Es ist sinnvoll, in diesem Fall durch Linearkombination zu neuen Generatoren überzugehen. In unserem Beispiel mit den 2 Generatoren definieren wir: \[ \theta_{a} := \frac{1}{\sqrt{2}} \, \left( \theta_{1} + i \, \theta_{2} \right) \] \[ \theta_{b} := \frac{1}{\sqrt{2}} \, \left( \theta_{1} - i \, \theta_{2} \right) \] Analog verfährt man bei mehr Generatoren (falls eine gerade Anzahl vorliegt). Man kann nun das komplexe Konjugieren von Grassmann-Zahlen einführen. Wir bezeichnen es mit einem hochgestellten \( * \) (analog zum komplexen Konjugieren bei komplexen Zahlen). Es soll die folgenden Eigenschaften haben: \[ (\theta^{*})^{*} = \theta \] \[ (\theta \, \theta' )^{*} = \theta' ^{*} \, \theta^{*} \] \[ (x \, \theta)^{*} = x^{*} \theta^{*} \] (dabei sind \(\theta\) und \(\theta'\) Grassmann-Zahlen, \(x\) ist eine komplexe Zahl und \(x^{*}\) die dazu komplex konjugierte Zahl (d.h. \(i\) wird gegen \( - i \) ausgetauscht). Außerdem soll für die ursprünglichen Generatoren gelten: \[ \theta_{1}^{*} = \theta_{1} \] \[ \theta_{2}^{*} = \theta_{2} \] Man spricht auch von reellen Generatoren. Für die neuen Generatoren gilt: \[ \theta_{b} = \theta_{a}^{*} \] Man spricht in diesem Fall von einer 1-dimensionalen komplexen Grassmann-Algebra, da man \(\theta_{a}\) und \(\theta_{a}^{*}\) nicht getrennt zählt. Es sind aber dennoch wie zuvor zwei linear unabhängige Generatoren vorhanden, nämlich \(\theta_{a}\) und \(\theta_{a}^{*}\), und man kann jederzeit zu den alten Generatoren \(\theta_{1}\) und \(\theta_{2}\) zurückkehren.
Es ist interessant, sich die Matrixdarstellung der neuen Generatoren (in der alten Basis) anzusehen: \[ \theta_a = \frac{1}{\sqrt{2}} \, \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ i & 0 & 0 & 0 \\ 0 & -i & 1 & 0 \end{pmatrix} \] \[ \theta_b = \frac{1}{\sqrt{2}} \, \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ -i & 0 & 0 & 0 \\ 0 & i & 1 & 0 \end{pmatrix} \] Die Matrizen gehen also hier durch komplexes Konjugieren der Matrixelemente ineinander über.
Analog zu den ursprünglichen reellen Generatoren antivertauschen auch \(\theta_{a}\) und \(\theta_{a}^{*}\): \[ \theta_{a}^{*} \, \theta_{a} = \] \[ \frac{1}{2} \, ( \theta_{1} - i \, \theta_{2} ) \cdot ( \theta_{1} + i \, \theta_{2} ) = \] \[ = i \, \theta_{1} \, \theta_{2} = \] \[ = - \theta_{a} \, \theta_{a}^{*} \] Die Matrixdarstellung für das Produkt der neuen Generatoren lautet also: \[ \theta_{a} \, \theta_{a}^{*} = - \theta_{a}^{*} \, \theta_{a} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ -i & 0 & 0 & 0 \end{pmatrix} \] Das komplexe Konjugieren der Matrixelemente liefert hier nicht das komplex konjugierte der linken Seite, denn die ändert sich durch komplexes Konjugieren nicht. Die Matrixdarstellung ist also ganz interessant, wenn man sich fragt, was Grassmann-Zahlen eigentlich sind, (oder wie man sie sich vorstellen kann) aber für konkrete Rechnungen doch eher ungeeignet.
Um eine Quantenfeldtheorie zu konstruieren, geht man meist von einer klassischen Feldtheorie aus, also von einem Wirkungsintegral einer Lagrangefunktion. Dafür braucht man klassische Felder, die Funktionen in der Raumzeit sind, beispielsweise ein skalares Bosonfeld \(\phi(x)\) oder ein Weyl-Spinorfeld \(\psi(x)\) oder \(\eta(x)\).
Man kann nun alleine mit diesen Feldern in der Raumzeit arbeiten, um die Aktion der Supersymmetrie darauf darzustellen. So kann man Supersymmetrie-Transformationen definieren, die aus einem skalaren Bosonfeld ein fermionisches Spinorfeld machen und umgekehrt, wobei diese Transformation durch die obigen Grassmann-Zahlen parametrisiert werden. Genau so sind wir weiter oben beim Wess-Zumino-Modell vorgegangen: \[ \delta \phi = \theta \, \psi \] Diese Vorgehensweise ist jedoch recht mühsam, da die Supersymmetrie in dem Formalismus nicht eingebaut ist (so wie die elektrischen und magnetischen Felder nicht an den Umgang mit Poincarétransformationen angepasst sind, im Gegensatz zum Feldstärketensor). Man kann jedoch einen Formalismus aufbauen, der an die Supersymmetrie angepasst ist. Er arbeitet mit Superfeldern auf einer Super-Raumzeit.
Betrachten wir dazu noch einmal Darstellungen der Poincarétransformationen auf Feldern, beispielsweise \[ (T_{g,a} \, \xi)(x) := g \, \xi(\Lambda^{- 1} (x - a)) \] Die Poincaré-Transformation des Raumzeit-Argumentes des Feldes induziert dabei (zusammen mit der Multiplikation mit \(g\)) eine Darstellung auf dem Feld. Anschaulich muss das so sein, damit z.B. aus einem Wellenpaket nach einer Drehung auch ein räumlich gedrehtes Wellenpaket wird.
Nun kann man versuchen, analog auch Supersymmetrie-Transformationen darzustellen. Dazu definiert man Superfelder auf einer erweiterten Super-Raumzeit. Zu den 4 Raumzeitkoordinaten kommen 4 komplexe Grassmannvariablen hinzu (d.h. wir brauchen eine komplexe Grassmann-Algebra mit 4 Generatoren). Es ist nützlich, diese 4 Grassmann-Variablen in Form eines Weyl-Spinors und eines konjugierten Weyl-Spinors darzustellen.
Der Raum aus 4 Raumzeitkoordinaten und 4 komplexen Grassmannvariablen ist keine übliche Mannigfaltigkeit mehr, sondern ein komplexeres Gebilde (eine Supermannigfaltigkeit). Insofern darf man sich nicht vorstellen, dass die Raumzeit einfach um weitere Dimensionen erweitert wird. Stattdessen wird sie durch ein komplexeres mathematisches Objekt ersetzt, das einerseits die Raumzeit umfasst, das aber aufgrund der Grassmann-Zahlen auch andere algebraische Strukturen enthält. Mehr dazu siehe beispielsweise Jose Miguel Figueroa-o'Farrill: Busstepp Lectures on Supersymmetry, arXiv:hep-th/0109172 v1 21 Sep 2001, ab Seite 31.
Die Superfelder sind nun Funktionen auf dieser Super-Raumzeit, hängen also von den 4 Raumzeitkoordinaten und den 4 Grassmann-Variablen ab. Damit kann man nun die supersymmetrische Erweiterung der Poincaré-Transformationen auf diesen Superfeldern definieren, ganz analog zu den Darstellungen der Poincarégruppe vorher. Schematisch könnte eine solche Supersymmetrietransformation \(S\) eines Superfeldes \(\Psi\) beispielsweise so aussehen (das Beispiel zeigt schematisch eine Supertranslation): \[ (S \, \Psi)(x, \theta) \, \sim \, \Psi( x + \theta' \theta , \, \theta + \theta' ) \] Die Verwendung von solchen Superfeldern auf der Superraumzeit hat den Vorteil, dass man in den entsprechenden Formeln sofort sieht, ob ein Ausdruck supersymmetrisch ist oder nicht. Analog hatte man ja auch bei den Poincarétransformationen mit kovarianten und kontravarianten Raum-Zeit-Indices eine Formulierung gewählt, bei der man die Transformationseigenschaften sofort ablesen kann. Einstein hatte es da am Anfang noch schwerer, als er noch explizit mit elektrischen und magnetischen Feldern hantierte. Erst die Formulierung mit dem Feldstärketensor ermöglichte es später, effektiv mit relativistischen Transformationen in der Elektrodynamik umzugehen.
So ist es auch bei der Supersymmetrie: Man muss sie nicht mit Superfeldern auf einem Superraum formulieren, aber es erleichter die Sache ungemein. Die zusätzlichen Grassmann-Dimensionen des Superraums sind dabei aber wohl eher formaler Natur und haben nach heutigem Wissen wohl keine direkte physikalische Bedeutung.
© Jörg Resag, www.joerg-resag.de
last modified on 12 December 2023