Kapitel 13
Topologie und Differentialformen: de-Rham-Kohomologie und harmonische Formen

• Gebiete ohne Löcher und das Lemma von Poincaré
• Beispiel mit Loch: das Magnetfeld eines stromführenden Leiters
• Topologie und die de Rham'sche Kohomologiegruppe
• Beispiele für de Rham'sche Kohomologiegruppen
• Der Satz von Hodge

Gebiete ohne Löcher und das Lemma von Poincaré

Wir hatten in Kapitel 11: Höhere Differentialformen und der Integralsatz von Stokes das Lemma von Poincaré kennengelernt. Es besagt, dass auf einem sternförmigen Gebiet jede geschlossene p-Form zugleich exakt ist.

Das bedeutet: wenn eine p-Form $\omega$ auf einem sternförmigen Gebiet die Integrabilitätsbedingung $$d\omega =0$$ erfüllt, so besitzt sie dort eine Stammform (ein Potential) $\pi$ mit $$\omega =d\pi$$ Umgekehrt gilt auf jedem Gebiet: Ist eine p-Form exakt, so ist sie auch geschlossen, denn die zweifache Anwendung des d-Operators ergibt wegen der Symmetrie der zweiten Ableitungen und der Antisymmetrie der Formen immer Null. Notieren wir also in Kurzform:

Lemma von Poincaré: G sternförmiges Gebiet und $$d\omega =0$$ $\Rightarrow$ es gibt Stammform $\pi$ mit $$\omega =d\pi$$ Immer gilt: $$\omega =d\pi \Rightarrow d\omega =0$$

Besitzt nun jede geschlossene Form $\omega$ (d.h. $d\omega =0$ ) eine Stammform? Zumindest steht im Lemma von Poincaré eine Zusatzbedingung: das betrachtete Gebiet $G$ muss sternförmig sein. Im wesentlichen bedeutet das, dass $G$ keine Löcher enthalten darf.

Schauen wir uns dazu ein Gegenbeispiel an, bei dem $G$ nicht sternförmig ist:

Beispiel mit Loch: das Magnetfeld eines stromführenden Leiters

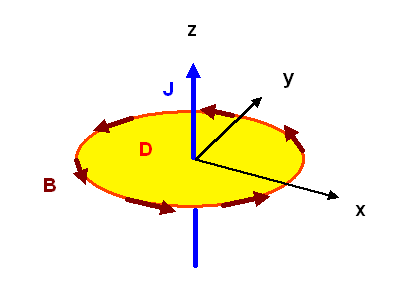
In der Elektrodynamik kennt man das Magnetfeld $\mathit{B}$ eines geraden unendlich langen Leiters, den wir uns als unendlich dünnen Draht in z-Richtung vorstellen. Das Magnetfeld umschließt diesen Leiter ringförmig, wobei die Feldlinien senkrecht zur z-Achse stehen. Die entsprechende Formel erhält man aus der statischen Maxwellgleichung $$\mathrm{r}\mathrm{o}\mathrm{t}\mathit{B}=\mathit{j}/c$$ indem man eine kreisförmige Fläche $D$ senkrecht zur z-Achse betrachtet und den Integralsatz von Stokes in ebenen Polarkoordinaten $$x=r\cos \theta$$ $$y=r\sin \theta$$ auswertet: $${\int }_{\mathrm{\partial }D}⟨\mathit{B},\mathit{d}\mathit{x}⟩={\int }_D⟨\mathit{j}/c,\mathit{d}\mathit{A}⟩$$

Wir stellen uns nun vor, dass der Leiter unendlich dünn wird, also gleichsam mit der z-Achse verschmilzt, und betrachten das Magnetfeld außerhalb der z-Achse, d.h. die Kreisscheibe $D$ soll einen Radius ungleich Null haben. Das Integral $${\int }_D⟨\mathit{j}/c,\mathit{d}\mathit{A}⟩$$ auf der rechten Seite ist dann gleich dem Gesamtstrom $I$ durch den Leiter (Vorfaktoren ignorieren wir). Setzt man rechts den Ansatz $$\mathit{B}=|\mathit{B}|{\mathit{e}}_{\theta }$$ ein mit $${\mathit{e}}_{\theta }=\left(\begin{array}{c}-\sin \theta \\ \cos \theta \\ 0\end{array}\right)$$ so erhält man $$2\pi r|\mathit{B}|=I$$ oder nach $|\mathit{B}|$ freigestellt $$\mathit{B}=\frac{a}{r}{\mathit{e}}_{\theta }=\frac{a}{r^2}\left(\begin{array}{c}-y\\ x\\ 0\end{array}\right)$$ mit $a=\frac{I}{2\pi }$ und dem Abstand $r$ von der z-Achse.

Da die gesamte Anordnung nicht von z abhängt, genügt es, sich eine Ebene senkrecht zur z-Achse herauszusuchen, so wie dies die Kreißcheibe $D$ im obigen Bild andeutet. Im Ursprung liegen dann (unendlich dicht zusammengedrängt) die Durchstoßpunkte der 2-Form $j$, die den Stromfluss repräsentiert, und gegen den Uhrzeigersinn verlaufen kreisförmig die Feldlinien von $\mathit{B}$.

Die entsprechende 1-Form lautet: $$B=⟨\mathit{B},\mathit{d}\mathit{x}⟩=\frac{a}{r^2}(-ydx+xdy)$$ Sie ist nur außerhalb des Ursprungs definiert, also in ${\mathbb{R}}^2\setminus \{0\}$. Unser betrachtetes Gebiet hat also im Ursprung ein Loch! Überall in diesem Gebiet (ohne den Ursprungspunkt $0$ ) gilt nun die Gleichung $$dB=0$$ d.h. $B$ ist geschlossen.

Das muss auch so sein, denn wir waren ja von der Gleichung $\mathrm{r}\mathrm{o}\mathrm{t}\mathit{B}=\mathit{j}/c$ ausgegangen und hatten dann die Stromflussdichte $\mathit{j}$ auf einen unendlich dünnen Bereich um die z-Achse herum beschränkt, so dass überall außerhalb der z-Achse $\mathrm{r}\mathrm{o}\mathrm{t}\mathit{B}=0$ erfüllt ist.

Und jetzt sind wir zur entscheidenden Frage vorgestoßen: Hat die 1-Form $B$ eine Stammform?

Wir suchen also eine 0-Form (eine Funktion) $\varphi$, so dass $$d\varphi =B$$ ist, oder anders ausgedrückt: $$\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi =\mathit{B}$$ Vorsicht! Hier darf man sich nicht verwirren lassen. Wir suchen hier keine Stammform zur 2-Form $$⟨\mathit{B},\mathit{d}\mathit{A}⟩$$ Eine solche Stammform existiert nämlich wegen $$d⟨\mathit{B},\mathit{d}\mathit{A}⟩=(\mathrm{d}\mathrm{i}\mathrm{v}\mathit{B})dV=0$$ immer! Man nennt diese Stammform oft $$A:=⟨\mathit{A},\mathit{d}\mathit{x}⟩$$ und bezeichnet $\mathit{A}$ als Vektorpotential von $\mathit{B}$ (nicht mit dem Flächenelement $\mathit{d}\mathit{A}$ verwechseln!). Das ist hier also nicht gesucht!

Wir suchen vielmehr eine Stammform zur 1-Form $$B=⟨\mathit{B},\mathit{d}\mathit{x}⟩$$ die (zur Unterscheidung von der 2-Form) auch oft mit $H$ bezeichnet wird.

Eine solche Stammform (Stammfunktion) der 1-Form $B$ ist scheinbar nicht schwierig zu finden: sie lautet $$\varphi (x,y)=b\theta$$ mit einer geeigneten Konstante $b$.

Die Funktion verläuft also wie eine Wendeltreppe, die gegen den Uhrzeigersinn mit wachsendem Winkel $\theta$ ansteigt. Ihr Anstieg verläuft daher kreisförmig entlang der Feldlinien von $\mathit{B}$. In drei Dimensionen haben wir das entsprechende Bild im letzten Kapitel bereits gesehen; wir zeigen es hier erneut (siehe das Bild rechts):

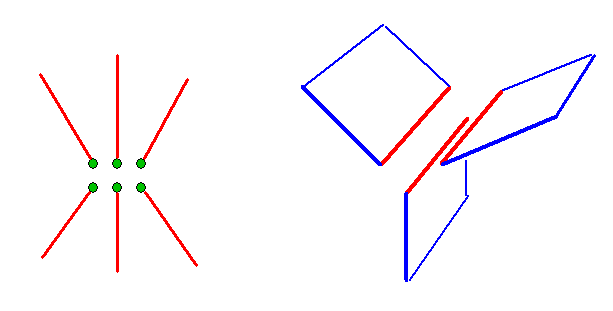
Die blauen 2-Flächen, die die 1-Form B im rechten Bild darstellen, entsprechen den Flächen mit konstanten $\varphi$, und die roten Entstehungskanten dieser Flächen entsprechen der 1-Flussform $J$.

Da wir in unserem Beispiel alle Entstehungskanten in der z-Achse zusammengeschoben haben, gilt außerhalb der z-Achse $dB=0$. In unserer zweidimensionalen x-y-Schnittfläche senkrecht zur z-Achse werden aus den Entstehungskanten die Durchtoßpunkte von $J$ im Ursprung, und aus den Flächen von $B$ werden die radial verlaufenden Schnittlinien dieser Flächen mit unserer zweidimensionalen x-y-Ebene. Diese Schnittlinien stellen in der x-y-Ebene die 1-Form $B$ dar. Gleichzeitig sind die Schnittlinien die Äquipotentiallinien von $\varphi$, also gleichsam die Treppenstufen der Wendeltreppe, wie das folgende Bild darstellt:

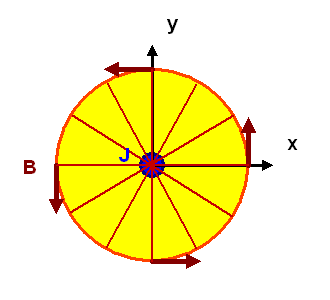
Es gibt allerdings ein Problem: Was geschieht nach einem Umlauf? Es entsteht ein Sprung in der Funktion $\varphi$, denn die Wendeltreppe befindet sich ja nun eine Etage höher! Und das bedeutet: es gibt eben keine in ganz ${\mathbb{R}}^2\setminus \{0\}$ definierte Stammform von $B$!

Die Ursache für das Fehlen einer Stammform ist das Loch im Ursprung. Hier konnten wir die Stromquelle für unser Magnetfeld verstecken!

Topologie und die de Rham'sche Kohomologiegruppe

Halten wir also fest: Bei nicht-sternförmigen Gebieten (z.B. bei vorhandenen Löchern) gilt das Lemma von Poincaré nicht! Wählen wir dagegen ein Teilgebiet des ${\mathbb{R}}^2$, das den Ursprung nicht enthält oder umschließt, so gilt das Lemma von Poincaré wieder, denn dann ist $\varphi (x,y)=b\theta$ eine in diesem Teilgebiet wohldefinierte Funktion.

Das ist interessant: offenbar können uns Differentialformen etwas über die großräumige Struktur (die Topologie) einer Mannigfaltigkeit sagen!

Schauen wir uns diesen Zusamenhang etwas genauer an:

Wir haben gerade gesehen, dass uns insbesondere geschlossenen p-Formen (also $d\omega =0$ ) etwas über die Topologie der Mannigfaltigkeit verraten können. Die Eigenschaft, dass sie keine Stammform besitzen, zeigt die Existenz von Löchern in der Mannigfaltigkeit an.

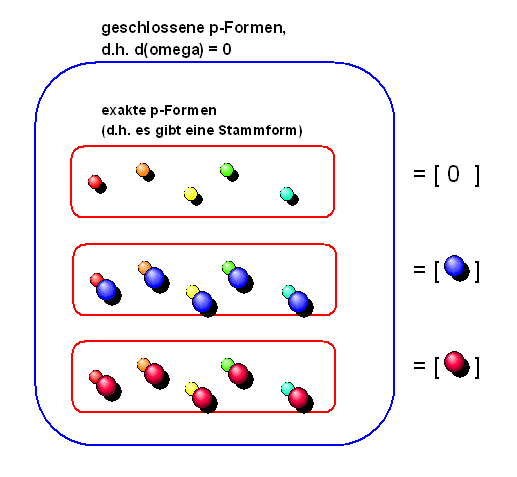
Die Menge der geschlossenen p-Formen der Mannigfaltigkeit $M$ wollen wir im Folgenden mit $${\mathrm{\Theta }}^p(M)$$ bezeichnen (nicht mit dem Winkel $\theta$ von oben verwechseln!).

Die geschlossenen p-Formen können wir nun in verschiedene Untergruppen (Teilmengen) aufteilen. Die Idee dabei ist folgende:

Wir interessieren uns für Integrale $${\int }_{\mathrm{\partial }G}\omega$$ geschlossener p-Formen über den Rand $\mathrm{\partial }G$ eines Gebietes $G$ (das aber ein Loch enthalten darf; korrekter wäre es daher, statt vom Rand $\mathrm{\partial }G$ besser von einer geschlossenen Kette (closed chain) zu sprechen; wichtig ist dabei die Eigenschaft, dass diese Kette keinen Rand besitzt, d.h. $\mathrm{\partial }\mathrm{\partial }G=\varnothing$ ).

Wenn nun das Gebiet G kein Loch enthält, d.h. wenn $G$ eine berandete Mannigfaltigkeit im Sinne des Integralsatzes von Stokes ist, so gilt nach diesem Integralsatz: $${\int }_{\mathrm{\partial }G}\omega ={\int }_{G}d\omega =0$$ Das bedeutet umgekehrt: Wenn $${\int }_{\mathrm{\partial }G}\omega \ne 0$$ ist (und natürlich $d\omega =0$ ), so kann $\mathrm{\partial }G$ nicht der Rand einer Mannigfaltigkeit (eines Gebietes) $G$ im Sinne des Integralsatzes von Stokes sein, d.h. $G$ enthält beispielsweise ein Loch.

Nun gibt es aber geschlossene p-Formen, bei denen das obige Integral immer gleich Null ist: die exakten p-Formen, also diejenigen Formen mit einer zugehörigen Stammform $\pi$, so dass $$\omega =d\pi$$ gilt. In diesem Fall ist nämlich $${\int }_{\mathrm{\partial }G}\omega ={\int }_{\mathrm{\partial }G}d\pi ={\int }_{\mathrm{\partial }\mathrm{\partial }G}\pi =0$$ da $\mathrm{\partial }G$ als geschlossene Kette oder als Rand eines Gebietes selbst keinen Rand hat.

Beispielsweise ist das Integral einer exakten 1-Form $d\varphi$ über einen geschlossenen Weg Null, da Anfangs- und Endpunkt des Weges identisch sind (anders gesagt: der geschlossene Weg hat keinen Rand, also keine verschiedenen Anfangs- und Endpunkte).

Daher kann man zu jeder geschlossenen p-Form $\omega$ eine exakte p-Form $d\pi$ hinzuaddieren, ohne dass sich der Wert von ${\int }_{\mathrm{\partial }G}\omega$ ändert: $${\int }_{\mathrm{\partial }G}(\omega +d\pi )={\int }_{\mathrm{\partial }G}\omega +{\int }_{\mathrm{\partial }G}d\pi ={\int }_{\mathrm{\partial }G}\omega$$ Man kann daher auch sagen:

• Alle geschlossenen p-Formen $\omega$, die sich nur um eine exakte p-Form $d\pi$ unterscheiden, ergeben dasselbe Integral über eine geschlossene Kette (z.B. einen geschlossenen Weg oder über den Rand eines Gebietes) und enthalten daher dieselbe Information über die topologische Struktur (z.B. Löcher) innerhalb dieser Kette. Exakte p-Formen $d\pi$ enthalten keine topologische Information. Das passt zu unserer Beobachtung oben, dass die Nichtexistenz einer Stammform (also die Nicht-Exaktheit der p-Form) auf Löcher in der Mannigfaltigkeit hinweist.

Es ist daher naheliegend, alle geschlossenen p-Formen jeweils zu einer Gruppe (Äquivalenzklasse) zusammenzufassen, wenn sie sich nur um eine exakte p-Form unterscheiden. Halten wir fest:

de Rham'sche Kohomologiegruppe: In einer Äquivalenzklassen $[\omega ]$ fassen wir jeweils alle diejenigen geschlossenen p-Formen zusammenzufassen, die sich nur um eine exakte p-Form unterscheiden. Dabei ist $\omega$ ein beliebiges Element der Äquivalenzklasse, das wir als Repräsentanten der Klasse auswählen. Formal ist also $$[\omega ]:=\{\sigma \in {\mathrm{\Theta }}^p(M):\mathrm{\exists }d\pi :\sigma =\omega +d\pi \}$$ (zur Erinnerung: ${\mathrm{\Theta }}^p(M)$ waren die geschlossenen p-Formen auf $M$, d.h. $d\omega =0$ ). Die Menge all dieser Äquivalenzklassen mit festem p bezeichnen wir mit $$H^p(M)$$ Diese Menge trägt den Namen p-te de Rham'sche Kohomologiegruppe, wobei sich der Gruppenbegriff auf die Addition von p-Formen bezieht. Mathematiker verwenden für diese Mengenbildung aus Äquivalenzklassen auch gerne den Begriff Quotientenraum und schreiben $$H^p(M):={\mathrm{\Theta }}^p(M)/d{\mathrm{\Theta }}^{p-1}(M)$$ Dabei ist $d{\mathrm{\Theta }}^{p-1}(M)$ die Menge der exakten p-Formen auf M, also diejenigen Formen mit einer Stammform, wobei wir für den Fall p = 0 die Festlegung $d{\mathrm{\Theta }}^{-1}(M):=\{0\}$ verwenden (dabei ist $0$ die Nullfunktion, die überall den Wert Null hat). Die Menge $d{\mathrm{\Theta }}^{p-1}(M)$ im formalen Nenner enthält also gleichsam die unwichtige Information, die man gerne aus der Menge ${\mathrm{\Theta }}^p(M)$ herausdividieren möchte, indem man die Elemente mit derselben wichtigen Information zu Äquivalenzklassen zusammenfasst (die Elemente innerhalb einer Äquivalenzklasse unterscheiden sich dann nur noch durch die unwichtige Information). Die Elemente von $H^p(M)$ sind also Gruppen von geschlossenen 1-Formen, die pro Gruppe dieselbe topologische Information tragen. Das Integral $${\int }_{\mathrm{\partial }G}\omega$$ hat für alle $\omega$ einer bestimmten Äquivalenzklasse denselben Wert, ist also letztlich eine Funktion der Äquivalenzklasse und nicht der einzelnen $\omega$.

Beispiele für de Rham'sche Kohomologiegruppen

Man bezeichnet das Studium von Mannigfaltigkeiten mittels Kohomologiegruppen als algebraische Topologie, da algebraische bzw. analytische Werkzeuge wie Differentialformen für topologische Untersuchungen eingesetzt werden. Schauen wir uns beispielhaft an, welche topologischen Informationen in den Kohomologiegruppen stecken:

Betrachten wir unser Beispiel von oben: die zweidimensionale reelle Ebene ohne den Nullpunkt $$M={\mathbb{R}}^2\setminus \{0\}$$ Beginnen wir mit den geschlossenen Null-Formen, also den skalaren Funktionen $\varphi$ mit $d\varphi =0$. Hier entfällt die Bildung von Äquivalenzklassen, da es keine (- 1)-Formen gibt – entsprechend hatten wir oben $$d{\mathrm{\Theta }}^{-1}(M):=\{0\}$$ gesetzt. Aus $d\varphi =0$ folgt, dass $\varphi$ auf ${\mathbb{R}}^2\setminus \{0\}$ konstant ist. Zu jeder reellen Zahl $a$ gibt es eine solche konstante Funktion und umgekehrt. Die Menge der geschlossenen Null-Formen entspricht also hier der Menge der reellen Zahlen: $$H^0({\mathbb{R}}^2\setminus \{0\})\sim \mathbb{R}$$ (das Zeichen $\sim$ bedeutet hier soviel wie ist isomorph zu, lässt sich also eins-zu-eins aufeinander abbilden).

Daraus kann man die Anzahl der Zusammenhangskomponenten von ${\mathbb{R}}^2\setminus \{0\}$ ablesen: sie ist gleich 1, da alle Punkte über Wege miteinander verbunden werden können. Bei Mannigfaltigkeiten $M$ mit k Zusammenhangskomponenten ist dagegen $$H^0(M)\sim {\mathbb{R}}^k$$ da eine konstante Funktion durch k reelle Zahlen dargestellt werden muss (nämlich für jede Zusammenhangskomponente durch die reelle Zahl, die den Funktionswert dort angibt).

Weiter geht es mit den geschlossenen 1-Formen auf ${\mathbb{R}}^2\setminus \{0\}$. Diese 1-Formen sehen (bis auf die unwichtige Addition einer exakten 1-Form $d\pi$) wegen der Bedingung $d\omega =0$ alle wie unsere Magnetfeld-1-Form von oben aus: $$\omega =⟨\mathit{B},\mathit{d}\mathit{x}⟩=\frac{a}{r^2}(-ydx+xdy)$$ Dabei entspricht $a$ bis auf einen Faktor dem senkrecht durch den Ursprung fließenden Strom $I$, d.h. $a$ kann jede reelle Zahl annehmen (das Vorzeichen bestimmt dabei die Stromrichtung). Zu jeder reellen Zahl $a$ gehört also eindeutig eine 1-Form-Äquivalenzklasse $[\omega ]$ mit dem obigen Repräsentanten und umgekehrt. In diesem Sinne entspricht die Menge der geschlossenen 1-Form-Äquivalenzklassen der Menge der reellen Zahlen und wir schreiben: $$H^1({\mathbb{R}}^2\setminus \{0\})\sim \mathbb{R}$$ Man kann daraus die Zahl der null-dimensionalen Löcher (also die Zahl der fehlenden Einzelpunkte) ablesen: sie ist gleich 1 (enstprechend $\mathbb{R}={\mathbb{R}}^1$).

Ohne das Loch im Ursprung wäre dagegen $$H^1({\mathbb{R}}^2)=\{[0]\}\sim \{0\}$$ Dabei ist $[0]$ die Äquivalentklasse der 1-Form $\omega =0$, also die Klasse der exakten 1-Formen. Der Grund dafür ist klar: Ohne ein Loch ist die Menge ${\mathbb{R}}^2$ sternförmig, d.h. nach dem Lemma von Poincaré ist jede geschlossene Form auch zugleich exakt und gehört damit zu $[0]$. Es besteht ohne Löcher einfach nicht die Möglichkeit, Ströme gleichsam in den Löchern zu verstecken und so neue geschlossene 1-Formen zu erzeugen, die an den Löchern auch Pole (Singularitäten) aufweisen dürfen. So kann man verstehen, dass Löcher die Zahl der möglichen Differentialform-Sorten erhöhen und dass umgekehrt die möglichen Differentialform-Sorten (genau das ist nämlich die de Rham'sche Kohomologiegruppe) Auskunft über die vorhandenen Löcher geben.

Hier noch einmal das Lemma von Poincaré in der Sprache der Kohomologiegruppen:

Lemma von Poincaré: $$H^0({\mathbb{R}}^n)\sim \mathbb{R}$$ weil ${\mathbb{R}}^n$ genau eine Zusammenhangskomponente besitzt und man die konstanten Funktionen daher durch eine einzige reelle Zahl (den Funktionswert) charakterisieren kann (siehe oben). $$H^p({\mathbb{R}}^n)=\{[0]\}\sim \{0\}$$ (mit $p>0$), weil ${\mathbb{R}}^n$ sternförmig ist und daher jede geschlossene p-Form eine Stammform besitzt, d.h. jede geschlossene Form ist äquivalent zur Form $\omega =0$.

Zurück zu unseren obigen Überlegungen mit Löchern:

Wie sieht der Fall mit mehreren Löchern aus? Bei k verschiedenen Löchern hätte man für jedes Loch eine 1-Form wie oben mit einem ringförmig um das Loch laufenden Magnetfeld. Jede dieser 1-Formen wäre durch eine reelle Zahl (entsprechend dem durch das Loch fließenden Strom) gekennzeichnet. Die allgemeine 1-Form wäre dann die Summe dieser 1-Formen, entsprechend der Superposition der Magnetfelder, plus eine irrelevante exakte 1-Form $d\pi$. Diese allgemeine 1-Form wird durch die k reellen Zahlen charakterisiert, die die Stromstärken in den k Löchern darstellen. Daher schreiben wir analog zu oben: $$H^1({\mathbb{R}}^2\setminus \{p_1,p_2,...,p_k\})\sim {\mathbb{R}}^k$$ Diese Überlegung kann man auf den n-dimensionalen Raum erweitern. Es gilt: $$H^{n-1}({\mathbb{R}}^n\setminus \{p_1,p_2,...,p_k\})\sim {\mathbb{R}}^k$$ Der Beweis dazu ist für $n>2$ keineswegs trivial, sondern er ist eine Konsequenz aus einem tiefer liegenden Satz der Differentialtopologie, dem sogenannten Gradsatz von Hopf.

Ist nun die de Rham'sche Kohomologiegruppe etwas Exotisches oder etwas Zentrales im Bereich der Topologie? Es stellt sich heraus, dass sie etwas Zentrales ist, denn man kann zeigen, dass für eine kompakte Mannigfaltigkeit (also gleichsam endliche Mannigfaltigkeit; diese Voraussetzung ist wichtig!) die de Rham'sche Kohomologiegruppe mit anderen Kohomologiekonzepten übereinstimmt, für die die Topologie-Experten eine Vielzahl anderer Berechnungsmethoden kennen (siehe z.B. John Baez: This Week's Finds in Mathematical Physics (Week 182) June 19, 2002). Wer sich also mit der Topologie von Räumen befasst, wird sich oft gerne der de Rham'schen Kohomologiegruppe bedienen. Daher spielt sie auch in der mathematischen Physik (besonders in der Stringtheorie) durchaus eine Rolle.

Der Satz von Hodge

Um mit Hilfe der de Rham'schen Kohomologiegruppe etwas über die Topologie der Mannigfaltigkeit aussagen zu können, benötigt man allerdings einen Überblick über die Differentialformen, die auf der Mannigfaltigkeit möglich sind, oder genauer: einen Überblick über die verschiedenen Differentialform-Typen, die sich um mehr als nur eine exakte Form unterscheiden. Mit anderen Worten: man muss die de Rham'sche Kohomologiegruppe erst einmal haben!

Zum Glück kennt man eine Möglichkeit, wie man hier vorgehen kann:

Es gibt eine Differentialgleichung für p-Formen, deren Lösungen jeweils genau die verschiedenen Differentialform-Typen darstellen. Die Lösungen der Differentialgleichung ergeben jeweils genau einen Repräsentanten pro Äquivalenzklasse. Der Lösungsraum der Differentialgleichung ist also isomorph zur de Rham'schen Kohomologiegruppe.

Das ist sehr gut, denn nun kann man das Arsenal der Differentialgleichungen auf topologische Fragestellungen anwenden. Zwei Bereiche der Mathematik (Analysis und Topologie) berühren und bereichern sich hier gegenseitig, was zu vielen tieferen Einsichten führt.

Die gesuchte Differentialgleichung ist eine Verallgemeinerung der sogenannten Laplace-Gleichung, wie man sie beispielsweise für ein statisches elektrisches Potential $\varphi$ kennt. Hier ist diese bekannte Laplace-Gleichung (auch Potentialgleichung genannt): $$\mathrm{\Delta }\varphi =0$$ Dabei ist der Laplace-Operator $\mathrm{\Delta }$ definiert als $$\mathrm{\Delta }\varphi =\mathrm{d}\mathrm{i}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi )$$ und $\varphi$ ist eine skalare Funktion.

In der Elektrostatik ist beispielsweise $\varphi$ das Potential eines statischen elektrischen Feldes $\mathit{E}$, also $$\mathit{E}=\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi$$ (das sonst hier übliche Minuszeichen lassen wir aus Vereinfachungsgründen weg – es entspricht nur einer Richtungskonvention für das elektrische Feld), so dass $$\mathrm{\Delta }\varphi =\mathrm{d}\mathrm{i}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi )=\mathrm{d}\mathrm{i}\mathrm{v}\mathit{E}$$ ist. Die Laplacegleichung $\mathrm{\Delta }\varphi =0$ ist also gleichbedeutend mit $$\mathrm{d}\mathrm{i}\mathrm{v}\mathit{E}=0$$ d.h. $\mathit{E}$ ist ein statisches elektrisches Feld im ladungsfreien Raum ist das elektrostatische Potential dazu.

Meist wird dieses $\varphi$ dann durch irgendwelche Randwerte festgelegt, beispielsweise durch vorgegebene Potentialwerte auf Kondensatorplatten. Ein anderes Beispiel ist das Potential einer Punktladung, die man im Ursprung versteckt. Man betrachtet dann die Potentialgleichung in ${\mathbb{R}}^3\setminus \{0\}$.

Insgesamt verhält sich $\varphi$ aufgrund der Laplacegleichung sehr ähnlich zu einer Seifenblasenhaut, die man zwischen irgendwelchen Drähten einspannt (was die Randbedingungen ergibt). Es dürfen nirgendwo Berge oder Mulden in $\varphi$ vorhanden sein, da dies Quellen des elektrischen Feldes und damit Ladungen entsprechen würde.

Wenn wir die Operatoren div und grad in die Sprache der Differentialformen übersetzen (siehe Kapitel 12: Hodge-Sternoperator, Volumenform, Gradient, Divergenz, Rotation ), so ist $$d\varphi =:{\omega }^{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi }$$ $$d\varphi =⟨\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi ,\mathit{d}\mathit{x}⟩$$ $$d\star {\omega }^E=:(\mathrm{d}\mathrm{i}\mathrm{v}\mathit{E})dV$$ $$d⟨\mathit{E},\mathit{d}\mathit{A}⟩=(\mathrm{d}\mathrm{i}\mathrm{v}\mathit{E})dV$$ Die zweite und vierte Zeile zeigt jeweils die Schreibweise, wie man sie in der klassischen euklidischen dreidimensionalen Vektoranalysis kennt. Wir können nun Gradient und Divergenz kombinieren: $$d\star d\varphi =d\star {\omega }^{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi }=$$ $$=(\mathrm{d}\mathrm{i}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi ))dV=$$ $$=(\mathrm{\Delta }\varphi )dV$$
$$d\star d\varphi =d\star ⟨\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi ,\mathit{d}\mathit{x}⟩=$$ $$=d⟨\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi ,\mathit{d}\mathit{A}⟩=$$ $$=(\mathrm{d}\mathrm{i}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\varphi ))dV=$$ $$=(\mathrm{\Delta }\varphi )dV$$ Um die Volumenform $dV$ noch zu entfernen, können wir noch einmal den Sternoperator anwenden. Wegen $$\star dV=(-1{)}^s$$ (siehe Kapitel 12: Hodge-Sternoperator, Volumenform, Gradient, Divergenz, Rotation, $s$ ist die Zahl der negativen Eigenwerte der metrischen Matrix bzw. das Vorzeichen der Determinante dieser Matrix) erhalten wir: $$\star d\star d\varphi =(\mathrm{\Delta }\varphi )\star dV=(\mathrm{\Delta }\varphi )(-1{)}^s$$ oder anders sortiert $$\mathrm{\Delta }\varphi =(-1{)}^s\star d\star d\varphi$$ Den Operator $\star d\star d$ können wir nun nicht nur auf skalare Funktionen anwenden, sondern auf beliebige p-Formen: $d$ macht aus der p-Form eine (p + 1) -Form, $\star$ verwandelt sie in eine (n - p - 1) -Form, das nächste $d$ macht daraus eine (n - p) -Form, und $\star$ darauf angewendet ergibt schließlich eine p-Form.

Aus einer p-Form wird also durch $\star d\star d$ wieder eine p-Form.

Nur im Fall $p=n$ (dabei ist wie immer $n$ die Dimension der Manngfaltigkeit) gibt es Schwierigkeiten, denn das erste $d$ macht aus einer n-Form im n-dimensionalen Raum eine Null.

Man kann jedoch einen zu $\star d\star d$ eng verwandten Operator konstruieren, der die Lücke schließt, indem man einfach die Reihenfolge der Sternoperatoren und der d-Operatoren vertauscht: $$d\star d\star$$ Aus einer n-Form wird dabei erst einmal eine 0-Form gemacht, mit der es dann wie beim ursprünglichen Operator weitergeht (nur dass man auf letzten Stern verzichtet, so dass es eine n-Form bleibt). Schreiben wir die n-Form als $\phi dV$ mit einer skalaren Funktion $\phi$, so ergibt sich $$d\star d\star (\phi dV)=d\star d\phi (-1{)}^s=$$ $$=(\mathrm{\Delta }\phi )dV(-1{)}^s$$ Allerdings hat der neue Operator ebenfalls eine Lücke, nämlich bei den Null-Formen. Der Sternoperator verwandelt Null-Formen in n-Formen, und der anschließende d-Operator macht aus ihnen wieder eine Null.

Wenn wir also eine Verallgemeinerung des Laplaceoperators von 0-Formen auf p-Formen suchen, so bietet es sich an, beide Operatoren oben zu addieren, wobei man noch eine bestimmte Vorzeichenkonvention trifft (die sich allerdings offenbar von Text zu Text unterscheiden):

Hodge-Laplace-Operator für p-Formen: $$\mathrm{\Delta }\omega :=(-1{)}^{[s+n(p-1)]}(\star d\star d+d\star d\star )\omega$$

Bei Null-Formen (Funktionen) fällt der zweite Operator weg und es ergibt sich der weiter oben definierte Laplace-Operator. Bei n-Formen fällt der erste Operator weg, und es gilt (siehe oben) $(-1{)}^{s}d\star d\star (\phi dV)=(\mathrm{\Delta }\phi )dV$, also im Wesentlichen wieder der weiter oben definierte Laplace-Operator. Die obige Definition scheint also wirklich eine vernünftige Verallgemeinerung des Laplace-Operators auf p-Formen zu ergeben.

Und damit sind wir auch schon bei unserer Differentialgleichung angekommen, deren Lösungsraum isomorph mit der de Rham'schen Kohomologiegruppe ist, denn es gilt der folgende beeindruckende Satz:

Satz von Hodge: Jede Äquivalenzklasse der de Rham'schen Kohomologiegruppe enthält einen eindeutigen Repräsentanten $\alpha$, der die Hodge-Laplace-Differentialgleichung $$\mathrm{\Delta }\alpha =0$$ erfüllt. Da man die Lösungen der Hodge-Laplace-Differentialgleichung auch als harmonische Formen bezeichnet, kann man auch sagen: Jede Äquivalenzklasse enthält eine eindeutig bestimmte harmonische Form. Die de Rham'schen Kohomologiegruppe ist isomorph (eins-zu-eins abbildbar) zum Lösungsraum der Hodge-Laplace-Differentialgleichung. Gleichwertig dazu ist auch die folgende Formulierung: Jede geschlossene p-Form $\omega$ (also $d\omega =0$) lässt sich eindeutig schreiben als Summe einer harmonischen Form und einer exakten Form: $$\omega =\alpha +d\pi$$ mit $\mathrm{\Delta }\alpha =0$.

Ich möchte diesen Satz hier nicht beweisen, aber es ist sicher interessant, zumindest einige Ideen kurz darzustellen, die hinter diesem Beweis stecken.

Die erste Idee besteht darin, ein Skalarprodukt auf dem Raum der p-Formen einzuführen. Die Basis dafür bildet die Definition des Hodge-Stern-Operators aus Kapitel 12: Hodge-Sternoperator, Volumenform, Gradient, Divergenz, Rotation: $$\alpha \wedge (\star \omega ):=g(\alpha ,\omega )dV$$ mit der Volumenform $dV$ und der punktweise definierten Metrik $g(\alpha ,\omega )$. Die obige Gleichung gilt separat in jedem Punkt $p$ der Mannigfaltigkeit, d.h. der Hodge-Stern-Operator ist punktweise definiert und benötigt keine Umgebungen von Punkten.

Für Differentialoperatoren benötigt man jedoch auch Umgebungen von Punkten. Daher verwenden wir die obige punktweise gegebene Gleichung und integrieren sie über alle Punkte der Mannigfaltigkeit bzw. geeigneter Teilgebiete. Da es sich insgesamt um n-Formen handelt, sind solche Integrale über geeignete Parametrisierungen (z.B. gegeben über die Koordinatenabbildungen) wohldefiniert. Auf diese Weise entsteht ein Skalarprodukt von p-Formen, das wir mit $(,)$ bezeichnen: $$(\alpha ,\omega ):=$$ $$={\int }_M\alpha \wedge (\star \omega )=$$ $$={\int }_{M}g(\alpha ,\omega )dV$$ Aus der Funktionalanalysis bzw. aus der Quantenmechanik kennt man den Begriff des adjungierten Operators, den man über ein Skalarprodukt definiert. Genauso definieren wir hier den adjungierten d-Operator, den wir mit $\delta$ bezeichnen: $$(\alpha ,\delta \omega ):=(d\alpha ,\omega )$$ Das Adjungieren wirft den Operator also gleichsam auf die andere Seite des Skalarproduktes. Nun muss auf beiden Seiten des Skalarproduktes eine Form gleichen Grades stehen. Um also $(d\alpha ,\omega )$ bilden zu können, muss zu einer p-Form $\alpha$ eine (p + 1) -Form $\omega$ hinzugenommen werden, da der d-Operator aus einer p-Form eine (p + 1) -Form macht.

Die linke Seite $(\alpha ,\delta \omega )$ macht daher nur Sinn, wenn der \delta-Operator aus einer (p + 1) -Form wieder eine p-Form macht. Dies sieht man auch an der expliziten Formel für den $\delta$-Operator, die sich aus der Definition ergibt: $$\delta =(-1{)}^{[s+n(p-1)]}\star d\star$$ Der Laplaceoperator ist damit gleich $$\mathrm{\Delta }=\delta d+d\delta$$ und er ist selbstadjungiert: $$(\alpha ,\mathrm{\Delta }\omega ):=(\mathrm{\Delta }\alpha ,\omega )$$ Man kann nun zeigen, dass folgende Äquivalenz gilt: $$\mathrm{\Delta }\omega =0$$ $$\iff$$ $$d\omega =0\mathrm{u}\mathrm{n}\mathrm{d}\delta \omega =0$$ Und nun kommt der entscheidende Schritt:

Man kann zeigen, dass die Menge der harmonischen Formen (d.h. es gilt $\mathrm{\Delta }\omega =0$ ) endlich-dimensional ist, und dass sich jede (nicht unbedingt geschlossene) p-Form eindeutig in die Summe einer harmonischen p-Form $\alpha$ (also $\mathrm{\Delta }\alpha =0$), einer exakten p-Form $d\pi$ und einer ko-exakten p-Form $\delta \eta$ zerlegen lässt: $$\omega =\alpha +d\pi +\delta \eta$$ mit $\mathrm{\Delta }\alpha =0$.

Wir können hierauf den d-Operator anwenden und dann verwenden, dass $dd\pi =0$ ist und $d\alpha =0$ ist (denn oben hatten wir bereits gesagt, dass $\mathrm{\Delta }\alpha =0$ äquivalent ist zu $d\alpha =0$ und $\delta \alpha =0$ ): $$d\omega =d\alpha +dd\pi +d\delta \eta =d\delta \eta$$ Für die geschlossenen p-Formen (also $d\omega =0$) ist dann also $d\delta \eta =0$ und somit auch $$(d\delta \eta ,\eta )=(\delta \eta ,\delta \eta )=0$$ Da das Skalarprodukt nicht entartet ist, folgt $\delta \eta =0$. Das setzen wir oben in $\omega =\alpha +d\pi +\delta \eta$ ein, so dass sich also die geschlossenen p-Formen eindeutig schreiben lassen als Summe einer harmonischen Form und einer exakten Form: $$\omega =\alpha +d\pi$$ Bei der Äquivalenzklassenbildung spielt $d\pi$ keine Rolle mehr: $$[\omega ]=[\alpha ]$$ d.h. die Elemente der de Rham'schen Kohomologiegruppe entsprechen eins-zu-eins den Lösungen der Hodge-Laplace-Gleichung. Genau das ist der Satz von Hodge.

Literatur:

• Dan Piponi: On the Visualisation of Differential Forms

• Selfridge, Arnold, Warnick: Electromagnetics
  Enthält eine sehr gute Veranschaulichung von Differentialformen im dreidimensionalen Raum und ihre Anwendung auf die Elektrodynamik.

• Karl F. Warnick, Richard H. Selfridge, and David V. Arnold: Electromagnetics Made Easy: Differential Forms as a Teskhing Tool

• Dirk Ferus: Analysis III

• How to Write Maxwell's Equations an a T-Shirt

• John Baez: This Week's Finds in Mathematical Physics (Week 182) June 19, 2002

• David Bachman: A Geometric Approach to Differential Forms, arXiv:math/0306194 [math.GT]