Höhere Differentialformen und der Integralsatz von Stokes werden in praktisch jedem Mathematikbuch der mehrdimensionalen Analysis in einem umfangreichen Kapitel ausführlich behandelt. Die Darstellungsweise ist jedoch zumeist recht abstrakt und formal, und oft versteht man den eigentlichen Hintergrund nicht wirklich. Der elegante Formalismus erscheint bisweilen wie Zauberei.
Das Thema ist andererseits für Mathematik und Physik sehr wichtig. Ich möchte daher in diesem Kapitel versuchen, den Schwerpunkt auf die Hintergründe und die anschauliche Interpretation zu legen. Längere Rechnungen und Beweise werde ich weglassen (diese findet man dann in den Standard-Lehrbüchern) und an ihre Stelle kurze Beweisskizzen und anschauliche Begründungen setzen.
Beginnen wir mit Objekten, die wir bereits aus Kapitel 5: Co-Tangentialräume und Differentialformen kennen: den Co-Tangentialvektoren, die wir auch als 1-Formen bezeichnet hatten. Eine kurze Wiederholung:
Der Co-Tangentialraum im Punkt \(p\) (also \(T^{*}(p)\) ) ist der Dualraum zum Tangentialraum \(T(p)\), d.h. \(T^{*}(p)\) ist der Vektorraum aller Linearformen auf dem Tangentialraum \(T(p)\).
Das bedeutet:
Jedes Element \(\omega(p)\) des Co-Tangentialraums ist eine lineare Abbildung auf dem Tangentialraum,
die jedem Tangentialvektor \(u(p)\) die reelle Zahl
\[
\omega(p) \, u(p)
\]
zuordnet.
Man kann jedes Element \(\omega\) des Co-Tangentialraums nach einer Basis \(dx^{\nu}|_{p}\) entwickeln, d.h. \[ \omega(p) = \sum_{\nu} \, \omega_{\nu}(p) \, dx^{\nu}|_{p} \] wobei die Basis \(dx^{\nu}|_{p}\) durch die Eigenschaft \[ dx^{\nu}|_{p} \, \frac{\partial}{\partial x^{\mu}}\bigg|_{p} = \delta^{\nu}_{\,\mu} \] festgelegt ist (die rechte Seite \(\delta^{\nu}_{\,\mu}\) ist 1 bei gleichen Indizes und 0 sonst).
Die Basis wird also wie beim Tangentialraum auch durch eine Koordinatenfunktion \(f\) in einer Umgebung von \(p\) auf der Mannigfaltigkeit festgelegt. Schreibt man \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}}\bigg|_{p} \] so folgt \[ \omega(p) \, u(p) = \sum_{\mu} \, \omega_{\mu}(p) \, u^{\mu}(p) \]
Man kann jeden Co-Tangentialvektor \(\omega(p)\) mit einer skalaren Funktion \(\phi\) in Verbindung bringen, die in einer Umgebung von \(p\) definiert sein muss. Wir schreiben \[ \omega(p) := d\phi(p) \] Das Änderungsverhalten von \(\phi\) im Punkt \(p\) (anschaulich: Verlauf und Dichte der Höhenlinien \(\phi\) beim Punkt \(p\)) legt dabei den Co-Tangentialvektor \(\omega(p)\) fest, d.h. \( d\phi(p) \) angewendet auf einen Tangentialvektor \(u(p)\) ergibt die Veränderungsrate von \(\phi\) in \(u(p)\)-Richtung: \[ d\phi(p) \, u(p) := u(p) \, \phi = \] \[ = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] Dabei ist \(u(p)\) der zur Kurve \(\gamma\) gehörende Tangentialvektor mit \( p = \gamma(0) \). Anschaulich ergibt \( d\phi(p) \) angewendet auf \(u(p)\), wie viele Höhenlinien von \(\phi\) man in \(u(p)\)-Richtung beim Weitergehen durchstößt.
Für die Entwicklung nach den Basisvektoren dx^{\nu}|_{p} bedeutet das: \[ d\phi(p) = \sum_{\nu} \, \frac{\partial \phi(f^{ -1}(x))}{\partial x^{\nu}} \, dx^{\nu}|_{p} \] mit \[ dx^{\nu}|_{p} \, u(p) = \frac{df^{\nu}(\gamma(t))}{dt} \bigg|_{t = 0} = u^{\nu}(p) \] (\(f\) ist dabei die Koordinatenfunktion oder Karte auf der Mannigfaltigkeit) oder in Physiker-Kurzschreibweise \[ \omega = d\phi = \sum_{\nu} \, \frac{\partial \phi}{\partial x^{\nu}} \, dx^{\nu} \] mit \[ dx^{\nu} \, u = \frac{d\gamma^{\nu}(t)}{dt} = u^{\nu} \] Diese Kurzschreibweise gilt zunächst für einen Punkt \(p\), also lokal. Es kann sein, dass man an verschiedenen Punkten auch verschiedene skalare Funktionen \(\phi\) mit entsprechendem Änderungsverhalten in diesen Punkten braucht. Dabei ist zunächst unklar, ob man diese Funktionen zu einer einzigen Funktion zusammensetzen kann. Wir werden uns etwas weiter unten noch genauer ansehen, wann das möglich ist, so dass \( \omega = d\phi \) für alle Punkte \(p\) eines Teilgebietes der Mannigfaltigkeit mit einer dort überall definierten skalaren Funktion \(\phi\) gilt.
In der Beziehung \( \omega(p) = d\phi(p) \) können wir \( d \) als einen Ableitungsoperator verstehen, denn das Änderungsverhalten von \(\phi\) im Punkt \(p\) legt \(\omega(p)\) fest. Man spricht bei der \(d\)-Ableitung auch von der äußeren Ableitung. Wenn wir skalare Funktionen als Null-Formen bezeichnen, so macht \( d \) demnach aus einer Null-Form eine Eins-Form. Weiter unten werden wir diese Vorgehensweise auch auf andere Differentialformen erweitern.
Noch eine Bemerkung:
Man kann sogar in dem Ausdruck \( dx^{\nu}|_{p} \)
das \( d \) vor dem \( x \) als den \(d\)-Ableitungsoperator verstehen, wenn wir unter \(x^{\nu}\)
die Koordinatenfunktion \( x^{\nu} = f^{ \nu}(p) \) verstehen,
denn es ist
\[
df^{\nu}(p) \, u(p) = u(p) \, f^{ \nu}
=
\]
\[
=
\frac{df^{ \nu}(\gamma(t))}{dt} \bigg|_{t = 0} =
\]
\[
= u^{\nu}(p)
= dx^{\nu}|_{p} \, u(p)
\]
Man sieht, wie die Schreibweisen elegant zusammenpassen.
Um \[ \omega(p) = \sum_{\nu} \, \omega_{\nu}(p) \, dx^{\nu}|_{p} \] auswerten zu können, benötigt man im Punkt \(p\) eine Richtung, d.h. eine Kurve \(\gamma\) und den dadurch gegebenen Tangentialvektor \(u(p)\). Man kann das auch so interpretieren, dass der Tangentialvektor (die Kurve) erst die Richtung angibt, in die man den infinitesimalen Schritt \( dx = (dx^{\nu}) \) gehen soll (mehr dazu gleich).
Das Ergebnis ist eine reelle Zahl. Schreibt man \( \omega(p) = d\phi(p) \), so ist diese Zahl gerade die Richtungsableitung von \(\phi\) in Kurvenrichtung.
Man könnte nun auf die Idee kommen, die durch die Kurve \(\gamma\) und die 1-Form \(\omega\) definierten reellen Zahlen entlang der Kurve \(\gamma\) aufzusummieren (genauer: aufzuintegrieren). Dabei setzen wir natürlich voraus, dass \(\omega\) entlang der Kurve überall definiert ist. Uns interessiert also das Integral \[ I_{ \gamma(T)} := \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \] wobei natürlich \( u(\gamma(t)) \) der Tangentialvektor der Kurve \(\gamma\) im Punkt \(\gamma(t)\) ist. Weiterhin soll \(T\) das Intervall von \(a\) bis \(b\) sein, also der Parameterbereich, über den integriert wird. Und schließlich wollen wir generell die Kurve in positiver Parameterrichtung durchlaufen, d.h. es soll \( a \le b \) sein. Damit ist die Schreibweise eindeutig definiert.
Was geschieht nun mit diesem Integral, wenn wir die Parametrisierung der Kurve \(\gamma\) verändern? Die Kurvenpunkte auf der Mannigfaltigkeit sind dabei dieselben. Es wird über dasselbe Kurvenstück integriert, aber die Kurve wird mit einer anderen Geschwindigkeit durchlaufen. Eine Einschränkung wollen wir noch machen: die Kurve soll immer noch in derselben Richtung durchlaufen werden, d.h. die Umparametrisierung soll die Orientierung des Kurvenstücks nicht ändern. Wir werden bald sehen, warum das wichtig ist.
Umparametrisierung bedeutet, dass wir vom Kurvenparameter \(t\) zu einem neuen Kurvenparameter \(t'\) übergehen. Wir stellen uns vor, dass \(t\) von \(t'\) abhängt, also \[ t = \varphi(t') \] mit einer (umkehrbaren) skalaren Funktion \(\varphi\). Die Kurve wird bzgl. der neuen Parametrisierung durch eine neue Funktion \(\rho(t')\) beschrieben, wobei \[ \gamma(t) = \gamma(\varphi(t')) =: \rho(t') \] sein soll, d.h. \[ \gamma \circ \varphi = \rho \] Da wir die Kurve in derselben Richtung (nur mit anderer Geschwindigkeit) durchlaufen wollen, muss \(\varphi\) eine monoton wachsende Funktion sein, d.h. ein wachsender Parameter \(t'\) führt zu einem wachsenden Parameter \(t\).
Für die Parametermengen \(T\) und \(T'\) gilt: \[ T = \varphi(T') \] Dabei ist \( \gamma(t) = \rho(t') \) gleich der Menge der Kurvenpunkte, die durchlaufen werden.
Analog analog zu oben können wir uns nun das folgende Integral ansehen, das sich auf die neue Kurvenfunktion \(\rho\) bezieht: \[ I_{\rho(T')} := \int_{a'}^{b'} \, [\omega(\rho(t')) \, v(\rho(t'))] \, dt' \] Dabei ist \( v(\rho(t')) \) Tangentialvektor zur Kurve \(\rho\) im Punkt \(\rho(t')\), und \( a = \varphi(a') \) sowie \( b = \varphi(b') \), so dass die Integration im selben Kurvenpunkt startet und endet wie beim Integral \( I_{ \gamma(T)} \) oben. Da \(\varphi\) monoton wachsend ist, gilt \(a' \le b' \), so wie wir das für unsere Schreibweise auch verlangt haben.
Es stellt sich nun die Frage, wie die beiden Integrale \(I_{\gamma(T)}\) und \(I_{\rho(T')}\) miteinander zusammenhängen. Versuchen wir daher, im Integral \(I_{\rho(T')}\) den Tangentialvektor \(v\) durch den Tangentialvektor \(u\) auszudrücken: \[ v(\rho(t')) \, \phi = \] \[ = \frac{d \phi(\rho(t'))}{dt'} = \] \[ = \frac{d \phi(\gamma(\varphi(t')))}{dt'} = \] \[ = \frac{d \phi(\gamma(t))}{dt} \, \frac{d \varphi(t')}{dt'} = \] \[ = [u(\gamma(t)) \, \phi] \, \frac{d \varphi(t')}{dt'} = \] \[ = [u(\gamma(\varphi(t'))) \, \phi] \, \frac{d \varphi(t')}{dt'} =: \] \[ =: \left[\frac{d \varphi(t')}{dt'} \, u(\gamma(\varphi(t')))\right] \, \phi \] Wenn wir eine Einbettung der Mannigfaltigkeit voraussetzen, ist diese Beziehung unmittelbar einsichtig, denn dann können Tangentialvektoren direkt als Ableitung der Kurve schreiben: \[ v(\rho(t')) = \frac{d\rho(t')}{dt'} = \] \[ = \frac{d\gamma(\varphi(t'))}{dt'} = \] \[ = \frac{d\gamma(t)}{dt} \, \frac{d\varphi(t')}{dt'} = \] \[ = u(\gamma(t)) \, \frac{d\varphi(t')}{dt'} = \] \[ = u(\gamma(\varphi(t'))) \, \frac{d\varphi(t')}{dt'} \] Physiker würden sogar noch kürzer einfach schreiben: \[ \frac{\boldsymbol{dx}}{dt'} = \frac{\boldsymbol{dx}}{dt} \, \frac{dt}{dt'} \] Fassen wir das Ergebnis noch einmal zusammen:
|
Transformation von Tangentialvektoren bei Parametertransformation der Kurve: Wir gehen von einer Kurve \( \gamma(t) \) aus mit zugehörigen Tangentialvektoren \( u(\gamma(t)) \). Nun wechseln wir zu einem neuen Kurvenparameter \(t'\), indem wir \(t\) als abhängig von \(t'\) betrachten: \[ t = \varphi(t') \] Die Kurve wird nun bezüglich \(t'\) durch die Funktion \[ \rho(t') := \gamma(\varphi(t')) = \gamma(t) \] beschrieben. Die zu \(\rho\) gehörenden Tangentialvektoren nennen wir \( v(\rho(t')) \). Dann gilt: \[ v(\rho(t')) = \frac{d\varphi(t')}{dt'} \, u(\gamma(\varphi(t'))) \] |
Dieses Ergebnis können wir nun im Integranden von \( I_{ \rho(T')} \)
einsetzen, wobei wir
zusätzlich ausnutzen, dass \(\omega\) eine lineare Abbildung ist, so dass wir
den Faktor \( \frac{d\varphi(t')}{dt'} \) herausziehen können. Im letzten Schritt
können wir
dann die Substitutionsregel für Integrale verwenden:
\[
I_{ \rho(T')} =
\]
\[ =
\int_{a'}^{b'} \, [\omega(\rho(t')) \, v(\rho(t'))] \, dt' =
\]
\[
=
\int_{a'}^{b'} \, \left[\omega(\gamma(\varphi(t'))) \,
\left( \frac{d\varphi(t')}{dt'} \, u(\gamma(\varphi(t'))) \right) \right] \, dt' =
\]
\[
=
\int_{a'}^{b'} \left[\omega(\gamma(\varphi(t'))) \,
u(\gamma(\varphi(t'))) \right] \, \frac{d\varphi(t')}{dt'} \, dt' =
\]
\[
=
\int_{a}^{b} [\omega(\gamma(t)) \, u(\gamma(t)) ] \, dt =
\]
\[
= I_{ \gamma(T)}
\]
Das Kurvenintegral ändert sich also bei der orientierungserhaltenden Umparametrisierung nicht.
Physiker würden übrigens die obige Rechnung vermutlich
in der folgenden intuitiven Kurzschreibweise durchführen:
\[
I_{ \rho(T')} =
\]
\[
=
\int_{a'}^{b'} \, \left[ \omega \, \frac{d\boldsymbol{x}}{dt'} \right] \, dt' =
\]
\[
=
\int_{a'}^{b'} \, \left[ \omega \, \left( \frac{d\boldsymbol{x}}{dt} \, \frac{dt}{dt'} \right) \right] \, dt' =
\]
\[
=
\int_{a'}^{b'} \, \left[ \omega \, \frac{d\boldsymbol{x}}{dt} \right] \, \frac{dt}{dt'} \, dt' =
\]
\[
=
\int_{a}^{b} \, \left[ \omega \, \frac{d\boldsymbol{x}}{dt} \right] \, dt =
\]
\[
= I_{ \gamma(T)}
\]
Anmerkung:
Hätten wir eine monoton fallende Funktion \(\varphi\) verwendet
(d.h. hätten wir die Orientierung des Kurvenstücks geändert),
so hätten wir an einer Stelle in der obigen Rechnung die
Integrationsgrenzen vertauschen müssen, da wir ja die Schreibweise
so festgelegt hatten, dass immer in aufsteigender Parameterrichtung integriert
wird. Das hätte zu einem Minuszeichen geführt:
Der Wechsel der Orientierung führt zu einem Vorzeichenwechsel im Integral!
Fassen wir zusammen:
|
Kurvenintegrale über 1-Formen sind unabhängig von der Parametrisierung der Kurve: Das Kurvenintegral \[ I_{ \gamma(T)} := \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \] (dabei ist \(T\) das Intervall von \(a\) bis \(b\) mit \( a \lt b \), \(t \in T\) und \(u(\gamma(t))\) ist der Tangentialvektor zur Kurve \(\gamma\) im Punkt \(\gamma(t)\) ) ändert sich nicht, wenn wir eine richtungserhaltende Umparametrisierung der Kurve vornehmen. Das bedeutet: Wenn wir \(t\) als Funktion eines neuen Kurvenparameters \(t'\) betrachten, d.h. \[ t = \varphi(t') \] mit einer streng monoton wachsender Funktion \(\varphi\), und die Kurve mit Hilfe des neuen Parameters \(t'\) durch die Funktion \[ \rho(t') := \gamma(\varphi(t')) = \gamma(t) \] beschreiben (d.h. dieselbe Kurve wird jetzt in einer anderen Geschwindigkeit durchlaufen), so ist \[ I_{ \gamma(T)} = I_{ \rho(T')} \] mit \[ I_{ \rho(T')} := \int_{a'}^{b'} \, [\omega(\rho(t')) \, v(\rho(t'))] \, dt' \] Dabei ist \( v(\rho(t')) \) Tangentialvektor zur Kurve \(\rho\) im Punkt \(\rho(t')\) (das ist gewissermaßen die neue Kurvengeschwindigkeit), und \( a = \varphi(a') \) sowie \( b = \varphi(b') \). Da \(\varphi\) als streng monoton steigend vorausgesetzt wurde, ist auch \( a' \lt b' \) gesichert, d.h. die Kurve wird auch nach dem Parameterwechsel in derselben Richtung durchlaufen. Als neue Schreibweise führen wir ein: \[ I_{ \gamma(T)} =: \int_{\gamma(T)} \omega \] Dieses Kurvenintegral hängt dabei nur von dem durchlaufenen Kurvenstück auf der Mannigfaltigkeit ab sowie von der Orientierung, in der es durchlaufen wird. Das Integral hängt nicht von der Geschwindigkeit ab, mit der das Kurvenstück durchlaufen wird, d.h. es ändert seinen Wert bei richtungserhaltenden Umparametrisierungen der Kurve nicht.
|
Wir haben oben bereits mehrfach den Begriff der Orientierung kennengelernt.
Hier noch einmal eine saubere Definition:
In Kapitel 9: Abstände und Winkel: die Metrik haben wir bereits ein sehr ähnliches Integral kennengelernt: Die Länge \( L_{\gamma(T)} \) eines Kurvenstücks \( \gamma \) zwischen zwei Punkten \( p_{a} := \gamma(a) \) und \( p_{b} := \gamma(b) \) (im Metrik-Kapitel hatten wir die Bezeichnung \(L(\gamma,a,b)\) verwendet). Sie ist definiert durch \[ L_{\gamma(T)} := \int_{a}^{b} \, \sqrt{ g( u(\gamma(t)), u(\gamma(t)) } \, dt \] (wieder ist \(u\) der Tangetialvektor der Kurve und \( a \lt b \)). Die obige Rechnung lässt sich hier analog wiederholen, wobei allerdings das Ergebnis nicht von der Richtung abhängt, in der man die Kurve durchläuft. Daher hängt \( L_{\gamma(T)} \) nicht von der Parametrisierung der Kurve ab, wobei hier auch richtungsändernde Umparametrisierungen erlaubt sind. Man könnte daher analog zu oben die Schreibweise \[ L_{\gamma(T)} = \int_{\gamma(T)} \sqrt{g} \] einführen. Allerdings ist der Integrand \( \sqrt{g} \) keine Differentialform (1-Form), denn er ist nicht linear im Tangentialvektor \(u(\gamma(t))\). Dennoch ist das Integral unabhängig von der Parametrisierung. Es gibt also über die Differentialformen hinaus durchaus weitere sinnvolle Integranden, die zu Parametrisierungs-unabhängigen Kurvenintegralen (oder später Flächenintegralen etc.) führen.
In der Physik schreibt man das Kurvenintegral \[ I_{ \gamma(T)} = \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \] gerne noch ein wenig um. Dazu zieht man formal das infinitesimale Parameterintervall \(dt\) in den Integranden hinein: \[ I_{ \gamma(T)} = \int_{a}^{b} \, [\omega(\gamma(t)) \, (u(\gamma(t)) \, dt)] \] Wenn man sich \(dt\) als sehr kleine reelle Zahl vorstellt, ist das ja erlaubt, da \(\omega\) linear ist. Dann ist \( u(\gamma(t)) \, dt \) gleichsam ein sehr kleiner Tangentialvektor (wobei der Begriff ohne Metrik natürlich noch gar nicht definiert ist).
Anschaulicher wird das, wenn man von einer Einbettung der Mannigfaltigkeit im \(\mathbb{R}^{n}\) ausgeht. Dann ist \( u(\gamma(t)) \, dt \) einfach ungefähr gleich dem Vektor, der vom Punkt \( \gamma(t) \) zum Punkt \( \gamma(t + dt) \) führt. Man könnte auch sagen, \( u(\gamma(t)) \, dt \) ist das kleine Wegstück zwischen den beiden Punkten. Wir wollen dieses Wegstück mit \( \boldsymbol{dx} \) bezeichnen, also \[ \boldsymbol{dx} := u(\gamma(t)) \, dt = \frac{d\gamma(t)}{dt} \, dt \] Der Fettdruck soll andeuten, dass \(\boldsymbol{dx}\) ein Vektor im Einbettungsraum tangential zur Kurve ist.
Wir wollen nun \( \boldsymbol{dx} \) nach der Koordinatenbasis entwickeln. In einbettungsfreier Formulierung war die Zerlegung eines Tangentialvektors \(u(p)\) nach einer Koordinatenbasis gegeben durch \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, \frac{d(f^{ \mu} \circ \gamma)(t)}{dt} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] mit \( p = \gamma(t)\).
Bei einer Formulierung mit Einbettung wird aus \( \frac{\partial}{\partial x^{\mu}} \big|_{p} \) einfach der Vektor \(\frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \), der in die \(\mu\)-te Koordinatenrichtung im Einbettungsraum zeigt. Dabei ist dann \( x = f(p) \) und \( p = \boldsymbol{X}(x) = f^{-1}(x) \), d.h. \(\boldsymbol{X}\) liefert eine Parametrisierung der Mannigfaltigkeit im Einbettungsraum mit Hilfe der Koordinaten \(x\). (siehe Kapitel 4: Tangentialräume und Vektorfelder).
Zum (infinitesimalen) Tangentialvektor \(\boldsymbol{dx}\) gelangt man bei einer Einbettung nun, indem man einfach mit dem winzigen Intervall \(dt\) multipliziert: \[ \boldsymbol{dx} = \] \[ = \sum_{\mu} \, (u^{\mu}(p) \, dt) \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} = \] \[ = \sum_{\mu} \, \frac{d(f^{ \mu} \circ \gamma)(t)}{dt} \, dt \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} =: \] \[ =: \sum_{\mu} \, dx^{\mu} \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \] Anschaulich ist \( dx^{\mu} \) die Komponente des kleinen Wegstücks \(\boldsymbol{dx}\) in die \(\mu\)-te Koordinatenrichtung.
Das können wir nun einsetzen: \[ I_{ \gamma(T)} = \] \[ = \int_{a}^{b} \, [\omega(\gamma(t)) \, {u(\gamma(t)) \, dt}] = \] \[ = \int_{a}^{b} \, \sum_{\mu} \, \omega_{\mu}(\gamma(t)) \, (u^{\mu}(\gamma(t)) \, dt) = \] \[ = \int_{a}^{b} \, \sum_{\mu} \, \omega_{\mu}(\gamma(t)) \, dx^{\mu} \] Vorsicht: \( dx^{\mu} \) ist hier weiterhin die Komponente des kleinen Wegstücks \( \boldsymbol{dx} \) in die \(\mu\)-te Koordinatenrichtung, also gleich \( u^{\mu}(\gamma(t)) \, dt \).
Nun hatten wir oben andererseits die Schreibweise \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{\gamma(T)} \, \sum_{\mu} \, \omega_{\mu} \, dx^{\mu} \] eingeführt, die ganz ähnlich aussieht, bei der aber \(\omega\) und damit auch \( dx^{\mu} \) lineare Abbildungen auf den Tangentialvektoren sind. Nun wird verständlich, wie diese Schreibweise zu verstehen ist:
Setze für \( dx^{\mu} \) formal die \mu-te Komponente \( dx^{\mu} = u^{\mu}(\gamma(t)) \, dt \) des infinitesimalen Wegstücks \( \boldsymbol{dx} \) ein, und du erhälst automatisch die korrekte Formel \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \] für das Wegintegral.
Das läuft im Grunde darauf hinaus, dass man die lineare Abbildung \( dx^{\mu}|_{\gamma(T)} \) auf den infinitesimalen Kurven-Tangentialvektor \( u(\gamma(t)) \, dt \) anwendet, um daraus die \(\mu\)-te Komponente \( dx^{\mu} = u^{\mu}(\gamma(t)) \, dt \) des infinitesimale Wegstücks \(\boldsymbol{dx}\) zu gewinnen.
Da man nun in der Literatur (vor allem in der Physik-Literatur) in der Schreibweise meist nicht zwischen der Abbildung \( dx^{\mu}|_{\gamma(T)} \) und der Wegstück-Komponente \( dx^{\mu} = u^{\mu}(\gamma(t)) \, dt \) unterscheidet, führen 1-Formen hier manchmal ein merkwürdiges Doppelleben: Erst führt man sie als lineare Abildungen auf den Tangentialvektoren ein, und in Integralen haben sie auf einmal die Bedeutung von gewichtet aufsummierten Wegstück-Komponenten.
Ähnlich erging es uns ja bereits bei der Metrik in Kapitel 9: Abstände und Winkel: die Metrik mit dem Ausdruck \[ ds^{2} = \sum_{\mu\nu} \, g_{\mu\nu} dx^{\mu} dx^{\nu} \] Ich hoffe, die obige Darstellung konnte diese scheinbare Doppelnatur etwas aufklären.
Übrigens wird in der mathematischen Literatur oft der Pullback-Formalismus verwendet, um mit dieser Doppelnatur von \( dx^{\mu} \) umzugehen:
Man schreibt \[ \gamma^{*}dx^{\mu} := u^{\mu}(\gamma(t)) \, dt \] für die Wegstück-Komponente, d.h. \[ \gamma^{*}\omega := [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \] Man sagt, \( \gamma^{*} \) ist der Pullback der Parametrisierungsfunktion \( \gamma \).
Damit wird aus der Differentialform \( \omega \), die auf der Mannigfaltigkeit \(M\) definiert ist, die in den Parameterraum \(T\) zurückgeholte Differentialform \( \gamma^{*}\omega \) (die dann auf \(T\) definiert ist). Man kann sich \( \gamma^{*} \) auch als Einsetz-Abbildung veranschaulichen, denn es wird die Parametrisierung \( \gamma \) in \( \omega \) eingesetzt. Formal gilt dann: \[ I_{\gamma(T)} = \int_{T} \gamma^{*}\omega = \] \[ = \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt \]
Wir konnten bisher 1-Formen und Kurvenintegrale über 1-Formen vollkommen ohne den Begriff der Metrik formulieren. Oft hat man es aber ohnehin mit Mannigfaltigkeiten zu tun, die über eine Metrik verfügen. Wie wir in Kapitel 9: Abstände und Winkel: die Metrik gesehen haben, kann man mit Hilfe der Metrik jeder 1-Form \(\omega(p)\) einen eindeutigen Tangentialvektor (nennen wir ihn hier \( v_{\omega}(p) \)) zuordnen über die Beziehung \[ g( v_{\omega}(p), u(p) ) := \omega(p) \, u(p) \] die für alle \(u(p)\) erfüllt sein soll. In Komponenten ist \[ (v_{\omega})^{\mu}(p) = \sum_{\nu} \, g^{\mu\nu}(p) \, \omega_{\nu}(p) \] mit \[ g^{\mu\nu}(p) = [g^{-1}(p)]_{\mu\nu} \] Wir sprachen vom Hochziehen des Indexes. Oft schreibt man einfach \[ \omega^{\mu}(p) := (v_{\omega})^{\mu}(p) \] Wir können die Beziehung \( g( v_{\omega}(p), u(p) ) := \omega(p) \, u(p) \) nun in das Wegintegral über die 1-Form \(\omega\) einsetzen: \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt = \] \[ = \int_{a}^{b} \, g( v_{\omega}(\gamma(t)), u(\gamma(t)) ) \, dt \] Bei einer positiv definiten Metrik, die durch eine Einbettung induziert wird, ist diese Metrik durch das euklidische Skalarprodukt in n-dimensionalen reellen Einbettungsraum gegeben (siehe Kapitel 9: Abstände und Winkel: die Metrik): \[ g(u(p), v(p)) := \langle u(p), v(p) \rangle \] so dass wir das Wegintegral schreiben können als \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{a}^{b} \, \left\langle v_{\omega}(\gamma(t)), \frac{d\gamma(t)}{dt} \right\rangle \, dt = \] \[ = \int_{\gamma(T)} \langle v_{\omega}(\gamma(t)), \boldsymbol{dx} \rangle \] Diese Schreibweise ist bei Physikern sehr beliebt, da sie sehr intuitiv ist. Man multipliziert an jedem Kurvenpunkt den von außen vorgegebenen Vektor \(v_{\omega}\) mit dem Wegstück \(\boldsymbol{dx}\) und integriert über alle Wegstücke. Solche Ausdrücke braucht man beispielsweise, wenn man ausrechnen will, welche Energie man in einem Kraftfeld \(v_{\omega}\) entlang des Weges \(\gamma\) gewinnt oder verliert, wenn die Kraft nur vom Ort abhängt.
Man kann mit Hilfe der Metrik nun weiterhin das sogenannte Linienelement \(ds\) (auch Bogenlängenelement genannt) einführen (siehe wieder Kapitel 9) und mit ihrer Hilfe das Integral über die 1-Form noch weiter umschreiben. Formal schreibt man gerne \[ ds = \] \[ = \sqrt{ \sum_{\mu\nu} \, g_{\mu\nu} \, dx^{\mu} \, dx^{\nu} } = \] \[ = \sqrt{ \sum_{\mu\nu} \, g_{\mu\nu} \, u^{\mu} \, u^{\nu}} \, dt = \] \[ = \sqrt{ g(u,u) } \, dt \] und meint damit, dass das Integral \[ L_{\gamma(T)} = \int_{\gamma(T)} ds = \] \[ = \int_{a}^{b} \, \sqrt{ g( u(\gamma(t)), u(\gamma(t)) } \, dt \] die Länge der Kurve \(\gamma\) zwischen \(\gamma(a)\) und \(\gamma(b)\) angibt.
Vorsicht:
Bei positiv definiter Metrik (d.h. \( g(u,u) \gt 0 \), wenn \(u\) nicht der Nullvektor ist) ist das alles kein Problem und entspricht der anschaulichen Längeninterpretation.
Ist die Metrik aber nicht positiv definit (wie in der Relativitätstheorie), so muss man ggf. hier aufpassen, da \(g(u,u)\) gleich Null werden kann. Die Bogenlänge \(ds\) erhält in der Relativitätstheorie die Interpretation der Eigenzeit (siehe Kapitel 3.7: Die spezielle Relativitätstheorie: Geschwindigkeit, Zeitdilatation, Vierergeschwindigkeit und Eigenzeit ); das ist die Zeit, die für ein Objekt auf der Raum-Zeit-Kurve \(\gamma\) verstreicht. Für Objekte, die sich mit Lichtgeschwindigkeit bewegen (und die deshalb masselos sein müssen), ist diese Eigenzeit immer gleich Null – Licht altert nicht!
Im Folgenden wollen wir den Fall \( g(u,u) = 0 \) ausschließen.
Dann kann man die Bogenlänge auch als spezielle Parametrisierung der Kurve \( \gamma \)
ansehen. Wir können also wie oben einen speziellen Parameterwechsel durchführen,
bei dem wir
\[
t' = s = \varphi^{-1}(t) =
\]
\[
= \sqrt{ g( u(\gamma(t)), u(\gamma(t)) } \, t
\]
sowie \( \rho(s) = \gamma(t) \) setzen.
Rechnen wir damit das Integral auf die Bogenlängenparametrisierung um
(sein Wert ändert sich dabei ja nicht, wie wir wissen):
\[
I_{ \gamma(T)} =
\]
\[
=
\int_{a}^{b} \, [\omega(\gamma(t)) \, u(\gamma(t))] \, dt =
\]
\[
=
\int_{s(a)}^{s(b)} \,
[\omega(\rho(s)) \, u(\rho(s))] \, \frac{ds}{\sqrt{ g( u(\rho(s)), u(\rho(s)) }}
=
\]
\[
=
\int_{s(a)}^{s(b)} \,
\left[ \omega(\rho(s)) \, \frac{ u(\rho(s))} { \sqrt{ g( u(\rho(s)), u(\rho(s)) } } \right] \, ds
=
\]
\[
=:
\int_{s(a)}^{s(b)}
[\omega(\rho(s)) \, v(\rho(s))] \, ds
\]
Wie man sieht, ist der neue Tangentialvektor gegeben durch
\[
v := \frac{u}{\sqrt{ g(u,u) }}
\]
(nicht mit \(v_{\omega}\) verwechseln!).
Das ist ein Vektor vom Betrag (Metrik) Eins, also ein Einheitsvektor!
Die Bogenparametrisierung zeichnet sich also dadurch aus, dass man die
Kurve mit Geschwindigkeit Eins durchläuft.
Vergleicht man diesen Ausdruck nun mit der Einbettungs-Physiker-Schreibweise
\[
I_{ \gamma(T)}
=
\int_{\gamma(T)}
\, \langle
v_{\omega}(\gamma(t)), \boldsymbol{dx}
\rangle
\]
von oben, so sieht man, dass
\[
\boldsymbol{dx} = v \, ds
\]
ist.
Da \(v\) die Länge Eins hat, muss \(\boldsymbol{dx}\) die Länge \(ds\) haben, also die Länge des
kleinen Kurvenstücks, über das integriert wird.
Man schreibt daher auch
\[
|\boldsymbol{dx}| = ds
\]
Das macht erneut die anschauliche Bedeutung von \( \boldsymbol{dx} \) als
kleines Kurvenstück deutlich. Physiker verwenden die Schreibweise
\[
I_{ \gamma(T)}
=
\int_{\gamma(T)} \,
\langle
v_{\omega}, \boldsymbol{dx}
\rangle
\]
übrigens auch gerne, um die Parametrisierungs-Unabhängigkeit des Integrals
intuitiv zu demonstrieren, indem man formal mit \(dt\) erweitert und
\[
I_{ \gamma(T)}
=
\int_{\gamma(T)} \,
\langle
v_{\omega}, \boldsymbol{dx}
\rangle
=
\]
\[ =
\int_{\gamma(T)}
\left\langle
v_{\omega}, \frac{\boldsymbol{dx}}{dt}
\right\rangle \, dt
\]
schreibt. Da dabei \(t\) eine beliebige Parametrisierung sein darf,
kann es offenbar darauf nicht ankommen. Verwendet man die spezielle
Bogenlängen-Parametrisierung, d.h. \( dt = ds = |\boldsymbol{dx}| \),
so zeigt diese Schreibweise sehr schön, dass der Tangentialvektor
hier die Länge Eins hat:
\[
I_{ \gamma(T)}
=
\int_{\gamma(T)}
\langle
v_{\omega}, \boldsymbol{dx}
\rangle
= \]
\[
\int_{\gamma(T)} \,
\left\langle
v_{\omega}, \frac{\boldsymbol{dx}}{|\boldsymbol{dx}|}
\right\rangle \, ds
\]
An dieser Stelle noch eine Warnung vor zu unbedachtem Vorgehen:
Man kann keineswegs jedes Integral über eine Kurve als Integral
über eine 1-Form schreiben. Als Beispiel aus der Physik
nehmen wir die Arbeit, die notwendig ist, um sich entlang einer Kurve
gegen den Luftwiederstand fortzubewegen.
Diese Arbeit ist in Physiker-Kurzschreibweise gegeben durch
\[
W = \int_{\gamma(T)}
\langle
\boldsymbol{F}, \boldsymbol{dx}
\rangle
\]
Die Kraft \(\boldsymbol{F}\), die aufgrund des Luftwiderstandes wirkt, ist dabei
nicht vom Ort, sondern von der Geschwindigkeit \( \frac{\boldsymbol{dx}}{dt} \) abhängig.
Es gilt typischerweise
\[
\boldsymbol{F} = c \, \left|\frac{\boldsymbol{dx}}{dt}\right| \, \frac{\boldsymbol{dx}}{dt}
\]
mit einer (negativen) Konstanten \(c\). Der Luftwiderstand wächst also quadratisch
mit der Geschwindigkeit an. Setzen wir dies ein und verwenden
\( \boldsymbol{dx} = \frac{\boldsymbol{dx}}{dt} \, dt \), so ergibt sich
\[
W = \int_{\gamma(T)} \,
\langle
\boldsymbol{F}, \boldsymbol{dx}
\rangle
=\]
\[
= \int_{\gamma(T)} \,
\left\langle
c \, \left|\frac{\boldsymbol{dx}}{dt}\right| \, \frac{\boldsymbol{dx}}{dt} \, , \,
\frac{\boldsymbol{dx}}{dt}
\right\rangle \, dt
=
\]
\[
= \int_{\gamma(T)} \,
c \, \left|\frac{\boldsymbol{dx}}{dt}\right|^{3} \, dt
\]
Hier kann man \(dt\) nicht wegkürzen, d.h. das Integral ist nicht
invariant bei Umparametrisierungen der Kurve.
Es kommt hier darauf an, wie schnell man die Kurve durchfährt, denn je schneller
man ist, umso größer ist auch der Luftwiderstand.
Mathematiker würden übrigens dieses \(W\) schreiben als \[ W = \int_{a}^{b} \, c \, [g( u(\gamma(t)), u(\gamma(t)) )]^{3/2} \, dt \] Natürlich kann man auch in dieser Schreibweise die Parametrisierungs-Abhängigkeit leicht nachweisen.
Wir möchten uns nun mit ganz speziellen 1-Formen befassen, die eine besonders wichtige Rolle spielen: den 1-Formen, die sich in dem uns interessierenden Gebiet der Mannigfaltigkeit (nennen wir es \(G\)) als d-Ableitung einer (einzigen) skalaren Funktion \(\phi\) darstellen lassen (siehe oben): \[ \omega = d\phi \] für jeden Punkt im betrachteten Gebiet der Mannigfaltigkeit (also nicht nur lokal an einem Punkt \(p\)). Man bezeichnet \(\phi\) dann als Stammform (Stammfunktion). 1-Formen, die sich so schreiben lassen, nennt man exakt.
Für die Komponenten bedeutet das für jeden Punkt \(p\) \[ \omega_{\mu}(p) = \frac{\partial (\phi \circ f^{-1})}{\partial x^{\mu}}(f(p)) \] oder in Kurzschreibweise \[ \omega_{\mu} = \frac{\partial \phi}{\partial x^{\mu}} \] Bei einer gegebenen Metrik können wir auch \[ v_{\omega} = \mathrm{grad} \, \phi \] schreiben (siehe Kapitel 9: Abstände und Winkel: die Metrik zur Definition des Gradienten). Physiker schreiben bei einer Einbettung dann auch gerne \[ \omega = \langle \mathrm{grad} \, \phi, \, \boldsymbol{dx} \rangle \] Nun weiß man aus der Physik bzw. der klassischen dreidimensionalen Vektoranalysis bereits, dass sich nicht jedes Vektorfeld \(v_{\omega}\) als Gradient einer skalaren Funktion \(\phi\) schreiben lässt. Nur Vektorfelder mit verschwindender Rotation lassen sich so schreiben, d.h. sie dürfen keine Wirbelfelder sein!
Diese Bedingung kann man in den Formalismus der Differentialformen übertragen. Dazu versucht man, die skalare Funktion \( \phi \) explizit aus \( \omega \) zu konstruieren (so dass \( \omega = d\phi \) gilt) und schaut während der Rechnung nach, welche Bedingungen für \( \omega \) gelten müssen, damit das gelingt.
Es stellt sich heraus, dass man ein passendes \( \phi(p) \) als Integral \( \int_{\gamma(T)} \omega \) über eine Kurve \(\gamma\) konstruieren kann. Die Kurve startet dabei für \(t = 0\) in einem beliebigen Startpunkt \( \gamma(0) = q \) im Gebiet \(G\) und endet für \(t = 1\) in irgendeinem \( \gamma(1) = p \) (d.h. \(a = 0\) und \(b = 1\) wurde gewählt).
Bei gegebener Koordinatenfunktion \(f\) kann man die Kurve so festlegen, dass ihre Koordinaten eine gerade Linie von \(f(q)\) nach \(f(p)\) bilden, d.h. es ist \[ f(\gamma(t)) = f(q) + t \cdot [ f(p) - f(q) ] \] Das Gebiet \(G\) darf dabei natürlich nicht verlassen werden (man sagt, das Gebiet muss sternförmig bezüglich irgendeines Punktes \(q\) sein – es darf also z.B. keine Löcher enthalten). Außerdem soll das Gebiet G topologisch trivial sein, soll also keine Löcher wie ein Donut enthalten.
Nun muss man nachprüfen, dass \( \omega(p) = d\phi(p) \) für die so konstruierte Funktion \(\phi\) gilt. Man findet, dass das genau dann gilt, wenn im Gebiet \(G\) die Bedingungen \[ \frac{\partial \omega_{\mu}(f^{ -1}(x))}{\partial x^{\nu}} = \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial dx^{\mu}} \] für alle \(\mu\) und \(\nu\) erfüllt sind (dabei ist \(p = f(x)\) ). Für Vektorfelder im dreidimensionalen Raum ist dies genau die Bedingung, dass die Rotation des Vektorfeldes verschwinden muss.
Nun kann man die Bedingung noch etwas umformulieren, indem man den d-Operator auch auf 1-Formen geeignet definiert:
|
d-Operator für 1-Formen (Basis-abhängige Definition): Für eine 1-Form \[ \omega = \sum_{\nu} \, \omega_{\nu} \, dx^{\nu} \] (die in einer Umgebung von \(p\) definiert sein muss) definieren wir \(d\omega(p)\) durch \[ d\omega(p) := \sum_{\nu} \, d\omega_{\nu}(p) \wedge dx^{\nu}|_{p} \] In \( d\omega_{\nu}(p) \) werden die Koeffizientenfunktionen dabei wie skalare Funktionen behandelt, d.h. \[ d\omega_{\nu}(p) = \sum_{\mu} \, \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} \, dx^{\mu}|_{p} \] Das Dachprodukt \( \wedge \) ist so definiert, dass sich ausgeschrieben \[ d\omega(p) = \sum_{\mu\nu} \, \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} \, dx^{\mu}|_{p} \wedge dx^{\nu}|_{p} \] ergibt. Kurzschreibweise: \[ d\omega = \sum_{\mu\nu} \, \frac{\partial \omega_{\nu}}{\partial x^{\mu}} \, dx^{\mu} \wedge dx^{\nu} \] Eine Basis-unabhängige Definition werden wir weiter unten angeben. |
Zur Erinnerung (siehe Kapitel 8: Krümmung ):
Das Dachprodukt (äußere Produkt) von 1-Formen hatten wir definiert durch
\[
[ dx^{\mu} \wedge dx^{\nu} ] (u, v)
:= u^{\mu} \, v^{\nu} - u^{\nu} \, v^{\mu}
\]
(die Argumente \(p\) haben wir weggelassen).
Das äußere Produkt \( dx^{\mu} \wedge dx^{\nu} \) ist also eine antisymmetrische bilineare Abbildung auf dem Raum der Tangentialvektoren, deren Ergebniswert eine reelle Zahl ist.
Aus der Definition geht unmittelbar hervor, dass \[ dx^{\mu} \wedge dx^{\nu} = - dx^{\nu} \wedge dx^{\mu} \] ist. Man bezeichnet \( dx^{\mu} \wedge dx^{\nu} \) (bzw. Linearkombinationen davon) auch als 2-Formen. Der d-Operator macht also aus einer 1-Form eine 2-Form, so wie er oben aus einer 0-Form eine 1-Form gemacht hat. Weitere Details zu 2-Formen folgen weiter unten.
Diese antisymmetrische Definition von \(d\omega\) ist sehr nützlich, denn die Bedingung \[ \frac{\partial \omega_{\mu}(f^{ -1}(x))}{\partial x^{\nu}} = \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial dx^{\mu}} \] von oben lässt sich nun einfach schreiben als \[ d\omega(p) = 0 \] für alle \(p \in G\). Hier die Begründung:
Man kann die Doppelsumme über alle \(\mu\) und \(\nu\) in \(d\omega\) aufteilen in eine Summe mit \( \mu \lt \nu \) und eine Summe mit \( \mu \gt \nu \) (die Terme mit \(\mu = \nu\) sind wegen der Antisymmetrie sowieso gleich Null). Nun benennt man in der zweiten Summe die Indices um (\(\mu\) in \(\nu\) und umgekehrt) und vertauscht \(dx^{\mu}\) und \(dx^{\nu}\) im Dachprodukt, was ein Vorzeichen ergibt. Nun fasst man die beiden Summen wieder zusammen. Ergebnis: \[ d\omega = \sum_{\mu \lt \nu} \, \left( \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} - \frac{\partial \omega_{\mu}(f^{ -1}(x))}{\partial dx^{\nu}} \right) \cdot \] \[ \cdot dx^{\mu} \wedge dx^{\nu} \] Aus \( d\omega = 0 \) folgt dann die Bedingung \[ \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} - \frac{\partial \omega_{\mu}(f^{ -1}(x))}{\partial dx^{\nu}} = 0 \] Im dreidimensionalen Raum bedeutet das, dass die Rotation des Vektorfeldes verschwinden muss, wenn man es als Gradient einer skalaren Funktion schreiben möchte. Details sehen wir weiter unten noch genauer. Halten wir zunächst fest:
|
Integrabilitätsbedingung für 1-Formen (Lemma von Poincaré): Eine 1-Form \( \omega(p) \)ist dann in einem Gebiet \(G\) der Mannigfaltigkeit \(M\) exakt (lässt sich also überall in \(G\) als äußere Ableitung \[ \omega = d\phi \] einer Null-Form \(\phi\) schreiben), wenn \(G\) topologisch trivial und sternförmig ist (d.h. es gibt einen Punkt \(q\) in \(G\), so dass bezüglich eines Koordinatensystems \(f\) sich jeder Punkt \(p\) aus \(G\) durch eine gerade Linie von \(f(q)\) nach \(f(p)\) im Koordinatenraum erreichen lässt) und wenn in \(G\) gilt: \[ d\omega = 0 \] (man bezeichnet ein solches \(\omega\) auch als geschlossen). Die Umkehrung gilt ebenfalls, denn wegen der Antisymmetrie des Dachproduktes und wegen der Vertauschbarkeit der partiellen Ableitungen folgt aus \(\omega = d\phi\) direkt \[ d\omega = d(d\phi) = 0 \] Man bezeichnet \(\phi\) als Stammform (hier auch: Stammfunktion) von \omega. |
Komplikationen wie nicht-triviale Topologien oder die Notwendigkeit mehrerer
Koordinatensysteme haben wir hier erst einmal weggelassen – das Gebiet \(G\) soll einfach
so klein sein, dass wir uns darum nicht zu kümmern brauchen.
Man sieht, wie elegant die Formulierung mit Differentialformen ist. Diese Eleganz bleibt auch bei höheren Dimensionen erhalten, wie wir bald sehen werden. Zentral ist dabei die Antisymmetrie bei der Definition des d-Operators und bei der Definition der 2-Formen (und später der höheren Formen). Wir werden im weiteren Verlauf an mehreren Stellen sehen, dass diese Antisymmetrie noch weitere sehr elegante Formulierungen ermöglicht.
Für Kurvenintegrale exakter 1-Formen \(\omega\) gilt nun eine wichtige Eigenschaft: sie hängen nur vom Anfangspunkt \(\gamma(a)\) und vom Endpunkt \(\gamma(b)\) ab, nicht aber vom Verlauf der Kurve \(\gamma\) dazwischen. Das kann man leicht wie folgt sehen (dabei verwenden wir, dass nach Definition oben \( d\phi(\gamma(t)) \, u(\gamma(t)) = \frac{d}{dt} \phi(\gamma(t)) \) ist, und wir betrachten die Funktion \( \phi \circ \gamma \) einfach als skalare Funktion einer reellen Variablen, für die der Hauptsatz der Differential- und Integralrechnung gilt): \[ \int_{\gamma(T)} \omega = \int_{\gamma(T)} d\phi = \] \[ = \int_{a}^{b} d\phi(\gamma(t)) \, u(\gamma(t)) \, dt = \] \[ = \int_{a}^{b} \, \frac{d}{dt} \phi(\gamma(t)) \, dt = \] \[ = \phi(\gamma(b)) - \phi(\gamma(a)) =: \] \[ = \int_{\gamma(\partial T)} \phi \] Man bezeichnet den Zusammenhang \[ \int_{\gamma(T)} \omega = \int_{\gamma(\partial T)} \phi \] auch als Integralsatz von Stokes. Wie wir gesehen haben, ist dieser Satz bei exakten 1-Formen identisch mit dem Hauptsatz der Differential- und Integralrechnung.
Die Schreibweise \( \int_{\gamma(\partial T)} \phi \) soll dabei bedeuten, dass wir \(\phi\) über den (orientierten) Rand \( \gamma(\partial T) \) der Kurve \( \gamma \) integrieren, also über Anfangs- und Endpunkt der Kurve mit Vorzeichen summieren. Dabei ist \( \partial T \) der orientierte Rand des Intervalls \(T\) (also des Intervalls von \(a\) bis \(b\)), d.h. \(\partial T\) umfasst die \(t\)-Werte \(a\) und \(b\) inklusive einer Vorzeichenkonvention. Diese Schreibweise wird weiter unten bei höheren Dimensionen noch genauer erklärt und macht dort dann auch mehr Sinn. Halten wir fest:
|
Integralsatz von Stokes für exakte 1-Formen: \[ \int_{\gamma(T)} d\phi = \int_{\gamma(\partial T)} \phi = \] \[ = \phi(\gamma(b)) - \phi(\gamma(a)) \] |
Wichtig dabei ist, dass wir die Metrik an keiner Stelle benötigt haben.
Der Integralsatz von Stokes benötigt keine Metrik!
Ein Beispiel aus der Physik (mit Skalarprodukt formuliert): Das statische klassische Gravitationsfeld (nach Newton) \(\boldsymbol{F}\) lässt sich als Gradient einer skalaren Funktion \(\phi\) (das Gravitationspotential) schreiben: \[ \omega = \langle \boldsymbol{F}, \boldsymbol{dx} \rangle = \langle \mathrm{grad} \, \phi, \boldsymbol{dx} \rangle = d\phi \] Die Arbeit, die das Gravitationsfeld entlang eines Weges \(\gamma\) verrichtet, ist also allein gegeben durch den Potentialunterschied (Höhenunterschied) zwischen Start- und Zielpunkt: \[ \int_{\gamma(T)} \langle \boldsymbol{F}, \boldsymbol{dx} \rangle = \] \[ = \int_{\gamma(T)} \langle \mathrm{grad} \, \phi, \boldsymbol{dx} \rangle = \] \[ = \int_{\gamma(T)} d\phi = \int_{\gamma(\partial T)} \phi = \] \[ = \phi(\gamma(b)) - \phi(\gamma(a)) \] Es kommt also nur darauf an, wieviel man bergauf oder bergab geht, aber nicht auf den genauen Weg. Bei geschlossenen Wegen (d.h. Anfangs- gleich Endpunkt) ist dieses Integral gleich Null, d.h. man kann auf einer Rundreise im Gravitationsfeld keine Energie gewinnen.
Hätte das Kraftfeld dagegen einen Rotationsanteil (eine Wirbelstärke wie bei ständigem Rückenwind entlang des Weges), so könnte man auf einer Rundreise Energie gewinnen. Dann wäre aber auch \(d\omega\) ungleich Null. So etwas kommt beispielsweise bei elektrischen Feldern vor, die aufgrund eines sich ändernden Magnetfeldes entstehen, z.B. in einem Dynamo.
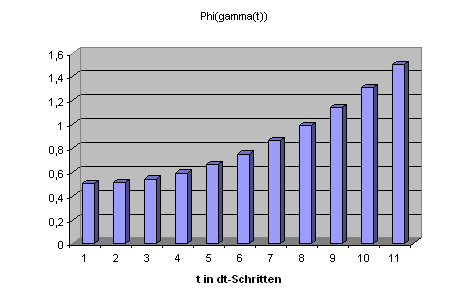
Man kann den Integralsatz von Stokes bei 1-Formen auch anschaulich gut verstehen: Dazu stellen wir uns wieder vor, dass wir das Kurvenparameter-Intervall von \(a\) nach \(b\) in viele sehr kleine Stückchen der Größe \(dt\) aufteilen. Das zugehörige Kurvenstück geht jeweils von \(\gamma(t)\) bis \(\gamma(t + dt)\). Das Integral können wir uns dann als Summe über all diese kleinen Kurvenabschnitte vorstellen, wobei jeder Kurvenabschnitt eine Zahl \[ d\phi = \frac{d}{dt} \phi(\gamma(t)) \, dt = \] \[ = \phi(\gamma(t + dt)) - \phi(\gamma(t)) \] zur Summe beiträgt (das zweite Gleichheitszeichen gilt streng genommen erst im Grenzübergang zu infinitesimal kleinen \(dt\)). Hier ist \(d\phi\) als die kleine Zahl zu verstehen, die der jeweilige Kurvenabschnitt zur Summe (zum Integral) beiträgt.
Der Ausdruck \(d\phi\) spielt also (wie oben bereits \(dx^{\mu}\)) eine Doppelrolle: Zunächst einmal ist er als Linearform auf Tangentialvektoren definiert. Im Kurvenintegral kann man ihn als Veränderung von \(\phi\) auf dem kleinen Kurvenstück interpretieren und erhält so automatisch die korrekte Bedeutung des Integrals \( \int_{\gamma(T)} d\phi \), so wie sie durch die formal saubere Definition \[ \int_{\gamma(T)} d\phi = \] \[ = \int_{a}^{b} d\phi(\gamma(t)) \, u(\gamma(t)) \, dt \] gegeben ist.
Wenn man nun \[ d\phi = \phi(\gamma(t + dt)) - \phi(\gamma(t)) \] über alle Kurvenabschnitte aufsummiert (also dabei den Kurvenparameter in \(dt\)-Schritten von \(a\) nach \(b\) wandern lässt), so heben sich in der Summe die \(\phi\)-Werte aller Zwischenpunkte auf, und man erhält das Ergebnis \( \phi(\gamma(b)) - \phi(\gamma(a)) \). So muss es auch sein, denn das Integral summiert ja alle Veränderungen von \(\phi\) entlang der Kurve auf, so dass man am Ende die Gesamtveränderung von \(\phi\) entlang der Kurve erhält.

Differentialformen haben oft den Ruf, nicht gerade anschauliche Objekte zu sein. Nur in bestimmten Fällen gelingt es, mit ihnen anschauliche Vorstellungen zu verbinden (z.B. wenn eine Metrik vorhanden ist und man sich eine 1-Form als Kraftwirkung entlang eines Wegstücks vorstellen kann, siehe oben).
Es gibt jedoch eine recht interessante Möglichkeit, zu einer anderen halbwegs anschaulichen Vorstellung zu gelangen, die nicht auf einer Metrik aufbaut, und die man auch auf höhere Dimensionen übertragen kann (siehe z.B. Dan Piponi: On the Visualisation of Differential Forms). Wir sind in Kapitel 5: Co-Tangentialräume und Differentialformen bereits darauf eingegangen und wollen hier die wichtigsten Aspekte noch einmal wiederholen (auch im Hinblick auf die Anwendung bei höherdimensionalen Formen).
Als Ausgangspunkt dient uns die Darstellung \[ \omega(p) \, u(p) = d\phi(p) \, u(p) = \] \[ = u(p) \, \phi = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] von oben, d.h. die Tatsache, dass man jede 1-Form \( \omega(p) \) lokal durch das Änderungsverhalten einer skalaren Funktion \( \phi \) beschreiben kann: \[ \omega(p) = d\phi(p) \] im Punkt \(p\).
Das Änderungsverhalten von \( \phi \) in einer sehr kleinen Umgebung von \(p\) können wir durch Höhenlinien oder Höhenflächen anschaulich darstellen, also in einer \(n\)-dimensionalen Mannigfaltigkeit \(M\) durch \((n - 1)\) - dimensionale Flächen, auf denen \(\phi\) konstant ist – wir werden zur Vereinfachung auch die \((n - 1)\) - dimensionalen Höhenflächen als Höhenlinien bezeichnen. Diese Höhenlinien bei \(p\) sollten also auch eine Veranschaulichung der 1-Form \( \omega(p) = d\phi(p) \) im Punkt \(p\) liefern.
Wenn das so ist, müssten wir aus den Höhenlinien von \(\phi\) bei \(p\) auch den Wert von \( \omega(p) u(p) \) ableiten können. Und tatsächlich geht das ganz einfach:
Wenn wir in Richtung von \(u(p)\) ein sehr kleines Stück vorangehen, so werden wir umso mehr Höhenlinien überschreiten, je schneller sich \(\phi\) in dieser Richtung ändert. Dabei zählen wir Höhenlinien positiv, wenn es bergauf geht, ansonsten negativ. Der Wert von \( \omega(p) \, u(p) \) entspricht also in diesem Bild der Zahl der Höhenlinien (mit Vorzeichen), die man in \(u(p)\)-Richtung überschreitet. So ergibt sich anschaulich für \( \omega(p) \, u(p) \) die Richtungsableitung von \(\phi\) im Punkt \(p\) in \(u(p)\)-Richtung.
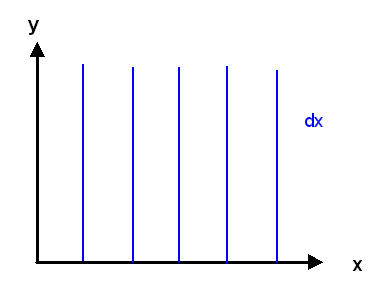
Nun gilt diese Vorstellung zunächst nur lokal, also nur in einer kleinen (sogar infinitesimalen)
Umgebung von \(p\). Wir können uns aber vorstellen, dass wir die Mannigfaltigkeit näherungsweise
mit sehr vielen sehr kleinen Umgebungen gleichsam pflastern und in jeder dieser Umgebungen
die 1-Form \(\omega\) durch Höhenlinien einer Funktion \(\phi\) darstellen.
Dabei ist \(\phi\) jeweils nur in dieser winzigen Umgebung definiert, und es kann sein,
dass wir in jeder Umgebung eine andere Funktion \(\phi\) brauchen.
Schauen wir uns ein einfaches Beispiel an: Die Mannigfaltigkeit \(M\) ist die zweidimensionale reelle Ebene \( \mathbb{R}^{2} \) mit den beiden Koordinaten \(x\) und \(y\), und die 1-Form \(\omega\) ist gegeben durch \[ \omega = x \, dy \] Nun ist \[ d\omega = dx \wedge dy \] hier ungleich Null. Nach dem Lemma von Poincaré kann es daher keine einzelne skalare Funktion \(\phi\) geben, so dass überall \( \omega = d\phi \) mit demselben \(\phi\) gilt. Nur lokal ist das möglich. Dazu wählen wir einen beliebigen Punkt \( p = (a,b) \) aus und betrachten die direkte Umgebung dieses Punktes. In dieser Umgebung definieren wir die skalare Funktion \(\phi\) als \[ \phi(x,y) = a \, y \] so dass \[ d\phi(x,y) = a \, dy \] ist. Damit haben wir erreicht, dass im Punkt \( p = (a,b) \) die gewünschte Beziehung \[ \omega(a,b) = d\phi(a,b) \] gilt.
Schauen wir uns die Höhenlinien von \( \phi(x,y) = a \, y \) nahe bei \( p = (a,b) \) an: \(\phi\) steigt nur in \(y\)-Richtung an, und zwar mit der Steigung \(a\). Der Anstieg wird also in Umgebungen bei Punkten weiter rechts immer steiler, aber gleichzeitig erfolgt der Anstieg immer nur in \(y\)-Richtung. So etwas ist nur mit unendlich vielen lokal definierten Funktionen \(\phi\) erreichbar, nicht aber mit einer einzigen Funktion \(\phi\), denn einen einzigen derart ansteigenden Berg gibt es nicht.
Die Höhenlinien liegen also parallel zur x-Achse, und ihre Dichte ist proportional zur Steigung \(a\). Je weiter rechts der Punkt \( p = (a,b) \) liegt, umso dichter sind die Höhenlinien der dort jeweils lokal definierten Funktion \(\phi\).
Wenn wir uns nun die gesamte Ebene mit kleinen Umgebungen gepflastert vorstellen und überall die Höhenlinien der entsprechenden lokalen \(\phi\)-Funktion einzeichnen, so erhalten wir folgendes Bild:
Je weiter rechts eine Umgebung liegt, umso mehr waagrechte Höhenlinien enthält sie, weil das lokal definierte \(\phi\) stärker in \(y\)-Richtung ansteigt. An den Grenzen der Umgebungen kommen also von links nach rechts immer neue Höhenlinien dazu. Wenn wir die Umgebungen unendlich klein werden lassen, so entspricht dies einer bestimmten Entstehungsdichte von nach rechts fortlaufenden Höhenlinien.
Diese Entstehung von neuen Höhenlinien ist die Ursache dafür, dass wir nicht die Höhenlinien einer einzigen Funktion \(\phi\) in der ganzen Ebene verwenden können. Daraus folgt auch, dass \( d\omega \ne 0 \) sein muss, denn sonst gäbe es nach dem Lemma von Poincaré eine einzige Funktion \(\phi\) mit \( \omega = d\phi \).
Also haben wir: Wenn neue Höhenlinien entstehen, so ist \( d\omega \ne 0 \). Wir werden später sehen, dass wir tatsächlich die Verteilung der Anfangspunkte von Höhenlinien als eine Veranschaulichung der 2-Form \( d\omega = dx \wedge dy \) ansehen können. Mehr dazu weiter unten.
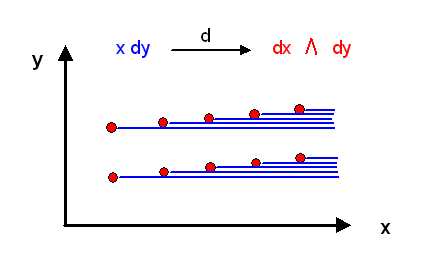
Das Höhenlinien-Bild lässt sich auch gut auf Kurvenintegrale
von 1-Formen anwenden. Bei einem solchen Kurvenintegral werden einfach die
auf dem Weg durchstoßenen Höhenlinien (ggf. mit negativem Vorzeichen beim Abstieg)
aufsummiert. Ist \( d\omega = 0 \), so gehören die Höhenlinien
zum Gebirge einer einzigen Funktion \(\phi\) und es ist egal, auf welchem Weg man von einem
Punkt zu einem anderen Punkt geht: man muss immer insgesamt denselben Höhenunterschied überwinden.
Das Kurvenintegral ist dann wegunabhängig (Integralsatz von Stokes für exakte 1-Formen).
Dies ist anders, wenn Höhenlinien neu entstehen können, so dass \( d\omega \ne 0 \)
ist. Hier kommt es sehr wohl auf den Weg an!
Damit haben wir 1-Formen und Kurvenintegrale im Detail besprochen. Wir wollen nun versuchen, die Begriffe und Ideen auch auf höhere Dimensionen zu übertragen. Dabei wollen wir schrittweise vorgehen und statt 1-Formen zunächst 2-Formen sowie statt Integralen über Kurven nun Integrale über zweidimensionale Flächen betrachten. Wenn wir das erst einmal verstanden haben, ist der Schritt zu beliebigen Dimensionen dann nicht mehr schwer.
Man kann alle oben für 1-Formen formulierten Begriffe und Zusammenhänge auf 2-Formen (und allgemein auf p-Formen) übertragen. Dabei sind 2-Formen einfach antisymmetrische bilineare Abbildung von den Tangentialräumen in die reellen Zahlen.
In dem Ausdruck \[ \omega(p) (u(p), v(p)) \] ist also \(\omega(p)\) die 2-Form im Punkt \(p\), weiter sind \(u(p)\) und \(v(p)\) Tangentialvektoren aus dem Tangentialraum \(T(p)\), und \( \omega(p) (u(p), v(p)) \) ist insgesamt eine reelle Zahl.
Die Abbildung \(\omega(p)\) ist dabei linear in jedem der beiden Argumente, und es gilt die Antisymmetrie \[ \omega(p) (u(p), v(p)) = - \omega(p) (v(p), u(p)) \] Diese Antisymmetrie entscheidend! Das haben wir bei der Definition der \(d\)-Ableitung und dem Integralsatz von Stokes bereits gesehen. Es wird sich weiter unten noch zeigen, dass man Integrale von 2-Formen über Flächen nur dann unabhängig von der Flächenparametrisierung definieren kann, wenn man die Antisymmetrie der 2-Form verwendet. Nur dann ist das Symmetrieverhalten nämlich verträglich mit der Substitutionsregel für Integrale, bei der die Determinante des Parameterwechsels auftritt.
Wir kennen 2-Formen das bereits aus Kapitel 8: Krümmung sowie oben von der Definition von \(d\omega\) mit der 1-Form \(\omega\). Schauen wir uns die Details noch einmal an:
Aus der Bilinearität der 2-Form \(\omega\) und der Antisymmetrie folgt (wir lassen die Argumente wie \(p\) zur Vereinfachung weg; \(u\) und \(v\) sind beliebige Tangentialvektoren): \[ \omega(u,v) = \] \[ = \sum_{\mu\nu} \, u^{\mu} \, v^{\nu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) = \] \[ = \sum_{\mu \lt \nu} \, u^{\mu} \, v^{\nu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) + \] \[ + \sum_{\mu \gt \nu} \, u^{\mu} \, v^{\nu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) = \] \[ = \sum_{\mu \lt \nu} \, u^{\mu} \, v^{\nu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) + \] \[ + \sum_{\nu \gt \mu} \, u^{\nu} \, v^{\mu} \, \omega \left( \frac{\partial}{\partial x^{\nu}}, \frac{\partial}{\partial x^{\mu}} \right) = \] \[ = \sum_{\mu \lt \nu} \, u^{\mu} \, v^{\nu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) + \] \[ - \sum_{\mu \lt \nu} \, u^{\nu} \, v^{\mu} \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) = \] \[ = \sum_{\mu \lt \nu} \, (u^{\mu} \, v^{\nu} - u^{\nu} \, v^{\mu}) \, \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) =: \] \[ =: \sum_{\mu \lt \nu} \, \omega_{\mu\nu} \, [ dx^{\mu} \wedge dx^{\nu} ] (u, v) \] Dabei haben wir verwendet, dass die Terme mit \(\mu = \nu\) wegen der Antisymmetrie gleich Null sind, und wir haben einmal die Indizes \(\mu\) und \(\nu\) ineinander umbenannt sowie die Antisymmetrie von \[ \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) \] verwendet, was den Vorzeichenwechsel bewirkt. Zusammengefasst haben wir also:
|
Basisentwicklung von 2-Formen: Wegen der Bilinearität und der Antisymmetrie kann man jede 2-Form \(\omega\) bei einer gegebenen Koordinatenfunktion \(f\) nach Basisformen \[ dx^{\mu} \wedge dx^{\nu} \] wie folgt entwickeln (die Argumente \(p\) haben wir weggelassen): \[ d\omega = \sum_{\mu lt \nu} \, \omega_{\mu\nu} \, dx^{\mu} \wedge dx^{\nu} \] mit \[ [ dx^{\mu} \wedge dx^{\nu} ] (u, v) := u^{\mu} \, v^{\nu} - u^{\nu} \, v^{\mu} \] sowie \[ \omega_{\mu\nu} := \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}} \right) \]
|
Wir hatten oben bereits gesehen, dass der d-Operator 1-Formen in 2-Formen verwandelt. Lokal (also in einer Umgebung eines festen Punktes \(p\)) geht das immer, d.h. man kann zu einer 2-Form \(\omega(p)\) immer eine 1-Form \(\pi\) finden, die in einer (kleinen) Umgebung von p definiert ist, so dass \( d\pi(p) = \omega(p) \) gilt. Zur Erinnerung hier die Basis-abhängige Definition des d-Operators von oben: \[ d\pi(p) = \] \[ := \sum_{\nu} \, d\pi_{\nu}(p) \wedge dx^{\nu}|_{p} = \] \[ = \sum_{\mu\nu} \, \frac{\partial \pi_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} \, dx^{\mu}|_{p} \wedge dx^{\nu}|_{p} = \] \[ = \sum_{\mu \lt \nu} \, \left[ \frac{\partial \pi_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} - \frac{\partial \pi_{\mu}(f^{ -1}(x))}{\partial x^{\nu}} \right] \cdot \] \[ \cdot dx^{\mu}|_{p} \wedge dx^{\nu}|_{p} = \omega(p) = \] \[ = \sum_{\mu \lt \nu} \, \omega_{\mu\nu}(p) \, dx^{\mu}|_{p} \wedge dx^{\nu}|_{p} \] so dass \[ \omega_{\mu\nu}(p) = \frac{\partial \pi_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} - \frac{\partial \pi_{\mu}(f^{ -1}(x))}{\partial x^{\nu}} \] ist. Wann eine solche Beziehung zwischen \(\pi\) und \(\omega\) über einen Punkt \(p\) hinaus in einem Gebiet \(G\) gilt, werden wir wieder weiter unten sehen (Integrabilitätsbedingung).
Die obige Basis-abhängige Definition ist leider etwas unanschaulich: Warum definiert man die d-Ableitung gerade so? Wir wollen daher noch eine zweite Basis-unabhängige Definition angeben und zeigen, dass sie zur obigen Basis-abhängigen Definition führt. Dazu schauen wir uns noch einmal die Basis-unabhängige Definition der d-Ableitung bei 0-Formen an: \[ d\phi(p) u(p) := u(p) \, \phi = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] mit \( p = \gamma(0) \). Die d-Ableitung der 0-Form \(\phi\) ist also so definiert, dass sich mit ihrer Hilfe die Richtungsableitung der Funktion \(\phi\) in eine beliebige Richtung ausrechnen lässt, indem man \(d\phi\) auf den entsprechenden Tangentialvektor anwendet.
Wie lässt sich das auf 1-Formen übertragen?
Schauen wir uns dazu den Ausdruck \[ \pi(p) \, u_{2}(p) \] mit einer 1-Form \(\pi\) an. Durch diesen Ausdruck wird eine skalare Funktion auf der Mannigfaltigkeit \(M\) definiert, denn \( \pi(p) \, u_{2}(p) \) ist für jeden Punkt \(p\) eine reelle Zahl. Wir wollen diese Funktion mit \[ \pi u_{2} \] bezeichnen, d.h. \[ [\pi u_{2}](p) := \pi(p) u_{2}(p) \] Da \(d\pi\) eine 2-Form werden soll, benötigen wir 2 Tangentialvektoren. Daher ersetzen wir die Kurve \( \gamma(t) \) durch eine Flächenparametrisierung \[ \gamma(t_{1}, t_{2}) \] mit zwei Parametern \( t_{1} \) und \( t_{2} \), d.h. \( \gamma \) ist eine Abbildung von \( \mathbb{R}^{2} \) in die Mannigfaltigkeit \(M\).
Zur Vereinfachung der Schreibweise schreiben wir \[ (t_{1}, t_{2}) = \boldsymbol{t} \] Wir setzen \[ p = \gamma(\boldsymbol{0}) = \gamma(0, 0) \] Die Tangentialvektoren in \(t_{i}\)-Richtung in \( \boldsymbol{t} = \boldsymbol{0} \) bezeichnen wir mit \( u_{i}(p) \).
Für die Funktion \( \pi u_{2} \) können wir nun analog zu \(\phi\) die Richtungsableitung beispielsweise in \(t_{1}\)-Richtung bilden: \[ \frac{d}{dt_1} [\pi(\gamma(\boldsymbol{t})) \, u_{2}(\gamma(\boldsymbol{t}))] \bigg|_{\boldsymbol{t} = \boldsymbol{0}} = u_{1}(p) \, [\pi u_{2}] \] Dieser Ausdruck ist linear in \(u_{2}\) (denn die skalare Funktion \( \pi(\gamma(\boldsymbol{t})) \, u_{2}(\gamma(\boldsymbol{t})) \) ist linear in \(u_{2}\)) und linear in \(u_{1}\) (so wie auch \( d\phi(p) \, u(p) \) linear in \(u(p)\) war). Er ist also bilinear in \(u_{1}\) und \(u_{2}\).
Allerdings können wir damit noch keine 2-Form definieren, denn der Ausdruck ist nicht unbedingt antisymmetrisch in \(u_{1}\) und \(u_{2}\). Außerdem fehlt noch die Ableitungen in \(t_1\)-Richtung, denn \(t_1\) und \(t_2\) und damit \(u_{1}\) und \(u_{2}\) sollten gleichberechtigt sein. Wir können aber leicht einen entsprechenden antisymmetrischen Ausdruck konstruieren: \[ d\pi(p) (u_{1}(p), u_{2}(p)) := \] \[ = u_{1}(p) \, [\pi u_{2}] - u_{2}(p) \, [\pi u_{1}] = \] \[ = \frac{d}{dt_1} [\pi(\gamma(\boldsymbol{t})) u_{2}(\gamma(\boldsymbol{t}))] \bigg|_{\boldsymbol{t} = \boldsymbol{0}} + \] \[ - \frac{d}{dt_2} [\pi(\gamma(\boldsymbol{t})) u_{1}(\gamma(\boldsymbol{t}))] \bigg|_{\boldsymbol{t} = \boldsymbol{0}} \] Dieser Ausdruck leistet das Gewünschte: er ist bilinear und antisymmetrisch in \(u_{1}\) und \(u_{2}\), und er enthält keine Ableitungen der Tangentialvektoren \(u_{i}\) mehr (wie wir gleich noch sehen werden). Hier sehen wir, wie sich in natürlicher Weise die Definition der d-Ableitung von 0-Formen auf 1-Formen übertragen lässt (und analog auf höhere Differentialformen). Besonders für den Integralsatz von Stokes wird sich weiter unten diese Basis-unabhängige Schreibweise noch als nützlich erweisen.
Wir wollen noch zeigen, dass die obige Definition tatsächlich unserer Basis-abhängigen Definition von oben entspricht, und dass die Ableitungen der Tangentialvektoren \(u_{i}\) wegfallen: \[ = \frac{d}{dt_1} [\pi(\gamma(\boldsymbol{t})) u_{2}(\gamma(\boldsymbol{t}))] + \] \[ - \frac{d}{dt_2} [\pi(\gamma(\boldsymbol{t})) u_{1}(\gamma(\boldsymbol{t}))] = \] \[ = \sum_{\mu} \, \bigg( \frac{d \pi_{\mu}(\gamma(\boldsymbol{t}))}{dt_1} \, u_{2}^{\mu}(\gamma(\boldsymbol{t})) + \] \[ + \pi_{\mu}(\gamma(\boldsymbol{t})) \, \frac{du_{2}^{\mu}(\gamma(\boldsymbol{t}))}{dt_{1}} + \] \[ - \frac{d\pi_{\mu}(\gamma(\boldsymbol{t}))}{dt_{2}} \, u_{1}^{\mu}(\gamma(\boldsymbol{t})) + \] \[ - \pi_{\mu}(\gamma(\boldsymbol{t})) \, \frac{du_{1}^{\mu}(\gamma(\boldsymbol{t}))}{dt_{2}} \bigg) = \, ... \] ... die Ableitungen von \(\pi_{\mu}\) rechnen wir mit Hilfe der Kettenregel aus, wobei wir \(\pi_{\mu}\) direkt als Funktion der Koordinaten \( x = f(\gamma(\boldsymbol{t})) \) auffassen (wir sparen uns also das explizite Einschieben der Koordinatenfunktion \(f\), um die Schreibweise nicht zu überfrachten; die formal saubere Schreibweise findet man weiter oben). Außerdem verwenden wir die Kurzschreibweise \[ u^{\mu}_{i} = \frac{d\gamma^{\mu}}{dt_{i}} = \frac{df^{ \mu}(\gamma(\boldsymbol{t})))}{dt_{i}} \] und lassen die Argumente \( \gamma^{\mu}(\boldsymbol{t}) \) weg. Die Ableitungsterme von \( u_{i} \) heben sich wegen der Vertauschbarkeit der Ableitungen nach \(t_{1}\) und \(t_{2}\) gegenseitig auf, denn \[ \frac{du_{2}^{\mu}}{dt_{1}} = \frac{d}{dt_1} \frac{d\gamma^{\mu}}{dt_{2}} = \frac{d}{dt_2} \frac{d\gamma^{\mu}}{dt_{1}} = \frac{du_{1}^{\mu}}{dt_{2}} \] Wir haben also: \[ \, ... = \sum_{\mu\nu} \, \bigg( \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \, \frac{d\gamma^{\nu}}{dt_{1}} \, u_{2}^{\mu} - \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \, \frac{d\gamma^{\nu}}{dt_{2}} u_{1}^{\mu} \bigg) = \] \[ = \sum_{\mu\nu} \, \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \, \left( u_{1}^{\nu} \,u_{2}^{\mu} - u_{1}^{\mu} \, u_{2}^{\nu} \right) = \] \[ = \sum_{\mu\nu} \, \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \, [dx^{\nu} \wedge dx^{\mu}] (u_{1}, u_{2}) = \] \[ = d\pi(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t}))) \] Fassen wir zusammen (wobei wir analog zur Basis-abhängigen Definition von oben wieder \(\omega\) statt \(\pi\) schreiben wollen):
|
d-Operator für 1-Formen (Basis-unabhängige Definition): Für eine 1-Form \[ \omega(p) = \sum_{\nu} \, \omega_{\nu}(p) \, dx^{\nu}|_{p} \] definieren wir den d-Operator durch \[ d\omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t}))) := \] \[ = \frac{d[\omega(\gamma(\boldsymbol{t})) \, u_{2}(\gamma(\boldsymbol{t}))]}{dt_{1}} - \frac{d[\omega(\gamma(\boldsymbol{t})) \, u_{1}(\gamma(\boldsymbol{t}))]}{dt_{2}} \] Dabei ist \[ \boldsymbol{t} := (t_{1}, t_{2}) \] und \( \gamma(\boldsymbol{t}) \) ist eine Flächenparametrisierung (also eine Abbildung zweier reeller Parameter in die Mannigfaltigkeit \(M\)). In einer Koordinatenbasis ausgeschrieben ergibt sich daraus die Basis-abhängige Definition von oben: \[ d\omega(p) = \sum_{\nu} \, d\omega_{\nu}(p) \wedge dx^{\nu}|_{p} = \] \[ = \sum_{\mu\nu} \, \frac{\partial \omega_{\nu}(f^{ -1}(x))}{\partial x^{\mu}} \, dx^{\mu}|_{p} \wedge dx^{\nu}|_{p} \] |
Diese Definition lässt sich leicht auch auf höhere Dimensionen verallgemeinern.
Details folgen weiter unten.
Um eine 2-Form \omega(p) auswerten zu können, benötigt man im Punkt p zwei Tangentialvektoren. Eine 2-dimensionale Untermannigfaltigkeit (Fläche) in unserer mindestens 2-dimensionalen Mannigfaltigkeit M liefert in jedem ihrer Punkte zwei solche Tangentialvektoren. Die Anwendung von \omega(p) auf diese beiden Tangentialvektoren liefert eine reelle Zahl. Wir können diese Zahlen nun über die Fläche (oder über einen Teil davon) aufsummieren (genauer: aufintegrieren), wobei wir wieder voraussetzen, dass \omega dort überall definiert ist.
Wie bei der Kurve wollen wir auch die Fläche (oder einen Teil davon) wieder durch eine Parameterdarstellung kennzeichnen, also durch eine Funktion \(\gamma\), die jeweils zwei reellen Zahlen (Flächenparametern) \(t_{1}\) und \(t_{2}\) einen Punkt \( p = \gamma(t_{1}, t_{2}) \) zuordnet. Wir schreiben im Folgenden wieder \( \boldsymbol{t} := (t_{1}, t_{2}) \), also z.B. \( p = \gamma(\boldsymbol{t}) \).
Dabei müssen wir noch den Zahlenbereich festlegen, den die beiden Flächenparameter überstreichen sollen. Wir wollen diesen Bereich analog zum eindimensionalen Fall mit \( T \) bezeichnen, d.h. es gilt \[ \boldsymbol{t} = (t_{1}, t_{2}) \in T \] und \(T\) ist eine geeignete Teilmenge von \(\mathbb{R}^{2}\).
Dabei bedeutet geeignet, dass \(T\) konvex ist oder das diffeomorphe Bild einer solchen Menge ist (konvex heißt, dass gerade Verbindungsstrecken zwischen zwei Punkten von \(T\) auch in \(T\) liegen).
Außerdem soll die Parameterfunktion \(\gamma\) differenzierbar und injektiv sein. Mit anderen Worten: wir wollen über ein vernünftiges zusammenhängendes Flächenstück integrieren und keine Probleme mit Löchern, Überlappungen, unzusammenhängenden Stücken etc. haben. Wir sprechen auch von einem einfachen 2-Flächenstück.
Und natürlich soll \(\gamma\) so sein, dass für jeden Punkt des Flächenstücks ein zweidimensionaler Tangentialraum existiert, der durch Tangentialvektoren in Richtung der beiden Parameter aufgespannt wird. Die Fläche soll also wirklich zweidimensional sein (auf was man so alles achten muss ... ). Später werden wir solche 2-Flächenstücke zu größeren Untermannigfaltigkeiten zusammensetzen. Dabei wird sich als wichtig erweisen, dass diese Untermannigfaltigkeiten orientierbar sind, also nicht wie das Möbiusband aussehen (Bild siehe weiter unten). Für das Möbiusband sind Flächenintegrale von 2-Formen nicht definiert.
Für das Integral brauchen wir noch ein geeignetes Integrationsmaß \( d\mu(\boldsymbol{t}) \) auf dem Parameterraum \(T\). Wie üblich verwenden wir das Standardmaß für karthesische Koordinaten im \(\mathbb{R}^{2}\): \[ d\mu(\boldsymbol{t}) = dt_{1} \, dt_{2} \] Das uns interessierende Flächenintegral definieren wir nun analog zum Kurvenintegral durch \[ I_{ \gamma(T)} := \] \[ := \int_{T} \, [\omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t})))] \, d\mu(\boldsymbol{t}) \] wobei natürlich \( u_{i}(\gamma(\boldsymbol{t})) \) der Tangentialvektor in \(t_{i}\)-Richtung ist, d.h. beispielsweise \( u_{1}(p) \, \phi = \frac{d}{dt_1} \phi(\gamma(\boldsymbol{t})) \) mit \(p = \gamma(\boldsymbol{t})\).
Es wäre schön, wenn dieses Integral analog zum eindimensionalen Fall nicht von der Parametrisierung der Fläche abhängen würde. Schauen wir uns also an, was bei einer Umparametrisierung der Fläche geschieht.
Umparametrisierung der Fläche bedeutet, dass wir das Parameterpaar \( \boldsymbol{t} = (t_{1}, t_{2}) \) als Funktion eines neuen Parameterpaars ansehen: \[ \boldsymbol{t} = (t_{1}, t_{2}) = \varphi(t_{1}', t_{2}') = \varphi(\boldsymbol{t}') \] mit einer umkehrbaren Funktion \(\varphi\), die von \(\mathbb{R}^{2}\) nach \(\mathbb{R}^{2}\) geht. So könnte man beispielsweise zu zweidimensionalen sphärischen Koordinaten übergehen, also \[ t_{1} = t_{1}' \, \cos{t_{2}'} \] \[ t_{2} = t_{1}' \, \sin{t_{2}'} \] verwenden.
Die Fläche wird bzgl. der neuen Parametrisierung durch eine neue Funktion \(\rho(\boldsymbol{t}')\) beschrieben, wobei \[ \gamma(\boldsymbol{t}) = \gamma(\varphi(\boldsymbol{t}')) =: \rho(\boldsymbol{t}') \] sein soll, d.h. \[ \gamma \circ \varphi = \rho \] (ganz analog zum eindimensionalen Fall).
Betrachten wir nun das folgende Integral, das sich auf die neue Flächenparametrisierung \(\rho\) bezieht: \[ I_{ \rho(T')} := \] \[ := \int_{T'} \, [\omega(\rho(\boldsymbol{t}')) (v_{1}(\rho(\boldsymbol{t}')), v_{1}(\rho(\boldsymbol{t}')))] \, d\mu(\boldsymbol{t}') \] Dabei sind \( v_{i}(\gamma(\boldsymbol{t}')) \) die Tangentialvektoren in die neuen Parameterrichtungen \(t_{i}'\) im Punkt \(\rho(\boldsymbol{t}')\), und \( T' \) ist der Parameterbereich der gestrichenen Parameter, so dass die Integration über dieselbe Fläche geht wie beim Integral \( I_{ \gamma(T)} \) oben (also \(T = \varphi(T') \)).
Wir hoffen natürlich, dass wie oben wieder \[ I_{ \gamma(T)} = I_{ \rho(T')} \] gilt. Also versuchen wir, den Nachweis dafür analog zum eindimensionalen Fall zu führen, indem wir wieder \(I_{ \rho(T')}\) durch Einsetzen von \( \gamma(\varphi(\boldsymbol{t}')) = \rho(\boldsymbol{t}') \) umschreiben: \[ I_{ \rho(T')} := \] \[ = \int_{T'} \, [\omega(\gamma(\varphi(\boldsymbol{t}'))) (v_{1}(\gamma(\varphi(\boldsymbol{t}'))), v_{2}(\gamma(\varphi(\boldsymbol{t}'))))] \, d\mu(\boldsymbol{t}') \] Wir wollen nun wieder die \(v\)-Tangentialvektoren durch die \(u\)-Tangentialvektoren ausdrücken: \[ v_{i}(\rho(\boldsymbol{t}')) \, \phi = \] \[ = \frac{d\phi(\rho(\boldsymbol{t}'))}{dt_{i}'} = \] \[ = \frac{d\phi(\gamma(\varphi(\boldsymbol{t}')))}{dt_{i}'} = \] \[ = \sum_{j} \, \frac{d\phi(\gamma(\boldsymbol{t}))}{dt_{j}} \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{i}'} = \] \[ = \sum_{j} \, [u_{j}(\gamma(\boldsymbol{t})) \, \phi] \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{i}'} = \] \[ = \sum_{j} \, [u_{j}(\gamma(\varphi(\boldsymbol{t}'))) \, \phi] \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{i}'} = \] \[ = \left[ \sum_{j} \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{i}'} \, u_{j}(\gamma(\varphi(\boldsymbol{t}'))) \right] \, \phi \] d.h. für die Umrechnung benötigen wir die Jacobimatrix der Umparametrisierungsfunktion \(\varphi\) mit den Matrixelementen \[ \frac{d\varphi_{j}(\boldsymbol{t}'))}{dt_{i}'} \] Physiker würden bei einer Einbettung kürzer einfach schreiben: \[ \frac{\boldsymbol{dx}}{dt_{i}'} = \sum_{j} \, \frac{\boldsymbol{dx}}{dt_{j}} \, \frac{dt_{j}}{dt_{i}'} \] Fassen wir das Ergebnis noch einmal zusammen:
|
Transformation von Tangentialvektoren bei Parametertransformation der Fläche: Wir gehen von einer Flächenparametrisierung \[ \gamma(\boldsymbol{t}) \] aus mit zugehörigen Tangentialvektoren \( u_{i}(\gamma(\boldsymbol{t})) \). Nun wechseln wir zu einem neuen Parameterpaar \(\boldsymbol{t}'\), indem wir \(\boldsymbol{t}\) als abhängig von \(\boldsymbol{t}'\) betrachten: \[ \boldsymbol{t} = \varphi(\boldsymbol{t}') \] Die Fläche wird nun bezüglich \(\boldsymbol{t}'\) durch die Funktion \[ \rho(\boldsymbol{t}') := \gamma(\varphi(\boldsymbol{t}')) = \gamma(\boldsymbol{t}) \] beschrieben. Die zu \(\rho\) gehörenden Tangentialvektoren nennen wir \(v_{i}(\rho(\boldsymbol{t}'))\). Dann gilt: \[ v_{i}(\rho(\boldsymbol{t}')) = \sum_{j} \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{i}'} \, u_{j}(\gamma(\varphi(\boldsymbol{t}'))) \]
|
Dieses Ergebnis können wir nun im Integranden von \( I_{ \rho(T')} \) oben einsetzen, wobei wir
wieder ausnutzen, dass \(\omega\) eine bilineare Abbildung ist:
\[
I_{ \rho(T')} =
\int_{T'} \, [\omega(\gamma(\varphi(\boldsymbol{t}')))
(v_{1}(\gamma(\varphi(\boldsymbol{t}'))),
\]
\[v_{2}(\gamma(\varphi(\boldsymbol{t}'))))] \,
d\mu(\boldsymbol{t}')
=
\]
\[
=
\int_{T'} \, \bigg[ \omega(\gamma(\varphi(\boldsymbol{t}')))
\bigg(
\sum_{j} \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{1}'}
\, u_{j}(\gamma(\varphi(\boldsymbol{t}')))
,
\]
\[
\sum_{k} \, \frac{d\varphi_{k}(\boldsymbol{t}')}{dt_{2}'}
\, u_{k}(\gamma(\varphi(\boldsymbol{t}')))
\bigg) \bigg] \,
d\mu(\boldsymbol{t}')
=
\]
\[
=
\int_{T'} \,
\sum_{jk} \,
\frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{1}'} \,
\frac{d\varphi_{k}(\boldsymbol{t}')}{dt_{2}'}
\]
\[
\omega(\gamma(\varphi(\boldsymbol{t}')))
( u_{j}(\gamma(\varphi(\boldsymbol{t}'))), \, u_{k}(\gamma(\varphi(\boldsymbol{t}')))) \,
d\mu(\boldsymbol{t}')
= \, ...
\]
Wir würden nun gerne für jeden Summanden die
Tangentialvektoren \(u_{j}\) und \(u_{k}\)
in \(\omega\) so vertauschen, dass \( \omega(u_{1}, u_{2}) \)
entsteht, so wie das in \( I_{ \gamma(T)} \) der Fall ist.
Wir wollen dies direkt so vornehmen, dass sich die Vorgehensweise
auf den höherdimensionalen Fall übertragen lässt.
Dazu verwenden wir den bekannten Begriff der Permutation: eine Permutation ist eine Umsortierung in einer geordneten Liste natürlicher Zahlen. So kann eine spezielle Permutation beispielsweise aus der Liste (2, 5, 11, 3) die neue Liste (11, 2, 3, 5) machen.
Nun kann man jede Permutation dadurch erzeugen, dass man nacheinander einzelne Zahlen miteinander vertauscht. In dem obigen Beispiel vertauscht man dazu zuerst die Zahlen 2 und 11 mit dem Ergebnis (11, 5, 2, 3) (damit ist die erste Zahl schon mal richtig), danach die Zahlen 2 und 5 mit dem Ergebnis (11, 2, 5, 3) , und zum Schluss noch die Zahlen 3 und 5 mit dem Ergebnis (11, 2, 3, 5) . Wir haben also drei Vertauschungen benötigt, um die Permutation zu erreichen.
Man kann nun das Signum (Vorzeichen) einer Permutation definieren: Für eine gerade Zahl von Vertauschungen ist das Signum der Permutation gleich 1 , bei einer ungeraden Zahl von Vertauschungen gleich - 1 . In unserem Beispiel wäre also das Signum der Permutation gleich - 1 . Übrigens macht die Signum-Definition natürlich nur Sinn, wenn in der Zahlenliste keine Zahl doppelt vorkommt, denn sonst wäre die Zahl der Vertauschungen nicht eindeutig festgelegt (man könnte ja zwei identische Zahlen miteinander vertauschen, ohne dass sich etwas ändert). Daher definieren wir das Signum für solche Fälle mit mehrfach vorkommenden Zahlen als Null.
In unserem Integranden oben können wir \( (j, k) \) als Permutation von \( (1, 2) \) betrachten (\(j\) und \(k\) sind ja gleich \(1\) oder \(2\), und die Terme mit \(i = j\) können wir aufgrund der Antisymmetrie von \(\omega\) sowieso weglassen. Wir schreiben einfach direkt \( (j, k) \) für diese Permutation. Dann gilt: \[ \omega(u_{j}, u_{k}) = \mathrm{sign}(j, k) \cdot \omega(u_{1}, u_{2}) \] Dabei ist der Fall \(j = k\) wegen \( \mathrm{sign}(j, j) = 0 \) direkt mit enthalten.
Das Verhalten von \(\omega\) beim Vertauschen der Argumente ist übrigens vollkommen identisch mit dem Verhalten einer Determinante beim Vertauschen der Spalten – auch im mehrdimensionalen Fall (siehe unten). In diesem Sinn sind Differentialformen verträglich mit Determinanten, und genau deshalb ergibt sich auch die Unabhängigkeit von der Parametrisierung, denn bei Umparametrisierungen von Integralen tritt gemäß der Transformationsformel die Jacobideterminante der Umparametrisierung auf. Die Details sehen wir gleich noch genauer.
Man könnte natürlich fragen, ob wir hier nicht mit Kanonen auf Spatzen geschossen haben. Schließlich sind oben nur die beiden Fälle \( \mathrm{sign}(1, 2) = 1 \) und \( \mathrm{sign}(2, 1) = - 1 \) interessant, und wir hätten alles auch ganz ohne Permutationen und den Signum-Begriff durchführen können. Bei mehr Dimensionen wird es aber immer schwieriger, sich zu Fuß durchzuschlagen. Daher haben wir schon hier alles so formuliert, wie wir es auch bei mehr Dimensionen brauchen. Setzen wir also unser Ergebnis oben ein: \[ ... \, = \int_{T'} \, \sum_{jk} \, \mathrm{sign}(j, k) \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{1}'} \, \frac{d\varphi_{k}(\boldsymbol{t}')}{dt_{2}'} \] \[ \omega(\gamma(\varphi(\boldsymbol{t}'))) ( u_{1}(\gamma(\varphi(\boldsymbol{t}'))), \, u_{2}(\gamma(\varphi(\boldsymbol{t}')))) \, d\mu(\boldsymbol{t}') = \] \[ =: \int_{T'} \, \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} \] \[ \omega(\gamma(\varphi(\boldsymbol{t}'))) ( u_{1}(\gamma(\varphi(\boldsymbol{t}'))), \, u_{2}(\gamma(\varphi(\boldsymbol{t}')))) \, d\mu(\boldsymbol{t}') = \, ... \] Dabei haben wir die Definition der Determinante der Jacobimatrix verwendet, also \[ \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} := \sum_{jk} \, \mathrm{sign(j, k)} \, \frac{d\varphi_{j}(\boldsymbol{t}')}{dt_{1}'} \, \frac{d\varphi_{k}(\boldsymbol{t}')}{dt_{2}'} \] In unserem zweidimensionalen Fall ist dann natürlich \[ \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} = \] \[ = \frac{d\varphi_{1}(\boldsymbol{t}')}{dt_{1}'} \, \frac{d\varphi_{2}(\boldsymbol{t}')}{dt_{2}'} - \frac{d\varphi_{2}(\boldsymbol{t}')}{dt_{1}'} \, \frac{d\varphi_{1}(\boldsymbol{t}')}{dt_{2}'} \] Man kann nun direkt die Transformationsregel für mehrdimensionale Integrale anwenden. Wir wollen hier diese Regel noch einmal kurz motivieren:
Wenn man im t-Parameterraum auf das zweidimensionale Einheitsquadrat mit Flächeninhalt gleich 1 eine 2 x 2 - Matrix \(A\) anwendet (d.h. aus jedem Punkt \(\boldsymbol{t}\) wird der Punkt \(A \, \boldsymbol{t} \) ) , so einsteht ein Parallelogramm, dessen Kanten durch die beiden Spaltenvektoren von \(A\) gegeben sind. Wie man in der Vektoranalysis zeigt, hat es den Flächeninhalt \( |\det{A}| \).
Analog ist es auch in höheren Dimensionen. Den Beweis führt man mit Hilfe der vollständigen Induktion, mit der man sich durch geeignete Zerlegung der Matrix \(A\) in den Dimensionen nach oben hangeln kann. Weiter unten werden wir für den zweidimensionalen Fall noch einmal explizit zeigen, dass \( \det{A} \) die Fläche des Parallelogramms ist (Stichwort: Gramsche Matrix).
Nun kann man die Abbildung \(\varphi\) lokal immer durch die 2 x 2 - Jacobi-Matrix \[ \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \] annähern. Wendet man daher \(\varphi\) auf ein sehr kleines Quadrat mit Kantenlängen \(dt_{1}'\) und \(dt_{2}'\) und Flächeninhalt \[ d\mu(\boldsymbol{t}') = dt_{1}' \, dt_{2}' \] an, so entsteht daraus ein Parallelogramm mit Flächeninhalt \[ d\mu(\boldsymbol{t}) = d\mu(\varphi(\boldsymbol{t}')) = \] \[ = \left| \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} \right| \, d\mu(\boldsymbol{t}') \] Das können wir oben verwenden und so im Integral zu den ungestrichenen Integrationsvariablen übergehen. Um dabei keine Vorzeichenprobleme zu bekommen, wollen wir uns auf solche Umparametrisierungen beschränken, die eine positive Jacobi-Determinante \( \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} \) haben, so dass wir die Betragsstriche weglassen können. Diese Umparametrisierungen bezeichnen wir als orientierungserhaltend: \[ I_{ \rho(T')} = \] \[ = \int_{T'} \, \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} \] \[ \omega(\gamma(\varphi(\boldsymbol{t}'))) ( u_{1}(\gamma(\varphi(\boldsymbol{t}'))), \, u_{2}(\gamma(\varphi(\boldsymbol{t}')))) \, d\mu(\boldsymbol{t}') = \] \[ = \int_{T} \, \omega(\gamma(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), \, u_{2}(\gamma(\boldsymbol{t})))] \, d\mu(\boldsymbol{t}) = \] \[ = I_{ \gamma(T)} \] Das Flächenintegral ändert sich also wieder bei der Umparametrisierung (mit positiver Jacobi-Determinante) nicht. Die Ursache dafür liegt darin, dass aufgrund der Antisymmetrie der 2-Form bei der Umparametrisierung genau die Jacobi-Determinante entsteht, die man für die Transformationsregel (also für die Umrechnung der kleinen Parameter-Flächenstücke im Integral in die neue Parametrisierung) benötigt. Fassen wir zusammen:
|
Flächenintegrale über 2-Formen sind unabhängig von der Parametrisierung der Fläche (wenn
die Orientierung erhalten bleibt): Wir betrachten das (orientierte) Flächenintegral \[ I_{ \gamma(T)} := \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), \, u_{2}(\gamma(\boldsymbol{t}))) \, d\mu(\boldsymbol{t}) \] Dabei ist die Parametermenge \(T\) eine Teilmenge des \(\mathbb{R}^{2}\), die offen und konvex ist oder das diffeomorphe Bild einer solchen Menge ist, und es ist \[ \boldsymbol{t} = (t_{1}, t_{2}) \] Die Flächenparametrisierung \(\gamma\) ist eine (gutartige) Funktion vom Parameterraum \(T\) in die Mannigfaltigkeit \(M\). Weiter ist \(\omega\) eine 2-Form, \(u_{i}\) sind die Tangentialvektoren in \(t_{i}\)-Richtung und \[ d\mu(\boldsymbol{t}) = dt_{1} \, dt_{2} \] ist das übliche 2-dimensionale Integrationsmaß. Das obige Integral ändert sich bei einer orientierungserhaltenden Umparametrisierung der Fläche nicht. Das bedeutet: Wenn wir \(\boldsymbol{t}\) als Funktion eines neuen Flächenparameterpaars \(\boldsymbol{t}'\) betrachten, \[ \boldsymbol{t} = \varphi(\boldsymbol{t}') \] mit positiver Jacobi-Determinante \[ \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right)} \] und die Fläche mit Hilfe des neuen Parameterpaars \(\boldsymbol{t}'\) mit der Funktion \[ \rho(\boldsymbol{t}') := \gamma(\varphi(\boldsymbol{t}')) = \gamma(\boldsymbol{t}) \] beschreiben, so ist \[ I_{ \gamma(T)} = I_{ \rho(T')} \] mit \[ I_{ \rho(T')} := \] \[ = \int_{T'} \, \omega(\rho(\boldsymbol{t}')) (v_{1}(\rho(\boldsymbol{t}')), \, v_{1}(\rho(\boldsymbol{t}'))) \, d\mu(\boldsymbol{t}') \] Dabei sind \( v_{i} \) die Tangentialvektoren in die neuen Parameterrichtungen \(t_{i}'\), und \( T' \) ist der Parameterbereich der gestrichenen Parameter, so dass die Integration über dieselbe Fläche geht wie beim Integral \(I_{ \gamma(T)}\) oben (also \(T = \varphi(t') \) ). Als neue Schreibweise führen wir analog zu den 1-Formen ein: \[ I_{ \gamma(T)} =: \int_{\gamma(T)} \omega = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), \, u_{2}(\gamma(\boldsymbol{t}))) \, d\mu(\boldsymbol{t}) \] \( \int_{\gamma(T)} \omega \) hängt dabei nur von dem durchlaufenen Flächenstück auf der Mannigfaltigkeit ab sowie von der durch die Funktion \(\gamma\) gegebenen Orientierung, in der es durchlaufen wird. Das Integral hängt nicht von der Geschwindigkeit ab, mit der das Flächenstück durchlaufen wird (d.h. es ändert seinen Wert bei orientierungserhaltenden Umparametrisierungen der Kurve nicht). Der Grund dafür liegt darin, dass das Symmetrieverhalten der 2-Form dem einer Determinante entspricht. |
In der mathematischen Literatur findet man oft andere elegant aussehende
Formulierungen für die obige Aussage, die mit Hilfe des sogenannten
Pullbacks von Differentialformen formuliert sind – wir sind bei den 1-Formen
oben bereits kurz darauf eingegangen.
Im Prinzip kennen wir den Pullback bereits aus Kapitel 10: Lie-Ableitung und Killingsche Vektorfelder, nur dass die dortige Flussabbildung hier durch die Umparametrisierung \(\varphi\) zu ersetzen ist. Wir wollen hier nicht näher darauf eingehen, da wir dadurch inhaltlich nichts Neues erfahren würden (von dem manchmal etwas kryptischen Formalismus einmal abgesehen). Das Kapitel ist sowieso schon lang genug.
Versuchen wir, analog zu den 1-Formen vorgehen. Dazu schreiben wir \( d\mu(\boldsymbol{t}) = dt_{1} \, dt_{2} \), ziehen die \(dt_{i}\) unter die 2-Form und verwenden \( \boldsymbol{dx}_{i} := u_{i} \, dt_{i} \) (anschaulich ist dann \( \boldsymbol{dx}_{i} \) ein kleiner Tangentialvektor in t_{i}-Richtung): \[ I_{ \gamma(T)} = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), \, u_{2}(\gamma(\boldsymbol{t}))) \, d\mu(\boldsymbol{t}) = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})) \, dt_{1}, \, u_{2}(\gamma(\boldsymbol{t})) \, dt_{2}) = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( \boldsymbol{dx}_{1}, \boldsymbol{dx}_{2} ) = \] \[ = \int_{T} \, \sum_{\mu\nu} \, \omega_{\mu\nu}(\gamma(\boldsymbol{t})) \, dx^{\mu}_{1} \, dx^{\nu}_{2} \] Hier ist die Ähnlichkeit mit \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{\gamma(T)} \, \sum_{\mu \lt \nu} \, \omega_{\mu\nu} \, dx^{\mu} \wedge dx^{\nu} \] auf den ersten Blick noch nicht so überzeugend wie bei den 1-Formen. Wenn wir jedoch wie in Kapitel 9: Abstände und Winkel: die Metrik die Schreibweise \[ dx^{\mu} \wedge dx^{\nu} = \] \[ = dx^{\mu} \circ dx^{\nu} - dx^{\nu} \circ dx^{\mu} \] mit dem Tensorprodukt \[ [dx^{\mu} \circ dx^{\nu}] (u, v) := \] \[ = [dx^{\mu} u] \, [dx^{\nu} v] = u^{\mu} \, v^{\nu} \] verwenden, so ist \[ \omega = \sum_{\mu\nu} \, \omega_{\mu\nu} \, dx^{\mu} \circ dx^{\nu} \] und wir haben \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{\gamma(T)} \, \sum_{\mu\nu} \, \omega_{\mu\nu} \, dx^{\mu} \circ dx^{\nu} \] Das sieht unserem obigen Ausdruck \[ I_{ \gamma(T)} = \int_{T} \, \sum_{\mu\nu} \omega_{\mu\nu}(\gamma(\boldsymbol{t})) \, dx^{\mu}_{1} \, dx^{\nu}_{2} \] schon sehr ähnlich, wobei die Indices 1 und 2 anzeigen, dass zwei verschiedene Tangentialvektoren zu verwenden sind, da man ja über eine Fläche integriert.
Zum Vergleich: Bei der Metrik \[ g = \sum_{\mu\nu} \, g_{\mu\nu} \, dx^{\mu} \circ dx^{\nu} \] und dem entsprechenden Integral \[ L_{\gamma(T)} = \int_{\gamma(T)} \sqrt{ g } \] integriert man über eine Kurve (also nicht über eine Fläche) und hat es deshalb nur mit einem Tangentialvektor zu tun – daher gibt es hier keinen Index 1 oder 2.
Bei den 1-Formen konnte man bei einer vorhandenen Metrik nun weiter die Bogenlänge einführen und \( \boldsymbol{dx} \) als Wegstück der Länge \(ds\) ansehen. Bei 2-Formen hätten wir sicher gerne analog so etwas wie ein Flächenstück. Außerdem konnte man 1-Formen im Wegintegral dann sehr schön als Skalarprodukt eines Vektors mit dem Wegstück \( \boldsymbol{dx} \) verstehen. Bei 2-Formen geht das offenbar nicht ganz so einfach, aber wir wollen uns im Folgenden ansehen, was sich erreichen lässt.
Wie bei 1-Formen wollen wir uns ansehen, was geschieht, wenn wir auf der Mannigfaltigkeit eine Metrik zur Verfügung haben (siehe Kapitel 9: Abstände und Winkel: die Metrik ). Kann man analog zum Bogenmaß ein Flächenmaß finden? Lassen sich 2-Formen anschaulich über das Skalarprodukt interpretieren?
Dazu stellen wir uns die Fläche \(\gamma(\boldsymbol{t})\) eingebettet in den dreidimensionalen euklidischen Raum vor, so dass wir uns die beiden kleinen Wegstücke \[ \boldsymbol{dx}_{1} := u_{1} \, dt_{1} \] \[ \boldsymbol{dx}_{2} := u_{2} \, dt_{2} \] (siehe oben) anschaulich als zwei sehr kleine Tangentialvektoren vorstellen können. Wir können uns weiter vorstellen, dass wir die Fläche \(\gamma(\boldsymbol{t})\) in sehr viele sehr kleine Fast-Parallelogramme mit solchen Kantenvektoren aufteilen können. Diese Kanten haben die Längen \[ |\boldsymbol{dx}_{i}| = ds_{i} = \sqrt{ g(u_{i}, u_{i}) \, dt_{i} } \] Schauen wir uns zum Vergleich ein Parallelogramm im \(\mathbb{R}^{2}\) mit Kantenvektoren \(\boldsymbol{a}_{1}\) und \(\boldsymbol{a}_{2}\) an. In karthesischen Koordinaten (hier geht die Metrik ein!) ist die Fläche dieses Parallelogramms gegeben durch die Determinante der Matrix \(A\) mit den Spaltenvektoren \(\boldsymbol{a}_{1}\) und \(\boldsymbol{a}_{2}\), d.h. \(A\) hat die Komponenten \[ A_{ij} = (\boldsymbol{a}_{j})_{i} \] mit den karthesischen Vektorkomponenten \( (\boldsymbol{a}_{j})_{i} \) (genauer müssten wir den Betrag der Determinante nehmen, da die Fläche positiv sein soll).
Es wäre nun ungünstig, karthesische Koordinaten voraussetzen zu müssen. Daher wollen wir \( \det{A} \) noch etwas umrechnen. Dazu verwenden wir die transponierte Matrix \(A^{T}\), so dass \[ A^{T}_{ij} := A_{ji} \] ist. Die Matrix \(A^{T} A \) hat dann die Komponenten \[ (A^{T} A)_{ij} = \sum_{k} \, A^{T}_{ik} \, A_{kj} = \] \[ = \sum_{k} \, A_{ki} \, A_{kj} = \sum_{k} \, (\boldsymbol{a}_{i})_{k} \, (\boldsymbol{a}_{j})_{k} = \] \[ = \langle \boldsymbol{a}_{i}, \boldsymbol{a}_{j} \rangle =: G_{ij} \] Das vorletzte Gleichheitszeichen ist dabei die Präzisierung der Aussage, dass wir mit karthesischen Vektorkomponenten \( (\boldsymbol{a}_{j})_{i} \) gearbeitet haben, denn nur dann ergibt die Summe über \(k\) auch das euklidische Skalarprodukt. Man bezeichnet \(G\) als Gramsche Matrix.
Bilden wir nun die Determinante: \[ \det{G} = \det{(A^{T} A)} = \] \[ = \det{A^{T}} \, \det{A} = \] \[ = \det{A} \, \det{A} = \] \[ = [\det{A}]^{2} \] d.h. die Fläche des Parallelogramms (gegeben durch \( \det{A} \) ist auch gleich \( \sqrt{ \det{G} } \).
Diese Formulierung hat den Vorteil, dass keine karthesischen Koordinaten mehr gebraucht werden, denn \[ \langle \boldsymbol{a}_{i}, \boldsymbol{a}_{j} \rangle = g(\boldsymbol{a}_{i}, \boldsymbol{a}_{j}) \] können wir in beliebigen Koordinaten auswerten.
Außerdem kann man im zweidimensionalen Fall direkt verifizieren, dass \( \sqrt{ \det{G} } \) anschaulich die Fläche des Parallelogramms sein muss. Diese Fläche ist nämlich gegeben durch die Länge der Grundseite (also z.B. \( |\boldsymbol{a}_{1}| \) ) mal der Höhe des Parallelogramms über dieser Grundseite, also mal \[ |\boldsymbol{a}_{2} - \langle \boldsymbol{e}_{1}, \boldsymbol{a}_{2} \rangle \, \boldsymbol{e}_{1}| \] mit dem Einheitsvektor \[ \boldsymbol{e}_{1} = \frac{\boldsymbol{a}_{1}}{|\boldsymbol{a}_{1}|} \]
Rechnen wir das Quadrat dieses Betrages (also der Höhe) aus:
\[
|\boldsymbol{a}_{2} -
\langle
\boldsymbol{e}_{1}, \boldsymbol{a}_{2}
\rangle \boldsymbol{e}_{1}|^{2} =
\]
\[
=
\langle
\boldsymbol{a}_{2} -
\langle
\boldsymbol{e}_{1}, \, \boldsymbol{a}_{2}
\rangle \, \boldsymbol{e}_{1}
\, , \,
\boldsymbol{a}_{2} -
\langle
\boldsymbol{e}_{1}, \, \boldsymbol{a}_{2}
\rangle \, \boldsymbol{e}_{1}
\rangle
=
\]
\[
=
\langle
\boldsymbol{a}_{2}, \boldsymbol{a}_{2}
\rangle
-
2
\langle
\boldsymbol{e}_{1}, \boldsymbol{a}_{2}
\rangle^{2}
+
\langle
\boldsymbol{e}_{1}, \boldsymbol{a}_{2}
\rangle^{2}
=
\]
\[
=
\langle
\boldsymbol{a}_{2}, \boldsymbol{a}_{2}
\rangle
-
\langle
\boldsymbol{e}_{1}, \boldsymbol{a}_{2}
\rangle^{2}
\]
Das mulitiplizieren wir mit dem Betragsquadrat der Grundseite, also
mal \( \langle
\boldsymbol{a}_{1}, \boldsymbol{a}_{1}
\rangle \) und erhalten so als
Quadrat der Fläche den Ausdruck
\[
\langle
\boldsymbol{a}_{1}, \boldsymbol{a}_{1}
\rangle
\cdot
\left(
\langle
\boldsymbol{a}_{2}, \boldsymbol{a}_{2}
\rangle
-
\langle
\boldsymbol{e}_{1}, \boldsymbol{a}_{2}
\rangle^{2}
\right)
=
\]
\[
=
\langle
\boldsymbol{a}_{1}, \boldsymbol{a}_{1}
\rangle
\,
\langle
\boldsymbol{a}_{2}, \boldsymbol{a}_{2}
\rangle
-
\langle
\boldsymbol{a}_{1}, \boldsymbol{a}_{2}
\rangle^{2}
=
\]
\[
= \det{G}
\]
d.h. die Wurzel dieses Ausdrucks entspricht der anschaulichen geometrischen
Flächendefinition des Parallelogramms als Grundseite mal Höhe.
Im Folgenden wollen wir nun an Stelle des euklidischen Skalarproduktes des Einbettungsraums wieder die Metrik der Mannigfaltigkeit verwenden, um uns von der Einbettung zu lösen. Dabei setzen wir voraus, dass die Metrik positiv definit ist, um Komplikationen zu vermeiden (für die Relativitätstheorie mit ihrer indefiniten Metrik muss man also bei Bedarf darüber nachdenken, unter welchen Voraussetzungen sich die Überlegungen auch dort anwenden lassen).
Damit ist die Fläche \( dA \) jedes der winzigen Parallelogramme mit Kantenvektoren \[ \boldsymbol{dx}_{1} = u_{1} \, dt_{1} \] \[ \boldsymbol{dx}_{2} = u_{2} \, dt_{2} \] gleich \[ dA := \sqrt{ \det{g(\boldsymbol{dx}_{i}, \boldsymbol{dx}_{j})} } = \] \[ = \sqrt{ \det{g(u_{i}, u_{j})} } \, dt_{1} \, dt_{2} \] in Analogie zur Länge \(ds\) eines Kurvenstücks. Achtung: der Faktor \( dt_{1} \, dt_{2} \) steht nicht mehr unter der Wurzel, denn die \(dt\)-Faktoren kommen in der Determinante häufiger vor! Und: die Schreibweise \( \det{g(u_{i}, u_{j})} \) bedeutet, dass man die Determinante einer Matrix bildet, die die Matrixelemente \(g(u_{i}, u_{j}) \) hat.
Wie bei der Kurvenlänge \( L_{\gamma(T)} \) können wir nun auch die Fläche \( A_{\gamma(T)} \) eines Flächenstücks \(\gamma(T)\) definieren über \[ A_{\gamma(T)} = \int_{T} \, dA = \] \[ = \int_{T} \, \sqrt{ \det{ g( u_{i}(\gamma(\boldsymbol{t})), u_{j}(\gamma(\boldsymbol{t}))) } } \, dt_{1} \, dt_{2} \] Auch hier ist – wie bei der Bogenlänge – der Integrand nichtlinear in den Tangentialvektoren. Es handelt sich also nicht um ein Integral über eine Differentialform. Dennoch ist das Integral unabhängig von der Parametrisierung (und von der Orientierung).
Versuchen wir, das Flächenintegral unserer 2-Form \(\omega\) so zu parametrisieren, dass \( dA \) als Integrationsmaß verwendet werden kann. Dazu erweitern wir mit der Gramschen Determinante, so dass wir das Flächenelement \(dA\) erhalten, und werten das Ergebnis als eine Umparametrisierung der Fläche analog zu oben: \[ I_{ \gamma(T)} = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), \, u_{2}(\gamma(\boldsymbol{t}))) \, d\mu(\boldsymbol{t}) = \] \[ = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t}))) \cdot \] \[ \cdot \sqrt{ \det{ g( u_{i}(\gamma(\boldsymbol{t})), u_{j}(\gamma(\boldsymbol{t}))) } } \cdot \] \[ \cdot \frac{d\mu(\boldsymbol{t})}{ \sqrt{ \det{ g( u_{i}(\gamma(\boldsymbol{t})), u_{j}(\gamma(\boldsymbol{t}))) } } } = \] \[ = \int_{T} \, \omega(\rho(\boldsymbol{t}')) ( v_{1}(\rho(\boldsymbol{t}')), \, v_{2}(\rho(\boldsymbol{t}')))] \, \, dA(\boldsymbol{t}') \] Die Umparametrisierung \[ \boldsymbol{t} = \varphi(\boldsymbol{t}') \] wurde dabei gerade so gewählt, dass \[ d\mu(\boldsymbol{t}) = d\mu(\varphi(\boldsymbol{t}')) = \] \[ = \left| \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right) } \right| \, d\mu(\boldsymbol{t}') = \] \[ = \sqrt{ \det { ( g( u_{i}(\gamma(\boldsymbol{t})), u_{j}(\gamma(\boldsymbol{t})) ) ) } } \, dA(\boldsymbol{t}') \] ist mit \[ d\mu(\boldsymbol{t}') = dA(\boldsymbol{t}') \] und \[ \left| \det{ \left( \frac{d\varphi(\boldsymbol{t}')}{\boldsymbol{dt}'} \right) } \right| = \] \[ = \sqrt{ \det { ( g( u_{i}(\gamma(\boldsymbol{t})), u_{j}(\gamma(\boldsymbol{t})) ) ) } } \] (d.h. \(\varphi\) muss entsprechend gewählt werden).
Anschaulich legt die spezielle \(\boldsymbol{t}'\)-Parametrisierung ein Netz aus kleinen Parallelogrammen über die Fläche, so dass jedes Mini-Paralellogramm auf der Fläche (gegeben durch die Tangentialvektoren \( v_{1} \, dt_{1} \) und \( v_{2} \, dt_{2} \) ) eine Fläche \(dA\) aufweist, die identisch ist mit der Fläche \( d\mu(\boldsymbol{t}') = dt_{1} \, dt_{2} \). Man könnte sagen, dass das rechteckige Koordinaten-Gitternetz aus dem Parameterraum flächentreu über die Fläche gelegt wird.
Im eindimensionalen Fall konnten wir das Skalarprodukt (die Metrik) weiter dazu verwenden, um unter dem Integral 1-Formen als Skalarprodukt eines Vektors mit den Linienelement \( \boldsymbol{dx} \) zu schreiben: \[ I_{ \gamma(T)} = \int_{\gamma(T)} \omega = \] \[ = \int_{\gamma(T)} \, \langle v_{\omega}(\gamma(t)), \boldsymbol{dx} \rangle \] Dabei konnten wir \( \boldsymbol{dx} \) mit der Bogenlänge in Verbindung bringen: \( |\boldsymbol{dx}| = ds \).
Können wir analog auch bei 2-Formen vorgehen und unsere obige Schreibweise \[ I_{ \gamma(T)} = \int_{T} \, \omega(\gamma(\boldsymbol{t})) ( \boldsymbol{dx}_{1}, \boldsymbol{dx}_{2} ) = \] \[ \int_{T} \, \sum_{\mu\nu} \, \omega_{\mu\nu}(\gamma(\boldsymbol{t})) \, dx^{\mu}_{1} \, dx^{\nu}_{2} \] mit dem Flächenelement \(dA\) in Verbindung bringen?
Nun, zunächst haben wir natürlich von oben bereits den Zusammenhang \[ dA = \sqrt{ \det { g(\boldsymbol{dx}_{i}, \boldsymbol{dx}_{j}) }} \] d.h. \(dA\) ist die Fläche des kleinen Parallelogramms mit den Kantenvektoren \(\boldsymbol{dx}_{1}\) und \(\boldsymbol{dx}_{2}\).
Oben haben wir gesehen, wie sich das Integral dann durch Umparametrisierung als Integral über \(dA\) schreiben lässt. Wir würden aber gerne noch weitergehen und aus den Kantenvektoren \(\boldsymbol{dx}_{1}\) und \(\boldsymbol{dx}_{2}\) einen Flächenelement-Vektor \boldsymbol{dA} mit Länge \(dA\) machen. Dann lässt sich vielleicht der Integrand wieder als Skalarprodukt schreiben, beispielsweise als \( \langle \boldsymbol{v}, \boldsymbol{dA} \rangle \) mit einem geeigneten Vektor \(\boldsymbol{v}\).
Es stellt sich heraus, dass sich unser Ziel erreichen lässt, wenn die Dimension der Mannigfaltigkeit, in der unsere Fläche liegt, um eins größer ist als die Fläche, über die integriert wird. In unserem Fall ist die Fläche zweidimensional (wir integrieren ja eine 2-Form), d.h. die Mannigfaltigkeit muss dreidimensional sein. Die Rolle des Skalarproduktes übernimmt dann die Metrik der Mannigfaltigkeit.
Wenn die Mannigfaltigkeit nur zweidimensional ist und das Integral über ein zweidimensionales Teilgebiet läuft, so kann man eine Einbettung zu Hilfe nehmen und den Einbettungsraum \(\mathbb{R}^{3}\) mit seinem euklidischen Skalarprodukt als Mannigfaltigkeit verwenden. Wir wollen diese beiden Fälle im Folgenden nicht unterscheiden. Wichtig ist lediglich, dass wir im Tangentialraum genau eine Dimension mehr zur Verfügung haben, als die Dimension der Differentialform und damit der Integrationsfläche ist.
Schauen wir uns an, wie sich in diesem Fall das Flächenintegral schreiben lässt. Dazu wollen wir zunächst die 2-Form \(\omega\) in einer speziellen Weise mit Hilfe der Antisymmetrie umschreiben: \[ \omega = \sum_{\mu \lt \nu} \, \omega_{\mu\nu} \, dx^{\mu} \wedge dx^{\nu} = \] \[ = \omega_{2,3} \, dx^{2} \wedge dx^{3} + \] \[ + \omega_{3,1} dx^{3} \wedge dx^{1} + \] \[ + \omega_{1,2} \, dx^{1} \wedge dx^{2} \] (dabei sind wie immer \(x^{1}, x^{2}, x^{3}\) die Koordinaten auf der Mannigfaltigkeit).
Diese Schreibweise lässt sich leicht auf mehr Dimensionen verallgemeinern. Bei 3-Formen im vierdimensionalen Raum wäre z.B. der zweite Summand gegeben durch \[ \omega_{3,4,1} \, dx^{3} \wedge dx^{4} \wedge dx^{1} \] d.h. man macht immer eine zyklische Rundreise durch alle Koordinaten-Indices, wobei im i-ten Summanden der Index \(i\) nicht vorkommt. Das Verfahren funktioniert immer, wenn man eine (n-1)-Form im n-dimensionalen Raum hat.
Wir können nun das Flächenintegral in dieser Schreibweise ausdrücken: \[ \int_{\gamma(T)} \omega = \] \[ = \int_{T} \, [\omega_{2,3} \, dx^{2} \wedge dx^{3} + \] \[ + \omega_{3,1} \, dx^{3} \wedge dx^{1} + \] \[ + \omega_{1,2} \, dx^{1} \wedge dx^{2}] \] \[ (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t}))) \, dt_{1} dt_{2} = \] \[ =: \int_{T} \, (\Omega_{1} \, dA^{1} + \Omega_{2} \, dA^{2} + \Omega_{3} \, dA^{3} ) \] mit \[ \Omega_{1} := \omega_{2,3} \] usw. (zyklisch) sowie \[ dA^{1} := [dx^{2} \wedge dx^{3}] (u_{1}, u_{2}) \, dt_{1} dt_{2} = \] \[ = (u_{1}^{2} \, u_{2}^{3} - u_{1}^{3} \, u_{2}^{2}) \, dt_{1} \, dt_{2} \] usw. (zyklisch)
Wenn die Mannigfaltigkeit \(M\) der euklidische Raum \(\mathbb{R}^{3}\) ist, dann können wir in euklidischen Koordinaten \(x^{\mu}\) die \( dA^{\mu} \) als Komponenten des Vektors \[ \boldsymbol{dA} := \boldsymbol{dx}_{1} \times \boldsymbol{dx}_{2} \] ansehen. Dabei ist \( \times \) das übliche Vektor-Kreuzprodukt. Man kann zeigen, dass \( \boldsymbol{dA} \) senkrecht auf auf \( \boldsymbol{dx}_{1} \) und \( \boldsymbol{dx}_{2} \) steht und dass er auch die richtige Länge hat, d.h. diese Länge ist gleich der durch \( \boldsymbol{dx}_{1} \) und \( \boldsymbol{dx}_{2} \) aufgespannten Parallelogrammfläche. Daher bezeichnet man \( \boldsymbol{dA} \) auch als Normalenvektor des Flächenelements.
Weiter kann man im euklidischen dreidimensionalen Raum auch die \( \Omega_{\mu} \) als Komponenten eines Vektors \( \boldsymbol{\Omega} \) ansehen und das Flächenintegral schreiben als \[ \int_{\gamma(T)} \omega = \int_{\gamma(T)} \langle \boldsymbol{\Omega}(\gamma(t)), \boldsymbol{dA} \rangle \] Man kann sich vorstellen, dass \( \boldsymbol{\Omega} \) eine Flüssigkeits-Stromdichte darstellt, und dass \( \langle \boldsymbol{\Omega}(\gamma(t)), \boldsymbol{dA} \rangle \) den Durchfluss durch das Flächenelement \(dA\) ergibt. Dabei wird durch das Skalarprodukt automatisch berücksichtigt, dass der Durchfluss am größten ist, wenn die Fläche senkrecht (also \(\boldsymbol{dA}\) parallel) zum Strom \(\boldsymbol{\Omega}\) steht.
Bleiben wir im euklidischen dreidimensionalen Raum: Man verwendet dort auch gerne die Schreibweise \[ dA^{1} := dx^{2} \wedge dx^{3} \] (usw. (zyklisch)), ohne diese \( dA^{\mu} \) in der Schreibweise von den Komponenten des Flächen-Normalenvektors \( dA^{\mu} \) von oben zu unterscheiden.
Das ist analog zur Doppelbedeutung von \( dx^{\mu} \) bei den 1-Formen. Man muss sich einfach merken: In Flächenintegralen werden aus den 2-Formen \( dA^{\mu} \) durch Anwenden auf die beiden Tangentialvektoren \( u_{1} \, dt_{1} \) und \( u_{2} \, dt_{2} \) die Flächen-Normalenvektor-Komponenten \( dA^{\mu} \) wie oben angegeben, so dass die korrekte Definition des Flächenintegrals für 2-Formen automatisch entsteht. Man braucht die beiden Tangentialvektoren ja, um zu wissen, wie die Fläche in der Mannigfaltigkeit liegt.
Interpretiert man die \( dA^{\mu} \) als 2-Formen, so kann man in \( \mathbb{R}^{3} \) in euklidischen Koordinaten die 2-Form \( \omega \) formal als Skalarprodukt schreiben: \[ \omega = \langle \boldsymbol{\Omega}, \boldsymbol{dA} \rangle \] in Analogie zur 1-Form-Schreibweise \[ \omega = \langle v_{\omega}, \boldsymbol{dx} \rangle \] Gilt für eine 1-Form, dass sie die d-Ableitung einer 0-Form (Funktion) ist, also \( \omega = d\phi \), so konnten wir gleichwertig auch \[ d\phi = \langle \mathrm{grad} \, \phi, \boldsymbol{dx} \rangle \] schreiben.
Bei der d-Ableitung einer 1-Form \( \omega = \langle v_{\omega} , \boldsymbol{dx} \rangle \) schreiben wir im euklidischen \( \mathbb{R}^{3} \) analog \[ d \langle v_{\omega} , \boldsymbol{dx} \rangle = \langle \mathrm{rot} \, v_{\omega} , \boldsymbol{dA} \rangle \] In euklidischen Koordinaten kann man leicht nachrechnen, dass sich die übliche Definition der Rotation eines Vektorfeldes ergibt.
Etwas weiter unten werden wir auch noch die d-Ableitung einer 2-Form kennenlernen. Hier ein kurzer Vorgriff darauf: Wenn wir im \( \mathbb{R}^{3} \) in euklidischen Koordinaten \[ dV := dx^{1} \wedge dx^{2} \wedge dx^{3} \] schreiben, so ergibt diese d-Ableitung die Form \[ d \langle \boldsymbol{\Omega} , \boldsymbol{dA} \rangle = (\mathrm{div} \, \boldsymbol{\Omega}) \, dV \] mit der üblichen Definition der Divergenz eines Vektorfeldes in euklidischen Koordinaten. Die obigen Formeln machen die anschauliche Bedeutung der d-Ableitung vielleicht etwas klarer. Wir kommen unten noch einmal darauf zurück.
Anmerkung:
Für die korrekte Definition von \(\boldsymbol{dA}\) und \(\boldsymbol{\Omega}\)
sowie der obigen Beziehungen für Divergenz und Rotation
in krummlinigen Koordinaten
(z.B. in einer gekrümmten dreidimensionalen Mannigfaltigkeit)
muss man sorgfältiger
vorgehen und eine koordinaten-unabhängige Definition
verwenden (die obige Definition benötigte
euklidische Koordinaten). Bei den 1-Formen und dem Gradienten
ist uns dies ja bereits gelungen
(siehe Kapitel 9: Abstände und Winkel: die Metrik).
Dafür werden wir den sogenannten Hodge-Sternoperator benötigen.
Wir kommen im nächsten Kapitel darauf zurück.
Wir möchten uns nun analog zu den 1-Formen die exakten 2-Formen \(\omega\) anschauen, also die 2-Formen, die sich in jedem Punkt in dem uns interessierenden Gebiet \(G\) der Mannigfaltigkeit \(M\) als d-Ableitung einer einzigen 1-Form (Stammform) \(\pi\) darstellen lassen: \[ \omega = d\pi \] Ausgeschrieben bedeutet das (den d-Operator für 1-Formen hatten wir oben bereits definiert; wir lassen die Argumente wie \(p\) und \(x\) hier weg): \[ \omega = d\pi = \] \[ = \sum_{\nu} \, d\pi_{\nu} \wedge dx^{\nu} = \] \[ = \sum_{\nu} \, \left( \sum_{\mu} \, \frac{\partial \pi_{\nu}}{\partial x^{\mu}} \, dx^{\mu} \right) \, \wedge dx^{\nu} = \] \[ = \sum_{\mu\nu} \, \frac{\partial \pi_{\nu}}{\partial x^{\mu}} \, dx^{\mu} \wedge dx^{\nu} = \] \[ = \sum_{\mu \lt \nu} \, \left( \frac{\partial \pi_{\nu}}{\partial x^{\mu}} - \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \right) \, dx^{\mu} \wedge dx^{\nu} \] Für die Komponenten bedeutet das für jeden Punkt \(p\) \[ \omega_{\mu\nu} = \frac{\partial \pi_{\nu}}{\partial x^{\mu}} - \frac{\partial \pi_{\mu}}{\partial x^{\nu}} \] Bei karthesischen Koordinaten ist das die Rotation eines Vektorfeldes.
Wie bei den 1-Formen kann man auch bei den 2-Formen Bedingungen herleiten, die garantieren, dass eine 2-Form \( \omega \) exakt ist, also eine Stammform \(\pi\) besitzt. Die Idee ist vollkommen analog zu den 1-Formen: Man konstruiert die Stammform \(\pi\) explizit aus \(\omega\) durch geeigntete Integration über eine Kurve, die genauso wie bei den 1-Formen von einem beliebigen (aber dann festen) Startpunkt \(q\) zum betrachteten Punkt \(p\) führt, wobei die Koordinaten eine Gerade im Koordinatenraum beschreiben. Daher muss das betrachtete Gebiet wieder sternförmig sein. Nun muss man wieder nachprüfen, ob \( \omega(p) = d\pi(p) \) für die so konstruierte 1-Form \(\pi\) gilt. Man findet erneut, dass das genau dann gilt, wenn im Gebiet \(G\) die Bedingungen \[ d\omega = 0 \] erfüllt ist (die relativ lange Rechnung dazu wollen wir hier überspringen; sie steht in jedem Lehrbuch über Differentialformen). Dabei ist der d-Operator für 2-Formen in in Analogie zu den 1-Formen definiert:
| d-Operator für 2-Formen: \[ d\omega = = \] \[ = \sum_{\mu \lt \nu} \, d\omega_{\mu\nu} \, \wedge dx^{\mu} \wedge dx^{\nu} = \] \[ = \sum_{\mu \lt \nu} \, \left( \sum_{\rho} \, \frac{\partial \omega_{\mu\nu}}{\partial x^{\rho}} \, dx^{\rho} \right) \wedge dx^{\mu} \wedge dx^{\nu} \] Der d-Operator macht also aus einer 2-Form eine 3-Form (Details zu höherdimensionalen Formen folgen weiter unten). Natürlich kann man die Summenterme noch so umordnen und umbenennen, dass eine Summe mit \( \sum_{\mu \lt \nu \lt \rho} \) entsteht. Wir wollen uns das hier ersparen. Das 3-fache Dachprodukt ist dabei definiert durch die Determinante \[ [ dx^{\mu} \wedge dx^{\nu} \wedge dx^{\rho} ] (u, v, w) := \] \[ := \det{ (u, v, w)^{\mu\nu\rho} } \] wobei die Matrix \( (u, v, w)^{\mu\nu\rho} \) wie folgt aufgebaut ist: \[ (u, v, w)^{\mu\nu\rho} = \begin{pmatrix} u^{\mu} & v^{\mu} & w^{\mu} \\ u^{\nu} & v^{\nu} & w^{\nu} \\ u^{\rho} & v^{\rho} & w^{\rho} \end{pmatrix} \] d.h. \(\mu, \nu, \rho\) sind die Zeilenindizes und \(u, v, w\) sind die Spaltenvektoren. |
Im dreidimensionalen Raum (euklidische Koordinaten) bedeutet \(d\omega = 0\),
dass die Divergenz des Vektorfeldes \( \boldsymbol{\Omega} \) (siehe oben) verschwinden muss.
Ein divergenzfreies (also quellenfreies) Vektorfeld lässt sich daher als Rotation eines
anderen Vektorfeldes (genannt Vektorpotential) schreiben, wie man
als Physiker beispielsweise in der Elektrodynamik lernt.
Fassen wir zusammen:
|
Integrabilitätsbedingung für 2-Formen (Lemma von Poincaré): Eine 2-Form \( \omega(p) \) ist dann in einem Gebiet \(G\) der Mannigfaltigkeit \(M\) exakt (lässt sich also in \(G\) als äußere Ableitung \[ \omega = d\pi \] einer 1-Form \(\pi\) schreiben), wenn \(G\) topologisch trivial und sternförmig ist (d.h. es gibt einen Punkt \(q \in G\), so dass bezüglich eines Koordinatensystems \(f\) sich jeder Punkt \(p \in G\) durch eine gerade Linie von \(f(q)\) nach \(f(p)\) im Koordinatenraum erreichen lässt) und wenn in \(G\) gilt: \[ d\omega = 0 \] (man bezeichnet ein \(\omega\) mit \(d\omega = 0\) auch als geschlossen). Die Umkehrung gilt ebenfalls, denn wegen der Antisymmetrie des Dachproduktes und wegen der Vertauschbarkeit der partiellen Ableitungen gilt \[ d\omega = d(d\pi) = 0 \] Man bezeichnet \(\pi\) als Stammform von \(\omega\).
|
Das Ergebnis sieht also formal genauso aus wie bei den 1-Formen, wobei wir
Komplikationen wie nicht-triviale Topologien oder die Notwendigkeit mehrerer
Koordinatensysteme wieder erst einmal weggelassen haben.
Generell können wir uns merken, dass das obige Ergebnis auch in mehr Dimensionen
weiter gilt.
Bei den 1-Formen hatten wir gesehen, dass das Kurvenintegral über die exakte 1-Form \(d\phi\) nur von den \(\phi\)-Werten am Anfangs- und Endpunkt des Kurvenstücks \(\gamma(T)\) abhängt (wir sprachen vom Rand \(\gamma(\partial T)\) des Kurvenstücks): \[ \int_{\gamma(T)} d\phi = \] \[ = \phi(\gamma(b)) - \phi(\gamma(a)) =: \] \[ =: \int_{\gamma(\partial T)} \phi \] Anschaulich konnten wir uns vorstellen, wie man über viele kleine Kurvenstücke die \( \phi \)-Veränderungen \(d\phi\) entlang der Kurve aufsummiert und so den \(\phi\)-Unterschied zwischen Start- und Zielpunkt bestimmt. Die Form der Kurve dazwischen spielt dabei keine Rolle.
Wie wir sehen werden, kann man dieses Ergebnis auch auf exakte 2-Formen (und generell auf alle höherdimensionalen Differentialformen) übertragen. Wir wollen uns bei den 2-Formen ansehen, wie es dazu kommt, und was unter dem Integral über den Rand zu verstehen ist. Dazu betrachten wir ein Rechteck \(T\) im Parameterraum, so dass das Bild \(\gamma(T)\) des Rechtecks die Eckpunkte \[ p_{1} = \gamma(a_{1}, a_{2}) \] \[ p_{2} = \gamma(b_{1}, a_{2}) \] \[ p_{3} = \gamma(b_{1}, b_{2}) \] \[ p_{4} = \gamma(a_{1}, b_{2}) \] besitzt. Die Reihenfolge der Punkte ist so gewählt, dass wir im Parameterraum gegen den Uhrzeigersinn um das Rechteck \(T\) herumlaufen (das hat etwas mit dem Begriff der Orientierung zu tun, auf den wir weiter unten noch eingehen).
Übrigens muss das Bild \( \gamma(T) \) des Rechtecks \(T\) kein Parallelogramm sein, da die Seiten nicht parallel sein müssen im Sinn der Parallelverschiebung (siehe Kapitel 7: Torsion ). Wir erinnern uns: ein richtiges Parallelogramm kann ja aufgrund von Torsion eine Lücke (wie eine Schraubenversetzung) aufweisen. Das kann bei unserem Rechteck nicht passieren.
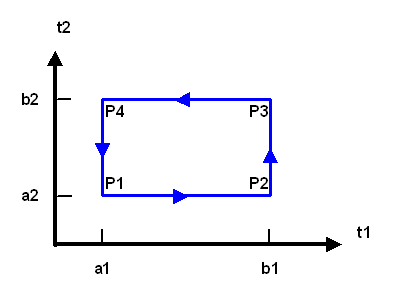
Den Rundweg von \(p_{1}\) über \(p_{2}, p_{3}\) und
\(p_{4}\) wieder zurück nach \(p_{1}\) (in dieser Reihenfolge!) wollen wir als
\( \gamma(\partial T) \) oder als Rand von \( \gamma(T) \) bezeichnen.
Den Rand von \(T\) im Parameterraum bezeichnen wir analog als \( \partial T \).
Im 1-dimensionalen Fall oben wird eine Null-Form \(\phi\) über den Rand eines Kurvenstücks integriert, d.h. Anfangs- und Endpunkt werden betrachtet. Analog wollen wir nun im zweidimensionalen Fall eine 1-Form \(\omega\) über den Rand des Rechtecks integrieren, also über den obigen Rundweg \( \gamma(\partial T) \) entlang der Rechteck-Kanten. Um das Randintegral \[ \int_{\delta\gamma(T)} \omega \] auszurechnen, teilen wir es in vier Teilintegrale auf, entsprechend den vier Teilwegen entlang der einzelnen Kanten. Die entsprechenden Tangentialvektoren wollen wir wie bisher mit \(u_{1}\) und \(u_{2}\) (ggf. mit Vorzeichen) bezeichnen, je nachdem, ob sie in \(t_{1}\) oder in \(t_{2}\)-Richtung zeigen. Als Kurvenparameter verwenden wir analog entweder \( t_{1} \) oder \( t_{2} \), je nachdem, in welche Richtung wir laufen. Also haben wir: \[ \int_{\gamma(\partial T)} \omega = \] \[ = \int_{a_{1}}^{b_{1}} \, [\omega(\gamma(t_{1}, a_{2})) \, u_{1}(\gamma(t_{1}, a_{2}))] \, dt_{1} + \] \[ + \int_{a_{2}}^{b_{2}} \, [\omega(\gamma(b_{1}, t_{2})) \, u_{2}(\gamma(b_{1}, t_{2}))] \, dt_{2} + \] \[ - \int_{a_{1}}^{b_{1}} \, [\omega(\gamma(t_{1}, b_{2})) \, u_{1}(\gamma(t_{1}, b_{2}))] \, dt_{1} + \] \[ - \int_{a_{2}}^{b_{2}} \, [\omega(\gamma(a_{1}, t_{2})) \, u_{2}(\gamma(a_{1}, t_{2}))] \, dt_{2} = \] ... die negativen Vorzeichen berücksichtigen, dass die Kanten 3 und 4 entgegen der Parameterrichtung durchlaufen werden. Wir können nun Term 1 und 3 sowie Term 2 und 4 zusammenfassen und die Differenz jeweils durch ein Integral ausdrücken, so dass aus den Differenzen der eindimensionalen Kantenintegrale ein zweidimensionales Integral über das Rechteck \(T\) wird. An dieser Stelle kommt der Hauptsatz der Differential- und Integralrechnung ins Spiel, analog zu den Kurvenintegralen oben! Daran erkennt man, dass der Integralsatz von Stokes eigentlich nur eine geschickte Übertragung dieses Hauptsatzes auf mehrdimensionale Integrale ist. Es ergibt sich: \[ = \int_{a_{1}}^{b_{1}} \, \big\{ [\omega(\gamma(t_{1}, a_{2})) \, u_{1}(\gamma(t_{1}, a_{2}))] + \] \[ \quad \quad - [\omega(\gamma(t_{1}, b_{2})) \, u_{1}(\gamma(t_{1}, b_{2}))] \big\} \, dt_{1} + \] \[ + \int_{a_{2}}^{b_{2}} \, \big\{ [\omega(\gamma(b_{1}, t_{2})) \, u_{2}(\gamma(b_{1}, t_{2}))] + \] \[ \quad \quad - [\omega(\gamma(a_{1}, t_{2})) \, u_{2}(\gamma(a_{1}, t_{2}))] \big\} \, dt_{2} = \] \[ = \int_{a_{1}}^{b_{1}} \, \int_{b_{2}}^{a_{2}} \, \left( \frac{d}{dt_2} [\omega(\gamma(t_{1}, t_{2})) \, u_{1}(\gamma(t_{1}, t_{2}))] \right) \, dt_{1} \, dt_{2} + \] \[ + \int_{a_{2}}^{b_{2}} \, \int_{a_{1}}^{b_{1}} \, \left( \frac{d}{dt_1} [\omega(\gamma(t_{1}, t_{2})) \, u_{2}(\gamma(t_{1}, t_{2}))] \right) \, dt_{1} \, dt_{2} = \] ... im ersten Term vertauschen wir die Grenzen \(b_{2}\) und \(a_{2}\), was ein Minuszeichen bewirkt, und fassen die beiden Integrale zusammen: \[ = \int_{a_{2}}^{b_{2}} \, \int_{a_{1}}^{b_{1}} \, \bigg( \frac{d}{dt_1} [\omega(\gamma(t_{1}, t_{2})) \, u_{2}(\gamma(t_{1}, t_{2}))] + \] \[ \quad \quad - \frac{d}{dt_2} [\omega(\gamma(t_{1}, t_{2})) \, u_{1}(\gamma(t_{1}, t_{2}))] \bigg) \, dt_{1} \, dt_{2} = \] ... zur Vereinfachung der Schreibweise wollen wir wieder \( (t_{1}, t_{2}) = \boldsymbol{t} \) sowie \( \int_{a_{2}}^{b_{2}} \int_{a_{1}}^{b_{1}} dt_{1} \, dt_{2} = \int_{T} d\mu(\boldsymbol{t}) \) schreiben: \[ = \int_{T} \, \bigg( \frac{d}{dt_1} [\omega(\gamma(\boldsymbol{t})) u_{2}(\gamma(\boldsymbol{t}))] + \] \[ \quad \quad - \frac{d}{dt_2} [\omega(\gamma(\boldsymbol{t})) u_{1}(\gamma(\boldsymbol{t}))] \bigg) \, d\mu(\boldsymbol{t}) = \] ... der Integrand ist identisch mit der Basis-unabhängigen Darstellung von \( d\omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t})) \) (siehe oben). Wir haben also: \[ = \int_{T} \, d\omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t})) \, d\mu(\boldsymbol{t}) = \] \[ = \int_{\gamma(T)} d\omega \] Wir haben also mit dieser sehr einfachen Rechnung gezeigt:
|
Integralsatz von Stokes für exakte 2-Formen und rechteckige Parametergebiete: Für ein Rechteck \(T\) im zweidimensionalen Parameterraum und eine beliebige auf der berandeten Fläche \(\gamma(T)\) definierte 1-Form \(\omega\) gilt: \[ \int_{\gamma(\partial T)} \omega = \int_{\gamma(T)} d\omega \] Dabei ist \(\gamma(\partial T)\) der Rand der Fläche \(\gamma(T)\). Die Flächenparametrisierung \(\gamma\) muss dabei hinreichend gutartig (z.B. injektiv) sein, um Fälle wie das Möbiusband zu vermeiden, bei dem 2 Kanten durch \(\gamma\) verkehrt herum zusammenkleben.
|
Man kann diesen Satz leicht auf andere Parameterbereiche verallgemeinern.
So kann man durch Parametertransformationen aus dem Rechteck andere
Integrationsgebiete gewinnen. Man kann auch viele sehr kleine Rechtecke verwenden
und das gewünschte Integrationsgebiet damit gleichsam pflastern.
Die Kantenbeiträge an den gemeinsamen Kanten der Pflasterstücke heben sich
dabei gegenseitig auf, so dass nur die Kantenbeiträge am Außenrand der Pflasterfläche
übrig bleiben. Die Pflasterfläche muss dabei noch nicht einmal zusammenhängend sein.
Wie weit man diese Verallgemeinerung treiben kann, wollen wir hier nicht untersuchen. Anschaulich können wir uns vorstellen:
|
Integralsatz von Stokes für exakte 2-Formen auf (berandeten) Untermannigfaltigkeiten: Der Integralsatz von Stokes für exakte 2-Formen gilt für alle (ggf. berandeten) Untermannigfaltigkeiten, die man im Prinzip mit einem Rechteckpflaster überziehen kann, d.h. der Parameterbereich ist die Vereinigungsmenge von endlich vielen Rechtecken, so dass sich die Rand-Integralbeiträge der inneren Kanten aufheben (d.h. die Untermannigfaltigkeit muss orientierbar sein).
|

Auch hier sind Verallgemeinerungen denkbar, z.B. mehrere verträgliche Pflasterungen,
Dreiecke statt Rechtecke
oder infinitesimal kleine Rechtecke.
Die letzte Bedingung, dass sich die Rand-Integralbeiträge der inneren Kanten aufheben müssen, bedeutet, dass die Fläche orientierbar sein muss. Für das Möbiusband gilt der Integralsatz von Stokes also nicht. Wir werden uns im n-dimensionalen Fall noch einmal genau ansehen, was es mit der Orientierung und Rändern sowie mit den Vorzeichen der einzelnen Randterme auf sich hat. Für den Moment wollen wir uns mit der Anschauung begnügen, die im zweidimensionalen Fall noch einigermaßen funktioniert.
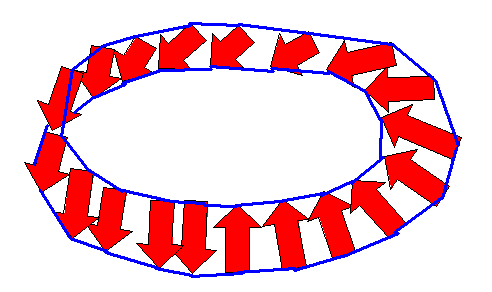
Wir hatten oben eine Veranschaulichung für 1-Formen angegeben, wie man sie beispielsweise in Dan Piponi: On the Visualisation of Differential Forms findet. Dabei haben wir eine 1-Form \( \omega \) in einer n-dimensionalen Mannigfaltigkeit durch \((n - 1)\) -dimensionale Höhenlinien (Flächen) dargestellt.
Dahinter stand die Idee, dass eine um einen Punkt \(p\) herum definierte skalare Funktion \(\phi\) entlang der Höhenlinien bei \(p\) konstant ist, und dass der Wert von \( \omega(p) \, u(p) \) gleich der Richtungsableitung von \(\phi\) in \(p\) in \(u(p)\)-Richtung ist. Der Wert von \[ \omega(p) \, u(p) \] entspricht dann der Dichte der Höhenlinien in \(u(p)\)-Richtung, also der Zahl der Höhenlinien (mit Vorzeichen), die man bei einem kleinen Schritt in \(u(p)\)-Richtung durchstößt (die Schrittlänge wird dabei durch \(u(p)\) bestimmt). Ein Kurvenintegral über \(\omega\) zählt demnach die durchstoßenen Höhenlinien (mit Vorzeichen) auf dem Weg.
Wir wollen dieses Bild nun auf 2-Formen übertragen. Eine 2-Form \(\omega\) in einer n-dimensionalen Mannigfaltigkeit werden wir also durch \((n - 2)\) -dimensionale Flächen darstellen. Wir wollen diese Flächen als Blätter bezeichnen. Der Wert von \[ \omega(p) (u_{1}(p), u_{2}(p)) \] ist dann durch die Zahl der Blätter gegeben, die von einer kleinen, durch \(u_{1}(p)\) und \(u_{2}(p)\) aufgespannten Fläche durchstoßen werden. Ein Flächenintegral über \( \omega \) zählt demnach die von der Fläche durchstoßenen Blätter, wobei noch Vorzeichen ins Spiel kommen können (je nach Orientierung der Tangentialvektoren und der Blätter). Auf Details wollen wir lieber verzichten.
Warum dieses Bild Sinn macht, ist nicht ganz einfach zu begründen. Und: Wenn die Begründungen für Veranschaulichungen zu kompliziert werden, macht die Veranschaulichung selbst oft auch keinen Sinn mehr. Schauen wir uns daher lieber an, wie weit wir mit diesem Bild kommen.
Bei den 1-Formen hatten wir als Mannigfaltigkeit den zweidimensionalen reellen Raum \( \mathbb{R}^{2} \) betrachtet. Darin hatten wir uns die 1-Form \[ \omega = x \, dy \] angesehen. Die Höhenlinien zu dieser 1-Form lagen alle parallel zur x-Achse, und nach rechts kamen ständig neue Höhenlinien dazu.
Schauen wir und nun die zugehörige 2-Form \( d\omega \) an. Wir wollen dazu die Basis-unabhängige Definition des d-Operators verwenden: \[ d\omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t}))) = \] \[ = \frac{d}{dt_1} [\omega(\gamma(\boldsymbol{t})) u_{2}(\gamma(\boldsymbol{t}))] + \] \[ - \frac{d}{dt_2} [\omega(\gamma(\boldsymbol{t})) u_{1}(\gamma(\boldsymbol{t}))] \] In unserem einfachen Beispiel setzen wir einfach \( t_{1} = x \) und \( t_{2} = y \) sowie \[ u_{1} = \frac{\partial}{\partial x} \] \[ u_{2} = \frac{\partial}{\partial y} \] Also haben wir: \[ d\omega(x,y) \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right) = \] \[ = \frac{\partial}{\partial x} \left[\omega(x,y) \frac{\partial}{\partial y}\right] + \] \[ - \frac{\partial}{\partial y} \left[\omega(x,y) \frac{\partial}{\partial x}\right] \] Rechnen wir die eckigen Klammern auf der rechten Seite für \( \omega = x dy \) aus: \[ \omega(x,y) \frac{\partial}{\partial y} = (x \, dy) \, \frac{\partial}{\partial y} = x \] \[ \omega(x,y) \frac{\partial}{\partial x} = (x \, dy) \frac{\partial}{\partial x} = 0 \] sodass \[ d\omega(x,y) \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right) = \frac{\partial}{\partial x} x = 1 \] Dieses Ergebnis konnten wir erwarten, denn die Höhenlinien, die \(\omega\) darstellen, liegen parallel zur x-Achse, und es geht nur in y-Richtung bergauf (und zwar mit der Steigung x). Wir erinnern uns: eine 1-Form angewendet auf einen Tangentialvektor ergibt die Steigung einer lokal definierten skalaren Funktion in die Tangentialvektor-Richtung. Genau dies stellt das Höhenlinienbild ja dar.
Nun nimmt die Steigung in y-Richtung proportional zu \(x\) zu. Genau diese Veränderung der Steigung misst der erste Term \[ \frac{\partial}{\partial x} \left[\omega(x,y) \frac{\partial}{\partial y}\right] \] (der zweite Term ist sowieso Null). Daher misst der erste Term die Rate, mit der neue Höhenlinien bei wachsendem \(x\) hinzukommen, um die Steigung in y-Richtung zu vergrößern. Dies legt die Vermutung nahe, dass \[ d\omega(x,y) \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right) \] etwas mit der Anzahl der neu entstehenden (oder verschwindenden) Höhenlinien zu tun hat. Vermutlich kommen auch noch Vorzeichen hinzu, je nachdem, ob Höhenlinien entstehen oder verschwinden. Da die Höhenlinien bei einer n-dimensionalen Mannigfaltigkeit \((n - 1)\) -dimensionale Flächen sind, sind die Anfangs- oder Endkanten dieser Flächen \((n - 2)\) -dimensionale Objekte. Wir wollen diese Anfangs- oder Endkanten als Blätter der 2-Form \(d\omega\) interpretieren. Damit erhält der d-Operator eine recht anschauliche Bedeutung
Diese Interpretation macht sogar den Integralsatz von Stokes anschaulich verständlich: In unserem zweidimensionalen Beispiel \( \omega = x \, dy \) ist das Integral \[ \int_{G} d\omega \] gleich der Zahl der Anfangspunkte für die im Gebiet \(G\) neu entstehenden Höhenlinien. Diese Höhenlinien durchstoßen den Rand von \(G\). Daher wird ihre Zahl auch vom Randintegral \[ \int_{\partial G} \omega \] erfasst, d.h. es muss \[ \int_{G} d\omega = \int_{\partial G} \omega \] sein.
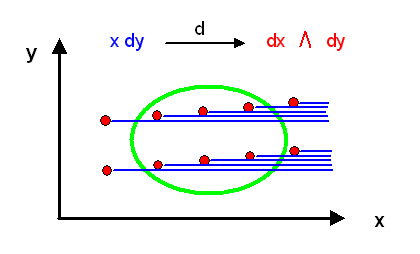
Auch auf p-Formen (Näheres dazu siehe unten) kann man diese Veranschaulichung übertragen:
Sie werden durch \((n - p)\) -dimensionale Blätter dargestellt,
und p-dimensionale Flächenintegrale entsprechen der Zahl der
Blätter, die von der p-dimensionalen Fläche durchstoßen werden, wobei noch
Regeln für die Vorzeichen beachtet werden müssen (abhängig von der
Orientierung von Blättern und Flächenstück).
Wir werden hier allerdings nicht weiter darauf eingehen,
zumal unsere Anschauung bei mehr Dimensionen sowieso schnell
an ihre Grenzen stößt.
Man muss bei der obigen Veranschaulichung etwas aufpassen (siehe z.B. David Bachman: A Geometric Approach to Differential Forms, arXiv:math/0306194 [math.GT]):
Die Vorstellung, eine p-Form im n-dimensionalen Raum durch \((n - p)\) -dimensionale Blätter darzustellen, gilt im Allgemeinen nur lokal. Man kann sich vorstellen, dass man die Mannigfaltigkeit in sehr viele sehr kleine n-dimensionale Parzellen einteilt, und in jeder dieser Parzellen \((n - p)\) -dimensionale zueinander parallele Flächen (Blätter) einzeichnet, die durch ihre Dichte den dortigen Wert \(\omega(p)\) der p-Form \(\omega\) repräsentieren.
Diese parallelen Blätter werden durch diejenigen Tangentialvektoren \(v(p)\) aufgespannt, für die \( \omega(p) \, v(p) = 0 \) gilt (denn ein solcher Tangentialvektor durchstößt dann gar keine Blätter von \(\omega\), da er ja parallel zu den Flächen liegt). Man sagt auch, die lokalen Blätter werden vom Kern der p-Form aufgespannt.
Wenn wir nun die Gesamtheit dieser vielen Parzellen der Mannigfaltigkeit betrachten und uns den Grenzübergang zu unendlich kleinen Parzellen vorstellen, so ergeben die sehr vielen lokal definierten Flächen ein sogenanntes Flächenfeld (plane field). Dieses Flächenfeld korrespondiert zu unserer p-Form \(\omega\), denn die Richtung der Flächen in einem Punkt \(p\) entspricht dem Kern der linearen Abbildung \(\omega(p)\) (d.h. die Tangentialvektoren mit \( \omega(p) \, v(p) = 0 \) spannen die Flächen auf), und ihre Dichte legt den Wert von \( \omega(p) \, u(p) \) fest (entsprechend der Anzahldichte der von \(u(p)\) durchstoßenen Flächen).
Bleibt die Frage, ob man all diese in den kleinen Parzellen definierten Flächenstücke nicht an den Parzellengrenzen jeweils zusammenkleben kann, so dass beim Übergang zu unendlich kleinen Parzellen daraus \((n - p)\) -dimensionale Flächen werden, die die gesamte Mannigfaltigkeit durchziehen. Die Mannigfaltigkeit würde durch diese Flächen gleichsam in (unendlich dünne unendlich viele) Schichten zerlegt (man spricht in der englischsprachigen Literator von foliations). Falls das geht, sagt man auch, das Flächenfeld ist integrabel.
Im \( \mathbb{R}^{2} \) ist die Antwort auf diese Frage positiv: Dort ist jedes Flächenfeld (oder besser: Linienfeld) integrabel.
Im dreidimensionalen Raum gilt diese Aussage allerdings nicht mehr. Man findet beispielsweise: Ein Flächenfeld im \( \mathbb{R}^{3} \), das zu einer 1-Form \(\omega\) gehört, kann nur dann integrabel sein, wenn \[ \omega \wedge d\omega = 0 \] gilt.
Hier ist ein Beispiel für eine 1-Form in \(\mathbb{R}^{3}\), die ein nicht-integrables Flächenfeld besitzt (ein solches Flächenfeld nennt man auch Kontaktstruktur (contact structure)): \[ \omega = x \, dy + dz \] Bei \( x = 0 \) ist dies einfach gleich \( dz \), dargestellt durch Flächen senkrecht zur z-Richtung. Je größer \(x\) wird, umso wichtiger wird der Term \(x \, dy \), der für sich einem Flächenfeld entspricht, bei dem die Flächen senkrecht zur y-Richtung stehen und mit wachsendem \(x\) immer dichter werden (die Grafik dazu hatten wir bereits weiter oben).
Zusammengenommen bedeutet das: Je größer \(x\) wird, umso mehr kippen die Flächen senkrecht zur y-Richtung, und umso dichter werden sie. In y- und z-Richtung ändert sich dagegen nichts. Die lokal definierten Flächen dieser 1-Form lassen sich nirgends zu global definierten Flächen zusammensetzen, die den Raum in Schichten aufteilen. Das folgende Bild zeigt, dass jeder Versuch zu Überschneidungen in den Flächen führen muss:
Bei den obigen Betrachtungen zu 2-Formen konnten wir sehen, dass sich die meisten Aussagen problemlos auf mehrdimensionale Flächen übertragen lassen. An die Stelle von 2-Formen treten dann die p-Formen, also p-lineare Abbildungen \( \omega \) von \(p\) Tangentialvektoren in die reellen Zahlen. So wie jede 2-Form antisymmetrisch in den beiden Argumenten sein muss, so muss analog jede p-Form antisymmetrisch bei Vertauschung zweier beliebiger Argumente sein. Man nennt eine solche Abbildung total antisymmetrisch oder schiefsymmetrisch oder auch alternierend.
Anders ausgedrückt: Bei Vertauschungen der Argumente verhält sich eine p-Form genauso wie sich eine Determinante mit \(p\) Spalten bei Spaltenvertauschungen verhält. Damit stellen wir sicher, dass mehrdimensionale Flächenintegrale über p-Formen wieder unabhängig von der Flächenparametrisierung sind (abgesehen von der Orientierung), und dass der Integralsatz von Stokes auch für p-Formen gilt. Die Details schauen wir uns weiter unten an.
Weiter oben hatten wir uns bereits mit dem Begriff der Permutation beschäftigt. Wenn wir nun in einer p-Form die \(p\) Argumente \( u_{i}, u_{j}, u_{k}, \, ... \) solange untereinander vertauschen, bis sich die Reihenfolge \( u_{1}, u_{2}, u_{3},\, ... \) ergibt, so führt jede Vertauschung zu einem Vorzeichenwechsel. Das Vorzeichen, das sich so insgesamt ergibt, hatten wir als Signum der Permutation bezeichnet. Es gilt also: \[ \omega(u_{i}, u_{j}, u_{k}, \, ...) = \] \[ = \mathrm{sign}(i, j, k, \, ...) \, \omega(u_{1}, u_{2}, u_{3}, \, ...) \] Natürlich kann man auch eine p-Form wieder nach Basisformen \( dx^{\mu} \wedge dx^{\nu} \wedge dx^{\rho} \wedge \, ... \) entwickeln (mit p verschiedenen Indices): \[ \omega = \sum_{\mu \lt \nu \lt \rho \lt \, ...} \, \omega_{\mu, \nu, \rho, \, ...} \, dx^{\mu} \wedge dx^{\nu} \wedge dx^{\rho} \wedge \, ... \] Dabei ist \[ \omega_{\mu, \nu, \rho, ...} = \omega \left( \frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}}, \frac{\partial}{\partial x^{\rho}}, \, ... \right) \] und \[ [ dx^{\mu} \wedge dx^{\nu} \wedge dx^{\rho} \wedge \, ... ] (u_{1}, u_{2}, u_{3}, \, ...) \] ist die Determinanten mit der Matrix, die in der k-ten Spalte die Einträge \[ u_{k}^{\mu}, u_{k}^{\nu}, u_{k}^{\rho}, \, ... \] hat. Wir verzichten hier auf den etwas mühsamen Beweis dieser Aussagen, da die Ideen dieselben sind wie bei den 2-Formen.
Die äußere Ableitung (d-Operator) kann man auf einer \((p - 1)\) -Form \(\omega\) in der Basis-abhängigen Schreibweise vollkommen analog zu den 2-Formen definieren: \[ d\omega = \sum_{\mu \lt \nu \lt \rho \lt \, ...} \, d\omega_{\mu, \nu, \rho, \, ...} \, \wedge dx^{\mu} \wedge dx^{\nu} \wedge dx^{\rho} \wedge \, ... \] Für die Basis-unabhängige Schreibweise schreiben wir wieder \[ \boldsymbol{t} := (t_{1}, t_{2}, \, ... , t_{p}) \] und verwenden eine Flächenparametrisierung \( \gamma(\boldsymbol{t}) \) (also eine Abbildung der \(p\) reellen Parameter in die Mannigfaltigkeit \(M\)). Die Tangentialvektoren nennen wir wie immer \( u_{i}(\gamma(\boldsymbol{t})) \). Sie entsprechen jeweils der Richtungsableitung in \(t_{i}\)-Richtung. Damit haben wir (wir lassen die Argumente \( \gamma(\boldsymbol{t}) \) hier weg): \[ d\omega (u_{1}, u_{2}, \, ...\, , u_{p}) = \] \[ = \frac{d}{dt_1} [\omega (u_{2}, u_{3}, \, ...\, , u_{p})] + \] \[ - \frac{d}{dt_2} [\omega (u_{1}, u_{3}, \, ...\, , u_{p})] + \] \[ + \frac{d}{dt_3} [\omega (u_{1}, u_{2}, \, ...\, , u_{p})] + \] \[ - \, ... \, + \] \[ + \frac{d}{dt_p} [\omega (u_{1}, u_{2}, \, ... \, , u_{p - 1})] \, (- 1)^{p - 1} = \] \[ = \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, \frac{d}{dt_i} [\omega ( \, ... \mathrm{ohne} \, u_{i} \, ... \,)] = \] \[ = \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, u_{i} \, [\omega ( \, ... \mathrm{ohne} \, u_{i} \, ... \,)] \] Man findet diese Formel beispielsweise in Wikipedia: Exterior derivative. Dabei ist zu beachten, dass in unserem Fall die dort auftretende Lie-Klammer \( [u_{i}, u_{j}] = 0 \) ist, denn wir können ja die \(t_{i}\) als Koordinaten ansehen, so dass in diesen Koordinaten \( u_{i} = \frac{d}{dt_{i}} \) ist. Die Ableitungen \( \frac{d}{dt_{i}} \) und \( \frac{d}{dt_{j}} \) vertauschen aber miteinander, d.h. die \(u_{i}\) bilden eine holonome Basis des Tangentialraums. Wäre die Lie-Klammer ungleich Null, so kämen noch Terme mit Lie-Klammern dazu.
In der Formel oben wechselt das Vorzeichen von Term zu Term, und es fehlt im i-ten Term (der Term, in dem nach \(t_{i}\) abgeleitet wird) im Argument jeweils der i-te Tangentialvektor. Den Beweis, dass sich daraus die obige Basis-abhängige Form reproduzieren lässt, wollen wir uns hier ersparen (für \( p = 2 \) hatten wir den Beweis weiter oben explizit durchgeführt). Schauen wir uns lieber einige Spezialfälle an:
Für \(p = 2\) erhalten wir unsere alte Formel für die Ableitung einer 1-Form zurück: \[ d\omega(u_{1}, u_{2}) = u_{1} \, [\omega u_{2}] - u_{2} \, [\omega u_{1}] \] Die Antisymmetrie in \(u_{1}\) und \(u_{2}\) ist direkt zu sehen.
Schauen wir uns den Fall \(p = 3\) an: \[ d\omega(u_{1}, u_{2}, u_{3}) = \] \[ = u_{1} \, \omega(u_{2}, u_{3}) + \] \[ - u_{2} \, \omega(u_{1}, u_{3}) + \] \[ + u_{3} \, \omega(u_{1}, u_{2}) \] Die Antisymmetrie bei Vertauschung von \(u_{1}\) und \(u_{2}\) bzw. Vertauschung von \(u_{2}\) und \(u_{3}\) ist wieder direkt zu sehen. Bei Vertauschung von \(u_{1}\) und \(u_{3}\) muss man etwas genauer hinschauen: Der zweite Term ist dabei antisymmetrisch. Erster und dritter Term ergeben nach Vertauschung: \[ u_{3} \, \omega(u_{2}, u_{1}) + u_{1} \, \omega(u_{3}, u_{2}) = \] \[ = - u_{3} \, \omega(u_{1}, u_{2}) - u_{1} \, \omega(u_{2}, u_{3}) = \] \[ = - \big( u_{1} \, \omega(u_{2}, u_{3}) + u_{3} \, \omega(u_{1}, u_{2}) \big) \] d.h. auch hier haben wir Antisymmetrie. Analog kann man auch für höhere p-Werte die Antisymmetrie nachweisen.
Man kann zeigen, dass auch für p-Formen das Lemma von Poincaré gilt, d.h. auf einer sternförmigen Menge folgt aus \[ d\omega = 0 \] die Existenz einer Stammform \(\pi\) mit \[ d\pi = \omega \]
Auch die Definition der p-dimensionalen Flächenintegrale lässt sich von 2-Formen problemlos auf p-Formen erweitern. Dazu braucht man p reelle Parameter \[ \boldsymbol{t} = (t_{1}, t_{2}, \, ... \, , t_{p}) \] aus einem p-dimensionalen reellen Parameterbereich \(T\) sowie wie bei den 2-Formen eine Flächen-Parametrisierungsfunktion \(\gamma\). Das Flächenintegral ist dann gegeben durch \[ I_{ \gamma(T)} := \int_{T} \, d\mu(\boldsymbol{t}) \] \[ \omega(\gamma(\boldsymbol{t})) (u_{1}(\gamma(\boldsymbol{t})), u_{2}(\gamma(\boldsymbol{t})), \, ... \, , u_{p}(\gamma(\boldsymbol{t}))) \] mit \[ d\mu(\boldsymbol{t}) = dt_{1} \, dt_{2} \, ... \, dt_{p} \] Bei einem orientierungserhaltenden Parameterwechsel (d.h. die Determinante der Jacobimatrix des Parameterwechsels ist positiv) ändert sich der Wert dieses Integrals nicht. Der Beweis verläuft vollkommen analog zum zweidimensionalen Fall.
Ist eine (positiv definite) Metrik vorhanden, so lassen sich die Überlegungen zum Flächenmaß von oben ebenfalls direkt auf p-Formen übertragen. Aus dem Flächenmaß wird dann ein entsprechendes p-dimensionales Volumenmaß. Die Gramsche Matrix \(G\) ist dann eine p-mal-p-Matrix mit Komponenten \( G_{ij} = g(u_{i}, u_{j}) \).
Der Integralsatz von Stokes gilt auch im p-dimensionalen Fall (warum, werden wir gleich noch sehen):
|
Integralsatz von Stokes für exakte p-Formen: Für eine berandete p-dimensionale orientierbare kompakte Unter-Mannigfaltigkeit \(G\) und einer darauf definierten exakte p-Form \(d\omega\) (d.h. \(\omega\) ist die \((p - 1)\) -dimensionale Stammform) gilt: \[ \int_{\partial G} \omega = \int_{G} d\omega \] Dabei ist \(\partial G\) der Rand des Integrationsgebietes \(G\), und \(G\) ist eine Unter-Mannigfaltigkeit der Mannigfaltigkeit \(M\).
|
Hier tauchen nun einige Begriffe auf, die noch genauer definiert
werden müssen. Man kann dies z.B. tun, indem man die Unter-Mannigfaltigkeit
in Teile aufteilt, die jeweils eine eigene Parametrisierung \(\gamma\) besitzen.
Den zugehörigen Parameterbereich \(T\) teilt man in p-dimensionale Quader auf.
Nun zeigt man für einen quaderförmigen Parameterbereich, dass der Satz
von Stokes gilt, so wie wir dies bei den 2-Formen oben für das Rechteck getan haben.
Setzt man nun die Quader zusammen, so heben sich die Randterme für die zusammenstoßenden Randflächen auf, da sie jeweils das entgegengesetzte Vorzeichen tragen (das gilt, wenn die Unter-Mannigfaltigkeit orientierbar ist, was man zugleich auch als Definition für den Begriff orientierbar ansehen kann). Es bleiben also insgesamt nur die Terme der äußeren Quader-Randflächen übrig. Der Rand der Unter-Mannigfaltigkeit wird entsprechend durch diese äußeren Quader-Randflächen parametrisiert, wobei man noch aufpassen muss, wie die Mannigfaltigkeit sich aus den verschiedenen parametrisierbaren Teilen zusammensetzt.
Diese Methode ist zwar recht anschaulich, aber technisch kompliziert. Deshalb wird zumeist eine andere Methode angewendet, um die obigen Begriffe zu definieren und den Satz von Stokes zu beweisen. Diese Methode trägt den Namen Zerlegung der Eins.
Dazu überdeckt man das Integrationsgebiet \(G\) auf der Mannigfaltigkeit mit endlich vielen, hinreichend kleinen, einander teilweise überlappenden offenen Mengen \(U_{k}\) (das geht, da wir das Integrationsgebiet als kompakt vorausgesetzt haben; die \(U_{k}\) sind dabei Untermengen der Mannigfaltigkeit \(M\)). Achtung: da die Mengen \(U_{k}\) als offen vorausgesetzt werden, besitzen sie keinen Rand bzw. der Rand gehört nicht zur Menge dazu!
Damit liegt nun jeder Punkt des Integrationsgebietes \(G\) in mindestens einem \(U_{k}\). Die \(U_{k}\) dürfen dabei ruhig über den Rand des Integrationsgebietes hinausreichen (müssen sie sogar, da sie keinen Rand besitzen).
Die Überdeckung der Mannigfaltigkeit mit sich überlappenden offenen Mengen (ohne Rand) ersetzt das obige Aufteilen der Mannigfaltigkeit in nicht-überlappende Teile (ggf. mit Rand). Für praktische Berechnungen wird man natürlich immer die Mannigfaltigkeit in geeignete Teile zerschneiden; für die folgende theoretische Diskussion ist aber das Überdecken mit offenen Mengen einfacher. Dabei werden wir jede der Mengen \(U_{k}\) so klein wählen, dass der von ihr überdeckte Teil von \(G\) sich auf einfache Weise parametrisieren lässt – das ist der Sinn dieser Überdeckung!
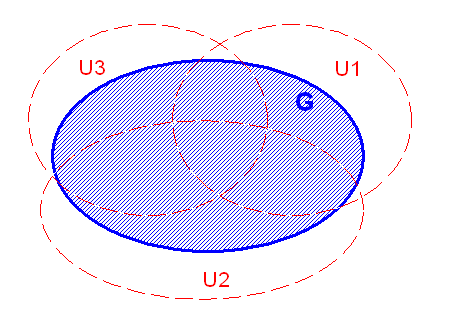
Als Nächstes wollen wir die Integrale
\[
\int_{G} d\omega
\]
und
\[
\int_{\partial G} \omega
\]
in Teilintegrale aufteilen, so dass das k-te Teilintegral
nur über den Teil von \(G\) bzw. \(\partial G\) integriert, der zu dem zugehörigen
\(U_{k}\) dazugehört.
Das können wir erreichen, indem wir den Integranden mit einer sanften
Einschaltfunktion \(g_{k}\) versehen, die nur in \(U_{k}\)
ungleich Null (genauer: größer als Null) ist.
Außerdem soll für jeden Punkt \(p\) aus dem Integrationsgebiet \(G\)
\[
\sum_{k} \, g_{k}(p) = 1
\]
gelten (daher kommt der Ausdruck Zerlegung der Eins).
Das stellt eine Art Normierung für die \(g_{k}\) dar.
Wenn also insbesondere ein Punkt \(p\) nur in einem einzigen \(U_{k}\) liegt,
so ist dort \( g_{k}(p) = 1 \).
Wir können nun wie beabsichtigt
jede Differentialform \(\omega\), die auf dem Integrationsgebiet \(G\) definiert ist,
in einzelne Summanden
\[
\omega = \left( \sum_{k} g_{k} \right) \, \omega
= \sum_{k} \, ( g_{k} \, \omega )
\]
aufteilen,
so dass jeder Summand \( g_{k} \, \omega \)
nur in dem Teil des Integrationsgebietes \(G\) ungleich Null ist, der
auch gleichzeitig im zugehörigen \( U_{k} \) liegt.
Da das Integral linear ist, gilt damit auch
\[
\int_{G} \omega
=
\int_{G} \, \sum_{k} \, g_{k} \, \omega
=
\sum_{k} \, \int_{G} g_{k} \, \omega
\]
(wir werden noch sehen, dass genau genommen durch diese Gleichung das Integral
\( \int_{G} \omega \) erst definiert wird).
Wichtig ist nun, dass in den Integralen rechts jeder Integrand \( g_{k} \, \omega \) nur in dem Teil von \(G\) ungleich Null ist, der vom zugehörigen \( U_{k} \) überdeckt wird. Wir fordern nun, dass wir die Überdeckung so wählen können, dass jeder von \( U_{k} \) überdeckte Bereich von \(G\) eine einfache Parametrisierung \(\gamma\) besitzt (genau müssten wir \( \gamma_{k} \) schreiben, da jeder Bereich seine eigene Parameterfunktion besitzt). Damit meinen wir folgendes:
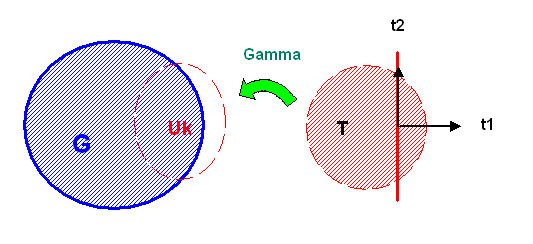
Diese Aussagen definieren im Grunde den Begriff berandete orientierbare Untermannigfaltigkeit erst
sauber. Wir erkennen hier die Definition der Mannigfaltigkeit aus
Kapitel 3: Mannigfaltigkeiten wieder.
Dabei spielt die Umkehrfunktion \( \gamma^{-1} \) der Parametrisierung die
Rolle der Koordinatenfunktion \(f\), denn wir können den Parametervektor \(\boldsymbol{t}\) als
Koordinatenvektor des Punktes \(\gamma(\boldsymbol{t})\) ansehen.
Die von den einzelnen \( U_{k} \) überdeckten Bereiche von \(G\)
entsprechen dann den Bereichen der Mannigfaltigkeit mit verschiedenen
Koordinatensystemen. Nur eines ist neu: der Begriff des Randes von \(G\).
Die obige Überlegung umfasst übrigens auch Gebiete \(G\) ohne Rand, denn dann werden einfach
ausschließlich offene Parametermengen verwendet.
Da nun jeder Integrand \( g_{k} \, \omega \) nur in dem Teil von \(G\) ungleich Null ist, der vom zugehörigen \( U_{k} \) überdeckt wird, und da dieser Bereich eine einfache Parametrisierung \( \gamma \) besitzt (so wie gerade beschrieben), können wir nun jedes Integral \( \int_{G} g_{k} \, \omega \) mit Hilfe dieser Parametrisierung wie gehabt definieren: \[ \int_{G} g_{k} \, \omega := \int_{\gamma(T)} g_{k} \, \omega \] (genauer müssten wir natürlich wieder \( \gamma_{k}(T_{k}) \) schreiben, aber wir wollen die Schreibweise nicht überfrachten).
In dem Ausdruck rechts ist also die Parametrisierung des von dem jeweiligen \( U_{k} \) überdeckten Teils von \(G\) konkret einzusetzen, so wie wir das von oben ja kennen. Das Gesamtintegral \[ \int_{G} \omega \] ist dann durch die Summe all dieser Integrale definiert. Das macht Sinn, da man zeigen kann, dass jede beliebige Überdeckung mit den obigen Eigenschaften (mit zugehörigen Funktionen \(g_{k}\)) denselben Wert für das Gesamtintegral ergibt (der Beweis ist einfach, aber wir wollen ihn hier überspringen).
Wir wollen diese Überlegung nun dazu nutzen, um den Integralsatz von Stokes \[ \int_{\partial G} \omega = \int_{G} d\omega \] zu beweisen. Dazu müssen wir die beiden Integrale wie gerade gesehen durch die Zerlegung der Eins aufteilen, die Parametrisierungen konkret einsetzen und die einzelnen Summanden ausrechnen.
Für den links stehenden Ausdruck \( \int_{\partial G} \omega \) ist die Zerlegung unmittelbar möglich, denn auch \( \partial G \) ist eine Mannigfaltigkeit, die von den \( U_{k} \) überdeckt wird (denn \( \partial G \) ist eine Unter-Mannigfaltigkeit von \(G\)). Als Parametrisierungsfunktionen dienen die einzelnen \(\gamma\)-Funktionen, und als Parameterbereiche dienen die Schnittflächen \( \partial T \) der einzelnen \(T\)-Mengen, also der Teil von \(T\) mit \( t_{1} = 0 \). Also haben wir: \[ \int_{\partial G} \omega = \] \[ = \int_{\partial G} \, \sum_{k} \, g_{k} \, \omega = \] \[ = \sum_{k} \, \int_{\partial G} g_{k} \, \omega = \] \[ = \sum_{k} \, \int_{\gamma(\partial T)} g_{k} \, \omega \] Anmerkung: Falls es keinen Rand von \(G\) gibt, so ist einfach \( \int_{\partial G} \omega = 0 \) zu setzen.
Analog wollen wir auch das andere Integral \( \int_{G} d\omega \) aufteilen. Zunächst einmal haben wir wieder (wie zuvor beim Integral \( \int_{G} \omega \)): \[ \int_{G} d\omega = \] \[ = \int_{G} \, \sum_{k} \, g_{k} \, d\omega = \] \[ = \sum_{k} \, \int_{G} g_{k} \, d\omega \] (im Grunde definiert diese Gleichung ja erst das Integral \( \int_{G} d\omega \)). Die Summe \( \sum_{k} \, g_{k} \, d\omega \) können wir allerdings noch umschreiben: Statt die Zerlegung der Eins (also \( 1 = \sum_{k} \, g_{k} \) ) vor dem d-Operator einzuschieben, können wir sie auch hinter dem d-Operator einschieben:
Einschieben vor dem d-Operator ergab:
\[
d\omega =
\left( \sum_{k} g_{k} \right) \, d\omega
=
\sum_{k} \, g_{k} \, d\omega
\]
Einschieben nach dem d-Operator ergibt
wegen der Linearität des d-Operators:
\[
d\omega =
d \left[ \left( \sum_{k} \, g_{k} \right) \, \omega \right]
=
\]
\[ =
d \left( \sum_{k} \, g_{k} \, \omega \right)
=
\sum_{k} \, d(g_{k} \, \omega)
\]
so dass wir zusammengenommen folgendes Ergebnis haben:
\[
\sum_{k} \, g_{k} \, d\omega
=
\sum_{k} \, d(g_{k} \, \omega)
\]
Wir können das Integral über \( d\omega \) daher auch so schreiben:
\[
\int_{G} d\omega
=
\]
\[ =
\int_{G} \, \sum_{k} \, d(g_{k} \, \omega)
= \]
\[ =
\sum_{k} \, \int_{G} \, d(g_{k} \, \omega)
\]
Die einzelnen Integrale rechts sind wieder über die Parametrisierung definiert,
die jeweils zu dem von \( U_{k} \) überdeckten Teil von \(G\) gehört,
denn nur dort ist \( d(g_{k} \, \omega) \) ungleich Null
( \( g_{k} \) soll ja in ganz \(G\) differenzierbar sein, so dass es in den Überlappungsbereichen an
den Grenzen von \(U_{k}\) ohne Ecken auf Null abfällt):
\[
\int_{G} d(g_{k} \omega) =
\int_{\gamma(T)} d(g_{k} \, \omega)
\]
Nun sind wir fast am Ziel:
Wir können den Satz von Stokes
\[
\int_{\partial G} \omega
= \int_{G} d\omega
\]
schreiben als
\[
\sum_{k} \, \int_{\gamma(\partial T)} g_{k} \, \omega
=
\sum_{k} \, \int_{\gamma(T)} d(g_{k} \, \omega)
\]
Wenn wir die Gleichheit für die einzelnen Summanden zeigen können,
so wäre damit auch die Gültigkeit dieser Gleichung gezeigt, und wir hätten den Satz von
Stokes bewiesen. Versuchen wir also,
\[
\int_{\gamma(\partial T)} g_{k} \, \omega
=
\int_{\gamma(T)} d(g_{k} \, \omega)
\]
zu beweisen, indem wir die Integrale mit Hilfe der Parametrisierung konkret ausschreiben.
Beginnen wir mit dem Integral auf der rechten Seite und verwenden wir von oben die Basis-unabhängige Formel für den d-Operator (das Argument \(\gamma(\boldsymbol{t})\) lassen wir teilweise weg und wir schreiben später \( d\mu(\boldsymbol{t}) \) explizit aus als \( d\mu(\boldsymbol{t}) = dt_{1} \, dt_{2} \, ... \, dt_{p} \) ): \[ \int_{\gamma(T)} d(g_{k} \, \omega) = \] \[ = \int_{T} d(g_{k} \, \omega)(u_{1}, \, ... \, , u_{p}) \, d\mu(\boldsymbol{t}) = \] \[ = \int_{T} \, \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, \frac{d}{dt_i} [(g_{k} \, \omega) ( \, .. \, \mathrm{ohne} \, u_{i})] \, d\mu(\boldsymbol{t}) = \] \[ = \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, \int_{T} \, \frac{d}{dt_i} [(g_{k} \omega) (\, .. \, \mathrm{ohne} \, u_{i})] \] \[ \quad dt_{1} \, dt_{2} \, ... \, dt_{p} = \] ... die Integration über die konvexe Parametermenge \(T\) bedeutet nun, dass der Parameter \(t_{i}\) von einem kleinsten Wert \(a_{i}\) bis zu einem größten Wert \(b_{i}\) läuft. Wir wollen dieses Integral über \(t_{i}\) zuerst ausführen, wobei wir den Hauptsatz der Differential- und Integralrechnung verwenden: \[ = \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, \int dt_{1} dt_{2} \, ... \, dt_{p} \, (\mathrm{ohne} \, dt_{i}) \] \[ \int_{a_{i}}^{b_{i}} dt_{i} \frac{d}{dt_i} [(g_{k} \omega) (\, .. \, \mathrm{ohne} \, u_{i})] = \] \[ = \sum_{i = 1}^{p} \, (- 1)^{i - 1} \, \int dt_{1} dt_{2} \, ... \, dt_{p} \, (\mathrm{ohne} \, dt_{i}) \] \[ \big[ [(g_{k} \omega) (\, .. \, \mathrm{ohne} \, u_{i})]_{t_{i} = b_{i}} + \] \[ - [(g_{k} \omega) (\, .. \, \mathrm{ohne} \, u_{i})]_{t_{i} = a_{i}} \big] = \] Wir brauchen also für gegebenes \(i\) und bei festgehaltenen Werten für die anderen Parameter den Wert von \[ [(g_{k} \, \omega) (\, .. \, \mathrm{ohne} \, u_{i})] \] an den Stellen \( t_{i} = b_{i} \) und \( t_{i} = a_{i} \).
Diese Parameterpunkte liegen jeweils an der Grenze des Integrationsgebietes \(T\), denn sie entsprechen dem minimalen und maximalen Wert des Parameters \(t_{i}\) (bei festgehaltenen Werten für die anderen Parameter).
Nun können diese Grenz-Parameterpunkte zu \(T\) gehören oder auch nicht. Das bedeutet: Falls \(U_{k}\) kein Randstück überdeckt, ist \(T\) offen und die Grenz-Parameterpunkte gehören nicht zu \(T\). Im anderen Fall geht \(T\) aus einer offenen Menge \(T'\) hervorgeht, bei der alle Punkte mit \( t_{1} \gt 0 \) weggeschnitten wurden. Daher gehören dann nur die Grenz-Parameterpunkte mit \( t_{1} = 0 \) zu \(T\) dazu (sie liegen auf der Schnittfläche \(\partial T\)).
Nur für \( \boldsymbol{t} \in \partial T \) (also auf dem Rand) erlauben wir, dass \( g_{k} \, \omega \) ungleich Null sein darf! Das ist der Sinn der Einschalt-Funktion \(g_k\)!
Die anderen Grenz-Parameterpunkte gehören dagegen entweder zu Grenzen der \(U_{k}\) im Inneren von \(G\) (dann muss dort \(g_{k}\) gleich Null sein) oder zur Grenze von \(G\) (dann muss \(\omega\) gleich Null sein).
Vorsicht: Der Begriff Grenze soll andeuten, dass diese Punkte nicht mehr dazu gehören (anders als der Rand). Möchte man an der Grenze von \(G\) aber \(\omega\) ungleich Null haben, so muss man diese Grenze mit zu \(G\) hinzunehmen und so aus ihr einen Rand von \(G\) machen. Die \(U_{k}\) und die Parametrisierungen müssen dann so gewählt werden, dass dieser Rand durch die jeweilige Parameter-Schnittfläche mit \( t_{1} = 0 \) parametrisiert wird.
Ein Beispiel:
Wenn \(G\) das offene Intervall von 0 bis 1 ist, so muss
\(\omega\) bei 0 und bei 1 gleich Null sein.
Will man \(\omega\) an diesen Grenzpunkten
ungleich Null haben,
so muss man für \(G\) das geschlossene Intervall von 0 bis 1 wählen, so dass
0 und 1 zum Rand von \(G\) werden. Genau so ist der Integralsatz von Stokes zu verstehen!
Schauen wir uns also die obige Summe an:
Falls \(U_{k}\) kein Randstück überdeckt, ist \( g_{k} \omega \) an den Grenz-Parameterpunkten gleich Null, und die ganze Summe ergibt demnach auch Null. Wir werden diesen Fall später einfach dadurch berücksichtigen, dass wir für die Parameter-Schnittfläche \( \partial T \) die leere Menge nehmen.
Falls aber \(U_{k}\) ein Randstück überdeckt, so bleibt in der Summe oben nur der Term mit \(i = 1\) übrig, also der Term mit \( t_{1} = b_{1} = 0 \). Nur dort befinden wir uns nämlich auf dem Rand \( \partial T \).
Hier zeigt sich, wie günstig die Vorgehensweise mit der Zerlegung der Eins und der speziellen Wahl der Parametrisierung ist! Man muss sich (anders als bei der Würfel-Vorgehensweise) nicht ständig mit vielen Termen und Vorzeichen herumschlagen! Schreiben wir also unser Ergebnis auf: \[ = \int dt_{2} \, ... \, dt_{p} \, [(g_{k} \, \omega) (u_{2}, \, ... \, , u_{p})]_{t_{1} = 0} = \] \[ = \int_{\partial T} \, [(g_{k} \, \omega) (u_{2}, \, ... \, , u_{p})] \, dt_{2} \, ... \, dt_{p} = \] \[ = \int_{\gamma(\partial T)} g_{k} \, \omega \] Damit ist also gezeigt, dass \[ \int_{\gamma(\partial T)} g_{k} \, \omega = \int_{\gamma(T)} d(g_{k} \, \omega) \] gilt. Also gilt die Gleichheit auch für die Summe dieser Terme \[ \sum_{k} \, \int_{\gamma(\partial T)} g_{k} \, \omega = \sum_{k} \, \int_{\gamma(T)} d(g_{k} \, \omega) \] und schließlich auch \[ \int_{\partial G} \omega = \int_{G} d\omega \] Der Integralsatz von Stokes ist damit bewiesen, und alle darin vorkommenden Begriffe sind im Beweisverlauf sauber definiert worden!
Wie wir gesehen haben, ist der Beweis eigentlich recht einfach. Wenn man die Vorüberlegung mit der Überdeckung von \(G\) durch die \(U_{k}\) und das zugehörige Ein- und Ausblenden von \( \omega \) durch die Funktionen \( g_{k} \) erst einmal gemacht hat, ist die nachfolgende Rechnung recht kurz und übersichtlich, denn in jedem Teilbereich können wir eine für unsere Zwecke ideal passende Parametrisierung wählen.
Aus dem Beweis kann man noch eine wichtige Informationen ablesen: Die Orientierung von G induziert eine Orientierung des Randes \(\partial G\). Der Grund ist:
In jeder von einem \(U_{k}\) überdeckten Teilmenge von \(G\) induziert die Parametrisierung (definiert durch die Funktion \(\gamma\) und die Parametermenge \(T\)) eine Orientierung (legt also das Vorzeichen des Integrals fest).
Dieselbe Parametrisierung können wir aber auch für den Rand \(\partial G\) verwenden, indem wir den Parameterraum auf \(\partial T\) einschränken. Daher induziert sie auch eine Orientierung auf dem Rand \(\partial G\) (legt also das Vorzeichen des Randintegrals fest). Nur mit dieser induzierten Orientierung gilt der Integralsatz von Stokes in der obigen Form (also mit diesem Vorzeichen).
Schauen wir uns die Parametrisierungen unter diesem Blickwinkel noch einmal an:
Wenn ein \(U_{k}\) einen Teil von \(G\) mit Rand überdeckt, so haben wir diesen Teil von \(G\) mit Hilfe der Parametermenge \(T\) und der Funktion \(\gamma\) parametrisiert. Der Parametervektor lautet \[ (t_{1}, t_{2}, \, ... \, , t_{p}) \] mit \( t_{1} \le 0 \).
Der Rand von \(G\) wird dann durch die Parameter \[ (0, t_{2}, \, ... \, , t_{p}) \] dargestellt. Wenn wir mit \(t_{1}\) bei negativen Werten starten und den Wert langsam vergrößern, so durchstoßen wir bei \( t_{1} = 0 \) den Rand von \(G\) und verlassen \(G\).
Der Tangentialvektor \(u_{1}\), der auf \(G\) einer Ableitung in \(t_{1}\)-Richtung entspricht, zeigt also in den Randpunkten von \(G\) nach außen.
Das wird in anderen Texten häufig dazu verwendet, um die Orientierung von \( \partial G \) festzulegen. Tatsächlich kommt es auf die anderen Parameter gar nicht an, denn sie verlaufen ja im Inneren und auf dem Rand in derselben Weise. Lediglich der Parameter, der auf dem Rand einen konstanten Wert annimmt, ist entscheidend: er muss von innen nach außen anwachsen und bei einem gewissen maximalen Wert den Rand durchstoßen.
Für eine Vollkugel beispielsweise könnten wir Kugelkoordinaten \(\theta, \varphi, r\) verwenden. Die Winkel \( \theta, \varphi \) parametrisieren die Kugeloberfläche sowie (zusammen mit dem Radius \(r\)) das Kugelinnere. Der Radius \(r\) entspricht dem Parameter \(t_{1}\) (bis auf eine additive Konstante). Da \(r\) den maximalen Wert auf der Kugeloberfläche annimmt (also auf dem Rand der Vollkugel), passen diese Parameter und die durch sie induzierten Orientierungen zu unserer Formulierung des Stokes'schen Integralsatzes. Für den Bereich am Kugelmittelpunkt bei \(r=0\) muss man sich übrigens eine andere Parametrisierung ausdenken, um kompatibel mit unseren Forderungen an die Parametrisierung von oben zu sein.
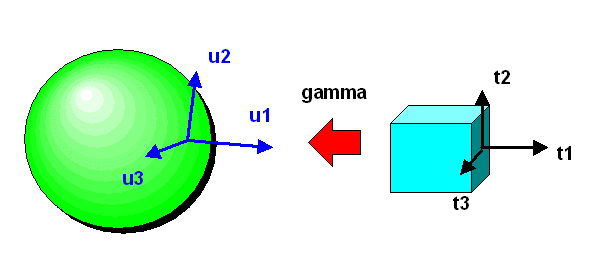
Damit sind wir am Ende dieses umfangreichen und sicher nicht ganz einfachen Kapitels
angekommen. Ich hoffe, ich konnte Ihnen, lieber Leser, den Begriff der Differentialformen
etwas näher bringen und zeigen, dass man auch einen Satz wie den Integralsatz
von Stokes verstehen kann und dass ihm keineswegs ein verschlungener und
unzugänglicher Beweis zugrunde liegt.
Im nächsten Kapitel wollen wir uns dann noch etwas weiter mit
Differentialformen befassen und den Hodge-Stern-Operator und seine Verbindung
zu Divergenz und Rotation kennenlernen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 25 October 2023