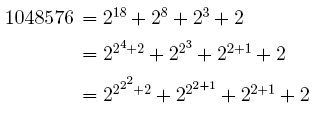
Vorbemerkung
Goodstein-Folgen
Beweis des Satzes von Goodstein mit Hilfe von Ordinalzahlen
Transfinite Induktion
Anhang: Eine andere graphische Darstellung von Ordinalzahlen
Aus den vorausgehenden Kapiteln wissen wir, dass Gödels Unvollständigkeitssatz kein merkwürdiges Ergebnis am Rande der Mathematik ist, sondern dass er ganz entscheidend zum Verständnis axiomatischer Systeme beiträgt. Unentscheidbare Aussagen müssen nicht wie Gödels Aussage \(G\) (ich bin nicht beweisbar, siehe Kapitel 2.5) mühsam konstruiert werden, sondern sie tauchen als sinnvolle Fragestellungen immer wieder von alleine auf. Ein Beispiel dafür ist die Kontinuumshypothese in der Mengenlehre.
Auch in der Peano-Arithmetik gibt es Aussagen über natürliche Zahlen, die sich in ihr nicht entscheiden lassen. In den bisherigen Kapiteln konnte man allerdings vielleicht den Eindruck gewinnen, dass diese unentscheidbaren Aussagen doch etwas konstruiert sind – man denke an Gödels Aussage \(G\) oder an die diophantischen Gleichungen aus Kapitel 3.5. Gibt es denn auch bei den natürlichen Zahlen Aussagen, die auf den ersten Blick so aussehen, als ob die Peano-Arithmetik sie im Griff haben sollte, die sich dann aber als unentscheidbar in der Peano-Arithmetik herausstellen?
Ein Beispiel, auf das diese Beschreibung zutreffen könnte, sind die Goodstein-Folgen. Diese Folgen sind relativ leicht zu verstehen und man kann hier eine Menge über die Gründe der Unvollständigkeit, über Mengenlehre und über transfinite Induktion lernen. Wir wollen sie uns daher in diesem Kapitel genauer ansehen.
Zunächst müssen wir verstehen, was die iterierte Darstellung
einer natürlichen Zahl \(n\) zu einer Basis \(b\)
sein soll.
Nehmen wir beispielsweise die Zahl \( n = 35 \).
Wie gewohnt haben wir diese Zahl im Dezimalsystem geschrieben,
also in einem Stellenwertsystem zur Basis 10.
Rechts stehen die Einer, links daneben die Zehner, dann die Hunderter, die Tausender usw..
Das ist so selbstverständlich, dass wir kaum noch darüber nachdenken:
\[
n = 35 = 3 \cdot 10 + 5 \cdot 1
\]
Wir können \(n\) aber auch im Stellenwertsystem zu einer anderen Basis darstellen,
beispielsweise zur Basis 2 (also als Binärstring). Dann ist
\begin{align}
n &= 35 = \\
&= 32 + 2 + 1 = \\
&= 2^5 + 2^1 + 2^0
\end{align}
Der Binärstring von \(n\) lautet also \(100011\).
Nun taucht im Exponent beispielsweise die Zahl 5 auf. Diese Zahl können wir
natürlich ebenfalls zur Basis 2 darstellen: \( 5 = 2^2 + 1 \).
Also ist
\[
n = 35 = 2^{2^2 + 1} + 2^1 + 2^0
\]
Man nennt dies die iterierte Darstellung der Zahl 35 zur Basis 2.
Hier ist ein anderes komplizierteres Beispiel:
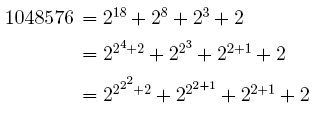
Natürlich kann man auch die iterierte Darstellung zu einer anderen Basis bilden. Die iterierte Darstellung von \(n = 35\) zur Basis 3 sieht beispielsweise so aus: \[ n = 35 = 3^3 + 2 \cdot 3^1 + 2 \] Das Schema für die iterierte Darstellung einer Zahl \(n\) funktioniert also so: Man fängt erst einmal an, die natürliche Zahl \(n\) zur Basis \(b\) darzustellen. Dabei ist \(b\) eine natürliche Zahl, z.B. 2 oder 10. Das sieht dann schematisch so aus: \[ n = a_m \cdot b^m + ... + a_2 \cdot b^2 + a_1 \cdot b^1 + a_0 \] Dabei sind die Koeffinzienten \(a_i\) natürliche Zahlen, die Werte von \(0\) bis \( b - 1 \) haben können. Im nächsten Schritt geht man nun hin und stellt auch die Exponenten genauso dar. Die dabei auftretenden Exponenten der Basis stellt man dann wieder so dar, und so fährt man fort, bis keine Zahlen größer als die Basis \(b\) mehr auftreten. Zur Verdeutlichung hier noch ein selbstgebasteltes Beispiel zur Basis 3: \begin{align} & \, n = 61085 = \\ &= 59049 + 2 \cdot 729 + 2 \cdot 243 + 81 + 9 + 2 = \\ &= 3^{10} + 2 \cdot 3^6 + 2 \cdot 3^5 + 3^4 + 3^2 + 2 = \\ &= 3^{3^2+1} + 2 \cdot 3^{2 \cdot 3} + 2 \cdot 3^{3+2} + 3^{3+1} + 3^2 + 2 \end{align}
Zurück zu unserem Beispiel \(n = 35\) mit Basis 2 von oben: \[ n = 35 = 2^{2^2 + 1} + 2^1 + 2^0 \] Wir könnten nun auf die Idee kommen, die Basis 2 überall durch die Basis 3 zu ersetzen und so eine neue Zahl \(n'\) zu erzeugen: \begin{align} n' &= 3^{3^3 + 1} + 3^1 + 3^0 = \\ &= 3^{28} + 3^1 + 1 = \\ &= 22.876.792.454.965 \end{align} Es ist kaum zu fassen, wie groß diese Zahl plötzlich geworden ist, obwohl wir doch nur die Basis um 1 vergrößert haben. Man spricht deshalb auch vom Aufblähen der Basis. Ganz allgemein können wir den Aufbläh-Operator \(B_b\) definieren, der in der iterierten Darstellung einer Zahl \(n\) zur Basis \(b\) diese Basis \(b\) durch \(b+1\) ersetzt und so eine neue Zahl \(n'\) erzeugt: \[ n' = B_b(n) \] Im obigen Beispiel ist also \[ B_2(35) = 22.876.792.454.965 \] Nun sind wir bereit, die Goodstein-Folge zur natürlichen Zahl \(n\) zu definieren. Dazu starten wir mit einer natürlichen Zahl \(n\) und definieren das erste Folgenglied als \[ g_1(n) := n \] Das zweite Folgenglied berechnen wir nun so: Schreibe das vorherige Folgenglied (also hier \(n\)) in der iterierten Darstellung zur Basis 2 auf, blähe die Basis danach auf (d.h. ersetze die Basis 2 in der iterierten Darstellung durch die Basis 3) und ziehe von dem Ergebnis am Schluss eine Eins ab. Analog geht es auch bei den höheren Folgengliedern, d.h. es gilt: \[ g_i(n) := B_i (g_{i-1}(n)) - 1 \] für \(i > 1\) und \( g_{i-1}(n)> 0 \). Nochmal in Worten: Bilde das \(i\)-te Glied der Goodstein-Folge so: Schreibe das vorherige Folgenglied in der iterierten Darstellung zur Basis \(i\) auf, blähe die Basis danach auf (d.h. ersetze die Basis \(i\) in der iterierten Darstellung durch die Basis \(i+1\) ) und ziehe von dem Ergebnis am Schluss eine Eins ab. Dazu kommt noch eine Sonderregel: tiefer als Null geht es nicht, d.h. wenn ein Folgenglied Null ist, so sind alle späteren Folgenglieder auch Null
Hier sind einige Goodsteinfolgen für verschiedene Startwerte \(n\):
\begin{align}
n &= 1 \; \Rightarrow \; 1, \, 0 \\
n &= 2 \; \Rightarrow \; 2, \, 2, \, 1, \, 0 \\
n &= 3 \; \Rightarrow \; 3, \, 3, \, 3, \, 2, \, 1, \, 0 \\
n &= 4 \; \Rightarrow \; 4, \, 26, \, 41, \, 60, \, 83, \\
& 109, \, 139, \, 173, \, 211, \, 253, \, 299, \, 348, \, ... \\
\end{align}
Für \(n = 1, 2\) oder \(3\) passiert noch nicht viel, denn sehr schnell ist die Basis so groß,
dass das Folgenglied kleiner als die Basis wird. Dann taucht die Basis aber in der iterierten Darstellung
gar nicht mehr auf (nämlich nur mit Exponent Null), so dass die Basisersetzung nichts mehr verändert.
Bei \(n = 4\) sieht das schon anders aus. Die Folgenglieder wachsen hier schnell genug, so dass
die iterierte Darstellung genügend Basisterme hat. Wie man sich die Goodstein-Folgenglieder zu \(n = 4\)
als Baum vorstellen kann, werden wir weiter unten noch sehen (dann wird auch das Bildungsgesetz transparenter werden).
Wie geht es mit der Goodsteinfolge zu \(n = 4\) weiter? Hier noch einige Folgenglieder: \begin{align} g_{100}(4) &= 12.412 \\ g_{1000}(4) &= 1.020.533 \end{align} Es sieht so aus, als würde die Folge ewig weiter wachsen. Doch vergessen wir nicht: Es findet hier ein Wettlauf statt zwischen wachsendem Folgenglied und wachsender Basis. Wenn jemals die Basis größer wird als das Folgenglied, so taucht die Basis nicht mehr in der iterierten Darstellung auf, d.h. die Basisvergrößerung hat keine Auswirkung mehr und es wird in jedem weiteren Schritt einfach um Eins heruntergezählt, bis man bei Null ankommt. Der Aufbläh-Operator \(B_b\) bewirkt also nicht immer ein starkes Wachstum. Er tut das nur dann, wenn die Basis häufig in der iterierten Darstellung der jeweiligen Zahl vorkommt. Je größer also die Zahl und je kleiner die Basis \(b\) ist, umso aufblähender wirkt sich \(B_b\) aus. Kein Wunder also, dass \(B_2(35)\) so groß wird (siehe oben). Dagegen ergibt beispielsweise \begin{align} B_5(35) &= B_5(5^2 + 2 \cdot 5^1) = \\ &= 6^2 + 2 \cdot 6^1 = \\ &= 36 + 12 = 48 \end{align} Das Wachstum durch den Aufbläh-Operator ist hier also nur gering, denn die Basis 5 ist für die Darstellung der Zahl 35 schon recht groß. Sobals die Basis größer als die Zahl wird, ändert der Aufbläh-Operator nichts mehr: \begin{align} B_{36}(35) - 1 &= B_{36}(35 \cdot 36^0) = \\ &= 35 \cdot 37^0 = 35 \cdot 1 = 35 \end{align} Wie geht nun dieser Wettlauf zwischen wachsenden Folgengliedern und wachsender Basis bei den Goodstein-Folgen aus? Wächst jede Goodstein-Folge immer weiter an, oder gewinnt die größer werdende Basis und die Folgenglieder werden irgendwann wieder kleiner (weil ja immer eine Eins abgezogen wird), um schließlich gleich Null zu werden?
Es zeigt sich, dass die obige Goodstein-Folge zu \(n = 4\) sehr lange anwächst, nämlich bis
die Basis den Wert \( 3 \cdot 2^{402.653.209} \) erreicht.
Dann bleibt sie noch einmal doppelt
solange konstant, und fällt dann ab, bis bei der Basis
\( 3 \cdot 2^{402.653.211} - 1 \) der Wert Null erreicht wird. Die
Anzahl der benötigten Schritte ist hier also selbst eine Zahl mit mehr als 121
Millionen Dezimalstellen (siehe
Wikipedia: Goodstein-Folge). Mit einem Computerprogramm,
das die Goodsteinfolge Schritt für Schritt ausrechnet, wird man dieses Verhalten der Folge
wohl nie direkt beobachten können. Bis man bei den entsprechenden riesigen Folgengliedern
angekommen ist, dürfte unsere Lebenszeit schon lange abgelaufen sein.
Man kann es aber anders herausbekommen, nämlich durch systematisches Nachdenken.
Wie, das steht beispielsweise in John Baez: Week 236,
http://math.ucr.edu/home/baez/week236.html.
Nun gut, die Goodsteinfolge zu \(n = 4\) wächst also eine Ewigkeit lang an, um dann doch in den fernen Tiefen der Unendlichkeit schließlich einzuknicken und gegen Null zu schrumpfen. Aber wie sieht es beispielsweise mit der Goodsteinfolge zu \(n = 19\) aus? In Wikipedia: Goodstein-Folge wird gezeigt, wie rasend schnell diese Folge bereits in den ersten Folgengliedern anwächst. Klar: die Basis ist hier zumindest am Anfang deutlich kleiner als die Folgenglieder, und wegen des rasanten Wachstums der Folge bleibt das wohl noch sehr lange so. Entsprechend stark wirkt sich das Aufblähen der Basis in jedem Schritt aus. Die Folge erklimmt also sehr schnell Zahlenbereiche, die jenseits jeder Vorstellungskraft liegen. Knickt auch diese Folge irgendwann ein, wobei irgendwann sehr sehr weit weg liegen kann?
Sie tut es tatsächlich, denn es gilt:
|
Unglaublich! Trotz des rasanten Wachstums gewinnt irgendwann die größer werdende Basis und zwingt die Folge wieder in die Knie. Und jetzt kommt das Beste: Die Peano-Arithmetik weiß nichts davon, denn man kann den Satz von Goodstein mit den Mitteln der Peano-Arithmetik zwar formulieren, aber nicht beweisen! Gödels Unvollständigkeitssatz schlägt also zu!
Da haben wir unser Beispiel! Wir haben konkrete Zahlenfolgen vor uns, die wir beliebig weit berechnen können, und in der Peano-Arithmetik ist nicht entscheidbar, ob die Folgen alle ewig weiter wachsen oder wieder auf Null schrumpfen. Dies ist offenbar ein Aspekt der natürlichen Zahlen, den die Peano-Arithmetik nicht erfassen kann. Zur Klarstellung: Mit Peano-Arithmetik ist das folgende Axiomensystem erster Ordnung gemeint (siehe Kapitel 2.1, 4.2 und 4.4).
Ausdrücklich nicht gemeint ist das von Neumannsche Modell der natürlichen Zahlen im Rahmen der Mengenlehre (siehe Kapitel 4.2 und 4.4). Zur Erinnerung: In diesem Modell sieht insbesondere das Induktionsaxiom anders aus: Es gilt für überabzählbar viele Eigenschaften (Teilmengen) der natürlichen Zahlen, während es in der Peano-Arithmetik nur für die abzählbar vielen Aussagen gilt, die man dort über natürliche Zahlen aufstellen kann. Wir hatten diesen Unterschied in Kapitel 4.2 und 4.4 eingehend diskutiert. Insbesondere kann man in der Peano-Arithmetik nicht von der Menge der natürlichen Zahlen sprechen.
Es ist nicht leicht, zu beweisen, dass man den Satz von Goodstein mit den Mitteln der Peano-Arithmetik nicht herleiten kann. Dies ist erst im Jahre 1982 Laurie Kirby und Jeff Paris gelungen (Satz von Kirby und Paris). Dabei verwendeten sie ein Nichtstandardmodell der Peano-Arithmetik, also eines mit unendlich großen Zahlen – wir kennen das schon aus den Kapiteln 3.1 und besonders 4.5 (Nichtstandard-Analysis). Im Beweis zeigt man, dass in gewissem Sinn die Größe von Goodsteinfolgen zu schnell anwächst, als dass diese Entwicklung von der Peano-Arithmetik erfasst werden kann. Man stellt dazu einen Zusammenhang zwischen den Goodstein-Folgengliedern und den möglichen Beweisen aus der Peano-Arithmetik auf. Wenn man nun wüsste, dass jede Goodsteinfolge irgendwann bei Null endet, dann führt der Zusammenhang mit den Beweisen dazu, dass man auch weiß, dass jeder Peano-Beweis korrekt ist (also keinen Widerspruch herleitet) und dass damit die Peano-Arithmetik widerspruchsfrei ist. Das ist bemerkenswert! Wenn jede Goodsteinfolge irgendwann bei Null endet, dann ist die Peano-Arithmetik widerspruchsfrei!
Die Widerspruchsfreiheit der Peano-Arithmetik kann man aber nach Gödel nicht innerhalb der Peano-Arithmetik beweisen, also kann man dort auch nicht beweisen, dass alle Goodsteinfolgen bei Null enden. Siehe dazu [Examples of] unprovable statements).
Woher wissen wir dann, dass der Satz von Goodstein richtig ist, also dass jede Goodsteinfolge irgendwann gegen Null geht?
Die Antwort lautet: Wir wissen es, wenn wir den Mitteln der Mengenlehre vertrauen, denn mit diesen Mitteln kann man den Satz von Goodstein beweisen. Das ist nicht allzu schwer und gelang bereits im Jahr 1944 dem englischen Logiker Reuben Louis Goodstein, nach dem der Satz und die Folgen benannt sind. Schauen wir uns diesen Beweis einmal genauer an:
Den Beweis des Satzes von Goodstein findet man an viele Stellen im Internet. Besonders gut hat mir beispielsweise die Darstellungen in John Baez: Week 236 gefallen. Hier nun also meine Version:
Die Beweisidee ist folgende: Wir konstruieren bestimmte Objekte (unendliche Mengen, auch Ordinalzahlen genannt), die in einem klar definierten Sinn größer als alle natürlichen Zahlen sind (so etwas kommt uns doch aus dem letzten Kapitel irgendwie bekannt vor, auch wenn die Details jetzt anders aussehen werden). Wenn wir nun in der iterierten Darstellung eines Goodsteinfolgenglieds die ständig wachsende Basis durch das kleinste dieser unendlichen Objekte ( \( \omega \) genannt) ersetzen, so können wir damit hoffentlich eine Aussage darüber gewinnen, was mit der Folge für unendlich große Basiszahlen passiert.
Damit die Idee funktioniert, benötigen wir andere unendlich große Objekte als in Kapitel 4.5. Man bezeichnet diese Objekte als Ordinalzahlen. Sie werden analog zu den natürlichen Zahlen mit Hilfe von Mengen konstruiert, sind also selber unendlich große Mengen. Also: Bitte nicht durch den Begriff unendliche Zahl verwirren lassen. Zahlen im eigentlichen Sinn sind endlich. Wir haben es jetzt mit neuen Objekten zu tun, die durch unendliche Mengen modelliert werden.
Schauen wir uns noch einmal an, wie die natürlichen Zahlen durch Mengen modelliert werden
(siehe Kapitel 4.2). Ausgangspunkt ist die leere Menge,
die wir mit \( \varnothing \) bezeichnen.
Dann definieren wir:
\begin{align}
0 &:= \varnothing \\
1 &:= \{ \varnothing \} = \{ 0 \} \\
2 &:= \{ \varnothing , \{ \varnothing \} \} = \{ 0, 1 \} \\
3 &:= \{ \varnothing , \{ \varnothing \}, \{ \varnothing , \{ \varnothing \} \} \} = \{ 0, 1, 2 \} \\
& ...
\end{align}
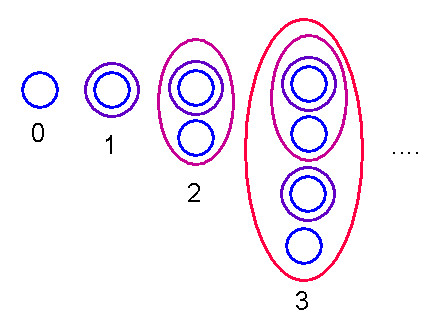
Die Mengen haben wir dabei so benannt wie die Zahlen, die durch sie dargestellt werden sollen.
Die Konstruktionsvorschrift für den Nachfolger \( ()^* \) einer Zahl ist damit klar:
\[
n^* = n \cup \{n\}
\]
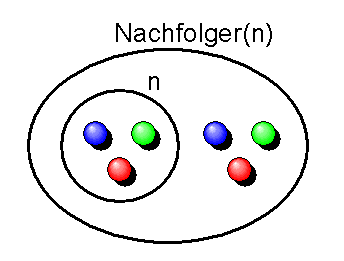
Dabei bezeichnet \( n \cup \{n\} \) die Menge, die alle Elemente von \(n\) und als zusätzliches Element die Menge \(n\) selbst enthält. Das Symbol \( \cup \) steht für das Bilden der Vereinigungsmenge. Die Konstruktion bewirkt also, dass jede neue Menge einfach die Menge ist, die alle ihre Vorgänger als Elemente enthält.
Man kann nun mithilfe der ZFC-Axiome der Mengenlehre zeigen, dass sich die Menge all dieser Mengen konstruieren lässt. Wie üblich bezeichnen wir diese Menge aller natürlichen Zahlen als \( \mathbb{N} \), d.h. \begin{align} \mathbb{N} &= \{ 0, 1, 2, 3, ... \} = \\ &= \{ \varnothing , \{ \varnothing \} , \{ \varnothing , \{ \varnothing \} \} , ... \} \end{align} Das ist das von Neumannsches Modell der natürlichen Zahlen im Rahmen der Mengenlehre. Der Einfachheit halber zählen wir die Null dabei zu den natürlichen Zahlen hinzu.
Analog zu Kapitel 4.5 definiert die Teilmengenbeziehung wieder eine Ordnungsrelation auf den natürlichen Zahlen. Wir sagen, eine Zahl \(n\) ist kleiner-gleich einer Zahl \(n'\), wenn die Menge \(n\) Teilmenge von \(n'\) ist: \[ n \leq n' \; \Leftrightarrow \; n \subseteq n' \] Das entspricht unserer Intuition, denn rechts steht ja die größere Menge. Die kleiner-gleich-Relation liefert nun eine Wohlordnung auf der Menge \( \mathbb{N} \), d.h. es gilt für alle \( m, n \in \mathbb{N} \) immer \( m \leq n \) oder \( n \leq m \) , und zusätzlich hat jede Teilmenge von \( \mathbb{N} \) ein kleinstes Element.
Die Möglichkeit, die Menge \( \mathbb{N} \) aller natürlichen Zahlen konstruieren zu können, ist eine typische Eigenschaft der Mengenlehre. In der Mengenlehre kann eine neue Menge häufig (aber nicht immer) als Vereinigungsmenge unendlich vieler Mengen definiert werden. Genauso definiert man die Menge \( \mathbb{N} \), nämlich als Vereinigungsmenge aller Mengen, die natürliche Zahlen darstellen. Auf diese Weise ist die Mengenlehre in der Lage, unendliche Objekte zu formulieren und mit ihnen formal umzugehen. Tatsächlich können wir die Menge \( \mathbb{N} \) im obigen Sinn als die erste unendliche Zahl (Menge) ansehen, die nach den natürlichen Zahlen kommt. Sie ist größer als jede natürliche Zahl, denn jede natürliche Zahl ist eine spezielle Teilmenge von \( \mathbb{N} \) (nämlich die Teilmenge, die aus all ihren Vorgängern besteht). So ist z.B. \( 4 = \{ 0, 1, 2, 3 \} \) eine Teilmenge von \( \mathbb{N} = \{ 0, 1, 2, 3, 4, ... \} \) . Gleichzeitig ist \(4\) auch ein Element von \( \mathbb{N} \).
Es ist üblich, für die nun folgende Argumentation die Menge \( \mathbb{N} \) als \(\omega\) zu bezeichnen:
\[
\omega := \mathbb{N}
\]
Man sagt, \(\omega\) ist die erste unendliche Ordinalzahl.
Die endlichen Ordinalzahlen sind entsprechend einfach die natürlichen Zahlen.
Es gibt eine schöne Möglichkeit, \(\omega\) graphisch darzustellen. Dazu macht man für jede
natürliche Zahl einen Strich und verkürzt die Abstände dann so, dass man alle natürlichen
Zahlen auf einer endlichen Strecke unterbringen kann. Die Menge \( \mathbb{N} \) bzw. \(\omega\)
sieht dann so aus:
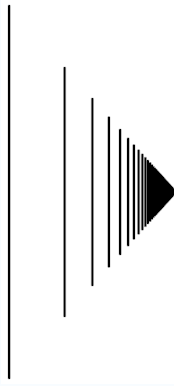
Die unendliche Zahl (Menge) \(\omega\) ist eine sogenannte Grenz-Ordinalzahl, denn sie besitzt keinen Vorgänger (wohl aber einen Nachfolger, denn den gibt es immer). Insofern ist sie etwas Besonderes! Es gibt keine andere Ordinalzahl, so dass \(\omega\) der Nachfolger dieser Zahl ist. Klar: das müsste ja die größte natürliche Zahl sein, und die gibt es nicht. Grenz-Ordinalzahlen definiert man als Vereinigungsmenge aller kleineren Ordinalzahlen. Immer wenn man bei der Aufzählung von Ordinalzahlen "und so weiter" (bzw. ... ) sagt, so kann man als Vereinigungsmenge all dieser und-so-weiter-Objekte eine neue Grenz-Ordinalzahl definieren und erklimmt damit eine neue Stufe der Unendlichkeit. Genau das geschieht, wenn man bei der Aufzählung der natürlichen Zahlen "und so weiter" sagt und dann \(\omega\) definiert. Die natürlichen Zahlen (also \(\omega\)) sind 1, 2, 3 und so weiter.
Nun kann uns keiner dazu zwingen, mit \(\omega\) aufzuhören. Das obige Schema funktioniert weiterhin und ermöglicht es uns, weitere Nachfolger zu konstruieren. Im Sinne der üblichen Schreibweise wollen wir dabei den Nachfolger von \(\omega\) als \(\omega + 1\) schreiben, analog \(\omega + 2\) usw.: \begin{align} \omega + 1 &:= \omega \cup \{ \omega \} = \\ & = \{ 0, 1, 2, 3, ... , \omega \} \\ & \\ \omega + 2 &:= (\omega + 1) \cup \{ (\omega + 1) \} = \\ &= \{ 0, 1, 2, 3, ... , \omega, (\omega + 1) \} \\ & ... \\ \end{align} Dies können wir wieder bis ins Unendliche fortsetzen, d.h. wir sagen wieder "und so weiter". Analog zu \( \mathbb{N} \) können wir daher auch jetzt die Vereinigungsmenge all dieser Mengen bilden. Diese Menge nennen wir \( \omega \cdot 2 \) oder auch \( \omega; + \omega \) : \[ \omega \cdot 2 = \omega + \omega = \] \[ = \{ 0, 1, 2, 3, ... , \omega , (\omega + 1), (\omega + 2), ... \} \]
Nicht verwirren lassen: hier steht einfach nur eine doppelt unendliche Liste von Mengen, bei denen jede Menge weiter rechts größer ist als alle Mengen weiter links. Die Mengen weiter links sind also Teilmengen der Mengen weiter rechts. Da man auch aus unendlich vielen Mengen wieder eine neue Menge bilden kann, ist es möglich, dass rechts von den natürlichen Zahlen eine Menge ω steht, die diese unendlich vielen Zahlen (Mengen) enthält.
Die graphische Darstellung der Menge \( \omega \cdot 2 \) anaolg zu oben sieht
dann so aus:


Wie es nun weitergeht, ist klar: Wir können immer wieder alle natürlichen Zahlen durchzählen
und dann die Menge all dieser Mengen bilden:
\[
\omega \cdot 3 = \omega + \omega + \omega =
\]
\[ =
\{ 0, 1, 2, 3, ... , \]
\[
\omega , (\omega + 1), (\omega + 2), ... , \]
\[
(\omega \cdot 2), (\omega \cdot 2 + 1), ... \}
\]
So kommen wir auch zu \( \omega \cdot 4 \), \( \omega \cdot 5 \), \( \omega \cdot 6 \) usw..
Wenn wir schließlich alle Zahlen hinter dem \( \omega \) durchgezählt haben, kommen wir gleichsam
bei \( \omega \cdot \omega = \omega^2 \) an:
\[
\omega^2 = \omega + \omega + \omega + \, ... \, =
\]
\[ =
\{ 0, 1, 2, 3, ... , \]
\[
\omega , (\omega + 1), (\omega + 2), ... , \]
\[
(\omega \cdot 2), (\omega \cdot 2 + 1), ... ,
\]
\[
(\omega \cdot 3), (\omega \cdot 3 + 1), ... ,
\]
\[
... \}
\]
Die Sprünge überwinden wir dabei, indem wir immer die Menge aller unendlich vielen Elemente
links davon bilden. So sieht die entsprechende graphische Darstellung aus:

Das Spiel können wir nun beliebig weitertreiben. An die Stelle des jedes einzelnen ω-Blocks im Bild oben können wir das komplette Bild, also den \( \omega^2 \)-Block einsetzen und so eine noch viel größere Menge bilden: die Menge \( \omega^3 \). Man kann sich vorstellen, dass man ein Bücherregal mit \(\omega\) Enzyklopädien hat, die jeweils aus \(\omega\) Bänden mit je \(\omega\) Seiten bestehen. Die Menge \( \omega^4 \) wäre dann eine Bibliothek mit \(\omega\) Bücherregalen mit je \(\omega\) Enzyklopädien, die jeweils aus \(\omega\) Bänden mit je \(\omega\) Seiten bestehen.
Können Sie sich vorstellen, wie das aussieht, wenn wir dies unendlich oft durchgeführt haben und so die
Menge \( \omega^\omega \) gebildet haben? Man hat unendlich oft das vorhergehende Bild genommen
und dieses Bild dann wieder unendlich oft hintereinandergehängt, wobei man es jeweils halbiert.
Das erinnert mich an die Verkleinerungs-Kopiermaschine, mit der man fraktale Bilder
erzeugen kann (siehe
Das Unteilbare – zu diesem Bild, mehr dazu ganz am Schluss dieses Kapitels).
In Wikipedia: Ordinal number
findet man die folgende schöne Darstellung:
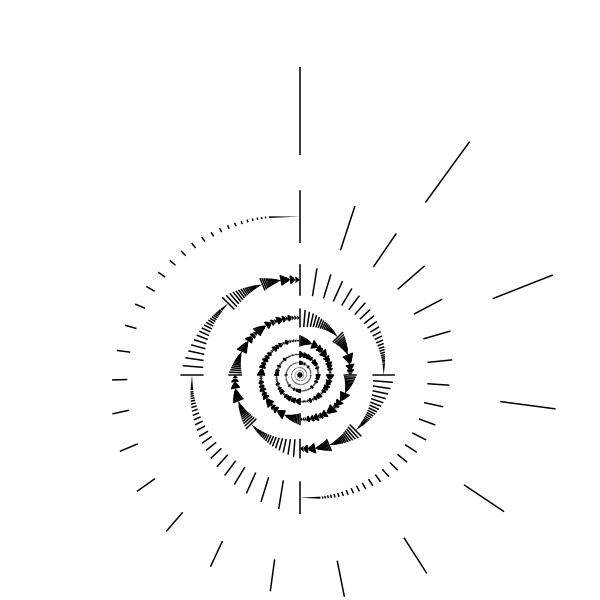
Darstellung von \( \omega^\omega \).
Quelle:
Wikimedia Commons: File:Omega-exp-omega.svg , dort Public Domain.
Wie kann man zu noch höheren Ordinalzahlen vordringen?
Nun, man kann beispielsweise die Menge \( \omega^{\omega^2} \) konstruieren
(das ist so zu lesen, dass im Exponent \( \omega^2 \) steht).
Hier stößt die obige Darstellung an ihre Grenzen.
Aber vielleicht gibt es ja noch eine bessere Möglichkeit.
Versuchen wir es mit Baumstrukturen – damit kann man Iterationen ja häufig gut darstellen.
Die Menge \( \omega \) der natürlichen Zahlen stellen wir dann
durch einen Knotenpunkt mit unendlich vielen Abzweigungen dar.
Wir können sie uns wie einen Fächer vorstellen, bei dem die Linien nach rechts immer dichter werden.
Nennen wir diese Darstellung den \( \omega \)-Fächer:
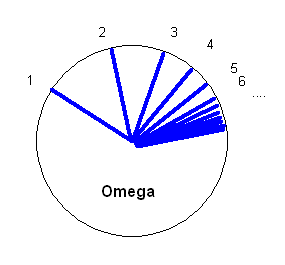
Diese Darstellung hat nun den Vorteil, dass man an den Enden der Linien
wieder neue \( \omega \)-Fächer ansetzen kann. So entsteht die Menge \( \omega^2 \):
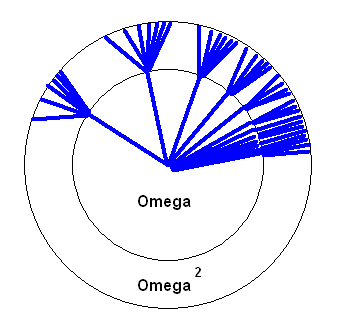
Welche Menge man jeweils vor sich hat, kann man sich leicht so überlegen: Stellen wir uns vor, wie hätten nur endlich viele Linien in jedem Fächer und \( \omega \) wäre die endliche Anzahl dieser Linien. Dann enden am Außenkreis im oberen Bild offenbar \( \omega^2 \) Linien, denn wir haben \( \omega \) Fächer mit je \( \omega \) Linien gezeichnet. Wenn wir uns nun vorstellen, \( \omega \) wird unendlich groß, dann ergibt sich im Grenzfall die Menge \( \omega^2 \), deren Größe ja die Zahl der Linienenden im obigen Bild darstellen soll. Dabei sollen die Linien in jedem Fächer nach rechts immer dichter werden, so dass unendlich viele Linien Platz haben.
Klar, wie es nun weitergeht: Wir fügen immer wieder an die Linienenden neue Fächer an
und erzeugen so die Mengen \( \omega^3 \), \( \omega^4 \), \( \omega^5 \) usw..
Im Grenzfall, dass wir dies unendlich oft tun, erhalten wir schließlich die Menge \( \omega^\omega \).
Dies können wir im Bild dadurch darstellen, dass wir die weiter außen liegenden Fächer immer kleiner zeichnen,
so dass wir im Prinzip unendlich viele Fächerschalen unterbringen können:
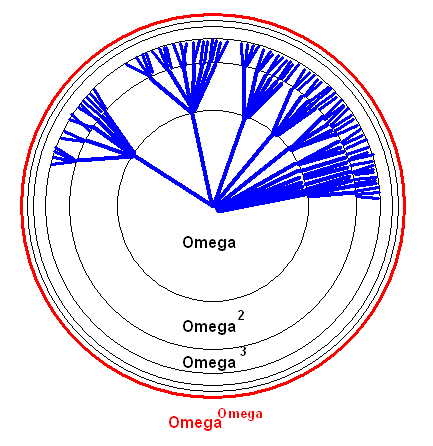
Wenn Ihnen die vielen Unendlichkeiten auch manchmal zu viel sind, hilft vielleicht wieder die Vorstellung, dass \( \omega \) erst einmal endlich ist. Jeder Fächer hat dann nur endlich viele Linien, und es gibt nur endlich viele Schalen, d.h. es werden nur endlich viele Fächer hintereinander gehängt. Die Zahl der ganz außen endenden Linien ist dann \( \omega^\omega \). Nun lässt man \( \omega \) wachsen: Die Zahl der Linien pro Fächer wächst, und zugleich wächst die Zahl der geschachtelten Schalen und damit die Zahl der hintereinandergehängten Fächer.
Wie aber kommen wir nun zu der Menge \( \omega^{\omega^2} \) , bei der
\( \omega^2 \) im Exponenten steht?
Für diese Menge brauchen wir \( \omega^2 \) ineinander geschachtelte Schalen, denn jede neue Schale
vervielfacht die Zahl der Enden um den Faktor \(\omega\). Wie \( \omega^2 \) aussieht, haben wir oben im
Bild mit den senkrechten Linien gesehen. Jede solche Linie begrenzt nun gleichsam eine Schale.
Wir müssen also im obigen Bild die rote Schale einfach \( \omega \)-oft ineinander schachteln
(die blauen Fächerlinien und die dazwischen liegenden unendlich vielen schwarzen Kreislinen
lassen wir weiter außen aus Darstellungsgründen weg).
Nach unendlich vielen solchen Schachtelungen erreichen wir die dick
eingezeichnete grüne Außenschale:
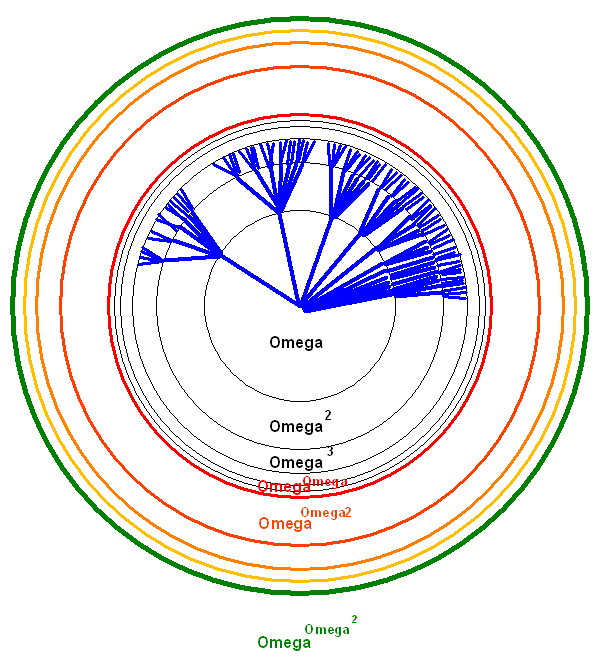
Wenn wir nun diesen ganzen Schachtelungsprozess außerhalb der grünen Schale einmal wiederholen, so erhalten wir die Menge \( \omega^{\omega^3} \). Wiederholen wir den Schachtelungsprozess unendlich oft, so erhalten wir die Menge \( \omega^{\omega^\omega} \). Um diese Menge könnten wir nun einen noch dickeren Kreis zeichnen.
Wir erkennen nun das Schema: Vor uns haben wir jeweils einen bestimmten Schachtelungsprozess. Wenn wir diesen Prozess wiederholen, wird in unserem Term der Menge eine bestimmte Zahl um Eins hochgezählt. Wenn wir den Schachtelungsprozess unendlich oft wiederholen, so wird aus der hochgezählten Zahl ein \(\omega\). Damit haben wir eine neue Qualität der Schachtelung erhalten, d.h. einen neuen unendlich viel tieferen Schachtelungsprozess. Die vor uns liegende Menge ist eine Grenz-Ordinalzahl. Sie wird als Vereinigungsmenge aller vorherigen Mengen gebildet. Den neuen tieferen Schachtelungsprozess können wir nun wieder als neue Einheit handhaben und mehrfach wiederholen – wieder wird hochgezählt, und nach unendlich vielen Schachtelungen entsteht wieder ein \(\omega\). Wir haben erneut die nächste Qualitätsstufe der Schachtelungen erreicht. Auch diesen Schachtelungsprozess können wir wiederholen: einmal, zweimal, ... , \(\omega\)-mal – nächste Schachtelungsstufe erreicht.
Auf diese Weise gelingt es uns, die Zahl der Exponenten beliebig hoch zu schrauben: \[ \omega^{\omega^{\omega^{...}}} \] Es ist mühsam und verwirren, die Schachtelungsdetails bei höheren Schachtelungstiefen im Detail zu verfolgen, aber die Vorgehensweise sollte nun ungefähr klar sein. Notfalls hilft es immer, \(\omega\) als endliche Zahl anzusehen und anwachsen zu lassen. Der obige Term spiegelt dann wieder, wie rasant die Zahl der Linienenden außen zunimmt.
Die Mengenlehre ist nun ausgesprochen mächtig: Sie erlaubt es sogar, den Grenzfall all dieser immer hochwertigeren Schachtelungsqualitäten formal als Vereinigungsmenge zu definieren. Diese Menge heißt \( \epsilon_0 \). Sie enthält alle Mengen der Form \( \omega^{\omega^{\omega^{...}}} \), bei denen nach beliebig (aber endlich) vielen Exponentierungen Schluss ist. Die Menge \( \epsilon_0 \) selbst kann man sich als Grenzfall vorstellen, bei der es nach oben im Exponenten unendlich weit geht. So unvorstellbar groß \( \epsilon_0 \) auch sein mag: sie ist immer noch eine abzählbare Menge!
Ich wage nicht, die Menge \( \epsilon_0 \) graphisch darzustellen. Irgendwie müsste sie wohl im obigen Sinn wie eine Zwiebel mit unendlich vielen Zwiebelschalen aussehen, bei der jede weiter außen liegende Schale eine neue Schachtelungsqualität beinhaltet, also eine neue Stufe, die die darunter liegende Schachtelungsart unendlich oft umfasst. Wenn man so will, enthält die Menge \( \epsilon_0 \) alles, was sich mit der oben beschriebenen Schachtelungs-Vorgehensweise erreichen lässt. Wenn man also mit den Worten "und so weiter ..." einen Prozess definiert, und diesen Prozess dann zweimal, dreimal "und so weiter ..." ausführt und so wieder einen neuen Prozess definiert, und wenn man das Prozess-neu-definieren endlich oft macht, dann ist dieser zuletzt definierte Prozess in \( \epsilon_0 \) enthalten.
Nach dieser Vorarbeit wollen wir nun versuchen, den Satz von Goodstein zu beweisen. Dazu wollen wir uns ansehen, was geschieht, wenn wir in der iterierten Darstellung einer Zahl \(n\) zur Basis \(b\) diese Basis \(b\) durch \(\omega\) ersetzen. Wir führen also ein Aufblähen der Basis durch, aber nicht nur um Eins wie in der Goodstein-Folge, sondern gleich bis zur unendlich großen Zahl \(\omega\). Analog zu oben schreiben wir für diesen Aufblähoperator \(B_b^\omega\). Betrachten wir dazu unser Beispiel von oben – die iterierte Darstellung der Zahl 35 zur Basis 2: \[ n = 35 = 2^{2^2 + 1} + 2^1 + 1 \] Wenn wir hier die Basis bis \(\omega\) aufblähen, erhalten wir \[ B_b^\omega(35) = \omega^{\omega^\omega + 1} + \omega^1 + 1 \]
Um diesen Term im Detail zu verstehen, müssten wir genau genommen noch die Addition und die Multiplikation von Ordinalzahlen sauber definieren. Unser schrittweiser Aufbau der Ordinalzahlen oben zeigt uns bereits die Vorgehensweise. Am anschaulichsten wird die Idee in der Baumdarstellung der Ordinalzahlen:
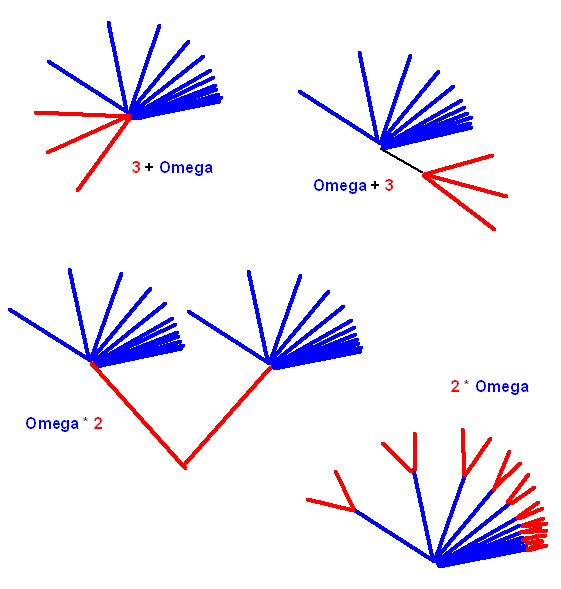
Bei der Addition \( a + b \) kommt links erst der Baum der Zahl \(a\) und dann rechts der Baum der Zahl \(b\). Erst müssen also alle Linienenden des \(a\)-Baums durchlaufen werden, dann erst die des \(b\)-Baums. Daher ist auch \( 3 + \omega = \omega \), denn hier kommen einfach nur drei neue Linien links an den \(\omega\)-Fächer dran, was denselben unendlichen Fächer ergibt (man beschriftet ihn nur neu mit den natürlichen Zahlen, wobei man vorne anfängt; siehe auch die Grafik unten). Dagegen kommen bei \( \omega + 3 \) die drei neuen Linien erst rechts, nachdem alle unendlich vielen Linien des \(\omega\)-Fächers bereits durchlaufen wurden. Daher gibt es neben der \(0\) noch ein weiteres Element ohne Vorgänger, nämlich die erste der drei hinzugefügten Linien. Entsprechend war oben in unserer Konstruktion auch \( \omega + 3 > \omega \).
Ähnlich ist es bei der Multiplikation:
Bei \( a \cdot b \) zeichnen wir erst den Baum der Zahl \(b\) und hängen dann an jedes Linienende
den Baum der Zahl \(a\) dran – so wollen wir es festlegen.
Daher ist \( \omega \cdot 2 = \omega + \omega \), d.h.
wir durchlaufen zwei ω-Bäume nacheinander. Neben der \(0\) gibt es ein weiteres Element ohne
Vorgänger, nämlich die erste Linie des zweiten \(\omega\)-Baums.
Anders ist es bei \( 2 \cdot \omega \) : Hier wird erst der \(\omega\)-Fächer gezeichnet,
und hier kommt dann an jedes Linienende der Baum der Zahl 2 dran, also eine Stimmgabel aus
zwei Linien. Die Linienenden haben dann dieselbe Struktur wie beim \(\omega\)-Baum, d.h. es ist
\( 2 \cdot \omega = \omega \).
Wie das Exponentieren nun geht, ist klar: \( \omega^3 = \omega \cdot \omega \cdot \omega \), also drei ineinander geschachtelte \(\omega\)-Fächer. Das kennen wir bereits von oben. Anders dagegen bei \( 3^\omega \). Hier werden Dreier-Gabeln unendlich oft ineinandergeschachtelt. Da dabei keine neuen Linien ohne Vorgänger entstehen, ist dieser Baum gleichwertig zum \(\omega\)-Fächer, hat also genauso viele Linienenden: \( 3^\omega = \omega \). Details findet man z.B. in Wikipedia: Ordinal arithmetic.
Zurück zum Aufblähen der Basis in der iterierten Darstellung:
Dieses Aufblähen bis zur Zahl \(\omega\) kann man sich im Baumbild
gut anschaulich vorstellen. Dazu zeichnet man zunächst den Baum
der iterierten Darstellung und ersetzt dann jeden Fächer, der \(b\) Linien trägt
(\(b\) ist die Basis der Darstellung),
durch den \(\omega\)-Fächer. Außerdem muss man \(b\)
Schachtelungen durch unendlich viele Schachtelungen ersetzen.
Schauen wir uns dazu ein einfaches Beispiel an: die iterierte Darstellung von 17 zur Basis 3:
\begin{align}
17 &= 3^2 + \, 3 \cdot 2 + 2
\\
B_3^\omega(17) &= \omega^2 + \omega \cdot 2 + 2
\end{align}
Hier die entsprechende Baumdarstellung. Man sieht sehr schön im oberen Bild, wie die
iterierte Darstellung sich auf die Baumstruktur auswirkt: Sie wird mit Dreierfächern aufgebaut,
passend zur Basis 3. Insgesamt entstehen so 17 Linienenden.
Im unteren Bild ist dann jeder Dreierfächer durch
den unendlichen \(\omega\)-Fächer ersetzt:
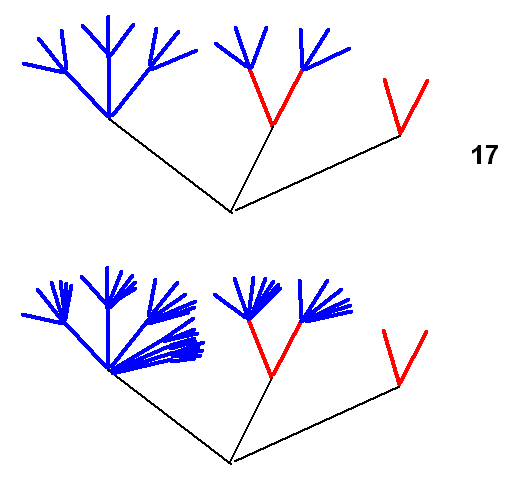
Wir sehen, dass es wichtig ist, in der iterierten Darstellung die Reihenfolge der Faktoren (hier \(3 \cdot 2\) ) festzulegen, um \(B_b^\omega\) eindeutig zu definieren. Wir treffen hier die Festlegung, dass die Potenzen von \(b\) immer zuerst kommen sollen, also \(3 \cdot 2\) und nicht \(2 \cdot 3\).
Ein wichtiger Punkt ist nun:
Das Basis-Aufblähen verändert die Größenverhältnisse nicht.
Betrachten wir beispielsweise zwei natürliche Zahlen \(n\) und \(m\), bei denen \(n < m\) ist.
Wenn wir diese Zahlen in ihrer iterierten Darstellung schreiben und die Basis schrittweise vergrößern,
so ist die aus \(m\) entstehende Zahl größer als die aus \(n\) entstehende Zahl.
Wir wollen das hier nicht beweisen, aber es ist sehr einleuchtend, wenn man sich die Zahlen
als Baum im obigen Sinn vorstellt. Die größere Zahl wird in der iterierten Darstellung
die Basis gleich oft oder öfter enthalten, so dass ein Aufblähen
der Basis sich bei der größeren
Zahl mindestens so stark auswirkt wie bei der kleineren Zahl.
Das gilt sogar dann, wenn wir die Basis
unendlich stark vergrößern und sie durch \(\omega\) ersetzen,
wie uns das Baumbild anschaulich bestätigt:
\[
n < m \quad \Rightarrow \quad B_b^\omega(n) < B_b^\omega(m)
\]
Das Aufblähen der Basis bis \(\omega\) können wir nun auch bei den Folgengliedern der
Goodstein-Folgen durchführen. Für das Folgenglied \(g_i(n)\) wird dabei die Zahl
\( i + 1 \) als Basis verwendet,
also die Basis, die durch den Bildungsprozess der Goodsteinfolge sowieso nahegelegt wird
(auf diese Basis wurde nämlich gerade per Basisersetzung hochgegangen).
Bei der Goodsteinfolge zu \(n = 4\) bilden wir also
\begin{align}
i &= 1 \\
g_1(4) &= 4 = \\
&= 2^2 \\
B_2^\omega(4) &= \omega^\omega \\
& \\
i &= 2 \\
g_2(4) &= 3^3 - 1 = 26 = \\
&= 3^2 \cdot 2 + 3 \cdot 2 + 2 \\
B_3^\omega(26) &= \omega^2 \cdot 2 + \omega \cdot 2 + 2 \\
& \\
i &= 3 \\
g_3(4) &= 4^2 \cdot 2 + 4 \cdot 2 + 2 - 1 = 41 = \\
&= 4^2 \cdot 2 + 4 \cdot 2 + 1 \\
B_4^\omega(41) &= \omega^2 \cdot 2 + \omega \cdot 2 + 1\\
& \\
i &= 4 \\
g_4(4) &= 5^2 \cdot 2 + 5 \cdot 2 + 1 - 1 = 60 = \\
&= 5^2 \cdot 2 + 5 \cdot 2 \\
B_5^\omega(60) &= \omega^2 \cdot 2 + \omega \cdot 2 \\
& \\
i &= 5 \\
g_5(4) &= 6^2 \cdot 2 + 6 \cdot 2 - 1 = 83 = \\
&= 6^2 \cdot 2 + 6 + 5 \\
B_6^\omega(83) &= \omega^2 \cdot 2 + \omega + 5
\end{align}
Wenn man das Verhalten oben verfolgt, so sieht man, wie Schritt für Schritt
die Subtraktion der Eins dafür sorgt, dass niedrigere Potenzen der Basis auftreten.
Genau so sind die Goodsteinfolgen nämlich konstruiert.
Besonders deutlich wird dies, wenn wir die Folgenglieder in einer Zifferndarstellung
zur jeweiligen Basis darstellen, analog zum Dezimalsystem oder dem Binärsystem.
Ein Beispiel:
\[
(423)_5 := 5^2 \cdot 4 + 5^1 \cdot 2 + 3
\]
Dann haben wir für die obige Goodsteinfolge:
\begin{align}
g_1(4) &= (100)_2 \\
g_2(4) &= (222)_3 \\
g_3(4) &= (221)_4 \\
g_4(4) &= (220)_5 \\
g_5(4) &= (215)_6
\end{align}
Die Zahlen werden zwar absolut gesehen immer größer, aber die Ziffern in der Zifferndarstellung
werden immer kleiner. Irgendwann werden sie komplett heruntergezählt sein!
Dies zeigt auch die Baumdarstellung der ersten Folgenglieder: Man sieht, wie die blauen Fächer
zwar immer mehr Linien enthalten, wie aber andererseits die Fächer
nach und nach angeknabbert werden, so dass die Zahl der Fächer abnimmt:
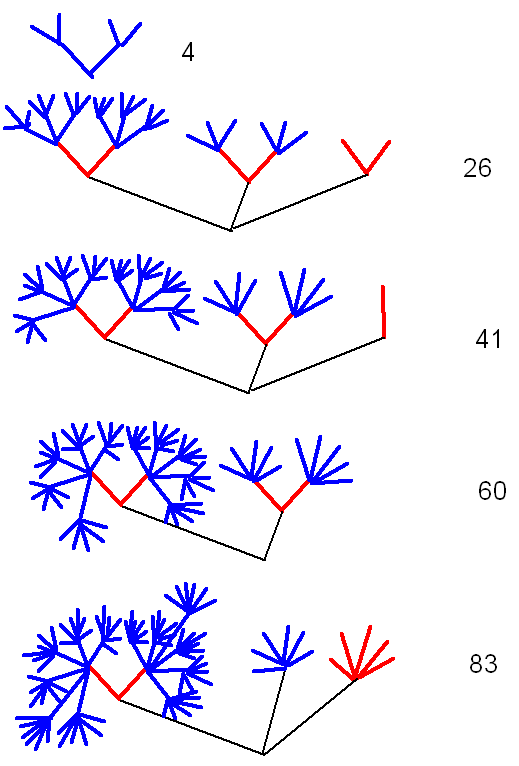
Genau dieses Anknabbern der Fächer spiegeln die Ordinalzahlen wieder, bei denen die jeweilige Basis durch \(\omega\) ersetzt ist (d.h. die blauen Fächer oben durch \(\omega\)-Fächer ersetzt werden). In jedem Schritt wird die Ordinalzahl kleiner. Auf diese Weise gelingt es den Ordinalzahlen, das Verhalten der Zifferndarstellung bzw. das Verhalten der Baumdarstellung geeignet einzufangen. Die Zunahme der Linien in den blauen Fächern wird in den Ordinalzahlen einfach ignoriert, indem man \(\omega\)-Fächer verwendet und so die Fächer als Einheit behandelt.
Man kann leicht mit dem Bildungsgesetz der Goodsteinfolge überprüfen, dass die
entsprechenden Ordinalzahlen tatsächlich schrittweise kleiner werden.
Dieses Bildungsgesetz lautete für
\(i > 1 \) und \( g_{i-1}(n) > 0 \) (siehe oben):
\[
g_i(n) = B_i (\, g_{i-1}(n) \, ) - 1
\]
Wenn wir nun die Basis auf \(\omega\) aufblähen, geschieht Folgendes:
\begin{align}
& B_{i+1}^\omega ( \, g_i(n) \, ) = \\
= \, & B_{i+1}^\omega ( \, B_i (g_{i-1}(n)) - 1 \, ) = \, ...
\end{align}
Nun verwenden wir, dass das Basis-Aufblähen bis \(\omega\)
die Größenverhältnisse nicht ändert (siehe oben).
Wenn wir also die Subtraktion von Eins weglassen, wird die Ordinalzahl größer:
\[
... \, < \, B_{i+1}^\omega ( \, B_i (g_{i-1}(n)) \, ) = \, ...
\]
Dieser Term bedeutet:
Ersetze in der iterierten Darstellung des Folgenglieds die Basis \(i\) durch \(i+1\) und ersetze dann diese
Basis \(i+1\) durch \(\omega\) (genauso lief es ständig oben in unserem Beispiel).
Statt dessen könnten wir auch in einem Schritt die Basis \(i\) gleich durch \(\omega\) ersetzen:
\[
... \, = \, B_i^\omega ( \, g_{i-1}(n) \, )
\]
Zusammengefasst haben wir also
\[
B_{i+1}^\omega ( \, g_i(n) \, ) < B_i^\omega ( \, g_{i-1}(n) \, )
\]
Das ist genau das Ergebnis, das wir oben in unserem Beispiel gesehen haben:
Die Ordinalzahlen, bei denen die jeweilige Basis durch \(\omega\) ersetzt ist, werden
in jedem Schritt kleiner.
Aber bedeutet das, dass die Ordinalzahlenfolge irgendwann auf Null heruntergeht? Immerhin sind Ordinalzahlen ja unendlich große Objekte. Wenn man da jedesmal Eins abzieht, dann wird man ja wohl nicht bei Null ankommen, sondern ewig weiter herunterzählen?!
Diese Überlegung enthält einen Denkfehler: Wir ziehen nicht jedesmal Eins ab! Das tun wir nämlich nur, wenn die Ordinalzahl einen Vorgänger hat, also eine um Eins kleinere Ordinalzahl existiert. Sobald wir aber bei einer Grenz-Ordinalzahl wie beispielsweise \(\omega\) ankommen, gibt es keinen Vorgänger. Die nächstkleinere Ordinalzahl wird einfach eine der unendlich vielen Ordinalzahlen sein, die kleiner als die Grenzzahl sind. Von dieser Zahl aus können wir dann wieder herunterzählen, bis die nächste Grenzzahl in endlich vielen Schritten erreicht ist und der nächste Sprung nach unten bevorsteht.
Es ist schon etwas verwirrend: Zählt man von unten nach oben, so kann man unendlich lange zählen,
ohne die nächste Grenzzahl zu erreichen, denn man findet immer einen Nachfolger, der
kleiner als die nächste Grenzzahl ist. Hat man dagegen eine absteigende Folge von Ordinalzahlen,
so muss man bei jeder Grenzzahl einen Sprung nach unten machen, denn einen direkten Vorgänger gibt es nicht:


Man sieht das auch sehr schön an unserem Beispiel von oben. Dort hatten wir: \begin{align} B_2^\omega(4) &= \omega^\omega \\ & \\ B_3^\omega(26) &= \omega^2 \cdot 2 + \omega \cdot 2 + 2 \\ & \\ B_4^\omega(41) &= \omega^2 \cdot 2 + \omega \cdot 2 + 1\\ & \\ B_5^\omega(60) &= \omega^2 \cdot 2 + \omega \cdot 2 \\ & \\ B_6^\omega(83) &= \omega^2 \cdot 2 + \omega + 5 \end{align} In der ersten und vierten Zeile wird eine Grenzzahl erreicht und es erfolgt ein Sprung auf eine kleinere Ordinalzahl.
Allgemein gilt: Jede strikt absteigende Folge von Ordinalzahlen erreicht nach endlich vielen Schritten ihr kleinstes Folgenelement und bricht dann ab. Tiefer als Null geht es dabei nicht, denn Null ist die kleinste Ordinalzahl.
Das kann man natürlich auch streng beweisen.
Dazu stellt man zunächst fest, dass die Ordinalzahlen analog zu den
natürlichen Zahlen wohlgeordnet sind
d.h. es gilt für alle Ordinalzahlen \(m\) und \(n\)
immer \( m \leq n \) oder \( n \leq m \), und zusätzlich
hat jede Menge aus Ordinalzahlen ein kleinstes Element.
Genau so haben wir die Ordinalzahlen oben ja konstruiert.
Nun ist eine absteigende Ordinalzahlenfolge genau so eine Teilmenge, hat also ein kleinstes Element
und muss demnach bei diesem Element abbrechen.
Achtung: die Menge aller Ordinalzahlen gibt es nicht (siehe unten)!
Hier reicht aber die Menge \(\epsilon_0\) aus, also die Menge aller Ordinalzahlen, die man
als iterierte Potenz von \(\omega\) schreiben kann (siehe oben).
Nur solche Ordinalzahlen können entstehen, wenn wir in der iterierten Darstellung der Goodstein-Folgenglieder
die Basis durch \(\omega\) ersetzen.
Damit haben wir alle Zutaten für den Beweis zusammen, der nun einfach so aussieht:
|
Was ist nun von diesem Beweis zu halten? Wie sicher sind wir jetzt, dass Goodsteinfolgen wirklich alle bei Null enden? Immerhin ist ein Beweis in der Peano-Arithmetik ja unmöglich und wir brauchen zum Beweis diese merkwürdigen Ordinalzahlen, also unendlich große Objekte.
Aus formaler Sicht gilt: Wenn wir den Mengenbegriff akzeptieren, so wie er durch die Zermelo-Fränkel-Axiome festgelegt wird (d.h. wir akzeptieren auch den Umgang mit unendlichen Mengen), wenn wir zusätzlich den Gesetzen der Logik trauen und wenn wir schließlich zustimmen, dass sich die natürlichen Zahlen im von-Neumannschen-Modell (siehe oben) durch Mengen darstellen lassen, dann akzeptieren wir auch den obigen Beweis.
Der entscheidende Punkt ist dabei für mich: Akzeptieren wir den Umgang mit unendlichen Mengen, also mit aktual unendlichen Objekten? Trauen wir den Ordinalzahlen?
Wenn wir es bei der rein abstrakten Definition als Menge belassen, so könnten letzte Zweifel bestehen bleiben. Wenn wir aber die Ordinalzahlen in der obigen Baumstruktur darstellen, dann werden aus ihnen anschaulich erfassbare Objekte. Wir können uns anschaulich vorstellen, dass die unendlichen \(\omega\)-Fächer in den Baumstrukturen Einheiten sind, die wir als Ganzes erfassen und manipulieren können. Auch unendlich tiefe Schachtelungen wie bei \(\omega^\omega\) können wir uns in ihrer Struktur noch recht gut vorstellen.
Damit wird klar, was der obige Beweis anschaulich macht: Er untersucht die Baumstruktur der endlichen Goodstein-Folgenglieder in ihrer iterierten Darstellung und betrachtet, wie sich diese Baumstruktur ändert, wenn wir in der Goodsteinfolge voranschreiten. Dabei wird ausgenutzt, dass es langfristig nicht darauf ankommt, wie viele Linien jeder endliche Fächer in der Baumstruktur aufweist. Diese Zahl der Linien in den Fächern wächst zwar ständig an (da die Basis der iterierten Darstellung ständig vergrößert wird), aber die Zahl der Fächer wird langsam aber sicher immer geringer, bis auch der letzte Fächer sich schließlich auflöst. Die Goodsteinfolge zu \(n=4\) hat das oben beispielhaft gezeigt.
Das Auflösen der Fächer kann man aber nur erkennen, wenn man die Fächer als Einheit erfassen kann. Die Ordinalzahlen tun genau das: Sie betrachten die Fächer als handhabbare Objekte (repräsentiert durch \(\omega\)) und spiegeln die Größenverhältnisse so wieder, wie sie sich bei immer größer werdenden Fächern (und anwachsender Iterationstiefe) einstellen würden. Die Peano-Arithmetik kann das nicht: Sie kann nur in einem einzigen unendlichen Fächer schrittweise von links nach rechts laufen und dabei den Fächer beliebig weit abtasten. Sie kann aber nicht aus einem unendlichen Fächer heraustreten und diesen Fächer als Ganzes erfassen. Genau deshalb ist die Peano-Arithmetik auch nicht in der Lage, die natürlichen Zahlen komplett zu erfassen, denn erst der komplette \(\omega\)-Fächer spiegelt die natürlichen Zahlen korrekt wieder.
Wenn man sich die Beweismethode auf diese Weise veranschaulicht, so scheint sie vollkommen natürlich zu sein. Warum sollte man auf eine solche Argumentation verzichten? Man darf nur keine Angst davor haben, die natürlichen Zahlen (also den \(\omega\)-Fächer) als ein handhabbares Objekt anzusehen. Also: keine Angst vor unendlichen Mengen! Diese Angst haben wir ja sonst auch nicht – man denke an die Konstruktion der reellen Zahlen über Äquivalenzklassen von Cauchyfolgen oder über den Dedekind'schen Schnitt (siehe Kapitel 4.5). Reelle Zahlen sind als Menge gesehen mindestens so merkwürdig wie Ordinalzahlen! Immerhin sind die hier verwendeten Ordinalzahlen bis \( \epsilon_0 \) sogar abzählbar, im Gegegensatz zur Menge der reellen Zahlen.
Der obige Beweis hat Ähnlichkeit mit einer Beweismethode, die transfinite Induktion genannt wird. Da wir uns mit Ordinalzahlen bereits so gut auskennen, wollen wir uns das hier nicht entgehen lassen.
Transfinite Induktion verallgemeinert die normale Induktion, die wir von den natürlichen Zahlen her kennen, auf allgemeine wohlgeordnete Mengen (z.B. Mengen aus Ordinalzahlen). Das Induktionsaxiom der Peano-Arithmetik kennen wir schon von oben: \[ [ A(0) \, \land \,(\forall n : (A(n) \Rightarrow A(n^*) )] \] \[ \Rightarrow \, [ \forall n : (A(n) ] \] In Worten: Wenn die Ausage \(A\) für \(0\) gilt und wenn sich diese Aussage von jeder natürlichen Zahl auf deren Nachfolger überträgt, dann gilt sie für alle natürlichen Zahlen.
Dabei ist \(A(n)\) eine beliebige Aussage über die natürliche Zahl \(n\). Im von-Neumannschen-Modell der natürlichen Zahlen ist dann \(n\) die Mengendarstellung der natürlichen Zahl \(n\) und aus dem obigen Induktionsaxiom im Modell ein beweisbarer Satz: \begin{align} & \forall A: \, [ \, (0 \in A) \, \land \, \forall n : \, [(n \in \mathbb{N}) \Rightarrow \\ & \quad \quad \quad ( (n \in A) \Rightarrow ( n^* \in A)) \, ]] \Rightarrow [ \mathbb{N} \subseteq A ] \end{align} Wenn wir statt \( \mathbb{N} \) irgendeine wohlgeordnete Menge \(M\) betrachten, so formuliert man das transfinite Induktionsprinzip in Worten so:
|
Das transfinite Induktionsprinzip ist kein Axiom, sondern es folgt aus der Wohlordnung der Menge \(M\) (so wie im von-Neumannschen-Modell das Induktionsaxiom kein Axiom mehr ist, sondern ein wahrer Satz). Der Beweis ist ganz einfach:
Angenommen, die Aussage \(A\) gelte nicht für alle Elemente von \(M\) (obwohl die kursiv gedruckte Bedingung erfüllt ist). Dann kann man die Teilmenge dieser Elemente von \(M\) bilden, für die \(A\) nicht gilt. Da \(M\) wohlgeordnet ist, muss diese Teilmenge ein kleinstes Element (nennen wir es \(a'\) ) besitzen, d.h. \(a'\) ist das kleinste Element, für das die Aussage \(A\) nicht gilt. Für alle kleineren Elemente als \(a'\) gilt \(A\) also (denn \(a'\) ist ja das kleinste Element, für das \(A\) nicht gilt). Wegen der kursiv gedruckten Bedingung muss dann aber \(A\) auch für \(a'\) gelten – ein Widerspruch. Also muss die Aussage \(A\) doch für alle Elemente von \(M\) gelten.
Transfinite Induktion ist also nichts Geheimnisvolles, sondern einfach eine Eigenschaft wohlgeordneter Mengen. Sie gilt auch für beliebig große Mengen aus Ordinalzahlen, z.B. für die Menge \(\epsilon_0\), denn diese Mengen sind wohlgeordnet.
Vorsicht! Die Menge aller Ordinalzahlen gibt es nicht, und zwar aus folgendem einfachen Grund: Die Menge aller Ordinalzahlen wäre nach unserer Konstruktionsvorschrift von Grenz-Ordinalzahlen (als Menge aller kleineren Ordinalzahlen) selbst eine Grenz-Ordinalzahl, die größer ist als alle in ihr enthaltenen Ordinalzahlen. Da die Menge aller Ordinalzahlen aber als Grenz-Ordinalzahl in sich selbst enthalten sein müsste, müsste sie auch größer als sie selbst sein – ein Widerspruch. Außerdem darf es nach dem Regularitätsaxiom (Fundierungsaxiom, siehe Kapitel 4.2) sowieso keine Mengen geben, die sich selbst als Element enthalten. Man könnte sagen, die Gesamtheit aller Ordinalzahlen ist zu groß, um sie zu einer Menge zusammenfassen zu können. Insbesondere gibt es keine größte Ordinalzahl, und man kann noch sehr viel größere Ordinalzahlen als beispielsweise \(\epsilon_0\) definieren (siehe z.B. Wikipedia: Large countable ordinal). Zur Erinnerung: \(\epsilon_0\) war die Menge, die alle Ordinalzahlen enthält, die sich als \( \omega^{\omega^{\omega^{...}}} \) mit beliebig vielen Exponentierungen schreiben lassen.
Im Beweis der Endlichkeit von Goodsteinfolgen hatten wir oben verwendet, dass jede streng absteigende Folge aus Ordinalzahlen, die sich als iterierte Potenz von \(\omega\) schreiben lassen, nach endlich vielen Schritten abbricht. Man kann dies als eine Form der transfiniten Induktion ansehen, denn sowohl transfinite Induktion als auch die Endlichkeit absteigender Goodsteinfolgen sind eine Folge der Wohlordnung der Ordinalzahlen. Da nur Ordinalzahlen eine Rolle spielen, die kleiner als \(\epsilon_0\) sind (also die in \(\epsilon_0\) enthalten sind), spricht man auch von transfiniter Induktion bis \(\epsilon_0\). Der Satz von Kirby und Paris aus dem Jahr 1982 besagt, dass man transfinite Induktion bis \(\epsilon_0\) braucht, um den Satz von Goodstein zu beweisen. Die Peano-Arithmetik kann das nicht (wir haben es oben bereits erwähnt), denn sie kann nur transfinite Induktion bis \(\omega\), also die gewohnte Induktion innerhalb der natürlichen Zahlen.
Bei transfiniter Induktion bis \(\epsilon_0\) ist die betrachtete wohlgeordnete Menge also die Menge \(\epsilon_0\), d.h. alle Ordinalzahlen, die wir wie oben beschrieben als Baum mit \(\omega\)-Fächern darstellen können. Transfinite Induktion bis \(\epsilon_0\) ist also gleichsam Induktion entlang von solchen Baumstrukturen. Es ist also durchaus möglich, sich dieses Induktionsverfahren zu veranschaulichen. Damit verwandelt es sich von einer merkwürdigen logischen Verallgemeinerung des gewohnten Induktionsverfahrens in ein anschaulich nachvollziehbares und korrektes Verfahren.
Im Jahr 1936 ist es Gerhard Gentzen gelungen, mit diesem Verfahren die Konsistenz (Widerspruchsfreiheit) der Peano-Arithmetik nachzuweisen (siehe z.B. Wikipedia: Gentzen's consistency proof ). Dabei hat er alle Beweise, die in der Peano-Arithmetik möglich sind, in Baumstrukturen untergebracht, denen sich eine Ordinalzahl kleiner als \(\epsilon_0\) zuordnen lässt. So kann man sich vorstellen, dass die logische Teilaussage Für alle natürlichen Zahlen gilt ... zu einem \(\omega\)-Fächer im Baum führt. Per transfiniter Induktion hat er dann nachgewiesen, dass keiner dieser Beweise einen Widerspruch herleitet. Wenn nämlich einer der Beweise einen Widerspruch herleiten würde, so hätte das zu einer unendlich weit absteigenden Folge von Ordinalzahlen geführt. Von oben wissen wir aber bereits, dass es so eine Folge nicht gibt.
Der Beweis von Gentzen weist Ähnlichkeiten zum Beweis von Kirby und Paris auf, in dem man einen Zusammenhang zwischen den Goodstein-Folgengliedern und den möglichen Beweisen aus der Peano-Arithmetik aufstellt. Beim Beweis von Gentzen stellt man dagegen einen Zusammenhang zwischen Ordinalzahlen und den möglichen Beweisen aus der Peano-Arithmetik auf. Aus den Goodstein-Folgengliedern kann man aber leicht Ordinalzahlen machen, indem man die Basis zu \(\omega\) aufbläht. In beiden Fällen führt dann ein Abbruch der Folge dazu, dass die Widerspruchsfreiheit der Peano-Arithmetik feststeht, da dann kein Peano-Arithmetik-Beweis für einen Widerspruch vorhanden sein kann.
Innerhalb der Peano-Arithmetik sind beide Beweise nicht möglich, denn kein System kann seine eigene Widerspruchsfreiheit beweisen (siehe Gödels zweiter Satz in Kapitel 2.6). Transfinite Induktion bis \(\epsilon_0\) geht über die Peano-Arithmetik hinaus, die nur bis \(\omega\) gehen kann.
Noch eine Anmerkung: Die Widerspruchsfreiheit der Peano-Arithmetik folgt auch bereits aus der Tatsache, dass es für sie ein Modell im Rahmen der Mengenlehre gibt, z.B. das von-Neumannsche-Modell (siehe oben und Kapitel 4.2). Die Axiome werden im Modell zu wahren Sätzen und die Regeln der Logik sind so aufgebaut, dass sich aus diesen wahren Sätzen nur ebenfalls wahre Sätze ableiten lassen. Ein Widerspruch (also eine Aussage der Form \(A \land \neg A\) ) hat jedoch immer den Wahrheitswert "falsch" und kann demnach nicht abgeleitet werden (siehe Kapitel 4.4 sowie Wikipedia: Gentzen's consistency proof).
In gewissem Sinn ist die Ordinalzahl \(\epsilon_0\) ein Maß für die Komplexität der Peano-Arithmetik. Man braucht transfinite Induktion bis \(\epsilon_0\), um die Widerspruchsfreiheit der Peano-Arithmetik zu beweisen. Die Bäume der Ordinalzahlen kleiner als \(\epsilon_0\) stellen die Beweisstrukturen dar, die in der Peano-Arithmetik möglich sind.
Allgemein kann man auf diese Weise Ordinalzahlen dazu verwenden, um die Komplexität formaler Systeme und die Struktur der darin möglichen Beweise zu charakterisieren. Mehr dazu siehe beispielsweise Wikipedia: Large countable ordinal.
Man könnte an dieser Stelle noch sehr viel weiter fortschreiten. Die aktuelle Forschung hat ein ganzes Teilgebiet der Mathematik hervorgebracht, das sich mit diesen Dingen beschäftigt: die Beweistheorie. Es würde hier jedoch zu weit führen, darauf näher einzugehen, zumal ich kein Experte auf diesem Gebiet bin. Wer mehr wissen möchte, findet viele weitere Informationen zu dem Thema beispielsweise hier (vergleiche John Baez: Week 236):
Beim Experimentieren mit Veranschaulichungen stieß ich noch auf eine andere Möglichkeit, Ordinalzahlen darzustellen. Ich habe diese Idee zwar wieder verworfen, da die Baumdarstellung besser geeignet ist, möchte sie aber zum Abschluss dieses Kapitels kurz zeigen:
Die Menge \(\omega\) stellen wir durch eine Reihe von Punkten dar,
die wir entlang einer Geraden immer enger aufreihen:
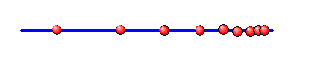
Wenn wir die Linie von links nach rechts durchlaufen, so kommen wir
dabei an allen natürlichen Zahlen vorbei.
Für die folgenden Zwecke ist es nützlich, die Linie zu einer oberen Kreishälfte
zu verbiegen – nennen wir ihn \(\omega\)-Kreis.
Die untere Kreishälfte brauchen wir eigentlich gar nicht.
Ich habe sie nur eingezeichnet, da es so leichter zu zeichnen ist (und aus einem anderen Grund,
der weiter unten sichtbar wird – ich möchte nämlich gerne ein Bild aus
dem Zusatzmaterial von
Die Entdeckung des Unteilbaren wiederverwenden).
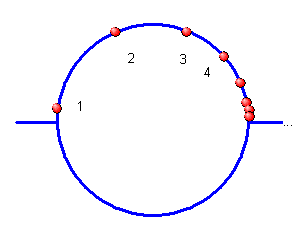
Die Menge \(\omega^2\) entsteht nun dadurch, dass wir jeden roten Punkt auf der
Geraden oben durch einen \(\omega\)-Kreis ersetzen, d.h. an die Stelle jeder natürlichen Zahl
treten \(\omega\) Elemente. Es werden also \(\omega\) Elemente \(\omega\)-oft durchlaufen:
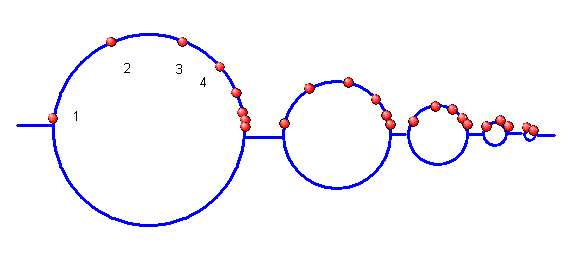
Das Spiel können wir fortsetzen: Wenn wir wieder jeden roten Punkt durch einen \(\omega\)-Kreis
ersetzen, entsteht die Menge \(\omega^3\)
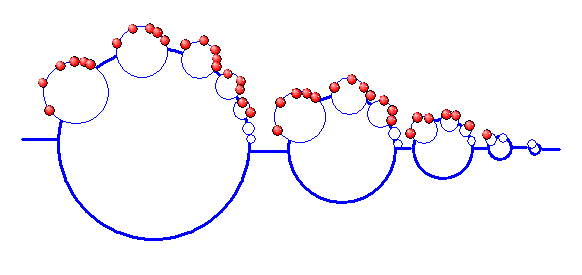
Und wenn wir das ganze Spiel \(\omega\)-oft durchführen, entsteht die Menge \(\omega^\omega\),
die dann ungefähr so aussieht (siehe auch
Das Unteilbare – zu diesem Bild):

Dabei haben wir die roten Punkte weggelassen und außerdem wurde die Ersetzungsregel auch für die unteren Halbkreise durchgeführt (das war für die Erzeugung des Bildes einfacher). Das stört uns aber nicht, wenn wir uns nur ganz am oberen Rand der Figur von links nach rechts bewegen. Jeder Halbkreis ist dabei eine Menge \(\omega\), die wir durchlaufen, und diese Mengen sind am oberen Rand des Bildes unendlich tief ineinander geschachtelt. Das Bild ist also ein Fraktal.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 25 March 2023