
Quelle: Wikimedia Commons File:Skytale.png, CC BY-SA 3.0.
Zwei große Zahlen miteinander zu multiplizieren ist relativ einfach, zumindest für einen handelsüblichen Computer mit passender Software. Aus dem Ergebnis der Multiplikation umgekehrt diese beiden Faktoren wieder herauszulesen, ist schwierig. Bei großen Zahlen mit mehreren Hundert Dezimalstellen ist es so schwierig, dass heutige Computer auch nach Jahren Rechenzeit daran scheitern. Lediglich Quantencomputer könnten dieses Problem noch einigermaßen effektiv lösen, wie wir aus dem vorherigen Kapitel wissen.
Diese Eigenschaft der Multiplikation nutzt man heute, um mit dem gängigen RSA-Verfahren wichtige Daten zu verschlüsseln, beispielsweise im Internet. Vielleicht haben Sie sich an dieser Stelle auch schon gefragt: Wie soll das gehen? Was hat die Faktorisierung großer Zahlen mit Verschlüsselung zu tun? Dieser Frage wollen wir im aktuellen Kapitel genauer nachgehen. Dabei wollen wir uns allerdings auch etwas allgemeiner mit dem Thema Verschlüsselung beschäftigen, um einen besseren Überblick zu gewinnen und damit das RSA-Verfahren besser einordnen zu können.
Wie kann man eine Nachricht so verschlüsseln, dass möglichst nur der beabsichtigte Empfänger diese verstehen kann? Schon Kinder sind von dieser Frage begeistert und basteln an eigenen Geheimschriften. Auch unsere Vorfahren standen oft vor dieser Frage, beispielsweise wenn es darum ging, militärische Botschaften vor dem Zugriff Fremder zu schützen.
Die einfachste Methode ist natürlich, die Nachricht zu verstecken: Zettel im Schuhabsatz, Tätowierung auf die Kopfhaut und dann Haare wachsen lassen, Zitronensaft als Tinte und vieles mehr. Auf solche Ideen sind unsere Vorfahren natürlich schon vor langer Zeit gekommen.
Will man sich nicht darauf verlassen, dass die Nachricht unentdeckt bleibt,
dann muss man sie für einen zufälligen Entdecker unverständlich machen.
Eine einfache Möglichkeit besteht darin, die Schriftzeichen (Buchstaben) nach
einem bestimmten System durch andere Schriftzeichen zu ersetzen (Substitution) oder sie
anders anzuordnen (Transposition).
So verwendete der spartanische General Pasanius etwa 475 v.Chr.
eine sogenannte Skytale,
also einen Holzstab mit einem darum gewickelten
Papyrusstreifen. Der Papyrusstreifen erscheint erst dann lesbar, wenn man ihn um eine
Skytale gleichen Durchmessers wickelt:

Quelle: Wikimedia Commons File:Skytale.png,
CC BY-SA 3.0.
Julius Caesar verwendete um 50 v.Chr. eine einfache Substitutionsvorschrift zur Verschlüsselung: Verschiebe das Alphabet um \(n\) Zeichen, nimm also statt dem A beispielsweise ein D, statt dem B ein E usw., wobei nach dem Z wieder das A kommt. Hier gibt es sogar schon einen einfachen Schlüssel, den man zum Entziffern braucht, nämlich die Zahl \(n\), um die verschoben wird.
Statt nur um \(n\) Stellen zu verschieben, kann man auch eine Übersetzungstabelle angeben,
bei der das Alphabet vollkommen willkürlich durcheinandergewirbelt wird.
Wenn man diese Übersetzungstabelle (also den Schlüssel) nicht kennt, dann hat man schon große
Mühe, gleichsam von Hand einen entsprechend verschlüsselten Text zu entziffern.
Einen Ansatzpunkt zum Knacken dieses Codes liefert der Umstand,
dass die Buchstaben in jeder Sprache eine
bestimmte statistische Häufigkeitsverteilung haben, wie jeder Scrabble-Spieler weiß.
Ist der verschlüsselte Text lang genug, so kann man damit die Übersetzungstabelle erraten.
Enthält der verschlüsselte Text beispielsweise sehr oft den Buchstaben X,
so könnte das X für das häufige E stehen.
Im neunten Jahrhundert wurden bereits Texte nach diesem Verfahren entschlüsselt.
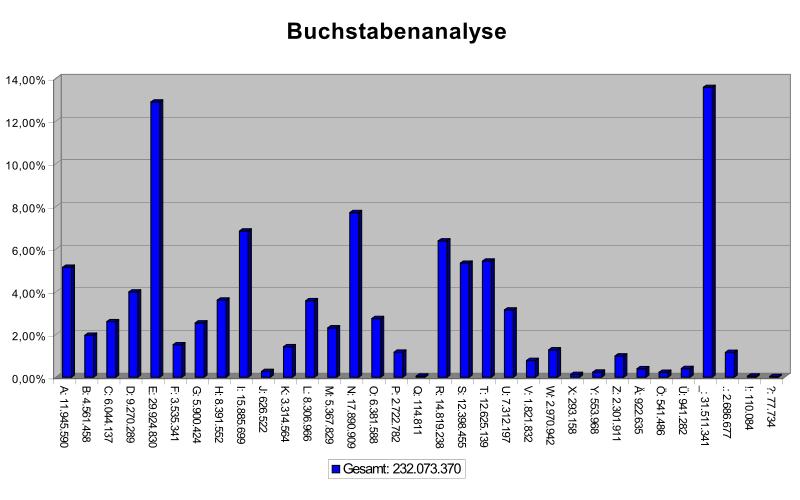
Urheber: Arbeitsgruppe EBUSS (Potsdam, Mosbach),
Quelle:
File:Alphabet haufigkeit.svg, Urheber: Arbeitsgruppe EBUSS (Potsdam, Mosbach),
GNU-Lizenz für freie Dokumentation.
Um dieser Entschlüsselungsmethode zu entgehen, kann man versuchen, die Übersetzungstabelle komplizierter zu gestalten und beispielsweise statt Buchstaben Zahlen verwenden, wobei man die überflüssigen Zahlen zufällig als Dummy-Zeichen im Text einstreut. Hier gibt es noch viele weitere Möglichkeiten, die alle ihre Vor- und Nachteile haben. Aber mit dem entsprechenden Aufwand lassen sich doch viele von ihnen über Häufigkeitsanalysen entschlüsseln.
Um statistischen Häufigkeitsanalysen zu entgehen, kann man die
Übersetzungstabelle während der Verschlüsselung nach einigen Buchstaben immer wieder ändern.
Etwas Ähnliches wurde beispielsweise von Leon Battista Alberti im Jahr 1466 vorgeschlagen.
Als Übersetzungstabelle diente dabei die folgende Scheibe, bei der sich die
Ringe gegeneinander verdrehen lassen, so dass sich die Buchstabenzuordnung leicht verändern lässt:

Quelle:
Wikimedia Commons File:UnionCipherDisk.nsa.jpg, Foto von Austin Mills,
CC BY-SA 2.0.
Zum Entschlüsseln muss man jetzt also wissen, wie die Scheibe aussieht und wann sie wie verdreht wurde – das ist der Schlüssel. Die abgebildete Scheibe ist allerdings nur eine Form von Caesars Buchstabenverschiebung, bei der die Verschiebezahl \(n\) flexibel verändert werden kann. Man könnte die Buchstaben auf einem der Ringe jedoch auch in anderer Reihenfolge anordnen und so eine Übersetzungstabelle mit Caesars Verschiebezahl kombinieren.
Noch geschickter ist es, mehrere komplette Übersetzungstabellen zu haben und immer wieder zwischen diesen zu wechseln. So könnte man im Text versteckt angeben, wann man zu welcher Tabelle wechseln muss. Solche Ideen kamen bereits um das Jahr 1500 herum auf. Verfeinert wurden diese Ideen im Jahre 1585 von Blaise de Vigenère (siehe Wikipedia: Vigenère-Chiffre ). Er verwendete 26 Übersetzungstabellen, durchnummeriert mit den Buchstaben des Alphabetes, wobei die Übersetzungstabellen meist einfache Verschiebetabellen nach dem Vorbild Caesars waren. Ein Schlüsselwort legt nun für jede Buchstabenposition im Ursprungstext fest, mit welcher Tabelle er zu verschlüsseln ist. Ist das Schlüsselwort beispielsweise "QUARK", so ist der erste Buchstabe des Ursprungstextes mit Tabelle Nummer Q zu verschlüsseln, der zweite Buchstabe mit Tabelle Nummer U usw.. Beim sechsten Buchstaben des Ursprungstextes fangen wir wieder mit Tabelle Q an und so fort. Natürlich sollte man möglichst lange Schlüsselwörter verwenden – QUARK wäre doch etwas zu kurz. Damit erreicht man recht wirkungsvolle Verschlüsselungen, die allerdings oft auch recht fehleranfällig sind, wenn man sich mal vertut.
Allerdings ist auch die obige Verschlüsselung nach Vigenère nicht absolut sicher. Wenn man nämlich die Länge des Schlüsselwortes kennt, dann weiß man, welche Buchstaben nach derselben Übersetzungstabelle verschlüsselt wurden, und kann dann wieder eine Häufigkeitsanalyse durchführen. Um die Länge des Schlüsselwortes zu erraten, kann man verschiedene statistische Untersuchungen am verschlüsselten Text vornehmen. Man kann beispielsweise nach Wiederholungen identischer Buchstabenfolgen suchen.
Man müsste also ein Schlüsselwort haben, das so lang wie der zu verschlüsselnde Text selbst ist, und das idealerweise aus einer zufälligen Buchstabenkombination besteht. Dann wäre die Suche nach Wiederholungen sinnlos. Dabei braucht man bei einem so langen zufälligen Schlüsselwort komplizierte Übersetzungstabellen gar nicht mehr, sondern es genügt, für jeden Buchstaben des Ursprungstextes Caesars Verschiebe-Regel anzuwenden. Ein A im Schlüsselwort sagt dann: verschiebe um 1, ein B sagt: verschiebe um 2 usw.. Für jeden Buchstaben des Ursprungstextes gibt es dabei einen eigenen Buchstaben des Schlüsselwortes, der angibt, um wieviel der Buchstabe im Alphabet verschoben werden muss. Da das Schlüsselwort zufällig ist, wird jeder Buchstabe des Ursprungstextes zufällig verändert, so dass es keine Angriffspunkte für eine Entschlüsselung gibt, wenn man das Schlüsselwort nur ein einziges Mal zum Verschlüsseln eines Textes verwendet. Dieses Verschlüsselungssystem ist daher so perfekt, wie eine Verschlüsselung nur sein kann. Wegen der Einmal-Verwendung nennt man das Schlüsselwort auch ein One Time Pad.
Das One Time Pad -Verschlüsselungssystem ist zwar theoretisch das sicherste denkbare Verschlüsselungssystem, aber es hat auch offensichtliche Nachteile. Sehr lange Schlüsselwörter (so lang wie der Text selbst) müssen sowohl dem Sender als auch dem Empfänger bekannt sein und ggf. sicher zwischen diesen übertragen werden, und man braucht ständig neue Schlüsselwörter, die auch noch zufällig sein sollen. Damit ist klar, dass sich das System eher für kurze Nachrichten und sehr hohe Sicherheitsansprüche eignet.
Viele weitere Verschlüsselungssysteme wurden im Laufe der Zeit erfunden, die zumeist
Variationen der obigen Ideen waren. Eines der Berühmtesten ist sicher die
ENIGMA,
die von den Deutschen im zweiten Weltkrieg verwendet wurde.

Quelle:
Wikimedia Commons File:EnigmaMachineLabeled.jpg, fotografiert von Karsten Sperling (2004),
dort Public Domain.
Diese Maschine substituiert über mehrere drehbare Walzen Buchstaben, wobei wegen der Walzendrehung für jeden Buchstaben eine eigene Übersetzungstabelle realisiert wird. Trotz ihrer scheinbaren Sicherheit konnte der Code im Jahre 1940 von den Alliierten geknackt werden, wobei auch der uns mittlerweile gut bekannte Alan Turing eine wichtige Rolle spielte. Mehr dazu findet man in Wikipedia: Enigma (Maschine).
Nach dem zweiten Weltkrieg spielten Computer eine immer stärkere Rolle. Es entstand u.a. der Lucifer-Verschlüsselungsstandard, der im Jahr 1976 in den Data Encryption Standard (DES) mündete. Da dieser später den Anforderungen nicht mehr genügte, wurde er im Jahr 2001 durch den Advanced Encryption Standard (AES) ersetzt. DES und AES sind Block-Substitutionsverfahren, d.h. es werden nicht einzelne Buchstaben ersetzt, sondern ganze Buchstabengruppen bzw. ganze Bit-Blöcke (beispielsweise Blöcke von 64 Bit Länge bei DES). Da es bei 64 Bit bis zu \(2^{64}\) verschiedene Blöcke gibt, wird es nur sehr wenige Blöcke geben, die in einem Ursprungstext sowie in dem verschlüsselten Text mehrfach vorkommen. Eine statistische Häufigkeitsanalyse wie bei Buchstaben-Ersetzungen wird bei Blöcken daher scheitern. Allerdings kann man für das Ersetzen der Blöcke keine Übersetzungstabelle wie bei Buchstaben verwenden – eine solche Tabelle wäre viel zu groß. Stattdessen wendet man einen komplizierten Ersetzungs-Algorithmus an, der seinerseits einen Schlüssel benötigt. Zum Entschlüsseln kehrt man diesen Algorithmus um, wobei derselbe Schlüssel verwendet wird (symmetrisches Verfahren). Der Schlüssel muss also zwischen Sender und allen Empfängern ausgetauscht werden – eine potentielle Schwachstelle. Abgesehen davon gilt zumindest AES mit hinreichend langem Schlüssel als sicher und wird weltweit überall eingesetzt.
Wie lässt sich nun aber die Schwachstelle mit der Schlüsselübertragung ausschalten? Das ist genau die Stelle, bei der das Faktorisierungsproblem ins Spiel kommt. Schauen wir uns die Details an.
Die Idee ist folgende: Der Empfänger besitzt einen privaten Schlüssel, den
nur er kennt und den er zum Entschlüsseln verwendet.
Außerdem besitzt er einen dazu passenden öffentlichen Schlüssel, den
er jedem öffentlich zur Verfügung stellt, der ihm eine verschlüsselte Nachricht
übersenden möchte. Er ruft also gleichsam in die Welt hinaus:
"Hallo Leute – wer mir eine verschlüsselte Nachricht schicken möchte, die keiner außer mir
wieder entschlüsseln kann, der verwende bitte zum
Verschlüsseln den folgenden öffentlichen Schlüssel ..."
Jeder kann also mit dem öffentlichen Schlüssel eine Nachricht verschlüsseln, und nur der Besitzer des dazu passenden privaten Schlüssels kann diese Nachricht wieder entziffern. Zum Entschlüsseln ist der öffentliche Schlüssel also nutzlos. Daher ist keine Schlüsselübertragung notwendig, denn der öffentliche Schlüssel zum Verschlüsseln ist allgemein bekannt, während der geheime private Schlüssel zum Entschlüsseln nur dem Empfänger bekannt sein muss. Man bezeichnet solche Verfahren als asymmetrische Verfahren oder auch als Public-Key-Verfahren.
Das bekannteste Verfahren zur Umsetzung dieser Idee ist das RSA-Verfahren, das 1977 entwickelt wurde und breite Anwendung findet. Das Verfahren erfordert ein gewisses mathematisches Verständnis. Daher wollen wir schrittweise vorgehen und uns das Verfahren an einem vereinfachten Beispiel anschauen (das Beispiel stammt aus Wikipedia: RSA-Kryptosystem).
Wir wollen also einen Text verschlüsseln. Da es sich bei dem RSA-Verfahren um einen Rechenalgorithmus handelt, müssen wir Teile des Textes zunächst in Zahlen umwandeln. In unserem Beispiel nehmen wir einfach die Position der Buchstaben im Alphabet: A = 01, B = 02, ... , Z = 26. In der Realität wird man analog zum DES- und AES-Verfahren (siehe oben) ganze Textblöcke durch Zahlen darstellen und so mit größeren Zahlen arbeiten. Das verringert die Gefahr, dass der Code durch Häufigkeitsanalysen geknackt werden kann.
Um eine solche Zahl (nennen wir sie \(K\) für Klartext) zu verschlüsseln, brauchen wir den öffentlichen Schlüssel, den uns der Empfänger zur Verfügung stellt. Dieser Schlüssel besteht aus zwei natürlichen Zahlen:
öffentlicher Schlüssel:
|
In der Realität verwendet man natürlich weit größere Zahlen, beispielsweise einen 5-stelligen Exponenten \(e\) und ein Modul \(N\) mit mehreren Hundert Stellen (d.h. \(N\) ist größer als die Zahl der Atome im sichtbaren Universum). Wie man auf ein passendes \(N\) und \(e\) kommt, sehen wir uns später an. Jedenfalls ist \(e\) deutlich kleiner als \(N\). Damit können wir nun die Klartextzahl \(K\) nach der folgenden Formel verschlüsseln:
Verschlüsselung:
|
In unserem Beispiel mit RSA-Modul \(N = 143\) und Verschlüsselungsexponent \(e = 23\) ergibt die Verschlüsselung des siebten Buchstabens "G" (also \(K = 7\)) \[ C = 7^{23} \;\mathrm{mod}\; 143 \] Dabei müssen wir glücklicherweise die riesige Zahl \(7^{23}\) nicht wirklich berechnen, sondern es gibt dazu ein effizientes Rechenverfahren, das wir anwenden wollen (siehe Wikipedia: Diskrete Exponentialfunktion sowie Wikipedia: Schnelles Potenzieren). Insbesondere muss man nicht zuerst die komplette Potenz bilden, sondern man kann zwischendurch auch \( \mathrm{mod}\; N \) anwenden, um die Zahl wieder zu verkleinern, bevor man weitere Faktoren \(K\) heranmultipliziert. Man kann nämlich jedes zu potenzierende Zwischenergebnis \(x\) (eine natürliche Zahl) schreiben als \[ x = (x \;\mathrm{mod}\; N) + k \cdot N \] mit einer passenden natürlichen Zahl \(k\) (die sagt, wie oft \(N\) in \(x\) hineinpasst). Dann erhält man beim Potenzieren \begin{align} & x^m \;\mathrm{mod}\; N = \\ &= ((x \;\mathrm{mod}\; N) + k \cdot N)^m \;\mathrm{mod}\; N = \\ &= ((x \;\mathrm{mod}\; N)^m + k' \cdot N) \;\mathrm{mod}\; N = \\ &= (x \;\mathrm{mod}\; N)^m \;\mathrm{mod}\; N \end{align} Analog ist es auch beim Multiplizieren: \begin{align} & (a \cdot b \cdot c) \;\mathrm{mod}\; N = \\ &= (((a \cdot b) \;\mathrm{mod}\; N) \cdot c) \;\mathrm{mod}\; N = \\ &= (a \cdot ((b \cdot c) \;\mathrm{mod}\; N)) \;\mathrm{mod}\; N \end{align} denn Vielfache von \(N\) werden durch das Multiplizieren mit anderen natürlichen Zahlen immer nur zu anderen Vielfachen von \(N\), die am Schluss sowieso alle abgezogen werden. Man kann sie also auch vorher jederzeit in den Klammern schon wegnehmen. Die Multiplikation modulo \(N\) erfüllt demnach das Assoziativgesetz (und natürlich auch das Kommutativgesetz). Wir werden unten noch sehen, dass man das nutzen kann, um eine endliche Gruppe aufzubauen, die diese Multiplikation modulo \(N\) als Gruppenoperation enthält. Die Elemente dieser Gruppe werden alle Zahlen von \(1\) bis \(N\) sein, die teilerfremd zu \(N\) sind. Man spricht von der multiplikativen Gruppe modulo \(N\) oder auch einer primen Restklassengruppe und schreibt sie als \( \mathbb{Z}_N^* \). Die Eigenschaften dieser Gruppe sind letztlich der Grund dafür, dass das RSA-Verfahren funktioniert – schließlich ist die Verschlüsselung ja gerade die \(e\)-fache Gruppenmultiplikation von \(K\) mit sich selbst. Mehr dazu weiter unten.
Man kann also bei der zu potenzierenden Zahl jederzeit ein möglichst großes Vielfaches des Moduls \(N\) abziehen, denn dieses würde beim Potenzieren oder Multiplizieren seinerseits nur ein anderes Vielfaches von \(N\) ergeben, das am Schluss wegen \( \mathrm{mod}\; N \) sowieso wieder abgezogen wird.
Das Potenzieren geht am schnellsten, wenn wir es durch mehrfaches Quadrieren geeignet ersetzen und nach jedem Quadrieren \( \mathrm{mod}\; N \) anwenden, um ein möglichst großes Vielfaches von \(N\) loszuwerden. In unserem Beispiel (Verschlüsselung des Buchstabens "G" = \(7\) über die Formel \[ C = 7^{23} \;\mathrm{mod}\; 143 \] sieht die Verschlüsselungsrechnung folgendermaßen so aus (wer will, kann diese Details gerne überspringen – ich wollte es aber selber einmal explizit durchrechnen):
Den Exponenten \(23\) können wir schreiben als \begin{align} 23 &= 16 + 4 + 2 + 1 = \\ &= 2^4 + 2^2 + 2 + 1 = \\ &= ((2 \cdot 2 + 1) \cdot 2 + 1) \cdot 2 + 1 \end{align} entsprechend der Binärzahl \( 10111 \). Bei Potenzieren mit \(23\) entsteht so (durch Anwenden der Potenzgesetze von links nach rechts): \begin{align} 7^{23} &= 7^{ ( (2 \cdot 2 + 1) \cdot 2 + 1) \cdot 2 + 1} = \\ &= 7^{ ( (2 \cdot 2 + 1) \cdot 2 + 1 ) \cdot 2 } \cdot 7 = \\ &= \left( 7^{ ( 2 \cdot 2 + 1 ) \cdot 2 + 1} \right)^2 \cdot 7 = \\ &= \left( 7^{ ( 2 \cdot 2 + 1 ) \cdot 2 } \cdot 7 \right)^2 \cdot 7 = \\ &= \left( \left( 7^{2 \cdot 2 + 1 } \right)^2 \cdot 7 \right)^2 \cdot 7 = \\ &= \left( \left( 7^{2 \cdot 2 } \cdot 7 \right)^2 \cdot 7 \right)^2 \cdot 7 = \\ &= \left( \left( \left( 7^2 \right)^2 \cdot 7 \right)^2 \cdot 7 \right)^2 \cdot 7 \end{align} Rechnen wir das nun modulo \(N = 143\) aus, wobei wir in jedem Schritt versuchen, ein möglichst großes Vielfaches von \(N = 143\) abzuziehen (kann man natürlich gerne beim Lesen überspringen – solche Rechnungen macht normalerweise ein kleines Computerprogramm): \begin{align} & 7^{23} \;\;\mathrm{mod}\; 143 = \\ &= (( (7^{2})^{2} \cdot 7 )^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= (( 2401 \cdot 7 )^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= (( (2401 - 16\cdot143) \cdot 7 )^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= (( 113 \cdot 7 )^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( 791^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( (791 - 5\cdot143)^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( 76^{2} \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( 5776 \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( (5776 - 40\cdot143) \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= ( 56 \cdot 7 )^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= 392^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= (392 - 2\cdot143)^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= 106^{2} \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= 11236 \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= (11236 - 78\cdot143) \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= 82 \cdot 7 \;\;\mathrm{mod}\; 143 = \\ &= 574 \;\;\mathrm{mod}\; 143 = \\ &= (574 - 4\cdot143) = \\ &= 2 \end{align} Uff – ich kann es kaum glauben, dass ich mich nicht verrechnet habe, aber dieses Ergebnis steht auch in Wikipedia: RSA-Kryptosystem so drin! Man kann die obige Verschlüsselungsrechnung also tatsächlich sogar von Hand mit einem Taschenrechner und etwas Geduld durchziehen. Das bedeutet: Verschlüsseln ist nicht schwer, schon gar nicht für einen Computer.
Da man in die Verschlüsselungsformel
\[
C = K^e \;\mathrm{mod}\; N
\]
die Basis \(K\) hineinsteckt und dazu das Ergebnis \(C\) berechnet, spricht
man von einer Potenzierung modulo \(N\). Dabei handelt es sich um eine sogenannte
Einwegfunktion, d.h. bei gegebenem Exponenten e und Modul \(N\) kann man aus der Basis \(K\)
mit einem Computer relativ leicht das Ergebnis \(C\) ausrechnen,
aber es gibt (bei größeren \(e\) und \(N\)) kein effektives Verfahren, um
aus dem Ergebnis \(C\) wieder die ursprüngliche Basis \(K\) zu berechnen, selbst wenn wir
den Exponenten \(e\) und das Modul \(N\) kennen. Wir haben es also
tatsächlich mit einer Verschlüsselung
zu tun, die sich selbst bei Kenntnis des öffentlichen
Schlüssels (\(e\) und \(N\)) nicht mit heutigen Computern
umkehren lässt. Das hat damit zu tun, dass die Potenzierung modulo \(N\) fast chaotische Sprünge
macht – die Ergebnisse für \(C\) sehen für verschiedene Eingabewerte \(K\) wie zufällig aus,
und genau das soll eine Verschlüsselung ja auch tun. Die Verschlüsselung wirkt also
wie eine fast zufällige Verwürfelung, wie die folgende Beispielgrafik für
\(e = 7\) und \(N = 15\) zeigt:
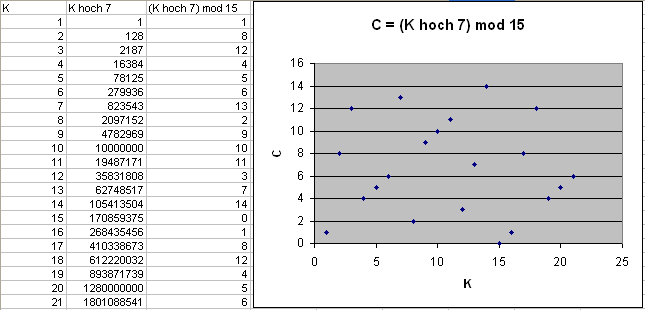
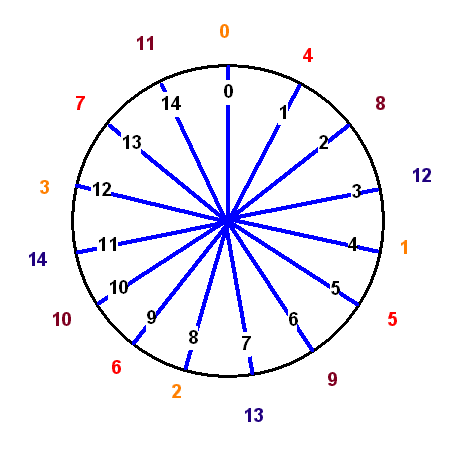
Man kann sich die Potenzierung modulo \(N\) auch gut an einem Rad mit \(N\) Speichen voranschaulichen, wobei wir die Speichen wie bei einer Uhr von \(0\) bis \(N-1\) durchnummerieren (die \(N\)-te Speiche ist dann wieder identisch mit der \(0\)-ten Speiche, siehe Bild weiter unten). Die Nummern der Speichen schreiben wir zusätzlich auf ein Gummiband, das wir einmal um das Rad wickeln, so dass die Nummern über den passenden Speichen liegen. Bei einer Multiplikation mit \(K\) und anschließendem modulo \(N\) geschieht nun Folgendes: Wir nehmen das Gummiband ab, strecken es um das \(K\)-fache (das entspricht der Multiplikation mit \(K\)) und wickeln es \(K\)-mal um das Rad (das entspricht der Operation modulo \(N\)). Die Zahlen auf dem Gummiband landen dann an neuen Speichenpositionen, die genau das Ergebnis der Multiplikation dieser Zahlen mit \(K\) und anschließendem modulo \(N\) angeben.
Wenn wir das Ganze \(e\) mal wiederholen, landet die Zahl \(1\) des Gummibandes genau bei Speichenposition \( C = K^e \;\mathrm{mod}\; N \). Das Gummiband wird dabei \(e\)-mal um das \(K\)-fache gestreckt und nach jeder Streckung (oder alternativ am Schluss) wieder komplett um das Rad gewickelt. Das wirkt wie wiederholtes Ausrollen und Falten bei einem Knet-Kuchenteig: Nummern, die nahe beieinander lagen, entfernen sich durch das Strecken voneinander und landen durch das Aufwickeln fast wie zufällig an neuen Orten. Letztlich werden die Zahlen auf dem Gummiband dabei kräftig durchgemischt.
Da bei einer realen Verschlüsselung
\(e\) eine fünfstellige Zahl ist und das Rad extrem viele Speichen hat
(mehr als es Atome im sichtbaren Universum gibt), wird man
nach den vielen tausend Streckungen und Wiederaufwicklungen
aus der Endposition \(C\) der 1-Speiche kaum noch ermitteln
können, um welches \(K\) man bei jeder Drehung dehnen muss, um gerade diese Endposition
zu erreichen. Man kann höchstens noch verschiedene \(K\) ausprobieren, und das ist bei der großen
Zahl der Speichen und damit den extrem vielen möglichen \(K\)-Werten (die zwischen
\(2\) und \(N - 1\) liegen können) aussichtslos.
Dieses Bild eines Rades wird uns weiter unten bei der
multiplikativen Gruppe modulo \(N\) noch einmal wiederbegegnen.
Wie aber soll der Empfänger nun die Nachricht entschlüsseln, also aus \(C\) wieder das ursprüngliche \(K\) berechnen? Alleine mit der Kenntnis des öffentlichen Schlüssels \(N\) und \(e\) geht das nicht mit realen Mitteln, denn sonst wäre die Verschlüsselung ja unsicher. Das Entschlüsseln geht, weil die obige Einwegfunktion eine Hintertür (Falltür, Trapdoor) bereithält – zumindest wenn man bestimmte Module \(N\) und dazu passende Exponenten \(e\) wählt und eine Zusatzinformation zu \(N\) und \(e\) besitzt. Und das tut der Empfänger, der \(e\) und \(N\) als öffentlichen Schlüssel zur Verfügung gestellt hat. Er wählt nämlich \(N\) und \(e\) nicht zufällig, sondern er startet mit zwei großen Primzahlen \(p\) und \(q\) und multipliziert diese, um das Modul \(N\) zu berechnen (zum öffentlichen Exponenten \(e\) kommen wir gleich): \[ N := p \cdot q \] Im Gegensatz zu \(N\) und \(e\) werden die Primzahlen \(p\) und \(q\) aber nicht veröffentlicht, sondern vom Empfänger geheim gehalten – mit ihrer Hilfe kann er nämlich die verschlüsselte Nachricht wieder entschlüsseln (wie, kommt gleich). Und hier genau schlägt das Faktorisierungsproblem zu: Wäre es einfach, auch ein großes \(N\) in seine Primfaktoren zu zerlegen, so könnte jeder aus dem öffentlichen Schlüssel \(N\) die beiden geheimen Primfaktoren \(p\) und \(q\) errechnen und so ebenfalls die Nachricht entschlüsseln. Nach heutigem Wissen ist aber das Berechnen der Primfaktoren \(p\) und \(q\) bei großen Zahlen zu aufwendig für normale Computer, so dass nur der Empfänger die Nachricht entschlüsseln kann (er kennt ja \(p\) und \(q\)), nicht aber alle anderen, die nur das Produkt \(N = p \cdot q \) kennen.
Bleibt noch der zweite öffentliche Schlüssel, der Exponent \(e\). Diesen muss der Empfänger passend zu den beiden geheimen Primzahlen \(p\) und \(q\) wählen. Dazu braucht er zunächst eine Hilfsgröße, nämlich das Produkt der beiden Zahlen unterhalb von \(p\) und \(q\), also \( (p - 1) \cdot (q - 1) \). Dieses Produkt nennt man auch Eulersche Phi-Funktion und schreibt
Diese Größe hat auch eine wichtige anschauliche Bedeutung: \( \varphi(N) \) ist die Anzahl an Zahlen von \(1\) bis \(N\), die teilerfremd zu \(N\) sind, d.h. deren Primfaktorzerlegung für unser spezielles \(N\) weder die Primzahl \(p\) noch die Primzahl \(q\) enthält.
Dass das so ist, kann man so sehen: Als gemeinsame Teiler einer Zahl mit der Zahl \( N= p \cdot q \) kommen nur die beiden Primzahlen \(p\) und \(q\) in Frage (denn \(N\) hat keine anderen Teiler). Folgende Zahlen bis \(N\) haben den gemeinsamen Teiler \(p\) mit \(N\): \[ p, \, 2p, \, 3p, \, ... \, , qp \] Das sind \(q\) Zahlen. Analog haben folgende Zahlen bis \(N\) den gemeinsamen Teiler \(q\) mit \(N\): \[ q, \, 2q, \, 3q, \, ... \, , pq \] Das sind \(p\) Zahlen. Allerdings haben wir \(qp = pq\) doppelt gezählt – es gibt also insgesamt \( q + p - 1 \) Zahlen bis \(N\), die nicht teilerfremd zu \(N\) sind. Ziehen wir das von \(N=pq\) ab, so haben wir die Anzahl der Zahlen bis \(N\), die teilerfremd zu \(N\) sind, also \begin{align} & \quad N - (q + p - 1) = \\ &= p q - q - p + 1 = \\ &= (p - 1) (q - 1) = \\ &= \varphi(N) \end{align} Für den öffentlichen Exponenten \(e\) nimmt der Empfänger nun irgendeine Zahl unterhalb von \(\varphi(N)\), die keinen gemeinsamen Teiler mit \(\varphi(N)\) haben darf. Die Primfaktorzerlegung von \(e\) muss also aus komplett anderen Primzahlen bestehen als die von \(\varphi(N)\). Das brauchen wir gleich für den sogenannten Entschlüsselungsexponenten. Meist nimmt man für \(e\) einfach eine nicht allzu große Primzahl, die in der Primfaktorzerlegung von \(\varphi(N)\) nicht vorkommt (das kann man mit einem Computer leicht testen, indem man \(\varphi(N)\) durch solche kleineren Primzahlen teilt und schaut, ob dabei ein Rest übrig bleibt).
Wie geht nun die Entschlüsselung mit Hilfe der geheimen Primzahlen \(p\) und \(q\) vor sich? Wäre die Verschlüsselungsfunktion einfach die normale Exponentialfunktion \(C = K^e \) (also ohne dass ein möglichst großes Vielfaches von \(N\) abgezogen wird), dann könnte man einfach einen Entschlüsselungsexponenten \( d = 1/e \) wählen (sodass \( e d = 1 \) ist) und hätte die Entschlüsselung \(K = C^d = C^{1/e}\).
Das wäre natürlich keine besonders sinnvolle Verschlüsselung gewesen, denn zum Entschlüsseln bräuchten wir nur den Kehrwert des öffentlichen Exponenten \(e\) zu bilden. Daher wird beim Verschlüsseln noch ein möglichst großes Vielfaches von \(N\) abgezogen, was beim obigen Rad dem Aufwickeln des Gummibandes entspricht. Statt \(C = K^e \) wird also \( C = K^e \;\mathrm{mod}\; N \) zum Verschlüsseln verwendet. Das Interessante ist nun, dass man auch die anderen Formeln ähnlich modifizieren kann, so dass alles zusammenpasst (warum das so geht, kommt später): Aus \( e d = 1 \) und \(K = C^d \) wird:
| Entschlüsselung: \[ K = C^d \;\mathrm{mod}\; N \] wobei der geheime Entschlüsselungsexponent \(d\) (wie \(e\) ebenfalls eine natürliche Zahl) die folgende Formel erfüllen muss: \[ (e \cdot d) \;\mathrm{mod}\; \varphi(N) = 1 \] |
Das Produkt der Exponenten \(e \cdot d\) muss also gleich Eins plus einem Vielfachen von \(\varphi(N)\) sein. Wie die Verschlüsselung erfolgt also auch die Entschlüsselung durch Potenzierung modulo \(N\), wobei man für die Bestimmung des Entschlüsselungsexponenten \(d\) die Zahl \(\varphi(N) = (p-1) (q-1) \) braucht. Dafür braucht man aber die beiden Primfaktoren \(p\) und \(q\). Der Empfänger kennt diese und hat deshalb keine Probleme beim Entschlüsseln, aber alle anderen, die nur die öffentlichen Schlüssel \(e\) und \(N\) kennen, müssen dafür das Faktorisierungsproblem für \(N\) lösen, also \(p\) und \(q\) berechnen. Da das auf heutigen Computern bei großen Zahlen aussichtslos ist, scheitern sie und können den Entschlüsselungsexponenten \(d\) nicht berechnen.
Die Bedingung \((e \cdot d) \;\mathrm{mod}\; \varphi(N) = 1\) bedeutet, dass der Verschlüsselungsexponent \(e\) teilerfremd zu \(\varphi(N)\) sein muss. Würde nämlich \(e\) einen gemeinsamen Teiler mit \(\varphi(N)\) haben (nennen wir ihn \(g\)), dann wäre \(e\) ein Vielfaches von \(g\) und auch das Produkt \( e d \) wäre ein Vielfaches von \(g\). Die \(\mathrm{mod}\; \varphi(N)\)-Operation zieht davon dann ein anderes Vielfaches von \(g\) ab (denn \(\varphi(N)\) wäre ja auch ein Vielfaches von \(g\)), so dass am Schluss irgendein Vielfaches von \(g\) oder aber Null übrig bleibt. Nun ist \(g\) aber größer als Eins (es soll kein trivialer Teiler sein) und somit kann am Schluss nie genau Eins übrig bleiben, was aber gefordert ist. Diese Argumentation wird uns unten beim Thema inverses Element noch einmal begegnen.
Schauen wir uns nochmal unser obiges Beispiel aus Wikipedia: RSA-Kryptosystem an. Wie hat der Empfänger den öffentlichen Schlüssel \(N = 143\) und \(e = 23\) hergestellt? Das ist bei so kleinen Zahlen nicht schwer herauszufinden: Er hat die beiden Primzahlen \(p = 11\) und \(q = 13\) verwendet, so dass \[ N = 11 \cdot 13 = 143 \] ist. Für den öffentlichen Verschlüsselungsexponenten \(e\) brauchen wir Eulers Phi-Funktion \[ \varphi(143) = 10 \cdot 12 = 120 = \] \[ = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \] Die Zahl \(e\) muss nun kleiner als \(\varphi(143)\) und teilerfremd zu \(\varphi(143)\) sein. Die obige Primfaktorzerlegung von \(\varphi(143)\) zeigt, dass die Primzahl \( e = 23 \) die Bedingung erfüllt (natürlich gibt es noch mehr Möglichkeiten).
Oben ergab die Verschlüsselung des Beispiel-Buchstabens "G" (also \(7\)) den Wert \[ C = 7^{23} \;\mathrm{mod}\; 143 = 2 \] Zum Entschlüsseln brauchen wir den Entschlüsselungsexponenten \(d\), der die Formel \[ (e \cdot d) \;\mathrm{mod}\; 120 = 1 \] erfüllen muss. Das kann man effektiv mit dem erweiterten euklidischen Algorithmus auswerten – Details lassen wir hier weg (mehr dazu siehe unten beim Thema inverses Element der Gruppe \( \mathbb{Z}_N^* \) und im Anhang ganz unten). Als Ergebnis erhält man \[ d = 47 \] sodass \begin{align} & \quad (e \cdot d) \;\mathrm{mod}\; 120 = \\ &= (23 \cdot 47) \;\mathrm{mod}\; 120 = \\ &= (1081) \;\mathrm{mod}\; 120 = \\ &= (9 \cdot 120 + 1) \;\mathrm{mod}\; 120 = \\ &= 1 \end{align} die Bedingung erfüllt. Die Entschlüsselung lautet dann also \[ K = 2^{47} \;\mathrm{mod}\; 143 = 7 \] was man mit dem oben bei der Verschlüsselung beschriebenen Rechenverfahren nachrechnen kann.
Dass die Ver- und Entschlüsselung funktioniert, können wir noch einmal
an dem sehr einfachen Beispiel
mit \( e = 7 \) und \( N = 15 \) von oben nachvollziehen.
Hier sieht man noch leicht,
dass zu \( N = 15 \) die beiden Primfaktoren \( p = 5 \) und \( q = 3 \)
gehören. Dann ist \( \varphi(15) = 4 \cdot 2 = 8 \).
Der Verschlüsselungsexponent \( e = 7 \)
ist dann wie verlangt kleiner als \(\varphi(15)\) und außerdem teilerfremd dazu.
Wie sieht dann ein passender Entschlüsselungsexponent \(d\) aus? Er muss
\( (7 \cdot d) \;\mathrm{mod}\; 8 = 1 \) erfüllen.
Der Wert \( d = 7 \) erfüllt den Zweck, denn \( e \cdot d = 7 \cdot 7 = 49 = 6 \cdot 8 + 1 \).
Zufällig ist also hier\( e = d \). Die folgende mit einem Tabellenkalkulationsprogramm
berechnete Tabelle zeigt, dass diese Entschlüsselung in diesem Beispiel funktioniert, solange man
mit dem zu verschlüsselnden Startwert \(K\) unterhalb
von \(N\) bleibt (danach wiederholt sich die Verschlüsselungsfunktion ja,
so dass die Entschlüsselung nur unterhalb von \(N\) funktionieren kann):
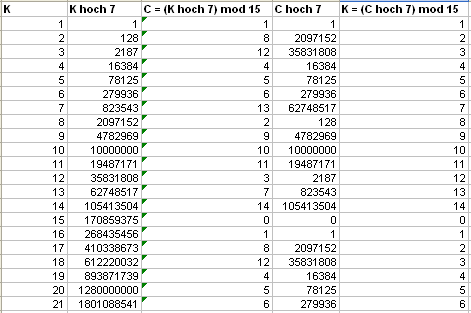
Bleibt die Frage: Warum funktionieren die obigen Ver- und Entschlüsselungs-Formeln eigentlich? Auf Anhieb ist das nämlich keineswegs zu sehen! Tasten wir uns also schrittweise heran: Verschlüsseln ging mit \[ C = K^e \;\mathrm{mod}\; N \] Setzen wir dies in die Entschlüsselungsformel \[ K = C^d \;\mathrm{mod}\; N \] ein, so folgt \begin{align} K &= C^d \;\mathrm{mod}\; N = \\ &= (K^e \;\mathrm{mod}\; N)^d \;\mathrm{mod}\; N = \\ &= K^{ed} \;\mathrm{mod}\; N \end{align} wobei wir im letzten Schritt wieder die Eigenschaften der Multiplikation modulo \(N\) verwendet haben, die wir von oben schon kennen: Es ist egal, ob man in Zwischenprodukten oder erst am Schluss ein möglichst großes Vielfaches von \(N\) abzieht, denn beim Multiplizieren erzeugen Vielfache von \(N\) nur andere Vielfache von \(N\), die aber am Schluss sowieso alle wegfallen.
Das obige Ver- und Entschlüsselungsverfahren funktioniert also, wenn die Formel \[ K = K^{ed} \;\mathrm{mod}\; N \] gilt. Schreiben wir auch diese Formel noch etwas um, indem wir die Bedingung \[ (e \cdot d) \;\mathrm{mod}\; \varphi(N) = 1 \] schreiben als \[ (e \cdot d) = b \cdot \varphi(N) + 1 \] mit einer passenden natürliche Zahl \(b\) (inclusive Null). Damit ist \begin{align} & \quad \; K^{ed} \;\mathrm{mod}\; N = \\ &= K^{b \cdot \varphi(N) + 1} \;\mathrm{mod}\; N = \\ &= K \cdot (K^{\varphi(N)})^b \;\mathrm{mod}\; N = \\ &= K \cdot (K^{\varphi(N)} \;\mathrm{mod}\; N )^b \;\mathrm{mod}\; N = \\ &=: (*) \end{align} Nun kommt der entscheidende Schritt: Nach dem Satz von Euler gilt für teilerfremde Zahlen \(K\) und \(N\) die Beziehung
|
Satz von Euler: \[ K^{\varphi(N)} \;\mathrm{mod}\; N = 1 \] |
Die Beweisskizze dazu kommt gleich. Das können wir oben einsetzen und erhalten \begin{align} (*) &= K \cdot 1^b \;\mathrm{mod}\; N = \\ &= K \;\mathrm{mod}\; N = \\ &= K \end{align} denn \(K\) muss kleiner als \(N\) sein (sonst funktioniert die Entschlüsselung nicht). Die Formel \[ K = K^{ed} \;\mathrm{mod}\; N \] ist damit bewiesen, d.h. das RSA-Verfahren funktioniert.
Man kann sich sogar überlegen, dass \(K\) nicht unbedingt teilerfremd zu \(N\) sein muss, damit das RSA-Verfahren funktioniert – wir lassen diese Bedingung trotzdem hier stehen, denn man kann die Primzahlen \(p\) und \(q\) immer groß genug wählen, so dass jedes zu kodierende \(K\) kleiner als \(p\) und \(q\) und somit teilerfremd zu \(N = p \cdot q\) ist.
Und nun kommen wir wie versprochen zur Beweisskizze des Satzes von Euler, der ja den Kern der obigen Argumentation bildet:
(die hier vorgestellte Beweißkizze findet man verkürzt in Wikipedia: Satz von Euler). Schauen wir uns die sogenannte multiplikative Gruppe modulo N ( prime Restklassengruppe) an, die wir oben bereits kurz erwähnt und mit \( \mathbb{Z}_N^* \) bezeichnet hatten. Diese Gruppe besteht aus allen natürlichen Zahlen von \(1\) bis \(N\), die teilerfremd zu \(N\) sind (wobei 1 als teilerfremd zu \(N\) zählt). Von oben wissen wir bereits, dass es \( \varphi(N) \) dieser teilerfremden Zahlen gibt. Beim Beispiel \( N = 15 = 3 \cdot 5 \) hätten wir also \[ \mathbb{Z}_{15}^* = \{ 1, 2, 4, 7, 8, 11, 13, 14 \} \] d.h. alle Vielfachen von \(3\) und \(5\) lassen wir weg. Damit enthält \( \mathbb{Z}_{15}^* \) insgesamt 8 Elemente, so wie es \( \varphi(15) = 2 \cdot 4 = 8 \) angibt.
Wir können diese Gruppe wieder mit unserem Rad von oben darstellen.
Dabei lassen wir jetzt aber alle Speichen weg, die nicht teilerfremd
zu \(N = 15\) sind:
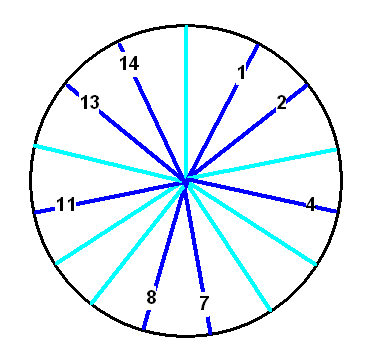
Als Gruppenoperation (schreiben wir sie als \( \circ \) ) nehmen wir die übliche Multiplikation, aber Modulo \(N\), d.h. es wird noch ein möglichst großes Vielfaches von \(N\) abgezogen: \[ a \circ b := (a \cdot b) \;\mathrm{mod}\; N \] Nun müssen wir natürlich zunächst nachweisen, dass diese Gruppenoperation die Eigenschaften aufweist, die sie haben muss (siehe z.B. Wikipedia: Gruppentheorie ; kann man auch gerne einfach glauben und überspringen):
Kann \begin{align} a \circ b &= (a \cdot b) \;\mathrm{mod}\; N = \\ &= a b - i N \end{align} (mit einer passenden natürlichen Zahl \(i\)) einen gemeinsamen Teiler (beispielsweise \(p\)) mit \(N\) haben (dann würde eine Zahl jendeits der Gruppe entstehen, was nicht sein darf)? Falls ja, dann wäre \( a \circ b \) ein Vielfaches dieses Teilers \(p\), d.h. es gibt eine natürlich Zahlen \(j\), so dass \[ a b - i N = j p \] ist. Außerdem wäre auch \(N\) ein Vielfaches von \(p\), d.h. es gibt eine natürliche Zahl \(k\) mit \[ N = k p \] Wenn wir dieses \(N\) oben einsetzen, so ergibt das \[ a b − i k p = j p \] oder umgestellt \[ a b = j p + i k p = (j + i k) p \] d.h. auch \(ab\) müsste ein Vielfaches des gemeinsamen Teilers \(p\) mit \(N\) sein. Das kann aber nicht der Fall sein, denn \(a\) und \(b\) haben als Elemente von \(\mathbb{Z}_N^*\) beide keinen gemeinsamen Teiler mit \(N\), sind also keine Vielfache eines solchen Teilers \(p\), so dass auch ihr Produkt kein Vielfaches eines solchen Teilers \(p\) sein kann.
Fazit: Die Annahme muss falsch sein, d.h. \( a \circ b \) kann keinen gemeinsamen Teiler mit \(N\) haben. Die \(\mathrm{mod}\; N\)-Operation sorgt außerdem dafür, dass die Zahl kleiner als \(N\) bleibt. Damit ist \( a \circ b \) wieder ein Element von \(\mathbb{Z}_N^*\), d.h. die Abgeschlossenheit ist erfüllt.
Anschaulich bedeutet die Abgeschlossenheit im obigen Rad-Bild: Wenn man das Gummiband, das die Speichen-Nummerierung enthält, um das \(a\)-fache drehnt und \(a\) dabei einer dunkelblauen Speichennummer entspricht, dann landen die Zahlen der dunkelblauen Speichen beim Aufwickeln wieder über dunkelblauen Speichen.
Dass das Assoziativgesetz (Klammergesetz) \[ a \circ (b \circ c) = (a \circ b) \circ c \] gilt, wissen wir bereits von oben: Vielfache von \(N\) werden durch das Multiplizieren mit anderen natürlichen Zahlen immer nur zu anderen Vielfachen von \(N\), die am Schluss wegen \(\mathrm{mod}\; N\) sowieso alle wieder abgezogen werden. Man kann sie also auch vorher jederzeit in den Klammern schon wegnehmen, also auch in der Klammer \(\mathrm{mod}\; N\) bilden.
Die ganz normale natürliche Zahl \( 1 \) ist das neutrale Element, d.h. \[ a \circ 1 = 1 \circ a = a \]
Es muss zu jeder Zahl \(a\) aus der Gruppe eine Zahl \(a'\), aus der Gruppe geben, so dass \[ a \circ a' = a' \circ a = 1 \] ist. Die Zahl \(a'\) ist dann das inverse Element zu \(a\).
Eine Vorbemerkung: Das inverse Element ist der Grund dafür, warum die Gruppe nur Zahlen enthalten darf, die keinen gemeinsamen Teiler mit \(N\) haben. Wäre beispielsweise eine Zahl \(a\) dabei, die den Teiler \(p\) mit \(N\) gemeinsam hat, so ergäbe jede Multiplikation dieser Zahl mit einer anderen Zahl \(b\) ein Vielfaches des Teilers \(p\), und die \(\mathrm{mod}\; N\)-Operation zieht davon dann ein Vielfaches von \(N\) (und damit ein Vielfaches von \(p\)) ab, so dass am Schluss ein Vielfaches von \(p\) oder aber Null übrig bleibt. Also ist \( a \circ b \) ein Vielfaches des Teilers \(p\) oder aber Null und damit niemals gleich \(1\) (denn \(p\) soll ja ein nicht-trivialer Teiler größer als \(1\) sein). Zu \(a\) gäbe es also kein inverses Element.
Gibt es nun zu jeder Zahl \(a\) aus der Gruppe ein passendes inverses Element \(a'\) in der Gruppe? Ja, und man es mit Hilfe des erweiterten euklidischen Algorithmus auch explizit berechnen. Wie das geht, wird im Anhang am Ende dieses Kapitels dargestellt.
Wir wissen also jetzt, dass \(\mathbb{Z}_N^*\) eine endliche Gruppe ist, und können das beim Beweis verwenden. Dazu nehmen wir irgendein festes \(K\) aus \(\mathbb{Z}_N^*\) heraus und multiplizieren alle Elemente von \(\mathbb{Z}_N^*\) mit diesem festen \(K\) (wobei wir natürlich noch \(\mathrm{mod}\; N\) anwenden). Da das genau die Gruppenoperation ist, entsteht so jeweils wieder ein Element von \(\mathbb{Z}_N^*\).
Es entsteht sogar für jedes Startelement ein anderes Ergebniselement, denn wenn zwei Ergebniselemente \( K \circ a \) und \( K \circ b \) gleich wären, so kann man mit dem inversen Element von \(K\) multiplizieren (wie immer \(\mathrm{mod}\; N\)) und erhält \(a = b\), d.h. nur gleiche Startelemente ergeben auch gleiche Ergebniselemente.
Die Gruppenmultiplikation mit \(K\) vertauscht also lediglich die Elemente von \(\mathbb{Z}_N^*\). Schauen wir uns das an unserem Beispiel \(\mathbb{Z}_{15}^*\) mit \( K = 2 \) an: \[ \{ 1, 2, 4, 7, 8, 11, 13, 14 \} \] \[ \downarrow \; 2 \circ \] \[ \{ 2, 4, 8, 14, 1, 7, 11, 13 \} \] Das kann man auch sehr schön an unserem ersten Rad-Bild weiter oben erkennen, bei dem die Multiplikation mit \(4\) (modulo \(15\)) zu einer Umsortierung der Speichennummern führt.
Was geschieht nun, wenn wir alle Ergebniselemente der unteren Zeile miteinander multiplizieren? Nun, dann enthält dieses Produkt alle Startelemente von \(\mathbb{Z}_{15}^*\) (obere Zeile), nur in anderer Reihenfolge. Bezeichnen wir die Elemente von \(\mathbb{Z}_{15}^*\) mit \(r_i\) , wobei \(i\) von \(1\) bis \( \varphi(N) \) läuft (denn die Menge enthält ja \( \varphi(N) \) Elemente). Die mit \(K\) gruppenmultiplizierten Elemente sind dann \( K \circ r_i \) und für das (normale) Produkt gilt: \[ r_1 \cdot r_2 \cdot \, ... \, \cdot r_{\varphi(N)} = \] \[ = (K \circ r_1) \cdot (K \circ r_2) \cdot \, ... \, \cdot (K \circ r_{\varphi(N)}) \] denn die Faktoren \( K \circ r_i \) umfassen zusammen alle Elemente \( r_i \) , nur in anderer Reihenfolge.
Nun können wir auf beiden Seiten \(\mathrm{mod}\; N\) anwenden und so aus der normalen Multiplikation die Gruppenoperation machen. Da diese kommutativ ist, dürfen wir die Faktoren rechts vertauschen und so alle Faktoren \(K\) nach rechts ziehen. Da \(K\) insgesamt \varphi(N) mal im Produkt vorkommt, entsteht so: \[ r_1 \circ r_2 \circ \, ... \, \circ r_{\varphi(N)} = \] \[ = (K \circ r_1) \circ (K \circ r_2) \circ \, ... \, \circ (K \circ r_{\varphi(N)}) = \] \[ = r_1 \circ r_2 \circ \, ... \, \circ r_{\varphi(N)} \circ (K^{\varphi(N)} \mathrm{mod}\; N) \] Da es zu jedem \(r_i\) ein inverses Element gibt, können wir auf beiden Seiten mit dem Produkt aller inversen Elemente gruppenmultiplizieren und so das Produkt der \(r_i\) entfernen. Übrig bleibt: \[ 1 = K^{\varphi(N)} \mathrm{mod}\; N \] Das ist genau der Satz von Euler. Der Beweis war gar nicht so schwer, wenn man die Gruppenstruktur von \(\mathbb{Z}_N^*\) verwendet, wobei der entscheidende Punkt die Existenz der inversen Elemente ist. Letztlich haben wir in dem obigen Beweis gezeigt, dass bei einer endlichen Gruppe mit \(m\) Elementen das \(m\)-fache Gruppenprodukt eines Elementes mit sich selbst gleich \(1\) (dem neutralen Element) ist. Das ist ein allgemeiner Satz aus der Theorie endlicher Gruppen, und der Satz von Euler ist lediglich die Anwendung dieses Satzes auf die Gruppe \(\mathbb{Z}_N^*\), wobei dann \( m = \varphi(N) \) ist.
Wie steht es mit der Sicherheit des RSA-Verfahrens? Das RSA-Verfahren ist sicher, solange es mit den verfügbaren Computern und Algorithmen in der Praxis aussichtslos ist, aus der Kenntnis des öffentlichen Schlüssels \(N\) die beiden Primfaktoren \(p\) und \(q\) zu berechnen, also \(N\) in \(p\) mal \(q\) zu zerlegen und damit das Faktorisierungsproblem für große \(N\) zu lösen. Damit hatten wir uns bereits in Kapitel 5.8 genauer beschäftigt. Bis heute ist kein Algorithmus bekannt, der das Faktorisierungsproblem auf einem gewöhnlichen Computer in polynomialer Zeit löst, so dass die Lösungszeit nur polynomial mit der Größe von \(N\) wächst. Daher gilt das RSA-Verfahren als sicher, wenn man für die Primzahlen \(p\) und \(q\) Zahlen mit mehreren hundert Dezimalstellen verwendet. Für den Verschlüsselungsexponenten \(e\) verwendet man häufig die Primzahl \( e = 2^{16} + 1 = 65537 \). Im Normalfall ist diese Primzahl dann kein Teiler von \(\varphi(N)\), so wie verlangt. Diese Zahl für \(e\) ist groß genug, um ein Knacken der Verschlüsselung zu verhindern, aber zugleich klein genug, um eine noch relativ effiziente Verschlüsselung zu erlauben.
Auf einem Quantencomputer gibt es dagegen einen polynomialen Faktorisierungs-Algorithmus: den Shor-Algorithmus (siehe Kapitel 5.8 ). Wenn es also eines Tages gelingt, brauchbare Quantencomputer zu bauen, die große Zahlen in vernünftiger Zeit faktorisieren können, dann wäre das RSA-Verfahren für die Verschlüsselung damit unbrauchbar geworden. Dasselbe gilt, falls doch noch jemand einen polynomialen Faktorisierungsalgorithmus für heutige Computer findet – es ist nämlich nicht bewiesen, dass es keinen solchen Algorithmus gibt, auch wenn heute fast jeder davon ausgeht.
Im realen Leben verwendet man das RSA-Verfahren meist nicht für die Verschlüsselung längerer Texte, denn es ist etwa 1000-mal langsamer als die weiter oben beschriebenen DES und AES-Verfahren, die aber als symmetrische Verfahren einen geheimen Schlüsselaustausch brauchen. Genau für diesen Schlüsselaustausch kann man aber nun das RSA-Verfahren verwenden und dann anschließend mit dem schnelleren AES-Verfahren längere Texte ver- und entschlüsseln. Auch komplexere Mischverfahren werden in der Praxis angewendet. Ein Beispiel ist das Pretty-Good-Privacy-Verschlüsselungsverfahren, das man beispielsweise für Emails anwenden kann.
Gibt es ein absolut sicheres Verfahren, um einen geheimen Schlüssel (oder gar ein komplettes One-Time-Pad, siehe oben) zwischen zwei Parteien auszutauschen? Die Natur selbst könnte ein solches Verfahren zur Verfügung stellen, wenn man sich ihre Quanteneigenschaften zu Nutze macht. Schauen wir uns das am Beispiel verschränkter Teilchenpaare genauer an (es gibt hier auch andere Vorgehensweisen):
Aus Kapitel 5.8 wissen wir, wie ein Quantensystem aus zwei Teilchen beschrieben werden kann: mit Hilfe einer Tabelle, die die möglichen Messwerte für beide Teilchen gemeinsam auflistet und die zu jeder Messwertkombination einen Pfeil enthält. Dieser Pfeil ist die Wahrscheinlichkeitsamplitude für die jeweilige Messwertkombination. Seine quadrierte Länge gibt die Wahrscheinlichkeit dafür an, die zugehörige Messwertkombination für beide Teilchen bei einer Messung vorzufinden. Die Pfeilorientierungen für die verschiedenen Messwertkombinationen relativ zueinander werden bei sogenannten Interferenzen wichtig, d.h. wenn mehrere Messwertkombinationen als ununterscheidbare Möglichkeiten zu einem anderen Messergebnis beitragen (man denke an das berühmte Doppelspalt-Experiment).
Verschränkung bedeutet nun, dass es Korrelationen im Verhalten der beiden Teilchen gibt:
das Verhalten des einen Teilchens hängt vom Verhalten des anderen Teilchens ab und umgekehrt.
Es gibt sogar die Möglichkeit, dass sich beide Teilchen genau entgegengesetzt
zueinander verhalten, wie die folgende Tabelle zeigt (die uns schon öfter begegnet ist):
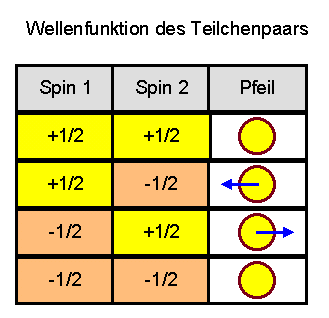
Man kann nun dieses entgegengesetzte Verhalten von Teilchenpaaren dazu verwenden,
um einen geheimen Schlüssel für zwei Partner zu erzeugen (es gibt auch andere Verfahren,
die mit nur einem Teilchen arbeiten, aber die wir wollen wir hier nicht betrachten).
Nehmen wir dazu eine Teilchenquelle, die solche entgegengesetzten Teilchenpaare erzeugt,
wobei das eine Teilchen jeweils vom ersten Partner und das zweite Teilchen vom zweiten Partner
aufgefangen und sein Spin von beiden Partnern in derselben Richtung gemessen wird
(sagen wir in z-Richtung). Das kann man beispielsweise durch ein Magnetfeld
in diese Richtung machen, wobei das Teilchen dann je nach Spinwert entweder nach oben oder nach
unten abgelenkt wird, wie das folgende Bild zeigt:
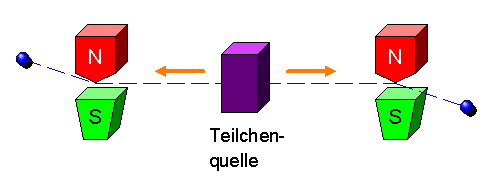
Statt Teilchen mit Spin 1/2 und Magnetfelder kann man auch Photonen und Polarisationsfilter verwenden. Das wäre nur eine andere technische Umsetzung – das dahinterstehende Prinzip bleibt dasselbe. Übrigens kann auch durchaus einer der beiden Partner die Teilchenquelle überwachen, d.h. es wird keine dritte Partei zum Erzeugen der Teilchenpaare benötigt.
Jeder Partner notiert sich nun für eine Reihe von Teilchenpaaren, ob das Teilchen nach oben oder nach unten abgelenkt wurde. Partner A notiert eine 1 bei Ablenkung nach oben und eine 0 bei Ablenkung nach unten, Partner B macht es umgekehrt. Auf diese Weise entsteht bei beiden Partnern dieselbe zufällige Bitfolge, die beide dann als Schlüssel oder als One-Time-Pad verwenden können. Die Bitfolge ist deshalb zufällig, weil das Verhalten des einzelnen Teilchens quantenmechanisch nicht festliegt: es wird rein zufällig nach oben oder unten abgelenkt. Das ist genau die prinzipielle Zufälligkeit in der Quantenmechanik. Mehr dazu siehe in Das Unteilbare, Kapitel 3.8 (John Steward Bell und die Suche nach verborgenen Informationen).
Ist dieser Zufallsschlüssel nun wirklich geheim, also nur den beiden Partnern bekannt, die auch die Messung durchführen, oder kann eine dritte Person ebenfalls versteckt eine Messung an den Teilchenpaaren durchführen und so den Schlüssel mitschreiben, ohne dass die beiden Partner etwas davon merken?
Wenn ein Spion heimlich mithören will, so muss er eine Messung an mindestens einem der beiden Teilchen durchführen. Er kann dabei ebenfalls den Spin in z-Richtung messen und das Teilchen dann an den entsprechenden Partner weiterleiten. Dieser merkt bei seiner Spinmessung in z-Richtung dann nichts davon, dass da jemand heimlich diesen Spin bereits vorher gemessen hat.
Allerdings wird durch die heimliche Messung durch den Spion
der Quantenzustand der beiden Teilchen unvermeidbar verändert, denn dieser Quantenzustand muss nun
die Information widerspiegeln, die durch die Messung gewonnen wurde.
Die obige Quantentabelle ist ungültig geworden.
Bei Spin-Messungen in z-Richtung
merken das die beiden Partner A und B allerdings nicht.
Messbar wird die Spionage und damit der veränderte Quantenzustand
erst, wenn die beiden Partner die Messrichtung
gegeneinander verdrehen, ohne dass der Spion das bei seiner Messung schon weiß.
So könnte Partner A weiter in z-Richtung messen, während Partner B zufällig bei jedem neuen Teilchenpaar zwischen
den folgenden drei Messrichtungen wechselt:
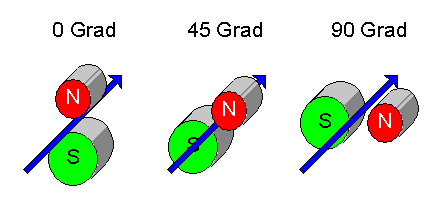
Nachdem beide Partner nun viele Teilchenpaare so gemessen haben, teilt Partner B seinem Partner A mit, wann er welche Messrichtung verwendet hat. Das kann er sogar öffentlich tun, denn der Spion kann sich nun nicht mehr mit seiner Messrichtung darauf einstellen – die Messungen sind vorbei. Damit können die beiden Partner nun ihre Messungen statistisch analysieren und die sogenannte Bellsche Ungleichung überprüfen (Details dazu siehe in Das Unteilbare, Kapitel 3.8 ).
Wenn nun ein Spion mitgemessen hat, so kann er den ursprünglichen Quantenzustand der beiden Teilchen nicht mehr rekonstruieren (würde er das tun, so wäre der Spin in seiner Messrichtung wieder ungewiss und er würde damit seine Messung wertlos machen). Der Spion kann zwar sicherstellen, dass die Teilchen sich in der von ihm gewählten Messrichtung weiter so verhalten, wie auch er es gemessen hat, so dass die beiden Partner in dieser Messrichtung dasselbe Ergebnis messen würden wie er. Er kann aber nicht sicherstellen, dass sich die Teilchen nach seinem Mitlauschen auch in allen anderen Messrichtungen noch statistisch so verhalten, wie sie es ohne sein Mitlauschen tun würden. Würde er beispielsweise versuchen, den Teilchen passende Informationen aufzuprägen, so würden diese Teilchen dann statistisch die Bellsche Ungleichung verletzen und sich somit anders verhalten als ohne sein Mitlauschen.
Der Spion schafft es also prinzipiell nicht, dass seine Information nützlich bleibt und zugleich sich die Teilchen so verhalten, als hätte er nicht gelauscht. Mit anderen Worten: Der Lauschangriff des Spions verändert die Mess-Statistik in verschiedene Raumrichtungen zwangsläufig so, dass die beiden Partner das bemerken. Er hinterlässt einen unvermeidlichen Fingerabdruck im statistischen Verhalten der Teilchen. Bei Messungen in zufällig gegeneinander verdrehte Messrichtungen verhalten sich unbelauschte Teilchenpaare statistisch anders als belauschte.
Wenn die beiden Partner nun nach der statistischen Analyse ihrer Messungen sicher sind, dass die Bellsche Ungleichung erfüllt ist und demnach niemand mitgehört haben kann, dann verwenden sie zur Schlüsselgenerierung einfach nur noch die Messergebnisse, bei denen sie beide zugleich in z-Richtung gemessen haben (über die verwendeten die Messrichtungen haben sie sich ja nach der Messung bereits gegenseitig informiert). Bei diesen Messungen in z-Richtung verhalten sich die beiden Teilchen dann entgegengesetzt zueinander, so dass beide Partner denselben Schlüssel generieren können.
Quantenkryptographie besitzt also Eigenschaften, die sie inhärent sicher machen können. Tatsächlich gibt es schon einige praktische Beispiele, in denen sie real angewendet wurde, auch wenn sie sicher noch in den Kinderschuhen steckt. Mehr dazu findet man beispielsweise in Wikipedia: Quantenkryptografie.
Der euklidische Algorithmus ist ein uralter Algorithmus, um den größten gemeinsamen Teiler zweier Zahlen zu bestimmen. Er war bereits im antiken Griechenland bekannt. Schauen wir uns dazu das folgende Beispiel an (stammt aus dem obigen Wikipedia-Link):
Wir wollen den größten gemeinsamen Teiler der beiden Zahlen \(44\) und \(12\) finden. Wenn wir uns beide Zahlen als Streckenlängen vorstellen, geht es also darum, eine (möglichst große) Teilstrecke zu finden, die \(n\)- bzw. \(m\)- mal in beide Streckenlängen hineinpasst. Nennen wir sie die ggT-Strecke (wobei ggT für größter gemeinsamer Teiler steht).
Schauen wir uns zunächst an, ob die kürzere der beiden Strecken (die 12) vielleicht schon die gesuchte ggT-Strecke ist, d.h. wie oft die kleinere Strecke \(12\) in die größere Strecke \(44\) hineinpasst und ob dabei ein Rest übrig bleibt. Das Ergebnis ist \[ 44 = 3 \cdot 12 + 8 \] (siehe die zweite Zeile in der Grafik etwas weiter unten). Also passt die \(12\) nicht ohne Rest in die \(44\) hinein, und wir haben damit neben den beiden bisherigen Strecken \(44\) und \(12\) eine weitere Strecke als Divisionsrest hinzubekommen, nämlich die \(8\).
Diese neue Rest-Strecke ist garantiert kleiner als die zuvor kürzeste Strecke (die \(12\)), denn sie entstand ja als Rest beim Einfügen von möglichst vielen \(12\)-er-Strecken. Die gesuchte ggT-Strecke (nennen wir sie \(g\) ) muss auch Teiler dieser neuen Rest-Strecke sein, denn nur dann kann sie zugleich Teiler von \(44\) und \(12\) sein. Das sieht man schon optisch in der Grafik etwas weiter unten, kann man aber auch leicht nachrechnen, denn wenn \( 44 = n g \) und \( 12 = m g \) ist, so folgt aus der obigen Gleichung \( n g = 3 m g + 8 \) und freigestellt nach dem Rest \( 8 = n g - 3 m g \) \( = (n - 3 m) g \).
Schauen wir uns daher analog zu oben wieder an, ob die neue Rest-Strecke (die \(8\)) vielleicht schon die gesuchte ggT-Strecke ist. Dazu reicht es, nachzusehen, ob sie Teiler der zuvor kürzesten Strecke \(12\) ist, denn dann wäre sie automatisch auch Teiler der längeren Strecke \(44\) (sie war ja gerade der Rest beim Auffüllen der \(44\) mit \(12\)-er-Strecken, siehe Bild unten). Rechnen wir nach: \[ 12 = 1 \cdot 8 + 4 \] (siehe dritte Zeile in der gleich folgenden Grafik). Es bleibt also wieder ein noch kleinerer Rest übrig: die \(4\). Mit dieser neuen Reststrecke können wir die obige Argumentation nun wiederholen: Passt sie in die bisher kürzeste Strecke (die \(8\)) mehrfach hinein, oder bleibt wieder ein Rest übrig? Wir haben Glück, denn \( 8 = 2 \cdot 4 \) ohne Rest. Die bisher kürzeste Reststrecke \(4\) teilt also die \(8\) und teilt damit auch die \(12\) und teilt damit auch die \(44\) (wie die obigen Gleichungen zeigen). Damit haben wir den größten gemeinsamen Teiler von \(44\) und \(12\) gefunden: die \(4\).
Das Verfahren funktioniert analog auch bei anderen Zahlen.
Da die Reststrecken in jedem Schritt garantiert immer kürzer werden,
endet das Verfahren spätestens bei der kürzest-möglichen Reststrecke \(1\)
(in diesem Fall wären die beiden Startzahlen teilerfremd).
Hier die versprochene Grafik, die das Verfahren noch einmal darstellt:

Nun zum
erweiterten euklidischen Algorithmus.
Dieser beruht darauf, dass man im obigen euklidischen Algorithmus
jede der dabei konstruierten Strecken
als ganzzahlige Linearkombination der beiden Ausgangsstrecken \(44\) und \(12\) schreiben kann.
So war die nächstkürzere Strecke (die \(8\)) als Rest beim Einfügen von \(12\)-en
in die 44 entstanden:
\[
44 = 3 \cdot 12 + 8
\]
(siehe zweite Zeile in der Grafik).
Das können wir natürlich nach dem Rest 8 freistellen:
\[
8 = 44 - 3 \cdot 12
\]
Analog ist es bei der nächstkürzeren Strecke \(4\), die als Rest beim Einfügen von
\(8\)-en in die \(12\) entstand:
\[
12 = 1 \cdot 8 + 4
\]
was wir nach dem Rest \(4\) freistellen können:
\[
4 = 12 - 1 \cdot 8
\]
Die \(8\) rechts hatten wir gerade als ganzzahlige
Linearkombination der beiden Ausgangsstrecken \(44\) und \(12\)
dargestellt (nämlich \(8 = 44 - 3 \cdot 12\)) und können dies hier einsetzen:
\begin{align}
4 &= 12 - 1 \cdot 8 = \\
&= 12 - 1 \cdot (44 - 3 \cdot 12) = \\
&= 12 - 1 \cdot 44 + 1 \cdot 3 \cdot 12 = \\
&= 4 \cdot 12 - 1 \cdot 44
\end{align}
Insbesondere die kleinste Strecke, also der größte gemeinsame Teiler \(4\), lässt sich
demnach als Linearkombnination der beiden Ausgangsstrecken
\(44\) und \(12\)
schreiben.
Nennen wir die beiden Ausgangsstrecken allgemein \(a\) und \(b\), so lässt sich deren
größter gemeinsamer Teiler \( \mathrm{ggT}(a,b) \) also schreiben als
\[
\mathrm{ggT}(a,b) = s a + t b
\]
mit passenden ganzen (auch negativen) Zahlen \(s\) und \(t\), die wir wie gerade gezeigt schrittweise
berechnen können.
Was hat das nun mit dem inversen Element in unserer multiplikativen Gruppe \(\mathbb{Z}_N^*\) zu tun? Nehmen wir dazu ein Element \(a\) aus dieser Gruppe und wenden den gerade gezeigten erweiterten euklidischen Algorithmus auf dieses Element \(a\) und den Gruppenmodul \(N\) an. Als Ergebnis erhalten wir den größten gemeinsamen Teiler \(\mathrm{ggT}(a,N)\) von \(a\) und \(N\) sowie die beiden ganzen Zahlen \(s\) und \(t\), so dass \[ \mathrm{ggT}(a,N) = s a + t N \] ist. Nun wissen wir aber bereits, dass \(a\) und \(N\) teilerfremd sind, denn so war die Gruppe \(\mathbb{Z}_N^*\) gerade definiert. Die beiden Zahlen \(a\) und \(N\) haben also außer der \(1\) keinen gemeinsamen Teiler, d.h. \(\mathrm{ggT}(a,N) = 1 \) und somit \[ 1 = s a + t N \] Wir hätten nun gerne, dass \(s\) aus der Gruppe \(\mathbb{Z}_N^*\) ist, aber das muss in unserer Rechnung nicht unbedingt so herauskommen. Wir verschieben es daher um ein passendes \(k\)-faches Vielfaches von \(N\), bis das Ergebnis (nennen wir es \(a'\)) zwischen \(1\) und \(N\) liegt: \[ a' := s + k N \] (\(k\) darf auch Null sein, falls nicht verschoben werden muss). Dieses \(a'\) ist das verschobene \(s\) (wir haben es extra nicht \(s'\) genannt, weil \(a'\) sich gleich als unser inverses Element zu \(a\) entpuppen wird). Wenn wir das nach \(s\) freistellen (also \(s = a' - k N\)) und oben einsetzen ergibt sich \begin{align} 1 &= s a + t N = \\ &= (a' - k N) a + t N = \\ &= a' a - k N a + t N = \\ &= a' a - (k a + t) N = \\ &= a' a - t' N \end{align} mit der ganzen Zahl \( t' = k a + t \). Da \(a'\) in den positiven Zahlenbereich gelegt wurde, muss \(t'\) positiv (oder Null) sein, d.h. es wird ein passendes Vielfaches von \(N\) abgezogen, so dass \( a' a \) danach \(1\) ergibt. Das ist genau unsere Gruppenmultiplikation, d.h. \[ a' \circ a = 1 \] Jetzt müssen wir nur noch überprüfen, ob \(a'\) auch wirklich in der Gruppe \(\mathbb{Z}_N^*\) liegt. Durch das Verschieben liegt es irgendwo von \(1\) bis \(N\), d.h. wir müssen nur noch sichergehen, dass \(a'\) teilerfremd zu \(N\) ist. Das aber wissen wir bereits von oben:
Wenn \(a'\) einen gemeinsamen Teiler \(p\) (größer als Eins) mit \(N\) hätte, so wäre \(a'\) und damit auch \( a' a \) ein Vielfaches dieses Teilers \(p\), und auch \(N\) und damit \( t' N \) wäre ein Vielfaches von \(p\), so dass die Differenz \( a' a - t' N \) ebenfalls ein Vielfaches des Teilers \(p\) wäre. Dann kann diese Differenz aber nicht gleich \(1\) sein, wie gefordert. Also ist \(a'\) teilerfremd zu \(N\) und liegt zudem im Bereich von \(1\) bis \(N\), ist also damit Element unserer Gruppe \(\mathbb{Z}_N^*\). Damit ist \(a'\) das gesuchte inverse Element zu \(a\), womit zugleich seine Existenz bewiesen ist.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 19 April 2023