Klassische Computer sind uns heute gut vertraut – fast jeder hat einen auf seinem Schreibtisch stehen. Abstrakt gesehen ist ein klassischer Computer eine Maschine, die Informationen mit Bits in seinem Speicher darstellt und diese über seinen Prozessor nach einem gegebenem Programm manipuliert. Der Prototyp für einen solchen Computer ist die Turingmaschine (siehe Kapitel 2.3 ).
Oft hört man von einem neuartigen Computertyp, der einem solchen herkömmlichen Computer weit überlegen sein soll: dem Quantencomputer. Ich möchte in diesem Kapitel versuchen, mit möglichst anschaulichen (aber dennoch präzisen) Mitteln zu erklären, was ein Quantencomputer ist und was er wirklich besser kann als ein üblicher Computer.
Um es gleich zu sagen: Große Quantencomputer, die es mit herkömmlichen Computern aufnehmen könnten, gibt es bis heute noch nicht. Bisher sind wir eher noch im Bereich der Grundlagenforschung, in der man versucht, noch relativ wenige Quantenbits (Qubits) physikalisch zu realisieren und zu manipulieren. Das physikalische Prinzip der Quantencomputer ist jedoch gut bekannt: die Quantenmechanik. Über die Grundlagen der Quantenmechanik habe ich bereits einige Kapitel geschrieben (siehe z.B. Die Symmetrie der Naturgesetze, speziell Kapitel 4.2 ). Die mathematischen Details braucht man aber für das Verständnis hier gar nicht. Es genügt, analog zu Das Unteilbare (Kapitel 3) mit Tabellen und Pfeilen zu arbeiten.
Was unterscheidet einen Quantencomputer von einem üblichen Computer? Wir hatten es bereits oben erwähnt: Ein Quantencomputer stellt Informationen nicht mit Bits dar, sondern mit Quantenbits (Qubits), oder genauer: mit einem Quantenregister. Ein solches Quantenregister mit \(n\) Qubits kann im Prinzip simultan für jede der \(2^n\) möglichen klassischen Bitkombinationen einen Eintrag enthalten und diese Einträge teilweise parallel verändern – er rechnet in diesem Sinn parallel mit allen möglichen Bitkombinationen. Genau darin liegt die theoretische Überlegenheit eines Quantencomputers. Allerdings liefert eine Messung des Quantenregisterzustandes immer nur eine bestimmte Bitkombination, was diesen Vorteil wieder zunichte machen kann. Man muss also die Information im Quantenregister vor der Messung geeignet aufbereiten, so dass man auch die gewünschte Information erhält – und das ist nicht ganz einfach. Letztlich führt es dazu, dass Quantencomputer nur bei bestimmten Rechnungen ihre Vorteile auch ausspielen können.
Um ein Qubit physikalisch zu realisieren, braucht man ein physikalisches Objekt, das (mindestens) zwei unterschiedliche Quantenzustände einnehmen kann. Diese Quantenzustände müssen möglichst leicht messbar und manipulierbar sein. Ein Beispiel wäre ein Atom, das zwei verschiedene Energiezustände annehmen kann, oder ein Teilchen mit Spin in einem Magnetfeld, bei dem die Spinrichtung parallel zum Magnetfeld eine andere Energie aufweist als die Spinrichtung antiparallel zum Magnetfeld.
Ein solches Objekt könnte zunächst auch einfach ein gewöhnliches Bit darstellen: Befindet sich das Objekt im höheren Energiezustand, so hätte das Bit beispielsweise den Wert 1, im niedrigeren Energiezustand dagegen den Wert 0.
In der Quantenmechanik ist es aber auch möglich, dass sich das Objekt weder ausschließlich in dem höheren noch in dem niedrigeren Energiezustand befindet. Würde man seine Energie messen, so würde man das Objekt mit einer gewissen Wahrscheinlichkeit entweder im höhreren oder im niedrigeren Energiezustand finden. Eine präzise Angabe seiner Energie wäre dann vor der Messung nicht möglich. Es ist sogar so, dass diese Information vor der Messung dann gar nicht existiert: das Objekt kennt seine eigene Energie selbst nicht, und es sind prinzipiell nur Wahrscheinlichkeitsaussagen darüber möglich. Mehr dazu siehe Das Unteilbare (Kapitel 3.8).
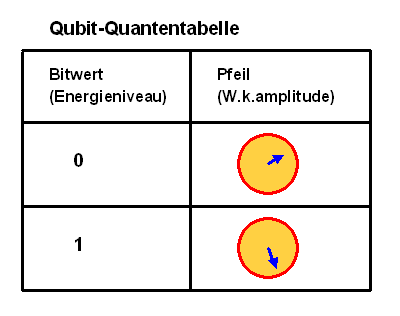
In der Quantenmechanik wird ein solches Objekt durch einen Quantenzustand beschrieben. In unserem Fall mit den beiden Energieniveaus ist das einfach eine Tabelle mit zwei Spalten und zwei Zeilen.
Die erste Spalte steht für die Messgröße Energie bzw. das dadurch repräsentierte Bit – hier tragen wir in den beiden Zeilen jeweils die möglichen Energiemesswerte ein, also das höhere und das niedrigere Energieniveau. Alternativ können wir auch einfach den zugehörigen Bitwert 1 oder 0 reinschreiben, für den das jeweilige Energieniveau steht. Die erste Spalte könnte demnach statt Energie aus klassischer Bitwert heißen. Genau genommen enthält die erste Spalte die quantenmechanischen Basiszustände, also die möglichen Messwertkombinationen für die gewählten Messgrößen – hier die Energie. Jede Zeile entspricht einem Basiszustand.
In die zweite Spalte tragen wir nun die sogenannte Wahrscheinlichkeitsamplitude ein:
das ist nichts anderes als ein Pfeil, der eine bestimmte Länge und einen bestimmten Drehwinkel
aufweist, analog zum Zeiger einer Uhr.
Der Pfeil repräsentiert eine komplexe Zahl. Die zweite Spalte ist also
die Darstellung des Quantenzustandes als Spaltenvektor in der Basis, wie sie die erste Spalte angibt.

Was bedeutet ein solcher Pfeil? Seine quadrierte Länge gibt an, wie wahrscheinlich es bei einer Energiemessung ist, den jeweiligen Energiezustand zu messen. Oder anders ausgedrückt: Sie gibt an, wie wahrscheinlich es ist, den dadurch repräsentierten Bitwert zu finden, wenn man nachschaut. Da die Summe aller Wahrscheinlichkeiten gleich Eins sein muss (irgendeinen Bitwert misst man garantiert), muss auch die Summe der quadrierten Pfeillängen gleich Eins sein. Entsprechend hat jeder einzelne Pfeil eine Länge unterhalb von Eins.
Neben der Länge ist auch die Ausrichtung der Pfeile wichtig, oder genauer: ihre relative Ausrichtung zueinander. Bei Energiemessungen merkt man davon nichts, sehr wohl aber bei anderen Messungen. Ein Beispiel: Wir betrachten einen Spin und messen, ob dieser parallel oder antiparallel zur z-Achse ausgerichtet ist (es gibt immer nur diese beiden Möglichkeiten – mehr dazu unten). Die beiden Pfeile in der Tabelle würden dann für diese beiden Möglichkeiten stehen, wobei die quadrierten Pfeillängen die entsprechenden Wahrscheinlichkeiten angeben. Die relative Ausrichtung der beiden Pfeile ist dabei egal. Man könnte nun aber auch messen, ob der Spin parallel oder antiparallel zu einer anderen Raumrichtung ausgerichtet ist, beispielsweise zur x-Richtung. Die Wahrscheinlichkeiten für diese beiden Möglichkeiten kann man aus den Pfeilen der Tabelle berechnen, wobei auch die relative Ausrichtung der Pfeile zueinander eingeht. Wie das gehen könnte, sehen wir weiter unten (Stichwort Bloch-Kugel und Drehung eines Spins).
Damit ist klar, dass ein Qubit-Zustand wesentlich mehr Informationen enthält als ein klassisches Bit, denn man muss zwei Pfeile angeben, also zwei Pfeillängen und den relativen Winkel zwischen den beiden Pfeilen. Man kann diese komplette Information aber nur dann ermitteln, wenn man viele verschiedene Messungen mit verschiedenen Messgrößen an vielen identischen Qubits durchführt. Eine einzige Messung liefert auch nur ein Bit an Information (z.B. hohe oder niedrige Energie), und nach der Messung ist das Qubit so verändert, dass es die alte Information nicht mehr enthält (wohl aber die durch die Messung gewonnene neue Information).
Falls Sie gerne einmal die mathematischen Details sehen wollen:
Die obige Quantenzustandstabelle lässt sich leicht in die übliche Schreibweise der Quantenmechanik übersetzen. Jede Zeile ergibt dabei einen Summanden, bei dem der Energiemesswert bzw. Bitwert der ersten Spalte den Basisvektor \( | 0 \rangle \) oder \( | 1 \rangle \) festlegt, und der Pfeil in der zweiten Spalte den komplexen Vorfaktor \(c_0\) bzw. \(c_1\) darstellt. So ergibt die oben dargestellte Tabelle den Zustandsvektor \[ | Q \rangle := c_0 \, | 0 \rangle + c_1 \, | 1 \rangle \] Der Buchstabe \(Q\) steht hier links für Qubit bzw. weiter unten auch für Quantenregister. Nicht verwirren lassen: Diese Schreibweise bedeutet genau dasselbe wie unsere Qubit-Tabelle. Sie ist für Rechnungen mit Quantenzuständen allerdings praktischer. Mehr dazu findet man in Die Symmetrie der Naturgesetze, Kapitel 4.5: Das mathematische Gerüst der Quantentheorie.
Den Quantenzustand des Qubits kann
man sich gut mit Hilfe der
Bloch-Kugel veranschaulichen.
Dazu drückt man die beiden Pfeile (komplexen Zahlen)
\(c_0\) und \(c_1\) durch reelle
Kugelkoordinaten-Winkel \(\theta\) und \(\varphi\) aus:
\begin{align}
c_0 &= \sin (\theta/2) \, e^{- i \varphi/2} \\
c_1 &= \cos (\theta/2) \, e^{+ i \varphi/2}
\end{align}
Dabei nimmt der Winkel \(\theta\) im Bogenmaß Werte zwischen \(0\) und \(\pi\) (also 180 Grad)
und der Winkel \(\varphi\) Werte zwischen \(0 \)und \(2\pi\) (also 360 Grad) an.
Die Verbindung zu den Pfeilen in der Tabelle kommt so zustande:
\( \sin (\theta/2) \) ist die Länge des Pfeils \(c_0\) und
\( \cos (\theta/2) \) ist die Länge des Pfeils \(c_1\).
Damit ist sichergestellt, dass die Summe der quadrierten Pfeillängen gleich Eins ist.
Man halbiert den Winkel \(\theta\) dabei, damit er Werte von \(0\) und \(\pi\) annehmen kann,
analog zu dem Winkel eines 3D-Vektors in Kugelkoordinaten (mehr dazu gleich).
Der Winkel \(\varphi\) ist wiederum der Winkel zwischen den beiden Pfeilen – nur auf diesen kommt es
ja an. Die absolute Ausrichtung der Pfeile ist egal, so dass die obige Darstellung einfach den Pfeil
\(c_0\) um \(\varphi/2\) nach rechts und den Pfeil
\(c_1\) um \(\varphi/2\) nach links dreht.
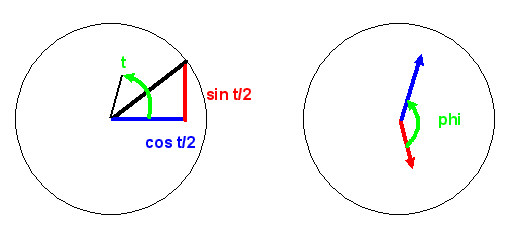
Rechts: Der Winkel \(\varphi\) (phi) ist der Winkel zwischen
beiden Pfeilen \(c_0\) (rot) und \(c_1\) (blau).
Er legt damit die relative Orientierung der beiden Pfeile zueinander fest.
Die absolute Orientierung spielt keine Rolle, d.h. man kann das Bild rechts insgesamt um einen
beliebigen Winkel drehen, ohne den Informationsgehalt des Qubits zu ändern.
Interpretiert man \(\theta\) und \(\varphi\) als Kugelkoordinaten-Winkel
eines Einheitsvektors im dreidimensionalen Raum, so
entspricht den beiden Pfeilen \(c_0\) und \(c_1\) zusammen genau ein Punkt auf der Einheitskugel,
auf den der Vektor zeigt
(hier auch Bloch-Kugel genannt).
Dabei ist \(\theta\) der Winkel zur z-Achse (gleichsam der Breitengrad)
und \(\varphi\) der Winkel am Äquator zur x-Achse (gleichsam der Längengrad).
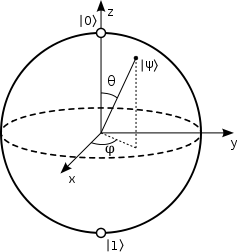
Quelle:
Wikimedia Commons File:Bloch sphere.svg, von Wikimedia-User Smite-Meister,
CC BY-SA 3.0.
Bei einem Teilchenspin, mit dem man ein Qubit ja physikalisch realisieren kann, hat das Bild der Bloch-Kugel auch eine ganz anschauliche Bedeutung. Wir können uns nämlich in einem bestimmten Sinn vorstellen, dass der Teilchenspin analog zur Drehachse eines rotierenden Körpers in die Richtung zeigt, die \(\theta\) und \(\varphi\) auf der Kugel angeben.
Allerdings kann man nicht einfach die Ausrichtung eines Spins im Raum messen, so wie man die Richtung einer klassischen Drehachse messen könnte. Man muss für eine Spinmessung erst eine Raumrichtung festlegen (z.B. durch ein Magnetfeld) und findet dann den Spin immer parallel oder antiparallel zu dieser gewählten Raumrichtung – der Quantenzustand des Spins sagt dann, mit welchen Wahrscheinlichkeiten das so ist.
Nehmen wir als Beispiel einen Spin, der zum Nordpol der Kugel ausgerichtet ist (also \(\theta = 0\), wobei \(\varphi\) beliebig ist, so dass wir es gleich Null setzen können). Dann ist \( c_0 = 0 \) und \( c_1 = 1 \), d.h. bei jeder Messung in z-Richtung finden wir, dass das Bit gesetzt ist und entsprechend der Spin parallel zur z-Achse liegt.
Kippt man den Spin komplett (wählt also \(\theta = \pi\) und wieder \(\varphi = 0\)) , so wird \( c_0 = 1 \) und \( c_1 = 0 \), d.h. das Bit ist nun immer gleich Null. So wollten wir es haben: Spin nach oben (in z-Richtung) bedeutet Bit = 1 und Spin nach unten bedeutet Bit = 0 (im obigen Bild ist es leider genau umgekehrt gewählt).
Was geschieht, wenn wir den zum Nordpol ausgerichteten Spin nicht komplett kippen, sondern ihn nur um den Winkel \(\theta\) von der z-Achse weg zur x-Achse hin kippen und dann in Äquatorebene um den Winkel \(\varphi\) nach links drehen, so dass eine Messung des Teilchenspins in diese neue Richtung diesen nun immer parallel zu dieser neuen Richtung finden würde? Durch das Drehen des Teilchenspins verändern sich \( c_0 \) und \( c_1 \). Man kann zeigen (siehe Die Symmetrie der Naturgesetze, Kapitel 4.8 ), dass sie nun durch die obigen Formeln gegeben sind, und zwar genau mit den Winkelwerten, um die der Spin gedreht wurde.
Eine Messung in z-Richtung würde daher den Spinzustand nun mal in und mal gegen die z-Richtung finden, so wie das die quadrierten Pfeillängen für die aktuellen \(\theta\) und \(\varphi\)-Werte angeben: parallel zur z-Richtung finden wir den Spin nun mit der Wahrscheinlichkeit \[ |c_1|^2 = (\cos (\theta/2))^2 \] und antiparallel mit der Wahrscheinlichkeit \[ |c_0|^2 = (\sin (\theta/2))^2 \] Auf der Bloch-Kugel entspricht "Spin in z-Richtung" dem z-Wert \(+1\) und "Spin gegen die z-Richtung" dem z-Wert \(-1\). Der Mittelwert der Spinmessungen in z-Richtung ergäbe demnach \[ (+ 1) \cdot (\cos (\theta/2))^2 + (- 1) \cdot (\sin (\theta/2))^2 = \] \[ = (1 + \cos \theta)/2 - (1 - \cos \theta)/2 = \cos \theta \] d.h. der Mittelwert der Spinmessungen in z-Richtung ist gerade die Projektion der gedrehten Spinrichtung auf die z-Achse (zu den Formeln siehe Wikipedia: Formelsammlung Trigonometrie ).
Nehmen wir die x- und y-Richtung hinzu: Würde man bei dem gedrehten Spinzustand sehr viele Messungen in x- , y- sowie in z-Richtung machen, so findet man den Spin mal parallel und mal antiparallel zu der vorgegebenen Richtung, aber die jeweiligen Mittelwerte für jede dieser drei Richtungen ergeben zusammen die Komponenten eines Vektors, der genau in die durch \(\theta\) und \(\varphi\) angegebene Richtung auf der Bloch-Kugel zeigt (dabei ist für die x- und y-Richtung auch der Winkel \(\varphi\) wichtig – Details lassen wir hier weg). Die Spinrichtung ist also eine Richtung, die den Mittelwerten vieler Messungen in verschiedenen Raumrichtungen entspricht. Wählt man diese Spinrichtung direkt als Messrichtung für den Spin aus, so findet man diesen immer parallel dazu. Mehr zum Thema Spin findet man in Das Unteilbare, Kapitel 3.8.
Für einen Computer benötigt man mehrere Bits, für einen Quantencomputer also mehrere Qubits – wir wollen von einem Quantenregister sprechen. Physikalisch kann man das beispielsweise durch mehrere Atome oder mehrere Spins in einem Magnetfeld realisieren. Zu jedem Atom oder Spin gehören dabei zwei Energieniveaus, die wir mit den Bitwerten 1 (für das höhere Energieniveau) und 0 (für das niedrigere Energieniveau) identifizieren.
Um den Quantenzustand eines Quantenregisters darzustellen, muss man die obige Qubit-Tabelle
passend erweitern: In die Felder der ersten Spalte tragen wir
alle Energiewert-Kombinationen der Quantenregister-Teilchen ein, oder gleichwertig dazu die entsprechenden Bit-Kombinationen
(Bitstring).
In der zweiten Spalte
tragen wir dann wieder die zugehörige
Wahrscheinlichkeitsamplitude ein, also einen Pfeil.
Für jede mögliche Bitkombination brauchen wir also eine Zeile, bei \(n\) Bits (\(n\) Atomen) also
\(2^n\) Zeilen.
Jeder Bitstring spezifiziert dabei
einen quantenmechanischen Basiszustand für das gesamte Quantenregister.
Die Spalte rechts ist also
die Darstellung des Quantenzustandes als Spaltenvektor in der gegebenen Basis, wie sie die Spalte links angibt.
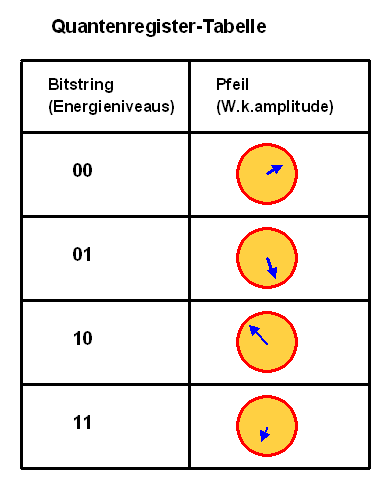
Der Pfeil in der zweiten Spalte hat nun analog zu oben die folgende Bedeutung: Seine quadrierte Länge gibt an, wie wahrscheinlich es bei einer Energieniveau-Messung aller Atome ist, die Energiezustands-Kombination in der Zeile zu messen – oder gleichbedeutend, die dadurch repräsentierte Bitwert-Kombination zu finden. Wieder muss die Summe aller Wahrscheinlichkeiten (quadrierten Pfeillängen) gleich Eins sein, so dass jeder einzelne Pfeil eine Länge unterhalb von Eins hat.
Auch die relative Ausrichtung der Pfeile zueinander ist wichtig. Manchmal trägt sie sogar die entscheidende Information und muss dann erst für eine Messung zugänglich gemacht werden (z.B. durch eine Quanten-Fouriertransformation, siehe unten).
Man sieht hier einen entscheidenden Unterschied zum gewöhnlichen Computer: Der Zustand eines klassischen Registers enthält genau eine Bitkombination. Das ist beim Quantenregister anders: Es kann für jede mögliche Bitkombination einen Pfeil enthalten, also bei \(n\) Bits \(2^n\) Pfeile. Die Zahl der Pfeile (und damit die vorhandene Informationsmenge) wächst also exponentiell mit der Zahl der Bits (Atome). In gewissem Sinn rechnet ein Quantencomputer parallel mit jeder möglichen Bitkombination – mehr dazu unten.
In der Literatur findet man hier oft den Ausdruck Verschränkung und sagt,
dass man einen verschränkten Zustand nicht als Produkt einzelner Qubit-Zustände
schreiben kann. Das bedeutet, dass man nicht einzelne Qubit-Tabellen hinschreiben kann
und durch entsprechende Pfeilmultiplikation (Drehstreckungen) die Pfeile
der Quantenregistertabelle erhält (die Details interessieren hier nicht).
Vereinfacht gesagt: Die Wahrscheinlichkeit für eine Bitkombination ist nicht das Produkt
von Einzelwahrscheinlichkeiten für die einzelnen Bits.
So kann ein Quantenregister mit zwei Bits in einem Zustand sein, bei dem
nur die beiden Bitkombinationen \(1 0\) und \(0 1\)
gemessen werden, während \(0 0\) und \(1 1\)
nicht vorkommen, siehe das folgende Bild:
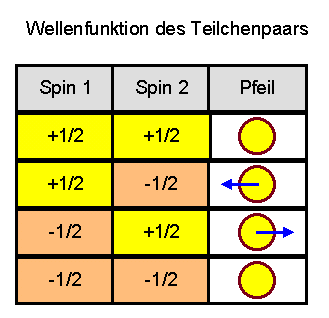
Jedes einzelne Bit kann in diesem Beispiel zufällig gleich 0 oder 1 sein, aber zusätzlich verhalten sich beide Bits entgegengesetzt zueinander: ist eines gleich 0, so ist das andere gleich 1 oder umgekehrt. Man sagt, die beiden Bits sind miteinander verschränkt, also miteinander untrennbar verflochten. Ein Quantenregister ist also mehr als eine Ansammlung von einzelnen Qubits! Die Atome bzw. Bits müssen als Gesamtheit betrachtet werden und es sind Korrelationen zwischen den Wahrscheinlichkeiten für die einzelnen Bits möglich.
Wie entsteht aus einem Quantenregister wieder ein gewöhnliches Register? Ganz einfach: Man lässt einen einzigen Pfeil in der Tabelle auf die Länge Eins wachsen und alle anderen Pfeile auf die Länge Null schrumpfen (sie verschwinden also; die Ausrichtung des Pfeils ist dabei egal). Genau das geschieht, wenn man die Bitbelegung (die Energieniveaus) des Quantenregisters durch eine Einzelmessung komplett bestimmt, also das Quantenregister ausliest. Nach der Messung sieht der Zustand des Quantenregisters genau so aus. Dabei ist die Zeile mit dem Pfeil die klassische Belegung des Registers.
Anmerkung:
Auch hier kann man die Quantenzustandstabelle leicht in die übliche Schreibweise der
Quantenmechanik übersetzen. Jede Zeile ergibt dabei
wieder einen Summanden, bei dem die Bitwert-Kombination
der ersten Spalte den Basisvektor festlegt
und der Pfeil der zweiten Spalte den komplexen Vorfaktor
darstellt:
\begin{align}
| Q \rangle
= &c_{0...00} \, | 0...00 \rangle + \\
+ &c_{0...01} \, | 0...01 \rangle + \\
+ &c_{0...10} \, | 0...10 \rangle + \\
+ &\, ... \, + \\
+ &c_{1...11} \, | 1...11 \rangle
\end{align}
Statt der Bitstrings (Binärstrings)
kann man auch die dadurch dargestellte natürliche Zahl verwenden:
\(0...00 = 0 \), \(0...01 = 1 \), \(0...10 = 2 \) usw..
Dies entspricht zugleich der Zeilennummer in der Tabelle, wenn man mit \(0\) bei der obersten Zeile anfängt.
Dann haben wir:
\[
| Q \rangle =
\sum_{j=0}^{N-1} \, c_j \, | j \rangle
\]
wobei \( N = 2^n \) die Anzahl Zeilen ist
(\(n\) war die Anzahl Bits im Register, also die Länge der Binärstrings).
In einem klassischen Computer bedeutet Rechnen, dass man die Bitwerte in einem Register verändert und so aus einer alten Information (z.B. zwei Zahlen) eine neue Information macht (z.B. deren Summe). Analog ist es auch beim Quantencomputer, nur dass man hier die Pfeile in der Tabelle verändert: Man streckt, staucht und dreht sie, wobei die Quadrate der Pfeillängen in Summe immer Eins ergeben müssen, denn die Summe aller Wahrscheinlichkeiten muss Eins bleiben. Wenn man also einen Pfeil verlängert, so müssen sich die anderen Pfeile entsprechend verkürzen. Drehungen dagegen können beliebig erfolgen. Mathematiker sprechen hier von einer unitären Operation.
In der Praxis erreicht man solche Veränderungen des Quantenregister-Zustandes beispielsweise durch Einwirkung von Magnetfeldern auf Teilchenspins oder durch Einstrahlung von Laserpulsen.
Eine Rechenoperation auf einem Quantenregister kann im Prinzip deutlich effektiver sein als eine gewöhnliche Rechenoperation auf einem normalen Register, denn es werden nicht nur \(n\) Bits verändert, sondern gleichzeitig bis zu \(2^n\) Pfeile. Man kann daher bestimmte Rechenalgorithmen auf einem Quantencomputer theoretisch wesentlich effektiver durchführen als auf einem normalen Computer. Prinzipiell lässt sich aber jeder Quantencomputer durch einen gewöhnlichen Computer simulieren, denn dieser muss ja nur die Pfeilveränderungen nachvollziehen. Was für einen normalen Computer prinzipiell nicht berechenbar ist, ist daher auch für einen Quantencomputer prinzipiell nicht berechenbar.
Beim klassischen Computer enthält der Prozessor einzelne Logikgatter (Gates), die ein oder zwei Bits als Eingang haben und ein Bit als Ausgang. Diese Gatter werden dann miteinander verschaltet und können so zusammen komplexere Aktionen auf den Bits des Registers ausführen.
Auch beim Quantencomputer gibt es die Idee, dass man elementare Operationen auf einigen wenigen (ein oder zwei) Qubits definiert und physikalisch realisiert (z.B. durch Manipulieren einzelner Atome über Magnetfelder etc.). In Analogie zum klassischen Computer stellt man diese elementaren Operationen oft durch sogenannte Quantengatter dar. Führt man mehrere solcher elementaren Operationen nacheinander auf verschiedenen Atomen (Qubits) aus, so lassen sich auch komplexere Manipulationen des Quantenregister-Zustandes erreichen. Das kann man mit Hilfe der Quantengatter auch durch einen formalen Quantengatter-Schaltplan graphisch darstellen.
Ein einfaches Beispiel für ein Quantengatter, das nur ein Qubit manipuliert,
ist das Hadamard-Gatter. Formal macht dieses Gatter
aus den beiden Pfeilen \(c_0\) und \(c_1\) die beiden
Pfeile
\begin{align}
c_0' &:= (c_0 + c_1) / \sqrt{2} \\
c_1' &:= (c_0 - c_1) / \sqrt{2}
\end{align}
Für die neuen Pfeile hängt man also die beiden
ursprünglichen Pfeile \(c_0\) und \(c_1\) aneinander,
wobei man bei \(c_1'\) den Pfeil \(c_1\)
zuvor umdreht. Dann wird noch mit \(1/\sqrt{2}\) gestaucht, damit die
Summe der quadrierten Pfeillängen gleich \(1\) bleibt.
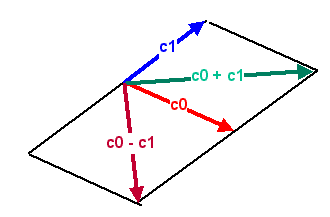
Wichtig ist, dass das Hadamard-Gatter aus einem klassischen Bitzustand einen überlagerten Qubit-Zustand macht. Das Hadamard-Gatter erzeugt also eine Verschränkung, was man später für die Initialisierung des Quantengatters gut gebrauchen kann. Ist z.B. das Qubit garantiert Eins (also \(c_0 = 0\) und \(c_1 = 1\), entsprechend dem Nordpol der Bloch-Kugel), so ist anschließend \( c_0' = 1/\sqrt{2} \) und \( c_1' = - 1/\sqrt{2} \). Die Pfeile sind also gleich lang (d.h. \( \theta = \pi/2\) = 90 Grad auf der Bloch-Kugel), aber entgegengesetzt gerichtet (d.h. \( \varphi = \pi \) = 180 Grad , den gemeinsamen Vorfaktor \(i\) kann man ignorieren). Der Nordpol der Bloch-Kugel landet also auf dem Äquator auf der negativen x-Achse. Analoge Überlegungen kann man für die anderen Punkte der Bloch-Kugel anstellen. Wer sich oben die Anmerkungen zur Spindrehung angesehen hat, der hat jetzt vielleicht eine Idee, wie sich das Hadamard-Gatter physikalisch realisieren lässt: durch Drehung eines Spins. So entspricht die Wirkung des Hadamard-Gatters genau der Drehung eines Spins von der z-Richtung in die negative x-Richtung.
Ein anderes wichtiges Ein-Qubit-Gatter ist das allgemeine Phasengatter. Dieses Gatter macht aus den Pfeilen \(c_0\) und \(c_1\) die Pfeile \begin{align} c_0' &:= c_0 \\ c_1' &:= c_1 \, e^{2 \pi i/m} \end{align} Mit dem \(c_0\)-Pfeil passiert also gar nichts, während der \(c_1\)-Pfeil um den Winkel \(2 \pi /m\) nach links gedreht wird, also um ein \(m\)-tel des Vollkreises (\(m\) ist dabei irgendeine natürliche Zahl). Der Winkel \(\varphi\) zwischen den beiden Pfeilen wächst also um den Winkel \(2 \pi /m\) an. Auf der Bloch-Kugel entspricht dies einer Rotation um den Winkel \(2 \pi /m\) um die z-Achse, d.h. der Qubit-Quantenzustand ändert sich analog zu einem Spinzustand, den man entsprechend um die z-Achse dreht.
Ein wichtiges zwei-Qubit-Quantengatter ist das CNot-Gatter (Controlled Not Gate). Dieses Gatter lässt die Pfeile in den ersten beiden Spalten der 2-Qubit-Tabelle (also zu den Bitkombinationen \( 0 0 \) und \( 0 1 \)) unverändert und vertauscht die beiden Pfeile in den beiden anderen Spalten \( 1 0 \) und \( 1 1 \)). Das erste Bit ist also gleichsam ein Kontroll-Bit: Nur wenn es gesetzt ist, werden die entsprechenden Pfeile für das zweite Bit vertauscht. Eine Liste der Quantengatter findet man unter Wikipedia: Liste der Quantengatter.
Was geschieht nun bei mehreren Qubits? Wie würde sich beispielsweise die Manipulation eines einzelnen Qubits auf den gesamten Quantenregisterzustand aus mehreren Qubits auswirken? Ganz einfach: Man fasst die Zeilen der Tabelle zu Zeilenpaaren zusammen, deren Binärstrings sich jeweils nur in dem zu manipulierenden Bit unterscheiden. Mit jedem dieser Zeilenpaare führt man nun die Operation so durch, wie man sie auch mit der zweizeiligen Qubit-Tabelle eines einzelnen Qubits durchführt. Damit wird die Veränderung des Qubits allen entsprechenden Pfeil-Paaren der Tabelle parallel in gleicher Weise aufgeprägt. Bei dem Hadamard-Gatter wäre das beispielsweise: \begin{align} c_{a0b}' &:= (c_{a0b} + c_{a1b}) / \sqrt{2} \\ c_{a1b}' &:= (c_{a0b} - c_{a1b}) / \sqrt{2} \end{align} wobei \(a\) und \(b\) für den jeweiligen Rest des Binärstrings in dem Zeilenpaar stehen (verschiedene Zeilenpaare unterscheiden sich dann in \(a\) oder \(b\) oder beiden). Bei dem allgemeinen Phasengatter wäre es noch einfacher: In allen Zeilen, in denen das zu manipulierende Qubit gleich Eins ist, wird der Pfeil um den Winkel \(2\pi/m\) nach links gedreht.
Analog geht man auch bei einem zwei-Qubit-Quantengatter vor, das zwei bestimmte Qubits eines Quantenregisters manipuliert: Man bildet Vierergruppen aus Binärstrings, die sich nur in den beiden manipulierten Bits unterscheiden, und verfährt mit diesen Gruppen wie mit der entsprechenden zwei-Qubit-Quantentabelle.
Man kann zeigen, dass man mit Manipulationen einzelner Qubits sowie mit der Manipulation von Qubit-Paaren über das CNot-Gatter in der Lage ist, jede mögliche Veränderung eines beliebigen Quantenregisters zu realisieren (siehe Wikipedia: Quantengatter).
Wie wir gesehen haben, führt die Manipulation eines (oder auch zweier) Qubits zu einer parallelen Änderung aller Pfeile einer Quantenregister-Tabelle. In diesem Sinn führt der Quantencomputer eine bestimmte Operation simultan für sämtliche Bitkombinationen aus. Das ist genau die Art von Parallelität, die bei ganz bestimmten Rechnungen (aber nicht bei allen) zu einer Überlegenheit des Quantencomputers über gewöhnliche Computer führt. Schauen wir uns nun die beiden bekanntesten Erfolgs-Beispiele an, und betrachten wir danach auch die Probleme, bei denen ein Quantencomputer vermutlich nicht helfen kann:
Stellen wir uns vor, wir wollen ein Zahlenschloss öffnen und suchen nach der richtigen Zahlenkombination. Oder wir haben eine Telefonnummer und suchen in einem riesigen Telefonbuch den passenden Namen dazu (wobei das Telefonbuch nicht nach den Telefonnummern sortiert ist). Oder allgemeiner: Wir haben eine große unsortierte Datenmenge vor uns und suchen nach einem bestimmten Datensatz darin. Wie gehen wir vor?
Es bleibt uns gar nichts anderes übrig, als nach und nach alle Möglichkeiten oder Datensätze durchzuprobieren, bis wir den richtigen gefunden haben. Auch ein klassischer Computer kann hier nichts anderes tun.
Ein Quantencomputer kann dagegen in gewissem Sinn alle Möglichkeiten gleichzeitig durchprobieren. Den entsprechenden Algorithmus nennt man Grover-Algorithmus. Schauen wir uns genauer an, wie dieser Algorithmus es schafft, den Datensatz schneller zu finden:
Zunächst einmal repräsentieren wir die verschiedenen Möglichkeiten durch entsprechende Binärstrings, d.h. wir nummerieren die Möglichkeiten binär durch. In einer Quantenregister-Tabelle entspricht also jede Zeile einer bestimmten Möglichkeit, die wir überprüfen wollen (überflüssige Zeilen streichen wir ggf. einfach weg).
Um mit allen Möglichkeiten gleichzeitig zu arbeiten, versehen wir das Quantenregister mit einem passenden Initialzustand: Jede Zeile der Tabelle enthält dabei denselben Pfeil, so dass alle Möglichkeiten mit gleicher Wahrscheinlichkeit gemessen würden. Die Pfeile sollen gleich orientiert sein (z.B. nach rechts), um den Initialzustand möglichst einfach zu halten. Man sagt auch, man muss die einzelnen Qubits miteinander verschränken.
Wie kann man diese Initialisierung erreichen? Das geht mit dem Hadamard-Gatter, das wir oben kennengelernt haben (also beispielsweise durch das Kippen einzelner Spins). Man startet mit einem klassischen Zustand, bei dem sich jedes Teilchen des Quantenregisters im energetisch tiefsten Zustand befindet. Jedes Bit ist also auf Null gesetzt – die Quantenregister-Tabelle enthält also nur in der ersten Zeile (entsprechend dem Binärstring \(0000...00\)) eine Pfeil der Länge Eins, den wir uns nach rechts ausgerichtet denken können. Dieser Zustand lässt sich leicht durch Energieentzug erreichen, denn er ist der energetische Grundzustand des Quantenregisters. Nun wendet man das Hadamard-Gatter der Reihe nach von hinten nach vorne auf jedes Qubit einzeln an. Schauen wir uns bei einem Zwei-Qubit-Register an, was dadurch geschieht (dabei ist \(c_{00}\) der Pfeil zum Binärstring \(00\) usw.):
Man kann sich überlegen, dass das auch bei mehr Qubits funktioniert. Der gewünschte Initialzustand lässt sich also aus dem Grundzustand durch Manipulation der einzelnen Qubits mit dem Hadamard-Gatter präparieren – man spricht auch von der Walsh-Hadamard-Transformation. Physikalisch kann man sich vorstellen, dass man zunächst mehrere Spins parallel in z-Richtung ausgerichtet hat und diese dann Spin für Spin um 90 Grad kippt.
Jetzt können wir mit der eigentlichen Rechnung loslegen. Nehmen wir an, die Bitkombination \(01\) repräsentiert die gesuchte Möglichkeit. Dann brauchen wir ein sogenanntes Orakel, d.h. es muss eine Möglichkeit geben, dass unser Quantenregister-Zustand etwas von dieser gesuchten Möglichkeit bemerkt, aber ohne dass eine klassische Messung durchgeführt wird – die Quantenregister-Tabelle soll also immer noch überall Pfeile haben.
Wie ein solches Orakel funktionieren könnte, wollen wir hier überspringen (Stichwort: wechselwirkungsfreie Messung, siehe Grovers Originalarbeit weiter unten). Wir wollen einfach nur festhalten, dass das Orakel den Pfeil in der entsprechenden Tabellenzeile umdreht. Wir haben in unserer Tabelle also jetzt vier Pfeile mit den Werten \begin{align} 00: \quad &1/2 \\ 01: \quad &-1/2 \\ 10: \quad &1/2 \\ 11: \quad &1/2 \end{align} stehen. Wichtig ist: Die Wahrscheinlichkeiten wurden dadurch nicht geändert, d.h. immer noch sind alle vier Möglichkeiten mit gleicher Wahrscheinlichkeit in unserem Quantenregister repräsentiert (denn dafür wird ja die quadrierte Pfeillänge verwendet). Wir müssen also eine andere Möglichkeit finden, das Minuszeichen messbar zu machen.
Die Details sind etwas länglich – wir wollen sie daher hier weglassen. Man kann jedenfalls mit Hilfe des Hadamard-Gatters sowie des Phasenverschiebungsoperators den durch das Orakel umgedrehten Pfeil am Mittelwert aller Pfeile spiegeln. In unserem Beispiel liegt dieser Mittelwert bei \[ (1/2 + (-1/2) + 1/2 + 1/2) / 4 = 1/4 \] Die Differenz zwischen diesem Mittelwert \(1/4\) und dem umgedrehten Pfeil \(-1/2\) lautet \(1/4 - (-1/2) = 3/4 \). Dieser Wert kommt bei der Spiegelung zum Mittelwert hinzu, d.h. aus \(-1/2\) wird \(1/4 + 3/4 = 1\). Die anderen Pfeillängen werden entsprechend reduziert, so dass die Summe aller quadrierten Pfeillängen gleich \(1\) ist. Das ist hier einfach, denn da wir ja schon einen Pfeil der Länge 1 haben, bleibt für die anderen Pfeile nichts übrig – sie sind Null. Unsere Quantengatter-Tabelle enthält also nur noch für den gesuchten Bitstring einen Pfeil und eine Messung würde diesen Bitstring daher jetzt garantiert ermitteln.
Bei mehr Qubits würde die Spiegelung am Mittelwert den Pfeil
des gesuchten Bitstrings ebenfalls verlängern und alle anderen verkürzen;
sie würden allerdings nicht auf Null schwinden.
Daher wendet man das Orakel und die Spiegelung am Mittelwert mehrfach an,
bis der Pfeil des gesuchten Bitstrings ungefähr die Länge \(1\) hat
(und alle anderen nahezu die Länge Null). Dafür sind bei \(N\) Bitstrings etwa
\(\sqrt{N}\) Wiederholungen nötig. Statt also beispielsweise
\( N = 1.000.000 \) Bitstrings auszuprobieren,
genügen etwa \(\sqrt{N} = 1000 \) Wiederholungen, um per Quantencomputer
die gesuchte Möglichkeit zu finden und so beispielsweise das Zahlenschloss zu öffnen
(sofern es dafür ein Orakel gibt).
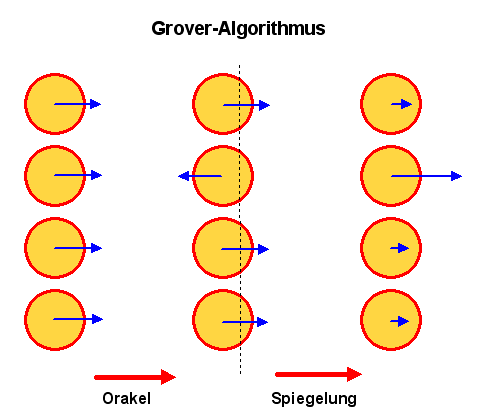
Mehr zum Grover-Algorithmus findet man beispielsweise in
Eine mögliche Rolle könnten Quantencomputer beim Knacken von gängigen Verschlüsselungen spielen, und solche Verschlüsselungen benutzt heute im Zeitalter des Internets fast jeder von uns. Moderne Verschlüsselungsverfahren basieren oft darauf, dass es auf normalen Computern zwar einfach ist, große Zahlen zu multiplizieren, aber umgekehrt sehr aufwändig ist, große Zahlen in Faktoren zu zerlegen (der Zeitaufwand wächst exponentiell mit der Anzahl Dezimalstellen der zu zerlegenden Zahl; mehr zu diesen Verschlüsselungsverfahren siehe das nächste Kapitel). Oder hätten Sie gewusst, dass die RSA-200 -genannte Zahl
aus den folgenden beiden Faktoren besteht:
und
Es war ein enormer Rechenaufwand erforderlich, um diese beiden Faktoren herauszubekommen (siehe Wikinews: Two hundred digit number factored, siehe auch Wikipedia: RSA numbers). Ein Quantencomputer könnte dies mit dem Shor-Algorithmus deutlich effizienter schaffen und damit die gängigen Verschlüsselungsverfahren in Frage stellen (der Zeitaufwand wächst nur noch ungefähr quadratisch mit der Anzahl Dezimalstellen).
Die Details der Rechnung sind etwas länglich – sie bestehen aus Rechnungen auf einem gewöhnlichen Computer und einem Rechenanteil für den Quantencomputer. wir verzichten hier auf die Details (siehe z.B. Daniel Truhn: Einführung in den Shor-Algorithmus). Einer der Quantenschritte ist wieder das Initialisieren des Quantenregisters, d.h. die Quantenregister-Tabelle (oder zumindest ein Teil davon) soll wieder in jeder Zeile einen Pfeil enthalten, so dass gleichzeitig mit allen Möglichkeiten gerechnet werden kann. Wie das geht, haben wir oben bereits gesehen. Nun werden wieder einzelne Qubits geignet manipuliert und dadurch viele Pfeile der Quantenregister-Tabelle simultan beeinflusst. Da die Zahl der Pfeile sich mit jedem neuen Qubit verdoppelt, kann man so bei genügend vielen Qubits mit einer enormen Menge an Pfeilen simultan rechnen und so auch sehr große Zahlen darstellen und manipulieren.
Das gewünschte Rechenergebnis ist dann zunächst in einer Dreh-Periodizitäten der Pfeile versteckt, d.h. von Zeile zu Zeile drehen sich die Pfeile annähernd um einen bestimmten Winkel. Dieser Winkel enthält die gewünschte Information. Leider ist er nicht direkt messbar, d.h. er muss noch in eine messbare Wahrscheinlichkeit (Pfeillänge) umgewandelt werden. Dazu dient die sogenannte Quanten-Fouriertransformation. Sie macht die Phaseninformationen des Quantenregister-Zustandes messbar.
Was macht diese Quanten-Fouriertransformation? Schauen wir uns dazu die Quantenregister-Tabelle für \(n\) Qubits an. Diese Tabelle hat \(2^n\) Zeilen, die jeweils die Pfeile für die einzelnen Bitkombinationen enthalten. Wir können die Zeilen der Tabelle durchnummerieren, wobei wir mit \(0\) beginnen: \( 0, 1, 2, \, ... \, , 2^n-1 \). Die Zeilennummer ist dann genau die Zahl, die durch die Bitkombination in der Zeile üblicherweise dargestellt wird (siehe die Anmerkung zur üblichen Quantenschreibweise oben).
Welcher Pfeil steht nun nach der Transformation in der Zeile Nummer \(k\)? Dazu nimmt man sich alle Pfeile der Tabelle, dreht jeden dieser Pfeile um einen bestimmten Winkel (kommt gleich) und hängt alle diese gedrehten Pfeile schließlich aneinander (man addiert sie). Zum Schluss staucht man das Ergebnis um den Faktor \(1/\sqrt{N}\), wobei \(N = 2^n\) die Anzahl Zeilen ist – das dient dazu, damit die Summe der quadrierten Pfeillängen wieder gleich 1 wird.
Nun zum Drehwinkel, um den wir den Pfeil in jeder \(j\)-ten Tabellenzeile drehen müssen, wenn wir insgesamt den neuen Gesamtpfeil für die \(k\)-te Tabellenzeile ausrechnen wollen: Dazu teilen wir den 360-Grad-Winkel in \(N\) gleiche Teile auf, wobei \(N\) die Gesamtzeilenanzahl war. Bei \(10\) Qubits (also \(N = 2^{10} = 1024 \approx 1000\)) ergäbe das beispielsweise etwa \(0,36\) Grad, also etwa ein-tausendstel-Vollkreis. Diesen Winkelanteil multiplizieren wir mit der Ergebnis-Zeilennummer \(k\). Für die Ergebniszeile \(500\) wäre der Winkelanteil also etwa \(180\) Grad, oder allgemein für die \(k\)-te Ergebniszeile \( 360 \, \mathrm{Grad} \cdot k/N \). Der Winkelanteil hängt also von der Ergebniszeile ab: Er ist sehr klein bei den ersten Ergebniszeilen und wächst schrittweise an, bis er für die letzte Ergebniszeite bei fast 360 Grad liegt. Und nun kommt es: Für die \(k\)-te Ergebniszeile drehen wir den Pfeil in der ersten Zeile um einen solchen Winkelanteil, den in der zweiten Anfangszeile um zwei solche Winkelanteile usw. und hängen am Schluss alle diese Pfeile aneinander.
Anschaulich ermittelt die Quanten-Fouriertransformation die Dreh-Periodizitäten der Pfeile auf die folgende Weise: Stellen wir uns vor, wir hätten es mit einer Quantentabelle zu tun, bei der die Pfeile von Zeile zu Zeile immer um denselben Winkel \( \Delta \varphi \) weitergedreht sind, ihre Länge aber weitgehend konstant ist. Das wäre dann eine Quantentabelle mit einer sehr deutlichen Dreh-Periodizität. Die Quantenfouriertransformation probiert nun ganz viele Zusatz-Drehwinkel aus und findet denjenigen heraus, der die Dreh-Periodizität \( \Delta \varphi \) am besten neutralisiert und die Pfeile so parallelisiert, dass ihre Summe einen möglichst langen Pfeil ergibt.
Genauer: Sie probiert für jede Zahl \(k\) aus, was geschieht, wenn man von Zeile zu Zeile einen weiteren Drehwinkel \( 360 \, \mathrm{Grad} \cdot k/N \) anwendet und am Schluss alle Pfeile aneinanderfügt. Schon bei relativ wenigen Qubits ist \(N\) sehr groß und es werden in sehr kleinen Schritten alle möglichen Zusatz-Drehwinkel ausprobiert. Wenn nun der Zusatz-Drehwinkel \( 360 \, \mathrm{Grad} \cdot k/N \) den Winkel \( \Delta \varphi \) passend neutralisiert (z.B. indem beide zusammen eine Volldrehung ergeben), so haben alle Pfeile nach der Drehung dieselbe Orientierung und ergeben einen entsprechend langen Ergebnispfeil für Zeile \(k\). Passt dagegen der Zusatz-Drehwinkel nicht gut zu \( \Delta \varphi \), dann löschen sich die Pfeile untereinander oft weitgehend aus. Im Ergebnis wird also in der Zeile \(k\) mit dem passenden Zusatz-Drehwinkel \( 360 \, \mathrm{Grad} \cdot k/N \) der längste Ergebnispfeil stehen, was sich in einer entsprechend hohen Messwahrscheinlichkeit ausdrückt. Wir wissen dann, dass die ursprünglichen Pfeile eine entsprechende Dreh-Periodizität aufgewiesen haben müssen.
Ein Quantencomputer macht dieses Drehen nicht für einzelne Pfeile, sondern simultan für viele Pfeile, indem er das allgemeine Phasengatter (siehe oben) auf einzelne Qubits anwendet: Wenn die Bitdarstellung von \(j\) an letzter Stelle eine 1 enthält, drehen wir um einen Winkelanteil von \( 360 \, \mathrm{Grad} \cdot k/N \), bei einer 1 an vorletzter Stelle drehen wir um zwei weitere Winkelanteile, bei einer 1 an drittletzter Stelle drehen wir um vier weitere Winkelanteile usw.. Zum Aneinanderhängen der Pfeile braucht man dann noch das Hadamard-Gatter (siehe oben). Insgesamt braucht man für die Quanten-Fouriertransformation also nur die Manipulation einzelner Qubits.
Hier das Ganze nochmal als Formel mit komplexen Zahlen:
\[ c_k' = \frac{1}{\sqrt{N}} \, \sum_{j=0}^{N-1} \, e^{k \cdot j \cdot 2\pi i/N} \, c_j \]
Dabei ist \( c_k' \) der Ergebnispfeil in Zeile \(k\) und \( c_j \) ist jeweils der ursprüngliche Pfeil in Zeile \(j\) . Man erkennt den Stauchfaktor (Normierungsfaktor) \( 1/\sqrt{N} \), die Drehung jedes Pfeils \( c_j \) um den Drehwinkel \( k \cdot j \cdot 2\pi i/N \) (Bogenmaß) durch die komplexe \(e\)-Funktion und das Aneinanderhängen der gedrehten Pfeile durch die Summe.
Schaut man sich die obigen beiden Beispiele (Grover- und Shor-Algorithmus) an, so stellt man fest, dass beide Quantenalgorithmen genau auf das zu lösende Problem zugeschnitten sind und dessen Struktur geschickt ausnutzen. Beim Faktorisieren großer Zahlen gelingt es dem Shor-Algorithmus dabei sogar, den exponentiell mit der Stellenzahl wachsenden Zeitaufwand in einen nur noch etwa quadratisch wachsenden Zeitaufwand abzumildern.
Das Problem, eine (große) Zahl in Faktoren zu zerlegen, gehört zur Problemklasse NP (nichtdeterministisch polynomial). Diese Problemklasse kennen wir bereits gut aus Kapitel 5.1: Die Komplexität von Problemen (ist P = NP ?). Hier kurz das Wesentliche:
Bei Problemen der Klasse NP ist es einfach, bei einem Lösungsvorschlag zu überprüfen, ob dieser das Problem wirklich löst. Dabei bedeutet einfach, dass der klassische Rechenaufwand zur Überprüfung nur polynomial mit der Problemgröße wächst (das erklärt das P = polynomial in NP). So kann man relativ leicht nachrechnen, ob zwei Faktoren zusammen die Ausgangszahl ergeben – man muss sie nur miteinander multiplizieren.
Ob es auch einfach ist, eine Lösung zu finden, bleibt bein NP-Problemen offen, d.h. es ist unklar, ob das Problem auch zur Problemklasse P gehört (das sind die Probleme, bei denen der Lösungsaufwand auf einem klassischen Computer nur polynomial mit der Problemgröße wächst). Man weiß nur, dass man Lösungsvorschläge relativ effizient auf einem klassischen Computer überprüfen kann. Man weiß aber nicht, ob es einen effizienten (also polynomialen) Weg gibt, eine Lösung zu finden (dann wäre P = NP), oder ob man schlimmstenfalls sogar alle möglichen Lösungen ausprobieren muss. Ob NP = P ist, das ist eines der großen ungelösten Probleme der Mathematik. Man weiß nur, dass P auf jeden Fall in NP enthalten ist, denn kann man eine Lösung effizient finden, so ist sie damit auch effizient geprüft. Die Vermutung ist, dass P kleiner als NP ist, d.h. dass es Probleme in NP gibt, für die es keinen effizienten Weg zum Finden der Lösung gibt – man muss im Wesentlichen raten! So gibt es bis heute keinen klassischen Computeralgorithmus, der eine große Zahl mit nur polynomial wachsendem Aufwand in Faktoren zerlegen kann. Genau darauf beruht die Sicherheit gängiger Verschlüsselungsmethoden.
Der Shor-Algorithmus kann nun große Zahlen auf einem Quantencomputer mit etwa quadratisch wachsendem Aufwand in Faktoren zerlegen – man sagt, das Faktorisierungsproblem gehört zur Klasse BQP (bounded-error quantum polynomial time). Wenn also ein Quantencomputer das NP-Problem der Faktorisierung in polynomialer Zeit lösen kann, wie sieht es dann mit den anderen NP-Problemen aus? Kann er sie ebenfalls effizient lösen, d.h. gehört jedes NP-Problem zu BQP?
Man vermutet heute, dass das nicht der Fall ist.
So ist der Shor-Algorithmus sehr speziell auf das Faktorisierungsproblem zugeschnitten,
lässt sich also nicht auf andere NP-Probleme übertragen.
Vielleicht findet man noch andere Spezialfälle in NP, die sich mit speziellen
Quantenalgorithmen effizient lösen lassen (die also zu BQP gehören),
aber es ist heute kein Ansatz erkennbar, der bei allen NP-Problemen greift.
Das gilt besonders für die schwierigsten NP-Probleme:
die NP-vollständigen Probleme (hat man für irgendein
NP-vollständiges Problem einen polynomialen Algorithmus, so kann man diesen
auf alle NP-Probleme übertragen).
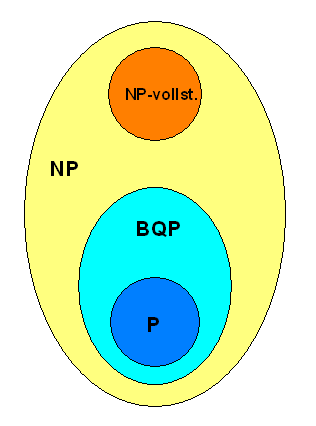
Im Prinzip könnte BQP auch Anteile außerhalb von NP haben, d.h. möglicherweise gibt es
Probleme außerhalb von NP, die ein Quantencomputer effizient lösen kann.
Ein Beispiel dafür ist bisher allerdings nicht bekannt.
Eines aber ist sicher: Alle dargestellten Problemklassen (P, NP, BQP) gehören
zu den PSPACE-Problemen, d.h. der benötigte Computerspeicher wächst nur polynomial
mit der Problemgröße.
Es ist also keineswegs einfach, die Parallelität eines Quantencomputers auch auszunutzen. Zwar kann dieser sehr viele mögliche Lösungen simultan durch die Pfeile der Quantenregister-Tabelle repräsentieren, aber er muss ohne klassische Messung alle diese Lösungen auch parallel testen können (vgl. das Orakel im Grover-Algorithmus oben), und er muss dann die entsprechende Veränderung der Pfeile in messbare Wahrscheinlichkeiten (Pfeillängen) umwandeln. Das gelingt bisher nur bei speziellen Problemen durch Algorithmen, die genau auf diese Probleme zugeschnitten sind. Quantencomputer können also wohl nur in bestimmten Fällen etwas bewirken. Ein sehr naheliegendes Anwendungsfeld könnten dabei Rechnungen im Bereich der Quantentheorie selbst sein, beispielsweise die Berechnung von Molekül- oder Festkörper-Eigenschaften – nicht unwichtig, wenn man an Nanotechnik oder das Design von Molekülen denkt.
Mehr dazu siehe auch Scott Aaronson: Die Grenzen der Quantencomputer, Spektrum der Wissenschaft, Juli 2008, S.90.
Warum ist es so schwierig, brauchbare Quantencomputer zu bauen? Dafür gibt es mehrere Gründe:
Ein Quantenregister muss man möglichst gut von seiner Umwelt abschirmen. Jede Störung verändert den Quantenzustand, wobei insbesondere die relative Ausrichtung der Pfeile zueinander sehr schnell unkontrolliert verändert wird – man spricht von Dekohärenz. Dabei wird ein Quantenzustand umso empfindlicher gegen Störungen, je mehr Teilchen (Qubits) er umfasst. Das entspricht auch unserer Alltagserfahrung: Makroskopische Objekte aus vielen Teilchen befinden sich praktisch nie in einem reinen Quantenzustand. Die unvermeidliche Wechselwirkung mit der Umgebung würde diesen sofort zerstören. Schrödingers Katze gibt es real nicht! Mehr dazu siehe auch Die Symmetrie der Naturgesetze, Kapitel 7.1 Was ist Entropie?, Anhang 2 (Dekohärenz).
Das Problem der Dekohärenz konnte durch sogenannte Quantenfehlerkorrekturen zumindest für kleine Quantenregister teilweise entschärft werden. Dabei wird Quanteninformation auf weitere Qubits verteilt, und zwar so, dass Messungen an diesen Qubits mögliche Veränderungen aufdecken und beseitigen können. Nachteil: Man braucht Quantenregister mit mehr Qubits.
Das möglichst gut isolierte Quantenregister muss man nun andererseits sehr präzise kontrollieren und manipulieren können, was eine intensive und sehr gut bekannte Wechselwirkung erfordert, die praktisch frei von zufälligen Einflüssen sein muss. Dabei muss die Manipulation während der Rechnung den Quantencharakter des Registers erhalten, darf also nicht wie eine klassische Messung wirken.
Beide Forderungen (Isolation und präzise Kontrolle) lassen sich oft nur für wenige Qubits und mit hohem Aufwand realisieren. Je mehr Qubits hinzukommen, umso empfindlicher wird der Quantenzustand und umso schwieriger wird die physikalische Umsetzung. Schauen wir uns an, wie weit man trotz dieser Schwierigkeiten heute bereits gekommen ist.
Eine Möglichkeit zur Realisierungen eines Quantencomputers ist das Einfangen von Teilchen in einer sogenannten Ionenfalle. Dabei werden elektisch geladene Atome (Ionen) in einem geeigneten elektromagnetischen Feld gleichsam im luftleeren Raum festgenagelt und wie an einer Perlenkette aufgereiht. Das ist dann das Quantenregister. Dabei repräsentiert ein niedriger Ion-Energiezustand den Bitwert Null, ein höherer Ion-Energiezustand den Bitwert Eins. Damit die Ionen in diesem Feld nicht schwingen, werden sie mit Lasern zusätzlich gleichsam gekühlt. Die Manipulation der Ionen (Qubits) erfolgt nun mit geeigneten Laserpulsen. Damit lassen sich Superpositionen (Verschränkungen) der beiden Energiezustände je Ion erzeugen. Auch das Auslesen funktioniert mit Lasern. Hört sich alles einfach an, ist aber in der Praxis äußerst anspruchsvoll und trickreich! Besonders aufpassen muss man, dass die Ionen möglichst gut von der Umwelt abgeschirmt sind, da es sonst zur Dekohärenz kommt und die Quanteninformation verloren geht.
Eine andere Möglichkeit bietet die Nuclear Magnetic Resonance (NMR) (Kernspinresonanzspektroskopie), die auf demselben Prinzip wie die Kernspintomographie aus der Medizin beruht. Dabei arbeitet man nicht mit einzelnen Teilchen wie oben, sondern mit makroskopischen Flüssigkeitsmengen, also mit beispielsweise 1020 Molekülen. Natürlich kann dann nicht jedes Molekül ein Qubit darstellen, sondern jedes Molekül ist selbst ein komplettes Quantenregister, wobei alle Moleküle möglichst synchron arbeiten. Die Spins der Atomkerne im Molekül bilden dabei die Qubits. Ein Molekül mit \(n\) Atomen kann also bis zu \(n\) Qubits zur Verfügung stellen. Die anderen identischen Moleküle in der Flüssigkeit liefern dann keine zusätzlichen Qubits, sondern sie arbeiten alle synchron – man hat es also gleichsam mit sehr vielen synchronen Quantenregistern zu tun, die alle dasselbe machen. Jedes Molekül ist gleichsam ein winziger Quantencomputer.
Ein von außen angelegtes Magnetfeld sorgt dafür, dass je Atomkern
zwei Energieniveaus entstehen: Eines mit Spin parallel und eines mit Spin antiparallel zum
Magnetfeld. Die Beeinflussung der Kernspins und damit der Qubits erfolgt dann
über kurze Radiofrequenzpulse mit passender Frequenz und Dauer im Mikrosekunden-Bereich.
Zusätzlich gibt es noch schwache Wechselwirkungen zwischen den verschiedenen Kernspins eines Moleküls,
so dass sich auch zwei-Qubit-Quantengatter realisieren lassen.

Quelle:
Wikimedia Commons File:NMR-Spectrometer.JPG, Andel Früh & Andreas Maccagnan (2006),
CC BY-SA 3.0.
Diese Vorgehensweise hat zwei Vorteile: Durch die große Teilchenmenge erhält man gut messbare Signale, wobei es keine Rolle spielt, wenn mal der eine oder andere Kernspin aus der Reihe fällt. Und: Kernspins sind von Natur aus durch die sie umgebende Elektronenhülle sehr gut von ihrer Umgebung isoliert, d.h. das Gezappel der Moleküle in der Flüssigkeit wirkt sich kaum auf die Kernspins aus.
Allerdings hat die NMR-Methode auch einen Nachteil: Da die Qubits des Quantenregister aus den verschiedenen Kernspins eines Moleküls besteht, braucht man umso größere Moleküle, je größer das Quantenregister ist. Dabei ist nicht jedes Molekül geeignet, und es ist nicht leicht, passende Moleküle mit genügend vielen brauchbaren Kernspins zu finden oder sogar speziell zu designen.
Es gibt noch viele weitere Ideen, wie man Quantencomputer physikalisch realisieren kann (supraleitende Qubits, optische Gitter kalter Atome, Quantenpunkte in Halbleitern, ... ). Große IT-Konzerne und internationale Forscherteams liefern sich hier ein Wettrennen, und es bleibt spannend, welche Durchbrüche sie auf diesem herausfordernden Forschungsgebiet noch erzielen werden.
© Jörg Resag, www.joerg-resag.de
last modified on 17 April 2023