
Quelle: Wikimedia Commons File:Einstein1921 by F Schmutzer 2.jpg, demnach gemeinfrei
Zusammenfassung des Buchkapitels:
Was würde passieren, wenn man versucht, einem Lichtstrahl hinterherzulaufen? Ist es eigentlich möglich, einen Lichtstrahl zu überholen? Mit solchen Fragen beschäftigte sich Albert Einstein in den Jahren bis 1905.

Quelle:
Wikimedia Commons File:Einstein1921 by F Schmutzer 2.jpg,
demnach gemeinfrei
Macht man entsprechende Experimente, so stellt man fest:
Egal wie schnell man einem Lichtstrahl hinterherläuft, er
fliegt (aus Sicht des Verfolgers) immer mit derselben Geschwindigkeit.
Man kann Licht daher niemals einholen, und schon gar nicht überholen.
Trotzdem hat Licht eine endliche Geschwindigkeit, nämlich immer etwa
300 000 km/s.
Wie kann das sein? Wir müssen wir unseren Blickwinkel ändern, um hinter das Geheimnis der immer gleichbleibenden Lichtgeschwindigkeit zu kommen. Es war Einsteins Verdienst, diese Tatsache als erster erkannt und formuliert zu haben. Hier sind seine beiden Postulate:
|
Ein Inertialsystem ist dabei ein Bezugssystem, in dem ein sich kräftefrei bewegender Körper eine konstante Geschwindigkeit besitzt.
Aus Postulat 2 folgt wegen Postulat 1, dass die maximale Ausbreitungsgeschwindigkeit für Wirkungen in jedem Inertialsystem die gleiche sein muss. Diese maximale Geschwindigkeit stellt eine zu messende universelle Naturkonstante dar, deren Wert aber nicht durch die Postulate festgelegt ist. Man kann mit den Maxwellgleichungen zeigen, dass es sich um die Lichtgeschwindigkeit handelt.
Es ist interessant, dass das erste Postulat auch auf die durch Newton begründete klassische Mechanik zutrifft. Allerdings gibt es dabei noch keine obere Grenze für die Geschwindigkeit einer Bewegung, und Licht wird durch die Newtonsche Gesetze der Mechanik sowieso nicht beschrieben.
Treffen Einsteins Postulate in der Realität auch wirklich zu? Alle Experimente geben darauf eine positive Antwort, und es gibt heute nicht den geringsten Zweifel an ihrer Gültigkeit. Somit stellt die spezielle Relativitätstheorie zusammen mit der Quantenmechanik das Fundament dar, auf dem jede physikalische Theorie der Materie aufgebaut sein muss.
Aus der speziellen Relativitätstheorie folgen eine ganze Reihe merkwürdiger Phänomene. Erscheinen zum Beispiel zwei Ereignisse aus einem Inertialsystem heraus betrachtet als gleichzeitig, so gilt dies keineswegs automatisch für alle anderen Inertialsysteme. Andere Phänomene sind die sogenannte Zeitdilatation und die Längenkontraktion.
Ein bekanntes Ergebnis der speziellen Relativitätstheorie ist die Äquivalenz von Energie und Masse, wie sie Einsteins berühmte Formel \[ E = m c^{2} \] (mit der Lichtgeschwindigkeit \(c\)) ausdrückt. Man kann sich die Bedeutung dieser Formel an einem elektrisch aufgeladenen Kondensator veranschaulichen:
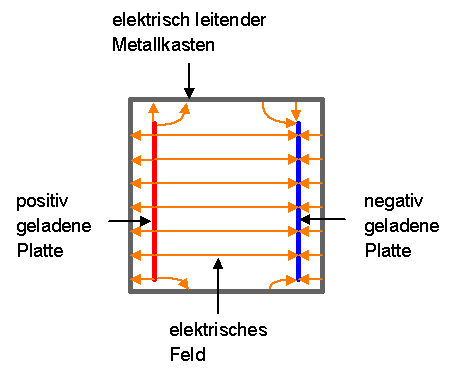
Wenn wir nun diesen Kondensator
in Bewegung versetzen, so folgt aus den Maxwellgleichungen, dass das
darin eingeschlossene elektrische Feld eine Trägheit besitzt.
Der Kondensator verhält sich bei Beschleunigungen so, als
ob er die Masse
\[
m = \frac{E}{c^{2}}
\]
hätte, wobei \(E\) die
Energie des elektromagnetischen Feldes des ruhenden Kondensators ist
(mehr dazu in den Zusatzinfos unten).
Nicht nur Masse, sondern auch Energie
besitzt eine gewisse Trägheit.
Einsteins Theorie erlaubt die Existenz von Objekten, die die Masse Null aufweisen, beispielsweise das Photon. Masselose Teilchen transportieren Energie und Impuls und bewegen sich dabei immer mit der Lichtgeschwindigkeit.
In der relativistischen Mechanik gelten zwischen der relativistischen Gesamtenergie \(E\), dem Impuls \(p\), der Masse \(m\) und der Geschwindigkeit \(v\) die Zusammenhänge (Herleitung siehe unten)
| Allgemein gilt: \[ E = \sqrt{ (mc^{2})^{2} + (pc)^{2} } \] Für \(m \gt 0\) gilt außerdem \[ p = m \gamma v \] \[ E = m \gamma c^{2} \] mit dem Lorentzfaktor \[ \gamma = \sqrt { \frac{1}{1 - (v/c)^{2}} } \] |
Die erste Formel ergibt für massive Teilchen in Ruhe (also \(p = 0\)) wieder
\( E = m c^{2} \). Für masselose Teilchen ergibt sie dagegen
\( E = p c \).
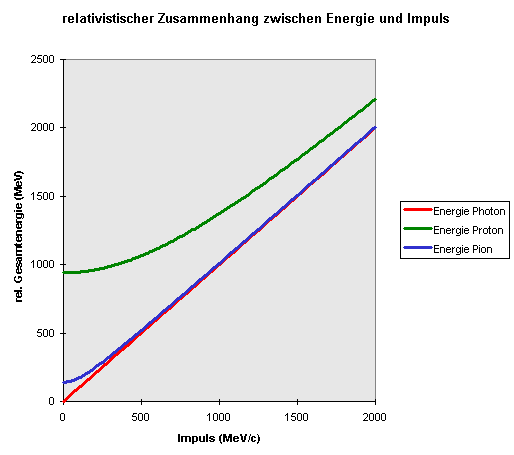
Der Zusammenhang zwischen relativistischer
Gesamtenergie \(E\) und Impuls \(p\) eines Teilchens
mit Masse \(m\) ist hier für das masselose Photon, das
etwa 940 MeV schwere Proton und das nur etwa 140 MeV
schwere Pion dargestellt. Man sieht, dass beim Photon
(\(m = 0\)) Energie und Impuls
genau proportional zueinander sind. Bei allen drei Teilchen
ist die relativistische Gesamtenergie im Ruhezustand
(Impuls \(p = 0\)) gleich der Teilchenmasse (in MeV ausgedrückt).
Wenn man die Formel \( E = m \gamma c^{2} \) nach der Geschwindigkeit \(v\) auflöst, erhält man die Formel
| \[ v = c \cdot \sqrt{ 1 - \left( \frac{mc^{2}}{E} \right)^{2} } \] |
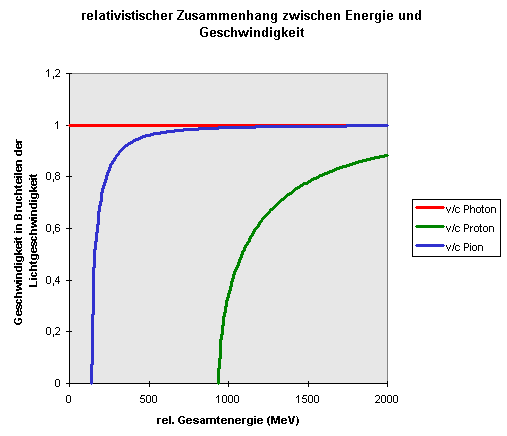
Der Zusammenhang zwischen relativistischer
Gesamtenergie \(E\) und Geschwindigkeit \(v\) eines Teilchens
mit Masse \(m\) ist hier wieder für das masselose Photon, das
etwa 940 MeV schwere Proton und das nur etwa 140 MeV
schwere Pion dargestellt.
Wie man sieht, nähert sich die Teilchengeschwindigkeit
bei zunehmender Energie immer mehr der Lichtgeschwindigkeit,
ohne sie aber je zu überschreiten.
Das masselose Photon bewegt sich dagegen bei jeder Energie
immer mit Lichtgeschwindigkeit.
Der Satz von der Erhaltung der
Energie sowie der Satz von der Erhaltung der Masse
verschmelzen in der Relativitätstheorie zu einem einzigen Erhaltungssatz
für die relativistische Gesamtenergie \(E\).
Es gibt Reaktionen, bei denen sich Masse komplett in Energie umwandelt.
Umgekehrt kann aus Energie auch wieder Masse entstehen.
Ein Beispiel für die Umwandlung von Masse in Energie ist der Zerfall des neutralen Pions. Dieses Teilchen hat Spin 0 und ist mit einer Masse von 135 MeV etwa 200-mal schwerer als das Elektron oder 8 mal leichter als das Proton. Es zerfällt nach einer mittleren Lebensdauer von einigen zehntausendstel milliardstel Milisekunden (genauer \(8 \cdot 10^{-17}\) s) bevorzugt in zwei masselose Photonen, also in reine elektromagnetische Strahlung.
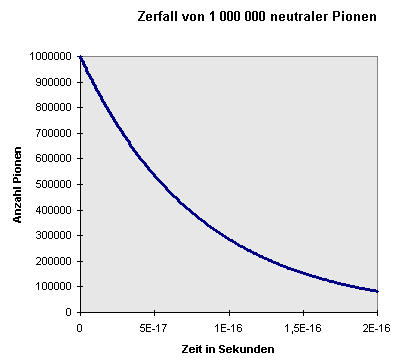
Beispiel für einen Zerfallsprozess:
Neutrale Pionen zerfallen mit einer mittleren Lebensdauer
von \(8 \cdot 10^{-17}\) Sekunden bevorzugt in zwei Photonen.
Das bedeutet, dass nach Ablauf dieser Zeit von den noch vorhandenen
Pionen etwa 2/3 zerfallen sind, so dass nur noch etwa 1/3 diese Zeit
überlebt hat. Von diesem Drittel bleibt nach Ablauf von
weiteren \(8 \cdot 10^{-17}\) Sekunden wiederum nur 1/3 übrig, d.h.
die Pionenzahl hat sich nun auf 1/9 reduziert. Wann ein einzelnes
Pion zerfällt, ist dabei nicht vorherbestimmt: ein Pion
altert nicht.
Man findet häufig die
Aussage, Einsteins Formel \( E = m c^{2} \) wäre für die enormen bei
der Kernspaltung freiwerdenden Energiemengen verantwortlich.
Diese Schlussfolgerung ist jedoch irreführend, denn
auch in einer Kerzenflamme wird Masse gemäß \( E = m c^{2} \)
in Energie umgewandelt.
Einsteins Formel sagt lediglich aus, dass wegen des
Erhaltungssatzes der relativistischen Gesamtenergie jede
Energiefreisetzung mit einem entsprechenden Massenverlust
einhergeht.
Die Ursache für die unterschiedlichen Energiefreisetzungen liegt
in der unterschiedlichen Stärke der jeweils wirkenden Kräfte.
All mass is interaction
(Richard Feynman, zitiert in Genius: The Life and Science of Richard Feynman (1992) von James Gleick)
a) Vierervektoren, Weltlinien, Energie und Impuls
b) Herleitung und Bedeutung von E = mc^{2}
c) Lorentztransformationen, Gleichzeitigkeit, Zeitdilatation und Lorentzkontraktion
Die Grundideen der speziellen Relativitätstheorie und ihre mathematische Beschreibung durch Vierervektoren im Minkowski-Raum finden Sie in Die Symmetrie der Naturgesetze, Kapitel 3: Die spezielle Relativitätstheorie und insbesondere in Kapitel 3.1: Die Poincaré-Gruppe. Die daran anschließenden Kapitel 3.2 etc. befassen sich dann mit den verschiedenen Lorentztransformationen (Boosts und Drehungen), Kapitel 3.7 geht auf Vierergeschwindigkeit und Eigenzeit ein und Kapitel 3.8 beschäftigt sich mit dem Viererimpuls.
Hier ist eine Kurzfassung (spezielle Relativitätstheorie in a nutshell):
Da es um den Vergleich verschiedener Inertialsystem (gleichförmig bewegter Bezugssysteme) geht und da die Lichtgeschwindigkeit in jedem Inertialsystem denselben Wert haben soll, ist es hilfreich, Raum und Zeit gemeinsam zu betrachten und die vierdimensionale Raumzeit einzuführen. Ein Ereignis zur Zeit \(t\) am Ort \(\boldsymbol{x}\) ist dann ein Punkt \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} ct \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \] in dieser Raumzeit. Die Indizes dieser karthesischen Raumzeit-Koordinaten werden oben geschrieben und man zählt sie von Null an. Die nullte Koordinate \[ x^{0} = c t \] repräsentiert die Zeitdimension \(t\) (multipliziert mit der Lichtgeschwindigkeit \(c\), um eine Längendimension zu erhalten).
In einem anderen Inertialsystem (z.B. ein gleichmäßig fahrender Zug) wird dieses Ereignis mit anderen Raumzeit-Koordinaten beschrieben, also durch einen neuen Vierervektor \(x'\). Die Koordinaten \(x\) und \(x'\) des Ereignisses müssen sich ineinander umrechnen lassen. Dabei gilt: eine geradlinig-gleichförmige (d.h. unbeschleunigte) Bewegung ist auch vom fahrenden Zug aus betrachtet geradlinig-gleichförmig. Und: Ein Lichtstrahl hat immer dieselbe Geschwindigkeit, ob nun am Bahnhof oder im Zug gemessen. Daraus folgt, dass \(x\) und \(x'\) über eine affine Transformation der Form \[ x' = \Lambda x + d \] ineinander umgerechnet werden. Dabei ist \(\Lambda\) eine reelle 4-mal-4-Matrix (eine Lorentzmatrix), die ausdrücklich auch Raum- und Zeitkoordinaten bei der Umrechnung miteinander mischen darf.
Die Bewegung eines Objektes in Raum und Zeit kann man durch eine Kurve \[ x(\tau) = \begin{pmatrix} x^0(\tau) \\ \boldsymbol{x}(\tau) \end{pmatrix} = \begin{pmatrix} c \, t(\tau) \\ \boldsymbol{x}(\tau) \end{pmatrix} \] in der Raumzeit darstellen (man spricht auch von einer Weltlinie). Dabei ist \(\tau\) ein Kurvenparameter und \( x^{0}(\tau) \) ist die Zeit (mal \(c\)), zu der sich das Objekt am Ort \( \boldsymbol{x}(\tau) \) befindet. Man kann nun den Tangentialvektor in einem Kurvenpunkt bilden: \[ u := \frac{dx(\tau)}{d\tau} = \begin{pmatrix} u^0 \\ \boldsymbol{u} \end{pmatrix} = \begin{pmatrix} c \, \frac{dt}{d\tau} \\ \frac{d\boldsymbol{x}}{d\tau} \end{pmatrix} \] d.h. man rechnet die Veränderungsrate aller 4 Kurvenkoordinaten für anwachsenden Kurvenparameter aus.
Man kann den Tangentialvektor \(u\) mit der räumlichen Geschwindigkeit \[ \boldsymbol{v} = \frac{d\boldsymbol{x}}{dt} \] in Beziehung setzen: \[ \frac{\boldsymbol{v}}{c} = \frac{d\boldsymbol{x}}{c \, dt} = \frac{d\boldsymbol{x}}{dx^{0}} = \] \[ = \frac{d\boldsymbol{x}}{d\tau} \, \frac{d \tau}{dx^0} = \frac{\boldsymbol{u}}{u^{0}} \] Das können wir uns gut in der folgenden Grafik veranschaulichen:
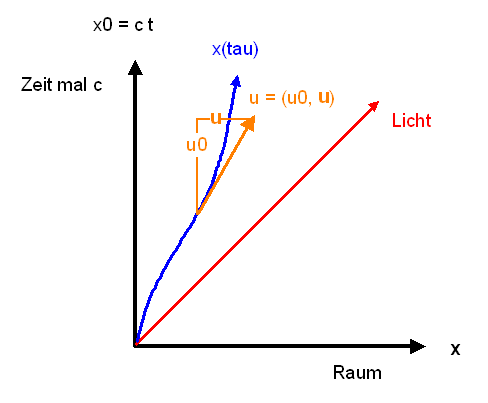
Bei Geschwindigkeiten unterhalb der Lichtgeschwindigkeit
ist demnach immer
\[
u^{0} \gt |\boldsymbol{u}|
\]
und bei Lichtgeschwindigkeit ist
\[
u^{0} = |\boldsymbol{u}|
\]
Die Kurvenparametrisierung wollen wir dabei generell so wählen, dass \( u^{0} = c \, dt/d\tau \)
positiv ist, d.h. mit wachsendem Kurvenparameter \(\tau\) soll also auch die Zeit \(t\) anwachsen.
Überlichtgeschwindigkeit würde \( u^{0} \lt |\boldsymbol{u}| \)
bedeuten, was wir hier ausschließen, denn
man könnte sonst Lorentztransformationen \(\Lambda\) finden, die zu negativem \(u^{0}\)
führen, d.h. es hinge vom Bezugssystem ab, ob ein Objekt
vorwärts oder rückwärts durch die Zeit fliegt.
Aus der Unabhängigkeit der Lichtgeschwindigkeit vom Bezugssystem (und weiteren Zusatzüberlegungen) folgt eine Bedingung für die Lorentzmatrix \(\Lambda\): Sie darf die Minkowski-Metrix \(g(u,w)\) zweier Vierervektoren \(u\) und \(w\) nicht ändern: \[ g(u,w) = g(\Lambda u, \Lambda w) \] mit \[ g(u,w) := u^{0} \, w^{0} - \boldsymbol{u \, w} = \] \[ = u^{0} \, w^{0} - \left( u^{1} \, w^{1} + u^{2} \, w^{2} + u^{3} \, w^{3} \right) \] Oft schreibt man auch \( u \, w \) statt \(g(u,w)\) und \( u^{2} \) (sprich \(u\)-Quadrat, also hier kein Index!) statt \(g(u,u)\).
Gängig ist auch die Verwendung der folgenden Komponentenschreibweise, wobei über doppelt vorkommende Indizes summiert wird (Einsteinsche Summenkonvention), also \[ u = u^{\mu} \, e_{\mu} = \sum_{\mu = 0}^3 \, u^{\mu} \, e_{\mu} \] mit den vier Basisvektoren \(e_{\mu}\) in der Raumzeit, wobei Indizes mit der metrischen Matrix \( g_{\mu\nu} \) hoch- und heruntergezogen werden können: \[ g(u,w) = g( u^{\mu} \, e_{\mu} , \, w^{\nu} \, e_{\nu} ) = \] \[ = u^{\mu} \, w^{\nu} \, g(e_{\mu},e_{\nu}) = \] \[ = u^{\mu} \, w^{\nu} \, g_{\mu\nu} = \] \[ = u^{\mu} \, w_{\mu} = u_{\mu} \, w^{\mu} \] In karthesischen Raumzeit-Koordinaten ist dabei die metrische Matrix \( g_{\mu\nu} \) diagonal mit \[ g := (g_{\mu\nu}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \] Die Minkowski-Metrik zweier Vierervektoren ändert sich also nicht, wenn man das Bezugssystem wechselt. Dabei ist ein vierdimensionaler Vektor ein Vierervektor, wenn er beim Bezugssystemwechsel mit der Lorentzmatrix \(\Lambda\) umgerechnet wird. Da die Koordinaten \(x(\tau)\) bei einem Bezugssystemwechel mit \(\Lambda\) umgerechnet werden, wird auch \(u\) beim Bezugssystemwechel mit \(\Lambda\) multipliziert, d.h. der Tangentialvektor \(u\) ist ein Vierervektor. Der Kurvenparameter \(\tau\) ändert sich per Definition dabei nicht.
Damit folgt, dass sich ein Objekt, das sich in einem Bezugssystem mit Lichtgeschwindigkeit bewegt, auch in jedem anderen Bezugssystem mit Lichtgeschwindigkeit bewegt, denn \[ u^{0} = |\boldsymbol{u}| \] ist gleichbedeutend mit \[ g(u,u) = 0 \] und \(g(u,u)\) ändert sich nicht durch den Bezugssystemwechsel.
Für massive Teilchen (d.h. \( g(u,u) \gt 0 \)) kann man die die Parametrisierung der Kurve so wählen, dass die Minkowskimetrik des Tangentialvektors für jedes \(\tau\) gleich dem Quadrat der Lichtgeschwindigkeit ist: \[ g(u,u) = c^{2} \] für \(m \gt 0\)
Bei dieser Parametrisierung für massive Teilchen hat der Kurvenparameter \(\tau\) eine physikalische Bedeutung: er gibt die Zeit auf einer Uhr an, die mit dem Objekt mitfliegt. Das sieht man, wenn man sich in das momentane Ruhesystem des Objektes begibt, so dass \( \boldsymbol{u} = 0 \) ist und damit \[ c^{2} = g(u,u) = \] \[ = (u^{0})^{2} - \boldsymbol{u}^{2} = (u^{0})^{2} = \] \[ = c^2 \, \left( \frac{dt}{d\tau} \right)^{2} \] gilt. Da \(u^{0} \gt 0\) sein soll, können wir die Wurzel ziehen und durch \(c\) teilen mit dem Ergebnis \[ \frac{dt}{d\tau} = 1 \] Im lokalen Ruhesystem ist also \[ dt = d\tau \] d.h. die Zeitintervalle \(dt\) für einen mitbewegten Beobachter entsprechen den Intervallen \(d\tau\) des Kurvenparameters \(\tau\). Man nennt \(\tau\) daher auch Eigenzeit. Den Tangentialvektor \(u\) nennt man dann Vierergeschwindigkeit.
Allgemein kann man für massive Teilchen mit der Bedingung \[ g(u,u) = c^{2} \] unsere Geschwindigkeits-Beziehung \[ \frac{\boldsymbol{v}}{c} = \frac{\boldsymbol{u}}{u^{0}} \] von oben konkretisieren:
Quadrieren und Freistellen nach \(\boldsymbol{u}^{2}\) ergibt \[ \boldsymbol{u}^{2} = (u^{0})^{2} \, \left( \frac{v}{c} \right)^{2} \] mit \( v = |\boldsymbol{v}| \). Das können wir nun für Teilchen mit positiver Masse in \( g(u,u) = c^{2} \) einsetzen und \(u^{0}\) ausklammern: \[ c^{2} = g(u,u) = (u^{0})^{2} - \boldsymbol{u}^{2} = \] \[ = (u^{0})^{2} - (u^{0})^{2} \, \left( \frac{v}{c} \right)^{2} = \] \[ = (u^{0})^{2} \, \left(1 - \left( \frac{v}{c} \right)^{2} \right) \] Freigestellt nach \((u^{0})^{2}\) ergibt \[ (u^{0})^{2} = \frac{c^{2}}{1 - (v/c)^{2}} =: \gamma^{2} c^{2} \] mit der Abkürzung (Lorentzfaktor) \[ \gamma = \sqrt{\frac{1}{1 - (v/c)^{2}}} \] \(u^{0}\) ist positiv, so dass wir die Wurzel ziehen können und \[ u^0 = \gamma c \] erhalten. Das können wir nun in unsere obige Beziehung \[ \boldsymbol{u} = u^{0} \, \frac{\boldsymbol{v}}{c} \] einsetzen und erhalten \[ \boldsymbol{u} = \gamma c \, \frac{\boldsymbol{v}}{c} = \gamma \boldsymbol{v} \] Insgesamt erhält man für Teilchen mit positiver Masse also die Beziehung \[ u = \begin{pmatrix} u^0 \\ \boldsymbol{u} \end{pmatrix} = \begin{pmatrix} \gamma c \\ \gamma \boldsymbol{v} \end{pmatrix} = \gamma \, \begin{pmatrix} c \\ \boldsymbol{v} \end{pmatrix} \] Für masselose Teilchen hatten wir dagegen oben bereits \( |\boldsymbol{u}| = u^{0} \) hergeleitet, so dass einfach \[ u = \begin{pmatrix} u^0 \\ \boldsymbol{u} \end{pmatrix} = \begin{pmatrix} u^0 \\ u^0 \boldsymbol{e} \end{pmatrix} = u^0 \, \begin{pmatrix} 1 \\ \boldsymbol{e} \end{pmatrix} \] mit \(|\boldsymbol{e}| = 1 \) ist. Ansonsten ist \(u^{0}\) hier eine beliebige positive Zahl.
Aus der Beziehung \[ c \, \frac{dt}{d\tau} = u^{0} = \gamma c \] folgt direkt \[ \frac{dt}{d\tau} = \gamma \] Im Ruhesystem ist \(\gamma = 1\), d.h. dort ist dann \( dt = d\tau \), was wir von oben bereits kennen und was zur Interpretation von \(\tau\) als Eigenzeit geführt hat.
Bei \(v \gt 0\) wird dagegen \(\gamma \gt 1\), so dass \( dt \gt d\tau \) wird. Ein Zeitintervall \(d\tau\) auf einer mitbewegten Uhr (z.B. 1 sec) entspricht also einem größeren Zeitintervall \(dt\) aus Sicht einer anderen ruhenden Uhr, gegenüber der sich die mitbewegte Uhr mit der Geschwindigkeit \(v\) bewegt. Das nennt man Zeitdilatation.
Geht \(v\) gegen die Lichtgeschwindigkeit \(c\), so geht \(\gamma\) gegen unendlich und \(d\tau\) geht für gegebenes \(dt\) gegen Null. Könnte sich eine Uhr mit einem Lichtstrahl mitbewegen, so würde auf ihr keine Zeit vergehen. Man sagt auch, Photonen altern nicht. Aber auch andere massive Teilchen zerfallen langsamer, wenn sie sich schnell genug bewegen. Ein Beispiel sind die Myonen der kosmischen Höhenstrahlung, die uns in Kapitel 4.1 begegnen werden.
Den Viererimpuls \( p \) eines Teilchens mit positiver Masse \(m\) definiert man als
| \[ p = \begin{pmatrix} p^0 \\ \boldsymbol{p} \end{pmatrix} = \begin{pmatrix} E/c \\ \boldsymbol{p} \end{pmatrix} := \] \[ := m u = m \gamma \, \begin{pmatrix} c \\ \boldsymbol{v} \end{pmatrix} \] |
Dabei ist \(E = p^0 c\) die relativistische Gesamtenergie und \(\boldsymbol{p}\) der räumliche Impuls. Da \(m\) konstant ist, ist \(p\) wie \(u\) ein Vierervektor.
Den Fall \(m = 0\) erhält man durch Grenzübergang \(m\) gegen Null (mit konstantem \(E\)). Man verwendet dazu die Beziehung \[ \frac{E}{c} = m \gamma c \] und stellt sie nach der Geschwindigkeit \(v\) (in \(\gamma\)) frei: \[ v = c \, \sqrt{ 1 - \left( \frac{mc^{2}}{E} \right)^{2} } \] Bei konstantem \(E\) und \(m\) gegen Null wird demnach \(v = c\). Der räumliche Impuls \(\boldsymbol{p}\) wird also zu \[ \boldsymbol{p} = m \gamma \boldsymbol{v} = m \gamma c \, \boldsymbol{e} = \frac{E}{c} \boldsymbol{e} \] mit dem Einheitsvektor \(\boldsymbol{e}\). Wir haben also für masselose Teilchen \[ p = \frac{E}{c} \cdot \begin{pmatrix} 1 \\ \boldsymbol{e} \end{pmatrix} \] Es gilt nun die relativistische Energie-Impuls-Erhaltung: Die Summe der Viererimpulse aller Teilchen vor und nach einer Teilchen-Wechselwirkung ist dieselbe. Dieses physikalische Gesetz ist konsistent mit dem Transformationsverhalten der Viererimpulse, denn alle Viererimpulse transformieren sich in gleicher Weise bei Bezugssystemwechseln. Aus diesem Gesetz folgt, dass sich Masse in Energie umwandeln kann und umgekehrt. Hauptsache, die Summe der relativistischen Gesamtenergien ändert sich nicht. Mehr dazu etwas weiter unten.
Aus der Normierung \( g(u,u) = c^{2} \) für \(m \gt 0\) folgt aus \(p = mu\) \[ g(p,p) = m^{2} \, g(u,u) = m^{2}c^{2} \] Zugleich ist die Minkowskimetrik \(g(p,p)\) definiert als \[ g(p,p) = (p^0)^{2} - \boldsymbol{p}^{2} = (E/c)^{2} - \boldsymbol{p}^{2} \] so dass sich \[ (E/c)^{2} - \boldsymbol{p}^{2} = m^{2}c^{2} \] ergibt. Freigestellt nach \(E^{2}\) ist das die wichtige Beziehung
| \[ E^{2} = (mc^{2})^{2} + (\boldsymbol{p}c)^{2} \] |
Der masselose Fall ergibt sich wieder als Grenzübergang \(m\) gegen Null, was man hier sofort einsetzen kann.
Einstein leitete die Formel \( E = mc^{2} \) mit folgendem Gedankenexperiment her (siehe Literaturangaben unten):
Wir starten mit einem ruhenden Objekt der Masse \(m\) (das kann ein Raumschiff, ein Atom oder auch ein Teilchen sein – wir wollen von einem Teilchen ausgehen). Dieses Objekt sendet nun zeitgleich zwei gleich starke Lichtblitze der Energie \(E_{\gamma}\) in genau entgegengesetzte Richtungen aus. Statt der Lichtblitze kann man sich auch zwei Photonen vorstellen, was wir im Folgenden tun wollen.
Beim Aussenden der beiden Photonen soll die Erhaltung von Energie und Impuls gelten, d.h. vor dem Aussenden hat das ruhende Teilchen die innere Energie \[ E \] und danach die innere Energie \[ E' = E - 2 E_{\gamma} \] (wir schreiben innere Energie, da es sich hier nicht um Bewegungsenergie handelt – das Teilchen ruht ja; mehr zu diesem Begriff siehe weiter unten). Der Impuls des Teilchens ändert sich dabei nicht, da die beiden ausgesendeten Photonen jeweils entgegengesetzten Impuls tragen – das Teilchen ruht also immer noch.
Wir können uns nun diesen Vorgang auch aus einem fahrenden Zug heraus ansehen, der sich in Richtung eines der beiden Photonen bewegt (dem Photon also hinterherfährt). Das ruhende Teilchen besitzt in diesem Bezugssystem dann die Geschwindigkeit \(v\). Gleichwertig dazu könnten wir auch das Teilchen in einen (entgegengesetzt fahrenden) Zug setzen und uns den Vorgang vom Bahnhof aus ansehen. Das Teilchen hat jetzt jedenfalls vor und nach dem Aussenden der beiden Photonen die Geschwindigkeit \(v\).
Der entscheidende Schritt kommt nun durch die Betrachtung der Impulsbilanz zustande. Da wir in der speziellen Relativitätstheorie einen inneren Massenbegriff verwenden wollen, der unabhängig von der Teilchengeschwindigkeit sein soll und der bei kleinen Geschwindigkeiten gleich dem nichtrelativistischen Massenbegriff ist, brauchen wir dafür den Anschluss an die nichtrelativistischen Formel für den Impuls des Teilchens. Daher gehen wir im Folgenden davon aus, dass die Geschwindigkeit \(v\) klein gegenüber der Lichtgeschwindigkeit \(c\) ist, so dass man die nichtrelativistische Impulsformel \(p = mv\) für das aussendende Teilchen anwenden kann.
Beim ruhendem Teilchen ist alles ganz einfach, denn beide Photonen haben entgegengesetzt-gleichen Impuls, so dass das Teilchen seinen Impuls (nämlich Null) nicht ändert.
Beim Betrachten der Situation aus dem fahrenden Zug heraus ändert sich das jedoch, denn die beiden Photonen tragen nun nicht mehr entgegengesetzt-gleichen Impuls (der Zug fährt ja einem der beiden Photonen hinterher). Das einzelne Photon wird zwar nicht schneller oder langsamer (denn es fliegt in jedem Bezugssystem mit Lichtgeschwindigkeit), aber der Impuls des einen wegfliegende Photons (das in Bewegungsrichtung des aussendenden Teilchens wegfliegt) vergrößert sich, der des anderen Photons (dem wir hinterherfahren) verringert sich vom Zug aus gesehen.
Das kann man sich aufgrund des Dopplereffektes für die zugehörige Lichtwelle erklären: Die Wellenberge der ausgesendeten Lichtwelle rücken in Bewegungsrichtung (des aussendenden Teilchens) enger zusammen, da das nun als bewegt gesehene Teilchen der Welle hinterherläuft und der nächste Wellenberg immer etwas weiter in Bewegungsrichtung abgesetzt wird.
Man kann aus dem Dopplereffekt für kleine Geschwindigkeiten (gegenüber \(c\)) ableiten, dass aus der Lichtfrequenz \(f\) bei ruhendem Teilchen die Lichtfrequenzen \[ f \cdot (1 \pm v/c) \] in und gegen die Bewegungsrichtung bei mit \(v\) bewegtem Teilchen werden (siehe auch Wikipedia: Dopplereffekt).
Nun ist der Impuls eines Photons bzw. Lichtblitzes proportional zur Frequenz der zugehörigen Welle, so dass aus den beiden Photonimpulsen \[ \pm p_{\gamma} \] bei ruhendem Sende-Teilchen die Photonimpulse \[ p_{\gamma}' = \pm p_{\gamma} \cdot (1 \pm v/c) \] bei mit \(v\) bewegtem Teilchen werden (Zugsichtweise) (man kann beispielsweise die Maxwellgleichungen verwenden, um den Impuls des Lichtblitzes auszurechnen).
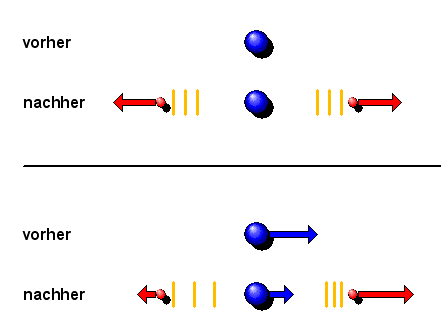
Obere Hälfte:
Ein ruhendes Teilchen (blau) sendet zwei Photonen (rot) aus, die mit
entgegengesetzt-gleichem Impuls (rote Pfeile) auseinanderfliegen,
so dass das sendende Teilchen auch anschließend weiterhin ruht.
Die den Photonen zugeordneten Lichtwellen (orange) haben dieselbe Wellenlänge.
Untere Hälfte: Dieselbe Situation, diesmal aber aus einem fahrenden Zug heraus betrachtet,
so dass das Teilchen (blau) vorher und nachher die Geschwindigkeit \(v\) hat.
Der Dopplereffekt führt dazu, dass die Lichtwellenlänge des einen Photons gestaucht, die
des anderen Photons gedehnt wird. Entsprechend haben die beiden Photonen nicht mehr denselben
Impuls (rote Pfeile). Ein Teil des Impulses des sendenden Teilchens geht also auf die Photonen über,
so dass das sendende Teilchen Impuls verliert (blaue Pfeile).
Wie lautet nun also die Impulsbilanz, wenn das bewegte Teilchen diese beiden Photonen aussendet?
Der Impuls vorher muss gleich dem Impuls nachher plus den beiden Photonimpulsen sein.
Sicherheitshalber räumen wir dabei die Möglichkeit ein, dass die Teilchenmasse
sich durch das Aussenden der Photonen ändert – ob das zutrifft, werden wir gleich sehen:
\[
mv =
\]
\[
=m'v + p_{\gamma} \, (1 + v/c) - p_{\gamma} \, (1 - v/c) =
\]
\[
= m'v + 2 p_{\gamma} \, (v/c)
\]
Der Impuls des Teilchens hat sich also beim Aussenden der beiden Photonen geändert, denn diese haben nun
unterschiedliche Impulse und tragen daher Impuls weg. Allerdings kann sich die Geschwindigkeit \(v\)
des Teilchens
durch das Aussenden der Photonen nicht geändert haben, denn das ruhende Teilchen ändert seine
Geschwindigkeit (Null) dabei auch nicht, und wir
betrachten dieselbe Situation ja nur aus einem anderem Blickwinkel (nämlich aus dem Zug heraus).
Die einzige Möglichkeit zur Impulsänderung ist daher
die Änderung der Teilchenmasse –
gut, dass wir bereits \( m' \) eingeführt hatten.
Nun ist bei einem Photon dessen Impuls gleich seiner Energie (durch \(c\)), wie man bei Lichtblitzen auch aus den Maxwellgleichungen herleiten kann. Wir setzen also \( p_{\gamma} = E_{\gamma}/c \) oben ein und erhalten \[ mv = m'v + 2 E_{\gamma} \, (v/c^{2}) \] Von oben wissen wir außerdem, dass \( 2 E_{\gamma} = E - E' \) ist, d.h. die von den beiden Photonen weggetragene Energie führt zu einer Änderung der inneren Energie des Teilchens. Das ergibt (nach dividieren durch \(v\)) dann \[ m = m' + (E - E')/c^{2} \] und schließlich \[ E - E' = mc^{2} - m'c^{2} \] Die Änderung der inneren Energie des Teilchens entspricht also genau einer Änderung seiner Masse (mal \(c^{2}\)).
Nun ist die innere Energie eines Objektes ein Begriff aus der nichtrelativistischen Physik. Sie wird gebraucht, um beispielsweise den Anregungszustand eines Atoms darzustellen, das beim Übergang zu seinem Grundzustand Energie abgibt und dabei seine innere Energie ändert. Letztlich dient die innere Energie dazu, in der nichtrelativistischen Physik den Energieerhaltungssatz konsistent darzustellen und Energieformen wie innere Anregungszustände, Wärmeenergie etc. zu berücksichtigen. Dabei ist die innere Energie nur bis auf eine additive Konstante festgelegt, denn es können nur Differenzen der inneren Energie gemessen werden, die einer entsprechenden Energie-Zufuhr oder -Abgabe entsprechen.
In der relativistischen Physik brauchen wir den Begriff der inneren Energie nun nicht mehr, um den Energieerhaltungssatz konsistent darzustellen. Innere Energiedifferenzen entsprechen Massendifferenzen, d.h. wir können Änderungen der inneren Energie an der Änderung der Teilchenmasse erkennen. Daher können wir die innere Energie mit der Masse (mal \(c^{2}\)) des Teilchens gleichsetzen: \[ E = mc^{2} \] Statt von innerer Energie kann man hier einfach von der relativistischen Energie eines ruhenden Teilchens sprechen. Bewegt sich das Teilchen, so kommt die Bewegungsenergie hinzu, so dass bei kleinen Geschwindigkeiten die relativistische Energie durch \[ E = mc^{2} \, \left( 1 + \frac{1}{2} \left( \frac{v}{c} \right)^{2} \right) \] gegeben ist. Die maximale Energie, die ein ruhendes Teilchen mit Masse \(m\) abgeben kann, ist gleich \( mc^{2} \). Das geschieht beispielsweise, wenn das neutrale Pion vollständig in zwei Photonen zerfällt. Anders als bei der inneren Energie haben wir nun also einen natürlichen Nullpunkt für die relativistische Energie.
An welcher Stelle kommt nun bei der obigen Betrachtung die spezielle Relativitätstheorie ins Spiel? Es liegt an den masselosen Photonen (Lichtblitzen), die es so in der nichtrelativistischen Physik nicht gibt, denn sie tragen Energie und Impuls, aber keine Masse.
Da sie keine Masse tragen, würden wir zunächst erwarten, dass sich die Masse des aussenden Teilchens nicht ändern. Andererseits tragen sie Impuls, was nur aufgrund der speziellen Relativitätstheorie möglich ist.
Beim Wechsel des Bezugssystems (ruhend -> bewegt) ändern sich die beiden Photonimpulse – auch das kann man nur mit Hilfe der speziellen Relativitätstheorie verstehen, z.B. über die Maxwellgleichungen. Die Photonimpulse addieren sich nun nicht mehr zu Null, üben also zusammen einen Rückstoß auf das aussendende Teilchen aus, so dass sich auch dessen Impuls ändern muss, ohne dass sich aber seine Geschwindigkeit ändern darf (denn im ruhenden Bezugssystem tut sie das auch nicht). Das geht nur, wenn das Teilchen Masse (Trägheit) verliert. Die Rechnung zeigt dann, dass dieser Massenverlust (mal \(c^{2}\)) genau der Energie entspricht, die die beiden Photonen davontragen.
Mit Hilfe von Vierervektoren und Lorentzmatrizen könnte man die obige Diskussion wie folgt abkürzen: Wenn wir Energie (durch \(c\)) und Impuls eines Photons zu einem vierdimensionalen Vektor (Vierervektor) \[ \begin{pmatrix} E_{\gamma}/c \\ \boldsymbol{p}_{\gamma} \end{pmatrix} \] zusammenfassen, so wissen wir aus den Maxwellgleichungen, dass wir die Umrechnung beider Größen bei Wechsel des Bezugssystems als Multiplikation dieses Vierervektors mit einer 4-mal-4-Lorentzmatrix \(\Lambda\) schreiben können (das entspricht dann dem korrekten relativistischen Dopplereffekt).
Auch für das aussendende Teilchen können wir dessen Energie und Impuls zunächst formal zu einem solchen vierdimensionalen Vektor zusammenfassen, also auch dort \[ \begin{pmatrix} E/c \\ \boldsymbol{p} \end{pmatrix} \] schreiben. Wenn nun beim Aussenden der Photonen die Energie-Impuls-Erhaltung in jedem gleichförmig bewegten Bezugssystem gilt, so muss auch dieser Vierervektor sich beim Bezugssystemwechsel mit derselben Lorentzmatrix \(\Lambda\) umrechnen wie die Photonimpulse.
Nun wissen wir, dass eine Lorentzmatrix die Minkowski-Metrik nicht ändert (siehe oben; kann man auch aus den Maxwellgleichungen ableiten). Daher muss \[ (E/c)^{2} - \boldsymbol{p}^{2} \] für ein bestimmtes Teilchen immer denselben Wert aufweisen, unabhängig vom Bezugssystem und damit unabhängig von der Geschwindigkeit \(v\) des Teilchens. Die Ableitung dieses Ausdrucks nach der Geschwindigkeit \(v\) ist also Null: \[ \frac{d}{dv} \left( (E/c)^{2} - \boldsymbol{p}^{2} \right) = \] \[ = 2 \frac{E}{c^{2}} \, \frac{dE}{dv} - 2 p \, \frac{dp}{dv} = 0 \] Im Grenzfall kleiner \(v/c\) ist \[ \frac{dE}{dv} = mv = p \] \[ \frac{dp}{dv} = m \] (das ergibt die korrekte Verbindung mit den nichtrelativistischen Formeln und dem darin definierten Massenbegriff) und wir erhalten: \[ 2 \frac{E}{c^{2}} p - 2 p m = 0 \] Multiplikation mit \(c^{2}/(2p)\) und Umstellen ergibt \[ E = 2 p m \frac{c^2}{2p} = m c^2 \] und wir haben im Grenzfall kleiner \(v/c\):
| \[ E = m c^{2} \] |
In Ruhe (also \(p = 0\)) ist unser Vierervektor \[ \begin{pmatrix} E/c \\ \boldsymbol{p} \end{pmatrix} \] für ein massives Teilchen also gegeben durch \[ \begin{pmatrix} mc \\ \boldsymbol{0} \end{pmatrix} \] Für andere Geschwindigkeiten \(v\) kann man dann den entsprechenden Vierervektor durch Multiplikation mit der Lorentzmatrix \(\Lambda\) aus diesem Vierer-Ruhevektor berechnen (siehe oben).
In jedem Fall muss für beliebige Geschwindigkeiten \[ (E/c)^{2} - \boldsymbol{p}^{2} = (mc)^{2} \] gelten, denn der Term links ist ja unabhängig von \(v\) (siehe oben), also eine Konstante (rechte Seite), und diese Konstante ist dann durch den Grenzfall \(v = 0\) festgelegt. Freigestellt nach \(E^{2}\) ist das wieder unsere bekannte Beziehung \[ E^{2} = (\boldsymbol{p}c)^{2} + (mc^{2})^{2} \] Im Buchkapitel haben wir die Formel \( E = mc^{2} \) am Beispiel eines abgeschirmten elektrischen Kondensators erläutert (siehe oben). Die Argumentation war dabei etwas anders:
Mit Hilfe der Maxwellgleichungen lassen sich Energie \(E\) und Impuls \(p\) des elektromagnetischen Feldes in dem Kondensator berechnen, und zwar für verschiedene Geschwindigkeiten \(v\) des Kondensators. Dabei ergibt sich beispielsweise für kleine Geschwindigkeiten die Beziehung \[ p = \frac{E}{c^{2}} \, v \] d.h. \(E/c^{2}\) kann mit einer Masse \(m\) identifiziert werden, denn nichtrelativistisch gilt ja \( p = m v \).
Früher sprach man hier auch von der elektromagnetischen Masse, doch dann hat sich diese Unterscheidung von der "gewöhnlichen" Masse als überflüssig erwiesen.
In der Realität besitzt diese Rechnung allerdings durchaus gewisse Schwierigkeiten, da die Kräfte im Kondensator nicht ausgeglichen sind, wenn man nur das elektromagnetische Feld betrachtet (so ziehen sich die Kondensatorplatten gegenseitig elektrisch an). Man muss auch die Kräfte, die den Kasten und die Platten stabil halten, mit berücksichtigen, um konsistente Ergebnisse zu erhalten – man nennt diese Kräfte auch Poincaré-Spannungen. Mehr dazu siehe Feynman Vorlesungen über Physik, Band II, Kap. 28 (Feynman betrachtet an Stelle des Kondensators eine elektrisch geladene Kugel).
In dieser Argumentation wird die Masse in ihrer Bedeutung als Proportionalitätsfaktor zwischen Impuls und (kleiner) Geschwindigkeit verwendet. Masse kann man aber auch physikalisch anschaulicher direkt als Trägheit verstehen, d.h. ein Objekt mit Masse setzt dem Versuch, es durch eine Kraft zu beschleunigen, einen Widerstand entgegen. Woher kommt diese Trägheit beim elektromagnetischen Feld im Kondensator? Richard Feynman beschreibt die Ursache für diese Trägheit in seinen Feynman Vorlesungen über Physik, Band II, Kap. 28-4 sinngemäß so:
Im Kondensator wirken zwischen den geladenen Platten sowie zwischen Platten und Abschirmung elektrische Kräfte. Diese Kräfte addieren sich beim ruhenden oder gleichförmig bewegten Kondensator insgesamt zu Null, d.h. der Kondensator übt insgesamt auf sich selber keine Kraft aus, solange er nicht beschleunigt wird.
Beschleunigt man jedoch den Kondensator, so wirkt sich aus, dass sich nichts schneller als mit Lichtgeschwindigkeit fortpflanzen kann. Die Veränderung der elektromagnetischen Kräfte aufgrund der Beschleunigung kann sich also nur mit Verzögerung bemerkbar machen. Die eine Platte merkt also erst mit zeitlicher Verzögerung, dass sich die andere Platte bereits woanders befindet.
Die elektromagnetischen Kräfte zwischen den Platten sowie der Abschirmung verändern sich daher so, dass sie sich insgesamt nicht mehr zu Null addieren. Es entsteht eine Gesamtkraft, die proportional zur Beschleunigung anwächst und die dieser Beschleunigung entgegenwirkt. Der Kondensator hält sich gleichsam an den eigenen Schnürsenkeln fest und setzt der Beschleunigung eine Gegenkraft entgegen, so dass man eine gleichstarke entgegengesetzte Kraft von außen anlegen muss, um die Beschleunigung überhaupt erzielen zu können.
Fazit: Der Kondensator besitzt aufgrund seines elektromagnetischen Feldes eine Trägheit (Masse). Wieder einmal finde ich es faszinierend, wie in der Natur alles wunderbar zusammenpasst. Die spezielle Relativitätstheorie erweist sich in allen diesen Aspekten als konsistente Theorie.
Von oben wissen wir: Beim Wechsel von einem Inertialsystem in ein anderes Inertialsystem werden die zugehörigen Raum-Zeit-Koordinaten durch eine Lorentztransformation (bei zusätzlicher Raumzeitverschiebung auch Poincarétransformation genannt) \[ x' = \Lambda x + d \] ineinander umgerechnet. Dabei ist \(d\) ein Verschiebungsvektor, der den räumlichen und zeitlichen Ursprungspunkt ändert, und \(\Lambda\) ist eine reelle 4-mal-4-Matrix (die Lorentzmatrix). Damit sich die Lichtgeschwindigkeit beim Bezugssystemwechsel nicht ändert, muss \(\Lambda\) die Bedingung \[ g(u,w) = g(\Lambda u, \Lambda w) \] erfüllen, d.h. sie ändert die Minkowski-Metrik von Vierervektoren nicht.
Wie sieht die Matrix \(\Lambda\) nun konkret aus? Die genaue Analyse zeigt (siehe z.B. Die Symmetrie der Naturgesetze, Kapitel 3: Die spezielle Relativitätstheorie):
\( \Lambda \) umfasst neben den diskreten Raum- und Zeitspiegelungen zwei Arten von kontinuierlichen Transformationen: räumliche Drehungen und Boosts (Geschwindigkeitstransformationen). Da die räumlichen Drehungen keine relativistischen Besonderheiten aufweisen, wollen wir uns hier nur die Boosts genauer ansehen.
Um die Sache zu vereinfachen, betrachten wir Boosts in x-Richtung (oben \(x^1\)-Richtung genannt), so dass wir die y- und z-Koordinaten nicht weiter beachten müssen und im Folgenden einfach weglassen können. \(\Lambda\) ist dann einfach eine 2-mal-2-Matrix, die Zeitkoordinate und x-Koordinate vom alten in das neue Inertialsystem umrechnet.
Ein Boost in x-Richtung macht nun aus einem ruhenden Körper einen Körper, der sich mit der Geschwindigkeit \( v \) in x-Richtung bewegt. Aus der Vierergeschwindigkeit eines ruhenden Objekts \[ u = \begin{pmatrix} c \\ 0 \end{pmatrix} \] wird also nach dem Boost die Vierergeschwindigkeit \[ u = \begin{pmatrix} \gamma c \\ \gamma v \end{pmatrix} = \Lambda \, u = \Lambda \, \begin{pmatrix} c \\ 0 \end{pmatrix} \] Daraus können wir ablesen, dass die erste Spalte der Matrix \( \Lambda \) die Werte \( \gamma \) und \( \gamma \, v/c \) enthält: \[ \Lambda = \begin{pmatrix} \gamma & \Lambda^0_{\, 1} \\ \gamma \, v/c & \Lambda^1_{\, 1} \end{pmatrix} \] Die zweite Spalte von \(\Lambda\) ergibt sich nun aus der Bedingung, dass \(\Lambda\) die Minkowski-Metrik von Vierervektoren nicht ändert. Nehmen wir einen beliebigen Vierervektor \[ w = \begin{pmatrix} a \\ b \end{pmatrix} \] sodass \[ \Lambda w = \begin{pmatrix} \gamma & \Lambda^0_{\, 1} \\ \gamma \, v/c & \Lambda^1_{\, 1} \end{pmatrix} \, \begin{pmatrix} a \\ b \end{pmatrix} = \] \[ \begin{pmatrix} \gamma \, a + \Lambda^0_{\, 1} \, b \\ \gamma \, (v/c) \, a + \Lambda^1_{\, 1} \, b \end{pmatrix} \] Dann muss \[ g(w,w) = a^{2} - b^{2} = \] \[ = g(\Lambda w, \Lambda w) = \] \[ = \left( \gamma \, a + \Lambda^{0}_{\, 1} \, b \right)^{2} - \left( \gamma \, (v/c) \, a + \Lambda^{1}_{\, 1} \, b \right)^{2} \] gelten. Ausmultiplizieren der rechten Seite und Koeffizientenvergleich in \(a^{2}, b^{2}, a b \) ergibt dann \[ \Lambda^{0}_{\, 1} = \gamma \, v/c \] \[ \Lambda^{1}_{\, 1} = \gamma \] Insgesamt sieht die Lorentzmatrix für einen Boost in x-Richtung also so aus: \[ \Lambda = \begin{pmatrix} \gamma & \gamma \, v/c \\ \gamma \, v/c & \gamma \end{pmatrix} \] Dabei ist wie immer \[ \gamma = \frac{1}{\sqrt{1 - (v/c)^{2}}} \] der Lorentzfaktor. Nimmt man die y- und z-Koordinate hinzu, so erweitert sich diese Matrix um zwei Einsen in der Diagonalen, d.h. \(\Lambda\) ändert bei einem Boost in x-Richtung die y- und z-Koordinate nicht.
Um von dem neuen Bezugssystem wieder in das alte Bezugssystem zurückzuwechseln, benötigt man die inverse Lorentzmatrix \( \Lambda^{-1} \). Diese erhalten wir, indem wir in der Lorentzmatrix \(\Lambda\) einfach die Geschwindigkeit \( v \) durch die umgekehrte Geschwindigkeit \( - v \) ersetzen. Man kann leicht nachrechnen, dass dann wie gefordert \( \Lambda \, \Lambda^{-1} = 1 \) ist.
Beim Wechsel vom alten in das neue Bezugssystem wird demnach ein zuvor ruhendes Objekt zu einem mit Geschwindigkeit \(v\) bewegten Objekt, und beim Wechsel vom neuen Bezugssystem in das alte Bezugssystem wird aus einem im neuen System ruhenden Objekt ein mit Geschwindigkeit \( - v \) bewegtes Objekt, während das mit \(v\) bewegte Objekt wieder zum ruhenden Objekt wird. Die Situation bezüglich der beiden Bezugssysteme ist also vollkommen symmetrisch.
Da wir nun die explizite Umrechnungsformel für Raum- und Zeitkoordinate bei Boosts haben, können wir uns im Detail ansehen, wie sich diese Umrechung auf verschiedene Raumzeitpunkte (Ereignisse) auswirkt, wenn wir diese aus verschiedenen Bezugssystemen heraus betrachten, die sich in x-Richtung gleichförmig gegeneinander bewegen. Zur Veranschaulichung bieten sich Raumzeit-Diagramme an, in denen wir die Zeitkoordinate \(t\) (mal \(c\)) nach oben und die Raumkoordinate \(x\) nach rechts laufen lassen. Ein solches Raumzeit-Diagramm haben wir weiter oben bereits verwendet, um den Zusammenhang zwischen Vierergeschwindigkeit \(u\) und räumlicher Geschwindigkeit \(v\) abzuleiten.
Wir wollen zwei ruhende Uhren betrachten: Die erste Uhr soll sich im Ursprung des räumlichen Koordinatensystems befinden, und die zweite Uhr soll sich bei der x-Koordinate \(L\) befinden, so dass der Abstand zwischen den beiden Uhren gleich \(L\) ist.
In regelmäßigen Zeitintervallen (z.B. jede Sekunde) senden diese Uhren gleichzeitig je einen Lichtblitz aus, der damit ein Ereignis in der Raumzeit festlegt (nämlich Ort und Zeit der Lichtblitz-Entstehung). Diese Ereignisse können wir in unserem Raumzeit-Diagramm eintragen. Es entstehen zwei senkrecht verlaufende Ketten aus Lichtblitz-Entstehungspunkten: eine Kette bei \(x = 0\) für die erste Uhr und eine Kette bei \(x = L\) für die zweite Uhr (siehe unten das linke Bild). Die Punkte liegen dabei immer horizontal nebeneinander, da die Lichtblitze ja gleichzeitig (also bei gleicher Zeitkoordinate \(t\)) entstehen sollen.
Wir betrachten nun dieselbe Situation aus einem Raumschiff, das sich mit 3/4 Lichtgeschwindigkeit in die negative x-Richtung bewegt. Von diesem Raumschiff aus gesehen bewegen sich die beiden Uhren also mit 3/4 Lichtgeschwindigkeit in die positive x-Richtung. Die einzelnen Lichtblitz-Ereignisse müssen daher mit der obigen Boostmatrix \(\Lambda\) in unser neues Raumschiff-Bezugssystem umgerechnet werden, wobei \( v/c = 3/4 \) und \[ \gamma = \frac{1}{\sqrt{1 - (3/4)^{2}}} \approx 1,51 \] ist. Dabei entsteht das folgende Bild (rechts):
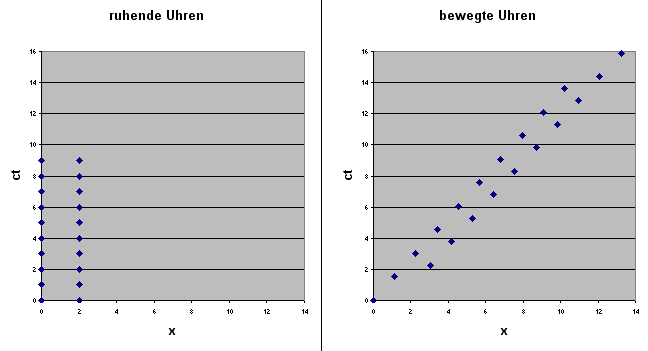
Links die beiden ruhenden Uhren, rechts dieselben Uhren, aber vom Raumschiff aus gesehen
Wir sehen rechts, dass beide Uhren sich wie gewünscht mit
zunehmender Zeit zu größeren x-Werten hin bewegen,
da sie nun mit 3/4 Lichtgeschwindigkeit nach rechts fliegen.
Zugleich sehen wir, dass zuvor gleichzeitig ausgesandte Lichtblitze (Punkte auf gleicher Höhe links im Bild) sich im rechten Bild nicht mehr auf gleicher Höhe befinden, also nicht mehr gleichzeitig sind. Die Ereignisse der rechten Uhr sind zu späteren Zeiten hin verschoben, verglichen mit der linken Uhr. Die Definition gleichzeitiger Ereignisse hat sich durch den Bezugssystemwechsel verändert! Gleichzeitigkeit hängt vom Bezugssystem ab!
Weiterhin sehen wir, dass die einzelnen Ereignisse im rechten Bild in zeitlich größerem Abstand aufeinander folgen als im linken Bild. Die Zeitabstände haben sich um den Faktor \(\gamma = 1,51\) vergrößert. Das ist genau die Zeitdilatation, die wir weiter oben bereits angesprochen hatten.
Räumliche Abstände werden zwischen gleichzeitigen Ereignissen definiert, d.h. sie sind im Raumzeit-Diagramm durch den horizontalen Abstand zwischen zwei Ereignissen mit gleicher Zeitkoordinate gegeben. Die Gleichzeitigkeit kann man beispielsweise dadurch sicherstellen, dass man im betrachteten Inertialsystem überall ruhende Uhren aufstellt und diese Uhren miteinander synchronisiert (das geht entweder mithilfe von Lichtsignalen oder durch Synchronisation der Uhren an einem Ort und anschließendem sehr langsamen Transport der Uhren an ihren Zielort). Diese Uhren liefern nun den Zeitmaßstab in diesem Inertialsystem, definieren also an jedem Ort die Zeitkoordinate für dortige Ereignisse. Den räumlichen Abstand dieser ruhenden Uhren untereinander kann man nun über die Laufzeit von Lichtsignalen ermitteln, denn das Licht bewegt sich garantiert mit Lichtgeschwindigkeit. Damit lassen sich dann auch die Ortskoordinaten der ruhenden Uhren festlegen.
Im Bild links beträgt der räumliche Abstand zwischen gleichzeitig ausgesandten Lichtblitzen 2 Einheiten. In diesem Sinne sind die beiden Uhren hier 2 Einheiten räumlich voneinander entfernt.
Im Bild rechts gelten nun aber andere Ereignisse als gleichzeitig. Denken wir uns im rechten Bild die einzelnen Lichtblitz-Ereignisse der linken Uhr durch eine schräge Linie verbunden (analog bei der rechten Uhr), so ist der horizontale Abstand zwischen diesen beiden Linien um den Faktor \( 1/\gamma = 0,66 \) kleiner als im Bild rechts. Das bezeichnet man als Lorentzkontraktion. In diesem Sinne ist der Abstand zwischen den beiden Uhren im Vergleich zur ruhenden Situation um den Faktor \( 1/\gamma \) geschrumpft. Hier die Rechnung dazu (eine anschauliche Begründung für Zeitdilatation, Lorentzkontraktion und die Relativität der Gleichzeitigkeit folgt weiter unten):
Im Inertialsystem links im Bild oben werden die Weltlinien der beiden Uhren durch die Raumzeit-Geraden \[ x_{1} = (ct_{1}, 0) \] \[ x_{2} = (ct_{2}, L) \] beschrieben. Dabei sind \(x_{1}\) und \(x_{2}\) Vierervektoren (bzw. wegen Weglassen der y- und z-Koordinaten zweikomponentige Vektoren). Der räumliche Abstand bei gleicher Zeitkoordinate \(t = t_{1} = t_{2}\) in diesem Bezugssystem beträgt \(L\) (im Bild oben links wurde \(L=2\) gewählt).
Im Inertialsystem rechts im obigen Bild bewegen sich beide Uhren mit der Geschwindigkeit \(\boldsymbol{v}\) nach rechts (wir hatten dort \(\boldsymbol{v} = 0,75 \, c\) gewählt). Die entsprechenden Weltlinien erhalten wir, indem wir die Boostmatrix \(\Lambda\) auf die ursprünglichen Weltlinien anwenden: \[ x_{1}' = \Lambda \, x_{1} = \] \[= \begin{pmatrix} \gamma & \gamma \, v/c \\ \gamma \, v/c & \gamma \end{pmatrix} \, \begin{pmatrix} ct_{1} \\ 0 \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma c t_{1} \\ \gamma v t_{1} \end{pmatrix} \] \[ x_{2}' = \Lambda \, x_{2} = \] \[= \begin{pmatrix} \gamma & \gamma \, v/c \\ \gamma \, v/c & \gamma \end{pmatrix} \, \begin{pmatrix} ct_{1} \\ L \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma c t_{2} + \gamma v L/c \\ \gamma v t_{2} + \gamma L \end{pmatrix} \] Bei gleichzeitigen Ereignissen (Lichtblitze der beiden Uhren) in diesem Bezugssystem muss \(t_1' = t_2'\) und somit \[ t_{1}' = \gamma c t_{1} = \] \[ = t_2' = \gamma c t_{2} + \gamma v L/c \] gelten, d.h. \[ t_{1} = t_{2} + v L/c^{2} \] Der räumliche Abstand dieser gleichzeitigen Ereignisse beträgt dann \[ L' = \gamma v t_{2} + \gamma L - \gamma v t_{1} = \] \[ = \gamma v t_{2} + \gamma L - \gamma v \, (t_{2} + v L/c^{2}) = \] \[ = \gamma v t_{2} + \gamma L - \gamma v t_{2} - \gamma v^{2} L/c^{2} = \] \[ = \gamma L \, (1 - v^{2}/c^{2}) = L / \gamma \] Bei der Interpretation dieser Lorentzkontraktion muss man immer daran denken, dass man im Bild rechts zur Ermittlung des räumlichen Abstandes andere Ereignisse miteinander vergleicht als im Bild links. Vergisst man diesen wichtigen Punkt, so kann man alle möglichen Paradoxien ableiten, indem man beispielsweise anschaulich starre Körper aus verschiedenen Bezugssystemen heraus betrachtet. In der speziellen Relativitätstheorie gibt es prinzipiell keine starren Körper mehr!
Betrachten wir beispielsweise bei beiden Uhren das Ereignis, bei dem der jeweils erste Lichtblitz ausgesendet wird. Bei den ruhenden Uhren geschieht dies gleichzeitig zur Zeit \(t = 0\) im räumlichen Abstand von zwei Einheiten.
Aus dem Raumschiff heraus betrachtet sendet die rechte Uhr ihren ersten Lichtblitz jedoch mehr als zwei Zeiteinheiten später ab als die linke Uhr, und zwar in einem räumlichen Abstand von mehr als 3 Einheiten relativ zum Entstehungsort des ersten Lichtblitzes der linken Uhr.
Insofern ist der räumliche Abstand zwischen diesen beiden Ereignissen nicht etwa geschrumpft, sondern sogar gewachsen, nur dass die beiden Ereignisse nun nicht mehr gleichzeitig sind.
Wir können dies nachrechnen, indem wir oben \(t_{1} = t_{2} = t\) verwenden und den räumlichen Abstand dieser beiden Ereignisse im rechten Bezugssystem ausrechnen: \[ L'' = \gamma v t_{2} + \gamma L - \gamma v t_{1} = \] \[ = \gamma v t + \gamma L - \gamma v t = \gamma L \] Der räumliche Abstand zweier Ereignisse, die im Ruhesystem gleichzeit waren, wächst also, wenn man diese Ereignisse aus einem bewegten Bezugssystem heraus betrachtet, wobei sie aber dann nicht mehr gleichzeitig sind.
Man ist hier schnell in Versuchung, Formulierungen wie "die Ereignisse erscheinen einem nicht mehr gleichzeitig" zu verwenden, womit man unterstellt, dass die Ereignisse eigentlich gleichzeitig sind. Das widerspricht jedoch der Grundidee der speziellen Relativitätstheorie, nach der alle Inertialsysteme vollkommen gleichberechtigt sind. Insofern würde man beispielsweise im Bild rechts zwei Lichtblitz-Ereignisse selbstverständlich dann als gleichzeitig ansehen, wenn man ihnen dieselbe Zeitkoordinate zuordnen kann. Das bedeutet beispielsweise, dass beide Lichtblitze gleichzeitig einen Punkt erreichen, der sich räumlich genau zwischen den beiden Punkten befindet, an denen der Lichtblitz ausgesandt wurde (immer bezogen auf das gerade verwendete Bezugssystem).
Die Veränderung der Gleichzeitigkeit, die Lorentzkontraktion und die Zeitdilatation sind keine scheinbaren, sondern ganz reale physikalische Phänomene im folgenden Sinn: Sie hängen zwar vom Bezugssystem ab und haben daher keinen absoluten Charakter, aber sie führen zu messbaren physikalischen Phänomenen im jeweiligen Bezugssystem. Schnell bewegte Myonen leben im Durchschnitt länger als ruhende Myonen, und eine bewegte Ladungsdichte ist aufgrund der Lorentzkontraktion größer als dieselbe Ladungsdichte, wenn man sich mit ihr mitbewegt, und sie muss entsprechend in den Maxwellgleichungen verwendet werden. Das das so ist, wissen wir aus den Zusatzinfos zu Kapitel 1.4 Abschnitt d) Der relativistische Ursprung des Magnetfeldes.
Lorentzkontraktion, Zeitdilatation und die Relativität der Gleichzeitigkeit sind eng miteinander verknüpft, wie wir oben bereits gesehen haben. Die schnellen Myonen, die in der oberen Atmosphäre in ca. 10 km Höhe durch die kosmische Strahlung entstehen, sind dafür ein schönes Beispiel (siehe Zusatzinfos zu Kapitel 4.1 ). Die hohe Energie der Myonen führt aufgrund der Zeitdilatation zu einer Verlängerung ihrer Lebensdauer, so dass sie sogar den Erdboden erreichen können. Ohne diese Lebensdauerverlängerung wären sie bereits nach wenigen hundert Metern größtenteils zerfallen und kämen praktisch nie bis zum Erdboden.
Betrachtet man dieselbe Situation aus dem Ruhesystem des Myons heraus, so haben wir ein ruhendes Myon mit entsprechend kurzer Lebensdauer vor uns. Dafür sind aber in diesem Bezugssystem Atmosphäre und Erdboden bewegt, so dass nun die Lorentzkontraktion dafür sorgt, dass der auf das frisch entstandene Myon zurasende Erdboden nicht mehr 10 km, sondern nur noch wenige hundert Meter entfernt ist und das Myon ihn meistens erreicht, bevor es zerfällt.
Im Ruhesystem der Erde sorgt also die Zeitdilatation dafür, dass das Myon bis zum Erdboden vordringen kann, im Ruhesystem des Myons liegt es dagegen an der Lorentzkontraktion. Es hängt vom Bezugssystem ab, welchen Effekt wir für das physikalische Ergebnis verantwortlich machen, aber im jeweiligen Bezugssystem wirkt sich der Effekt ganz real auf das physikalische Ergebnis aus.
anschauliche Begründung für die Zeitdilatation:
Man kann sich den Grund für die Zeitdilatation sehr schön mithilfe einer Lichtuhr veranschaulichen. Die Lichtuhr besteht dabei aus zwei idealen Spiegeln im Abstand \(d\), zwischen denen ein Lichtblitz ständig hin- und herpendelt, wobei die Uhr die Zahl der pro Spiegel ankommenden Lichtblitze zählt und entsprechend seinen Zeiger weiterbewegt. Der pendelnde Lichtblitz bestimmt also, wie schnell unsere Lichtuhr tickt.
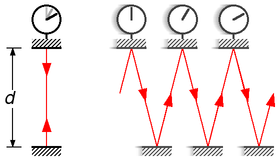
Quelle:
Wikimedia Commons File:Light-clock.png, Credit: Michael Schmid,
CC BY-SA 3.0 DEED
Betrachtet man die ruhende Lichtuhr links, so benötigt der Lichtblitz
für den Weg zwischen den beiden Spiegeln
die Zeit
\[
t = \frac{d}{c}
\]
Wenn wir aber nun die Uhr aus einem nach links bewegten Bezugssystem heraus betrachten, so dass sie sich
in diesem Bezugssystem mit der Geschwindigkeit v nach rechts bewegt, so muss das Licht nun einen längeren
schrägen Weg \(d'\) zwischen den Spiegeln zurücklegen
(siehe Bild oben rechts sowie die Grafik weiter unten).
Da die Lichtgeschwindigkeit auch in diesem Bezugssystem gleich \(c\) ist, benötigt das Licht für diesen längeren Weg auch eine längere Zeit \(t'\). Die bewegte Lichtuhr tickt langsamer als die ruhende Lichtuhr!
Aber auch jede andere bewegte Uhr tickt langsamer als dieselbe ruhende Uhr, denn wenn eine solche Uhr im ruhenden Bezugssystem synchron zur Lichtuhr läuft und wir diese beiden Uhren nun aus dem bewegten Bezugssystem heraus betrachten, so laufen beide Uhren immer noch synchron, auch wenn sie im neuen Bezugssystem nun beide nach rechts fliegen. Wäre es anders, so könnte man den Gangunterschied zweier relativ zueinander ruhender Uhren dazu verwenden, eine absolute Geschwindigkeit zu messen, und das widerspricht dem Relativitätsprinzip Einsteins.
Wie groß ist die Verlangsamung der Zeit? Nach Pythagoras (siehe Bild unten) ist die längere Strecke \(d'\) zwischen den mit Geschwindigkeit \(v\) nach rechts bewegten Spiegeln gleich \[ d' = \sqrt{d^{2} + (vt')^{2}} \] wobei \(t'\) die Zeit ist, die der Lichtstrahl für diese Längere Strecke \(d'\) benötigt, d.h. \[ d' = ct' \] (dabei setzen wir voraus, dass sich der direkte Abstand \(d\) zwischen beiden Spiegeln durch den Bezugssystemwechel nicht ändert, da er senkrecht zur Raumschiff-Bewegungsrichtung steht). Quadrieren und der Satz von Pythagoras ergeben \[ (d')^{2} = (ct')^{2} = \] \[ = d^{2} + (vt')^{2} \] also umgestellt \[ (ct')^{2} - (vt')^{2} = \] \[= d^{2} = (ct)^{2} \] und somit \[ t'^{2} \, (1 - (v/c)^{2}) = t^{2} \] d.h. \[ t' = \gamma t \] Das ist genau unser Ergebnis von oben.
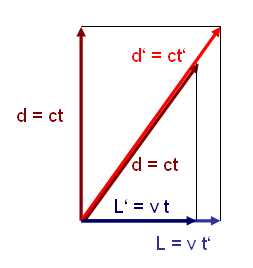
Im Ruhesystem der Spiegeluhr
legt der Lichtblitz die Strecke \(d\) zwischen den Spiegeln in der Zeit \(t\) zurück
und die Strecke \(L' = vt\) bewegt sich in dieser Zeit unter dem ruhenden unteren Spiegel hindurch.
Im bewegten Bezugssystem fliegt die Spiegeluhr gleichmäßig nach rechts,
so dass der Lichtblitz für die längere Strecke \(d'\) die Zeit \(t' = \gamma t\) benötigt.
In dieser Zeit \(t'\) überfliegt der untere Spiegel die (ruhende) Strecke \(L = vt'\).
anschauliche Begründung für die Lorentzkontraktion:
Die Lorentzkontraktion können wir direkt aus unserer obigen Veranschaulichung der Zeitdilatation ableiten. Dazu schauen wir uns das Bezugssystem an, in dem sich die Lichtuhr mit der Geschwindigkeit \(v\) nach rechts bewegt. Der Lichtblitz benötigt für den Weg zwischen den bewegten Spiegeln die Zeit \(t'\). In dieser Zeit legen die Spiegel den Weg \( L = v t' \) zurück, wobei diese Wegstrecke (also ihr Anfangs- und Endpunkt) sich bei vorgegebenem \(t'\)-Wert räumlich nicht bewegt – die Wegstrecke ruht in diesem Sinne in diesem Bezugssystem (deswegen haben wir den Strich bei \(L\) weggelassen, die Strecke also nicht \(L'\) genannt).
Betrachten wir speziell den bewegten unteren Spiegel, so sind Start- und Endpunkt der Strecke \(L\), die er zurücklegt, durch die x-Koordinaten definiert, die der untere Spiegel zu den Zeiten \(0\) und \(t'\) aufweist, also zu den Zeiten, an denen der Lichtblitz am unteren Spiegel startet bzw. beim oberen Spiegel ankommt. Dabei kommt die Gleichzeitigkeit ins Spiel, denn wir beurteilen den gleichzeitigen Ort beider Spiegel bei Start bzw. Ankommen des Lichtblitzes!
Nun wechseln wir zurück in das Bezugssystem, in dem die Lichtuhr ruht (siehe auch die Grafik oben). In diesem Bezugssystem bewegt sich diese Wegstrecke (also ihr Anfangs- und Endpunkt) von links nach rechts mit der Geschwindigkeit \( - v \) unter der ruhenden Lichtuhr hindurch. Zur Zeit Null (wenn also der Lichtblitz am unteren Spiegel startet) befindet sich dabei der linke Startpunkt der Strecke am Ort des ruhenden unteren Spiegels. Zur Zeit \(t\) (wenn also der Lichtblitz am oberen Spiegel ankommt) befindet sich dagegen der rechte Endpunkt der Strecke am Ort des ruhenden unteren Spiegels, während der linke Startpunkt um den Betrag \( L' = v t \) weiter nach links gewandert ist.
Nun wissen wir von oben, dass aufgrund der Zeitdilatation \( t' = \gamma t \) ist. Also ist \[ L' = v t = v t' / \gamma = L / \gamma \] Die sich bewegende Strecke \(L'\) erscheint also gegenüber der ruhenden Strecke \(L\) um den Faktor \( 1/\gamma \) verkürzt. Auch hier kommt die Gleichzeitigkeit ins Spiel, denn wir vergleichen den Aufenthaltsort der beiden sich bewegenden Endpunkte zur selben Zeit. Die Beurteilung der Gleichzeitigkeit ändert sich jedoch beim Wechsel des Bezugssystems.
anschauliche Begründung für die Relativität der Gleichzeitigkeit:
Betrachten wir zwei ruhende kleine Objekte, die sich im Abstand \(2L\) zueinander auf der räumlichen x-Achse befinden. Genau zwischen diesen Objekten starten wir einen Lichtblitz, der nach der Zeit \( L/c \) gleichzeitig bei den beiden Objekten ankommt, denn sie befinden sich ja beide in derselben Entfernung zur Lichtquelle, nur auf entgegengesetzen Seiten.
Nun betrachten wir dieselbe Situation wieder aus einem bewegten Bezugssystem heraus, das sich mit der Geschwindigkeit \(v\) nach links entlang der x-Achse bewegt. In diesem Bezugssystem bewegen sich die beiden Objekte also mit der Geschwindigkeit \(v\) nach rechts in x-Richtung. Da nun der in der Mitte ausgesendete Lichtblitz aber dem einen Objekt hinterherlaufen muss, während ihm das andere Objekt entgegenkommt, wird er nicht mehr gleichzeitig bei den beiden Objekten ankommen. Die beiden Ereignisse "Lichtblitz kommt beim jeweiligen Objekt an" sind nun nicht mehr gleichzeitig, obwohl sie es im anderen Bezugssystem waren. Hier ist das entsprechende Raumzeitdiagramm für \(v/c = 3/4\):
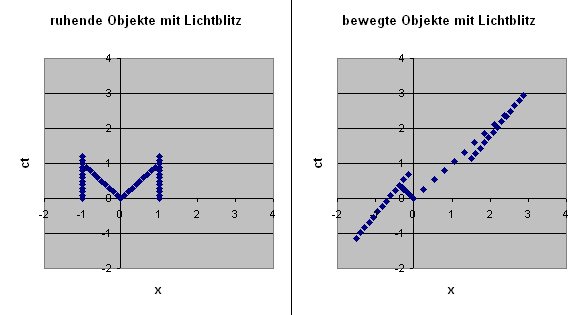
Relativität der Gleichzeitigkeit
Man sieht, wie der Lichtblitz in beiden Bezugssystemen vom Ursprungspunkt (0,0) ausgeht
und diagonal nach links und rechts oben läuft, also in beiden Bezugssystemen dieselbe
Geschwindigkeit c besitzt. Links ruhen die beiden Objekte bei x = 1 und -1, so dass ihre Weltlinien
senkrecht nach oben laufen und der Lichtblitz sie gleichzeitig trifft.
Rechts dagegen bewegen sie sich mit 3/4 Lichtgeschwindigkeit nach rechts,
so dass der Lichtblitz sie zu unterschiedlichen Zeitpunkten trifft.
Die einzelnen Punkte im Bild links und rechts gehören jeweils zu denselben Ereignissen
und wurden mithilfe der Lorentzmatrix in das jeweils andere Bezugssystem umgerechnet.
Wenn Sie sich mit Tabellenkalkulationsprogrammen (Excel & Co.) auskennen, können Sie selbst problemlos solche Raumzeit-Diagramme erstellen (die Umrechnung mithilfe der Lorentzmatrix ist ja recht einfach). Auf diese Weise können Sie selbst die unterschiedlichsten Situationen aus verschiedenen Bezugssystemen heraus grafisch darstellen und physikalisch beurteilen.
Noch eine Randbemerkung:
Zwei Ereignisse, die in irgendeinem Inertialsystem als gleichzeitig betrachtet werden können, hängen kausal nicht zusammen (egal in welchem Bezugssystem), da sich jede Information maximal mit Lichtgeschwindigkeit ausbreiten kann. Genau das ist die Lösung für viele scheinbare Paradoxa in der speziellen Relativitätstheorie.
Ein Beispiel dafür ist das Stab-Scheune-Paradoxon (Garagenparadoxon): Ein bewegter (und daher lorentzkontrahierter) Stab durchfliegt sehr schnell eine ruhende Scheune, die etwas größer als der Stab ist. Für ein gewisses Zeitintervall befinden sich also Anfangs- und Endpunkt des Stabes gleichzeitig innerhalb der Scheune. Im Ruhesystem des Stabes bewegt sich jedoch die Scheune, so dass nun diese lorentzkontrahiert ist. Daher kann es in diesem Bezugssystem bei genügend großer Geschwindigkeit geschehen, dass die Scheune kleiner als der Stab ist, so dass sich Anfangs- und Endpunkt des Stabes niemals gleichzeitig innerhalb der Scheune befinden.
Ein Widerspruch?
Nein, denn dieser Unterschied zwischen den beiden Bezugssystemen kann sich physikalisch nicht auswirken, da die beiden Ereignisse "vorderes Stabende verlässt die Scheune" und "hinteres Stabende betritt die Scheune" kausal nicht zusammenhängen, sofern der oben beschriebene Unterschied zwischen den beiden Bezugssystemen besteht.
Im Ruhesystem der Scheune betritt das hintere Stabende die Scheune und kurz danach verlässt das vordere Stabende die Scheune, im Ruhesystem des Stabes ist es umgekehrt. Die Relativität der Gleichzeitigkeit wirkt sich hier aus. Dabei kann sich – wie in diesem Fall – die zeitliche Reihenfolge von Ereignissen sogar umdrehen, sofern beide Ereignisse raumartig zueinander liegen, d.h. solange das Licht zeitlich keine Chance hat, Informationen vom einen Ereignis zum anderen Ereignis zu transportieren.
Dafür muss der Stab allerdings schon sehr schnell und Stab sowie Scheune müssen sehr groß sein – man denke da eher an Ausmaße wie beim Planeten Jupiter und nicht an handelsübliche Scheunen. Siehe auch Klaus Kassner: Das Stab-Scheune-Paradoxon, Wikipedia: Garagenparadoxon sowie Wikipedia: Ehrenfestsches Paradoxon und Wikipedia: Geschichte der speziellen Relativitätstheorie#Starre Körper und Realität der Längenkontraktion.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 03 January 2024