Darstellung der Polarisationswolke eines Elektrons mit Hilfe von Feynmangraphen. Die Zeit läuft hier ausnahmsweise nach rechts.
Die Eigenschaften eines physikalischen Teilchens ergeben sich durch das Zusammenwirken von zentralem Teilchen und seiner Polarisationswolke aus virtuellen Teilchen.
Beginnt man nun, die Beiträge der einzelnen Graphen zu berechnen, so macht man eine unangenehme Entdeckung: sobald beispielsweise ein virtuelles Elektron-Positron-Paar (eine Schleife) auftaucht, wird der Beitrag des entsprechenden Graphen unendlich groß, da die viertuellen Teilchen beliebig große Impulse besitzen können, deren Beiträge alle aufsummiert werden müssen!
Die Lösung des Problems gelang schließlich im Jahre 1948 den Physikern Julian Schwinger, Sin-Hiro Tomonaga und Richard P. Feynman. Wie man mit dem Problem fertig wurde, kann am Beispiel der geometrischen Reihe verdeutlicht werden.
Nehmen wir in unserem Beispiel an, dass als Ergebnis der unendlich langen Summe von Feynmangraphen für die physikalische Ladung des Elektrons die Formel
herausgekommen wäre. Dabei ist E die Ladung des Elektrons, die bei dem Viererimpulsquadrat x des ankoppelnden Photons auftritt, e ist die Ladung der nackten Elektronen, die als Linien in den Feynmangraphen auftreten, und P stellt die durch die Elektron-Positron-Loops auftretenden Unendlichkeiten dar. Wir müssen also zu einem geeigneten Zeitpunkt den Fall untersuchen, bei dem P beliebig groß werden kann.
Wie wir sehen, haben wir eine geometrische Reihe vor uns, die wir schreiben können als
Hier tritt nun die Unendlichkeit auf, die wir uns durch beliebig große Werte von P dargestellt denken wollen. Die physikalische Ladung E kann daher nur dann endlich bleiben, wenn mit wachsendem P gleichzeitig die nackte Ladung e immer kleiner wird. Dagegen ist nichts einzuwenden, da die nackte Ladung selbst ja keine physikalisch beobachtbare Größe ist. Der Haken bei der Angelegenheit liegt nun aber darin, dass sich die obige Formel nun nicht mehr zur Berechnung der physikalischen Ladung E eignet, da jeder beliebige Wert von E auf der linken Seite stehen kann. Dieser Wert für E hängt davon ab, auf welche Weise P wächst und e schrumpft.
Umgekehrt legt ein beliebiger Wert für E bei gegebenem x fest, auf welche Weise sich e bei wachsendem P verhalten muss. Der einzige Weg, hier weiter zu kommen, besteht daher in der Vorgabe einer Referenzladung E0 bei irgendeinem vorgegebenem Viererimpulsquadrat x0. Da sich ein solcher Wert offenbar nicht ausrechnen lässt, bleibt nur der Weg, ihn im Experiment zu bestimmen und gleichsam als Aufhängepunkt in die Rechnung einfließen zu lassen. Wir messen also, welche physikalische Ladung E0 beim Viererimpulsquadrat x0 des Photons auftritt. Man nennt einen solchen Punkt Renormierungspunkt. Für den Renormierungspunkt gilt also:
Wir könnten diese Beziehung nach der nackten Ladung e freistellen, sie in die Beziehung E = e / (1 − e (x+P)) einsetzen und so versuchen, gleichzeitig die nackte Ladung e und die Unendlichkeit P loszuwerden.
Schritt 1: Renormierungspunkt nach e freistellen ergibt:
Diese Gleichung legt nun fest, wie bei fest vorgegebenem Renormierungspunkt (feste Werte von E0 und x0) die nackte Ladung e schrumpfen muss, wenn P immer größer wird.
Schritt 2: Einsetzen von diesem e in E = e / (1 − e (x+P)) ergibt:
und nach kurzer Rechnung schließlich
|
Tatsächlich konnten wir sowohl die nackte Ladung e als auch die Unendlichkeit P eliminieren und haben eine Formel erhalten, die nur noch physikalisch messbare Größen enthält.
Es ist uns damit tatsächlich gelungen, unter Verwendung der am Renormierungspunkt x0 gemessenen Ladung E0 dem anfangs so sinnlos erscheinenden Ausdruck für die Ladung E einen präzisen Sinn zu geben und sie am Renormierungspunkt gleichsam zu verankern. Es ergibt sich eine Formel, die eine gleitende Ladung repräsentieren könnte. Die Tatsache, dass irgendein Renormierungspunkt x0 vorgegeben werden muss, bedeutet, dass durch die Renormierung der dimensionsbehaftete Parameter x0 in die Theorie hineingeraten ist, der vor der Renormierung nicht darin enthalten war. Man sagt, die Renormierung führt eine Skala in die Theorie ein. Es muss dabei vollkommen egal sein, welchen Renormierungspunkt man wählt. In der Quantenfeldtheorie führt diese Forderung zu einer mathematischen Struktur, die als Renormierungsgruppe bezeichnet wird.
Die obige Rechnung lässt sich auch durchführen, wenn wir die einzelnen geometrischen Reihen als unendliche Summe hinschreiben und nur einige wenige Terme berücksichtigen. Die Unendlichkeit lässt sich dann immer in den Term verschieben, den man bei dieser Näherung nicht mehr berücksichtigt. Genau so geht man in der Quantenfeldtheorie auch vor, wenn man nur bestimmte Feynmangraphen berücksichtigt. Im Buchkapitel finden sich Details dazu.
In der Quantenfeldtheorie sind nun die mathematischen Ausdrücke nicht so einfach wie in dem oben dargestellten einfachen Beispiel. Insbesondere muss hier zunächst überprüft werden, ob die Theorie überhaupt renormierbar ist, d.h. ob sich mit dem hier skizzierten Verfahren die Unendlichkeiten tatsächlich entfernen lassen. Die Quantenfeldtheorien des Standardmodells sind renormierbar. Bei der Gravitation gibt es dagegen Probleme, die man heute als Hinweise auf die Notwendigkeit einer umfassenderen fundamentaleren Theorie deutet (mehr dazu im Buch).
a) Renormierbarkeit und Renormierungsgruppe
Versuchen wir, die Idee der Renormierung noch etwas allgemeiner zu verstehen. Wir wollen als Beispiel eine Theorie mit nur einem Teilchen und nur einer Ladung betrachten, wobei m die physikalische Teilchenmasse und e(μ) die physikalische Ladung bei einem Referenzimpuls μ sein soll (die Bezeichnungen weichen im Folgenden von denen im Buchkapitel ab und orientieren sich an gängigen Bezeichnungen der Fachliteratur; μ entspricht dabei x0 und e(μ) entspricht E0 ). Als Beispiel können wir uns die Quantenelektrodynamik von Elektronen vorstellen, wobei wir das Photon und seine Masse sowie Teilchenspins nicht weiter beachten.
Die entsprechende Quantenfeldtheorie wird nun zunächst mit Hilfe der nackten Teilchenmasse m0 und der nackten Ladung e0 (im Buchkapitel als e bezeichnet) formuliert, d.h. jede beobachtbare Wahrscheinlichkeitsamplitude A ist zunächst durch einen entsprechenden mathematischen Ausdruck gegeben, der e0 und m0 enthält. Typischerweise ist dieser Ausdruck eine unendlich lange Störungsreihe mit wachsenden Potenzen von e0 , entsprechend den möglichen Feynmangraphen mit immer mehr Vertices. Die inneren Loops (Schleifen) in diesen Feynmangraphen führen dabei zu Unendlichkeiten, da die virtuellen Teilchen in diesen Loops beliebig große Impulse aufweisen können, die man in den zugehörigen Impulsintegralen alle berücksichtigen muss. Diese Unendlichkeiten muss man beseitigen, indem man nur Impulse bis zu einem Maximalwert M berücksichtigt oder diese ab da zumindest abschwächt (es gibt technisch auch noch andere Möglichkeiten; M kann man mit der Unendlichkeit P aus dem Buchkapitel identifizieren). Man führt also künstlich eine Maximalenergie (auch Cutoff oder Regularisierung genannt) M ein. Gleichbedeutend kann man auch sagen, dass man nur Abstände ab einem bestimmten Minimalabstand berücksichtigt. Die Amplitude A ist also zunächst gegeben durch eine Funktion (regularisierte Störungsreihe)
A( p, e0, m0, M )
wobei p stellvertretend für alle Teilchenimpulse steht, von denen die Amplitude abhängen kann. Nun darf der Energie-Cutoff M eigentlich keine Rolle spielen, wenn die Theorie auch für sehr große Energien noch gültig sein soll. Wir müssen die Theorie also so umformulieren, dass wir den Grenzwert unendlich großer M durchführen können. Die ursprüngliche regularisierte Störungsreihe A(p, e0, m0, M) gibt das allerdings zunächst nicht her, denn in ihr treten ja aufgrund der inneren Loops der Feynmangraphen die Unendlichkeiten auf. Diese Unendlichkeiten bei wachsendem M müssen wir irgendwie kompensieren. Wir fordern nun, dass diese Kompensation möglich ist, indem wir bei wachsendem M auch die nackte Ladung und die nackte Masse geeignet verändern. Dazu ersetzen wir e0 und m0 durch geeignete universelle Funktionen e0(M) und m0(M) und fordern, dass der folgende Grenzwert existiert:
|
Renormierbarkeit: Renormierbarkeit bedeutet, dass es universelle Funktionen e0(M) und m0(M) gibt, so dass für jede beobachtbare Wahrscheinlichkeitsamplitude A der Grenzwert der zugehörigen regularisierten Störungsreihe lim(M → ∞) A( p, e0(M), m0(M), M ) existiert, wobei die Funktionen e0(M) und m0(M) nicht von der betrachteten Amplitude A abhängen dürfen, sondern für jede beobachtbare Amplitude dieselben sein müssen (daher die Bezeichnung universell). |
Die Idee ist dabei, dass für wachsenden Cutoff M beispielsweise die nackte Ladung e0(M) immer kleiner (oder größer) wird, so dass der Gesamtausdruck immer endlich bleibt. Bei unendlich großem M wird schließlich e0(M) = e0 (analog bei der Masse), wobei e0 durchaus infinitesimal klein werden kann. In diesem Sinn existiert dann auch der ursprüngliche Ausdruck A(p, e0, m0, M) für unendlich großes M .
Ob diese Forderung erfüllt werden kann und geeignete universelle Funktionen e0(M) und m0(M) existieren, hängt von der betrachteten Theorie ab. Falls ja, dann ist die Theorie renormierbar.
Schauen wir uns an, wie man im Prinzip die Funktionen e0(M) und m0(M) findet und so die Unendlichkeiten beseitigt. Dazu benötigt man zwei physikalische Messgrößen, an denen man die gesamte Rechnung gleichsam aufhängt.
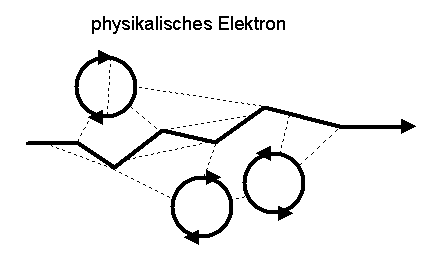
Eine dieser Messgrößen ist die physikalische Teilchenmasse m . In der Quantenfeldtheorie schlägt sich diese physikalische Teilchenmasse im physikalischen Teilchenpropagator nieder, der durch die Summe aller Feynmangraphen gegeben ist, bei denen ein nacktes Teilchen (mit nackter Masse m0 ) beliebig viele virtuelle Teilchen aussendet und wieder einfängt (Polarisationswolke). Ein möglicher Feynmangraph für den physikalischen Teilchenpropagator eines Elektrons in der QED ist in der Abbildung zu Beginn dieses Kapitels dargestellt.
Dabei tritt für die Vertices die nackte Ladung e0 und für innere Linien der nackte Propagator auf, der in natürlichen Einheiten durch
1 / (p2 − m02)
gegeben ist (siehe Zusatzinfos zu Kapitel 5.2; dabei ist p2 das Viererimpulsquadrat des Teilchens). Loops in diesen Graphen führen dabei zu Unendlichkeiten, die wir beseitigen können, indem wir den nackten Propagator formal durch den regularisierten (nackten) Propagator
1 / [ p2 − (m0(M))2 ] − 1 / [ p2 − M2 ]
sowie e0 durch e0(M) ersetzen. Die genaue Abhängigkeit der Funktionen m0(M) und e0(M) von M ist dabei noch unbekannt -- sie muss gleich noch durch physikalische Messgrößen fixiert werden.
Die obige Regularisierung bezeichnet man als Pauli-Villars-Regularisierung. Man kann sich dabei vorstellen, dass man formal ein weiteres sehr schweres Teilchen mit Masse M in die Theorie einfügt und dessen Propagator vom nackten Propagator des m0-Teilchens abzieht. Bei Impulsquadraten deutlich oberhalb von M2 geht der regularisierte Probagator weit schneller gegen Null als ohne Regularisierung, so dass die Loop-Integrale endlich bleiben, solange M endlich ist. In diesem Sinn verringert M den Einfluss der großen Impulse im Propagator, ist also gleichsam ein weicher Cutoff. Es gibt auch noch andere Möglichkeiten zur Regularisierung, beispielsweise die dimensionale Regularisierung, die besonders für Eichtheorien geeignet ist. Im Grenzfall unendlich großer M geht der regularisierte Propagator in den nackten Propagator über.
Man kann nun zeigen, dass sich der volle regularisierte Propagator (also die Summe aller Propagatorgraphen mit regularisiertem nackten Propagator) in der folgenden Form schreiben lässt:
1 / [ p2 − m2 − Σ( p2, e0(M), m0(M), M ) ]
Dabei haben wir bereits die physikalische Teilchenmasse m verwendet. Man kann weiter zeigen, dass der physikalische Propagator bei p2 = m2 einen Pol haben muss, so wie der nackte Propagator einen Pol bei der nackten Masse m0 besitzt, denn nur dann beschreibt er auch die Fortbewegung eines Teilchens (siehe Kapitel 5.2 ). Wir fordern nun, dass auch der volle regularisierte Propagator bei endlichem M diese Eigenschaft aufweisen soll. Entsprechend muss bei bei p2 = m2 für beliebige endliche M gelten:
| Σ( m2, e0(M), m0(M), M ) = 0 |
Dies ist die erste Forderung, die die Form der beiden Funktionen e0(M) und m0(M) festlegt, wobei die physikalische Teilchenmasse m als erster Aufhängepunkt dient (in der QED ergibt sich für das Photon und seine Masse eine analoge Forderung).
Die zweite Forderung kommt über die physikalische Ladung e(μ) zustande. Wir bilden dazu beispielsweise in der QED die Summe aller Feynmangraphen, die die Wechselwirkung eines Photons mit einem Elektron beschreiben:
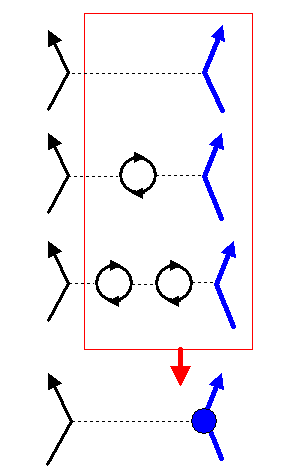
Die Unendlichkeiten in diesen Graphen beseitigen wir wieder wie oben, indem wir den
nackten Propagator durch den regularisierten Propagator sowie e0 durch e0(M) ersetzen.
Die Summe dieser Graphen ergibt dann einen Ausdruck
E( q, e0(M), m0(M), M ) ,
wobei q die Impulse von einlaufendem Elektron und Photon zusammenfasst
(die Bezeichnung E wurde in Analogie zum Buchkapitel gewählt, während die anderen Bezeichnungen abweichen:
q entspricht x, μ entspricht x0 und e0 entspricht e).
Diesen Ausdruck wollen wir im Grenzfall unendlicher M
als physikalische Elektronladung e(q) interpretieren, die man bei den
Impulsen q misst. Wir wollen nun einen Satz von Standardimpulsen μ wählen
(z.B. ein ruhendes Elektron und ein sehr energiearmes Photon) und die physikalische Ladung e(μ) bei diesen Impulsen
als zweiten Aufhängepunkt verwenden, d.h. wir fordern für beliebige endliche M:
| E( μ, e0(M), m0(M), M ) = e(μ) |
(dabei entspricht μ dem Wert x0 im Buchkapitel und e(μ) entspricht E0 im Buchkapitel). Dieser zweite Aufhängepunkt legt zusammen mit dem ersten Aufhängepunkt die beiden Funktionen e0(M) und m0(M) für beliebige M fest. Damit ist gesichert, dass auch für endliche M zumindest die physikalische Masse m und die physikalische Ladung e(μ) beim Standardimpuls μ durch die entsprechenden regularisierten Störungsreihen reproduziert werden. Im Grenzfall unendlicher M bleibt diese Eigenschaft bei renormierbaren Theorien erhalten, wobei dann die physikalische Ladung e(q) auch bei anderen Impulsen q richtig herauskommen muss:
lim(M → ∞) E( q, e0(M), m0(M), M ) = e(q)
Analog muss bei unendlichen M auch der Propagator (also die Funktion Σ( p2, e0(M), m0(M), M ) ) für alle Werte des Teilchenimpulses p stimmen, und nicht nur beim Pol p2 = m2 .
Wie kann man sich nun konkret die Ermittlung der beiden Funktionen e0(M)
und m0(M) vorstellen? Meist sind ja die beiden Bedingungen
Σ( m2, e0(M), m0(M), M )
= 0 und
E( μ, e0(M), m0(M), M ) = e(μ)
nicht so einfach, dass sie sich formal nach e0(M)
und m0(M) auflösen lassen (das Beispiel im Buchkapitel ist da einfacher).
Im Rahmen der Störungstheorie sind sie vielmehr durch unendlich lange Potenzreihen mit wachsenden
Potenzen in e0(M) gegeben. Diese Potenzreihen muss man
nach endlich vielen Gliedern abbrechen, d.h. man berücksichtigt die Bedingungen nur bis zu einer gewissen Ordnung.
Die gesuchten Funktionen e0(M) und
und m0(M) stellt man nun als Potenzreihen
|
e0(M) = ∑i ci(M,μ) (e(μ))i
m0(M) = ∑i di(M,μ) (e(μ))i |
in e(μ) dar und bricht diese ebenfalls bei derselben Ordnung ab wie die Bedingungs-Potenzreihen. Nun setzt man diese Potenzreihen für e0(M) und und m0(M) in die beiden Bedingungs-Potenzreihen ein und ermittelt z.B. über Koeffizientenvergleich die Koeffizientenfunktionen ci(M,μ) und di(M,μ) . Bis zu der anvisierten Genauigkeit (Ordnung der Potenzreihen) hat man damit die beiden Funktionen ermittelt und kann sie in andere Amplituden A( p, e0(M), m0(M), M ) einsetzen. Diese Amplituden sind ursprünglich Potenzreihen in der nackten Ladung e0(M) und werden durch das Einsetzen umgeschrieben in Potenzreihen in der physikalischen Ladung e(μ) . Dabei entstehen aus verschiedenen Koeffizienten der e0 -Potenzreihe jeweils neue Koeffizienten der e(μ)-Potenzreihe, indem man Terme mit gleicher Potenz von e(μ) zusammenfasst. Während die Koeffizienten der ursprünglichen e0 Potenzreihe noch Unendlichkeiten enthalten, wenn M unendlich wird, enthalten die daraus gebildeten Koeffizienten der e(μ)-Potenzreihe keine solchen Unendlichkeiten mehr, sodern streben für unendlich großes M einem definierten Grenzwert zu. Beim Zusammenstellen zu neuen Koeffizienten fallen also die Unendlichkeiten der alten Koeffizienten heraus oder heben sich gegenseitig auf, sofern die Theorie renormierbar ist -- das gilt zumindest für die Koeffizienten bis zu der betrachteten Ordnung der Potenzreihen.
Hier zwei Beispiele, wie die Unendlichkeiten herausfallen können: Im Buchbeispiel oben ergibt die Reihenentwicklung in der dortigen Schreibweise E = e + e2 (x + P) + ... . Einsetzen von e = E0 − E02 (x0 + P) + ... ergibt
E =
E0 − E02 (x0 + P) + E02 (x + P) + ...
=
=
E0 + E02 [(x + P) − (x0 + P)] + ...
=
=
E0 + E02 (x − x0) + ...
Übertragen in die Schreibweise dieses Abschnitts bedeutet das, dass in diesem Beispiel e0(M) den Koeffizienten c1(M,μ) = μ + M hätte, der aber beim Aufstellen der neuen Potenzreihe auf den Term p + M stößt, so dass bei der Differenzbildung die Regularisierung M herausfällt.
Ein zweites Beispiel kennen wir aus den Zusatzinfos zu Kapitel 5.4. Bei der Berechnung der gleitenden Ladung α(q2) tritt die Differenz ln( |μ2| / M2 ) − ln( |q2| / M2 ) = − ln( |q2| / |μ2| ) ] auf, bei der die Regularisierung M ebenfalls wegfällt.
Jede Amplitude A einer renormierbaren Theorie lässt sich mit Hilfe der Renormierung als Potenzreihe in e(μ) umschreiben, also letztlich als Funktion A' der physikalischen Ladung e(μ) und der Masse m sowie der relevanten Impulse p und μ:
| lim(M → ∞) A( p, e0(M), m0(M), M ) = A'( p, e(μ), m, μ ) |
Dabei wurden die physikalischen Parameter m und e(μ) als Aufhängepunkte (Renormierungspunkte) hineingesteckt, um die Funktionen e0(M) und m0(M) (die das Verhalten der nackten Parameter bei wachsendem Cutoff M beschreiben) überhaupt definieren zu können. Es muss dabei egal sein, bei welchem Referenzimpuls μ wir die Ladung e(μ) messen. Wir könnten auch einen anderen Referenzimpuls μ' wählen, bei dem die physikalische Ladung einen anderen Wert e(μ') aufweist, und diesen Referenzwert für die Renormierung verwenden. Das darf auf die physikalische Amplitude A keinen Einfluss haben, d.h. es muss gelten:
A'( p, e(μ), m, μ ) = A'( p, e(μ'), m, μ' )
Man kann also eine renormierbare Quantenfeldtheorie durch Ladungen e(μ) bei verschiedenen Impulsen μ parametrisieren. Bei Berücksichtigung aller Terme der e(μ)-Potenzreihe muss sie aber für verschiedene Renormierungspunkte μ und zugehörige Ladungen e(μ) immer dasselbe Ergebnis liefern, d.h. die μ-Abhängigkeit der Koeffizienten und die μ-Abhängigkeit der gleitenden Ladungen e(μ) muss sich in Summe gegenseitig kompensieren (zur gleitenden Ladung siehe Kapitel 5.4 ). Zusammenhänge dieser Art, die die Willkürlichkeit des Renormierungspunktes ausdrücken, bilden insgesamt eine mathematische Struktur, die man als Renormierungsgruppe bezeichnet.
Zur Berechnung von A'( p, e(μ), m, μ ) für einen bestimmten p-Impulsbereich ist es sinnvoll, auch den Renormierungspunkt μ aus demselben Impulsbereich zu wählen, da dann bereits die ersten Terme der Potenzreihe ein gutes Ergebnis liefern (sofern e(μ) deutlich kleiner als 1 ist). Das macht man beispielsweise in der QCD bei sehr hochenergetischen Prozessen -- entsprechend wählt man auch passende große μ-Werte, bei denen die starke Ladung e(μ) dann relativ kleine Werte aufweist, so dass die Störungsreihe funktioniert.
Muss eine Quantenfeldtheorie renormierbar sein? Früher hielt man diese Forderung für unverzichtbar, doch diese Ansicht hat sich mittlerweile geändert. Man glaubt heute, dass Quantenfeldtheorien sogenannte effektive Theorien sind, also Niederenergie-Grenzwerte einer fundamentaleren Theorie, in der der oben künstlich eingeführte Cutoff M eine reale physikalische Bedeutung hat, beispielsweise gleich der Planck-Energie ist. Der oben durchgeführte Grenzwert unendlicher M in der Quantenfeldtheorie ist also nichts Anderes als die Bedingung, dass die betrachteten Impulse deutlich kleiner als M sein müssen. Man kann mit Hilfe der Renormierungsgruppe zeigen, dass dann alle nicht-renormierbaren Wechselwirkungsanteile einer fundamentaleren Theorie stark unterdrückt sind und nur renormierbare Wechselwirkungsanteile übrig bleiben (siehe auch Die Symmetrie der Naturgesetze, Kapitel 4.15: Aufbau der Quantenfeldtheorie nach Steven Weinberg, Abschnitt 12 ). Kein Wunder also, dass das Standardmodell renormierbar ist, während die sehr viel schwächere Gravitation nicht-renormierbar ist. Entsprechend lässt sich in einer Quantentheorie der Gravitation auch der Grenzwert unendlicher M nicht durchführen, denn diese Theorie ist erst bei Impulsen der Größenordnung M (Planck-Masse) relevant.
Literatur:
last modified on 27 August 2010