
Quelle: Wikimedia Commons File:Steven weinberg 2010.jpg, Credit: Larry D. Moore, CC BY 4.0
Als ich
Steven Weinbergs Buch The Quantum Theory of Fields (Vol. 1) zum ersten Mal gesehen habe, war ich begeistert:
Endlich ein Buch, das historischen Ballast abwirft und versucht, die Quantenfeldtheorie methodisch so zu
entwickeln, wie man das aus heutiger Sicht machen würde.

Quelle: Wikimedia Commons
File:Steven weinberg 2010.jpg, Credit: Larry D. Moore,
CC BY 4.0
Die übliche Vorgehensweise orientierte sich bis dahin (und tut es oft immer noch) am historischen Werdegang der Quantenfeldtheorie: In Analogie zur nichtrelativistischen Wellenfunktion wird versucht, eine relativistische Wellenfunktion und eine zugehörige relativistische Differenzialgleichung zu finden. Man stößt auf die Klein-Gordon-Gleichung (KGG) bzw. die Diracgleichung (DGL). Dann stellt man fest, dass die Lösungen dieser Gleichungen sich nicht als Wellenfunktionen eignen, denn es treten negative Energien und teilweise (KGG) auch negative Aufenthaltswahrscheinlichkeiten auf. Sobald man Theorien mit Wechselwirkung untersucht, wirken sich diese Probleme verheerend aus. Den Grund kennen wir bereits: Bei den Lösungen der KGG und der DGL handelt es sich um Felder, nicht um Wellenfunktionen.
Die klassische Vorgehensweise startet also mit Feldern. Auch in der Quantenelektrodynamik ist das so: dort startet man mit dem elektromagnetischen Feld. Im nächsten Schritt versucht man, eine Quantentheorie zu konstruieren, die zu diesen Feldern passt. Die entsprechende Technik nennt man zweite Quantisierung, was laut Weinberg sehr verwirrend ist, denn man hätte ja nur dann eine erste Quantisierung bereits hinter sich, wenn die Felder bereits Wellenfunktionen wären. Der historische Hintergrund für diese Bezeichnung ist: In der nichtrelativistischen Quantenmechanik benutzt man diese Technik, um von einer Einteilchen-Theorie zu einer Vielteilchen-Theorie überzugehen. Bei relativistischen Theorien mit Wechselwirkung ist eine Quantentheorie aber immer eine Vielteilchen-Theorie, denn Energie kann zur Bildung neuer Teilchen verwendet werden. Deshalb gibt es dort auch keine erste Quantisierung (eine Einteilchen-Quantentheorie mit Wellenfunktionen), sondern nur eine zweite Quantisierung der Felder. Am Besten ist es laut Weinberg, den Begriff zweite Quantisierung hier komplett zu streichen, denn er suggeriert, dass man über einer erste Quantisierung zunächst Wellenfunktionen konstruiert, die man dann einer zweiten Quantisierung unterwirft und so zu einer Vielteilchentheorie gelangt. Korrekt ist aber, dass man relativistische Felder quantisiert, was automatisch zu einer Vielteilchentheorie führt.
Weinberg verwendet den Begriff zweite Quantisierung nicht, und er startet auch nicht mit Feldern und quantisiert diese. Statt dessen verwendet er eine direkte Konstruktion von Quantenfeldern mit Hilfe von Teilchen-Erzeugungs- und Vernichtungsoperatoren, so dass ein direkter Zusammenhang zwischen Quantenzuständen und Quantenfeldern hergestellt wird (siehe unten). Hier ein Zitat von Weinberg dazu aus What is Quantum Field Theory, and what did we think it is? Steven Weinberg, 1997, arXiv:hep-th/9702027v1 (im Internet leicht zu finden – sehr lesenswert, denn hier beschreibt Weinberg noch einmal sehr übersichtlich, wie er Quantenfeldtheorie sieht und warum sie so aussieht, wie sie ist):
"Although this is often talked about as second quantizaion, I would like to urge that this description should be banned from physics, because a quantum field is not a quantized wave function. Certainly the Maxwell field is not the wave function of the photon, and for reasons that Dirac himself pointed out, the Klein-Gordon fields that we use for pions and Higgs bosons could not be the wave functions of the bosons."
Weinberg geht folgendermaßen vor: Er startet mit den Prinzipien der Quantentheorie, also mit quantenmechanischen Zuständen und ihrer Darstellung durch Vektoren in einem Hilbertraum (analog zu Kapitel 4.5 Das mathematische Gerüst der Quantentheorie). Dann nimmt er die Prinzipien der speziellen Relativitätstheorie hinzu und formuliert sie als Symmetrien in der Quantentheorie (analog zu Kapitel 4.6 bis Kapitel 4.10). Als Ergebnis erhält er die Darstellungen der Poincarégruppe auf den Quantenzuständen (siehe bei uns Kapitel 4.10). Damit wissen wir, welche quantenmechanische Zustände es geben kann und wie sie sich bei Raum-Zeit-Transformationen verhalten. Die Quantenfelder werden nun als Hilfsmittel definiert, um Objekte zur Verfügung zu haben, die ein einfacheres Transformationsverhalten aufweisen als die Quantenzustände. Anders als bei der üblichen Vorgehesweise quantisiert Weinberg also keine klassischen Felder, um zu Quantenfeldern zu gelangen, sondern er konstruiert Quantenfelder direkt auf Basis der relativistischen Quantenzustände.
Soviel zur Grundidee von Weinbergs Buch. In vielen Aspekten entspricht diese Grundidee dem Weg, den ich in den letzten Kapiteln ebenfalls eingeschlagen habe, wobei Weinberg natürlich noch weit darüber hinaus geht. Ich möchte daher die einzelnen Kapitel in seinem Buch nun Schritt für Schritt durchgehen und kurz zusammenfassen, worum es in dem jeweiligen Kapitel geht:
Weinberg beantwortet die Frage Why another book on quantum field theory? mit dem Versuch, den begrifflichen Rahmen für die Quantenfeldtheorie so allgemein wie nur möglich zu entwerfen und präzise zu begründen, warum die Struktur der Quantenfeldtheorie gerade die dargestellte Form hat (... give the reader the clearest possible idea of why this theory takes the form it does ...). Der klassische Zugang über Felder lässt für Weinberg zu viele Fragen offen (und das geht sicher vielen Physik-Studenten so): Why should we believe in the rules of canonical quantization or path integration? Genau: das erschien mir auch immer wie ein Kochrezept zu sein, das man aus der nichtrelativistischen Quantenmechanik übernommen hat und das irgendwie funktioniert. Wer sich für dieses Kochrezept interessiert: siehe Quantenfeldtheorie und Eichfelder, Kapitel 4 und Kapitel 5.
Weinberg unternimmt dagegen in seinem Buch den Versuch, zu zeigen, dass sich die dargestellte Struktur der Quantenfeldtheorie fast zwingend aus den Prinzipien der Quantentheorie und der speziellen Relativitätstheorie ergibt (wenn man von punktförmigen Teilchen in der Raumzeit ausgeht und zusätzlich fordert, dass sich weit voneinander entfernte Experimente nicht kausal gegenseitig beeinflussen – siehe das Cluster Decomposition Principle weiter unten).
Verzichtet man auf punktförmige Teilchen, so gibt es ein bekanntes Gegenbeispiel, das Weinberg in What is Quantum Field Theory, and what did we think it is? Steven Weinberg, 1997, arXiv:hep-th/9702027v1 selbst anführt: die Stringtheorie. Geht man aber davon aus, dass bei niedrigen Energien (verglichen mit der Planck-Energie) die Strings wie punktförmige Teilchen aussehen, so ergibt sich in diesem Grenzfall aus der String-Theorie wieder eine Quantenfeldtheorie. Es ist also nicht zwingend (und auch unwahrscheinlich), dass die grundlegende Theorie der Natur eine Quantenfeldtheorie ist. Aber es liegt nahe, dass jede Quantentheorie, die bei niedrigen Energien und großen Abständen (verglichen mit Planck-Energie und Planck-Länge) Lorentz-invariant ist und das Cluster-Decomposition-Prinzip erfüllt, in diesem Grenzfall wie eine Quantenfeldtheorie aussieht. In diesem Sinne spricht man auch von effektiven Quantenfeldtheorien. Die Lagrangefunktionen des Standardmodells und der allgemeinen Relativitätstheorie wären dann nur die führenden Terme in einer effektiven Feldtheorie. Übrigens muss eine effektive Feldtheorie nicht unbedingt renormierbar im klassischen Sinn sein (mehr dazu unten).
Da Weinberg in seinem Buch nicht dem Weg folgt, wie sich Quantenfeldtheorie historisch entwickelt hat, gibt er in diesem Kapitel einen kurzen Überblick über die historische Entwicklung. Wer andere Standardwerke der Quantenfeldtheorie kennt, wird dort diese historische Entwicklung oft wiederfinden. So begegnet man dem Dirac-See, bei dem das Problem der negativen Energien in der Diracgleichung dadurch gelöst wurde, dass man alle negativen Energiezustände als gefüllt ansieht. Antiteilchen sind dann Löcher im Diracsee. Schade nur, dass dieser Weg bei Bosonen so nicht funktioniert. Und auf Seite 28 findet man den schönen Satz ... It would be a good thing if the misleading expression 'second quantization' were permanently retired. Das zum Trost für jeden Studenten, der diesen Begriff nie ganz verstanden hat.
Die Grundregeln und die mathematische Struktur der Quantentheorie werden in Kapitel 2.1 entwickelt, ähnlich wie wir das in den Kapiteln 4.1 bis 4.5 getan haben (nur sehr viel kürzer). Das grundlegende Objekt ist dabei nicht die Wellenfunktion, sondern der quantenmechanische Zustand, dargestellt durch einen Vektor im Hilbertraum. Wahrscheinlichkeitsamplituden entsprechen dem Skalarprodukt von solchen Vektoren.
In Kapitel 2.2 geht Weinberg auf die Darstellung von Symmetrien in der Quantentheorie ein, ganz analog zu unserer Vorgehensweise in Kapitel 4.6. Kernpunkt ist der Satz von Wigner, dass eine Symmetrie einem unitären oder anti-unitären Operator im Hilbertraum entspricht, wobei kontinuierliche Symmetrien immer einem unitären Operator entsprechen. Mathematisch bilden diese Operatoren eine projektive Darstellung (Strahldarstellung) der Symmetriegruppe auf dem Hilbertraum, d.h. bei zwei Transformationen hintereinander kann zusätzlich eine komplexe Phase auftreten. Interessant sind in diesem Zusammenhang Weinbergs Anmerkungen zu Superauswahlregeln.
In Kapitel 2.3 geht es direkt weiter zu der Darstellung der Lorentz- bzw. Poincaré-Transformationen, d.h. hier beginnt Weinberg, die Prinzipien der Quantentheorie und der speziellen Relativitätstheorie miteinander zu verknüpfen. Die Lie-Algebra der Poincaré-Gruppe wird in Kapitel 2.4 untersucht. Analog zu Kapitel 4.7 und Kapitel 4.8 kommt man so auf die Begriffe Impuls und Drehimpuls. Im nichtrelativistischen Limes ergibt sich die Darstellung der Galilei-Gruppe, die eine projektive Phase aufweist, welche von einer Zentralladung in der Lie-Algebra herrührt (siehe Kapitel 4.9).
Kapitel 2.5 (One Particle States) bildet das entscheidende Kernstück von Kapitel 2. Hauptergebnis ist Formel (2.5.1), die unserer unitären Einteilchen-Darstellung der Poincarégruppe aus Kapitel 4.10 entspricht (mit anderer Normierung): \[ T_{g} \, |\boldsymbol{p},\sigma\rangle = \sum_{\sigma'} \, |\Lambda\boldsymbol{p},\sigma'\rangle \, D_{\sigma'\sigma}(u) \] Die Formel sagt aus: der Teilchenimpuls ändert sich bei einer Lorentztransformation wie ein Vierervektor mit der Lorentzmatrix \(\Lambda\), während sich der Spin (bzw. die Helizität) \(\sigma\) mit einer Darstellungsmatrix \( D_{\sigma'\sigma}(u) \) der kleinen Gruppe transformiert. Die kleine Gruppe besteht aus allen Lorentztransformationen \(\Lambda_{u}\), die einen beliebig vorgegebenen Standardimpuls \(k\) nicht ändern: \[ \Lambda_{u} \, k = k \] (\(u\) ist dann die zugehörige \(SL(2,\mathbb{C})\)-Matrix aus der Überlagerungsgruppe, siehe unten). Gibt man \(k\) vor, so kann man zu jeder Lorentztransformation \(\Lambda\) das zugehörige Element \(\Lambda_{u}\) der kleinen Gruppe (die sogenannte Wigner-Rotation) so bestimmen: \[ \Lambda = \Lambda_{\Lambda p} \, \Lambda_{u} \, \Lambda_{p}^{-1} \] \(\Lambda_{p}\) ist dabei durch \[ \Lambda_{p} \, k = p \] festgelegt (macht also aus dem Standardimpuls \(k\) den Impuls \(p\)). Die Formel sagt also: Mache aus \(p\) den Standardimpuls \(k\), ändere diesen nicht und mache dann daraus den Impuls \(\Lambda p\).
Bei positiver Masse verwendet man \[ k = \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} \] für den Standardimpuls (also den Ruheimpuls des Teilchens) und verwendet für \(\Lambda_{p}\) per Konvention nur Boosts. Dann ist die kleine Gruppe einfach die Drehgruppe im Ruhesystem, die Darstellungsmatrix ist eine Drehmatrix und \(\sigma\) ist der Teilchenspin.
Bei Masse Null gibt es kein Ruhesystem, daher verwendet man \[ k = \begin{pmatrix} 1 \\ \boldsymbol{e}_3 \end{pmatrix} \] (z.B. der Photonimpuls eines Lichtstrahls in z-Richtung mit Photonenenergie 1 in natürlichen Einheiten). Hier besteht die kleine Gruppe aus den Drehungen um die z-Achse und den sogenannten Nulldrehungen (sind keine Drehungen im eigentlichen Sinn) und die Darstellungsmatrix \( D_{\sigma'\sigma}(u) \) ist diagonal in der Helizität \(\sigma\) und berücksichtigt nur die Drehungen um die z-Achse, nicht aber die Nulldrehungen. Wir kennen das alles bereits aus Kapitel 4.10.
In Kapitel 2.6 werden die nicht-kontinuierlichen Symmetrien einbezogen, also Raum- und Zeitspiegelungen. Dabei stellt sich heraus, dass Zeitspiegelungen (nicht aber Raumspiegelungen) durch einen antiunitären Operator dargestellt werden müssen.
Besonders interessant fand ich Kapitel 2.7, da man so etwas in anderen Büchern kaum findet: Eine präzise Untersuchung über die projektiven Phasen in der Strahldarstellung von Gruppen. Ich habe in meinen Kapiteln (besonders in Kapitel 4.10) versucht, die hier von Weinberg dargestellten Ergebnisse an den geeigneten Stellen einfließen zu lassen. Der Kernsatz lautet:
Es gibt zwei potentielle Ursachen für eine nicht zu beseitigende projektive Phase einer Strahldarstellung:
Den Beweis liefert Weinberg in Anhang B von Kapitel 2.
Nun untersucht Weinberg, ob bei den Strahldarstellungen der Poincarégruppe eine solche nicht zu beseitigende projektive Phase auftritt. Er zeigt, dass die Zentralladungen in der Lie-Algebra alle eliminiert werden können (anders als bei der Galileigruppe). Hier droht also keine projektive Phase. Aber die zweite Ursache trifft zu: die Poincarégruppe ist nicht einfach zusammenhängend. Ursache sind die Drehungen (siehe Kapitel 4.10 und Kapitel 4.8). Das kennt man aus der Quantenmechanik: bei Spin 1/2 ergibt eine volle Umdrehung einen Vorzeichenwechsel des Zustandsvektors, also eine Phase.
Man kann die topologischen projektiven Phasen aber loswerden, wenn man zur einfach zusammenhängenden universellen Überlagerungsgruppe \(SL(2,\mathbb{C})\) übergeht und deren unitäre Darstellungen betrachtet, anstatt sich mit den projektiven Darstellungen der Lorentzgruppe herumzuschlagen. Das macht man auch in der üblichen nichtrelativistischen Quantenmechanik: statt projektiver Darstellungen der Drehgruppe betrachtet man unitäre Darstellungen der Überlagerungsgruppe \(SU(2)\). Auch das kennen wir im Detail aus Kapitel 4.10.
Dieses Kapitel fasst wohlbekannte Resultate zur S-Matrix und zur Streutheorie zusammen.
Um Wechselwirkungen zwischen Teilchen beschreiben zu können, bietet sich in der Quantentheorie die Streutheorie an. Sie entspricht dem typischen Experiment in der Teilchenphysik, bei dem man vor und nach der Wechselwirkung freie (nicht wechselwirkende) ein- und auslaufende Teilchenzustände vorliegen hat. Wie diese freien Zustände aussehen, hat Kapitel 2 gezeigt. Weinberg stellt in Kapitel 3.1 die wohlbekannten Grundlagen der Streutheorie dar.
In Kapitel 3.2 ergibt sich so die bekannte S-Matrix (Streumatrix), die gerade die Wahrscheinlichkeitsamplituden dafür darstellt, dass vor der Wechselwirkung ein bestimmter freier Mehrteilchenzustand \(\alpha\) vorliegt und nach der Wechselwirkung ein anderer freier Mehrteilchenzustand \(\alpha'\) gemessen wird. Diese S-Matrix ist unitär (d.h. die Summe aller Wahrscheinlichkeiten ist 1, denn irgend etwas passiert garantiert).
Um Weinbergs Kapitel zu verstehen, sollte man sich noch einmal mit den Begriffen Heisenbergbild und Wechselwirkungsbild vertraut machen, denn Weinberg arbeitet hier mit dem Heisenbergbild. Zum Verständnis sollte man die Formeln einmal in das gewohnte Schrödingerbild zurückübersetzen. Auf Details möchte ich hier nicht eingehen.
Auf die Symmetrien der S-Matrix geht Weinberg in Kapitel 3.3 ein. Das Transformationsverhalten der S-Matrix unter Poincarétransformationen wird untersucht. Aus der Translationsinvarianz folgt dabei die Erhaltung des Gesamtimpulses. Für den räumlichen Impulsoperator und den Drehimpulsoperator gibt es keinen Unterschied zwischen dem Fall mit Wechselwirkung und dem Fall ohne Wechselwirkung. Beim Boostoperator aber gibt es einen solchen Unterschied (nur so kann der Hamiltonoperator \(H\) einen Wechselwirkungsanteil \(V\) besitzen). Ich erinnere mich noch an einen Ausspruch bei Teilchenmodellen, bei denen dieser Aspekt vernachlässigt wurde. Ergebnis: Boostet man das Teilchen, so bleibt die Polarisationswolke stehen (denn sie beruht auf dem Wechselwirkungsanteil).
Anschließend untersucht Weinberg den Einfluss von inneren Symmetrien, die zur Erhaltung ladungsartiger Quantenzahlen führen (Beispiel: die elektrische Ladung). Außerdem untersucht er den Einfluss von Ladungskonjugation, Raum- und Zeitspiegelung.
In Kapitel 3.4 schlägt Weinberg die Brücke zwischen S-Matrix und physikalisch messbaren Größen wie Reaktionsraten und Streuquerschnitte. Das ist alles wohlbekannt und man kann es in vielen Büchern zu dem Thema nachlesen.
Ähnlich ist es mit Kapitel 3.5, in dem Weinberg auf die klassische sowie die zeitabhängige Störungstheorie eingeht. Die klassische Störungstheorie (Stichwort Lippmann-Schwinger-Gleichung) ist nützlich, wenn man sich für Singularitäten (Pole) der S-Matrix aufgrund von Zwischenzuständen interessiert (Resonanzen). Möchte man dagegen den Einfluss der Lorentz-Invarianz untersuchen, so ist die zeitabhängige Störungstheorie geeigneter. Hier zerlegt man den Hamiltonoperator \(H\) in einen freien Anteil \(H_{0}\) und einen Wechselwirkungsanteil \(V\), also \[ H = H_{0} + V \] Dann definiert man im sogenannten Wechselwirkungsbild den zeitabhängigen Wechselwirkungsanteil \[ V(t) := e^{i H_{0} t} \, V \, e^{-i H_{0} t} \] Die S-Matrix lässt sich damit in Form der sogenannten Dyson-Reihe schreiben, also \[ S = T \, e^{-i \, \int dt \, V(t)} = \] \[ = 1 + (-i) \, \int dt \, V(t) + \] \[ + (-i)^{2}/2 \, \int dt \, dt' \, T(V(t),V(t')) + \, ... \] Dabei ist \(T\) der Zeitordungsoperator, d.h. die Faktoren sind nach der Größe der Zeitargumente von links nach rechts angeordnet (man nennt das auch zeitgeordnetes Produkt). So ist
Analog geht es für mehr Faktoren bei den weiteren Termen der Exponentialreihe.
Die S-Matrix soll nun Lorentz-invariant sein. Dazu macht man für \(V(t)\) den Ansatz \[ V(t) =: \int d^{3}x \, \mathcal{H}(t,\boldsymbol{x}) \] und definiert so den Hamilton-Dichteoperator \(\mathcal{H}(t,\boldsymbol{x})\) für die Wechselwirkung im Wechselwirkungsbild (Achtung: Bei masselosen Teilchen können hier noch nicht-kovariante Zusatzterme hinzukommen, um nicht-kovariante Propagatorterme zu kompensieren).
Dieser Dichteoperator soll sich bei Lorentz-Transformationen wie ein skalarer Operator verhalten. Die Existenz des Dichteoperators \(\mathcal{H}(t,\boldsymbol{x})\) , der nur von einem Raumzeitpunkt \( x := (t,\boldsymbol{x}) \) abhängt, ist wohl der entscheidende Schritt, der zu einer Quantenfeldtheorie führt und der punktförmige Teilchen voraussetzt. In der Stringtheorie muss das demnach irgendwie anders laufen.
Schreibt man \( x := (t,\boldsymbol{x}) \), so kann man mit \(\mathcal{H}(x)\) die Dyson-Reihe oben mit vierdimensionalen Raum-Zeit-Integralen schreiben: \[ S = \, T e^{-i \int d^{4}x \, \mathcal{H}(x)} = \] \[ = 1 + (-i) \, \int d^{4}x \, \mathcal{H}(x) + \] \[ + (-i)^{2}/2 \, \int d^{4}x \, d^{4}x' \, T(\mathcal{H}(x),\mathcal{H}(x')) + \, ... \] Ob dieser Ausdruck Lorentz-invariant ist, hängt vom Verhalten des zeitgeordneten Produktes ab.
Wenn \( (x - x') \)zeitartig ist, dann liegt es im Vorwärts- oder Rückwärts-Lichtkegel und die beiden Ereignisse \(x\) und \(x'\) sind kausal miteinander verbunden. Eine Lorentz-Transformation ändert hier die zeitliche Reihenfolge der beiden Ereignisse nicht. Damit ändert sich auch die Reihenfolge im zeitgeordneten Produkt nicht.
Wenn dagegen \( (x - x') \) raumartig ist, so dass die Ereignisse nicht kausal zusammenhängen können, dann kann eine Lorentz-Transformation die zeitliche Reihenfolge ändern. Damit kann sich auch die Reihenfolge im zeitgeordneten Produkt durch eine Lorentztransformation ändern. Wenn die Operatoren in diesem Produkt nicht kommutieren, dann zerstört das die Lorentzinvarianz der S-Matrix. Aus diesem Grund fordern wir, dass in diesem Fall die Operatoren kommutieren müssen. Um die Lorentzinvarianz der S-Matrix sicherzustellen, fordern wir also (Gleichung (3.5.14) bei Weinberg): \[ [\mathcal{H}(x), \mathcal{H}(x')] = 0 \] wenn \( (x - x') \) raumartig ist.
Man bezeichnet dies auch als Kausalitätsbedingung. Diese Gleichung besagt im Wesentlichen, dass Raumzeit-Punkte, die raumartig zueinander liegen, einander nicht beeinflussen können (dazu wäre Überlichtgeschwindigkeit notwendig).
In Kapitel 3.6 leitet Weinberg aus der Unitarität der S-Matrix einige bekannte Folgerungen für die Wechselwirkungsraten ab, woraufhin er in Kapitel 3.7 auf die Partialwellenzerlegung von Streuquerschnitten eingeht. In Kapitel 3.8 zeigt Weinberg, wie ein instabiles Teilchen, das während eines Streuexperiment kurzzeitig entsteht und wieder zerfällt, zu einem Peak (einer Resonanz) im Streuquerschnitt führt, wobei die Unitarität der S-Matrix eine wichtige Rolle spielt.
Noch eine Schlussbemerkung zur S-Matrix: In der Quantenfeldtheorie hat man oft den Eindruck, man könne alles mit der S-Matrix beschreiben. Doch Weinberg selbst schreibt: the S-matrix isn't everything (siehe What is Quantum Field Theory, and what did we think it is? Steven Weinberg, 1997, arXiv:hep-th/9702027v1). Bei endlicher Temperatur gibt es beispielsweise keine freien ein- und auslaufenden Teilchen. Und auch die Beschreibung der Raumzeit durch eine vierdimensionale relativ glatte Mannigfaltigkeit ist keineswegs selbstverständlich.
Bisher war es nicht notwendig, Details über die Wechselwirkung zu wissen – außer der Forderung, das sich \(V(t)\) als Integral über eine lokale Hamiltondichte \(\mathcal{H}(x)\) schreiben lässt.
Das ändert sich nun. Weinberg zeigt, dass sich jeder Vielteilchenoperator (also auch \(\mathcal{H}\)) als Summe von Produkten aus Teilchen-Erzeugungs- und Vernichtungs-Operatoren schreiben lässt, mit geeigneten Koeffizienten. Bei der traditionellen Vorgehensweise treten diese Erzeugungs- und Vernichtungs-Operatoren auf, wenn man vorgegebene klassische Felder quantisiert. Von Feldern ist aber hier bisher noch nicht die Rede.
Weinberg gibt einen tieferen Grund für das Auftreten der Erzeugungs- und Vernichtungs-Operatoren mit einem bestimmten Regularitätseigenschaften der zugehörigen Koeffizienten an, der ohne die Quantisierung von vorgegebenen Felder auskommt: Das Cluster Decomposition Principle. Dieses Prinzip sagt im Wesentlichen, dass entfernt voneinander ausgeführte Experimente sich nicht gegenseitig kausal beeinflussen (sonst würde ja der Ausgang eines Experiments am CERN in Genf womöglich von einem zugleich ausgeführten Experiment in Hamburg abhängen). Gälte dieses Prinzip nicht, so wäre Naturwissenschaft fast unmöglich, denn man könnte nie etwas über den Ausgang eines Experiments vorhersagen, ohne Alles über das gesamte Universum zu wissen.
Übrigens: das Prinzip schließt die Korrelation weit voneinander entfernter Teilchen nicht unbedingt aus, aber diese Teilchen müssen sich während ihrer Wechselwirkung einmal nahe gewesen sein, wobei das gemeinsame Entstehen der Teilchen auch als Wechselwirkung bezeichnet wird (vgl. das Einstein-Rosen-Podolsky-Paradoxon in Die Entdeckung des Unteilbaren, Kapitel 2.8).
Baut man den Hamiltonoperator aus Teilchen-Erzeugungs- und Vernichtungs-Operatoren auf (mit bestimmten Regularitätseigenschaften der zugehörigen Koeffizienten), so ist das Cluster Decomposition Principle automatisch erfüllt. Auf diese Weise erhält die relativistische Quantentheorie letztlich die Struktur einer Feldtheorie (wie Felder ins Spiel kommen, folgt gleich). Andere Versuche, das Cluster Decomposition Principle in einer relativistischen Quantentheorie zu garantieren, waren wenig erfolgreich.
Zunächst geht Weinberg in Kapitel 4.1 auf die Symmetrie von Quantenzuständen bei identischen Teilchen ein (siehe Kapitel 4.4). Dabei geht er sorgfältig auf die Frage ein, wie die Phase aussehen kann, die beim Vertauschen zweier identischer Teilchen beim Quantenzustand auftreten kann. Das bekannte Ergebnis lautet: Vertauschen von Bosonen ergibt keine Phase, Vertauschen von Fermionen ergibt ein Vorzeichen. Auf den Spin geht er dabei noch nicht ein. Auch den zweidimensionalen Fall erwähnt er, bei dem andere Phasen möglich sind als im dreidimensionalen Fall (darauf haben wir in Kapitel 4.4 ebenfalls bereits hingewiesen). In Kapitel 9.7 kommt er später im Detail noch einmal darauf zurück.
Die Teilchen-Erzeugungs- und Vernichtungs-Operatoren werden in Kapitel 4.2 definiert. So fügt der Erzeugungsoperator \[ a^{+}(q) \] ein Teilchen mit den durch \(q\) festgelegten Quantenzahlen zu einem Vielteilchenzustand hinzu, wobei das neue Teilchen den Teilchenindex 1 erhält (die übrigen Teilchen rücken dann nach hinten).
Dann zeigt Weinberg, dass der adjungierte Operator \[ a(q) \] entsprechend ein Teilchen mit den durch \(q\) festgelegten Quantenzahlen aus einem Vielteilchenzustand entfernt (annihiliert) – er ist also ein Vernichtungsoperator. Enthält dieser Zustand kein passendes Teilchen, so ist das Ergebnis Null.
Der Vakuumzustand ist nun der Zustand, der keine Teilchen enthält, d.h. jedes \(a(q)\) ergibt bei ihm Null.
Weinberg zeigt nun, dass die so definierten Erzeugungs- und Vernichtungs-Operatoren die gewohnten Kommutator- bzw. Antikommutator-Beziehungen erfüllen. Er weist darauf hin, dass man bei der historisch motivierten Vorgehensweise meist genau umgekehrt vorgeht (siehe z.B. Quantenfeldtheorie und Eichfelder, Kapitel 4): Man hat Felder und quantisiert diese, was zu entsprechenden Kommutator- bzw. Antikommutator-Beziehungen führt, die man als entsprechende (Anti-)Kommutatoren für Erzeugungs- und Vernichtungsoperatoren umschreiben kann. Nun baut man einen entsprechenden Vielteilchen-Hilbertraum auf (auch Fock-Raum genannt). Weinberg vermeidet diese Vorgehensweise, denn er will die Existenz von Feldern nicht voraussetzen, sondern sehen, an welcher Stelle sie unvermeidlich ins Spiel kommen, wenn man nur die Grundgesetze der Quantentheorie und der speziellen Relativitätstheorie für Teilchen voraussetzt.
Dann beweist Weinberg das Kerntheorem: Jeder Operator \(\mathcal{O}\) im Vielteilchen-Hilbertraum lässt sich als Summe von Produkten aus Teilchen-Erzeugungs- und Vernichtungs-Operatoren mit geeigneten Koeffizienten schreiben. Der Beweis läuft über vollständige Induktion und weist nach, dass man die Koeffizienten immer so wählen kann, dass jedes beliebige Matrixelement von \(\mathcal{O}\) reproduzieren lässt.
Schließlich leitet Weinberg das Transformationsverhalten der Teilchen-Erzeugungs- und Vernichtungs-Operatoren aus dem Transformationsverhalten der Zustände ab. In unserer Schreibweise und Normierung wäre das (ohne Translationen): \[ T_{g} \, a^{+}(\boldsymbol{p},\sigma) \, T_{g}^{-1} = \] \[ = \sum_{\sigma'} \, a^{+}(\Lambda\boldsymbol{p},\sigma') \, D_{\sigma'\sigma}(u) \] Damit ergibt sich sofort das obige Transformationsverhalten für die Einteilchenzustände \[ |\boldsymbol{p},\sigma\rangle = a^{+}(\boldsymbol{p},\sigma) \, |0\rangle \] wobei \( |0\rangle \) der Vakuumzustand ist (dabei ändert \( T_{g} \) bzw. \( T_{g}^{-1} \) diesen Vakuumzustand nicht – er ist Poincaré-invariant).
Was sagt nun das Cluster Decomposition Principle über die S-Matrix aus (Weinberg Kapitel 4.3)?
Das entspricht einer der Kernaussagen aus Kapitel 4.2: Dort, wo man in der normalen Wahrscheinlichkeitsrechnung einzelne Wahrscheinlichkeiten zu einer Gesamtwahrscheinlichkeit multipliziert, multipliziert man in der Quantentheorie einzelne Wahrscheinlichkeitsamplituden zu einer Gesamtamplitude. Damit ist zugleich garantiert, dass sich die verschiedenen Wahrscheinlichkeiten zu einer Gesamtwahrscheinlichkeit multiplizieren, so wie das in der Wahrscheinlichkeitsrechnung für unkorrellierte Ereignisse auch sein muss. Ein Beispiel: Die Wahrscheinlichkeit, mit Würfel A eine gerade Zahl und mit Würfel B eine 3 zu würfeln, ist gleich \(1/2 \cdot 1/6 = 1/12 \). Die Wahrscheinlichkeiten multiplizieren sich, denn die beiden Würfel sind unabhängig voneinander. Analog multiplizieren sich die S-Matrizen der einzelnen Orte, denn damit multiplizieren sich auch ihre Betragsquadrate und somit die Wahrscheinlichkeiten, d.h. die Experimente an den verschiedenen Orten sind unabhängig voneinander.
Um die obige Forderung besser handhaben zu können, schreibt man die S-Matrix in eine spezielle Summe um, indem man nicht-zerlegbare Anteile (connected parts) definiert. Die S-Matrix soll dabei in eine Summe aus Produkten zerlegt werden, wobei die Faktoren (nennen wir sie \(S^{C}(...) \) mit \(C\) für connected) in den Produkten nicht in eine solche Summe von Produkten zerlegbar sind (Achtung: das ist eine rekursive Definition, wie wir gleich sehen werden!). Dies nennt man die Cluster-Zerlegung (Cluster Decomposition) der S-Matrix. Wer Feynman-Graphen kennt: \( S^{C}(...) \) würde für einen Graphen stehen, bei dem alle Linien miteinander verknüpft sind. Schauen wir uns einige Beispiele dazu an:
Ein Teilchen:
Angenommen, wir haben nur ein einlaufendes Teilchen \(a\) und ein auslaufendes Teilchen \(a'\) (dabei kennzeichnen \(a\) und \(a'\) die zeitlich konstanten Quantenzahlen des entsprechenden Quantenzustandes, z.B. Energie, Impuls und Spin). Dann ist \[ S(a',a) =: S^{C}(a',a) = \delta(a',a) \] wobei rechts das Kronecker-Symbol steht (oder bei kontinuierlichen Quantenzahlen die Delta-Funktion). Mit anderen Worten: Es muss \(a = a'\) sein, d.h. der Einteilchen-Quantenzustand ändert sich nicht. Wie auch, denn es gibt ja bei einem Teilchen keinen Wechselwirkungs-Partner. Der nicht-zerlegbare Anteil S^{C}(a',a) ist in diesem Fall identisch ist mit der S-Matrix selbst.
Zwei Teilchen:
Bei zwei einlaufenden Teilchen kann man den Zweiteilchenzustand aus zwei Einteilchenzuständen \(a\) und \(b\) aufbauen. Analog ist es bei zwei auslaufenden Teilchen \(a'\) und \(b'\). Die Cluster-Zerlegung lautet: \[ S(a'b',ab) =: \] \[ =: S^{C}(a'b',ab) + S^{C}(a',a) \, S^{C}(b',b) \pm \] \[ \pm S^{C}(a',b) \, S^{C}(b',a) = \] \[ = S^{C}(a'b',ab) + \delta(a',a) \, \delta(b',b) \pm \] \[ \pm \delta(a',b) \, \delta(b',a) \] (das Minus-Zeichen gilt für identische Fermionen). Dadurch wird letztlich über die S-Matrix zweier Teilchen der nicht-zerlegbare Term \( S^{C}(a'b',ab) \) definiert, wobei wir von oben verwendet haben, dass der Ein-Teilchen-Term \( S^{C}(a',a) = \delta(a',a) \) ist.
Drei Teilchen:
Hier lautet die Cluster-Zerlegung \[ S(a'b'c',abc) =: \] \[ =: S^{C}(a'b'c',abc) + \] \[ + S^{C}(a'b',a,b) \, \delta(c',c) \pm \] \[ \pm \mathrm{Teilchenvertauschungen} + \] \[ + \delta(a',a) \, \delta(b',b) \, \delta(c',c) \pm \] \[ \pm \mathrm{Teilchenvertauschungen} \] Dies definiert über die S-Matrix dreier Teilchen den Term \( S^{C}(a'b'c',abc) \), denn die anderen Terme wie beispielsweise \( S^{C}(a'b',a,b) \) hatten wir oben bereits über die Einteilchen- bzw. Zweiteilchen-S-Matrix definiert (daher ist die Definition der nicht-zerlegbaren Teile rekursiv).
Es bietet sich an, die Cluster-Zerlegung durch Graphen darzustellen.
Hier sind die Graphen für die obigen drei Beispiele
(die S-Matrix ist in Rot, die nicht-zerlegbaren Anteile sind in Blau und die
\(\delta\)-Terme sind durch Linien dargestellt; unten stehen von
links nach rechts die Teilchenzustände \(a, b, \, ...\) und oben die
Teilchenzustände \(a', b', \, ... \)):
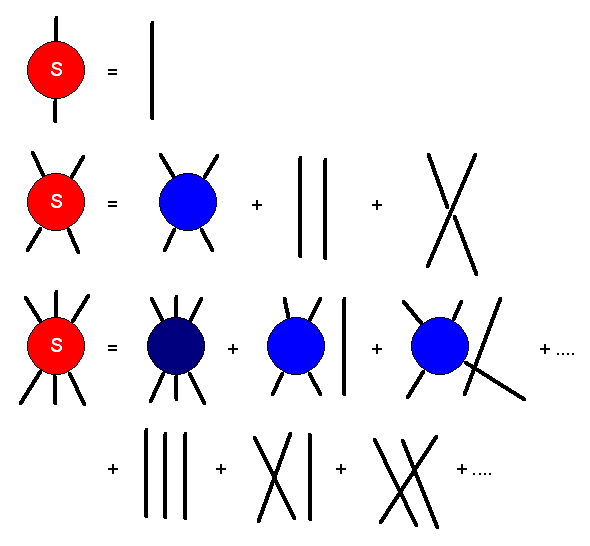
Wozu ist die Cluster-Zerlegung nun gut? Man kann damit das Cluster Decomposition Principle von oben umformulieren:
Anhand der obigen Beispiele kann man sich davon überzeugen, dass dann die S-Matrix genau die oben verlangte Produktstruktur hat. Weinberg zeigt das auch ganz allgemein.
In Kapitel 4.4 kommt Weinberg zum entscheidenden Punkt:
Es folgt ein ausführlicher Beweis mit Hilfe der zeitabhängigen Störungstheorie (Weinberg sagt, dass er keinen nicht-störungstheoretischen Beweis kennt). Dabei betont Weinberg, dass die Forderung an die Koeffizienten (nur eine Deltafunktion) keineswegs trivial ist und weitreichende Konsequenzen hat.
Nun hat Weinberg alle Zutaten zusammen, um zu zeigen, wozu Quantenfelder benötigt werden. So hatte er in Kapitel 3 gezeigt, dass die S-Matrix Poincaré-invariant ist, wenn man die Wechselwirkung über einen skalaren Raumzeit-abhängigen Hamiltondichte-Operator \( \mathcal{H}(x) \) darstellen kann, der die Kausalitätsbedingung erfüllt (d.h. \( [\mathcal{H}(x), \mathcal{H}(x')] = 0 \), wenn \( (x - x') \) raumartig ist, d.h. wenn man von \(x\) nach \(x'\) Überlichtgeschwindigkeit braucht). Und in Kapitel 4 hatte er gezeigt, dass man \(\mathcal{H}\) mit Teilchen-Erzeugungs- und Vernichtungs-Operatoren schreiben kann.
Problem:
Die Teilchen-Erzeugungs- und Vernichtungs-Operatoren transformieren sich mit einer Matrix
\( D_{\sigma'\sigma}(u) \), wobei \(u\) zur kleinen Gruppe gehört, d.h.
\(u\) ist Impuls-abhängig (siehe die Definition der
kleinen Gruppe in Kapitel 4.10).
Wie kann man daraus einen skalaren Ausdruck für \( \mathcal{H}(x) \) bilden?
Lösung:
Benutze als Bausteine für \( \mathcal{H}(x) \) sogenannte
Quantenfelder \( \psi_{k}^{\pm}(x) \)
(eines für die Erzeugungs- und eines für
die Vernichtungs-Operatoren), die sich mit einer Darstellungsmatrix \(D(g)\) der Lorentzgruppe
(bzw. der Überlagerungsgruppe \(SL(2,\mathbb{C})\) ) transformieren
(bei den masselosen Teilchen werden wir weiter unten noch sehen, dass
man dort ein allgemeineres Transformationsverhalten zulassen muss, um alle relevanten Fälle zu erfassen
– das Ergebnis sind die Eichfelder).
In unserer Normierung wäre das:
\[
\psi_{k}^{+}(x) :=
\sum_{\sigma n} \, \int \frac{d^{3}p}{2p^{0}}
\, \cdot
\]
\[ \cdot
\, u_{k}(x, \boldsymbol{p}, \sigma, n) \, a(\boldsymbol{p}, \sigma, n)
\]
\[
\psi_{k}^{-}(x) :=
\sum_{\sigma n} \, \int \frac{d^{3}p}{2p^{0}} \, \cdot
\]
\[ \cdot
\, v_{k}(x, \boldsymbol{p}, \sigma, n) \, a^{+}(\boldsymbol{p}, \sigma, n)
\]
Achtung: das hochgestellte \(+\) steht hier nicht für den adjungierten Operator.
Dabei ist \(\boldsymbol{p}\) der Impuls, \(x = (t, \boldsymbol{x})\) ein Punkt in der Raumzeit,
\(k\) der Index der Feldkomponente, \(\sigma\) die Spinkomponente in z-Richtung
bzw. die Helizität und \(n\) kennzeichnet verschiedene
Teilchenarten. Man sieht hier sehr schön, dass Feldindex \(k\) und Spinindex \(\sigma\) nicht identisch sind.
Der Feldindex \(k\) spielt eine Rolle im Transformationsverhalten
der beiden Quantenfelder, das folgendermaßen aussehen soll (diesmal schreiben wir die Translationen mit dazu):
\[
T_{g,a} \, \psi_{k}^{+}(x) \, T_{g,a}^{-1}
=
\]
\[ =
\sum_{k'} \, D_{k k' }(g^{-1}) \,
\psi_{k'}^{+}(\Lambda x + a)
\]
\[
T_{g,a} \, \psi_{k}^{-}(x) \, T_{g,a}^{-1}
=
\]
\[ =
\sum_{k'} \, D_{k k' }(g^{-1}) \,
\psi_{k'}^{-}(\Lambda x + a)
\]
Die Matrix \(D(g)\) ist eine Darstellungsmatrix der Lorentzgruppe
(oder genauer ihrer Überlagerungsgruppe \(SL(2,\mathbb{C})\), siehe Kapitel 4.10 ).
Diese Matrix ist nicht unbedingt unitär,
aber anders als \(D(u)\) impulsunabhängig (denn \(u\) ist impulsabhängig, \(g\) nicht).
Das Transformationsverhalten der Quantenfelder ist einfach genug, so dass sich daraus in
übersichtlicher Weise skalare Ausdrücke für
\( \mathcal{H}(x) \) aufbauen lassen.
Für die Koeffizientenfunktionen \(u_{k}\) und \(v_{k}\) ergeben sich aus dem geforderten Transformationsverhalten der Quantenfelder und dem oben angegebenen Transformationsverhalten der Erzeugungs- und Vernichtungs-Operatoren bestimmte Bedingungen, die diese Funktionen festlegen. Siehe Weinberg Gleichung (5.1.13) und (5.1.14) auf Seite 194. Diese Gleichungen wertet Weinberg dann speziell für Translationen, Boosts und Drehungen aus. Die Boosts verknüpfen dabei die Werte von \(u_{k}\) und \(v_{k}\) für verschiedene Impulse miteinander.
Nun zeigt Weinberg: Wenn man die Hamiltondichte \( \mathcal{H}(x) \) aus den Quantenfeldern aufbaut, dann hat sie genau die Form, die das Cluster Decomposition Principle verlangt. Insbesondere enthalten die Koeffizienten, die nun aus \(u_{k}\) und \(v_{k}\) gebildet werden, nur genau eine Delta-Funktion zur Erhaltung des Gesamtimpulses. Und: Jede Koeffizientenfunktion mit nur genau einer Delta-Funktion kann so aus \(u_{k}\) und \(v_{k}\) gebildet werden. Er schreibt: The cluster decomposition principle together with Lorentz invariance thus makes it natural that the interaction density should be constructed out of the annihilation and creation fields. Das ist der Grund, warum wir es mit einer Quantenfeldtheorie zu tun haben.
Weiteres Problem:
Die Kausalitätsbedingung muss erfüllt sein, d.h. \( [\mathcal{H}(x), \mathcal{H}(x')] = 0 \),
wenn \( (x - x') \) raumartig ist. Diese Bedingung
sichert die Lorentz-Invarianz der Theorie, wie Weinberg in Kapitel 3.5 zuvor gezeigt hatte.
Bildet man \( \mathcal{H}(x) \) beliebig aus den obigen Quantenfeldern \( \psi_{k}^{\pm}(x) \),
so ist die Kausalitätsbedingung aber nicht zwangsläufig erfüllt.
Lösung:
Verwende zum Aufbau der Hamiltondichte \( \mathcal{H}(x) \) Linearkombinationen
\[
\psi_{k}(x) :=
\kappa_{k} \, \psi_{k}^{+}(x) +
\lambda_{k} \, \psi_{k}^{-}(x)
\]
so dass für den (Anti-)Kommutator der Linearkombination gilt:
\[
[\psi_{k}(x), \psi_{k'}(y)]_{\pm}
=
[\psi_{k}(x), (\psi_{k'}(y))^{+}]_{\pm}
= 0
\]
wenn \( (x - y) \) raumartig ist.
Das hochgestellte \(+\) im (Anti-)Kommutator steht hier für den adjungierten Operator, und das tiefergestellte \(\pm\) für den Kommutator (bei Bosonen) bzw. Antikommutator (bei Fermionen). Dabei muss die weitere Analyse zeigen, ob man den Kommutator oder den Antikommutator verwenden muss, um \( [\mathcal{H}(x), \mathcal{H}(x')] = 0 \) für raumartige \( (x - x') \) garantieren zu können. Auch diese Bedingung wird oft als Kausalitätsbedingung bezeichnet – man spricht von kausalen Feldern. Diese Bezeichnung macht Sinn für messbare Felder wie das elektromagnetische Feld, weniger aber für nicht-messbare Felder wie das Diracfeld. Weinberg sagt dagegen einfach: Man braucht diese Bedingung für die Lorentz-Invarianz der S-Matrix.
Der Grund für Antiteilchen:
Eine Hürde gibt es noch für die Konstruktion passender Linearkombinationen: Es kann vorkommen, dass die Teilchen sogenannte erhaltene Quantenzahlen besitzen, beispielsweise eine elektrische Ladung. Der entsprechende Ladungsoperator \(Q\) muss dann mit \( \mathcal{H}(x) \) kommutieren (sonst wäre die Quantenzahl nicht erhalten). Das kann man (nur) so erreichen:
\( \mathcal{H}(x) \) besteht aus einer Summe (Integral) von Feldkomponenten-Produkten der Form \[ \psi_{k} \, \psi_{k'} \, ... \, \psi_{j}^{+} \, \psi_{j'}^{+} \, ... \] Wir fordern nun, dass jede Feldkomponente \( \psi_{k}(x) \) einen einfachen Kommutator mit dem Ladungsoperator \(Q\) hat: \[ [Q, \psi_{k}(x)] = - q_{k} \, \psi_{k}(x) \] mit reellem \(q_{k}\) (was diese Forderung bedeutet, kommt gleich). Adjungieren ergibt (mit \(Q^{+} = Q\) ) die Gleichung \[ [Q, \psi_{k}^{+}(x)] = q_{k} \, \psi_{k}^{+}(x) \] Bildet man nun \( [Q, \mathcal{H}(x)] \), so ergeben sich Terme \[ [Q, \psi_{k} \, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} ... ] = \] \[ = [Q, \psi_{k}] \, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... + \] \[ + \psi_{k} \, [Q, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... ] = \] \[ = - q_{k} \, \psi_{k} \, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... + \] \[ + \psi_{k} \, [Q, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... ] = \] \[ = \, ... \] \(Q\) immer weiter nach rechts durchtauschen \[ = (- q_{k} - q_{k'} - \, ... \, + q_{j} + q_{j'} + ...) \, \cdot \] \[ \cdot \, \psi_{k} \, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... \] Um \( [Q, \mathcal{H}(x)] = 0 \) zu erreichen, fordern wir also einfach \[ (- q_{k} - q_{k'} - \, ... \, + q_{j} + q_{j'} + \, ...) = 0 \] Was aber bedeutet unsere Forderung \( [Q, \psi_{k}(x)] = -q_{k} \psi_{k}(x) \) von oben für die Teilchen? Setzen wir dazu die Linearkombination für \( \psi_{k}(x) \) von oben ein. Wenn wir die Koeffinzienten \(\kappa_{k}\) und \(\lambda_{k}\) nicht weiter einschränken wollen, so muss separat \[ [Q, \psi_{k}^{\pm}(x)] = -q_{k} \, \psi_{k}^{\pm}(x) \] sein. Für die Feldkomponente \( \psi_{k}^{+}(x) \) bedeutet die Gleichung, dass die von dieser Feldkomponente vernichteten Teilchensorten alle dieselbe Ladung \( q_{k} \) besitzen. Analog bedeutet die Gleichung für \( \psi_{k}^{-}(x) \), dass die von dieser Feldkomponente erzeugten Teilchen alle dieselbe Ladung \( -q_{k} \) besitzen.
Bezeichnen wir die von \(\psi_{k}^{-}(x)\) erzeugten Teilchen als Antiteilchen. Dann folgt, dass die ladungsartigen Quantenzahlen der Antiteilchen entgegengesetzt zu den ladungsartigen Quantenzahlen der Teilchen sind. Fasst man alle Schritte zusammen, so folgt die Existenz von Antiteilchen mit entgegengesetzten ladungsartigen (d.h. erhaltenen) Quantenzahlen alleine aus der Lorentz-Invarianz der Theorie und dem Cluster Decomposition Principle (d.h. weit voneinander entfernte Vorgänge beeinflussen sich i.a. nicht).
This is the reason for antiparticles (Weinberg in Kapitel 5.1 auf S.199). Zugegeben: Weinbergs Argumentation ist sehr kompakt geschrieben und man müsste sie wohl mal ausführlich ausarbeiten und an Beispielen erproben, um sie wirklich zu verstehen.
Konzepte wie der Diracsee (siehe Die Entdeckung des Unteilbaren, Kapitel 5.1) wurden für die Existenz von Antiteilchen nicht benötigt – der Diracsee funktioniert ja auch nur bei Fermionen, nicht aber bei Bosonen. Kein Wunder, war der Diracsee ja auch eigentlich dazu gedacht, das Problem der negativen Energien bei der Diracgleichung zu lösen. Für negative Energien war aber bei Weinberg bisher überhaupt kein Bedarf: Alle Teilchenenergien sind positiv.
Man kann die Felder so festlegen, dass Untergruppen der Feldkomponenten einen irreduziblen Darstellungsraum für eine Teilchensorte bilden (sie transformieren sich also nur untereinander bei Lorentztransformationen). Solche Untergruppen bezeichnen wir ab sofort als ein Feld (z.B. ein Diracfeld).
Feldgleichungen:
Aus dem Transformationsverhalten der Felder bei Translationen folgt, dass jede Feldkomponente die Klein-Gordon-Gleichung \[ (\hat{P}^{2} - m^{2}) \, \psi_{k}(x) = 0 \] erfüllt (siehe Kapitel 4.12).
Gibt es mehr Feldkomponenten als zugehörige unabhängige Teilchen, dann erfüllen die Felder zusätzliche Gleichungen. Historisch begann man üblicherweise mit solchen Feldgleichungen, formulierte sie mit Poissonklammern im kanonischen Formalismus (siehe unten) und leitete mit ihrer Hilfe in der zweiten Quantisierung (Ersetzung der Poissonklammern durch Kommutatoren) Ausdrücke dür die Quantenfelder her, in denen diese von Teilchen-Erzeugern und -Vernichtern abhängen.
Weinberg dagegen startet mit Teilchenzuständen und den entsprechenden Erzeugern und Vernichtern und definiert damit die Quantenfelder. Aus deren gefordertem Transformationsverhalten und dem Transformationsverhalten der Teilchenzustände ergeben sich automatisch Gleichungen für die Felder, die man als Feldgleichungen umschreiben kann. Die Feldgleichungen ergeben sich daher fast zufällig als Nebenprodukt dieser Konstruktion (Weinberg Kapitel 5.1 Seite 200).
5.2 Causal Scalar Fields:
Weinberg betrachtet nun das einfachste Beispiel für ein Feld: ein skalares Feld \( \Phi(x) \) mit nur einer Komponente und der Darstellungsmatrix \[ D(g) = 1 \] sodass auch \(D(u) = 1\) ist, d.h. die Teilchenzustände entsprechen Spin = 0.
In unserer Normierung wäre dann \[ u(\boldsymbol{p}) = 1 \] \[ v(\boldsymbol{p}) = 1 \] (in Weinbergs Normierung ist \( u(\boldsymbol{p}) = \sqrt{2p^{0}} \) und \( v(\boldsymbol{p}) = \sqrt{2p^{0}} \)).
Nun kommt eine detaillierte Analyse der Bedingungen, die wir oben für Felder und die Hamiltondichte allgemein aufgestellt haben. Aus ihr folgt, dass bei einem Teilchen ohne ladungsartige Quantenzahlen das Feld \(\Phi(x)\) hermitesch gewählt werden kann.
Hat das Teilchen dagegen ladungsartige Quantenzahlen, so muss es ein anderes Teilchen mit entgegengesetzten ladungsartigen Quantenzahlen und gleicher Masse geben (das Antiteilchen). Das Feld \(\Phi(x)\) kann dann nicht hermitesch gewählt werden. Außerdem kommt heraus, dass für die Felder überall der Kommutator und nicht der Antikommutator verwendet werden muss, d.h. das Teilchen ist ein Boson.
5.3 Causal Vector Fields:
In diesem Fall soll sich der Feldindex \(k\) wie ein Lorentz-Index \(\mu\) verhalten, d.h. \[ D(g) = \Lambda \] (die Feldkomponenten transformieren sich also wie ein Vierervektor mit der Lorentzmatrix). So ein Feld braucht man beispielsweise für die massiven Vektorbosonen \(W^{+}, W^{-}, Z^{0}\) der schwachen Wechselwirkung und im masselosen Grenzfall für die Photonen der elektromagnetischen Wechselwirkung. Weinberg untersucht nun die Bedingungen für die Funktionen \( u^{\mu}(\boldsymbol{p}) \) und \( v^{\mu}(\boldsymbol{p}) \), die sich aus den Transformationsgesetzen ergeben. Ergebnis:
Es gibt zwei Möglichkeiten für Teilchenzustände, die sich zu einen Vierervektor-Quantenfeld kombinieren lassen:
Dann ist im Ruhesystem (also bei \(\boldsymbol{p} = 0\)) nur \(u^{0}\) und \(v^{0}\) ungleich Null. Weinberg zeigt, dass das Quantenfeld \( \Phi^{\mu}(x) \) einfach die Raum-Zeit-Ableitung des skalaren Feldes von oben ist: \[ \Phi^{\mu}(x) = \partial^{\mu} \Phi(x) \] Daher ist diese Fall bereits oben bei den skalaren Feldern mit enthalten und braucht nicht noch einmal separat betrachtet zu werden.
Dann ist im Ruhesystem (also bei \(\boldsymbol{p} = 0\)) nur \(u^{i}\) und \(v^{i}\) ungleich Null (mit i von 1 bis 3). Die Analyse zeigt, dass Spin 1 -Teilchen Bosonen sein müssen (d.h. der Kommutator muss bei den Feldern verwendet werden), und sie zeigt, dass die Quantenfelder neben der Klein-Gordon-Gleichung noch die Gleichung \[ \partial_{\mu} v^{\mu}(x) = 0 \] erfüllen müssen.
Im masselosen Grenzfall sind dies die Gleichungen für das Viererpotential der Elektrodynamik in der Lorentz-Eichung.
Weinberg weist aber darauf hin, dass nicht jede Theorie mit massiven Spin 1 -Teilchen im masselosen Grenzfall die Elektrodynamik ergibt. Als Beispiel verwendet er den Wechselwirkunsterm \( \mathcal{H}(x) = J_{\mu}(x) \, v^{\mu}(x) \) mit irgendeiner gegebenen Viererstromdichte \( J_{\mu}(x) \). Im masselosen Grenzfall muss diese Stromdichte die Bedingung \( \partial_{\mu} J^{\mu}(x) = 0 \) erfüllen, um zu verhindern, dass masselose Spin-1-Teilchen mit Helizität Null entstehen können (solche Teilchen gibt es ja prinzipiell nicht).
5.4 The Dirac Formalism:
Weinberg führt den Dirac-Formalismus ein, indem er letztlich die Spin-Gruppe zur Lorentz-Gruppe und damit die zugehörige Clifford-Algebra mit den Dirac-Matrizen konstruiert. Die Details dazu hatten wir bereits in Kapitel 4.11 kennengelernt.
5.5 Causal Dirac Fields:
Weinberg untersucht nun Felder, die sich wie ein Diracfeld verhalten, d.h. es gibt 4 Feldkomponenten und \(D(g)\) ist die 4-mal-4-Matrix der Spingruppe, die Weinberg in Kapitel 5.4 zuvor konstruiert hat. In Kapitel 4.11 hatten wir diese Matrix mit der Weyl-Darstellung der Diracmatrizen explizit ausgerechnet:
| \[ D(g) = S = \begin{pmatrix} g & 0 \\ 0 & (g^+)^{-1} \end{pmatrix} \] |
mit \(g\) aus \(SL(2,\mathbb{C})\). Weinberg verwendet nun wieder die Transformationseigenschaften der Felder, um die Koeffizientenfunktionen \(u_{k}\) und \(v_{k}\) in den Dirac-Quantenfeldern zu berechnen. Dabei stellt sich heraus, dass der Teilchenspin gleich 1/2 sein muss, und dass Antikommutatoren für die Felder verwendet werden müssen, d.h. die Teilchen sind Fermionen. Das Ergebnis für \(u_{k}\) und \(v_{k}\) zeigt, dass die Dirac-Quantenfelder automatisch die Diracgleichung erfüllen (siehe Kapitel 4.13).
5.6 General Irreducible Representations of the Homogeneous Lorentz Group:
Weinberg analysiert, welche endlich-dimensionalen Darstellungsmatrizen \(D(g)\) der Lorentzgruppe (bzw. ihrer Überlagerungsgruppe) es allgemein geben kann. Wir kennen diese Analyse bereits weitgehend aus Kapitel 4.10 und wissen, dass sich die Darstellungsmatrizen \(D(g)\) über analytische Fortsetzung in den Gruppenparametern aus dem zweifachen Tensorprodukt von Drehmatrizen gewinnen lassen.
Man bildet also das Tensorprodukt von zwei Drehimpulsen \(j\) und \(j'\) und setzt in den Drehmatrizen die Drehwinkel analytisch geeignet fort (braucht man für die Boosts). Deshalb kennzeichnet man Darstellungen der Lorentzgruppe auch häufig mit \( (j, j') \) und meint damit die beiden Drehimpulse der Drehmatrizen.
Bei den Darstellungen \( (j, 0) \) und \( (0, j) \) ist bei einer Drehung \(u\) die Matrix \(D(u)\) identisch mit der Drehmatrix, während bei einem Boost sich die beiden Darstellungen unterscheiden.
Bei \( (\frac{1}{2}, 0) \) ist \( D(g) = g \) einfach die \(SL(2,\mathbb{C})\)-Matrix \(g\) selbst (erste Fundamentaldarstellung), während bei \( (0, \frac{1}{2}) \) dann \( D(g) = (g^{+})^{-1} \) ist (zweite Fundamentaldarstellung).
Die Dirac-Darstellung wäre dann \( (\frac{1}{2}, 0) + (0, \frac{1}{2}) \), was der obigen Matrix \( D(g) = S \) entspricht. Weinberg geht im weiteren Verlauf auch darauf ein, wie verschiedene Tensordarstellungen mit \( (j, j') \) in Zusammenhang stehen.
5.7 General Causal Fields:
Analog zum skalaren Feld, dem Vektorfeld und dem Diracfeld konstruiert Weinberg nun allgemeine kausale Felder der Darstellung \( (j, j') \) für Teilchen mit Spin \(s\). Kausal bedeutet wie immer, dass die Feldkomponenten für zwei nicht kausal miteinander verbundene Ereignisse (also \( (x - x') \) raumartig) kommutieren müssen (siehe oben).
Ein wichtiges Ergebnis der Analyse ist, dass im Ruhesystem ( \( \boldsymbol{p} = 0 \) ) für Teilchen mit Spin \(s\) die Koeffizienten der Felder gleich Clebsch-Gordan-Koeffizienten \(C(...)\) sind, wobei statt dem Feldindex \(k\) ein Doppelindex \(m m'\) verwendet wird, passend zur Darstellung \((j, j')\). Mit geeigneter Normierung \(N\) gilt (Weinbergs Formel (5.7.4) auf Seite 234 mit etwas anderer Notation): \[ u_{m m'}(\boldsymbol{0},\sigma) = N \, C(s \sigma, j m j' m') \] Ist ja klar: Das Feld verhält sich bei Drehungen wie zwei gekoppelte Drehimpulse \(j\) und \(j'\), und das muss mit dem Drehverhalten des Teilchens mit Spin \(s\) zusammenpassen, d.h. \(j\) und \(j'\) müssen zu \(s\) verkoppelt werden.
Gibt man das Transformationsverhalten des Feldes (also \(j\) und \(j'\)) und den Teilchenspin vor, so ist das kausale Quantenfeld eindeutig festgelegt (Weinbergs Formel (5.7.31) auf Seite 238).
Gibt man aber nur den Teilchenspin \(s\) vor, so gibt es viele \((j, j')\)-Felder, die zu diesem Teilchenspin passen – Hauptsache, \(j\) und \(j'\) lassen sich über Clebsch-Gordan-Koeffizienten zu Spin s verkoppeln (es muss also \( |j - j'| \le s \le j + j' \) sein).
Ein Beispiel haben wir oben gesehen: zu Spin 0 passt ein skalares Feld oder ein bestimmtes Vektorfeld (das zur Darstellung \( (1/2, 1/2) \) gehört). Aber: das Vektorfeld bietet nichts Neues, denn es ist die Ableitung des skalaren Feldes. Das gilt auch generell: Es gibt zu einem Teilchen mit Spin \(s\) mehrere mögliche Quantenfelder, aber diese Felder repräsentieren keine physikalisch wirklich verschiedenen Alternativen, denn jedes \((j, j')\)-Feld zu einem Teilchen mit Spin \(s\) kann über einen Differentialoperator aus einem \((s, 0)\)-Feld oder einem \((0, s)\)-Feld abgeleitet werden.
5.8 The CPT Theorem:
Weinberg hat in den vorherigen Kapiteln neben den eigentlichen Lorentztransformationen (und ihrer Überlagerungsgruppe \(SL(2,\mathbb{C})\) ) auch die diskreten Transformationen Raumspiegelung \(P\), Zeitspiegelung \(T\) und Ladungsumkehr \(C\) untersucht (\(C\) macht aus Teilchen die zugehörigen Antiteilchen). Zusammengefasst erhält er das Ergebnis, dass sich alle drei diskreten Transformationen nacheinander auf ein \((j, j')\)-Feld \(\psi(x)\) so auswirken: \[ C P T \, \psi(x) \, (C P T)^{-1} = (- 1)^{2 j'} \, (\psi(- x))^{+} \] \(P\) und \(T\) bilden ja zusammen eine Raum-Zeit-Spiegelung, was aus dem Raumzeitvektor \( x = (t, \boldsymbol{x}) \) den Vektor \( - x \) macht. Die Ladungsumkehr \(C\) bewirkt dann den Übergang zum adjungierten Operator (hochgestelltes Kreuz), was etwas mit dem Austausch von Erzeugungs- und Vernichtungsoperatoren zu tun hat und damit den Wechsel von Teilchen zu Antiteilchen und umgekehrt bewirkt. Den Vorfaktor \( (- 1)^{2 j'} \) muss man in der genauen Analyse ermitteln.
Aus den \(\psi\)-Feldern muss man nun eine skalare hermitesche Hamiltondichte \(\mathcal{H}(x)\) aufbauen, indem man diese \((j,j')\)-Felder geeignet verkoppelt (wie bei der Drehimpulskoppelung). Man kann sich überlegen, dass dann die Summe der gestrichenen Drehimpulse \(j_{1}' + j_{2}' + \, ... \) der einzelnen Felder eine ganze Zahl sein muss. Entsprechend multiplizieren sich die Vorfaktoren zu \(1\), so dass \[ C P T \, \mathcal{H}(x) \, (C P T)^{-1} = \mathcal{H}(- x) \] gilt. Für den Hamilton-Wechselwirkungsanteil \[ V(0) =: \int d^{3}x \, \mathcal{H}(0,\boldsymbol{x}) \] gilt dann \[ C P T \, V(0) \, (C P T)^{-1} = V(0) \] Es war oben \[ V(t) := e^{i H_{0} t} \, V \, e^{-i H_{0}} \] d.h. \( V(0) = V \). Außerdem war \[ H = H_{0} + V \] Man kann sich weiter überlegen, dass auch für den freien Hamilton-Anteil \[ C P T \, H_{0} \, (C P T)^{-1} = H_{0} \] gilt. Also haben wir insgesamt \[ C P T \, H \, (C P T)^{-1} = H \] d.h. \( C P T \) kommutiert mit dem Hamiltonoperator. Das ist das berühmte CPT-Theorem der Quantenfeldtheorie.
Es gilt nur für die Kombination \( C P T \), nicht aber einzeln für \(C, P, T, CP\) usw. (man kennt entsprechende experimentelle Gegenbeispiele aus der schwachen Wechselwirkung). In Kapitel 3.3 (Seite 133) und Kapitel 3.6 (Seite 149) untersucht Weinberg die physikalischen Konsequenzen: \( C P T \) liefert den präzisen Zusammenhang zwischen Teilchen und Antiteilchen und sorgt beispielsweise dafür, dass beide dieselbe Masse besitzen.
Außerdem liefert es einen Zusammenhang zwischen einem Prozess und seinem inversen Prozess: Wenn man in der S-Matrix die Teilchen vorher und nachher vertauscht, zusätzlich die Spins umdreht und die Teilchen durch ihre Antiteilchen ersetzt, dann hat diese neue S-Matrix denselben Wert wie die alte S-Matrix zuvor. Zusammen mit der Drehinvarianz folgt so beispielsweise, dass ein instabiles Teilchen genau dieselbe Lebensdauer wie sein Antiteilchen hat.
5.9 Massless Particle Fields:
Weinberg geht hier detailliert auf masselose Teilchen und zugehörige Quantenfelder ein. So gibt es beim skalaren oder dem Dirac-Feld kein Problem, den masselosen Grenzfall durchzuführen (siehe z.B. Kapitel 4.13 ). Bei Vektorfeldern und Spin 1 dagegen war das anders, wie wir oben in Weinbergs Kapitel 5.3 gesehen haben. Weinberg zeigt nun den Grund dafür: Für Teilchenspin größer-gleich 1 kann man bei masselosen Teilchen mit den Erzeugungs- und Vernichtungs-Operatoren nicht alle die Quantenfelder aufbauen, die man bei Teilchen mit Masse aufbauen kann. Das führt zum Konzept der Eichinvarianz. Hier die Details:
Versucht man, ein allgemeines Quantenfeld aus den masselosen Erzeugern und Vernichtern aufzubauen, so ist wichtig, dass sich masselose Teilchen (und damit masselose Erzeugern und Vernichter) anders transformieren als Teilchen mit Masse: die Helizität ändert sich nicht und es tritt nur eine komplexe Phase \( e^{-i \varphi \sigma} \) auf, die von der Helizität \(\sigma\) und von einem Drehwinkel \(\varphi\) abhängt. Die sogenannten Nulldrehungen \( \Lambda_{N} \) der kleinen Gruppe verändern die Phase gar nicht (wohl aber den Impuls). Details siehe Kapitel 4.10 im Abschnitt die kleine Gruppe für masselose Teilchen. Für die Koeffizientenfunktionen für den Standardimpuls \(\boldsymbol{k}\) folgt daraus für die Nulldrehungen (Weinberg Seite 249 Gleichung (5.9.14) in der von mir verwendeten Notation in Matrixschreibweise für die Felder): \[ u(\boldsymbol{k},\sigma) = D(\Lambda_{N}) \, u(\boldsymbol{k},\sigma) \] Diese Gleichung fordert, dass sich die Darstellungsmatrix einer Nulldrehung auf den Wert der Feld-Koeffizientenfunktion im Standardimpuls nicht auswirkt. Diese Gleichung ist nicht für beliebige Helizitäten und Darstellungen \(D\) lösbar, wenn sich \(u\) auch bei anderen Lorentztransformationen korrekt transformieren soll!
Weinberg weist dies konkret an einem Vierervektorfeld für Spin 1 nach (d.h. \( D(\Lambda) = \Lambda \) und \( \sigma = \pm 1 \)) und zeigt, dass man aus masselosen Spin-1-Erzeugern und Vernichtern kein Vierervektor-Quantenfeld aufbauen kann.
Was geschieht, wenn man für Spin 1 die Nulldrehungen erst einmal ignoriert, also nur Lorentztransformationen betrachtet, deren kleines Gruppenelement (Wigner-Rotation) eine Drehung um die z-Achse ist? Dann kann man zunächst tatsächlich formal scheinbar ein masseloses Vierervektor-Quantenfeld (nennen wir es \( A^{\mu}(x) \)) für Spin 1 konstruieren.
Wie immer erfüllen die Feldkomponenten die Klein-Gordon-Gleichung (hier mit \(m = 0\)), also \[ \partial_{\nu} \partial^{\nu} A^{\mu}(x) = 0 \] (das ist gerade die relativistische Wellengleichung). Nimmt man nun die Nulldrehungen noch hinzu, so sind zusätzlich die folgenden Feldgleichungen erfüllt: \[ A^{0}(x) = 0 \] \[ \mathrm{div} \,\boldsymbol{A}(x) = 0 \] Das sind genau die Gleichungen für das elektromagnetische Viererpotential im ladungsfreien Raum in der Coulomb-Eichung (auch Strahlungseichung genannt). Nur zwei der vier Komponenten von \( A^{\mu}(x) \) sind demnach unabhängige Freiheitsgrade. Dann kann \( A^{\mu}(x) \) aber kein Vierervektorfeld mehr sein! Überprüft man das Transformationsverhalten des konstruierten Feldes \( A^{\mu}(x) \), so ergibt sich \[ T_{g} \, A_{\mu}(x) \, T_{g}^{-1} = A_{\nu}(\Lambda x) \, \Lambda^{\nu}_{\, \mu} + \partial_{\mu} \Omega(x) \] wobei \( \Omega(x) \) eine Linearkombination aus Erzeugern und Vernichtern ist, die auch noch von \( \Lambda \) abhängt – nur so kann man für jedes \( \Lambda \) immer \( A^{0}(x) = 0 \) sicherstellen. In Quantenfeldtheorie und Eichfelder, Kapitel 4 findet man die explizite Rechnung, wie man \( \Omega(x) \) wählen muss, um \( A^{0}(x) = 0 \) sicherzustellen (die richtige Stelle findet man unter dem Stichwort Strahlungseichung).
Die Transformationsformel sagt: Transformiere \( A_{\mu}(x) \) zunächst wie ein Vierervektorfeld, führe aber anschließend noch eine Eichtransformation aus, d.h. addiere einen geeigneten Term \( \partial_{\mu} \Omega(x) \) so, dass \( A^{0}(x) = 0 \) wird.
Ein Objekt, das sich so transformiert, nennt man ein Eichfeld. Da dieses Transformationsverhalten komplizierter ist als bei einem reinen Vierervektorfeld, sagt man auch, das Transformationsverhalten ist nicht mehr manifest kovariant. Dennoch hat man eine relativistisch korrekte Theorie vor sich: kein Bezugssystem wird ausgezeichnet.
Auch wenn man für Spin 1 im masselosen Fall kein Vierervektorfeld konstruieren kann, so kann man sehr wohl einen 4-mal-4-Tensor konstruieren. Ausgedrückt durch das Eichfeld lautet er \[ F_{\mu\nu} = \partial_{\mu} A_{\nu} - \partial_{\nu} A_{\mu} \] Das ist der bekannte Feldstärketensor. Beim Transformationsverhalten fallen die Eichterme hier weg.
Wenn man nun Quantenfeldtheorien mit masselosen Spin 1 -Teilchen betrachtet, so kann man Eichfelder \(A_{\mu}\) nicht ignorieren. Theorien ohne Eichfelder (z.B. nur mit dem Feldstärketensor \(F_{\mu\nu}\)) sind nicht allgemein genug, denn sie können keine langreichweitigen Kräfte wie die elektrische Kraft beschreiben. Man muss nur aufpassen, dass in den physikalischen Messgrößen keine Eichterme mehr vorkommen, d.h. die Theorie muss eichinvariant sein. Dann kann man nämlich die Eichfelder zunächst wie Vierervektorfelder transformieren und entsprechende kovariante Ausdrücke formulieren. Anschließend kann man über eine Eichtransformation die Eichbedingung sicherstellen, ohne dass diese Transformation sich in den physikalischen Messgrößen niederschlägt. Ein Beispiel ist der eichinvariante Feldstärketensor.
Auf Seite 253 macht Weinberg noch einige sehr interessante Bemerkungen: Für masselose Teilchen mit Spin 2 kann man langreichweitige Kräfte in einer Quantenfeldtheorie nur dann erreichen, wenn man analog zur Eichinvarianz bei Spin 1 so etwas wie die allgemeine Koordinaten-Kovarianz hat – in der allgemeinen Relativitätstheorie ist dies die Gleichwertigkeit aller Koordinatensysteme und damit die lokale Gleichwertigkeit aller frei fallenden Inertialsysteme (siehe Kapitel 5.2). Für Spin 3 und höher dagegen kann man überhaupt keine Quantenfeldtheorie mit langreichweitigen Kräften mehr erreichen.
Weinberg zeigt allgemein auf Seite 254: Will man aus masselosen Spin \(\sigma\) - Erzeugern und Vernichtern ein Quantenfeld konstruieren, dass sich wie ein \((j, j')\)-Feld transformiert, so muss \( j' - j = \sigma \) sein.
Um die S-Matrix für bestimmte Anfangs- und Endzustände näherungsweise auszurechnen, kann man die oben beschriebene zeitabhängige Störungstheorie verwenden. Sie hat den Vorteil, dass die Gültigkeit von Lorentz-Invarianz und Cluster-Decomposition-Prinzip ständig sichtbar bleiben. Die entsprechende Dyson-Reihe für die S-Matrix lautete (siehe oben Weinbergs Kapitel 3.5) \[ S = T e^{-i \int d^{4}x \, \mathcal{H}(x)} = \] \[ = 1 + (-i) \, \int d^{4}x \, \mathcal{H}(x) + \] \[ + (-i)^{2}/2 \, \int d^{4}x \, d^{4}x' \, T(\mathcal{H}(x),\mathcal{H}(x')) + \, ... \] Bildet man ein entsprechendes Matrixelement \[ \langle f | S | i \rangle \] zwischen einem Anfangs-Mehrteilchenzustand \( | i \rangle \) und einem End-Mehrteilchenzustand \( | f \rangle \), so kann man diese Anfangs- und Endzustände durch Einteilchen-Erzeugungsoperatoren aus dem Vakuum gewinnen und das Matrixelement entsprechend umschreiben. Es ergeben sich Vakuum-Matrixelemente der einzelnen S-Terme mit zusätzlichen Erzeugern für einlaufende Teilchen rechts und Vernichtern für auslaufende Teilchen links.
Die Wechselwirkungs-Hamiltondichte \( \mathcal{H}(x) \) besteht ihrerseits aus einer Summe (Integral) von Produkten der Form \[ \psi_{k} \, \psi_{k'} \, ... \, (\psi_{j})^{+} \, (\psi_{j'})^{+} \, ... \] (siehe oben), und diese Quantenfelder sind Impulsraum-Integrale mit Einteilchen-Erzeugern und -Vernichtern.
Man kann nun in allen Termen der Dyson-Reihe mit Hilfe der Kommutatoren und Anti-Kommutatoren die Vernichtungs-Operatoren schrittweise nach rechts durchtauschen. Dabei entstehen entsprechende Vertauschungsterme. Sobald dabei ein Vernichter rechts auf das Vakuum wirkt, ist der entsprechende Term Null, denn so ist das Vakuum ja gerade definiert.
Insgesamt entsteht eine lange Summe von komplexer werdenden Produkten, die immer wieder aus denselben Bausteinen bestehen. Diese Produkte kann man auch durch Diagramme charakterisieren, aus denen sich das Produkt ablesen lässt. Man bezeichnet sie als Feynman-Diagramme. Eine Linie entspricht dabei beispielsweise dem Vakuum-Matrixelement eines Erzeugers mit einem Vernichter (ein sogenannter Propagator, den Weinberg in Kapitel 6.2 explizit berechnet), und ein Kreuzungspunkt (Vertex) entspricht einem Faktor \( \mathcal{H}(x) \), also einer Wechselwirkung.
Man kann nun umgekehrt die Diagramme als Hilfsmittel dazu verwenden, um die Dyson-Reihe eines S-Matrix-Elementes bis zu einer bestimmten Ordnung aufzuschreiben. Dazu dienen die Feynman-Regeln. Sie geben an, welche Diagramme zu zeichnen sind und welche Terme sich daraus ergeben. Weinberg geht hier sehr detailliert darauf ein, und es zeigt sich, dass man gut aufpassen muss, um keine Fehler zu machen.
Die auftretenden Integrale über die Raum-Zeit-Koordinaten der Vertices kann man eliminieren und insgesamt alle Ausdrücke als Impuls-Integrale umschreiben. Man kann diese Ausdrücke auch direkt aus den Diagrammen ablesen, indem man entsprechende Impulsraum-Feynmanregeln formuliert. Dabei erkennt man, dass insbesondere der Viererimpuls an jedem Vertex erhalten ist. Die Viererimpulse der inneren Linien unterliegen keinen Beschränkungen (über sie wird integriert), während die Viererimpulse der ein- und auslaufenden Linien auf der Massenschale liegen müssen, also \( p^{2} = m^{2} \) mit der jeweiligen Teilchenmasse \(m\) erfüllen.
Oft ist es nützlich, auch für die ein- und auslaufenden Linien beliebige Viererimpulse zu betrachten. So wäre es ja beispielsweise, wenn diese Linien zu inneren Linien in einem größeren Diagramm würden. Außerdem werden solche Off-Shell-Diagramme wichtig, wenn äußere (klassische) Felder in den Feynmanregeln mit beschrieben werden sollen, oder wenn gebundene Zustände auftreten, die zu Polen in den Matrixelementen führen (siehe unten). Weinberg beweist in Kapitel 6.4 zudem ein wichtiges Theorem (Gleichung (6.4.3)), auf das wir unten bei Kapitel 10 noch einmal zurückkommen werden.
Der kanonische Formalismus ist der klassische Weg, über den man in der Vergangenheit meist eine Quantenfeldtheorie formuliert hat: Man beginnt mit einer Lagrangedichte und dem zugehörigen Wirkungsfunktional und führt die kanonische Quantisierung durch (Details dazu siehe Quantenfeldtheorie und Eichfelder, Kapitel 4 und Kapitel 5). Dieser historisch motivierte Weg ist aber keineswegs zwingend – deshalb geht Weinberg ja auch anders vor. Er schreibt: If we discovered a quantum field theory that led to a physically satisfactory S-matrix, would it bother us if it could not be derived by the canonical quantization of some Lagrangian?
Der wichtigste Vorteil des kanonischen Formalismus liegt darin, dass er es einfach macht, Lorentz-Invarianz und andere Symmetrien in der zugehörigen Quantentheorie sicherzustellen und eine passende Hamiltondichte zu formulieren. Weinberg betont, dass das keineswegs trivial ist, denn die Propagatoren erzwingen teilweise nicht-skalare Zusatzterme in \( \mathcal{H}(x) \), um entsprechende nicht-kovariante Terme in den Propagatoren zu kompensieren. Der kanonische Formalismus kann dies gewährleisten. Bei nicht-Abelschen Eichtheorien wäre es ohne den kanonischen Formalismus geradezu unmöglich, ein passendes \( \mathcal{H}(x) \) zu erraten. Hier kommt man ohne eine skalare und eichinvariante Lagrangedichte nicht weiter. In What is Quantum Field Theory, and what did we think it is? Steven Weinberg, 1997, arXiv:hep-th/9702027v1 schreibt Weinberg: Why do we enumerate possible theories by giving their Lagrangians rather than by writing down Hamiltonians? I think the reason for this is that it is only in the Lagrangian formalism (or more generally the action formalism) that symmetries imply the existence of Lie algebras of suitable quantum operators, and you need these Lie algebras to make sensible quantum theories.
In Kapitel 7.1 weist Weinberg nach, dass sich die freien Quantenfeldtheorien für skalare, Dirac- und Vierer-Vektorfelder in den kanonischen Formalismus umschreiben lassen. Zunächst zeigt er, dass sich aus ihnen die kanonisch konjugierten Operatoren \( p_{n}(x) \) und \( q^{n}(x) \) konstruieren lassen, die die bekannten Kommutatorregeln für gleiche Zeiten erfüllen (Weinberg Seite 293 Gleichung (7.1.1) bis (7.1.3) ), also insbesondere \[ [ q^{n}(t,\boldsymbol{x}) , p_{m}(t,\boldsymbol{y}) ]_{\pm} = \] \[ = i \, \delta^{3}(\boldsymbol{x} - \boldsymbol{y}) \, \delta^{n}_{m} \] Nun verwendet Weinberg den Kommutator, um formal eine quantenmechanische Funktionalableitung eines Funktionals von \( p_{n}(x) \) und \( q^{n}(x) \) zu definieren (Gleichungen (7.1.17) und (7.1.18) ). Dass das Sinn macht, kennen wir aus Quantenfeldtheorie und Eichfelder, Kapitel 3. Dort haben wir für die üblichen Operatoren \(x\) und \(p\) der nichtrelativistischen Quantenmechanik gezeigt, dass beispielsweise (mit \( \hbar = 1 \)) gilt: \[ - i [x, p^{n}] = n \, p^{n - 1} =: \frac{dp^{n}}{dp} \] wobei das zweite Gleichheitsheitszeichen als formale Definition des Ausdrucks \( \frac{dp^{n}}{dp} \) zu sehen ist, in Analogie zur üblichen Ableitung (hier sind \(x\) und \(p\) aber Operatoren!).
Wie man das auf kontinuierliche Operatoren \( p_{n}(x) \) und \( q^{n}(x) \) verallgemeinert, kann man unter dem Stichwort Funktionalableitung in Quantenfeldtheorie und Eichfelder, Kapitel 4 nachlesen. Die Funktionalableitung braucht man für die kanonische Formulierung einer Feldtheorie im Heisenberg-Bild in der Hamiltonschen Form, wie wir aus dem genannten Kapitel wissen.
Im nächsten Schritt muss der freie Hamiltonoperator identifiziert werden. Er hat immer die Form \[ H_{0} = \sum_{n,\sigma} \, \int d^{3}k \, k^{0} \, \cdot \] \[ \cdot \, a^{+}(\boldsymbol{k},\sigma,n) \, a(\boldsymbol{k},\sigma,n) \] (Weinberg Gleichung (7.1.23) ). Diese Form kann man nun durch die jeweils betrachteten Quantenfelder ausdrücken und so die gewohnten Formeln erhalten. Über die Legendre-Transformation (siehe Quantenfeldtheorie und Eichfelder, Kapitel 3 und Kapitel 4) gelangt man dann zur freien Lagrangedichte. Damit weiß man in der Störungstheorie immer, welcher Term als nullte Ordnung (d.h. als Term ohne Wechselwirkung) anzusehen ist, egal wie die gesamte Lagrangedichte aussieht.
In Kapitel 7.2 geht es nun darum, im kanonischen Formalismus geeignete Hamiltonoperatoren für wechselwirkende Felder zu erraten. Am einfachsten ist es, passende Lagrangedichten zu erraten und dann die Hamiltonoperatoren daraus zu berechnen. Dabei sind die Lagrangedichten Funktionale der Quantenfelder und deren Zeitableitungen. Ausgehend von der Lagrangedichte kann man nun mit dem Prinzip der kleinsten Wirkung die Feldgleichungen ermitteln (siehe Quantenfeldtheorie und Eichfelder, Kapitel 4). Weiterhin kann man zu den Feldern \(\psi(x)\) die kanonisch konjugierten Felder \(\pi(x)\) definieren (siehe das genannte Kapitel, Indizes lasse ich hier weg).
In Analogie zur klassischen Mechanik könnte man nun vermuten, dass man \(\psi(x)\) mit \(Q(x)\) und \(\pi(x)\) mit \(P(x)\) identifizieren kann. Für einfache skalare Felder stimmt das, aber im Allgemeinen ist die Sache nicht so einfach. Der Grund dafür ist, dass nicht zu jedem Feld \(\psi(x)\) auch dessen zeitliche Ableitung in der Lagrangedichte vorkommt, d.h. das entsprechende \(\pi(x)\) ist Null.
Das kennen wir aus Quantenfeldtheorie und Eichfelder, Kapitel 4: Dort hängt die Lagrangedichte des elektromagnetischen Potentials nicht von der zeitlichen Ableitung von \(A_{0}(x)\) ab, so dass \(\pi^{0}(x) = 0\) ist. Das entsprechende Feld \(A_{0}(x)\) muss also gesondert behandelt werden und entspricht nicht einem kanonischen Operator \(Q(x)\), sondern einem Feld \(C(x)\), dass man auch als Lagrange-Multiplier oder als Hilfsfeld bezeichnet und dem kein kanonisch konjugierter Impuls zugeordnet werden kann. Mehr dazu in dem genannten Kapitel.
Als Ergebnis des kanonischen Formalismus hat man nun im Heisenbergbild die kanonischen Bewegungsgleichungen (d.h. die Kommutatoren) für die \(P\)'s und \(Q\)'s sowie Nebenbedingungen aufgrund der \(C\)'s vorliegen. Um diese Gleichungen lösen zu können, geht man nun zur Störungstheorie über, d.h. man teilt den Hamiltonoperator auf in einen freien Teil \(H_{0}\) und einen Wechselwirkungsteil \(V\) und geht zum Wechselwirkungsbild über (siehe oben). Nun kann man die S-Matrix berechnen, wie wir es oben bereits kennengelernt haben. Beispiele gibt Weinberg in Kapitel 7.5 an.
In Kapitel 7.3 (Global Symmetries) geht Weinberg auf den eigentlichen Vorteil des kanonischen Formalismus ein: Er liefert einen geeigneten Rahmen, um Symmetrieprinzipien in einer Quantenfeldtheorie zu studieren. Grund dafür ist, dass die Bewegungsgleichungen sich aus einem Variationsprinzip herleiten lassen: dem Prinzip der kleinsten Wirkung (siehe oben). Symmetrien (Invarianzen) der Wirkung führen hier automatisch zu erhaltenen Strömen und zu zeitlich konstanten Erhaltungsgrößen (oft auch Ladungen genannt). Ist nicht nur die Wirkung invariant, sondern auch die Lagrangefunktion oder sogar die Lagrangedichte, so kann man explizite Formeln für die Ströme und Ladungen herleiten. Die Invarianz unter den 4 Raum-Zeit-Translationen führt beispielsweise zu 4 erhaltenen Strömen, die man zum Energie-Impuls-Tensor zusammenfassen kann (siehe auch Kapitel 5.3). Die zugehörigen Erhaltungsgrößen sind die Komponenten des Vierer-Gesamtimpulses.
Im kanonischen Formalismus stellt die Lorentz-Invarianz der skalaren Lagrangedichte automatisch die Lorentz-Invarianz der S-Matrix sicher. Dies zeigt Weinberg in Kapitel 7.4 (Lorentz Invariance). Dabei wird insbesondere der symmetrische Energie-Impuls-Tensor (Belinfante Tensor) eingeführt, den man im Rahmen der Einsteinschen Feldgleichungen als Quelle des Gravitationsfeldes interpretieren kann (siehe Kapitel 5.3).
In Kapitel 7.6 geht Weinberg auf eine Schwierigkeit ein, die bei der Herleitung des Hamiltonoperators aus der Lagrangefunktion auftritt: das Auftauchen von Nebenbedingungen. In Quantenfeldtheorie und Eichfelder, Kapitel 4 habe ich dies für das elektromagnetische Feld ausführlich dargestellt. Die Nebenbedingungen entstehen, wenn die Lagrangefunktion bestimmte zeitliche Feldableitungen nicht enthält (siehe oben). Die Ableitung der Lagrangefunktion nach diesen zeitliche Feldableitungen ist also Null – das ist die Nebenbedingung, die zu den Euler-Lagrange-Gleichungen der \(P\)'s und \(Q\)'s hinzukommt. Sie führt dazu, dass die \(P\)'s und \(Q\)'s im Allgemeinen keine unabhängigen Variablen mehr sind. In einfachen Fällen kann man noch versuchen, unabhängige \(P\)'s und \(Q\)'s zu finden.
Die bisherigen Methoden wendet Weinberg nun an, um die Quantentheorie des elektromagnetischen Feldes (die Quantenelektrodynamik) abzuleiten. Die klassische Vorgehensweise dazu kennen wir aus Quantenfeldtheorie und Eichfelder, Kapitel 4: Man beginnt mit den Maxwellgleichungen, formuliert diese im Rahmen des kanonischen Formalismus und quantisiert sie, indem man die \(P\)'s und \(Q\)'s als Operatoren eines Hilbertraums interpretiert und ihre Poissonklammern durch Kommutatoren ersetzt.
Weinberg geht anders vor: Er startet mit masselosen Teilchen mit Spin 1 (Photonen) und leitet die Notwendigkeit eines Eichprinzips explizit her. Die Idee dazu haben wir oben bereits kennengelernt, als wir für masselose Spin-1-Teilchen ein Vierer-Vektorfeld konstruieren wollten. Das Eichprinzip bestimmt dann wesentlich die Struktur der Theorie. Diese Vorgehensweise verwendet man beispielsweise in der Stringtheorie, bei der man unter den Stringzuständen gerade auf solche masselosen Zustände mit Spin 1 stößt. In What is Quantum Field Theory, and what did we think it is? Steven Weinberg, 1997, arXiv:hep-th/9702027v1 schreibt Weinberg dazu: ... what is the motivation for the special gauge invariant Lagrangians that we use in the standard model and general relativity? One possible answer is that quantum theories of mass zero, spin one particles violete Lorentz invariance unless the fields are coupled in a gauge invariant way, while quantum theories of mass zero, spin two particles violete Lorentz invariance unless the fields are coupled in a way that satisfies the equivalence principle. Entsprechende Anmerkungen kennen wir bereits aus Weinbergs Kapitel 5.9 (Massless Particle Fields) (siehe oben).
Danach geht Weinberg auch auf den alternativen konventionellen Weg ein, bei dem man mit dem lokalen Eichprinzip startet und daraus die Notwendigkeit eines Vierer-Vektorpotentials ableitet, das dann masselose Teilchen mit Spin 1 beschreibt. Siehe dazu auch Quantenfeldtheorie und Eichfelder, Kapitel 6
Welcher dieser beiden Wege besser der logischen Struktur der Natur entspricht, ist laut Weinberg heute noch offen. Freunde der Eichtheorie starten mit dem Eichprinzip, Freunde der Stringtheorie starten mit masselosen Spin-1-Teilchen.
In Kapitel 8.1 verfolgt Weinberg den ersten Weg und startet mit masselosen Spin-1-Teilchen. Von oben (Kapitel 5.9) wissen wir, dass man dann kein Vierervektor-Quantenfeld konstruieren kann, sondern nur ein Eichfeld (Eichpotential) \(A_{\mu}(x)\). Dieses transformiert sich zunächst wie ein Vierervektorfeld, aber es kommt noch eine Eichtransformation hinzu, mit der man beispielsweise die Eichbedingung \( A_{0}(x) = 0 \) in jedem Bezugssystem erzwingen kann. Bei dieser Eichbedingung ist die Eichtransformation also von der Lorentztransformation abhängig: jede Lorentztransformation führt zu einer Eichtransformation, um die Eichbedingung einzuhalten. Um die Lorentz-Invarianz der Theorie sicherzustellen, fordert man daher zusätzlich die Eichinvarianz der Theorie, denn dann kann die Eichtransformation und damit die sie erzeugende Lorentztransformation die Ergebnisse der Theorie nicht ändern.
Genauer: Man kann die Eichfelder \(A_{\mu}(x)\) zunächst Lorentz-invariant verkoppeln – damit wäre alles in Ordnung, wenn man die Eichfelder wie Vierervektorfelder transformiert. Nun kommt aber zu der Vierervektor-Transformation noch eine Eichtransformation der Eichfelder hinzu, mit der man beispielsweise die Eichbedingung \( A_{0}(x) = 0 \) sicherstellt. Nur wenn man die Eichfelder \(A_{\mu}(x)\) zugleich auch eichinvariant verkoppelt hat, stört diese Eichtransformation nicht, d.h. der Gesamtausdruck ist invariant unter der Vierervektor-Transformation und der anschließenden Eichtransformation von \(A_{\mu}(x)\), also unter dem Gesamt-Transformationsverhalten von \(A_{\mu}(x)\) bei Lorentz-Transformationen – der Gesamtausdruck ist damit erst Lorentz-invariant. Ein Beispiel für einen solchen invarianten Ausdruck wäre der Term \( F_{\mu\nu} F^{\mu\nu} \) mit dem Feldstärketensor \( F_{\mu\nu} = \partial_{\mu} A_{\nu} - \partial_{\nu} A_{\mu} \).
Eichinvariante Theorien mit Eichpotentialen \(A_{\mu}(x)\) und anderen Feldern \(\psi(x)\) (z.B. Materiefeldern) erhält man, wenn man in der Lagrangedichte Terme wie \(J_{\mu} A^{\mu}\) verwendet, wobei der Strom \(J_{\mu}\) erhalten ist (also \( \partial_{\mu} J^{\mu} = 0 \) gilt). Insgesamt findet man, dass eine lokale Eichtransformation der Eichpotentiale auch zu einer lokalen Transformation der Materiefelder führt, nämlich zu einer \(x\)-abhängigen Veränderung der Phase der Materiefelder (Weinberg Seite 342 Gleichungen (8.1.12) und (8.1.13)). Beim alternativen konventionellen Zugang über das lokale Eichprinzip startet man dagegen genau mit dieser lokalen Transformation der Materiefelder und fordert die Eichinvarianz, was die Einführung der Eichpotentiale erzwingt, sobald Raum-Zeit-Ableitungen der Materiefelder in der Lagrangedichte vorkommen.
Auf die Probleme, die durch Nebenbedingungen entstehen, geht Weinberg in Kapitel 8.2 ein. Wir hatten es oben bereits mehrfach erwähnt: Da \( \partial_{0} A_{0} \) in der Lagrangedichte nicht vorkommt, ist \( \pi^{0}(x) = 0 \). Weinberg nennt dies einen primary constraint. Er folgt direkt aus der Struktur der Lagrangedichte. Aus dem primary constraint folgt ein secondary constraint, nämlich \( \mathrm{div} \, \boldsymbol{\pi}(x) = J^{0}(x) \) oder anders geschrieben \( \mathrm{div} \, \boldsymbol{E}(x) = \rho(x) \). Details dazu siehe Quantenfeldtheorie und Eichfelder, Kapitel 4.
Um mit den Nebenbedingungen bei der Quantisierung fertig zu werden, kann man beispielsweise eine Eichfixierung fordern. Dies tut Weinberg in Kapitel 8.3 (Quantization in Coulomb Gauge). Die Vorgehensweise ist analog zu Quantenfeldtheorie und Eichfelder, Kapitel 4,, wobei Weinberg aber in den Folgekapiteln noch weiter geht und auch den Photonpropagator berechnet, die Feynman-Regeln der Quantenelektrodynamik in dieser Eichung herleitet und sogar die Compton-Streuung in niedrigster Ordnung berechnet (also die Streuung eines Elektrons mit einem Photon). Man erkennt, wie aufwendig der kanonische Formalismus bereits bei der einfachen Elektrodynamik wird – ein Grund, sich in Kapitel 9 nach alternativen Methoden umzusehen.
Zum Abschluss geht Weinberg in Kapitel 8.8 noch auf Eichpotentiale mit mehr als einem Raumzeitindex \(\mu\) ein. In mehrdimensionalen Räumen (Stringtheorie) spielen diese Eichpotentiale durchaus eine Rolle, aber in der vierdimensionalen Raumzeit liefern sie nichts Neues, wie Weinberg zeigt.
Lesenswert ist hier (wie auch bei vielen anderen Kapiteln) insbesondere Weinbergs Einleitung: Die vorherigen Kapitel haben gezeigt, dass der kanonische Formalismus schnell sehr unübersichtlich wird. Ausgehend von einer einfachen Lagrangedichte geht man über einen komplexen Hamiltonoperator und komplexe Bewegungsgleichungen mit Nebenbedingungen, um zum Schluss wieder einfache kovariante Feynmanregeln zu erhalten. Bei Theorien wie der nicht-Abelschen Eichtheorie (beispielsweise die Quantenchromodynamik QCD) macht diese Komplexität jedes Fortkommen unmöglich. Gibt es eine einfachere Methode, die den nicht-kovarianten Umweg über den Hamiltonoperator vermeidet und direkt von der kovarianten Lagrangedichte zu den kovarianten Feynmanregeln führt?
Ja, es gibt eine solche Methode: die Pfadintegrale, die zuerst von Richard Feynman verwendet wurden. Wir haben diese Methode in Quantenfeldtheorie und Eichfelder, Kapitel 3 und Kapitel 5 bereits kennengelernt. Heute gehört diese Methode fest zum Werkzeugkasten der theoretischen Physik, denn sie konnte Erfolge erzielen, die mit der kanonischen Formulierung nie zu erreichen gewesen wären: Quantisierung der nicht-Abelschen Eichtheorien und spontan gebrochener Eichtheorien sowie nicht-störungstheoretische Anteile der S-Matrix, die sich prinzipiell mit der Störungstheorie nicht erfassen lassen.
Dennoch kann man auf den kanonischen Formalismus nicht ganz verzichten, denn er garantiert die Unitarität der S-Matrix, was im Pfadintegral-Formalismus nicht so klar ist. Leitet man dagegen den Pfadintegral-Formalismus aus dem kanonischen Formalismus ab (was Weinberg tut), so ist die Unitarität der S-Matrix gesichert. Ohne den kanonischen Formalismus ist nicht bekannt, wie sich die Unitarität der S-Matrix allein mit Pfadintegral-Methoden nachweisen lässt.
Ein naives Anwenden der Pfadintegral-Methode ohne den kanonischen Formalismus liefert sogar teilweise schlicht falsche Feynmanregeln – ein weiterer Grund, mit dem kanonischen Formalismus zu starten und daraus sorgfältig die Pfadintegrale abzuleiten. Weinberg tut dies in Kapitel 9.1 in sehr ähnlicher Weise wie wir das aus Quantenfeldtheorie und Eichfelder, Kapitel 3 kennen.
In Kapitel 9.2 leitet er dann die entsprechenden Ausdrücke für die S-Matrix her und übersetzt die gefundene Hamilton'sche Version in Kapitel 9.3 in eine Lagrange-Version des Pfadintegrals (wobei einige Feinheiten zu beachten sind). Im Wesentlichen besteht dabei ein Pfadintegral aus einer Summe (Integral) über alle Möglichkeiten (Feldkonfigurationen), wobei jede Möglichkeit eine (passend gewichtete) Amplitude \( e^{i S[\psi]} \) beiträgt ( \(S[\psi]\) ist das Wirkungsfunktional und \( \hbar \) ist in natürlichen Einheiten hier gleich \(1\)).
Die Wirkung \(S\) teilt man nun auf in einen freien Anteil \(S_{0}\) und einen Wechselwirkungsanteil \(S_{1}\) und schreibt die Exponentialfunktion des Wechselwirkungsanteils als Exponentialreihe aus. Auf diese Weise gelang man in Kapitel 9.4 letztlich bis zu den Feynmanregeln.
In Kapitel 9.5 erweitert Weinberg den Formalismus auf Fermionen. Er tut dies sehr sorgfältig und zieht sich nicht alleine auf formale Analogien zum bosonischen Fall zurück. Dabei kommen Grassmann-Algebren ins Spiel, wie wir sie in Kapitel 6.1 kennenlernen werden (siehe auch Kapitel 4.11). In Kapitel 9.6 folgt die konkrete Berechnung des kovarianten Photon-Propagators mit Hilfe von Pfadintegralen.
Weinberg geht in diesem Kapitel auf Möglichkeiten ein, mit der man Ergebnisse erzielen kann, die in allen Ordnungen der Störungstheorie gültig sind und teilweise sogar über die Störungstheorie hinausgehen. Mit solchen Methoden kann man beispielsweise in bestimmten Fällen unendlich viele Feynmangraphen komplett erfassen. Beispiele, bei denen man das braucht, sind gebundene Zustände, Renormierung oder Formfaktoren.
Ausgangspunkt ist Gleichung (6.4.3), die Weinberg in Kapitel 6.4 herleitet. Dazu geht er davon aus, dass im Wechselwirkungsbild zu dem Wechselwirkungsanteil \(V(t)\) noch Operator-Terme \(o_{a}(x)\) hinzukommen, die über komplexwertigen Funktionen \(\epsilon_{a}(x)\) flexibel hinzugeschaltet werden (Gleichung 6.4.1): \[ V_{\epsilon}(t) = V(t) + \sum_{a} \, \int d^{3}x \, \epsilon_{a}(x) \, o_{a}(x) \] (alles im Wechselwirkungsbild mit der entsprechenden \(H_{0}\)-Zeitabhängigkeit der Operatoren \(o_{a}(x))\). Der Index \(\epsilon\) bei \(V_{\epsilon}(t)\) signalisiert die Abhängigkeit von dem Vektor der komplexwertigen Funktionen \( \epsilon(x) := (\epsilon_{a}(x)) \).
Entsprechend hängt auch ein S-Matrixelement zwischen einem Anfangszustand \(\alpha\) und einem Endzustand \(\beta\) von \(\epsilon\) ab, ist also ein Funktional \( S_{\beta \alpha}[\epsilon] \) dieser Funktionen. Definiert man nun zu den Wechselwirkungsbild-Operatoren \(o_{a}(x)\) die zugehörigen Heisenbergbild-Operatoren \(O_{a}(x)\) (mit der entsprechenden \(H\)-Zeitabhängigkeit), so gilt in beliebiger Ordnung der Störungstheorie der Zusammenhang (Gleichung 6.4.3) \[ \left[ \frac{\delta^{r} S_{\beta\alpha}[\epsilon]} {\delta\epsilon_{a}(x) \, \delta\epsilon_{b}(y) \, ... }\right]_{\epsilon = 0} = \] \[ = \langle \beta | T( -i O_{a}(x), -i O_{b}(y), \, ... ) | \alpha \rangle \] Links steht die Funktionalableitung (Variation) des S-Matrixelementes für infinitesimale Funktionswerte \(\epsilon_{a}(x)\), also die Änderung des S-Matrixelementes zwischen den Zuständen \(\alpha\) und \(\beta\) beim Einschalten der Zusatzwechselwirkung mit den Operatoren \(o_{a}(x)\). Mehr zur Funktionalableitung siehe Quantenfeldtheorie und Eichfelder, Kapitel 4.
Rechts steht das Matrixelement eines zeitgeordneten Operatorproduktes im Heisenbergbild (also mit Wechselwirkung), und zwar derjenigen Operatoren, die im \(\epsilon\)-Zusatzterm in der Wechselwirkung stehen. Die Gleichung sagt nun laut Weinberg aus: Dieses Matrixelement entspricht der Summe aller (unendliche vielen) Feynmangraphen, die an den Raum-Zeit-Punkten x, y usw. Zusatzvertices enthalten, wie sie den Operatoren \(o_{a}(x), o_{b}(x)\) usw. entsprechen.
Man kann nun die Fouriertransformation des Matrixelementes rechts in den Impulsraum bilden. Dann entspricht das Impulsraum-Matrixelement der Summe aller Feynmangraphen, bei denen die Operatoren \(O_{a}, O_{b} \, ... \) die Off-Shell-Impulse \(p_{a}, p_{b} \, ... \) über äußere Linien in die Graphen hineintragen. Falls die Operatoren Feldern der Lagrange-Funktion entsprechen, dann entsprechen diese Linien elementaren Teilchen der Theorie.
Entscheidend ist nun die Polstruktur der Matrixelemente im Impulsraum. Ein konkretes Beispiel: Nehmen wir 4 Operatoren \(O_{1}\) bis \(O_{4}\), und nehmen wir an, dass es einen Ein-Teilchen-Zustand mit Impuls \[ P = p_{1} + p_{2} = - (p_{3} + p_{4}) \] und Masse \(M\) gibt (Achtung: die Impulse \(p_{1}\) bis \(p_{4}\) dürfen off-shell sein, müssen also nicht \( p_{i}^{2} = m_{i}^{2} \) erfüllen).
Nehmen wir weiter an, dass die Matrixelemente \[ \langle 0 | T(O_{1}(x) O_{2}(y)) | P \rangle \] \[ \langle 0 | T(O_{3}(x) O_{4}(y)) | P \rangle \] ungleich Null sind (diese Matrixelemente werden auch als Bethe-Salpeter-Amplituden bezeichnet). Dann zeigt Weinberg, dass das Matrixelement \[ \langle 0 | T( O_{1}(x), O_{2}(y), O_{3}(x'), O_{4}(y') ) | 0 \rangle \] nach Fouriertransformation in den Impulsraum einen Pol bei \( P^{2} = M^{2} \) hat (er zeigt das ganz allgemein für beliebig viele Operatoren). Letztlich hat der Pol seinen Ursprung in den \(\Theta\)-Funktionen in der Zeit aufgrund des zeitgeordneten Produktes im Matrixelement. Über die Fourierdarstellung ergibt die \(\Theta\)-Funktion einen Pol.
Oft verwendet man für die Operatoren Felder der Lagrangedichte (entsprechend elementarer ein- und auslaufender Teilchen). Der Ein-Teilchen-Zustand mit Impuls \(P\) und Masse \(M\) muss aber keineswegs einem solchen elementaren Teilchenzustand entsprechen. Er kann auch ein zusammengesetztes Teilchen sein, z.B. ein aus Quarks zusammengesetztes Meson. Man spricht von gebundenen Zuständen.
Gebundene Zustände führen also zu Polen in entsprechenden Matrixelementen.
Das kann man mit reiner Störungstheorie in endlicher Ordnung nicht zeigen.
Man benötigt unendlich viele Graphen, d.h. dieses Ergebnis geht über die reine Störungstheorie hinaus.
Anschaulich wechselwirken die elementaren Bestandteile des gebundenen Zustandes
eben unendlich oft und unendlich lange miteinander – sonst wäre der Zustand nicht gebunden, sondern
würde zerfallen. Die folgende graphische Darstellung des Matrixelementes zeigt in der Mitte
diese unendliche Wechselwirkung, die zu dem gebundenen Zustand und damit zum Pol im
Matrixelement führt:
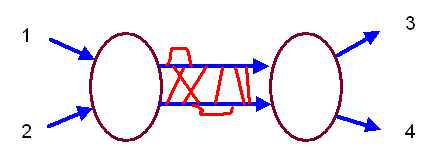
Wichtig ist, dass Pole sowohl von elementaren Teilchen stammen können (d.h. das zugehörige Quantenfeld steht im Lagrangian) als auch von zusammengesetzten Teilchen stammen können, zu denen es kein solches Quantenfeld im Lagrangian gibt. Solche Pole führen im nichtrelativistischen Grenzfall zu Kräften mit Reichweite \(1/M\) (Yukawa-Potential). Umgekehrt kann man aber aus der Existenz solcher Kräfte nicht auf ein elementares Teilchen (mit zugehörigem Quantenfeld im Lagrangian) schließen, denn auch ein zusammengesetztes Teilchen hat diese Auswirkung (Beispiel: die Rolle des Pions bei Kernkräften zwischen Nukleonen).
In Kapitel 10.3 betrachtet Weinberg Matrixelemente mit nur zwei Operatoren \[ \langle 0 | T( O_{1}(x), O_{2}(y)) | 0 \rangle \] also insbesondere Propagatoren.
Auch diese Propagatoren haben Pole. Setzt man für \(O_{1}(x)\) und \(O_{2}(x)\) die Felder des Lagrangians ein, so liegt dieser Pol bei der Masse des zugehörigen Teilchens dieser Felder. Nun kann man die Renormierung von Massen und Quantenfeldern betrachten, d.h. es wird berücksichtigt, dass die Selbstenergieanteile (ebenfalls unendlich viele Diagramme) den Massenpol und das Quantenfeld im Vergleich zu den nackten Massen und Feldern verändern. Der Kernsatz lautet (Seite 438): Thus a renormalized field is one whose propagator has the same behavior near its pole as for a free field, and the renormalized mass is defined by the position of the pole. Dabei muss die Position des Massenpols (also der Wert der renormierten Masse) als Information hineingesteckt werden. Weinberg betont, dass diese Renormierung zwingend notwendig ist, unabhängig davon, ob dadurch Divergenzen entstehen oder nicht.
Auch elektrische Ladungen müssen renormiert werden. Weinberg geht darauf in Kapitel 10.4 ein. Dabei leitet er die Ward-Takahashi-Identität her, die einen Zusammenhang zwischen der elektromagnetischen Vertexfunktion (Vertex mit Strahlungskorrekturen, also Ladung mit Polarisationswolke) und den Propagatoren (mit Polarisationswolke) der geladenen Fermionen herstellt.
In Kapitel 10.5 geht Weinberg schließlich auf Eichinvarianz und die Renormierung des Photonpropagators ein. Ein wichtiges Ergebnis ist, dass Strahlungskorrekturen dem Photon keine Masse verleihen, d.h. die Polarisationswolke des Photons ist gleichsam masselos wie das Photon selbst.
Elektromagnetische Formfaktoren behandelt Weinberg in Kapitel 10.6. Dabei untersucht man die Streuung eines Teilchens an einem äußeren elektromagnetischen Feld, wobei dieses Feld nur in erster Ordnung eingeht, aber die Polarisationswolke des Teilchens komplett eingehen soll – also müssen wieder alle unendlich vielen zugehörigen Feynmangraphen betrachtet werden.
In den weiteren Kapiteln 10.6 und 10.7 geht Weinberg noch auf Spezialthemen ein, die sich mit der analytischen Struktur von Matrixelementen (insbesondere Propagatoren) im Impulsraum befassen. Ich lasse das hier einfach weg.
Weinberg zeigt hier einige Standardrechnungen zu Ein-Schleifen-Korrekturen in der QED
(Vakuumpolarisation, Vertexkorrektur und Elektron-Selbstenergie).
Hier sind die entsprechenden Feynmangraphen (Photonlinien in Rot, Elektronlinien in Blau mit Pfeil):
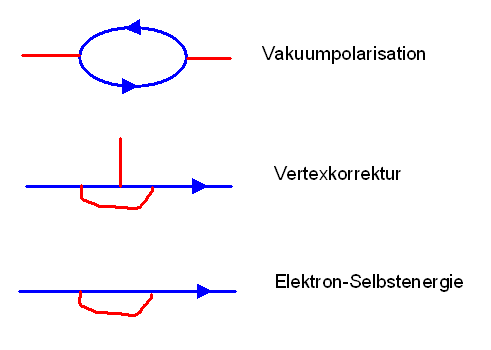
In Kapitel 11.2 startet Weinberg mit der Vakuumpolarisation, die durch Elektron-Positron-Loops im Photonpropagator entsteht. Der renormierte Photonpropagator \( \Delta' \) inklusive der Korrekturen durch virtuelle Teilchen hängt dabei mit dem nackten Photonpropagator \( \Delta \) über die Gleichung (11.2.1) \[ \Delta' = \frac{\Delta}{1 - \Pi^{*} \Delta} \] zusammen. Für \( \Pi^{*} = 0 \) wäre \( \Delta' = \Delta \), d.h. \(\Pi^{*}\) enthält den Einfluss der virtuellen Teilchen. In niedrigster Ordnung ist dies der Einfluss des Elektron-Positron-Loops, den Weinberg nun ausrechnet. Dabei muss ein Integral über den im Loop umlaufenden Fermion-Viererimpuls berechnet werden, wobei im Integranden die beiden Fermion-Propagatoren und die beiden Vertex-Matrizen mit elektrischen Ladungen stehen.
Um dieses Integral auszurechnen, kommen die Standardmethoden wie Wick-Rotation und dimensionale Regularisierung zum Einsatz. Bei der Wick-Rotation setzt man die auftretenden Integranden in \(p^{0}\) analytisch ins Komplexe fort und kann dann die Integrale berechnen. Dabei muss man auf die Pole der Propagatoren achten. Die Wick-Rotation hat den Vorteil, dass bei der Ersetzung von \(p^{0}\) durch \(i p^{0}\) die relativistische Metrik im Impulsraum zur euklidischen Metrik wird. Leider divergiert das Integral, da in dem Loop über beliebig große Impulse integriert werden muss.
Die dimensionale Regularisierung verwendet man nun, um aus dem divergierenden Integral ein endliches Integral zu machen. Ein einfacher Impuls-Cutoff als Regularisierung wäre ungeeignet, da dies die Eichinvarianz verletzen würde und zu einer endlichen Photonmasse führt. Bei der dimensionalen Regularisierung dagegen ersetzt man in den Formeln trickreich die Impulsraumdimension 4 durch eine beliebige Raumdimension \(d\) und kann sich dann später den Grenzfall für \(d\) gegen 4 ansehen. Zum Glück hängt die Stromerhaltung nicht von der Raumdimension ab – das ist der Grund, warum die dimensionale Regularisierung hier das geeignete Verfahren ist.
Das Auftreten von Divergenzen in solchen Schleifen signalisiert, dass die betrachtete Quantentheorie nicht bis zu beliebig hohen Impulsen (beliebig kleinen Abständen) physikalisch sinnvoll ist. Die Regularisierung (\(d\) ungleich 4) beseitigt zunächst formal die Divergenzen in den einzelnen Termen. Drückt man am Schluss der Rechnung alle Größen durch die renormierte Masse und Ladung aus (wobei man dafür deren experimentelle Werte braucht), so löschen sich die Divergenzen gegenseitig aus, d.h. man kann den Grenzfall \(d\) gegen 4 ausführen und erhält endliche Resultate. Eine anschauliche Beschreibung dieser Renormierung findet man in Die Entdeckung des Unteilbaren, Kapitel 6.3.
Im Detail sieht das Verschwinden der Divergenz hier so aus: Die Lagrangedichte, ausgedrückt durch die nackten (nicht renormierten) Felder \( A_{B}^{\mu} \) (\(B\) steht für Bare = nackt) enthält den Photonenterm \[ \mathcal{L} = - \frac{1}{4} \, {F_B}^{\mu\nu} {F_B}_{ \mu\nu} + \, ... \] mit dem Feldstärketensor \[ {F_{B}}_{ \mu\nu} = \partial_{\mu} {A_{B}}_{ \nu} - \partial_{\nu} {A_{B}}_{ \mu} \] Für die renormierten Felder machen wir den Ansatz (Gleichung 11.1.3) \[ A^{\mu} := {A_{B}}^{\mu} / \sqrt{Z_{3}} \] mit einem Renormierungsfaktor \(Z_{3}\). Ein renormiertes Feld ist dadurch gekennzeichnet, dass sein Propagator an seinem Pol dasselbe Verhalten aufweist wie ein freies Feld, mit der renormierten (experimentell ermittelten) Teilchenmasse als Pol (Weinberg Seite 438). Zu einem renormierten Feld gibt es also freie Teilchen mit der entsprechenden (experimentell ermittelten) Masse.
Für den Feldstärketensor haben wir entsprechend \[ F^{\mu\nu} = {F_{B}}^{\mu\nu} / \sqrt{Z_{3}} \] so dass wir die Lagrangedichte durch die renormierten Felder ausdrücken können: \[ L = - \frac{1}{4} \, {F_{B}}^{\mu\nu} {F_{B}}_{ \mu\nu} + \, ... = \] \[ = - \frac{1}{4} \, Z_{3} \, F^{\mu\nu} F_{ \mu\nu} + \, ... = \] \[ = - \frac{1}{4} \, F^{\mu\nu} F_{ \mu\nu} - (Z_{3} - 1) \, \frac{1}{4} \, F^{\mu\nu} F_{ \mu\nu} + \, ... \] Dabei haben wir im letzten Schritt die Lagrangedichte aufgeteilt in einen freien renormierten Photonterm \[ - \frac{1}{4} \, F^{\mu\nu} F_{ \mu\nu} \] und einen sogenannten Counterterm \[ - (Z_{3} - 1) \frac{1}{4} \, F^{\mu\nu} F_{ \mu\nu} \] Bei dem divergenten Ausdruck \( \Pi^{*} \) wurde aber nur der freie renormierte Photonterm und die entsprechenden Feynmanregeln berücksichtigt. Hinzu kommt ein weiterer Term, der von dem Counterterm verursacht wird. Insgesamt hat damit \( \Pi^{*} \) die folgende Struktur: \[ \Pi^{*}(q)^{ \mu\nu} = \] \[ = \{ f(d) \, I(q^{2},m,d) - (Z_{3} - 1) \} \, Q^{\mu\nu} \] mit der Lorentzstruktur \[ Q^{\mu\nu} = q^{2} g^{\mu\nu} - q^{\mu} q^{\nu} \] (Weinberg Gleichung (11.2.17) Seite 478). Dabei ist \(q\) der Photonimpuls, \(m\) die Elektronenmasse, \(d\) die Impulsraumdimension von der dimensionalen Regularisiserung, \( I(q^{2},m,d) \) eine endliche Funktion von \(q^{2}, m, d\), und \(f(d)\) eine Funktion der Raumdimension \(d\), die für \(d\) gegen 4 divergiert.
Nun soll der renormierte Photonpropagator \(\Delta'\) denselben Pol haben wie der nackte Photonpropagator \(\Delta\), nämlich bei \( q^{2} = 0 \) (der Photonmasse). Aus der Gleichung \[ \Delta' = \frac{\Delta}{1 - \Pi^{*} \Delta} \] von oben folgt, dass beide Propagatoren gleich werden, wenn \(\Pi^{*} = 0\) wird. Also muss für \( q^{2} = 0 \) die Vakuumpolarisation \(\Pi^{*}\) gegen Null gehen: \[ \Pi^{*}(0) = 0 \] Das bedeutet, dass in der obigen Formel für \( \Pi^{*}(q)^{ \mu\nu} \) die geschweifte Klammer für \( q^{2} = 0 \) gegen Null gehen muss (der Term \( Q^{\mu\nu} \) spielt bei diesen Betrachtungen keine Rolle, da er nur eine hier aus anderen Gründen erzwungene Lorentzstruktur sicherstellt): \[ \{ f(d) \, I(0,m,d) - (Z_{3} - 1) \} = 0 \] Diese Gleichung können wir nach \( (Z_{3} - 1) \) freistellen: \[ (Z_{3} - 1) = f(d) \, I(0,m,d) \] Nun können wir dieses Ergebnis oben in \( \Pi^{*}(q)^{ \mu\nu} \) einsetzen und \(f(d)\) ausklammern: \[ \Pi^{*}(q)^{ \mu\nu} = \] \[ = \{ f(d) \, I(q^{2},m,d) - (Z_{3} - 1) \} \, Q^{\mu\nu} = \] \[ = \{ f(d) \, I(q^{2},m,d) - f(d) \, I(0,m,d) \} \, Q^{\mu\nu} = \] \[ = f(d) \, \{ I(q^{2},m,d) - I(0,m,d) \} \, Q^{\mu\nu} \] Die Rechnung zeigt nun, dass für \(d\) gegen 4 die beiden Terme \(I(q^{2},m,d)\) und \(I(0,m,d)\) in der geschweiften Klammer gegen dieselbe reelle Zahl konvergieren, und dass deren Differenz in der geschweiften Klammer eine einfache Nullstelle in \(d\) aufweist (also proportional zu \( (d - 4) \) ist).
Diese Nullstelle kompensiert gerade den einfachen Pol \( 1/(d - 4) \) in \(f(d)\), so dass der Grenzwert \(d\) gegen 4 ausgeführt werden kann und eine endliche Funktion von \(q\) ergibt. Auf diese Weise kompensiert der divergente Counterterm die Divergenz der Vakuumpolarisation. Dass das funktioniert, haben wir im Grunde in die Rechnung hineingesteckt, denn wir hatten ja oben \( \Pi^{*}(0) = 0 \) gefordert, so dass der Counterterm zwangsläufig die Divergenz beseitigen muss.
Was bedeutet die Vakuumpolarisation physikalisch? Sie führt zu einer Art Abschirmung der nackten Ladungen durch virtuelle Teilchen wie in einem polarisierbaren Medium. Mehr dazu siehe Die Entdeckung des Unteilbaren, Kapitel 5.4.
In Kapitel 11.3 betrachtet Weinberg dann die Vertexkorrektur, bei der ein Photon an ein Fermion ankoppelt, wobei das Fermion aber zuvor ein virtuelles Photon aussendet und dieses nach dem Ankoppeln des anderen Photons wieder absorbiert. Hier genügt zur Regularisierung des divergenten Integrals ein einfacher Impuls-Cutoff, denn Eichinvarianz ist hier unwichtig. Das Diagramm beeinflusst im nichtrelativistischen Grenzfall das magnetische Moment des Fermions, also seine Wechselwirkung mit einem magnetischen Feld. Die Vakuumpolarisation beeinflusst dagegen seine Wechselwirkung mit einem elektrischen Feld im nichtrelativistischen Grenzfall.
Schließlich berechnet Weinberg in Kapitel 11.4 auch noch die Selbstenergie des Elektrons, die durch vom Elektron ausgesendete und wieder absorbierte virtuelle Photonen entsteht. Auch in der klassischen Elektrodynamik eines punktförmigen geladenen Teilchens gibt es eine solche Selbstenergie, die durch die Energie des elektrischen Feldes des Teilchens entsteht. Da das Teilchen punktförmig ist, divergiert diese Energie (d.h. in der klassischen Elektrodynamik darf es eigentlich keine punktförmigen Teilchen geben, oder man muss ihre Selbstenergie ignorieren). In der Quantenelektrodynamik divergiert die Selbstenergie ebenfalls, aber viel schwächer als in der klassischen Elektrodynamik (nämlich nur logarithmisch). Durch die Renormierung wird dann diese Divergenz beseitigt, denn der renormierte Elektronpropagator soll ja einen Pol bei der gemessenen Elektronmasse haben.
Noch eine Bemerkung von Seite 516 dazu (Kapitel 12.5): In der QED liefern die Elektronmasse, Elektronladung und Photonmasse natürlich ausgezeichnete Messwerte, um die Theorie zu renormieren. In anderen Theorien ist das nicht so naheliegend, beispielsweise in der Quantenchromodynamik (QCD). Dort gibt es keine freien Quarks oder Gluonen, und man muss bei der Messung der Quarkmasse oder Farbladung immer angeben, bei welchem Viererimpulsquadrat \(q^{2}\) man diese gemessen hat. Man kann sich nun irgendein solches \( q^{2} =: \mu^{2} \) wählen, um die entsprechenden Messwerte zur Renormierung der Theorie zu verwenden. Man hängt gleichsam die Renormierung an diesem Renormierungspunkt auf. Dabei müssen die physikalischen Ergebnisse unabhängig von der Wahl des Renormierungspunktes sein, was zur sogenannten Renormierungsgruppe führt. Ich habe diese Idee an einem einfachen Beispiel in Die Entdeckung des Unteilbaren, Kapitel 6.3 dargestellt.
Bereits bei den 1-Loop-Rechnungen in Kapitel 11 haben wir gesehen, dass divergente Integrale auftreten, da in den Loops bis zu unendlich großen Impulsen (unendlich kleinen Abständen) integriert wird. Drückt man jedoch alle Parameter der Theorie (Ladungen, Massen) durch renormierte Größen aus, so wie sie tatsächlich gemessen werden, so heben sich die Divergenzen gegenseitig auf. Man kann zeigen, dass das in der QED nicht nur für 1-Loop-Diagramme gilt, sondern für jede Ordnung der Störungstheorie. Solche Theorien nennt man renormierbar.
Früher dachte man, jede Quantenfeldtheorie müsse renormierbar sein, um physikalisch sinnvoll zu sein. Heute sieht man das laut Weinberg etwas anders, denn Quantenfeldtheorien werden als Nieder-Energie-Grenzfall von (noch unbekannten) fundamentaleren Theorien angesehen (Beispiel: Stringtheorie). Eine Quantenfeldtheorie ist dann eine effektive Feldtheorie, wobei eine solche Theorie alle unendlich vielen Wechselwirkungsterme im Lagrangian enthalten muss, die die zugrundeliegenden Symmetrien der Theorie respektieren. Die meisten dieser Terme sind nicht renormierbar. Dennoch heben sich die Divergenzen auf, solange man alle unendlich vielen Terme berücksichtigt. Bei Energien weit unterhalb der Planck-Energie sind jedoch vermutlich alle nicht-renormierbaren Terme unterdrückt, so dass eine renormierbare Quantenfeldtheorie übrig bleibt.
In Kapitel 12.1 schaut sich Weinberg systematisch die Divergenz von Loop-Integralen in Feynmangraphen an. Wenn diese Divergenzen immer schlimmer werden, je mehr Vertices ein Diagramm enthält, so lassen sich die Divergenzen in beliebiger Ordnung der Störungstheorie nicht mehr durch Redefinition (Renormierung) endlich vieler Parameter und Felder der Theorie beseitigen, und die Theorie wird nicht-renormierbar. Da bei effektiven Feldtheorien aber auch unendlich viele Wechselwirkungsterme mit unendlich vielen Parametern vorhanden sind, kann eine solche Theorie durchaus endliche Resultate liefern.
Bei renormierbaren Feldtheorien müssen normalerweise analog alle (endlich vielen) renormierbaren Terme im Lagrangian auftauchen, die die Symmetrie der Theorie zulässt (Kapitel 12.2). Auf Seite 517 gibt Weinberg dann eine Bedingung an, die die Terme im Lagrangian erfüllen müssen, um renormierbar zu sein. So muss für den i-ten Term gelten: \[ \Delta_{i} := \] \[ = 4 - d_{i} - \sum_{f} \, n_{if} \, (s_{f} + 1) \ge 0 \] Dabei bezeichnet \(f\) den Feldtyp, \(i\) den Wechselwirkungstyp (also die Nummer des Terms im Lagrangian), \(s_{f}\) ist der Spin des Feldes vom Typ \(f\), \(n_{if}\) ist die Zahl der Felder vom Typ \(f\) in der Wechselwirkung vom Typ \(i\), und \(d_{i}\) ist die Anzahl Feld-Ableitungen in der Wechselwirkung vom Typ \(i\).
Auf Seite 503 wendet Weinberg diese Formel auf die Terme des QED-Lagrangians an und zeigt damit, dass sie renormierbar sind. So gibt es in der QED zwei Feldtypen, nämlich das Photon-Potential \(A_{\mu}\) und das Elektron-Diracfeld \(\psi\).
Beim Feldtensor-Term \( F_{\mu\nu} F^{\mu\nu} \) taucht beispielsweise nur das Photon-Potential auf, dessen Ableitung dann den Feldstärketensor \(F_{\mu\nu}\) ergibt. Da der Tensor zweimal vorkommt, ist die Zahl der Ableitungen in dem Term \(d_{i}\) gleich 2, und zugleich die Zahl der Felder \(n_{if}\) (mit \(f\) = Photon) in dem Term gleich 2. Der Spin des Photonfeldes \(s_{f}\) (mit \(f\) = Photon) ist \(1\). Die Formel ergibt dann \( 2 \cdot 2 - 2 \cdot (1 + 1) = 0 \), d.h. die Bedingung ist für diesen Term erfüllt.
Insgesamt bedeutet die Formel: Die Renormierbarkeit eines Terms ist umso fraglicher, je mehr Felder ein Term enthält, je mehr Feldableitungen vorkommen und je größer der zugehörige Teilchenspin ist. Ein Beispiel: während die QED mit Photonspin 1 noch renormierbar ist, ist es die allgemeine Relativitätstheorie mit Gravitonspin 2 schon nicht mehr. Man kann sich sogar überlegen, dass es überhaupt keine sinnvollen renormierbaren Terme mit Spin größer 1 gibt.
Damit ist auch klar, dass es (bestimmte Symmetrien vorausgesetzt) nur wenige Terme geben wird, die renormierbar sind und die Symmetrien respektieren. Tatsächlich gibt Weinberg auf Seite 518 eine komplette Liste aller renormierbaren Terme an, die ein Lagrangian enthalten kann. Es sind nur 12 Terme! Damit wird klar, was für eine starke Einschränkung die Forderung nach Renormierbarkeit darstellt.
In einer effektiven Feldtheorie mit unendlich vielen, immer komplexer werdenden Termen im Lagrangian sind diese komlexen Terme im Allgemeinen nicht mehr renormierbar. Dennoch kann eine solche Theorie mit allen Termen zusammen endliche Resultate liefern (siehe oben), denn zu jedem Term gibt es einen Counterterm, der die Divergenzen wegheben kann. Allerdings braucht man für jeden Term eine weitere physikalische Information, um z.B. eine Teilchenmasse oder eine Ladung festzulegen.
Die heutige Sicht ist, dass renormierbare Quantenfeldtheorien nur Niederenergie-Grenzwerte weit unterhalb der Planck-Masse darstellen, und dass fundamentalere Quantenfeldtheorien immer effektive Feldtheorien mit unendlich vielen nicht-renormierbaren Termen sind, wobei die gesamte Theorie mit allen Termen zusammen renormierbar ist. Sonst könnte man beispielsweise niemals eine Quantenfeldtheorie der Gravitation finden, denn bereits der einfache Lagrangian der allgemeinen Relativitätstheorie ist nicht renormierbar, wie wir gerade gesehen haben.
Warum bleiben im Niederenergie-Grenzwert gerade die renormierbaren Terme übrig? Weinberg liefert dafür in Kapitel 12.3 ein handwaving argument, dass man wohl mit Hilfe der Renormierungsgruppe auf solide Füße stellen kann. Demnach verhalten sich die Kopplungskonstanten der Terme im Lagrangian einer effektiven Feldtheorie ungefähr wie \[ \left(\frac{k}{M}\right)^{- \Delta_{i}} \] wobei \(\Delta_{i}\) gerade unser Renormierungs-Bedingungsterm von oben ist. Dabei stellt \(k\) die typischen betrachteten Impulse dar und \(M\) ist eine fundamentale Masse der Theorie, z.B. die Planck-Masse. Nicht-renormierbare Terme haben \[ \Delta_{i} \lt 0 \] so dass diese Terme mindestens wie \( \frac{k}{M} \) unterdrückt sind für kleine \(k\) (im Vergleich zu \(M\)).
Umgekehrt zeigt der Erfolg des renormierbaren Standardmodells der Elementarteilchen, dass in einer fundamentaleren effektiven Feldtheorie die relevante Masse \(M\) deutlich größer sein muss als die heute experimentell untersuchten Teilchenenergien, denn sonst hätten die ersten nicht-renormierbaren Terme bereits Spuren im Experiment hinterlassen. Ein Beispiel für eine hinreichend große Masse wäre die Planck-Masse.
Gibt es experimentelle Hinweise auf nicht-renormierbare Terme im fundamentalen Lagrangian der physikalischen Gesetze? Weinberg nennt zwei solche Hinweise auf Seite 521:
Ein Argument gegen nicht-renormierbare Terme war immer, dass man unendlich viele experimentelle Informationen hineinstecken muss, um immer höhere Ordnungen in den Feynmangraphen berechnen und renormieren zu können. Mit unendlich vielen hineingesteckten Informationen kann man aber alles erklären, so dass die effektive Feldtheorie ihre Vorhersagekraft verliert. Das stimmt tatsächlich, wenn man Impulse \(k\) von der Größe der charakteristischen Masse \(M\) betrachtet. Bei deutlich kleineren Impulsen (Energien) dagegen kann man Potenzreihen-Entwicklungen in \(k/M\) vornehmen, unterdrückte Terme weglassen und so experimentelle Ergebnisse vorhersagen.
Bei Impulsen von der Größe der Masse \(M\) ist eine effektive Feldtheorie vermutlich keine brauchbare Theorie mehr, sondern neue Physik wird wichtig, d.h. eine neue fundamentalere Theorie wird gebraucht, die die effektive Feldtheorie als Niederenergie-Grenzwert besitzt. Diese fundamentalere Theorie muss noch nicht einmal eine Quantenfeldtheorie sein, wie die Stringtheorie gezeigt hat (die keine Quantenfeldtheorie ist).
Ein bekanntes Beispiel für eine effektive Feldtheorie ist die nicht-renormierbare Theorie der Kernkräfte auf der Basis von Nukleon- und Meson-Feldern, die man als Niederenergie-Grenzwert der fundamentaleren Quantenchromodynamik ansehen kann, die auf Quarks und Gluonen basiert. Im Niederenergie-Grenzwert werden die Freiheitsgrade der Quarks und Gluonen gleichsam weggemittelt und nur ihr kollektiver Einfluss in Form gebundener Teilchen (Nukleonen und Mesonen) berücksichtigt. Man könnte auch sagen: Nur die Struktur nahe der niederenergetischen Pole der Matrixelemente wird beachtet, nicht aber das genaue Verhalten der Matrixelemente bei höheren Impulsen.
Neben hohen Impulsen in inneren Loops spielen auch niedrige Photonimpulse eine besondere Rolle und können zu signifikanten Korrekturen und sogar zu Divergenzen führen. Da Photonen die Masse Null haben, kann man nämlich selbst winzige Energiemengen auf unbegrenzt viele Photonen verteilen, die dann entsprechend eine sehr lange Wellenlänge aufweisen und als weiche Photonen bezeichnet werden. Jedes einzelne Photon wirkt sich dabei kaum aus, aber ihr Gesamteffekt kann wichtig sein. Daher muss man auch ggf. den Effekt aller Photonen aufsummieren, also nicht-störungstheoretische Methoden anwenden.
In Kapitel 13.1 untersucht Weinberg, wie sich ein Matrixelement ändert, wenn eines der ein- oder auslaufenden Teilchen ein weiches Photon aussendet. Dabei kann man eine interessante Schlussfolgerung ziehen (Seite 537): Lorentz-Invarianz erzwingt, dass bei der Ankoppelung weicher Photonen die entsprechende Kopplungskonstante (also die elektrische Ladung) erhalten bleibt.
Weinberg erwähnt ein analoges Ergebnis, das man für Gravitonen (Masse Null, Spin 2) ziehen kann: Lorentz-Invarianz erzwingt, dass bei der Ankoppelung weicher Gravitonen die entsprechende Kopplungskonstante für alle Formen von Energie und Impuls gleich ist. Gravitation bei niedrigen Energien (also weit unterhalb der Planck-Energie) unterscheidet also nicht zwischen Teilchensorten, sondern hängt nur von deren Energie und Impuls ab. Das geht schon stark in Richtung der Einsteinschen Gravitationstheorie.
Auch die Ankoppelung weicher masseloser Teilchen mit Spin 3 und mehr kann man untersuchen. Lorentz-Invarianz erfordert hier die Erhaltung einer Größe, die es aus physikalischen Gründen nicht gibt, d.h. weiche masselose Teilchen mit Spin 3 und mehr können überhaupt nicht an andere Teilchen ankoppeln. Masselose Teilchen mit Spin 3 und mehr mögen vielleicht existieren, aber sie können keine Wechselwirkung mit anderen Teilchen haben, die bei niedrigen Energien überlebt. Sie können also insbesondere nicht in einer renormierbaren Quantenfeldtheorie auftauchen, die ja ein Niederenergie-Grenzwert einer effektiven Feldtheorie ist, und sie können auch keine langreichweitigen Kräfte wie Photonen bewirken. Weinberg ist in Kapitel 5.9 (Massless Particle Fields) bereits kurz darauf eingegangen (siehe oben).
In Kapitel 13.2 geht es nun darum, den Beitrag aller virtuellen weichen Photonen zu beschreiben, die zu einem Matrixelement beitragen. Es zeigt sich, dass hierbei Divergenzen auftreten, wenn man den Grenzwert beliebig kleiner Photonimpulse betrachtet (sogenannte Infrarot-Divergenzen).
In Kapitel 13.3 liefert Weinberg die Lösung für dieses Problem: Messbar ist immer nur ein Prozess, bei dem neben den gemessenen ein- und auslaufenden Teilchen noch weiche reelle Photonen vorhanden sind, deren Energie so gering ist, dass sie im Experiment nicht beobachtbar sind. Die Beiträge dieser unbeobachteten (aber dennoch prinzipiell vorhandenen) weichen reellen Photonen heben dann die Infrarotdivergenzen der weichen virtuellen Photonen auf, so dass die berechneten experimentellen Resultate endlich sind. Man sieht, wie sehr der Formalismus aufzeigt, ob man alles wirklich konsistent berücksichtigt hat und sich genau überlegt hat, was im Experiment messbar ist.
Tut man das nicht, entstehen Divergenzen. Dies zeigt Weinberg an verschiedenen Beispielen (andere masselose Teilchen oder beispielsweise in der QCD) in Kapitel 13.4.
In Kapitel 13.5 leitet Weinberg eine universelle Streuformel für niederenergetische Photonen an geladenen Teilchen her, und in Kapitel 13.6 zeigt Weinberg, wie man ein schweres geladenes Teilchen als Quelle eines äußeren elektromagnetischen Feldes interpretieren kann. Besonders interessant war für mich eine Bemerkung auf Seite 560 (Hintergrund: Ich habe mich in meiner Promotion mit gebundenen relativistischen Zuständen im Rahmen der Bethe-Salpeter-Gleichung beschäftigt): Man stellt sich die Wechselwirkung eines Elektrons und eines schweren Teilchens (z.B. eine Atomkern) oft so vor, dass virtuelle Photonen ausgetauscht werden, eines nach dem anderen. Im Rahmen der Bethe-Salpeter-Gleichung für gebundene Zustände spricht man von der Leiternäherung. Diese Näherung ist nach Weinberg aber nur dann gerechtfertigt, wenn beide Teilchen nichtrelativistisch sind. Ansonsten können auch komplexere verwobene Diagramme (z.B. der Über-Kreuz-Austausch von Photonen) genauso wichtig sein.
Um gebundene Zustände zu beschreiben, muss man über die Störungstheorie hinausgehen, denn gebundene Zustände führen zu Polen in Matrixelementen, und keine endliche Ordnung der Störungstheorie kann solche Pole erzeugen. Erst die Divergenz der kompletten Störungsreihe für ein bestimmtes \(P^{2}\) erzeugt den Pol. Also muss man unendlich viele Terme aufsummieren, um gebundene Zustände beschreiben zu können. Das macht man beispielsweise mit Hilfe der oben erwähnten Bethe-Salpeter-Gleichung. Weinberg geht hier nicht näher darauf ein, sondern er betrachtet den Spezialfall, dass in einem gebundenen System aus zwei Teilchen eines dieser Teilchen sehr viel schwerer ist als das andere Teilchen (beispielsweise wie im Wasserstoffatom). Ein solches System kann mit Hilfe der Dirac-Gleichung mit elektromagnetischem Potential beschrieben werden. Weinberg leitet diese Gleichung explizit im Rahmen der Feldtheorie her und untersucht weiter, wie man Strahlungskorrekturen in diesem Rahmen berücksichtigen kann.
Uff – geschafft. Wer bis hierher durchgehalten hat, der hat sicher einen guten Einblick in die Quantenfeldtheorie erhalten. Auch ich habe viele Zusammenhänge gelernt, die ich vorher gar nicht oder nur nebelhaft begriffen hatte. Besonders hat mir Weinbergs systematischer Einstieg in die Quantenfeldtheorie gefallen: Erst quantenmechanische relativistische Zustände definieren, dann Mehrteilchenzustände und entsprechende Erzeugungs- und Vernichtungsoperatoren betrachten und mit diesen Operatoren dann Quantenfelder definieren, um Operatoren mit einfachem Transformationsverhalten zu bekommen. Endlich weiß man, was ein Quantenfeld eigentlich ist!
Sehr schön fand ich auch Weinbergs Zugang zu Eichtheorien (und sogar zur allgemeinen Relativitätstheorie), indem er von masselosen Teilchen mit Spin 1 (bzw. 2) ausgeht und zeigt, dass man kein dazu passendes Vierervektor-Quantenfeld definieren kann, wohl aber ein Eichpotential.
Besonders wertvoll sind die Stellen, an denen Weinberg Hintergrundinformationen preisgibt. Ich habe versucht, diese Stellen weitgehend aufzuspüren und hier wiederzugeben. Allerdings gebe ich gerne zu, dass ich keineswegs alle Kapitel im Detail durchgegangen bin – Einiges mag mir also entgangen sein. Wer hier mehr wissen möchte, dem bleibt wohl nichts anderes übrig, als Weinbergs Buch selbst durchzuarbeiten. Dennoch hoffe ich, dass dieses Kapitel für alle diejenigen wertvoll war, die sich erst einmal einen Überblick verschaffen möchten, ohne gleich alle Details verstehen zu wollen.
Übrigens hat Weinberg noch zwei weitere Folgebände zur Quantenfeldtheorie geschrieben. Wer möchte, kann dort noch viel tiefer eintauchen in die komplexe Welt der Quantenfeldtheorie.
© Jörg Resag, www.joerg-resag.de
last modified on 30 August 2023