
Quelle: Wikimedia Commons File:Einstein1921 by F Schmutzer 2.jpg, Urheber: Ferdinand Schmutzer (1870-1928), Copyright abgelaufen.
Nachdem wir in Kapitel 3 die spezielle Relativitätstheorie kennengelernt haben, sind wir nach unserer mathematischen Vorbereitung aus Gekrümmte Räume (über die Grundlagen der Differentialgeometrie, Webbuch) nun gerüstet, uns an die Allgemeine Relativitätstheorie heranzuwagen, die Albert Einstein in den Jahren von 1907 bis 1915 entwickelte (In Die Entdeckung des Unteilbaren, Kapitel 3.2 Die spezielle Relativitätstheorie gibt es auch eine weniger mathematische Einführung in die Ideen der speziellen Relativitätstheorie).

Quelle:
Wikimedia Commons File:Einstein1921 by F Schmutzer 2.jpg,
Urheber: Ferdinand Schmutzer (1870-1928), Copyright abgelaufen.
Ich werde versuchen, die Ideen und Prinzipien möglichst klar und
ausführlich darzustellen und die notwendigen Grundlagen aus der speziellen
Relativitätstheorie und aus der Differentialgeometrie
dort, wo sie benötigt werden, jeweils noch einmal
kurz zu wiederholen.
Die Allgemeine Relativitätstheorie ist nämlich mathematisch und auch begrifflich
deutlich komplexer als die spezielle Relativitätstheorie, und auch Albert Einstein
hatte damit so seine Mühe. So schrieb er am 29. Oktober 1912 in einem Brief an
den Physiker Sommerfeld:
Ich beschäftige mich jetzt ausschließlich mit dem Gravitationsproblem und glaube nun, mit Hilfe eines hiesigen befreundeten Mathematikers aller Schwierigkeiten Herr zu werden. Aber das eine ist sicher, dass ich mich im Leben noch nicht annäherend so geplagt habe und dass ich große Hochachtung für die Mathematik eingeflößt bekommen habe, die ich bis jetzt in ihren subtileren Teilen in meiner Einfalt für puren Luxus ansah! Gegen dies Problem ist die ursprüngliche Relativitätstheorie eine Kinderei.
Der befreundete Mathematiker war übrigens Einsteins Studienfreund Marcel Grossmann.
Worum geht es in der Allgemeinen Relativitätstheorie?
Ziel ist es, eine Theorie der Gravitation (Schwerkraft) zu formulieren, die mit den Ideen der speziellen Relativitätstheorie verträglich ist. Newtons Gravitationstheorie (siehe Die Entdeckung des Unteilbaren, Kapitel 1.4 Kräfte und Wechselwirkungen ) ist nämlich nicht mit der speziellen Relativitätstheorie verträglich, da bei Newton sich die Gravitationskraft ohne jede Verzögerung durch den Raum ausbreitet. Es ist jedoch eine der Grundannahmen in der speziellen Relativitätstheorie, dass sich jede physikalische Wirkung (also auch die Gravitation) maximal mit Lichtgeschwindigkeit durch den Raum auswirkt.
Da sich diese Grundannahme experimentell immer wieder bestätigt, ist es sehr wahrscheinlich, dass sie auch auf die Gravitation zutrifft. Im Endergebnis wird sich herausstellen, dass die Synthese von Relativitätstheorie und Gravitation in der Allgemeinen Relativitätstheorie einen begrifflichen Rahmen schafft, der weit über die Beschreibung der Gravitation hinaus von großer Bedeutung ist: Man ist gezwungen, Naturgesetze in vollkommen Koordinaten-unabhängiger Form (man sagt auch: in tensorieller Form) zu formulieren, so dass sie sich dann in beliebigen (auch krummlinigen) Koordinaten ausschreiben lassen. So etwas wird man auch von jeder modernen Theorie verlangen, die über die Allgemeine Relativitätstheorie hinausgeht und die neben der Gravitation auch die anderen Wechselwirkungen umfasst. Ein Beispiel dafür ist die Stringtheorie.
Die große Aussagekraft und innere Eleganz der Allgemeinen Relativitätstheorie liegt darin begründet, dass sie auf einem neuen Prinzip beruht. So ist es bei vielen großen physikalischen Theorien: Sie enthalten eine neue fundamentale Einsicht in die Gesetze der Natur!
Um beispielsweise die Quantentheorie formulieren zu können, muss man erkennen, dass der Ausgang von Beobachtungen im Allgemeinen prinzipiell nicht feststeht, so dass man die Natur mit Hilfe von Wahrscheinlichkeiten beschreiben muss (siehe Kapitel 4). Weiter muss man erkennen, dass man diese Wahrscheinlichkeiten durch das Betragsquadrat komplexer Zahlen ausdrücken muss, die man als Wahrscheinlichkeitsamplituden bezeichnet. Bei ununterscheidbaren Möglichkeiten muss man diese Amplituden zunächst addieren – man sagt, sie interferieren miteinander.
In der Speziellen Relativitätstheorie besteht die neue Einsicht darin, dass man erkennt, dass alle gleichförmig bewegten (unbeschleunigten) Bezugssysteme (Inertialsysteme) zueinander gleichwertig sind, und dass es eine maximale Ausbreitungsgeschwindigkeit für physikalische Wirkungen gibt.
Und wie sieht es bei der Allgemeinen Relativitätstheorie aus? Sie soll ja Spezielle Relativitätstheorie und Gravitation geeignet umfassen. Daher werden wir auf jeden Fall fordern, dass bei verschwindender Gravitation sich die Spezielle Relativitätstheorie als Grenzfall ergibt. Und weiter erwarten wir, dass sich im Grenzfall kleiner Geschwindigkeiten und kleiner Gravitationskräfte das Newtonsche Gravitationsgesetz ergibt. Aber wo ist die neue zündende Idee, die eine solche Theorie zu begründen vermag?
Nachdem Einstein einige Zeit verschiedene Ansätze für eine relativistische Gravitationstheorie ausprobiert hatte und damit nicht zufrieden war, stieß er irgendwann im November 1907 auf diese entscheidende Idee:
Dann stieß ich auf den glücklichsten Gedanken meines Lebens, und zwar in der folgenden Form: Wie das elektrische Feld, das von der magnetoelektrischen Induktion hervorgerufen wird, besitzt auch das Gravitationsfeld nur eine relative Existenz. Für einen Beobachter, der sich im freien Fall vom Dach eines Hauses befindet, existiert – zumindest in seiner unmittelbaren Umgebung – kein Gravitationsfeld. Wenn nämlich der fallende Beobachter einige andere Körper fallen lässt, dann befinden sie sich im Bezug auf ihn im Zustand der Ruhe oder gleichförmigen Bewegung [...] .
Durch diese Betrachtungsweise erhält das eigentümliche experimentelle Gesetz, dass in einem Gravitationsfeld alle Körper mit der gleichen Beschleunigung fallen, mit einem Schlag eine tiefe physikalische Bedeutung. Und es folgt die Konsequenz: So ist die experimentell nachgewiesene Unabhängigkeit der Fallbeschleunigung ein starkes Argument für die Tatsache, dass das Relativitätspostulat auch auf Koordinatensysteme ausgedehnt werden muss, die sich zueinander in nicht gleichförmiger Bewegung befinden.
In seiner Kyoto-Vorlesung führt er im Dezember 1922 weiter aus:
Ich saß auf meinem Sessel im Berner Patentamt, als mir plötzlich folgender Gedanke kam: Wenn sich eine Person im freien Fall befindet, dann spürt sie ihr eigenes Gewicht nicht. Ich war verblüfft. Dieser einfache Gedanke machte auf mich einen tiefen Eindruck. Er trieb mich in Richtung einer Theorie der Gravitation. [...]
Als ich im Jahr 1907 an einem Überblicksartikel über die Konsequenzen der speziellen Relativitätstheorie schrieb, musste ich erkennen, dass alle natürlichen Phänomene mit Ausnahme des Gravitationsgesetzes in den Begriffen der speziellen Relativitätstheorie dargestellt werden konnten. Ich verspürte eine tiefe Sehnsucht den Grund dafür zu erkennen. [...]
Es war für mich außerordentlich unbefriedigend, dass im Rahmen der speziellen Relativitätstheorie die Beziehung zwischen Trägheit und Energie so schön hergeleitet werden kann, während es doch keine Relation zwischen Trägheit und Gewicht gibt. Ich vermutete, dass eine solche Beziehung im Rahmen der speziellen Relativitätstheorie nicht erklärt werden könne.
Schon Galilei hatte erkannt, dass alle Körper gleich schnell fallen. Moderne Experimente zeigen mit hoher Genauigkeit, dass träge und schwere Masse exakt gleich sind (wenn man die Maßeinheiten passend wählt). Das ist nicht selbstverständlich! So sind elektrische Ladung und träge Masse bei verschiedenen Objekten keineswegs gleich oder auch nur proportional zueinander. Die schwere Masse, also gleichsam die Ladung der Gravitation, ist dagegen gleich der trägen Masse. Das meint Einstein mit der Relation zwischen Trägheit und Gewicht.
Einstein hatte nun den inneren Grund für diese Gleichheit erkannt: Die Gravitation entspricht genau der Scheinkraft in einem beschleunigten Bezugssystem, ist also wie die Kraft, die einen in einer beschleunigenden Rakete im Weltraum in die Sitze drückt. Befindet man sich im freien Fall, so spürt man (zumindest lokal) die Gravitation nicht. Bei einer solchen Kraft, die das Resultat einer Beschleunigung ist, ergibt sich die Gleichheit von träger und schwerer Masse automatisch!
In Die Entdeckung des Unteilbaren, Kapitel 7.1 Einsteins Gravitationstheorie habe ich die Grundidee Einsteins bereits ausführlich dargestellt. Ich will daher hier nicht zu genau darauf eingehen. Der entscheidende Punkt ist:
|
Das Einsteinsche Äquivalenzprinzip: Im Inneren eines fensterlosen relativ kleinen Raumschiffs kann man prinzipiell nicht unterscheiden, ob das Raumschiff im leeren Weltraum gleichmäßig beschleunigt oder ob es noch auf der Startrampe im Gravitationsfeld der Erde steht. Ein Gravitationsfeld ist also lokal äquivalent zu einem gleichförmig beschleunigten Bezugssystem. Der Ausdruck lokal weist darauf hin, dass der betrachtete Raumbereich so klein sein soll, dass Inhomogenitäten des Gravitationsfeldes keine Rolle spielen. |
Diese Einsicht gilt für alle denkbaren physikalischen Messungen und geht insofern
über die reine Punktmechanik im Gravitationsfeld hinaus.
Man könnte den obigen Punkt auch etwas anders formulieren, wenn man an den freien Fall denkt:
| Die physikalischen Gesetze gelten in allen im freien Fall befindlichen Systemen, sofern diese hinreichend klein sind, in der gleichen Form. Wählt man lokal ein Raum-Zeit-Koordinatensystem, das einem im freien Fall befindlichen Raumschiff entspricht, so gelten darin lokal die Gesetze der speziellen Relativitätstheorie, d.h. im Raumschiff herrscht Schwerelosigkeit. |
Wenn man also lokal ein passendes Koordinatensystem in Raum und Zeit wählt, so sollte die Raumzeit in diesen Koordinaten dort wie der Minkowskiraum aus der speziellen Relativitätstheorie aussehen. Wie sieht dann lokal ein Koordinatensystem aus, das nicht dem freien Fall entspricht und in dem ein darin ruhender Beobachter eine Beschleunigung bzw. eine Gravitationskraft spürt? Es sollte einem beschleunigten Bezugssystem der speziellen Relativitätstheorie entsprechen, denn Gravitation ist ja nichts anderes als die Scheinkraft in einem solchen Bezugssystem.
Wenn wir also wissen wollen, wie man die Gravitation in Sinne des Äquivalenzprinzips formulieren muss, so ist es sicher eine gute Idee, wenn wir uns zur Vorbereitung beschleunigte Bezugssysteme in der speziellen Relativitätstheorie ansehen. Im Inneren einer gleichförmig beschleunigten Rakete soll ja dieselbe Physik herrschen wir lokal in einem statischen Gravitationsfeld. Schauen wir uns also die gleichförmig beschleunigte relativistische Rakete genauer an:
Stellen wir uns vor, wir befinden uns in einer Rakete weit draußen im leeren Weltraum. Alle Sterne und Planeten sollen so weit entfernt sein, dass wir ihre Gravitationsfelder vernachlässigen können. Die Rakete soll so beschleunigen, dass wir an einem festen Punkt in ihrem Inneren (nennen wir ihn den Ursprungspunkt der Rakete oder auch Ursprung des beschleunigten Bezugssystems) ständig eine konstante Beschleunigung in \(x^{3}\)-Richtung wahrnehmen (das entspricht der z-Richtung; wir schreiben die Koordinaten-Indizes wieder oben).
Warum die Einschränkung an einem festen Punkt in ihrem Inneren notwendig ist, und ob dieselbe konstante Beschleunigung auf die ganze Rakete übertragen werden kann, werden wir noch sehen. Man ahnt hier aber schon, wie sehr man aufpassen muss, wenn man versucht, anschauliche Vorstellungen in präzise Vorgaben umzusetzen. Es stellt sich nämlich schnell heraus, dass mehrere Forderungen, die aus derselben Anschauung stammen, einander widersprechen können. Eine der Ursachen dafür ist die Abhängigkeit des Begriffs Gleichzeitigkeit vom Bezugssystem. Ein anderer Aspekt ist der Effekt der Lorentz-Kontraktion, der bewirkt, dass bewegte Objekte in Bewegungsrichtung verkürzt sind, verglichen mit dem Ruhesystem des Objektes. Wir versuchen daher, so vorsichtig wie möglich vorzugehen.
Wenn die Beschleunigung im Ursprungspunkt der Rakete gerade etwa 10 m/s2 beträgt, so empfinden wir sie dort wie die Schwerkraft auf der Erdoberfläche. Nach dem Äquivalenzprinzip gibt es sogar zwischen der künstlichen Schwerkraft aufgrund der Beschleunigung der Rakete und der Schwerkraft auf der Erdoberfläche überhaupt keinen Unterschied, wenn man sich auf einen genügend kleinen Raumbereich beschränkt (da die Rakete sehr viel kleiner als die Erde ist, können wir diese Lokalitätsbedingung im Inneren der Rakete als erfüllt ansehen). In Anlehnung an die Erdbeschleunigung bezeichnen wir die konstante Beschleunigung der Rakete in \(x^{3}\)-Richtung im Ursprungspunkt mit \( g \). Im Inneren der Rakete empfinden wir die Beschleunigungsrichtung dann als die Richtung nach oben.
Versuchen wir nun, im Inneren der Rakete ein sich mitbewegendes beschleunigtes Bezugssystem mit Koordinaten \[ \xi^{0}, \, \xi^{1}, \, \xi^{2}, \, \xi^{3} \] zu definieren, das seinen räumlichen Nullpunkt im Ursprungspunkt der Rakete haben soll und das räumlich in einem gewissen Sinn starr sein soll.
Dazu definieren als Erstes die Zeitkoordinate, indem wir eine Uhr genau in dem Ursprungspunkt der Rakete aufstellen. Die auf dieser Uhr angezeigte Zeit (also die Eigenzeit \( \tau \) der Uhr) ist als Referenzzeit in unserem beschleunigten Bezugssystem definiert. Auch hier ist wieder Präzision wichtig: wir müssen diesmal genau sagen, wo die Referenzuhr steht! Warum, werden wir später noch sehen. (Gut, dass man diese Details alle jetzt schon korrekt berücksichtigen kann, wenn man das Endergebnis kennt. Ein Forscher wie Einstein, für den dieses alles Neuland war, hatte es da schon erheblich schwerer.)
Die zeitliche Koordinate \( \xi^{0} \) setzen wir dann gleich \[ \xi^{0} = c \tau \] mit der Lichtgeschwindigkeit \(c\). Zum Begriff der Eigenzeit siehe auch Kapitel 3.7 Geschwindigkeit, Zeitdilatation, Vierergeschwindigkeit und Eigenzeit.
Um weiterzukommen, müssen wir nun genau angeben, welche Eigenschaften das beschleunigte Raketen-Koordinatensystem haben soll. Nur dann können wir die entsprechenden Koordinaten auch mit einer dazu passenden physikalischen Interpretation versehen. Die Kernidee ist folgende:
Wir würden das beschleunigte Koordinatensystem \( \xi^{0}, \xi^{1}, \xi^{2}, \xi^{3} \) gerne so konstruieren, dass Raum-Zeit-Punkte mit derselben Zeitkoordinate \( \xi^{0} \) sich als gleichzeitige Ereignisse an verschiedenen Raumpunkten interpretieren lassen. Nun ist aber für beschleunigte Bezugssysteme der Begriff der Gleichzeitigkeit noch gar nicht definiert. Nur in gleichförmig bewegten Inertialsystemen haben wir in der speziellen Relativitätstheorie eine passende Definition, die auf dem Postulat beruht, dass die Lichtgeschwindigkeit in jedem Inertialsystem denselben konstanten Wert besitzt.
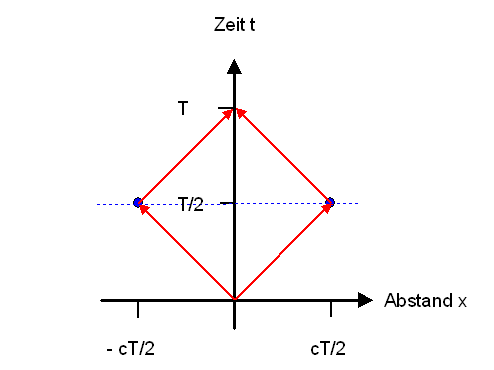
Betrachten wir ein Inertialsystem, das wir als unser Ruhesystem ansehen können. Senden wir darin beispielsweise einen Lichtblitz zugleich nach rechts (x-Richtung) und nach links (negative x-Richtung) aus, und kommt der Lichtblitz nach einer Zeit \(T\) wieder bei uns an, so wissen wir wegen der Konstanz der Lichtgeschwindigkeit, dass in der Entfernung \( x = cT/2 \) rechts und \( x' = - cT/2 \) links von uns ein Spiegel steht, an dem zur Zeit \( T/2 \) der Lichtblitz reflektiert wurde (so wird die räumliche Entfernung und der Zeitpunkt der beiden Reflexions-Ereignisse in diesem Inertialsystem definiert – man spricht auch von Radar-Koordinaten).
Die beiden Spiegelungen des Lichtblitzes an den Orten
\( x = cT/2 \) und \( x' = - cT/2 \) zur Zeit \( T/2 \)
sehen wir daher als gleichzeitig an.
Allerdings hängt die Gleichzeitigkeit von Ereignissen und deren räumliche Entfernung
vom Inertialsystem ab:
ein gleichförmig relativ zu uns bewegter Beobachter wird diese Ereignisse nicht als gleichzeitig ansehen.
Weiter unten im Abschnitt
Interpretation der Raumzeit-Koordinaten, Gleichzeitigkeit und räumliche Abstände
werden wir noch einmal im Detail auf diese Fragestellungen eingehen.
Schöne Darstellungen dazu findet man auch im Internet beispielsweise in Charles Francis
Conceptual Foundations of Special and General Relativity,
http://arxiv.org/ftp/physics/papers/9909/9909048.pdf.
Man kann nun die Definition der Gleichzeitigkeit in der speziellen Relativitätstheorie
von gleichförmig bewegten Inertialsystemen auf das beschleunigte Bezugssystem der Rakete übertragen,
indem wir uns zu jedem Zeitpunkt \( \xi^{0} \)
in das zugehörige momentane Ruhe-Inertialsystem
der Rakete begeben.
Die Rakete klinkt dieses Bezugssystem zum Zeitpunkt \( \xi^{0} = c \tau \) gleichsam aus, so dass es sich ab diesem Moment gleichförmig mit der Geschwindigkeit weiterbewegt, die die Rakete zum Ausklinkzeitpunkt besaß. Wir lassen uns gewissermaßen ab diesem Zeitpunkt in der Rakete frei fallen, sodass wir deren Beschleunigung nicht weiter spüren.
Man kann sich auch vorstellen, dass das momentane Ruhe-Inertialsystem schon vor dem Ausklinkzeitpunkt \(\tau\) da ist und sich von unten auf die Rakete zubewegt (die Rakete beschleunigt nach oben), so wie sich auf der Erde ein senkrecht nach oben geworfener Stein dem höchsten Punkt seiner Flugbahn nähert. Zum Zeitpunkt \(\tau\) ist dann das momentane Ruhe-Inertialsystem gerade relativ zur Rakete zur Ruhe gekommen (bzw. die Rakete hat gerade jetzt dieselbe Geschwindigkeit wie das gleichförmig bewegte momentane Ruhe-Inertialsystem erreicht). Nun beginnt das System, wieder nach unten zu fallen (so zumindest erscheint es von der Rakete aus gesehen). Diese Vorstellung müssen wir nun auf jeden Zeitpunkt \(\tau\) anwenden, d.h. wir haben es mit unendlich vielen solcher scheinbar aufsteigenden und wieder fallenden momentanen Ruhe-Inertialsysteme zu tun.
Nach Definition ist im momentanen Ruhe-Inertialsystem die Geschwindigkeit der Rakete zur Eigenzeit \(\tau\) gleich Null. Die Beschleunigung der Rakete ist jedoch nicht Null! Wir definieren nun im beschleunigten Bezugssystem zu jedem Zeitpunkt \( \xi^{0} = c \tau \) alle diejenigen Raum-Zeit-Punkte als gleichzeitig zu der im Ursprungspunkt der Rakete gemessenen Zeit \( \xi^{0} = c \tau \), die auch im momentane Ruhe-Inertialsystem zu diesem Zeitpunkt als gleichzeitig gelten.
Also konkret: wir betrachten ein Inertialsystem, das zum Zeitpunkt \( \xi^{0} \) dieselbe Geschwindigkeit wie die Rakete hat, d.h. genau in diesem Zeitpunkt ruht die Rakete für einen winzigen Augenblick in diesem gleichförmig bewegten Bezugssystem. Alle Ereignisse, die in diesem momentanen Ruhe-Inertialsystem als gleichzeitig zur Zeit \( \xi^{0} \) angesehen werden, definieren wir auch als gleichzeitig im beschleunigten Bezugssystem der Rakete.
Anmerkung:
Wie man die Gleichzeitigkeit von Ereignissen von der Rakete aus bestimmen kann, bleibt dabei offen.
Man muss im Grunde einen gleichförmig bewegten Beobachter fragen, den wir zufällig
im fraglichen Zeitpunkt genau mit der Geschwindigkeit Null in unserem Ursprungspunkt der Rakete treffen.
Dieser hätte dann theoretisch eine entsprechende Zeit- und Abstandsmessung mit Lichtstrahlen ausführen können.
Um daraus eine praktikable Messvorschrift für den Astronauten in der Rakete zu gewinnen,
ist gar nicht so einfach, siehe z.B.
David Alba, Luca Lusanna:
Generalized Radar 4-Coordinates and Equal-Time Cauchy Surfaces for Arbitrary Accelerated Observers,
arXiv:gr-qc/0501090.
Die Frage ist keineswegs rein akademisch und spielt beispielsweise beim Global Positioning System (GPS)
durchaus eine wichtige Rolle.
Analog zur Zeitkoordinate definieren wir auch die räumlichen Koordinaten \[ \xi^{1}, \, \xi^{2}, \, \xi^{3} \] im beschleunigten Bezugssystem der Rakete zu jedem Zeitpunkt \( \xi^{0} \): Sie sollen identisch sein mit den karthesischen räumlichen Koordinaten des momentanen Ruhe-Inertialsystems, das in diesem Moment ausgeklinkt wird. Auf diese Weise erreichen wir, dass wir diese Koordinaten als reine, senkrecht aufeinander stehende Raumkoordinaten und \( \xi^{0} \) als reine Zeitkoordinate (zumindest im Ursprungspunkt der Rakete) interpretieren können, wenn wir uns jeweils auf das momentane Ruhe-Inertialsystem zu diesem Zeitpunkt beziehen.

Nun sind die momentanen Ruhe-Inertialsysteme, die die beschleunigte Rakete
zu verschiedenen Zeiten gleichsam abwirft, nicht identisch, sondern sie
bewegen sich gleichförmig mit konstanter Geschwindigkeit relativ zueinander
(die Rakete beschleunigt ja ständig weiter, allerdings immer in dieselbe Richtung).
Daher lassen sie sich mit Hilfe einer Poincare-Transformation
aufeinander abbilden. Wir wollen die Koordinaten so wählen, dass
ein Boost mit einer eventuellen zusätzlichen Verschiebung
der Koordinaten ausreicht, d.h. das Koordinatensystem soll nicht
verdreht werden. Auf diese Weise erreichen wir, dass
die Rakete von Innen zu einem späteren Zeitpunkt genauso aussieht wie die
Rakete zu einem früheren Zeitpunkt.
Ein Beobachter im Ursprungspunkt der Rakete
sieht zu jedem Zeitpunkt einen räumlichen Koordinatenpunkt
\( \xi^{1}, \xi^{2}, \xi^{3} \)
an derselben Stelle relativ zu sich selbst, d.h. die Wände der
Rakete werden durch solche festen Koordinatenwerte im beschleunigten
Bezugssystem beschrieben – zumindest wenn die Rakete nicht allzu groß ist.
Im Grunde ist das so definierte beschleunigte Raketen-Koordinatensystem der Versuch, die Beschleunigung eines starren Körpers in der speziellen Relativitätstheorie zu beschreiben (das nennt man auch Bornsche Starrheit ). Doch Vorsicht: starre Körper gibt es in der Relativitätstheorie nicht, da sich ja jede Information nur mit Lichtgeschwindigkeit ausbreiten kann. Wir sollten also auf einige Überaschungen gefasst sein, die unserer Intuition widersprechen. Sobald die Abstände größer werden, gerät man mit der Interpretation eines starren Körpers in Schwierigkeiten, wie wir noch sehen werden. Dann ist es besser, sich vorzustellen, dass man viele kleine Raketen vor sich hat, die sich so bewegen, dass sie im obigen Koordinatensystem zu gleichen Zeiten denselben Abstand von der Hauptrakete (die sich bei \( \xi^{i} = 0 \) befindet) haben, wobei der Abstand über das momentane Ruhe-Inertialsystem der Hauptrakete definiert ist. Wir werden noch sehen, dass es einen kritischen Abstand gibt, ab dem das unmöglich wird.
Mathematisch kann man sich vorstellen, dass sich das beschleunigte Bezugssystem der Rakete mit den Koordinaten \( \xi^{\mu} \) (mit \(\mu\) von 0 bis 3) aus kleinen (infinitesimalen) Scheiben zusammensetzt. Die Scheiben entstehen durch Zerschneiden der Eigenzeit in infinitesimale Zeitscheiben. Jede der Scheiben entspricht einem momentanen Ruhe-Inertialsystem mit einem Zeitintervall der Dicke \( d\xi^{0} \). Die einzelnen Scheiben (momentanen Ruhe-Inertialsysteme) lassen sich durch einen passenden Boost (ggf. plus passende Nullpunktsverschiebung) aufeinander abbilden.
Beginnen wir mit dem momentanen Ruhe-Inertialsystem zur Zeit \( \xi^{0} = 0 \). Wir wollen diesen Zeitpunkt auch als Startzeitpunkt bezeichnen. Stellen wir uns vor, dass ein Beobachter außerhalb der Rakete genau in diesem System ruht, d.h. für ihn hat die Rakete zum Startzeitpunkt (noch) die Geschwindigkeit Null. Das Inertialsystem des äußeren Beobachters können wir daher identisch zum momentanen Ruhe-Inertialsystem des Startzeitpunktes wählen, wobei wir allerdings eine Verschiebung des Nullpunktes zulassen wollen (was sich später als günstig erweist), d.h. zum Startzeitpunkt muss sich die Rakete nicht im Ursprungspunkt des äußeren Inertialsystems befinden. Um die Diskussion einfach zu halten, verwenden wir in dem Inertialsystem des äußeren Beobachters wie gewohnt das karthesische Koordinatensystem des Minkowskiraums, also die vier Koordinaten \( x^{0}, x^{1}, x^{2}, x^{3} \) mit der Zeitkoordinate \( x^{0} = ct \) und den drei euklidischen Raumrichtungen.
Wir wollen uns zunächst die Bewegungskurve des Ursprungspunktes der Rakete im Inertialsystem dieses äußeren Beobachters ansehen, da diese Kurve den Äufhängungspunkt für das jeweilige momentane Ruhe-Inertialsystem bildet. Da an diesem Äufhängungspunkt die Uhr der Rakete steht, können wir die darauf angezeigte Eigenzeit \( \tau \) verwenden, um diese Bewegungskurve zu parametrisieren. Im karthesischen Koordinatensystem des externen Beobachters wird die Raumzeit-Bewegungskurve (Weltlinie) dann durch Koordinaten \[ x(\tau) := (x^{\mu}(\tau)) \] beschrieben. Dabei hatten wir \( x^{0}(0) = 0 \) gewählt, d.h. im Startmoment sind Raketenuhr und äußere Uhr synchron. Für die räumlichen Koordinaten des Raketen-Ursprungspunktes hatten wir zum Startzeitpunkt keine spezielle Bedingung gefordert.
Die Vierergeschwindigkeit \( u(\tau) \) und die Viererbeschleunigung \( a(\tau) \) dieses Fixpunktes in der Rakete (dort wo die Raketenuhr steht) sind im Inertialsystem des äußeren Beobachters gegeben durch \begin{align} u(\tau) &= \frac{dx}{d\tau} \\ a(\tau) &= \frac{du}{d\tau} = \frac{d^{2}x}{d\tau^{2}} \end{align} Dass passt zu der Eigenschaft der Eigenzeit, ein Lorentz-invarianter Kurvenparameter zu sein, der über die Normierung \[ g(u,u) = (u^{0})^{2} - \boldsymbol{u}^{2} = c^{2} \] mit der Minkowskimetrik \( g(u,u) \) festgelegt ist. Daher ist \[ 0 = \frac{d}{d\tau} c^2 = \frac{d}{d\tau} g(u,u) = \] \[ = 2 \ g\left(\frac{du}{d\tau},u\right) = 2 \, g(a,u) \] und somit \[ g(a,u) = 0 \] Sowohl \(x\) als auch \(u\) und \(a\) sind Vierervektoren, d.h. bei einem Bezugssystemwechsel transformieren sie sich alle in gleicher Weise mit der entsprechenden Lorentzmatrix. Der Zusammenhang zwischen Vierergeschwindigkeit \(u\) und der räumlichen Geschwindigkeit \(\boldsymbol{v}\) im Inertialsystem des äußeren Beobachters ist gegeben durch \[ u = \begin{pmatrix} \gamma c \\ \gamma \boldsymbol{v} \end{pmatrix} \] (siehe Kapitel 3.7 Geschwindigkeit, Zeitdilatation, Vierergeschwindigkeit und Eigenzeit ) mit dem Lorentzfaktor \[ \gamma = \sqrt{ \frac{1}{ 1 - (\boldsymbol{v}/c)^2 } } \] Im Startzeitpunkt \( t = \tau = 0 \) ist die Geschwindigkeit \( \boldsymbol{v} \) der Rakete noch gleich Null, d.h. \( \gamma = 1 \) und wir starten mit der Vierergeschwindigkeit \[ u(0) = \begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix} \] und die Vierer-Beschleunigung des Ursprungspunktes ist wegen \( \gamma = \frac{dt}{d\tau} \) und \( \frac{d \gamma}{dt}\big|_{t=0} = 0 \) sowie \( \gamma|_{t=0} = 1 \) zum Startzeitpunkt gegeben durch \[ a(0) = \frac{du}{d\tau}\bigg|_{\tau = 0} = \] \[ \frac{dt}{d\tau}\bigg|_{t=0} \, \frac{d}{dt} \begin{pmatrix} \gamma c \\ \gamma \boldsymbol{v} \end{pmatrix}_{t=0} = \] \[ = \gamma|_{t=0} \, \cdot \begin{pmatrix} \frac{d\gamma}{dt} \, c \\ \frac{d\gamma}{dt} \, \boldsymbol{v} + \gamma \, \frac{d\boldsymbol{v}}{dt} \end{pmatrix}_{t=0} = \] \[ = \begin{pmatrix} 0 \\ \frac{d\boldsymbol{v}}{dt} \end{pmatrix}_{t=0} = \begin{pmatrix} 0 \\ \boldsymbol{g} \end{pmatrix} \] (alles angegeben in den Koordinaten des äußeren Beobachters).
Zu einem späteren Zeitpunkt \(\tau\) bewegt sich die Rakete nun bereits mit einer Geschwindigkeit ungleich Null. Im momentane Ruhe-Inertialsystem zu diesem Zeitpunkt haben \(a\) und \(u\) aber immer noch dieselbe Form wie im Inertialsystem des äußeren Beobachters zum Zeitpunkt Null, d.h. für einen Beobachter im momentanen Ruhe-Inertialsystem (der also in der Rakete bei der Uhr sitzt) ruht der Ursprungspunkt der Rakete zur Zeit \(\tau\) und beschleunigt mit \(\boldsymbol{g}\). Dies präzisiert den Begriff der konstanten Beschleunigung.
Im Bezugssystem des äußeren Beobachters enstehen \(u\) und \(a\) zu einem Zeitpunkt \( \tau \) durch einen Boost aus \(u\) und \(a\) zur Zeit Null. Mit dem entgegengesetzten Boost kann man sie jederzeit in das momentane Ruhe-Inertialsystem der Rakete umrechnen.
Da die Rakete nur eine Beschleunigung in \( x^{3} \) -Richtung erfahren soll, ändern sich die räumlichen Koordinaten jedes Raumschiff-Fixpunktes senkrecht zur Bewegungsrichtung nicht: \( x^{1} = \xi^{1} \) und \( x^{2} = \xi^{2} \) sind konstant. Es genügt also im Folgenden, nur noch die Koordinaten \(x^{0}\) und \(x^{3}\) des ruhenden Beobachters bzw. \(\xi^{0}\) und \(\xi^{3}\) im momentanen Ruhe-Inertialsystem aus Sicht der Rakete zu betrachten.
Im Raum der Koordinaten \(x^{0}\) und \(x^{3}\) ist eine Boostmatrix \(\Lambda\) in \(x^{3}\)-Richtung gegeben durch \[ \Lambda = \begin{pmatrix} \cosh{\alpha} & \sinh{\alpha} \\ \sinh{\alpha} & \cosh{\alpha} \end{pmatrix} \] mit der Rapidität \( \alpha \) und den Hyperbelfunktionen \[ \sinh{\alpha} = \frac{1}{2} \, (e^{\alpha} - e^{-\alpha}) \] \[ \cosh{\alpha} = \frac{1}{2} \, (e^{\alpha} + e^{-\alpha}) \] Es gilt \[ (\cosh{\alpha})^{2} - (\sinh{\alpha})^{2} = 1 \] d.h. die Kurve \( (x(\alpha), y(\alpha)) = (\cosh{\alpha} , \, \sinh{\alpha}) \) ist eine Hyperbel mit \( x^{2} - y^{2} = 1 \) (siehe Kapitel 3.3 Die spezielle Relativitätstheorie: Boosts).
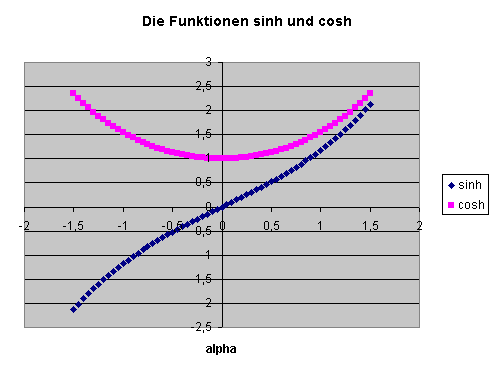
Die Hyperbelfunktionen
Da sich im Bezugssystem des äußeren Beobachters
die Situation zur Zeit \( \tau \gt 0 \) aus der Situation
zur Zeit \( \tau = 0 \) durch einen Boost \(\Lambda\) mit passender Rapidität \( \alpha \)
(plus Verschiebung) ergeben soll, und da \(x, u\) und \(a\) Vierervektoren sind, muss
im \(x^{0}\) - \(x^{3}\) - Bezugssystem des äußeren Beobachters gelten:
\[
u(\tau) = \Lambda \, u(0) =
\]
\[ =
\begin{pmatrix}
\cosh{\alpha} & \sinh{\alpha} \\
\sinh{\alpha} & \cosh{\alpha}
\end{pmatrix}
\,
\begin{pmatrix}
c \\
0
\end{pmatrix}
=
\]
\[ =
\begin{pmatrix}
c \, \cosh{\alpha} \\
c \, \sinh{\alpha}
\end{pmatrix}
\]
\[
a(\tau) = \Lambda \, a(0) =
\]
\[ =
\begin{pmatrix}
\cosh{\alpha} & \sinh{\alpha} \\
\sinh{\alpha} & \cosh{\alpha}
\end{pmatrix}
\,
\begin{pmatrix}
0 \\
g
\end{pmatrix}
=
\]
\[ =
\begin{pmatrix}
g \, \sinh{\alpha} \\
g \, \cosh{\alpha}
\end{pmatrix}
\]
Andererseits muss auch
\( a(\tau) = \frac{du(\tau)}{d\tau} \) gelten.
Da die Ableitung von \( \sinh \) gleich \( \cosh \) ist und umgekehrt,
erhalten wir
\[
a(\tau) =
\begin{pmatrix}
g \, \sinh{\alpha} \\
g \, \cosh{\alpha}
\end{pmatrix} =
\]
\[
= \frac{du(\tau)}{d\tau} =
\frac{d}{d\tau} \,
\begin{pmatrix}
c \, \cosh{\alpha} \\
c \, \sinh{\alpha}
\end{pmatrix} =
\]
\[
=
\begin{pmatrix}
c \, \sinh{\alpha} \\
c \, \cosh{\alpha}
\end{pmatrix}
\,
\frac{d\alpha}{d\tau}
\]
denn \(g\) und \(c\) sind ja konstant.
Beide Komponenten ergeben die Gleichung
\[
\frac{d\alpha}{d\tau} = \frac{g}{c}
\]
und somit
\[
\alpha(\tau) = \frac{g}{c} \, \tau + k
\]
mit einer beliebigen Konstante \(k\).
Die Rapidität wächst also bei einer konstant beschleunigten relativistischen Rakete linear mit der Eigenzeit, so wie dies für die Geschwindigkeit bei einer nichtrelativitsischen Rakete gilt. Man kann jedoch leicht nachrechnen, dass die Geschwindigkeit der relativistischen Rakete im Inertialsystem des äußeren Beobachters nicht linear mit der Eigenzeit wächst, sondern sich von unten der Lichtgeschwindigkeit immer weiter annähert.
Die Konstante \( k \) können wir noch durch die Bedingung festlegen, dass die Geschwindigkeit zum Startzeitpunkt \( \tau = 0 \) gleich Null sein soll, d.h. \[ u^{3}(0) = c \, \sinh{\alpha(0)} = \] \[ = c \, \sinh{k} = 0 \] sodass \( k = 0 \) sein muss und somit \[ \alpha(\tau) = \frac{g}{c} \, \tau \] ist.
Aus der Gleichung \[ \frac{dx}{d\tau} = u(\tau) = \] \[ = \begin{pmatrix} c \, \cosh{\alpha} \\ c \, \sinh{\alpha} \end{pmatrix} = \] \[ = \begin{pmatrix} c \, \cosh{\left(\frac{g}{c} \tau\right)} \\ c \, \sinh{\left(\frac{g}{c} \tau\right)} \end{pmatrix} \] können wir nun auch die Bahnkurve \( x(\tau) \) des Ursprungspunktes der Rakete (der Raketenuhr) im Inertialsystem des äußeren Beobachters durch Integrieren ausrechnen: \[ x(\tau) = \int_{0}^{\tau} d\tau' \, u(\tau') + x(0) = \] \[ = \int_{0}^{\tau} d\tau' \, \begin{pmatrix} c \, \cosh{\left(\frac{g}{c} \tau'\right)} \\ c \, \sinh{\left(\frac{g}{c} \tau'\right)} \end{pmatrix} + x(0) = \] \[ = \begin{pmatrix} \frac{c^2}{g} \, \sinh{\left(\frac{g}{c} \tau'\right)} \\ \frac{c^2}{g} \, \cosh{\left(\frac{g}{c} \tau'\right)} \end{pmatrix} \bigg|^{\tau'=\tau}_{\tau'=0} + x(0) = \] \[ = \begin{pmatrix} \frac{c^2}{g} \, \sinh{\left(\frac{g}{c} \tau\right)} \\ \frac{c^2}{g} \, \left( \cosh{\left(\frac{g}{c} \tau\right)} - 1 \right) \end{pmatrix} + x(0) = \] Setzen wir noch \( x^{0}(0) = 0 \), so haben wir: \[ x(\tau) = \begin{pmatrix} \frac{c^2}{g} \, \sinh{\left(\frac{g}{c} \tau\right)} \\ \frac{c^2}{g} \, \left( \cosh{\left(\frac{g}{c} \tau\right)} - 1 \right) + x^3(0) \end{pmatrix} \] Wir wollen dieses Ergebnis noch etwas umschreiben, indem wir die Raketenuhr-Eigenzeit \(\tau\) durch \[ \xi^{0} = c \tau \] ersetzen und die Abkürzung \[ L := \frac{c^2}{g} \] verwenden, sodass \[ \frac{g}{c} \, \tau = \frac{g}{c^2} \, \xi^{0} = \frac{\xi^{0}}{L} \] ist und somit: \[ x(\xi^{0}) = L \, \begin{pmatrix} \sinh{\frac{\xi^{0}}{L}} \\ \cosh{\frac{\xi^{0}}{L}} - 1 \end{pmatrix} + \begin{pmatrix} 0 \\ x^3(0) \end{pmatrix} \] Mit der Rapidität \[ \frac{\xi^{0}}{L} = \frac{g}{c} \, \tau = \alpha \] von oben können wir dies als Poincaretransformation schreiben: \[ x(\xi^{0}) = \Lambda \, \begin{pmatrix} 0 \\ L \end{pmatrix} + \begin{pmatrix} 0 \\ x^3(0) - L \end{pmatrix} \] wobei die Boostmatrix \( \Lambda \) von \(\alpha\) und damit von \(\xi^{0}\) abhängt, d.h. der Boost wird mit wachsender Eigenzeit immer stärker (denn die Rakete beschleunigt ja).
Man kann den Ursprung des Koordinatensystems des äußeren Beobachters nun auf verschiedene Weise weiter festlegen, indem man die Starthöhe \( x^{3}(0) \) des Raketen-Ursprungspunktes festlegt. Die Wahl \( x^{3}(0) = 0 \) führt zu sogenannten Möller-Koordinaten, die Wahl \( x^{3}(0) = L \) führt zu Rindler-Koordinaten (siehe z.B. Øyvind Grøn: Lecture Notes on General Relativity, Kap. 3.2). Wir verwenden hier Rindler-Koordinaten, d.h. der Raketen-Ursprungspunkt befindet sich zum Startzeitpunkt in der Höhe \( x^{3}(0) = L \) und wir haben die einfache Gleichung: \[ x(\xi^{0}) = \Lambda \, \begin{pmatrix} 0 \\ L \end{pmatrix} = \] \[ = L \, \begin{pmatrix} \sinh{\frac{\xi^{0}}{L}} \\ \cosh{\frac{\xi^{0}}{L}} \end{pmatrix} = \frac{c^2}{g} \, \begin{pmatrix} \sinh{\left(\frac{g}{c} \tau\right)} \\ \cosh{\left(\frac{g}{c} \tau\right)} \end{pmatrix} \] Trägt man die Zeitkoordinate \(x^{0}\) nach oben und die Höhenkoordinate \(x^{3}\) nach rechts in einem Koordinatensystem ein (siehe die Grafik etwas weiter unten), so ist die durch die Raketenuhr-Eigenzeit \(\tau\) parametrisierte Kurve eine Hyperbel, die im Abstand \(L\) die \(x^{3}\)-Achse schneidet. Im Raum-Zeit-Koordinatensystem des äußeren Beobachters beschreibt der Raketen-Ursprungspunkt der konstant beschleunigten Rakete (also die Raketenuhr) also eine Hyperbelbahn. Für große Eigenzeiten \(\tau\) nähert sich diese Bahn immer mehr dem Lichtkegel (also der Diagonalen) an. Die Geschwindigkeit des Raketen-Ursprungspunktes nähert sich entsprechend der Lichtgeschwindigkeit.
Die obige Formel können wir nun direkt dazu verwenden, um anzugeben, wo sich zur Zeit \( \xi^{0} \) im Inertialsystem des äußeren Beobachters die anderen Punkte der Rakete befinden, die im beschleunigten Bezugssystem der Rakete durch die festen Raum-Koordinaten \( \xi^{1}, \xi^{2}, \xi^{3} \) definiert sind:
|
Rindler-Koordinaten in einem konstant beschleunigten Bezugssystem (Rakete): Wir definieren ein konstant beschleunigtes (räumlich starres) Bezugssystem (Rakete) durch Raumzeit-Koordinaten \( \xi^{\mu} \) mit den folgenden Eigenschaften:
Das Inertialsystem eines äußeren Beobachters mit Raumzeit-Koordinaten \( x^{\mu} \) soll identisch sein mit dem momentanen Ruhe-Inertialsystem der Rakete zur Zeit \( \tau = 0 \) bis auf eine räumliche Verschiebung, so dass sich die mitbeschleunigte Uhr zu dieser Zeit in der Höhe \( x^{3} = L \) befindet. Der Zusammenhang zwischen den Rindler-Koordinaten \( \xi^{\mu} \) der Rakete und den Koordinaten des äußeren Beobachters \( x^{\mu} \) ist dann für \[ x = \begin{pmatrix} x^0 \\ x^3 \end{pmatrix} \] gegeben durch: \[ x(\xi^{0}, \xi^{3}) = \Lambda \, \begin{pmatrix} 0 \\ L + \xi^{3} \end{pmatrix} = \] \[ = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{\xi^{0}}{L}} \\ \cosh{\frac{\xi^{0}}{L}} \end{pmatrix} = \] \[ = \left(\frac{c^2}{g} + \xi^3\right) \, \begin{pmatrix} \sinh{\left(\frac{g}{c} \tau\right)} \\ \cosh{\left(\frac{g}{c} \tau\right)} \end{pmatrix} \] Für die übrigen beiden räumlichen Koordinaten gilt sowieso \[ x^{1} = \xi^{1} \] \[ x^{2} = \xi^{2} \] Zum Startzeitpunkt \( \xi^{0} = 0 \) ist damit \[ x(0, \xi^{3}) = \begin{pmatrix} 0 \\ L + \xi^{3} \end{pmatrix} \] d.h. die \(\xi^{3}\)-Höhenkoordinate entspricht zum Startzeitpunkt bis auf eine Verschiebung der \(x^{3}\)-Koordinate. Das momentane Ruhe-Inertialsystem der Rakete zu einem späteren Zeitpunkt ist vom äußeren Beobachter aus gesehen einfach ein sich gleichmäßig bewegendes Inertialsystem, das durch den Boost \(\Lambda\) entsteht. |
Aus der Gleichung
\[
x(\xi^{0}, \xi^{3}) =
(L + \xi^{3}) \,
\begin{pmatrix}
\sinh{\frac{\xi^{0}}{L}} \\
\cosh{\frac{\xi^{0}}{L}}
\end{pmatrix}
\]
kann man sehr schön die Form der Koordinatenlinien für konstantes \(\xi^{3}\)
(also feste Höhe in der Rakete) und laufende Raketenzeit \(\xi^{0}\)
sowie umgekehrt ablesen:
Halten wir die Höhenkoordinate \(\xi^{3}\) innerhalb der Rakete fest, so haben wir Hyperbeln, die durch die Eigenzeit \(\xi^{0}\) parametrisiert werden und die zur Startzeit \( \xi^{0} = 0 \) die \(x^3\)-Achse im Abstand \(L + \xi^{3} \) vom Nullpunkt schneiden. Diese Hyperbeln beschreiben im Inertialsystem des äußeren Beobachters die beschleunigte Bewegung von Punkten, die sich vom momentanen Ruhesystem der Rakete aus gesehen innerhalb der Rakete in der konstanten Höhe \(\xi^{3}\) befinden. Wir sehen also von außen, wie sich die einzelnen Teile der Rakete bewegen und wie sie beschleunigen.
Halten wir dagegen die Eigenzeit \(\xi^{0}\) fest, so haben wir Geraden, die durch \(\xi^{3}\) parametrisiert werden und die beim Wert \( \xi^{3} = -L \) immer durch den Nullpunkt gehen, unabhängig vom Wert der Eigenzeit \(\xi^{0}\). Diese Geraden sind die Ereignisse, die im entsprechenden momentanen Ruhe-Inertialsystem der Rakete als gleichzeitig zur zentralen Raketen-Uhrzeit angesehen werden, wie sie von der Uhr im Ursprungspunkt der Rakete angezeigt wird. Das sind also aus Sicht der Rakete die Räume der Gleichzeitigkeit:
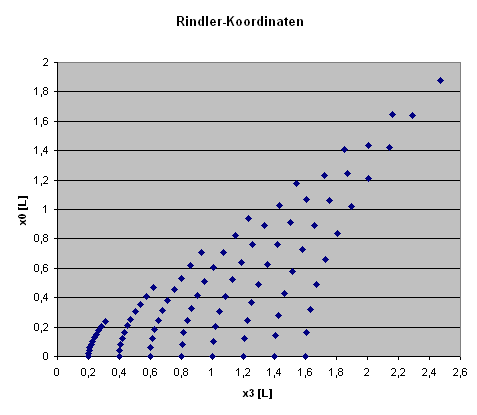
Darstellung der Raketenbeschleunigung (nach rechts):
\[
x(\xi^{0}, \xi^{3}) =
(L + \xi^{3}) \,
\begin{pmatrix}
\sinh{\frac{\xi^{0}}{L}} \\
\cosh{\frac{\xi^{0}}{L}}
\end{pmatrix}
\]
Dabei wird für verschiedene Raketenpunkte (\(\xi^{3}\)-Werte)
die Raketen-Eigenzeit \( \xi^{0} \) in 10 Schritten von \(0\) bis \(L\) erhöht, wobei sich die entsprechenden
Hyperbeln ergeben. Auf der horizontalen Achse ist hier die äußere
Höhenkoordinate \(x^{3}\) in Einheiten von \(L\) angegeben,
auf der vertikalen Achse analog die äußere Zeit \(x^{0}\) in Einheiten von \(L\).
Die Rakete beschleunigt in dem Bild also nach rechts,
während die Zeit des äußeren Beobachters nach oben läuft.
Die Bahn für den Ursprungspungt der Rakete (d.h. die Hyperbel für \( \xi^{3} = 0 \);
das ist genau die Bahn der zentralen Raketenuhr)
schneitet die horizontale Achse bei \( x^{3} = L\).
Schöne Darstellungen findet man auch im Internet unter
G. 't Hooft:
Introduction to General Relativity,
Kapitel 3 (The constantly accelerated elevator; Rindler space).
Ein sehr schönes animiertes GIF gibt es im Internet unter
http://www.phys.uu.nl/~thooft/rindler.html.
Hier noch eine etwas andere Darstellung:
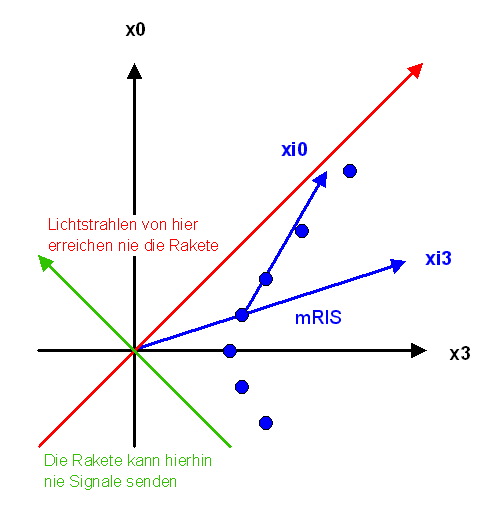
Dieses Bild zeigt analog zum Bild oben, wie sich der
Ursprungspunkt des beschleunigten Koordinatensystems (also die Raketenuhr)
in der Raumzeit für einen äußeren Beobachter bewegt (blauer Punkt).
Dabei läuft wieder die externe Beobachter-Zeit \(x^{0}\) nach oben und die Raketenuhr
beschleunigt nach rechts in \(x^{3}\)-Richtung.
Die blaue Bahn der Raketenuhr schneidet die \(x^{3}\)-Achse beim Wert \(x^{3} = L\),
d.h. in dieser Höhe startet sie aus Sicht des externen Beobachter
(bzw. dort ist sie zur Zeit Null).
Für einen bestimmten Zeitpunkt ist in Blau das
momentane Ruhe-Inertialsystem mRIS mit der \(\xi^{0}\)-Zeitachse und \(\xi^{3}\)-Raumachse
aus zentraler Raketensicht eingezeichnet.
Die eingezeichnete rote und grüne Linie sind sogenannte Ereignishorizonte.
Die Raum-Zeit-Punkte links oberhalb des roten Horizonts können den Ursprungspunkt der Rakete
niemals beeinflussen, da die Rakete diesem Signal immer hinreichend schnell davonfliegt.
Das Radiosignal ist zwar immer etwas schneller als die Rakete, aber da diese ständig beschleunigt,
kann das Signal die Rakete nicht einholen.
Umgekehrt kann ein Sender im Ursprungspunkt der Rakete niemals
die Raum-Zeit-Punkte links unterhalb des grünen Horizonts erreichen.
Solche Ereignishorizonte treten später auch
in Gravitationsfeldern auf, z.B. bei schwarzen Löchern. Das kommt nicht unerwartet, wenn
Gravitationskräfte lokal gleichwertig zu Scheinkräften in beschleunigten Bezugssystemen sind.
Nun hatten wir bei unserer Definition des beschleunigten Bezugssystems
keinerlei Einschränkung an die Werte der Höhenkoordinate \( \xi^{3} \) gemacht.
Das Bild oben legt allerdings nahe, dass nur Werte mit \( \xi^{3} \gt -L \)
unsere beabsichtigte Raketen-Interpretation aufweisen,
denn bei \( \xi^{3} = -L \) durchstößt jede
Gleichzeitigkeits-Linie (das sind die Geraden mit konstanter Eigenzeit \( \xi^{0} \))
den Nullpunkt des Koordinatensystems des externen Beobachters.
Ein Lichtblitz, der von diesem Nullpunkt ausgesendet wurde, kann den Ursprungspunkt der Rakete
gerade nicht mehr erreichen.
Das sieht alles sehr merkwürdig aus. Eine bessere Vorstellung bekommt man, wenn man für \(g\) die Erdbeschleunigung von etwa \( 10 \, \mathrm{m/s}^{2} \) einsetzt und \(L\) ausrechnet: \[ L = \frac{c^{2}}{g} = \] \[ = \frac{(3 \cdot 10^{8} \, \mathrm{m/s})^{2}}{10 \, \mathrm{m/s}^{2}} = 9 \cdot 10^{15} \, \mathrm{m} \] Dies entspricht einer Lichtlaufzeit von \[ t = \frac{L}{c} = \frac{c}{g} = \] \[ = \frac{3 \cdot 10^{8} \, \mathrm{m/s}}{10 \, \mathrm{m/s}^{2}} = 3 \cdot 10^{7} \, \mathrm{s} = \] \[ = 0,95 \, \mathrm{Jahre} \approx 1 \, \mathrm{Jahr} \] Wenn die Raketenuhr also mit Erdbeschleunigung beschleunigt (so dass die Beschleunigung sich für die Uhr wie die Schwerkraft auf der Erdoberfläche anfühlt), so ist \(L\) ungefähr gleich einem Lichtjahr.
Das ist weit größer als unser Sonnensystem und ist etwa ein Viertel der Strecke zu unserem nächsten Nachbarstern. Man müsste also eine 1 Lichtjahr lange Rakete bauen, die als starrer Körper beschleunigt wird, um in den Bereich von \( \xi^{3} = -L \) zu gelangen. In der Relativitätstheorie führt die Verwendung derart großer starrer Körper generell zu Problemen, z.B. auch bei der Rotation eines so langen Stabes (die Stab-Enden würden bei starrer Rotation und zu langem Stab schneller als mit Lichtgeschwindigkeit kreisen). Diese Probleme zeigen letztlich, dass es in der Relativitätstheorie keine absolut starren Körper gibt. Wie soll auch ein Körper absolut starr sein, wenn sich Informationen (z.B. über die Bewegung des einen Endes) nur mit Lichtgeschwindigkeit ausbreiten können?
Man darf also die Rakete nicht zu groß machen, wenn man sie sich noch anschaulich als starren Körper vorstellen möchte. Wir hatten es oben bereits angesprochen: Besser ist es bei großen Abständen, sich mehrere kleine Raketen vorzustellen, die sich so bewegen, dass sie im momentanen Ruhe-Inertialsystem der Hauprakete immer einen konstanten Abstand zu dieser haben. Wenn also eine Rakete im Abstand \(L\) unterhalb (oder besser hinter) der Hauptrakete versucht, den Abstand zu ihr konstant zu halten (aus Sicht des momentanen jeweils aktuellen momentanen Ruhe-Inertialsystems der Hauptrakete), so scheint es Probleme zu geben – wie wir noch sehen werden, schafft sie das nicht mehr. Unser Rindler-Koordinatensystem lässt sich unterhalb von \(L\) nicht mehr durch physikalische Objekte repräsentieren, die feste räumliche Koordinaten in diesem beschleunigten Koordinatensystem einnehmen. So etwas wird uns bei schwarzen Löchern unterhalb des Ereignishorizontes wiederbegegnen.
Um zu verstehen, was physikalisch los ist, schauen wir uns die Eigenzeit von Uhren an, die in verschiedener Höhe \(\xi^{3}\) innerhalb der Rakete (oder in festem Abstand zu ihr aus Raketensicht) fixiert sind. Oder anders ausgedruckt: Uhren, die sich in verschiedenen Raketen befinden, welche einen konstanten Abstand hinter der Haupt-Rakete einhalten (aus Sicht der Haupt-Rakete). Diese Eigenzeit wollen wir \( \tau' \) nennen. Eine Uhr in der Höhe \( \xi^{3} \) bewegt sich mit wachsender Hauptraketenuhr-Eigenzeit \(\tau\) nach unserer obigen Koordinatenformel auf der Bahnkurve \[ x(\xi^{0}, \xi^{3}) = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{\xi^{0}}{L}} \\ \cosh{\frac{\xi^{0}}{L}} \end{pmatrix} = \] \[ = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{c \tau}{L}} \\ \cosh{\frac{c \tau}{L}} \end{pmatrix} \] im Inertialsystem des äußeren Beobachters. Dabei ist \(\xi^{3}\) konstant und \( \xi^{0} = c \tau \) ist der Kurvenparameter.
Wichtig ist dabei: \(\tau\) ist die Eigenzeit der (Haupt-)Uhr im Ursprung der (Haupt-)Rakete (also bei \( \xi^{3} = 0 \)), und die Kurve jeder anderen Uhr, die sich bei \(\xi^{3}\) befindet, ist so parametrisiert, dass der Bahnkurvenpunkt \( x(c \tau, \xi^{3}) \) zu diesem \(\tau\) im momentanen Ruhe-Inertialsystem der Hauptuhr als gleichzeitig zur Hauptuhr-Zeit \(\tau\) angesehen wird.
Das bedeutet aber nicht unbedingt, dass die Uhr in der Höhe \(\xi^{3}\) auch die Eigenzeit \(\tau\) der Uhr in der Höhe Null anzeigt. Die Eigenzeit \( \tau' \) der Uhr in der Höhe \( \xi^{3} \) ist vielmehr gegeben durch die Bedingung, dass \[ g\left(\frac{dx}{d\tau'}, \frac{dx}{d\tau'}\right) = c^{2} \] sein muss (siehe Kapitel 3.7 Geschwindigkeit, Zeitdilatation, Vierergeschwindigkeit und Eigenzeit ). Daraus folgt \[ c^{2} = g\left(\frac{dx}{d\tau'}, \frac{dx}{d\tau'}\right) = \] \[ = g\left(\frac{dx}{d\tau}, \frac{dx}{d\tau}\right) \cdot \left(\frac{d\tau}{d\tau'}\right)^{2} \] Wir verlangen \( \frac{d\tau'}{d\tau} \gt 0 \) (die Zeitrichtung der Uhren soll ja gleich sein) und können die Wurzel ziehen: \[ \frac{d\tau'}{d\tau} = \frac{1}{c} \, \sqrt{ g\left( \frac{dx}{d\tau}, \frac{dx}{d\tau} \right) } = \] \[ = \frac{1}{c} \, \sqrt{ \left( \frac{dx^0}{d\tau} \right)^{2} - \left( \frac{dx^3}{d\tau} \right)^{2} } \] denn \(x^{1}\) und \(x^{2}\) hängen nicht von \(\tau\) ab. Für \(x\) setzen wir jetzt die obige Bahnkurve der Uhr ein: \[ x(\xi^{0}, \xi^{3}) = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{c \tau}{L}} \\ \cosh{\frac{c \tau}{L}} \end{pmatrix} \] Das ergibt für die Ableitungen \[ \frac{dx^0}{d\tau} = (L + \xi^{3}) \, \frac{c}{L} \, \cosh{\frac{c \tau}{L}} \] \[ \frac{dx^3}{d\tau} = (L + \xi^{3}) \, \frac{c}{L} \, \sinh{\frac{c \tau}{L}} \] Das setzen wir ein: \[ \frac{d\tau'}{d\tau} = \frac{1}{c} \, \sqrt{ \left( \frac{dx^0}{d\tau} \right)^{2} - \left( \frac{dx^3}{d\tau} \right)^{2} } = \] \[ = (L + \xi^{3}) \, \frac{1}{L} \, \sqrt{ \left( \cosh{\frac{c \tau}{L}} \right)^{2} - \left( \sinh{\frac{c \tau}{L}} \right)^{2} } = \] \[ = 1 + \frac{\xi^{3}}{L} \] Diese Gleichung können wir integrieren, wobei wir festlegen, dass zum Zeitpunkt Null alle Uhren synchron die Zeit Null anzeigen sollen:
|
Gleichzeitig angezeigte Eigenzeiten verschiedener Uhren im beschleunigten Bezugssystem: Die Eigenzeit \(\tau'\) einer Uhr, die aus Sicht der Hauptuhr (im deren momentanem Ruhe-Inertialsystem) in einem konstanten Abstand \(\xi^{3}\) vor/hinter der beschleunigten Hauptuhr fliegt, hängt mit der gleichzeitig angezeigten Eigenzeit \(\tau\) der Hauptuhr über die folgende Formel zusammen: \[ \tau' = \left( 1 + \frac{\xi^{3}}{L} \right) \, \tau \] (wobei der Abstand und die Gleichzeitigkeit über das momentane Ruhe-Inertialsystem der Hauptuhr definiert sind). Dabei ist \[ L = \frac{c^{2}}{g} \] mit der konstanten Beschleunigung \(g\). |
Bei \(\xi^{3} = 0\) ist also \(\tau' = \tau\) (so war es ja auch gemacht). Bei kleineren \(\xi^{3}\) (also in Richtung nach unten bzw. hinten) ist dagegen \( \tau' \lt \tau \), und bei \( \xi^{3} = -L \) ist sogar immer \( \tau' = 0 \). Man kann dies so interpretieren, dass aus Sicht eines Beobachters im Ursprungspunkt der Rakete Uhren weiter unterhalb langsamer laufen, und in der Entfernung \(L\) nach unten scheint die Uhr überhaupt nicht mehr zu laufen, d.h. die Physik scheint in Richtung des Punktes \(\xi^{3} = -L\) immer mehr einzufrieren. Nach dem Äquivalenzprinzip können wir daraus schließen, dass auch in einem Gravitationsfeld die Zeit weiter unten langsamer vergeht.
In den obigen Raum-Zeit-Diagrammen im Inertialsystem des äußeren Beobachters äußert sich der unterschiedliche Lauf der Uhren darin, dass die Linien der Gleichzeitigkeit (also \(\tau\) konstant) nach links hin enger zusammenrücken und im Nullpunkt sogar unendlich dicht zusammenliegen. So bewegt sich beispielsweise der Ursprungspunkt der Rakete vom Startzeitpunkt \(t = 0\) (waagrechte \(x^{3}\)-Achse) in eine kleine Zeit \(d\tau\) fast senkrecht nach oben entlang der Zeitachse bis zur nächsten Gleichzeitigkeitslinie. Ein Punkt weiter links bewegt sich jedoch nur ein kürzeres Stück bis zu dieser Gleichzeitigkeitslinie, was einem kleineren Eigen-Zeitintervall entspricht.
Nun beruht diese Analyse allerdings auf dem Begriff der Gleichzeitigkeit, wie er über das jeweilige momentane Ruhe-Inertialsystem definiert ist. Die Gleichzeitigkeit von Ereignissen ändert sich bei zunehmemder Geschwindigkeit im momentanen Ruhe-Inertialsystem gerade so, dass der obige Eigenzeit-Effekt entsteht. Nun ist die Gleichzeitigkeit von Ereignissen von der beschleunigten Rakete aus nicht unmittelbar messbar, da man ja dafür das momentane Ruhe-Inertialsystem braucht und dort im Grunde das weiter oben angegebene Experiment mit dem reflektierten Lichtstrahl ausführen muss – dafür aber braucht man genügend Zeit.
Was man jedoch auch in der beschleunigten Rakete messen kann, ist die Rotverschiebung eines Lichtsignals, das in \( \xi^{3} \lt 0 \) ausgesandt und in \( \xi^{3} = 0 \) empfangen wird. Die Frequenz des Lichtsignals ist gleichsam das Ticken der Uhr. Man kann zeigen, dass das Lichtsignal tatsächlich rotverschoben ankommt (siehe z.B. Marco Alberici: Clock rate comparison in a uniform gravitational field, arXiv:gr-qc/0409033), d.h. die Uhr weiter unten scheint von weiter oben aus gesehen langsamer zu ticken.
Man kann sich diesen Effekt auch klassisch-anschaulich über den Dopplereffekt erklären: Die Uhr, die das Lichtsignal weiter unten aussendet, hat noch eine geringere Geschwindigkeit als die Uhr, die weiter oben das Lichtsignal zu einer späteren Zeit empfängt. Diese Uhr fliegt dem Signal gleichsam immer schneller davon, so dass die Wellenlängen mit größeren Zeitabständen ankommen. Diese klassisch-anschauliche Erklärung ist jedoch mit Vorsicht zu genießen, da sie die Effekte der Relativitätstheorie nicht berücksichtigt. Und so kann man in der klassischen nichtrelativistischen Mechanik auch die Rotverschiebung des Lichtsignals nicht einfach als eine langsamer laufende Uhr interpretieren, denn die Zeit läuft dort überall gleich schnell. Erst die Relativitätstheorie mit ihrem Begriff der Gleichzeitigkeit, der vom Bezugssystem abhängt, erlaubt die Interpretation, dass die weiter unten in der Rakete befestigte Uhr langsamer läuft!
Neben der Eigenzeit ist es interessant, sich auch die in verschiedenen Höhen \( \xi^{3} \) empfundene Beschleunigung genauer anzusehen. Anders ausgedrückt: Welche Beschleunigung ist in unterschiedlicher Höhe notwendig, um den Abstand im momentanen Ruhe-Inertialsystem der Hauptuhr konstant zu halten?
Dazu betrachten wir wieder die Bahnkurve der in der Höhe \( \xi^{3} \) befestigten Uhr und setzen \[ \tau' = \left( 1 + \frac{\xi^{3}}{L} \right) \, \tau \] ein, sodass wir \[ \frac{c \tau}{L} = \] \[ = \frac{c}{L \, \left( 1 + \frac{\xi^{3}}{L} \right) } \, \tau' = \] \[ = \frac{c}{L + \xi^{3}} \, \tau' \] haben: \[ x(\xi^{0}, \xi^{3}) = \] \[ = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{c \tau}{L}} \\ \cosh{\frac{c \tau}{L}} \end{pmatrix} = \] \[ = (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{c}{L + \xi^{3}} \, \tau'} \\ \cosh{\frac{c}{L + \xi^{3}} \, \tau'} \end{pmatrix} \] Die Vierer-Beschleunigung \(a'\) in der Höhe \(\xi^{3}\) ist gegeben durch die zweite Ableitung nach der dort gemessenen Eigenzeit \( \tau' \): \[ a' = \frac{d^{2}}{d\tau'^{2}} \, (L + \xi^{3}) \, \begin{pmatrix} \sinh{\frac{c}{L + \xi^{3}} \, \tau'} \\ \cosh{\frac{c}{L + \xi^{3}} \, \tau'} \end{pmatrix} = \] \[ = (L + \xi^{3}) \, \left( \frac{c}{L + \xi^{3}} \right)^{2} \, \begin{pmatrix} \sinh{\frac{c}{L + \xi^{3}} \, \tau'} \\ \cosh{\frac{c}{L + \xi^{3}} \, \tau'} \end{pmatrix} = \] \[ = \frac{c^2}{L + \xi^{3}} \, \begin{pmatrix} \sinh{\frac{c}{L + \xi^{3}} \, \tau'} \\ \cosh{\frac{c}{L + \xi^{3}} \, \tau'} \end{pmatrix} \] Vergleichen wir diesen Ausdruck mit der Beschleunigung \(a\) im Ursprungspunkt \( \xi^{3} = 0 \). Diese Beschleunigung können wir aus dem obigen Ausdruck leicht ablesen, indem wir darin \( \xi^{3} = 0 \) und \( \tau' = \tau \) setzen: \[ a = \frac{c^2}{L} \, \begin{pmatrix} \sinh{\frac{c}{L} \, \tau} \\ \cosh{\frac{c}{L} \, \tau} \end{pmatrix} \] Wenn wir in \(a'\) wieder \( \tau' = (1 + \xi^{3}/L) \, \tau \) einsetzen, so erhalten wir: \[ a' = \frac{c^2}{L + \xi^{3}} \, \begin{pmatrix} \sinh{\frac{c}{L} \, \tau} \\ \cosh{\frac{c}{L} \, \tau} \end{pmatrix} = \frac{L}{L + \xi^{3}} \, a \] Wir sehen: wenn wir uns mit \( \xi^{3} \) dem Wert \(-L\) nähern, so wird die Viererbeschleunigung unendlich groß!
Wenn wir diese Beziehung im momentanen Ruhe-Inertialsystem zu irgendeinem Zeitpunkt auswerten, so ist \( a = (0, g) \) und \( a' = (0, g') \) und es folgt, dass im momentanen Ruhe-Inertialsystem der jeweiligen Uhr bei \(\xi^3\) die Beschleunigung \(g'\) immer größer wird und schließlich divergiert, wenn wir uns von oben dem Punkt \( \xi^{3} = -L \) nähern.
Man erkennt dies auch an den Hyperbeln mit konstanten \(\xi^{3}\): In der Nähe der waagrechten \(x^{3}\)-Achse (also bei kleinen \(t\)) werden diese Hyperbeln nach links hin immer spitzer, d.h. die Beschleunigung in \(x^{3}\)-Richtung wird immer größer.
Wenn man nun versuchen würde, jemanden (nennen wir sie Alice) in der beschleunigten Rakete langsam an einem Seil zum kritischen Punkt \( \xi^{3} = -L \) herabzulassen, so würde die Beschleunigung immer stärker an Alice ziehen, bis das Seil schließlich unweigerlich zerreist und Alice in den freien Fall übergeht (d.h. nicht mehr mit der Rakete mitbeschleunigt wird).
Für einen Beobachter im Ursprungspunkt der Rakete (nennen wir ihn Bob) sieht es dann so aus, als würde sich die fallende Alice immer langsamer auf den kritischen Punkt zubewegen (ihn aber nie erreichen), während ihre Bewegungen und überhaupt alle physischen Vorgänge bei ihr immer langsamer werden (da die Eigenzeit von Alice immer langsamer verstreicht im Vergleich zu der Eigenzeit von Bob). Aufgrund der immer stärkeren Rotverschiebung würde das von ihr ausgesandte Licht immer energieärmer werden, so dass Alice schließlich für Bob unsichtbar wird. Alice selbst merkt davon überhaupt nichts: sie bewegt sich friedlich geradlinig-gleichförmig durch den Raum. Ganz ähnlich ist es auch beim Ereignishorizont eines schwarzen Lochs!
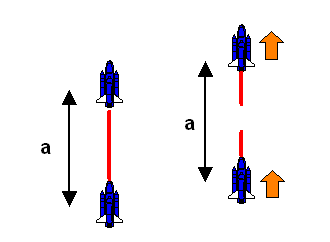
Die unterschiedliche Beschleunigung trotz festen Abstandes widerspricht unserer Anschauung. Dennoch ist es so: Eine zweite Rakete hinter unserer Hauptrakete muss stärker beschleunigen, um den Abstand im momentanen Ruhe-Inertialsystem der Hauptrakete konstant zu halten. Ist dieser Abstand größer als \(L\), so schafft sie es überhaupt nicht mehr, d.h. es gibt keine physikalischen Objekte, die in unserem beschleunigten Bezugssystem eine konstante \(\xi^{3}\)-Koordinate kleiner als \(-L\) haben können. Ab dem Abstand \(L\) gibt es keine Objekte mehr, die in unserem beschleunigten Bezugssystem statisch sein können. Das ist aber eine Eigenschaft unseres speziellen Bezugssystems. Bei schwarzen Löchern wird uns das wiederbegegnen (siehe Kapitel 7.3 ).
Die physikalische Ursache für dieses Phänomen liegt in der Lorentz-Kontraktion: Ein bewegter Körper ist in Bewegungsrichtung verkürzt, verglichen mit seiner Länge im Ruhesystem des Körpers. Das ist nicht nur Einbildung, sondern eine reale physikalische Tatsache, die man beispielsweise für Festkörper auch mit den Maxwellgleichungen begründen kann. Für einen äußeren ruhenden Beobachter wird also die beschleunigte Rakete immer kürzer, je schneller sie wird. Teile weiter hinten müssen also Teile weiter vorne immer mehr einholen, d.h. sie müssen entsprechend stärker beschleunigen. Würden alle Teile der Rakete gleich beschleunigen, so dass sie für den äußeren ruhenden Beobachter einen konstanten Abstand voneinander beibehielten, dann würde die Rakete in ihrem momentanen Ruhe-Inertialsystem immer mehr gedehnt werden und schließlich zerreißen. Das bezeichnet man auch als Bellsches Raumschiffparadoxon .
Im Inertialsystem des äußeren Beobachters ist die Bahnkurve \( x(\tau) = (x^{\mu}(\tau)) \) irgend eines Massenpunktes mit Masse \(m\) in einem Vierer-Kraftfeld \(F\) gegeben durch die Bewegungsgleichung \[ m \, \frac{d^{2}}{d\tau^{2}} \, x^{\mu}(\tau) = F^{\mu}(x(\tau)) \] Dabei ist \(\tau\) die Eigenzeit des Massenpunktes auf der Bahnkurve. Für die Eigenzeit der Uhr im Ursprungspunkt der Rakete wollen wir daher ab sofort nur noch die Koordinate \(\xi^{0}\) (und nicht mehr \(\tau\)) verwenden, damit es hier keine Verwechselungen gibt!
Die obige Gleichung ist in dieser Form nur in einem Inertialsystem gültig, denn sie bezieht sich auf die karthesischen Koordinaten dieses Inertialsystems. Für die Betrachtung von Poincaré-Transformationen reicht diese Schreibweise aus, denn die Gleichung ändert ihre Form bei diesen speziellen affinen Koordinatentransformationen nicht.
Wenn man die Gleichung allerdings in das beschleunigte Koordinatensystem der Rakete umformen möchte, so muss man explizit auf die neuen Koordinaten umrechnen. Es wäre daher sehr nützlich, wenn man die Gleichung in einer koordinaten-unabhängigen Form schreiben könnte, die sich dann in beliebigen Raum-Zeit-Koordinaten ausschreiben lässt. In der Physik spricht man auch davon, dass man die Gleichung in tensorieller Form schreiben möchte, d.h. in einer Form, die in beliebigen Koordinaten gültig ist. Die tensorielle Schreibweise ist einfach nur das Ausschreiben der koordinaten-unabhängigen Form in beliebigen Koordinaten. Da bei der Betrachtung der Gravitation nach dem Äquivalenzprinzip auch scheinbar-beschleunigte Koordinatensysteme eine Rolle spielen werden, wird es dort wichtig sein, eine koordinaten-unabhängige bzw. tensorielle Formulierung für die Naturgesetze zu finden.
Die Differentialgeometrie hält den passenden mathematischen Formalismus dafür bereit, denn die Minkowski-Raumzeit ist mathematisch eine differenzierbare Mannigfaltigkeit: Die Ereignisse kann man mit Punkten in dieser Mannigfaltigkeit identifizieren, die sich in beliebigen (differenzierbaren) Koordinatensystemen bezeichnen lassen. Wir werden unten sehen, dass sich der Formalismus auch auf die Raumzeit mit Gravitation übertragen lässt.
Die obige Bahnkurve ist in koordinaten-unabhängiger Schreibweise gegeben durch eine Kurve \( \gamma(\tau) \). Dabei ist \(\gamma\) eine Abbildung von den reellen Zahlen in die Mannigfaltigkeit der Minkowski-Raumzeit.
Man kann nun irgendeine Koordinatenfunktion \(f\) (auch Karte genannt) betrachten, die jedem Punkt \(p\) der Raum-Zeit-Mannigfaltigkeit (oder eines Teils der Mannigfaltigkeit) 4 reelle Koordinaten \[ x = (x^\mu) := f(p) \] zuordnet, d.h. \(x \in \mathbb{R}^{4}\). Es müssen dabei diesmal aber nicht unbedingt die üblichen Minkowski-Raumzeit-Koordinaten mit der Zeitkoordinate \(x^0 = ct\) und den drei karthesischen Raumkoordinaten \(x^1, x^2, x^3\) sein, sondern wir könnten auch unsere Raketen-Koordinaten \( \xi^\mu \) von oben nehmen.
In diesen beliebig wählbaren Koordinaten lautet die Bahnkurve dann \[ x(\tau) := f(\gamma(\tau)) \] oder ausführlich \[ x^{\mu}(\tau) := f^{\mu}(\gamma(\tau)) \] Aber nur wenn man karthesische Minkowski-Koordinaten verwendet, so erhält man für die Bahnkurve die obige Bewegungsgleichung \[ m \, \frac{d^{2}}{d\tau^{2}} \, x^{\mu}(\tau) = F^{\mu}(x(\tau)) \] Wie also kann man diese Bewegungsgleichung koordinaten-unabhängig formulieren? Dazu benötig man zunächst den Begriff des Tangentialvektors. Details dazu findet man in Tangentialräume und Vektorfelder. Hier eine kurze Wiederholung:
|
Tangentialvektoren: Ein Tangentialvektor \( u(p) \) im Punkt \(p\) der Mannigfaltigkeit (hier: der Raumzeit) wird über eine Kurve \( \gamma \) in der Mannigfaltigkeit definiert (mit \( \gamma(s) = p \) mit dem reellen Kurvenparameter \(s\)), so dass \( u(p) \) angewendet auf eine skalare Funktion \( \phi \) auf der Mannigfaltigkeit gerade die Richtungsableitung von \(\phi\) in Kurvenrichtung im Punkt \(p\) ergibt: \[ u(p) \, \phi := \frac{d\phi(\gamma(s))}{ds} \] Diese Formulierung hat den Vorteil, koordinaten-unabhängig zu sein und ohne eine Einbettung der Mannigfaltigkeit auszukommen. Man kann sich \( u(p) \) als kleinen Pfeil tangential zur Kurve \(\gamma\) im Punkt \(p\) vorstellen, der angewendet auf \(\phi\) die Richtungsableitung in Pfeilrichtung ergibt. Für \(\phi\) kann man z.B. die Koordinatenfunktionen \( f^{\mu} \) verwenden und erhält: \[ u(p) \, f^{\mu} := \frac{df^{\mu}(\gamma(s))}{ds} =: \] \[ =: \frac{dx^{\mu}(s)}{ds} =: u^{\mu}(p) \] Das sind die Komponenten des Tangentialvektors in Koordinatendarstellung. Es gilt die Zerlegung \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] mit \[ \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \, \phi := \frac{\partial \phi}{\partial x^{\mu}} \] auszuwerten im Punkt \( x = f(p) \). Der Tangentialraum \(T(p)\) ist der Vektorraum aller Tangentialvektoren in einem Punkt \(p\). Ein Tangentialvektorfeld \( u \) ist nun eine (differenzierbare) Abbildung, die jedem Punkt \(p\) der Mannigfaltigkeit einen Tangentialvektor \( u(p) \) zuordnet. |
Unsere Bahnkurve \( \gamma(\tau) \) von oben
definiert also auf diese Weise in jedem ihrer Punkte einen
Tangentialvektor \( u(\gamma(\tau)) \).
Wenn wir karthesische Minkowski-Koordinaten verwenden und für \(\tau\) die Eigenzeit verwenden, so sind die Komponenten \( u^{\mu} \) gerade die Komponenten der relativistischen Vierer-Geschwindigkeit, d.h. es ist \[ \frac{dx^{\mu}(\tau)}{d\tau} = u^{\mu}(\gamma(\tau)) =: u^{\mu}(\tau) \] Nun erfüllt die Vierer-Geschwindigkeit die Normierungsbedingung \[ g(u,u) = c^{2} \] mit der Minkowskimetrik (in karthesischen Minkowski-Koordinaten): \[ g(u,u) = (u^{0})^{2} - \boldsymbol{u}^{2} \] Wenn wir nun \( u \) als koordinatenfreien Tangentialvektor auffassen, so ist \( g(u,u) \) eine koordinatenfreie Metrik auf der Mannigfaltigkeit, ausgewertet auf dem Tangentialvektor \(u\). Zum Begriff der Metrik siehe Abstände und Winkel: die Metrik.
Mathematisch ist die Metrik eine bilineare symmetrische Abbildung, die aus zwei Tangentialvektoren eine reelle Zahl macht. Nur in karthesischen Minkowski-Koordinaten gilt dann \( g(u,u) = (u^{0})^{2} - \boldsymbol{u}^{2} \). Genau genommen definiert dies erst den Begriff karthesische Minkowski-Koordinaten.
Die koordinatenunabhängige Schreibweise für die Normierungsbedingung und damit für die Festlegung der Eigenzeit lautet daher einfach \( g(u,u) = c^{2} \). Die Metrik in der Raumzeit der speziellen Relativitätstheorie ist dadurch festgelegt, dass man die Existenz karthesischer Minkowski-Koordinaten auf der Mannigfaltigkeit fordert, so dass in diesen Koordinaten \( g(u,u) = (u^{0})^{2} - \boldsymbol{u}^{2} \) ist. Weiter unten werden wir sehen, dass sich diese Forderung bei Anwesenheit von Gravitation nicht mehr global, sondern nur noch lokal aufrecht erhalten lässt.
Die Bewegungsgleichung \[ m \, \frac{d^{2}}{d\tau^{2}} \, x^{\mu}(\tau) = F^{\mu}(x(\tau)) \] die so nur in karthesischen Minkowski-Koordinaten gilt, können wir mit Hilfe der Vierer-Geschwindigkeit \[ u^{\mu}(\tau) = \frac{dx^{\mu}(\tau)}{d\tau} \] in karthesischen Minkowski-Koordinaten schreiben als \[ m \, \frac{du^{\mu}}{d\tau} = F^{\mu}(x(\tau)) \] Die rechte Seite kann man als Komponente eines Tangentialvektors \(F\) ansehen, so dass man hier eine koordinatenfreie Darstellung erreichen kann. Bleibt das Problem: Wie schreibt man die linke Seite in koordinatenfreier Form? Schließlich steht dort explizit die Ableitung der einzelnen Komponenten, und die Ableitung eines koordinatenfreien Tangentialvektors ist zunächst gar nicht definiert.
Die Lösung kennen wir aus Kovariante Ableitung und Paralleltransport. Dort hatten wir die kovariante Ableitung definiert. Bei einer Einbettung der Mannigfaltigkeit in den \( \mathbb{R}^{n} \) (mit entsprechenden karthesischen Koordinaten darin) hatten wir gesagt:
Wenn \(v(p)\) ein Tangentialvektor zur Kurve \( \gamma \) im Punkt \( p = \gamma(s) \) ist, so ist die kovariante Ableitung \( D_{v(p)} u \) eines Tangentialvektorfeldes \(u\) im Punkt \(p\) in Richtung des Tangentialvektors \(v(p)\) definiert durch die Projektion von \[ \frac{du(\gamma(s))}{ds} \] auf den Tangentialraum in \(p = \gamma(s)\). Dabei ist \( \frac{du(\gamma(s))}{ds} \) über die Einbettung definiert, d.h. gemeint sind die Komponenten \( \frac{du^\mu(\gamma(s))}{ds} \) bezüglich der karthesischen Komponenten des Einbettungsraums.
Im Fall der Minkowski-Raumzeit brauchen wir den Einbettungsraum gar nicht, denn die Minkowski-Raumzeit mit ihren karthesischen Minkowski-Koordinaten ist selbst schon ein passender Einbettungsraum. Daher brauchen wir auch die Projektion nicht mehr und wir können direkt bezogen auf die karthesischen Minkowski-Koordinaten definieren: \[ (D_{v(p)} u)^{\mu} := \frac{du^\mu(\gamma(s))}{ds} \] Aus Kovariante Ableitung und Paralleltransport wissen wir, dass wir \( D_{v(p)} u \) auch koordinatenunabhängig definieren können, so dass sich in karthesischen Koordinaten gerade die obige Formel ergibt. Dazu fordert man bestimmte Eigenschaften: Die kovariante Ableitung soll algebraisch linear in \(v(p)\) sein, additiv in \(u\) sein und die Produktregel erfüllen. Als Ergebnis dieser Eigenschaften kann man die folgende eindeutige Darstellung in beliebigen Koordinaten ableiten:
|
kovariante Ableitung in beliebigen Koordinaten: Die kovariante Ableitung \( D_{v(p)}u \) eines Tangentialvektors \(u\) in Richtung des Tangentialvektors \(v(p)\) (festgelegt durch eine Kurve \(\gamma\) mit \(p = \gamma(s)\) ) ist in beliebigen Koordinaten gegeben durch \[ D_{v(p)} u = \sum_{\rho} \, \big\{ v(p) \, u^{\rho} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \big\} \, \frac{\partial}{\partial x^{\rho}}\bigg|_{p} \] Dabei sind die Christoffelsymbole \( \Gamma^{\rho}_{\nu\mu} \) definiert durch \[ D_{\frac{\partial}{\partial x^{\nu}}\bigg|_{p}} \, \frac{\partial}{\partial x^{\mu}} = \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \, \frac{\partial}{\partial x^{\rho}}\bigg|_{p} \] |
In karthesischen Koordinaten ist
\[
\Gamma^{\rho}_{\nu\mu}
=
\left[ D_{\frac{\partial}{\partial x^{\nu}}\bigg|_{p}} \,
\frac{\partial}{\partial x^{\mu}} \right]^{\rho} =
\frac{\partial}{\partial x^{\nu}} \, \delta^{\rho\mu}
= 0
\]
d.h. in karthesischen Koordinaten verschwinden die Christoffelsymbole,
da die Basisvektoren konstant sind,
und wir erhalten:
\[
[ D_{v(p)} u ]^{\rho} =
v(p) \, u^{\rho}
=
\frac{du^{\rho}(\gamma(s))}{ds}
\]
Die Christoffelsymbole reflektieren also den Umstand, dass in allgemeinen
Koordinaten die Basisvektoren sich entlang einer Kurve ändern können.
Das kennt man z.B. schon von zweidimensionalen Polarkoordinaten in der Ebene.
Wenn man in der klassischen Mechanik das Newtonsche Bewegungsgesetz
\[
m \, \frac{d}{dt} \boldsymbol{v} = \boldsymbol{F}
\]
nicht in karthesischen
Koordinaten, sondern in allgemeinen Koordinaten aufschreibt, so tritt
auch hier die kovariante Ableitung auf. Meist verzichtet man dort darauf,
um den Formalismus nicht zu überfrachten, ebenso wie in der speziellen
Relativitätstheorie, da man dort normalerweise auf karthesische Koordinaten
zurückgreifen kann. In der allgemeinen Relativitätstheorie ist das
i.a. nicht mehr möglich, wie wir weiter unten noch sehen werden.
Deshalb ist dann eine koordinaten-unabhängige (oder tensorielle)
Darstellung unverzichtbar. Man sollte aber nicht vergessen:
Jede physikalische Theorie kann man koordinaten-unabhängig (tensoriell)
darstellen! Koordinaten sind ja nur eine willkürliche Wahl, Raumpunkte (evtl. plus Zeit)
mit Zahlen zu bezeichnen.
Dass die kovariante Ableitung sich ganz automatisch ergibt, wenn man von karthesischen Koordinaten \(x^{\mu}\) in beliebige Koordinaten \(\xi^{\mu}\) umrechnet, kann man auch leicht selbst nachrechnen. Die Ableitung der krummlinigen Basisvektor-Komponenten ergibt dabei die Christoffelsymbole. Wir wollen uns hier diese Rechnung ersparen, da wir sie bereits in Kovariante Ableitung und Paralleltransport für einen Einbettungsraum durchgeführt haben.
Nach dieser Vorbereitung lautet unsere Bewegungsgleichung in koordinaten-unabhängiger Form:
|
Bewegungsgleichung in
koordinaten-unabhängiger Form: \[ m \, D_{u(\gamma(\tau))} u = F(\gamma(\tau)) \] oder kurz \[ m \, D_{u} u = F \] Dabei ist \( u(\gamma(\tau)) \) der Tangentialvektor zur Kurve \( \gamma \) im Punkt \( \gamma(\tau) \) und \(F\) ist ein Tangentialvektorfeld, das die auf den Massenpunkt (mit Masse \(m\)) wirkende Kraft darstellt. Besonders interessant ist der Fall mit \( F = 0 \), also die kräftefreie Bewegung. Dann ist nämlich \[ D_{u(\gamma(\tau))} u = 0 \] Ein Körper, auf den keine Kräfte einwirken, bewegt sich entlang einer geodätischen Linie. In karthesischen Koordinaten ist dies eine Gerade in der Raumzeit. |
In der speziellen Relativitätstheorie sind sowohl die Metrik als auch die
kovariante Ableitung über eine triviale Einbettung definiert
(die Raumzeit selbst ist der Einbettungsraum, da wir in ihr karthesische
Koordinaten einführen können, z.B. das Inertialsystem des äußeren Beobachters).
Daher erfüllen Metrik und kovariante Ableitung
automatisch die Verträglichkeitsbedinging, d.h. die Metrik
legt eindeutig die kovariante Ableitung fest und die Christoffelsymbole lassen sich
aus der metrischen Matrix berechnen
(siehe
Abstände und Winkel: die Metrik ):
\[
\Gamma^{\tau}_{\rho\mu}
=
\sum_{\nu} \,
\frac{1}{2} \, g^{\tau\nu} \, \cdot
\]
\[ \cdot \,
\left(
\frac{dg_{\nu\rho}}{dx^{\mu}} +
\frac{dg_{\nu\mu}}{dx^{\rho}} -
\frac{dg_{\rho\mu}}{dx^{\nu}} \right)
\]
Wie wir in Abstände und Winkel: die Metrik
weiter gesehen haben, folgt aus der Verträglichkeitsbedingun,
dass geodätische Linien (d.h. es gilt \( D_{u(\gamma(\tau))} u = 0 \) )
gleichzeitig auch Geodäten sind, d.h. die
Bogenlänge ist um die geodätische Linie herum bei Variationen in erster Ordnung stationär
(bei positiv definiter Metrik wäre die Bogenlänge z.B. minimal).
Daher kann man die Bewegungskurve eines kräftefreien Körpers auch über ein Variationsprinzip finden.
Bei zeitartigen Kurven (d.h. die Metrik des Tangentialvektors ist größer Null,
so wie bei der Vierergeschwindigkeit eines Körpers mit Masse) ist die Bogenlänge einer Kurve
(gebildet mit der Raum-Zeit-Metrik)
gleich der Eigenzeit einer entlang der Kurve bewegten Uhr. Ein kräftefreier Körper
bewegt sich also auf der Kurve mit extremaler Eigenzeit zwischen zwei Raum-Zeit-Punkten.
Man kann zeigen, dass in der speziellen und auch in der allgemeinen Relativitätstheorie die Eigenzeit für eine (zeitartige) Geodäte maximal ist, d.h. ein frei fallender Körper bewegt sich zwischen zwei Raum-Zeitpunkten auf einer Kurve maximaler Eigenzeit (siehe z.B. Feynman Vorlesungen über Physik, Band II Elektromagnetismus und Dtruktur der Materie, Kapitel 42 Der gekrümmte Raum ).
Im Fall der speziellen Relativitätstheorie können wir uns dies auch anschaulich klar machen. Dazu betrachten wir in einem Inertialsystem einen Raumpunkt mit festen Ortskoordinaten \(\boldsymbol{x}\) und lassen dort zu einer Zeit \(t_{1}\) eine kleine Uhr starten. Wir verlangen, dass diese Uhr zu einer vorgegebenen späteren Zeit \(t_{2}\) wieder am selben Raumpunkt \(\boldsymbol{x}\) ankommt. Wie muss sich die kleine Uhr bewegen, damit auf ihr eine möglichst große Zeitspanne (Eigenzeit) vergeht, während in unserem Inertialsystem die Zeitspanne \(t_{2} - t_{1}\) vergangen ist? Die Antwort lautet: Sie darf sich überhaupt nicht bewegen und bleibt die ganze Zeit über am Punkt \(\boldsymbol{x}\) stehen. Jede Bewegung würde zu einer Geschwindigkeit führen, und auf einer bewegten Uhr vergeht die Zeit langsamer, wie wir wissen (Zeitdilatation).
Wir können uns nun die ganze Situation aus einem anderen Inertialsystem heraus ansehen, das sich relativ zur ruhenden Uhr gleichförmig bewegt. Die Uhr bewegt sich in diesem Bezugssystem auf einer Raum-Zeit-Geraden zwischen den beiden Ereignissen Uhr startet und Uhr kommt an. Da die Eigenzeit, die von einer bewegten (oder ruhenden) Uhr angezeigt wird, nicht vom Bezugssystem abhängt (wie sollte sie auch), wissen wir: Die Uhr, die sich zwischen den beiden Ereignissen (Raum-Zeit-Punkten) Uhr startet und Uhr kommt an auf einer Geraden durch die Raumzeit bewegt, zeigt die längste Eigenzeit an. Jede andere Uhr, deren Bewegung von dieser Geraden abweicht, wird eine kürzere Eigenzeit anzeigen.
Genauso ist es auch, wenn wir und die Situation aus der beschleunigten Rakete heraus ansehen. In diesem beschleunigten Bezugssystem scheint die Uhr immer schneller nach unten zu fallen. Da es für die Eigenzeit auf das Bezugssystem nicht ankommt, gilt auch hier: Die Bewegungskurve der Uhr ist diejenige mit der längsten Eigenzeit zwischen vorgegebenen Ereignissen (Raum-Zeit-Punkten). Allerdings ist diese Kurve im beschleunigten Bezugssystem der Rakete keine Gerade mehr. Offenbar ist es in diesem Bezugssystem für eine maximale Eigenzeit günstiger, sich nicht auf einer Geraden zu bewegen. Auf diese Weise kann man nämlich ausnutzen, dass die Eigenzeit weiter oben schneller anwächst als weiter unten. Nach dem Äquivalenzprinzip gilt dasselbe lokal in einem Gravitationsfeld: Die Uhr bewegt sich zwischen zwei Ereignissen im freien Fall so, dass die Eigenzeit der Uhr maximal wird. Man nennt das auch das Trödelprinzip.
Soll eine Uhr nach einer gewissen Zeit im Inertialssystem wieder an ihrem Ausgangspunkt
ankommen, so ist die Eigenzeit maximal, wenn sich die Uhr gar nicht bewegt.
Daher ruht eine solche Uhr im Inertialsystem. Jede andere hypothetische
Bewegung (dargestellt durch die gelben Pfeile)
führt zu einer kürzeren Eigenzeit – daher bewegt sich die kräftefreie Uhr nicht so.
Die Eigenzeit ist die von der Uhr angezeigte Zeit – sie
hängt nicht vom Bezugssystem ab!
Rechts oben:
Betrachtet man dieselbe Uhr von einem anderen, gleichförmig bewegten Inertialsystem aus,
so führt sie eine geradlinig-gleichförmige Bewegung aus (in Blau dargestellt).
Diese Bewegung ist wie im anderen Bezugssystem
zuvor die Bewegung mit der längsten Eigenzeit.
Unten:
Aus einem beschleunigten Raumschiff heraus sieht die Bewegung mit der längsten Eigenzeit
krummlinig aus – die Uhr fällt. Die gelbe hypothetische Bewegung hat wie in den anderen Bezugssystemen auch
eine kürzere Eigenzeit.

Wir wollen die Christoffelsymbole für das beschleunigte Koordinatensystem
unserer Rakete explizit ausrechnen. Dazu berechnen wir zunächst die metrische Matrix
in den beschleunigten Raketenkoordinaten \( \xi^{\mu} \), indem wir auf die Minkowski-Metrik
der karthesischen Koordinaten \( x^{\mu} \) umrechnen:
\[
g_{\mu\nu} =
g\left( \frac{\partial}{\partial \xi^{\mu}}, \frac{\partial}{\partial \xi^{\nu}} \right) =
\]
\[
=
\sum_{\rho\sigma} \,
g\left(
\frac{\partial x^{\rho}}{\partial \xi^{\mu}}
\,
\frac{\partial}{\partial x^{\rho}} ,
\frac{\partial x^{\sigma}}{\partial \xi^{\nu}}
\,
\frac{\partial}{\partial x^{\sigma}}
\right) =
\]
\[
=
\sum_{\rho\sigma} \,
\frac{\partial x^{\rho}}{\partial \xi^{\mu}}
\,
\frac{\partial x^{\sigma}}{\partial \xi^{\nu}}
\,
g\left(
\frac{\partial}{\partial x^{\rho}} ,
\frac{\partial}{\partial x^{\sigma}}
\right) =
\]
\[
=
\frac{\partial x^{0}}{\partial \xi^{\mu}}
\,
\frac{\partial x^{0}}{\partial \xi^{\nu}}
-
\sum_{i=1}^{3} \,
\frac{\partial x^{i}}{\partial \xi^{\mu}}
\,
\frac{\partial x^{i}}{\partial \xi^{\nu}}
\]
Also müssen wir zunächst die karthesischen Komponenten der Raketen-Basisvektoren
\[
\frac{\partial x^{\rho}}{\partial \xi^{\mu}}
\]
ausrechnen. Zur Erinnerung:
Wir hatten
\[
x^{0}
=
(L + \xi^{3}) \, \sinh{ \frac{\xi^{0}}{L}}
\]
\[
x^{3}
=
(L + \xi^{3}) \, \cosh{ \frac{\xi^{0}}{L}}
\]
sowie
\[
x^{1} = \xi^{1}
\]
\[
x^{2} = \xi^{2}
\]
Damit ergibt sich:
\[
\frac{\partial x^{0}}{\partial \xi^{0}}
=
\left( 1 + \frac{\xi^{3}}{L} \right) \, \cosh{ \frac{\xi^{0}}{L}}
\]
\[
\frac{\partial x^{3}}{\partial \xi^{0}}
=
\left( 1 + \frac{\xi^{3}}{L} \right) \, \sinh{ \frac{\xi^{0}}{L}}
\]
\[
\frac{\partial x^{0}}{\partial \xi^{3}}
=
\sinh{ \frac{\xi^{0}}{L}}
\]
\[
\frac{\partial x^{3}}{\partial \xi^{3}}
=
\cosh{ \frac{\xi^{0}}{L}}
\]
und
\[
\frac{\partial x^{i}}{\partial \xi^{j}} = \delta_{ij}
\]
für \(i\) und \(j\) mit Werten im Bereich von 1 bis 2.
Für die metrische Matrix
\[
g_{\mu\nu} =
g\left( \frac{\partial}{\partial \xi^{\mu}}, \frac{\partial}{\partial \xi^{\nu}} \right) =
\]
\[
=
\frac{\partial x^{0}}{\partial \xi^{\mu}}
\,
\frac{\partial x^{0}}{\partial \xi^{\nu}}
-
\sum_{i=1}^{3} \,
\frac{\partial x^{i}}{\partial \xi^{\mu}}
\,
\frac{\partial x^{i}}{\partial \xi^{\nu}}
\]
in beschleunigten Raketenkoordinaten erhalten wir damit:
\[
g_{00} =
\frac{\partial x^{0}}{\partial \xi^{0}}
\,
\frac{\partial x^{0}}{\partial \xi^{0}}
-
\sum_{i=1}^{3} \,
\frac{\partial x^{i}}{\partial \xi^{0}}
\,
\frac{\partial x^{i}}{\partial \xi^{0}}
=
\]
\[
=
\left( 1 + \frac{\xi^{3}}{L} \right)^2 \, \left[\cosh{ \frac{\xi^{0}}{L}}\right]^2
+
\]
\[
-
\left( 1 + \frac{\xi^{3}}{L} \right)^2 \, \left[\sinh{ \frac{\xi^{0}}{L}}\right]^2
=
\]
\[
=
\left( 1 + \frac{\xi^{3}}{L} \right)^2
\]
\[
g_{03} = g_{30} =
\]
\[ =
\frac{\partial x^{0}}{\partial \xi^{0}}
\,
\frac{\partial x^{0}}{\partial \xi^{3}}
-
\sum_{i=1}^{3} \,
\frac{\partial x^{i}}{\partial \xi^{0}}
\,
\frac{\partial x^{i}}{\partial \xi^{3}}
=
\]
\[
=
\left( 1 + \frac{\xi^{3}}{L} \right) \, \cosh{ \frac{\xi^{0}}{L}} \, \, \sinh{ \frac{\xi^{0}}{L}}
+
\]
\[
-
\left( 1 + \frac{\xi^{3}}{L} \right) \, \sinh{ \frac{\xi^{0}}{L}} \, \, \cosh{ \frac{\xi^{0}}{L}}
=
\]
\[
=
0
\]
\[
g_{33} =
\frac{\partial x^{0}}{\partial \xi^{3}}
\,
\frac{\partial x^{0}}{\partial \xi^{3}}
-
\sum_{i=1}^{3} \,
\frac{\partial x^{i}}{\partial \xi^{3}}
\,
\frac{\partial x^{i}}{\partial \xi^{3}}
=
\]
\[
=
\left[\sinh{ \frac{\xi^{0}}{L}}\right]^2
-
\left[\cosh{ \frac{\xi^{0}}{L}}\right]^2
=
\]
\[
=
-1
\]
\[
g_{11} = g_{22} = -1
\]
Alle anderen Matrixelemente sind Null. Wir haben also:
|
Metrik in Rindler-Koordinaten in einer konstant beschleunigten Rakete: In beschleunigten Raketenkoordinaten (Rindler-Koordinaten) ist die Metrische Matrix eine Diagonalmatrix mit den Matrixelementen \[ g_{00} = \left( 1 + \frac{\xi^{3}}{L} \right)^2 \] \[ g_{11} = g_{22} = g_{33} -1 \] also \[ g = \begin{pmatrix} \left( 1 + \frac{\xi^{3}}{L} \right)^2 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \] d.h. die Metrische Matrix sieht fast aus wie in karthesischen Koordinaten (Minkowski-Metrik), nur dass die Zeitkomponente \(g_{00}\) statt der \(1\) den Wert \( \left( 1 + \frac{\xi^{3}}{L} \right)^2 \) trägt. In beschleunigten Raketenkoordinaten ist also die Metrik \( g(u,v) \) zweier Tangentialvektoren gegeben durch \[ g(u,v) = u^{0} \, v^{0} \, \left( 1 + \frac{\xi^{3}}{L} \right)^2 - \boldsymbol{u v} \] mit dem normalen euklidischen Skalarprodukt \( \boldsymbol{u v} \). In Tensorschreibweise kann man die Metrik auch so darstellen: \[ g = \left( 1 + \frac{\xi^{3}}{L} \right)^2 \, d\xi^{0} \otimes d\xi^{0} + \] \[ - \sum_{i=1}^{3} \, d\xi^{i} \otimes d\xi^{i} \] |
Wie können wir die metrische Matrix und damit die Koordinaten \(\xi^{\mu}\)
interpretieren?
Dazu schauen wir uns Koordinatenlinien mit konstantem \( \boldsymbol{\xi} = (\xi^{1}, \xi^{2}, \xi^{3}) \) und veränderlichem \(\xi^{0}\) an, d.h. \(\xi^{0}\) ist der Kurvenparameter dieser Kurven. Die Eigenzeit \(\tau'\) für einen Beobachter, der sich entlang dieser Kurve bewegt, war gegeben durch \[ c \, \frac{d\tau'}{d\xi^{0}} = \] \[ = \sqrt{g\left( \frac{\partial x}{\partial \xi^{0}}, \frac{\partial x}{\partial \xi^{0}} \right)} = \] \[ = \sqrt{g_{00}} = 1 + \frac{\xi^{3}}{L} \] Aus dem Matrixelement \(g_{00}\) können wir also ablesen, dass für die Koordinatenlinie der Hauptuhr \( \xi^{3} = 0 \) die Koordinate \( \xi^{0} \) gleich der Eigenzeit (mal \(c\)) der entsprechenden Bewegung ist.
Für andere \(\xi^{3}\)-Werte ist die Eigenzeit zumindest proportional zur Koordinate \(\xi^{0}\). In diesem Sinn kann man demnach die Koordinate \(\xi^{0}\) als Zeitkoordinate interpretieren: konstante \(\xi^{0}\)-Werte entsprechen gleichzeitigen Ereignissen. Allerdings ist \(g_{00}\) nicht gleich 1, so dass wir von krummlinigen Koordinaten sprechen. Zum Vergleich: bei ebenen Polarkoordinaten ist die metrische Matrix ebenfalls eine Diagonalmatrix, aber die Diagonal-Matrixelemente sind auch nicht alle gleich 1.
In jedem Raum-Zeit-Punkt kann man durch Multiplikation der \(\xi^{0}\)-Koordinate die Metrik auf Minkowski-Form bringen, ohne dass die räumlichen \( \boldsymbol{\xi} = (\xi^{1}, \xi^{2}, \xi^{3}) \) unter Beteiligung von \(\xi^{0}\) umgerechnet werden müssen (siehe den Stichpunkt nichtholonome Basisvektoren am Schluss des Kapitels). Daher repräsentieren diese drei Koordinaten direkt die räumlichen Koordinaten zum gegebenen Zeitpunkt, gesehen im momentanten Ruhe-Inertialsystem der Haupt-Raketenuhr. Da die metrische Matrix in den räumlichen Koordinaten diagonal gleich 1 ist, sind die drei Koordinaten euklidische Raumkoordinaten.
Das Matrixelement \(g_{00}\) ist das einzige Matrixelement, das von der üblichen Minkowskimetrik abweicht. Offenbar genügt es bereits, dass dieses eine Matrixelement ungleich 1 ist, um ein beschleunigtes Bezugssystem herbeizuführen – die Raumkoordinaten können euklidisch bleiben. Nach dem Äquivalenzprinzip manifestiert sich die zu der Beschleunigung gleichwertige Gravitationswirkung also hier in diesem Matrixelement. Im Grenzwert kleiner Geschwindigkeiten kann man daher aus diesem Matrixelement das klassische Gravitationspotential ablesen (die exakte Herleitung dazu findet man in praktisch jedem Text zur allgemeinen Relativitätstheorie).
Weiter unten werden wir noch einmal im Zusammenhang mit den Riemannschen Normalkoordinaten auf die Bedeutung der Metrik und die Interpretation der Koordinaten zurückkommen. Die Frage der Interpretation ist dabei gar nicht so einfach, denn eine einfache Interpretation haben die Koordinaten nur lokal, wenn dort die Minkowski-Metrik vorliegt (denn dann befindet man sich in einem lokalen momentanen Ruhe-Inertialsystem, also im freien Fall).
Kommen wir zu den Christoffelsymbolen:
Man kann mithilfe der metrischen Matrix \(g\) ausrechnen, dass die einzigen nicht-verschwindenden Christoffelsymbole die Folgenden sind: \[ \Gamma^{0}_{03} = \Gamma^{0}_{30} = \frac{1}{L + \xi^{3}} \] \[ \Gamma^{3}_{0 0} = \frac{L + \xi^{3}}{L^{2}} \]
Die kräftefreie Bewegungsgleichung \( (D_{u} u)^{\rho} = 0 \) in diesen Raketen-Koordinaten lautet nach kurzer Rechnung: \[ \frac{d^{2}\xi^{\rho}}{d\tau^{2}} + \sum_{\mu\nu} \, \frac{d\xi^{\mu}}{d\tau} \, \Gamma^{\rho}_{\nu\mu} \, \frac{d\xi^{\nu}}{d\tau} = 0 \] Achtung: \(\tau\) ist hier die Eigenzeit für die kräftefreie Bewegungskurve, muss also nicht proportional zu \(\xi^{0}\) sein! Setzen wir hier die obigen Christoffelsymbole ein, so erhalten wir: \[ \frac{d^{2}\xi^{0}}{d\tau^{2}} + \frac{2}{L + \xi^{3}} \, \frac{d\xi^{0}}{d\tau} \, \frac{d\xi^{3}}{d\tau} = 0 \] \[ \frac{d^{2}\xi^{3}}{d\tau^{2}} + \frac{L + \xi^{3}}{L^{2}} \, \left(\frac{d\xi^{0}}{d\tau}\right)^{2} = 0 \] \[ \frac{d^{2}\xi^{1}}{d\tau^{2}} = \frac{d^{2}\xi^{2}}{d\tau^{2}} = 0 \] Wenn wir beispielsweise im Ursprungspunkt der Rakete \( \xi^{i} = 0 \) mit \(i = 1, 2, 3 \) ein Objekt in der Rakete fallen lassen, so dass im Moment des Loslassens \( \frac{d\xi^{i}}{d\tau} = 0 \) ist, so gilt in diesem Moment nach der ersten Gleichung \[ \frac{d^{2}\xi^{0}}{d\tau^{2}} = 0 \] d.h. wir können für diesen Loslass-Moment \( \xi^{0} = c \tau \) setzen und erhalten für die zweite Gleichung \[ \frac{d^{2}\xi^{3}}{d\tau^{2}} + \frac{c^{2}}{L} = 0 \] und somit im Moment des Loslassens \[ \frac{d^{2}\xi^{3}}{d\tau^{2}} = - g \] Das hatten wir auch nicht anders erwartet, denn ein frei fallender Körper, den man im Ursprungspunkt der Rakete loslässt, sollte kurz nach dem Loslassen aus Sicht der Rakete mit \(g\) nach unten beschleunigen. Das beschleunigte Bezugssystem wirkt sich also auf frei fallende Körper tatsächlich genau wie die Gravitation aus! Verfolgen wir die Rechnung zurück, so stammt die Beschleunigung \(g\) vom Christoffelsymbol \( \Gamma^{3}_{00} \) das wiederum die Ableitung von \(g_{00}\) nach \(\xi^{3}\) enthält. In nichtrelativistischen Grenzfall enthält \(g_{00}\) das Gravitationspotential, und der Gradient dieses Potentials ergibt die Beschleunigung – genau das sehen wir hier! Man kann den nichtrelativistischen Grenzfall natürlich noch viel allgemeiner untersuchen. Da dies aber in fast allen Texten zur allgemeinen Relativitätstheorie ausführlich geschieht, wollen wir hier darauf verzichten.
Nach dem Einsteinschen Äquivalenzprinzip kann man in einem hinreichend kleinen Raumbereich nicht unterscheiden, ob ein Gravitationsfeld wirkt oder ob man sich einfach nur in einem beschleunigten Bezugssystem (einer Rakete) befindet. Oben hatten wir gesehen, dass bei einem beschleunigten Bezugssystem die metrische Matrix nicht identisch ist mit der Minkowski-Matrix. Daher sprachen wir auch von krummlinigen Koordinaten. Wir gehen deshalb davon aus, dass wir krummlinige Koordinaten mit einer entsprechenden metrischen Matrix brauchen, wenn wir ein Bezugssystem mit Gravitation beschreiben wollen, in dem frei fallende Körper beschleunigt erscheinen.
Wir wollen sogar beliebige krummlinige Koordinaten zulassen und die Naturgesetze in koordinaten-unabhängiger Form (gleichbedeutend mit tensorieller Form) formulieren, so dass wir problemlos zwischen allem möglichen Bezugssystemen hin- und herwechseln können. Dabei haben diese Koordinaten normalerweise nicht mehr eine direkte Bedeutung als Raum- oder Zeitkoordinate. Man könnte sich z.B. vorstellen, dass sich vier Uhren auf irgendwelchen Bahnen durch Raum und Zeit bewegen und dabei ständig ihre Uhrzeit per Radiosinal in die Welt hinausfunken. Bewegt sich nun ein Empfänger auf einer Bahn \( \gamma(\tau) \) durch den Weltraum (\( \tau\) ist dabei die Eigenzeit, die die Uhr des Empfängers anzeigt), so kann man die vier Uhrzeiten, die der Empfänger zur Eigenzeit \(\tau\) empfängt, als die vier Koordinaten des Punktes \( \gamma(\tau) \) definieren. Diese Idee ist keineswegs rein theoretisch: das Global Positioning System (GPS) arbeitet genau nach diesem Prinzip!

Wenn wir beliebige Koordinaten zulassen, so müssen wir etwas über die Christoffelsymbole bzw. die metrische Matrix in diesen Koordinaten aussagen, um z.B. die Bahn eines frei fallenden Objektes bestimmen zu können. Die Grundlage dafür liefert die folgende Umformulierung des Einsteinschen Äquivalenzprinzips:
Wenn wir also von der Beschreibung der Gravitation durch krummlinige Raum-Zeit-Koordinaten ausgehen, so muss es in jedem Punkt lokal möglich sein, neue Koordinaten so einzuführen, dass dort die Christoffelsymbole verschwinden und dass die metrische Matrix in diesem Punkt die Minkowski-Matrix aus der speziellen Relativitätstheorie ist. Mathematisch bedeutet das, dass auf der Raum-Zeit-Mannigfaltigkeit eine Metrik mit entsprechenden Vorzeichen der Eigenwerte existiert – dies ist eine koordinaten-unabhängige Eigenschaft der Metrik! Bei unserer Konvention muss es einen Eigenwert mit positivem Vorzeichen und drei Eigenwerte mit negativem Vorzeichen geben. Außerdem müssen die ersten Ableitungen der Metrik in \(p\) verschwinden, damit die Christoffelsymbole gleich Null sind, sodass lokal Schwerelosigkeit herrscht – man überlässt sich also im Freien Fall der Schwerkraft und spürt sie nicht mehr.
Man kann in der Differentialgeometrie zeigen, dass es generell möglich ist, Koordinaten so einzuführen, dass die metrische Matrix in einem beliebig vorgegebenem Punkt \(p\) eine Diagonalmatrix mit 1-en oder - 1-en in der Diagonalen ist (man nennt dies die kanonische Form der Matrix). Man bezeichnet diese Koordinaten als Riemannsche Normalkoordinaten zu einem Punkt \(p\).
In unserem Fall hat die metrische Matrix in diesen Koordinaten im Punkt \(p\) (und nur dort!) die Form der Minkowski-Matrix. Zusätzlich kann man erreichen, dass die Ableitungen der metrischen Matrixelemente nach den Riemannschen Normalkoordinaten (nennen wir sie \(\xi^{\mu}\) ) im Punkt \(p\) verschwinden: \[ \frac{dg_{\mu\nu}}{d\xi^{\sigma}}\bigg|_{p} = 0 \] so dass wie gefordert die Christoffelsymbole im Punkt \(p\) verschwinden – die Ableitungen der Chrisoffelsymbole dagegen verschwinden nicht unbedingt (siehe z.B. Sean M. Carroll: Lecture Notes on General Relativity, arXiv:gr-qc/9712019, Kapitel 2: Manifolds). Dies ist gemeint, wenn man davon spricht, ein lokales Inertialsystem (also ein frei fallendes Bezugssystem) zu verwenden. Es gibt mehrere Riemannsche Normalkoordinaten in einem Punkt, da eine Poincarétransformation die Minkowski-Matrix ja invariant lässt, wie wir aus der speziellen Relativitätstheorie wissen. Es gibt also in einem Punkt \(p\) mehrere dort lokal frei fallende Bezugssysteme, die sich durch eine Poincarétransformation ineinander umrechnen lassen. Sie entsprechen dem freien Fall durch das Ereignis \(p\) mit verschiedenen Geschwindigkeiten.
Bei den Rindler-Koordinaten der beschleunigten Rakete war es möglich, eine Transformation zurück in die karthesischen Koordinaten des äußeren Beobachters durchzuführen und so in jedem Punkt zugleich die metrische Matrix in ihre kanonische Form zu überführen. Das spiegelt wider, dass wir uns in der Raumzeit der speziellen Relativitätstheorie befinden, in der es keine Gravitation gibt.
Wenn wir dagegen die Raumzeit mit Gravitation betrachten, so können wir uns zwar in ein kleines frei fallendes Raumschiff setzen und so lokal in diesem Raumschiff Schwerelosigkeit erreichen (das Raumschiff könnte z.B. einen Planeten umkreisen). Wir sehen jedoch, dass weiter weg sich andere frei fallende Objekte (z.B. Monde oder andere Planeten) relativ zu unserem Raumschiff in einer beschleunigten Bewegung befinden. Lokal in unserem Raumschiff wird daher die Metrik sich auf kanonische Form bringen lassen, so dass frei fallende Objekte im Raumschiff nicht beschleunigt werden. Weiter weg weicht die Metrik jedoch im Allgemeinen immer mehr von der kanonischen Form ab und verwandelt sich in die Metrik beschleunigter Bezugssysteme, in der frei fallende Objekte relativ zum Raumschiff beschleunigen. Es wird daher nicht mehr möglich sein, überall in der Raumzeit zugleich karthesische Minkowski-Koordinaten einzuführen!
In der Kyoto-Vorlesung (Dezember 1922) erinnert er sich Albert Einstein:
Sind alle beschleunigten Systeme äquivalent, dann kann nicht in ihnen allen die euklidische Geometrie gelten. Die Geometrie aufzugeben und die physikalischen Gesetze beizubehalten, entspricht der Beschreibung von Gedanken ohne Worte. Wir müssen nach Worten suchen, ehe wir Gedanken darstellen können. Wonach müssen wir nun an dieser Stelle suchen? Dieses Problem blieb für mich bis 1912 unlösbar, als ich plötzlich erkannte, dass der Schlüssel zur Lösung des Mysteriums in der Gaußschen Flächentheorie zu finden war. Wie ich erkannte, haben die Gaußschen Flächenkoordinaten eine besondere Bedeutung. Allerdings wusste ich damals noch nicht, dass Riemann die Grundlage der Theorie in noch gründlicherer Weise untersucht hatte.
Einstein erkannte also den obigen Zusammenhang und suchte nach einer passenden mathematischen Sprache. Er fand diese im Formalismus der Riemannschen Geometrie, auf die wir im Webbuch Gekrümmte Räume (über die Grundlagen der Differentialgeometrie) detailliert eingehen und die wir auch bei der beschleunigten Rakete oben bereits angewendet haben.
Im Kapitel Krümmung haben wir den Begriff der Krümmung kennengelernt. Dabei sind wir auf einen sehr interessanten Zusammenhang gestoßen:
Dieser Zusammenhang gibt uns ein Kriterium an die Hand, das uns sagt, wann wir im gesamten Raum ein frei fallendes Inertialsystem einführen können, und wann nicht. Im ersten Fall haben wir einen Raumzeit ohne Gravitation, im zweiten Fall dagegen eine Raumzeit mit Gravitation, so wie sie beispielsweise ein Planet erzeugt. Wir können daher vermuten:
Wie die Krümmung der Raumzeit durch die darin vorhandene Materieverteilung festgelegt wird, ist in den Einsteinschen Feldgleichungen beschrieben, die wir uns im nächsten Kapitel genauer ansehen werden.
Man könnte natürlich fragen: was ist denn mit einem Gravitationsfeld, das keine Krümmung besitzt, weil es z.B. überall gleich ist (oder zumindest eine Metrik wie in der beschleunigten Rakete aufweist)? Ein solches Gravitationsfeld kann nicht durch Materie erzeugt werden, denn nach den Einsteinschen Feldgleichungen beeinflusst eine Materieverteilung nur die Krümmung, nicht aber direkt die Metrik (nur indirekt über die Krümmung). Daher ist ein solches Gravitationsfeld unphysikalisch.
Außerdem können wir bei verschwindender Krümmung überall zugleich karthesische Minkowski-Koordinaten einführen, d.h. es gibt ein globales frei fallendes Bezugssystem, in dem man überall keine Gravitation mehr spürt. Daher wäre ein solches Gravitationsfeld gleichwertig zu gar keiner Gravitation.
Man sieht hier sehr schön, dass Gravitation nicht mehr als Kraftfeld beschrieben wird. Gravitation bedeutet vielmehr die Unmöglichkeit, ein globales Bezugssystem zu finden, in dem sich alle frei fallenden Objekte unbeschleunigt bewegen. Bei Gravitation gibt es kein globales Inertialsystem mehr!
Nur so kann man vorgehen, wenn man das Einsteinsche Äquivalenzprinzip voraussetzt, denn dann kann man lokal Gravitationswirkung und Beschleunigung eines Bezugssystems nicht mehr unterscheiden – es gibt schließlich kein Referenzobjekt, das nicht der Gravitation unterliegt. Daher kann man auch keine durch die Gravitation erzeugte Beschleunigung mehr definieren, denn sie unterscheidet sich nicht von einer normalen Beschleunigung. Ein frei fallendes Bezugssystem ist lokal ununterscheidbar von einem unbeschleunigten Bezugssystem – daher fühlen sich die Astronauten in einem antriebslosen, um die Erde kreisenden Raumschiff auch völlig schwerelos. Gravitation bewirkt, dass man nicht überall zugleich in ein globales nicht-beschleunigtes Bezugssystem wechseln kann. In diesem Sinne ist der Gravitationsbegriff in der allgemeinen Relativitätstheorie ein anderer als in der Newtonschen Physik (daher gerät man auch in gewisse Schwierigkeiten, wenn man zugleich beide Gravitationsbegriffe verwendet).
Man zahlt einen Preis für die elegante Beschreibung der Gravitation durch die gekrümmte Raumzeit: Begriffe, die man in der speziellen Relativitätstheorie noch definieren konnte, sind in der allgemeinen Relativitätstheorie nicht mehr so einfach definierbar, da sie ein globales Inertialsystem voraussetzen. Ein Beispiel sind Geschwindigkeiten, die in unserem Formalismus durch Tangentialvektoren dargestellt werden. Man kann die Geschwindigkeit zweier weit voneinander entfernter Objekte bei vorhandener Gravitation nicht direkt miteinander vergleichen, denn zum Vergleich benötigt man wieder den Paralleltransport des einen Vektors hin zum anderen Vektor, und dieser Paralleltransport ist wegabhängig. Daher kann man nicht so einfach angeben, wie schnell sich das eine Objekt relativ zum anderen Objekt bewegt.
Ein anderes Beispiel ist die Interpretation der Raum-Zeit-Koordinaten. Nur dort, wo die metrische Matrix in diesen Koordinaten die Minkowski-Matrix ist, kann man diese Koordinaten direkt als getrennte Raum- und Zeitkoordinaten interpretieren. Da man aber bei Gravitation nicht überall zugleich ein solches Koordinatensystem einführen kann, ist diese Interpretation i.a. nur lokal möglich. Schauen wir uns dazu einige Details an (eine ausführliche Darstellung dazu findet man z.B. in Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie, Kapitel X Teilchen im Gravitationsfeld, §84 Entfernungen und Zeitintervalle ).
zeitartige Koordinaten:
Oben hatten wir bereits den Zusammenhang zwischen einer zeitartigen Koordinate \(x^{0}\) und der Eigenzeit \(\tau\) für eine Bewegung entlang der \(x^{0}\)-Koordinatenline kennengelernt (d.h. \(\tau\) ist hier die Zeit, die eine Uhr anzeigt, die sich bei konstanten räumlichen Koordinaten \(x^{i}\) befindet; die Raumzeit-Koordinaten müssen nicht karthesisch sein, aber es muss möglich sein, dass physikalische Objekte sich bei diesen konstanten räumlichen Koordinaten \(x^{i}\) aufhalten; ein Beispiel wären unsere Raketenkoordinaten \(\xi^\mu\), solange die Grenzentfernung \(L\) nicht überschritten wird). Leiten wir diesen Zusammenhang noch einmal kurz her:
Die Eigenzeit \(\tau\) war dadurch definiert, dass für den zugehörigen Tangentialvektor \(u\) entlang einer durch \(\tau\) parametrisierten Kurve die Normierungsbedingung \[ g(u,u) = c^{2} \] gilt. In allgemeinen \(x^{\mu}\)-Koordinaten bedeutet das: \[ g(u,u) = \] \[ = \sum_{\mu\nu} \, \frac{dx^{\mu}}{d\tau} \, \frac{dx^{\nu}}{d\tau} \, g_{\mu\nu} = c^{2} \] Für die Bewegung entlang der \(x^{0}\)-Koordinatenline ist für die räumlichen Koordinaten \[ \frac{dx^{i}}{d\tau} = 0 \] so dass die obige Gleichung sich zu \[ \left( \frac{dx^{0}}{d\tau} \right)^{2} \cdot g_{00} = c^{2} \] vereinfacht. Wir sehen hier, dass \( g_{00} \gt 0 \) sein muss, damit sich die \(x^{0}\)-Koordinate überhaupt zur Parametrisierung einer zeitartigen Bahnkurve (d.h. \( g(u,u) \gt 0 \)) eignet. Die Zusatzforderung \( \frac{dx^{0}}{d\tau} \gt 0 \) ermöglicht das Wurzelziehen mit dem Ergebnis
| Zusammenhang zwischen der Eigenzeit \(\tau\) und der \(x^{0}\)-Koordinate für eine Weltlinie mit konstanten räumliche Koordinaten \(x^i\) (\(x^{0}\)-Koordinatenlinie): \[ c \, \frac{d\tau}{dx^{0}} = \sqrt{ g_{00} } \] |
(diese Formel hatten wir oben für die Raketenkoordinaten \(\xi^{\mu}\) bereits angegeben).
Wir sehen also: nur wenn in den gewählten Koordinaten \( g_{00} = 1 \) gilt, ist die
zeitartige Koordinate \(x^{0}\) auch die Zeit, die am Ort fester räumlicher Koordinaten
\(x^{i}\) vergeht. Im Allgemeinen jedoch laufen Uhren an verschiedenen Raumpunkten
unterschiedlich schnell, d.h. sie bleiben nicht synchron. Das kennen wir bereits von der beschleunigten Rakete.
räumliche Abstände:
Wie sieht es mit dem Begriff des räumlichen Abstands zweier gleichzeitiger Ereignise aus? Schon in der speziellen Relativitätstheorie hängt dieser Begriff vom Bezugssystem ab. In der allgemeinen Relativitätstheorie kann man versuchen, über lokale Betrachtungen die Begriffe der speziellen Relativitätstheorie in die allgemeine Relativitätstheorie herüberzuretten. Schauen wir uns das genauer an:
Für die Definition des räumlichen Abstands müssen wir in einem Bezugssystem einen Lichtblitz aussenden, der eine winzige Strecke läuft und dann zum Ausgangspunkt zurückgespiegelt wird. Das Spiegelungsereignis wollen wir in unserem Bezugssystem mit den festen Koordinaten \[ x^{\mu} \] bezeichnen. Das Ereignis Lichtblitz erzeugen soll mit den Koordinaten \[ x^{\mu} + dx_{1}^{\mu} \] bezeichnet werden, das Ereignis Lichtblitz wieder empfangen soll entsprechend mit den Koordinaten \[ x^{\mu} + dx_{2}^{\mu} \] bezeichnet sein. Die Schreibweise \(dx_{1}^{\mu}\) und \(dx_{2}^{\mu}\) soll andeuten, dass es sich um sehr eng beeieinanderliegende Ereignisse handelt, so dass wir näherungsweise davon ausgehen können, dass die Begriffe der speziellen Relativitätstheorie anwendbar sind – die Koordinaten müssen allerdings nicht unbedingt karthesische Minkowskikoordinaten sein.
Der Lichtblitz soll nun an denselben räumlichen Koordinaten empfangen werden, an denen er auch ausgesendet wurde, so wie wir das von oben aus der speziellen Relativitätstheorie her kennen. Wir setzen also \[ dx_{1}^{i} = dx_{2}^{i} =: dx^{i} \] für i = 1, 2, 3. An die winzigen Zeitintervalle \( dx_1^0 \) uns \( dx_2^0 \) stellen wir dagegen keine Bedingung. Die folgende Grafik stellt die Weltlinien des Lichtblitzes (rot), des im Bezugssystem ruhenden Sende- und Empfangsgerätes sowie des im Bezugssystem ruhenden Spiegels (blau) dar:
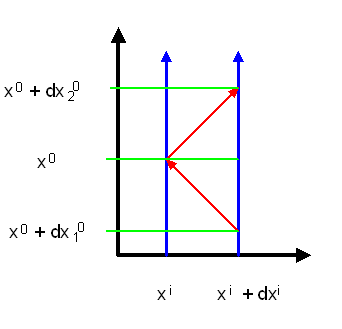
Da die Ereignisse über einen Lichtblitz miteinander verbunden sind, gilt \[ \sum_{\mu\nu} \, g_{\mu\nu} \, dx_k^{\mu} \, dx_k^{\nu} = 0 \] (mit \(k\) = 1 und 2; die Ereignisse sollen so nahe benachbart sein, dass wir die metrischen Matrixelemente in erster Näherung als konstant betrachten können).
Getrennt nach räumlichen Koordinaten \(x^{i}\) und zeitlicher Koordinate \(x^{0}\) ergibt das (unter Verwendung der Symmetrie der metrischen Matrix sowie \( dx_{1}^{i} = dx_{2}^{i} =: dx^{i} \)): \[ \sum_{ij} \, g_{ij} \, dx^{i} \, dx^{j} + \] \[ + 2 \, \sum_{i} \, g_{0i} \, dx_k^{0} \, dx^{i} + \] \[ + g_{00} \, dx_k^{0} \, dx_k^{0} = 0 \] Das ist eine quadratische Gleichung für \( dx_{k}^{0} \) mit den beiden Lösungen \[ dx_{1/2}^{0} = - \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \pm \] \[ \pm \sqrt{ \left( \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \right)^{2} - \sum_{ij} \, \frac{g_{ij}}{g_{00}} \, dx^{i} \, dx^{j} } \] Die beiden Lösungen entsprechen den beiden Zeitabschnitten für Hin- und Rückweg des Lichtblitzes. Das sieht man beispielsweise, wenn man Riemannsche Normalkoordinaten verwendet, so dass die metrische Matrix im Punkt \(x^{\mu}\) gleich der Minkowski-Matrix ist. In diesem Fall ist nämlich \[ dx_{1/2}^{0} = \pm \sqrt{ - \sum_{i} \, (-1) dx^{i} dx^{i} } = \pm |\boldsymbol{dx}| \] so wie man das auch erwartet. Hat man dagegen ein anderes Bezugssystem, in dem die Matrixelemente \( g_{0i} \), die räumliche und zeitliche Koordinaten mischen, nicht verschwinden, so entsprechen Hin- und Rückweg nicht unbedingt gleich großen Intervallen in der Koordinate \(x^{0}\). Das deutet bereits an, dass die Koordinate \(x^{0}\) in einem solchen Bezugssystem nur eingeschränkt als Zeitkoordinate interpretierbar ist.
Schauen wir uns die Differenz der Koordinaten zwischen empfangendem und sendendem Ereignis an: \[ (x^{\mu} + dx_{2}^{\mu}) - (x^{\mu} + dx_{1}^{\mu}) \] Wegen \[ dx_{1}^{i} = dx_{2}^{i} =: dx^{i} \] ist diese Differenz für die räumlichen Koordinaten gleich Null – so war das Ganze ja auch konstruiert, denn der Lichtblitz soll ja in unserem Bezugssystem an derselben Stelle gesendet und empfangen werden. Für die zeitliche Koordinate ergibt sich die Differenz \[ dx_{2}^{0} - dx_{1}^{0} = \] \[ = 2 \sqrt{ \left( \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \right)^{2} - \sum_{ij} \, \frac{g_{ij}}{g_{00}} \, dx^{i} \, dx^{j} } \] Das ist allerdings noch nicht die Zeitspanne \(d\tau\), die am Sende-Ort mit festen räumlichen Koordinaten zwischen Senden und Empfangen des Lichtblitzes abläuft. Von oben wissen wir, dass für diese Zeit \[ c \, \frac{d\tau}{dx^{0}} = \sqrt{ g_{00} } \] gilt, oder nach \(d\tau\) freigestellt: \[ d\tau = \sqrt{ g_{00} } \, dx^{0}/c \] Die Zeit zwischen Senden und Empfangen des Lichtblitzes ist demnach gegeben durch \[ d\tau = \sqrt{ g_{00} } \, (dx_{2}^{0} -dx_{1}^{0}) / c \] In dieser Zeit läuft der Lichtstrahl zum Spiegelungspunkt und wieder zurück. Daher definieren wir den räumlichen Abstand dl zum Spiegelungspunkt als c mal die halbe Laufzeit hin und zurück: \[ dl = \frac{c}{2} \, d\tau = \] \[ = \frac{c}{2} \, \sqrt{ g_{00} } \, (dx_{2}^{0} - dx_{1}^{0}) / c = \] \[ = \sqrt{ g_{00} } \, \sqrt{ \left( \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \right)^{2} - \sum_{ij} \, \frac{g_{ij}}{g_{00}} \, dx^{i} \, dx^{j} } = \] \[ = \sqrt{ \left( \sum_{i} \, g_{0i} \, dx^{i} \right)^{2} \frac{1}{g_{00}} - \sum_{ij} \, g_{ij} \, dx^{i} \, dx^{j} } = \] \[ = \sqrt{ \sum_{ij} \, \left( \frac{g_{0i} \, g_{0j}}{g_{00}} - g_{ij} \right) \, dx^{i} dx^{j} } = \] \[ =: \sqrt{ \sum_{ij} \, \gamma_{ij} \, dx^{i} \, dx^{j} } \] Halten wir fest:
| Definition des räumlichen Abstands zweier eng benachbarter gleichzeitiger Ereignisse in einem Bezugssystem: \[ dl = \sqrt{ \sum_{ij} \, \gamma_{ij} \, dx^{i} \, dx^{j} } \] Dabei bezeichnen wir \[ \gamma_{ij} := \frac{g_{0i} \, g_{0j}}{g_{00}} - g_{ij} \] als dreidimensionalen räumlichen metrischen Tensor. Wenn die raum-zeitlichen metrischen Matrixelemente \( g_{0i} \) im betrachteten Bezugssystem verschwinden, so wird der dreidimensionale räumliche metrische Tensor wieder allein durch die räumlichen metrischen Matrixelemente bestimmt: \( \gamma_{ij} = - g_{ij} \). |
Kann man nun über den infinitesimalen Abstand hinausgehen und den
räumlichen Abstand zweier weiter voneinander entfernter gleichzeitiger
Ereignisse definieren?
Dazu müsste man \(dl\) entlang einer raumartigen Kurve zwischen den beiden
Ereignissen aufintegrieren. Nun ist aber die Metrik \(g_{\mu\nu}\)
im Allgemeinen abhängig von \(x^{0}\). Das Integral über \(dl\) ist daher
normalerweise abhängig von der Kurve, entlang der integriert wird, so dass
der Abstandsbegriff wegabhäbgig wäre.
Nur wenn die Metrik \(g_{\mu\nu}\) nicht von \(x^{0}\) abhängt, kann man in einem entsprechenden Bezugssystem auch über das Infinitesimale hinaus einen räumlichen Abstandsbegriff definieren.
Wenn man ein Bezugssystem finden kann, in dem die metrische Matrix \(g_{\mu\nu}\) unabhängig von \(x^{0}\) ist, so nennt man das Gravitationsfeld zeitunabhängig und man bezeichnet \(x^{0}\) auch als Weltzeit, wobei diese Weltzeit nicht identisch ist mit der Eigenzeit, die auf einer Uhr bei festen räumlichen Koordinaten abläuft (siehe z.B. Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie, §88 Das zeitunabhängige Gravitationsfeld ). Ein zeitunabhängiges Gravitationsfeld kann aber nur entstehen, wenn nur ein einziger gravitationserzeugender Körper vorhanden ist.
Gleichzeitigkeit:
Man kann den obigen Gedankengang auch dazu verwenden, um den Begriff der Gleichzeitigkeit für eng beieinanderliegende Ereignisse zu definieren. So kann man am Sende- und Empfangsort diejenige Uhrzeit als gleichzeitig zum Zeitpunkt des Spiegelungsereignisses ansehen, die genau zwischen Sende- und Empfangszeit liegt. Das Spiegelungsereignis hatte die Raum-Zeit-Koordinaten \(x^{\mu}\). Am Sende- und Empfangsort mit räumlichen Koordinaten \( x^{i} + dx^{i} \) ist die Zeitkoordinate genau zwischen Sende- und Empfangszeit gegeben durch \[ x^{0} + \frac{1}{2} (dx_{1}^{0} + dx_{2}^{0}) \] Wir hatten oben \[ dx_{1/2}^{0} = - \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \pm \sqrt{...} \] Also ist \[ x^{0} + \frac{1}{2} (dx_{1}^{0} + dx_{2}^{0}) = \] \[ = x^{0} - \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \] Das bedeutet:
|
Gleichzeitigkeit infinitesimal benachbarter Ereignisse in einem Bezugssystem: Die infinitesimal benachbarten Ereignisse \[ \begin{pmatrix} x^0 \\ \boldsymbol{x} \end{pmatrix} \] (Spiegelungsereignis) und \[ \begin{pmatrix} x^0 - \sum_{i} \, \frac{g_{0i}}{g_{00}} \, dx^{i} \\ \boldsymbol{x} + d\boldsymbol{x} \end{pmatrix} \] (am Sende- und Empfangsort genau zwischen Sende- und Empfangszeitpunkt) betrachten wir als gleichzeitig. |
Man kann auf diese Weise nun entlang einer raumartigen Linie Uhren synchronisieren. Aber: wenn man eine geschlossene Kurve betrachtet und an den Ausgangspunkt zurückkehrt, so kann man so nicht alle Uhren synchronisieren: irgendwo gibt es einen Zeitsprung. Man kann in einem Bezugssystem nur dann in einem Raumbereich an allen Punkten die Uhren synchronisieren, wenn die Matrixelemente \( g_{0i} \) dort überall gleich Null sind. In diesem Fall zeigt die Formel oben nämlich, dass gleiche \(x^{0}\)-Koordinaten auch gleichzeitige Ereignisse kennzeichnen. Wie schon in der speziellen Relativitätstheorie hängen alle diese Aussagen natürlich vom jeweiligen Bezugssystem (Koordinatensystem) ab. Daher sind diese Aussagen Eigenschaften von Bezugssystemen, nicht Eigenschaften der Raumzeit. Es gilt sogar:
| Man kann immer (sogar auf unendlich verschiedene Weisen) Bezugssysteme und damit Koordinaten finden, in denen die Matrixelemente \( g_{0i} \) tatsächlich gleich Null sind. In solchen Fällen kann man die \(x^{0}\)-Koordinate zumindest im Sinne der Gleichzeitigkeit als Zeitkoordinate ansehen (wenn auch die Eigenzeit lokal positionierter Uhren schneller oder langsamer laufen kann, abhängig von \(g_{00}\)). Gleichzeitige Ereignisse haben dieselbe \(x^{0}\)-Koordinate. |
Wenn dann zusätzlich noch die metrischen Matrixelemente unabhängig von \(x^{0}\) sind (was nicht immer geht), dann kann man auch den räumlichen Abstand gleichzeitiger Ereignisse wie oben angegeben definieren. Man spricht von einem statischen Gravitationsfeld – das ist also ein zeitunabhängiges Gravitationsfeld, in dem zusätzlich \( g_{0i} = 0 \) gilt. Ein solches Gravitationsfeld entsteht dann, wenn nur ein einziger gravitationserzeugender Körper vorhanden ist, der zusätzlich noch im betrachteten Bezugssystem ruht (auch nicht rotiert). Ein rotierender achsensymmetrischer Körper dagegen erzeugt ein zeitunabhängiges Gravitatiosnfeld, in dem die \( g_{0i} \) i.a. nicht Null sind – man spricht von einem stationären Gravitationsfeld. In einem solchen zeitunabhängigen Gravitationsfeld kann man im gesamten Raum Uhren nicht überall zugleich synchronisieren!
Noch eine Randbemerkung: Interessant ist in diesem Zusammenhang der sogenannte Vielbein-Formalismus, bei dem man vier Basis-Tangentialvektorfelder (auch co-moving tetraed oder mitbewegtes Vielbein genannt) so wählt, dass die Metrik zwischen ihnen in jedem Punkt der Minkowski-Metrik entspricht, und dann durchgehend in dieser Basis rechnet. Man rechnet also an jedem Punkt zugleich in einem lokal definierten frei fallenden Inertialsystem. Die entsprechenden Kurvenparameter (die Tangentialvektoren sind ja in jedem Punkt über Kurven definiert) in einem jeden Punkt kann man daher genau dort als Orts- und Zeitangaben interpretieren.
Allerdings sind diese Basisvektoren nicht holonom, d.h. die Lie-Klammer zwischen ihnen ist nicht unbedingt gleich Null. Aus Kapitel Torsion wissen wir, dass sich dann infinitesimale Parallelogramme i.a. nicht schließen. Daher lassen sich die Kurven nicht zu einem globalen Koordinatennetz zusammensetzen.
Ein Beispiel:
Auf der zweidimensionalen Kugeloberfläche bilden die Kugelkoordinatenwinkel
\(\theta\) (Breitengrade) und \(\varphi\) (Längengrade) ein krummliniges Koordinatensystem.
Die Metrik in diesen Koordinaten lautet
\[
g = d\theta \otimes d\theta
+ (\sin{\theta})^{2} \, d\varphi \otimes d\varphi
\]
Anschaulich bedeutet das, dass man entlang der \(\varphi\)-Linien nach Osten
bei anwachsendem \(\varphi\) umso langsamer ist, je näher man sich
am Pol befindet.
Man kann nun aber den Faktor \( \sin{\theta} \) in nicht-holonome Basisvektoren
hineindefinieren:
\[
\omega^{\varphi} := (\sin{\theta}) \, d\varphi
\]
für den Cotangential-Basisvektor und entsprechend
\[
X_{\varphi} := \frac{1}{\sin{\theta}} \, \frac{\partial}{\partial \varphi}
\]
für den Tangential-Basisvektor, so dass
\[
\omega^{\varphi} \, X_{\varphi} = 1
\]
ist und wir
für die Metrik
\[
g = d\theta \otimes d\theta
+ \omega^{\varphi} \otimes \omega^{\varphi}
\]
haben.
Anschaulich bedeutet das, dass wir nun auch in \(\varphi-Richtung\) (nach Osten) immer gleich schnell laufen.
Den entsprechenden Kurvenparameter nennen wir
\[
\lambda := (\sin{\theta}) \, \varphi
\]
Leider können wir aber \( \lambda \) und \( \theta \) nicht als Koordinaten auf der Kugeloberfläche
verwenden, denn wenn wir in \(\theta\)-Richtung nach Süden laufen, so bleibt dabei \(\lambda\)
i.a. nicht konstant. Von einer Koordinatenlinie verlangen wir aber, dass sich entlang dieser Linie
nur die eine zugehörige Koordinate ändert.
Analog kann man auch bei unseren Raketenkoordinaten oben vorgehen und \[ \omega^{0} := \left(1 + \frac{\xi^{3}}{L} \right) \, d\xi^{0} \] sowie \[ X_{0} := \frac{1}{1 + \frac{\xi^{3}}{L}} \, \frac{\partial}{\partial \xi^{0}} \] definieren. Der entsprechende Kurvenparameter ist dann die lokal vergehende Eigenzeit \(\tau'\). Aber: \(\tau'\) und die räumlichen \(\xi^{i}\) bilden kein Koordinatensystem, denn in \(\xi^{3}\)-Richtung ändert sich \(\tau'\). In der Praxis erweist sich das Rechnen in nicht-holonomer Basis mit einfacher konstanter Minkowskimetrik oft als günstig. Man muss allerdings erst einmal beispielsweise die Krümmung auf diese Basis umrechnen. Den entsprechenden Formalismus bezeichnet man auch als Cartan-Formalismus.
Wie formuliert man nun Naturgesetze, beispielsweise die Bewegungsgleichung von frei fallenden Körpern, in der Raumzeit mit Gravitation? Da nach dem Äquivalenzprinzip alle Naturgesetze von der Gravitation betroffen sind, müssen wir diese in dem obigen Rahmen so formulieren, dass das Äquivalenzprinzip gilt: Die physikalischen Gesetze müssen in allen im freien Fall befindlichen Systemen, sofern diese hinreichend klein sind, in der gleichen Form gelten.
Nehmen, wir an, wir kennen ein Naturgesetz aus der speziellen Relativitätstheorie. Am Einfachsten ist es, wenn wir zunächst dieses Gesetz in eine koordinatenfreie (oder tensorieller) Form bringen, so dass es auch in krummlinigen (z.B. beschleunigten) Koordinaten gilt. Dazu ersetzen wir beispielsweise Richtungsableitungen durch kovariante Ableitungen in die entsprechende Tangentialvektorrichtung. Das haben wir oben für die Bewegungsgleichung eines frei fallenden Massenpunktes bereits getan. In dieser Form können wir das Gesetz sofort in die allgemeine Relativitätstheorie übertragen. Im Grenzfall verschwindender Krümmung ergibt sich so automatisch wieder das Gesetz aus der speziellen Relativitätstheorie.
Wenn man in der speziellen Relativitätstheorie ein Naturgesetz in koordinatenunabhängiger Form formuliert hat und dieses in die allgemeine Relativitätstheorie überträgt, so kann man allerdings anschließend noch Terme hinzufügen, die den Riemannschen Krümmungstensor enthalten (dieser enthält erste Ableitungen der Christoffelsymbole und wegen der Verträglichkeitsbedingung dann zweite Ableitungen der metrischen Matrix). Im Grenzfall verschwindender Gravitation oder bei so kleinen Raumbereichen, dass die Krümmung keine Rolle spielt und der Raum flach erscheint, erhält man so wieder das ursprüngliche Gesetz aus der speziellen Relativitätstheorie. Das Äquivalenzprinzip würde in dieser Interpretation also lediglich fordern, dass im Grenzfall verschwindender Krümmung die allgemeine in die spezielle Relativitätstheorie übergeht. Man kann das Äquivalenzprinzip auch schärfer interpretieren, so dass zusätzliche Krümmungsterme nicht so einfach möglich sind, da sie evtl. auch in beliebig kleinen frei fallenden Bezugssystemen messbar bleiben können. Reines Nachdenken löst diese Frage nicht – man muss nachsehen, wie sich die Natur entschieden hat.
Als erstes Beispiel betrachten wir den freien Fall eines Massenpunktes: Die entsprechende koordinatenfreie Bewegungsgleichung in der speziellen Relativitätstheorie hatten wir oben bereits kennengelernt. Es ist die Geodätengleichung \[ D_{u(\gamma(\tau))} u = 0 \] Dabei ist \( u(\gamma(\tau)) \) der Tangentialvektor zur Kurve \( \gamma \) im Punkt \( \gamma(\tau) \). Für die Bewegung eines Teilchens mit Masse kann man über die Normierung \( g(u,u) = c^{2} \) dem Kurvenparameter die Bedeutung der Eigenzeit geben.
Die Geodätengleichung gilt aber auch für masselose Teilchen, z.B. Licht. In diesem Fall ist \( g(u,u) = 0 \) und \( \tau \) ist ein sogenannter affiner Kurvenparameter (d.h. die Kurve wird mit gleichmäßiger Geschwindigkeit durchlaufen, so dass auf der rechten Seite der Geodätengleichung auch die Null steht – also keine Beschleunigung in Kurvenrichtung).
Ob sich diese Gleichung durch Hinzufügen von Krümmungstermen noch irgendwie verändern lässt, wollen hier etwas weiter unten noch untersuchen. Zunächst wollen wir einfach annehmen, dass dies bereits die richtige Gleichung ist (es ist zumindest schon mal die einfachste Gleichung): Ein Massenpunkt, der sich im freien Fall befindet, bewegt sich im Gravitationsfeld auf einer Geodäten. Letztlich muss das Experiment darüber entscheiden, ob dieses Gesetz on der Natur so gilt.
Man kann die Geodäte auch wie weiter oben wieder über die maximale Eigenzeit charakterisieren: Ein Körper bewegt sich zwischen zwei Ereignissen im freien Fall so, dass die in ihm ablaufende Eigenzeit der Uhr maximal wird. Wertet man diese Aussage mit Hilfe der Variationsrechnung aus, so erhält man für die Bewegungskurve gerade die obige Geodätengleichung. Da die Eigenzeit an unterschiedlichen Orten im Gravitationsfeld unterschiedlich schnell abläuft, kann man sich leicht vorstellen, dass eine Gerade nicht unbedingt die Kurve mit der längsten Eigenzeit sein muss. Und: da die Eigenzeit mit der \(x^{0}\)-Koordinate des jeweiligen Bezugssystems über die Beziehung \[ c \frac{d\tau}{dx^{0}} = \sqrt{ g_{00} } \] zusammenhängt, sehen wir, dass das metrische Matrixelement \(g_{00}\) ganz entscheidend für die Bahnkurve ist!
Ein anderes Beispiel ist das elektromagnetische Feld. In Hodge-Sternoperator, Volumenform, Gradient, Divergenz, Rotation haben wir eine koordinatenfreie Formulierung dafür kennengelernt: \[ dF = 0 \] \[ d {\star}F = j \] Dabei sind \(F, {\star}F, j \) 2-Formen, die das elektromagnetische Feld sowie den Ladungsfluss darstellen. Diese Formulierung macht sofort auch in der Raumzeit mit Gravitation Sinn.
Da zusätzliche Krümmungsterme durch das Äquivalenzprinzip nicht unbedingt festgelegt werden, steht man beispielsweise bei zweiten Ableitungen vor einem Sortierungsproblem, wenn man eine entsprechende Gleichung aus der speziellen in die allgemeine Relativitätstheorie übertragen will.
Nehmen wir an, die Gleichung in der speziellen Relativitätstheorie enthält den Term \[ \sum_{\mu\nu} \, u^{\mu} \frac{\partial}{\partial x^{\mu}} \, \frac{\partial}{\partial x^{\nu}} v^{\nu} \] Hier lassen sich die beiden Ableitungen noch problemlos vertauschen. Ersetzen wir die Ableitungen nun durch kovariante Ableitungen \[ D_{\mu} := D_{\frac{\partial}{\partial x^{\mu}}} \] so vertauschen diese Ableitungen nur noch in dem Fall, dass die Krümmung gleich Null ist, denn allgemein gilt (siehe Krümmung): \[ D_{\mu} D_{\nu} - D_{\nu} D_{\mu} = R\left(\frac{\partial}{\partial x^{\mu}}, \frac{\partial}{\partial x^{\nu}}\right) \] Hier tritt also durch die Sortierungsfrage automatisch die Frage nach einem zusätzlichen Krümmungsterm auf. Die Situation ist ganz ähnlich zu dem Anordnungsproblem, das man beim Übergang von der klassischen Hamiltonschen Mechanik zur Quantenmechanik hat. Die klassischen Größen Ort \(x\) und Impuls \(p\) sind in Produkten frei vertauschbar, aber die entsprechend hintereinandergeschalteten quantenmechanischen Operatoren sind nicht mehr frei vertauschbar. Auch hier können die klassischen Gleichungen nicht festlegen, ob in den entsprechenden quantenmechanischen Ausdrücken Zusatzterme mit Kommutatoren von \(p\) und \(x\) auftreten, denn genau diese Terme verschwinden wieder beim Grenzübergang zur klassischen Mechanik.
In diesem Sinne entsprechen Krümmungsterme in der allgemeinen Relativitätstheorie den Kommutatoren der Quantenmechanik: beide werden durch den entsprechenden Grenzfall (spezielle Relativitätstheorie bzw. klassische Mechanik) nicht festgelegt, da sie in diesem Grenzfall verschwinden.
Da wir sie auch im nächsten Kapitel brauchen, schauen wir uns einige Kandidaten für mögliche Zusatzterme an:
Zunächst haben wir den Riemannschen Krümmungstensor \( R^{\mu}_{\;\nu\rho\sigma} \) oder koordinatenfrei die Abbildung \( R(u,v) \) (so dass der Ausdruck \( R(u,v) \, w \) ein Tangentialvektor ist; Details siehe im Kapitel Krümmung ).
Man kann nun den Ricci-Tensor definieren. Seine Komponenten lauten \[ R_{\nu\sigma} := \sum_{\mu} \, R^{\mu}_{\;\nu\mu\sigma} \] und man schreibt \[ \mathrm{Ric}(w,v) := \sum_{\nu\sigma} \, R_{\nu\sigma} w^{\nu} v^{\sigma} \] Dieser Ausdruck hängt nicht vom Koordinatensystem ab. In der koordinatenfreien Formulierung kann man die obige Summation über den Index \(\mu\) als die Spur einer Abbildung definieren. Durch \[ A(w,v) \, u := R(u,v) \, w \] ist nämlich eine lineare Abbildung \(A(w,v)\) gegeben, die aus einem Tangentialvektor \(u\) den Tangentialvektor \( R(u,v) \, w \) macht. In Komponenten ausgeschrieben bedeutet das, dass man in \[ [R(u,v) \, w]^{\mu} = \sum_{\nu\rho\sigma} \, R^{\mu}_{\;\nu\rho\sigma} \, w^{\nu} u^{\rho} v^{\sigma} \] den Ausdruck \[ [A(w,v)]^{\mu}_{\;\rho} := \sum_{\nu\sigma} \, R^{\mu}_{\;\nu\rho\sigma} \, w^{\nu} v^{\sigma} \] als Komponentendarstellung dieses Abbildungstensors ansieht. Wir können nun die Spur von \(A(w,v)\) bilden (diese Spurbildung hängt nicht vom gewählten Koordinatensystem ab, auch wenn sie hier über ein beliebiges Koordinatensystem definiert wird; eine koordinatenfreie Einführung der Spur kann man wie bei der kovarianten Ableitung oder der bei der Determinante dadurch erreichen, dass man eine Reihe von Eigenschaften fordert, die die Spur eindeutig festlegen – wir verzichten hier darauf): \[ \mathrm{Spur}( A(w,v) ) := \] \[ = \sum_{\mu} \, [A(w,v)]^{\mu}_{\;\mu} = \] \[ = \sum_{\mu} \, R^{\mu}_{\;\nu\mu\sigma} w^{\nu} v^{\sigma} =: \] \[ =: \sum_{\nu\sigma} \, R_{\nu\sigma} w^{\nu} v^{\sigma} =: \] \[ =: \mathrm{Ric}(w,v) \] Man schreibt daher auch in diesem Sinne \[ \mathrm{Ric}(w,v) := \] \[ = \mathrm{Spur}( A(w,v) ) = \] \[ = \mathrm{Spur}( R( \; ,v) \, w ) \] Ohne Torsion (was in unserem Fall zutrifft) ist der Ricci-Tensor symmetrisch (analog zur Metrik). In 2 und 3 Dimensionen reicht der Ricci-Tensor zur Beschreibung der Krümmung vollständig aus. In 4 Dimensionen (also auch in der Raumzeit) benötigt man zur vollständigen Charakterisierung der Krümmung allerdings den Riemannschen Krümmungstensor von oben.
Man kann mit Hilfe der inversen metrischen Matrix auch die Spur über die Indices des Ricci-Tensors bilden und so den Ricci-Skalar (auch skalare Krümmung genannt) definieren: \[ R := \sum_{\nu\sigma} \, g^{\sigma\nu} R_{\nu\sigma} =: \mathrm{Spur}_{g} ( \mathrm{Ric} ) \] wobei das kleine \(g\) bei der Spur unten andeutet, dass vor der Spurbildung der erste Index mit der Metrik hochgezogen wird. Auch dieser Ausdruck hängt nicht vom Koordinatensystem ab. In 2 Dimensionen (also bei Flächen) reicht der Ricci-Skalar zur Beschreibung der Krümmung vollständig aus, aber nicht mehr in 3 Dimensionen.
Mit Hilfe dieser Objekte kann man nun alle möglichen Objekte zusammenbasteln und sie als Zusatzterme in den entsprechenden Gleichungen unterbringen. So könnte man die Gleichung \[ d {\star}F = j \] für das elektromagnetische Feld so abwandeln: \[ d {\star}(1 + kR) \, F = j \] mit einer Konstante \(k\) und dem Ricci-Skalar \(R\). Auch diese abgewandelte Gleichung geht bei verschwindender Krümmung in die Gleichung der speziellen Relativitätstheorie über. Bei der Übertragung von Gleichungen in die allgemeine Relativitätstheorie hat man also durchaus gewisse Freiheiten, und man muss durch das Experiment versuchen, herauszufinden, wofür die Natur sich entschieden hat. Im ersten Ansatz wird man es dabei natürlich mit den einfachsten Versionen versuchen, also möglichst ohne Zusatz-Krümmungsterme.
Damit sind wir am Ende dieses recht umfangreichen Kapitels angekommen. Wir wissen nun, wie das Äquivalenzprinzip zu einer ganz neuen Beschreibung der Gravitation im Rahmen der Riemannschen Geometrie führt, und dass Gravitation als die Unmöglichkeit beschrieben wird, in der gesamten Raumzeit ein einziges frei fallendes Inertialsystem zu finden. Mathematisch wird diese Unmöglichkeit durch eine nicht-verschwindende Krümmung dargestellt. Da wir nach dem Newtonschen Gravitationsgesetz davon ausgehen, dass Materie Gravitation erzeugt, müssen wir nun nach einem Zusammenhang zwischen Materieverteilung und Krümmung suchen. Das werden wir uns im nächsten Kapitel genauer ansehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 05 September 2023