Zusammenfassung des Buchkapitels:
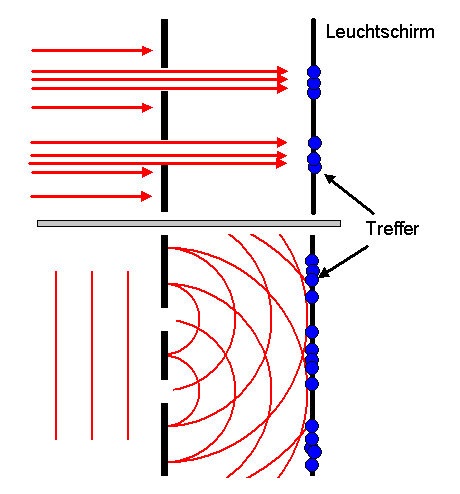
Licht weist Wellencharakter auf, besteht aber zugleich aus Teilchen. Die Umkehrung dieser Tatsache würde bedeuten, dass Elektronen nicht nur Teilchen sind, sondern auch Wellencharakter besitzen. Tatsächlich lässt sich diese Wellencharakter durch Interferenzexperimente wie bei Licht nachweisen:

Man findet, dass sich letztlich jedem Teilchen auf diese Weise eine
Wellenlänge zuordnen lässt, die umgekehrt proportional dem Produkt
aus seiner Masse mal seiner Geschwindigkeit (allgemeiner: seinem Impuls) ist.
Die Bewegung eines Teilchens durch den Raum wird dabei durch die
Ausbreitung dieser Welle dargestellt, deren Intensität an einem Ort die Wahrscheinlichkeit
dafür angibt, dieses Teilchen an diesem Ort nachzuweisen.
Flugbahnen gibt es nicht mehr. Genauer: Flugbahnen sind für Elektronen
analog zu Lichtstrahlen bei Licht zu betrachten. Sobald wir in Bereiche kommen,
die von der Größenordnung der Wellenlänge sind, werden Flugbahnen und Lichtstrahlen sinnlos.
Die entsprechende Theorie wurde in den Jahren nach 1926 mathematisch präzise formuliert. Sie trägt den Namen Quantenmechanik und bildet den theoretischen Rahmen jeder modernen Theorie über die Grundgesetze der Physik.
In der Quantenmechanik nennt man die obige Teilchenwelle auch Wellenfunktion. Mathematisch ist sie durch die Angabe eines oder auch mehrerer Pfeile (komplexer Zahlen, analog zu Uhrzeigern) an jedem Ort und für jeden Zeitpunkt gegeben.
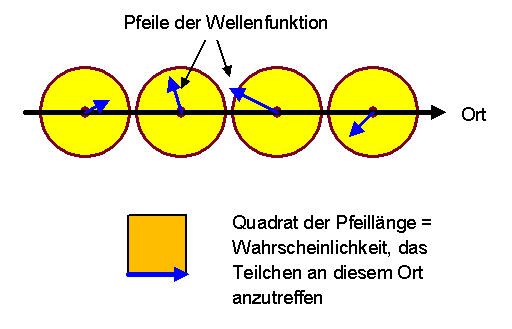
Wie eine Wellenfunktion von mehr als einem Teilchen aussieht und was man bei
Berücksichtigung des Spins tun muss, findet man im Buchkapitel.
Auch zu Schrödingers Katze findet man dort Interessantes.
Das Gesetz, das im nichtrelativistischen Bereich die zeitliche Veränderung der Pfeile festlegt, ist durch die sogenannte Schrödingergleichung gegeben (siehe unten).

Credit: Nobel foundation,
Quelle:
Wikimedia Commons File:Erwin Schrödinger (1933).jpg, dort Public Domain.
Quantenmechanik befasst sich grundsätzlich nur
mit Wahrscheinlichkeiten. Sie kann die Frage beantworten,
welche Ergebnisse eine bestimmte Messung haben kann und mit
welchen Wahrscheinlichkeiten die einzelnen Messergebnisse
eintreten können.
Dabei gibt es einen grundlegenden
Unterschied zur gewöhnlichen Wahrscheinlichkeitsrechnung:
Man arbeitet nicht direkt mit Wahrscheinlichkeiten, sondern
mit Wellenfunktionen, also mit Pfeilen (Wahrscheinlichkeitsamplituden).
Dort, wo man normalerweise Wahrscheinlichkeiten addieren würde, muss man
nun Pfeile addieren – so kommt Interferenz zustande!
Man könnte den Eindruck gewinnen, die Quantenmechanik sei lediglich eine vergröberte statistische Theorie, der eine fundamentalere und genauere Beschreibung der Physik zugrundeliegen müsse, die nicht bloß mit Wahrscheinlichkeiten hantiert. Wir werden noch sehen werden, ist dieser Eindruck vermutlich falsch.
I think I can safely say that nobody understands quantum mechanics.
(Richard Feynman in The Character of Physical Law (1965), Kap. 6)
Die Quantenmechanik ist sehr Achtung gebietend. Aber eine innere Stimme sagt mir, dass das noch nicht der wahre Jakob ist. Die Theorie liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher. Jedenfalls bin ich überzeugt, dass der Alte nicht würfelt.
(Albert Einstein in einem Brief an Max Born, 4. Dezember 1926, Einstein-Archiv 8-180, siehe z.B. Wikiquote: Albert Einstein)
Denn wenn man nicht zunächst über die Quantentheorie entsetzt ist, kann man sie doch unmöglich verstanden haben.
(Niels Bohr zitiert in "Der Teil und das Ganze. Gespräche im Umkreis der Atomphysik" von Werner Heisenberg, R. Piper & Co., München, 1969, S. 280, siehe Wikiquote: Niels Bohr)
Yeah, well, there are some people who spend an awful lot of time talking about the interpretation of quantum mechanics. My attitude [...] is that when I hear of Schrödinger's cat, I reach for my gun.
(Stephen Hawking in einer Konversation mit Timothy Ferris (4 April 1983), zitiert in The Whole Shebang (1998) von Timothy Ferris, S. 345)
a) Doppelspaltexperiment
b) Quantenmechanik und Schrödingergleichung
c) Gedanken zur Interpretation der Quantenmechanik
Was bei einem realen Doppelspaltexperiment mit 10, 200, 6000, 40000 und 140000 Elektronen herauskommt, zeigt die folgende Grafik (man erkennt, wie sich zunächst wenige Elektronen scheinbar zufällig, verteilen, während bei zunehmender Elektronenzahl langsam das Streifenmuster sichtbar wird):

Quelle:
Wikimedia Commons File:Double-slit experiment results Tanamura 2.jpg,
Creating User:Belsazar,
CC BY-SA 3.0 DEED
Lizenz.
Die beiden Spalte im Doppelspaltexperiment wirken für den Bereich
hinter dem Doppelspalt wie zwei fast punktförmige
Quellen für Kreiswellen. Die Überlagerung zweier
Kreiswellen kann man sich sehr schön mit Hilfe des
folgenden animierten GIFs veranschaulichen:
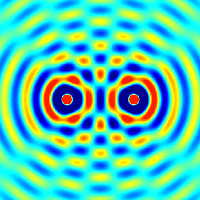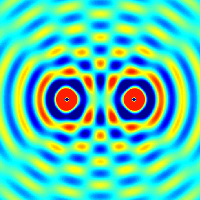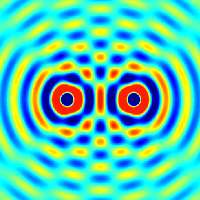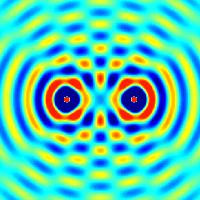
Quelle:
Wikimedia Commons File:Two sources interference.gif von Oleg Alexandrov, dort Public Domain.
Die obere Hälfte in diesem Bild entspricht dann der
Situation hinter dem Doppelspalt, wobei der Leuchtschirm
hier an der oberen Bildkante zu liegen kommt. Man erkennt sehr
schön die radial verlaufenden Streifen mit hoher
und niedriger Wellenintensität, die einer hohen bzw.
niedrigen Trefferquote für die Elektronen entsprechen..
Wenn Sie sich tiefer mit der Quantentheorie beschäftigen möchten, finden Sie weitere Informationen in meinem Online-Buch Die Symmetrie der Naturgesetze, speziell in Kapitel 4, sowie in Quantenfeldtheorie und Eichfelder. Die Schrödingergleichung finden Sie dort in Kapitel 3 Die Quantisierung der klassischen Mechanik.
Hier ist eine Motivation zur Schrödingergleichung (keine strenge Herleitung, sondern nur ein Plausibilitätsargument, siehe auch Wikipedia: Schrödingergleichung):
In der klassischen nichtrelativistischen Mechanik ist die Energie \(E\) eines Teilchens mit Impuls \[ \boldsymbol{p} = m \boldsymbol{v} \] am Ort \(\boldsymbol{x}\) in einem Potentialtopf \(V(\boldsymbol{x})\) gegeben durch \[ E = \frac{\boldsymbol{p}^{2}}{2m} + V(\boldsymbol{x}) \] Dabei ist \[ \frac{\boldsymbol{p}^{2}}{2m} = \frac{(m \boldsymbol{v})^{2}}{2m} = \frac{m}{2} \boldsymbol{v}^{2} \] die kinetische Energie und \( V(\boldsymbol{x}) \) die potentielle Energie des Teilchens. Das Gravitationsfeld der Erde oder auch die elektrische Anziehungskraft eines Atomkerns ergeben so einen Potentialtopf.
In der Quantenmechanik hat man es mit Wellen zu tun. Ein freies Teilchen mit Impuls \(\boldsymbol{p}\) und Energie \(E\) (ohne potentielle Energie) wird dabei durch eine ebene Welle der Form \[ \psi(t,\boldsymbol{x}) = e^{- \frac{i}{\hbar} (E t - \boldsymbol{p x})} \] beschrieben mit dem Planckschen Wirkungsquantum \(h\) und \[ \hbar = \frac{h}{2 \pi} \] und der Zusatzbedingung \[ E = \frac{\boldsymbol{p}^{2}}{2m} \] Das ist eine Welle mit Frequenz \[ \nu = \frac{E}{h} \] und Wellenlänge \[ \lambda = \frac{h}{|\boldsymbol{p}|} \] Dabei ist \( \psi(t,\boldsymbol{x}) \) eine komplexe Zahl (ein Zeiger), die sich an jedem festen Ort \(\boldsymbol{x}\) mit dieser Frequenz \(\nu\) dreht, und der sich zu jeder festen Zeit \(t\) in \(\boldsymbol{p}\)-Richtung einmal dreht, wenn man eine Wellenlänge λ in dieser Richtung zurücklegt. Es ist also eine Drehwelle.
Wenn man sich also die zeitliche Änderung der Welle ansieht, so erhält man die Frequenz und damit die Energie, und wenn man sich die räumliche Änderung ansieht, so erhält man die Wellenlänge und damit dem Impuls des Teilchens, das zu dieser ebenen Welle gehört. In Formeln ausgedrückt bedeutet das: \[ i \hbar \frac{d}{dt} \psi(t,\boldsymbol{x}) = E \, \psi(t,\boldsymbol{x}) \] \[ \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \, \psi(t,\boldsymbol{x}) = \boldsymbol{p} \, \psi(t,\boldsymbol{x}) \] Dabei ist \( \frac{d}{d\boldsymbol{x}} \) der Gradient. Im eindimensionalen Fall wird daraus einfach die räumliche Ableitung \( \frac{d}{dx} \) Damit die Bedingung \( E = \frac{\boldsymbol{p}^{2}}{2m} \) erfüllt ist, muss die Gleichung \[ i \hbar \frac{d}{dt} \psi(t,\boldsymbol{x}) = \frac{1}{2m} \, \left( \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \right)^{2} \, \psi(t,\boldsymbol{x}) \] erfüllt sein, denn die obige ebene Welle ist eine Lösung dieser Gleichung und ergibt \[ E \, \psi(t,\boldsymbol{x}) = \frac{\boldsymbol{p}^{2}}{2m} \, \psi(t,\boldsymbol{x}) \] und somit \[ E = \frac{\boldsymbol{p}^{2}}{2m} \] Damit haben wir bereits die Schrödingergleichung für ein spinloses freies Teilchen ohne Potentialtopf gefunden. Wir haben also einfach in \( E = \frac{\boldsymbol{p}^{2}}{2m} \) die Energie \(E\) durch die passende zeitliche Ableitung und den Impuls \(\boldsymbol{p}\) durch die passende räumliche Ableitung der Wellenfunktion ersetzt, um eine dazu passende Wellengleichung zu erhalten.
Wenn nun ein Potentialtopf \(V(\boldsymbol{x})\) vorhanden ist, so kommt die potentielle Energie hinzu, d.h. es gilt \[ E = \frac{\boldsymbol{p}^{2}}{2m} + V(\boldsymbol{x}) \] (siehe oben). Wir versuchen nun, analog zum freien Teilchen ohne Potentopf eine passende Wellengleichung aufzustellen, indem wir wieder die passenden Ableitungen verwenden. Das ergibt die Schrödingergleichung für ein spinloses Teilchen in einem Potentialtopf: \[ i \hbar \frac{d}{dt} \psi(t,\boldsymbol{x}) = \frac{1}{2m} \, \left( \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \right)^{2} \, \psi(t,\boldsymbol{x}) + \] \[ + V(\boldsymbol{x}) \, \psi(t,\boldsymbol{x}) \] Wäre die ebene Welle eine Lösung dieser Gleichung, so würde sich damit automatisch die richtige Beziehung \( E = \frac{\boldsymbol{p}^{2}}{2m} + V(\boldsymbol{x}) \) ergeben. Allerdings ist die ebene Welle normalerweise keine Lösung dieser Gleichung! Das bedeutet, dass ein Teilchen in diesem Potentialtopf keinen eindeutigen Impulswert mehr besitzt (eine feste Energie ist dagegen möglich). Immerhin kann man aber jede Lösung dieser Gleichung aus ebenen Wellen zusammensetzen. Jede dieser ebenen Wellen entspricht dann einem Impulswert für das Teilchen, der bei einer Messung auftreten könnte. Erst die Interferenz all dieser ebenen Wellen ergibt die Wellen, die im Potentialtopf das Teilchen korrekt beschreiben.
Ob die obige erratene Schrödingergleichung passt, muss man schrittweise untersuchen. Ergebnis: sie passt! Mit ihr kann man beispielsweise ein Elektron im Potentialtopf eines Atomkerns sehr gut beschreiben und so die Eigenschaften eines Wasserstoffatoms mit guter Genauigkeit berechnen.
Im Buchkapitel habe ich die gängige Standard-Interpretation der Quantenmechanik dargestellt:
Quantenmechanik befasst sich mit Wahrscheinlichkeitsamplituden (Pfeilen), deren Betragsquadrat die Wahrscheinlichkeit für das entsprechende Messergebnis angibt. Hinzu kommt die Interferenzregel, nach der bei ununterscheidbaren Möglichkeiten die entsprechenden Amplituden (Pfeile) zu einer Gesamtamplitude addiert werden, sowie die Multiplikationsregel, nach der Amplituden von Teilschritten multipliziert werden (siehe auch Buchkapitel 5.2). Die Interferenzregel führt dazu, dass sich die Amplituden zweier Möglichkeiten auch gegenseitig neutralisieren können, wie das Doppelspaltexperiment zeigt.
Genauer betrachtet ist die Quantenmechanik ein recht bizarres Konstrukt, das bis heute niemand wirklich verstanden hat, obwohl es in der Praxis ganz hervorragend funktioniert. So findet man in Feynmans Vorlesung über Physik Band III (Quantenmechanik), Kapitel 1-7:
Niemand hat irgendeinen Mechanismus hinter dem Gesetz (gemeint sind die Grundgesetze der Quantenmechanik) gefunden. Niemand kann mehr "erklären", als wir gerade "erklärt" haben. Niemand wird Ihnen irgendeine tiefergehende Darstellung der Verhältnisse geben. Wir haben keine Vorstellung von einem grundlegenderen Mechanismus, aus dem diese Resultate hergeleitet werden können.
Niemand weiß also bis heute, warum gerade die obigen Regeln gelten – es ist kein übergreifendes Prinzip bekannt, dass diese Regeln erzwingt (anders als in Einsteins spezieller und allgemeiner Relativitätstheorie, die aus sehr allgemeinen und anschaulichen Postulaten folgen). Warum sind Wahrscheinlichkeitsamplituden scheinbar die einzige Möglichkeit, die Natur zu beschreiben, zumindest bei den heute experimentell zugänglichen Phänomenen? Warum gelten die Interferenzregel und die Multiplikationsregel? Warum können wir nur von Wahrscheinlichkeiten sprechen? Oder um ein Zitat von Einstein abzuwandeln: Warum scheint Gott zu würfeln?
Ein Blick in Wikipedia: Interpretationen der Quantenmechanik zeigt, dass es eine große Vielfalt an Erklärungsversuchen gibt. Das ist meist ein sicheres Zeichen dafür, dass man nicht wirklich weiß, wie die Lösung aussieht. Wenn Sie eine Erkältung haben und in eine Apotheke gehen, so finden Sie eine Vielfalt an diversen Pillen, Tinkturen, Salben etc. – ebenfalls ein sicheres Zeichen dafür, dass es bis heute kein verlässliches Mittel gegen Erkältungen gibt. Jedes Mittel mag die eine oder andere Linderung verschaffen, aber die Viren muss ihr Immunsystem weitgehend selbst bekämpfen.
Irgendwie scheint die Schnittstelle zwischen Quantenwelt und klassischer Nicht-Quantenwelt eine entscheidende Rolle zu spielen. Die Quantenmechanik macht ja Aussagen über die Wahrscheinlichkeit von Messergebnissen, und dafür braucht man ein Messinstrument, das ein eindeutiges Messergebnis anzeigt und von uns Menschen abgelesen werden kann. Das Messinstrument muss daher klassisch beschrieben werden, so dass es eine eindeutig bestimmte Realität wiedergibt, beispielsweise einen Lichtblitz an einer bestimmten Stelle auf einem Leuchtschirm. Damit entsteht ein Bruch zwischen der Quantenwelt, in der sich Wellenfunktionen kontinuierlich mit der Zeit nach festen Regeln entwickeln, und dem klassischen Messapparat, bei dem sich plötzlich zufällig ein bestimmtes Messergebnis einstellt. Man spricht hier auch vom Messproblem.
Die Standardinterpretation (im Wesentlichen die Kopenhagener Interpretation, wie ich sie auch im Buch darstelle) ignoriert dieses Problem weitgehend. Kurz gesagt: Um von Messergebnissen reden zu können, braucht man nun mal die Begriffswelt der klassischen Physik. Wahrscheinlichkeitsamplituden spiegeln dann alles wider, was wir über ein Quantensystem im Rahmen dieser klassischen Begriffswelt wissen können (beispielsweise aufgrund vorhergehender Messungen).
Eine dahinterliegende Quantenrealität, die über dieses Wissen hinausgeht, gibt es demnach nicht, und John Stewart Bell hat ja tatsächlich gezeigt, dass es zumindest keine verborgenen lokalen Variablen wie beispielsweise eine Teilchenrotation gibt (siehe Kapitel 2.8 ). Wahrscheinlichkeitsamplituden (Wellenfunktionen) sind demnach auch keine realen physikalischen Objekte wie beispielsweise Teilchen, sondern sie spiegeln Informationen über diese Objekte wider, und solche Informationen ändern sich natürlich, wenn wir eine Messung vornehmen (Kollaps der Wellenfunktion). Diesen Standpunkt haben im Wesentlichen beispielsweise Niels Bohr, Werner Heisenberg oder auch Richard Feynman eingenommen.
Nun scheint es in der Natur aber keine klar definierte Grenze zwischen Quantenwelt und klassischem Messinstrument zu geben. Es gelingt in den letzten Jahren, mit immer größeren Objekten das Doppelspaltexperiment durchzuführen, beispielsweise mit C60-Fullerenen (das sind Fußball-ähnliche Moleküle aus 60 Kohlenstoffatomen, siehe Wikipedia: Fullerene), und so die Gültigkeit der Quantenmechanik auch für diese Objekte nachzuweisen.
Auch andere ausgeklügelte Experimente zeigen keinerlei Grenze für den Gültigkeitsbereich der Quantenmechanik auf – so konnte die quantenmechanische Verschränkung von Photonen über eine Entfernung von mehr als 100 km nachgewiesen werden (siehe Anton Zeilinger: Die Wirklichkeit der Quanten, Spektrum der Wissenschaft, November 2008, S.54).
Wenn man daher von der universellen Gültigkeit der Quantenmechanik auch für große Objekte ausgeht, so muss man letztlich auch das Messinstrument und letztlich sogar das gesamte Universum quantenmechanisch beschreiben und das Zustandekommen zufälliger Messergebnisse erklären. Hier ein Zitat von Steven Weinberg dazu (siehe Steven Weinberg: Einstein's Mistakes in Physics Today (2005); Abschnitt Contra quantum mechanics ):
Bohr's version of quantum mechanics was deeply flawed, but not for the reason Einstein thought. The Copenhagen interpretation describes what happens when an observer makes a measurement, but the observer and the act of measurement are themselves treated classically. This is surely wrong: Physicists and their apparatus must be governed by the same quantum mechanical rules that govern everything else in the universe. But these rules are expressed in terms of a wavefunction (or, more precisely, a state vector) that evolves in a perfectly deterministic way. So where do the probabilistic rules of the Copenhagen interpretation come from?
Eigene Übersetzung:
Bohrs Version der Quantenmechanik war zutiefst mangelhaft, aber nicht aus dem Grund, den Einstein im Sinn hatte. Die Kopenhagener Interpretation beschreibt, was geschieht, wenn ein Beobachter eine Messung vornimmt, doch sowohl der Beobachter als auch der Messvorgang selbst werden klassisch behandelt. Das ist sicherlich falsch: Physiker und ihre Messgeräte müssen denselben quantenmechanischen Gesetzen unterliegen, die auch alles andere im Universum regieren. Diese Gesetze werden jedoch durch den Begriff der Wellenfunktion (oder präziser den Zustandsvektor) ausgedrückt, die sich in vollkommen deterministischer Weise entwickelt. Woher also stammen die Wahrscheinlichkeitsregeln der Kopenhagener Interpretation?
In den letzten Jahren ist es tatsächlich gelungen, einige wichtige Fortschritte in dieser Richtung zu erzielen – nicht zuletzt auch deshalb, weil solche Fragen auch für Quantencomputer von Relevanz sind. Ein zentraler Aspekt ist dabei der Begriff der Dekohärenz. In Was ist Entropie? (Teil 2) (Anhang 1 und 2) finden Sie eine detaillierte Darstellung zur Dekohärenz. Die Kernidee kann man sich aber auch am Doppelspaltexperiment recht gut klarmachen:
Beim Doppelspaltexperiment tritt auf dem Leuchtschirm hinter dem Doppelspalt ein Interferenzmuster aus Streifen mit vielen und wenigen Teilchentreffern auf. Die Welle aus dem einen Spalt überlagert sich mit der Welle aus dem anderen Spalt, wobei je nach Ort auf dem Leuchtschirm die beiden Wellen dort gleichphasig ankommen und sich verstärken oder gegenphasig ankommen und sich auslöschen. Man kann auch sagen, die beiden Wahrscheinlichkeitsamplituden (Pfeile) zu den beiden Möglichkeiten (Spalt eins oder zwei) addieren sich, wobei es auf den relativen Winkel zwischen den Pfeilen ankommt, ob sie sich verstärken oder neutralisieren. Wir hatten in Buchkapitel 5.2 auch von der Interferenz ununterscheidbarer Möglichkeiten gesprochen.
Dabei ist für das Auftreten von Interferenz entscheidend, dass die beiden Möglichkeiten prinzipiell ununterscheidbar sind, d.h. dass wir prinzipiell nicht wissen können, welche Möglichkeit genommen wurde: Spalt eins oder zwei. Der Teilchendurchgang durch die Spalte darf keine makroskopisch erkennbaren Spuren in der Natur hinterlassen, da ansonsten das Interferenzmuster verloren geht und keine Wahrscheinlichkeitsamplituden mehr addiert werden dürfen, sondern klassische Wahrscheinlichkeiten, die sich nicht mehr gegenseitig auslöschen können.
Sicherzustellen, dass tatsächlich keine erkennbaren Spuren entstehen, wird immer schwieriger, je mehr Freiheitsgrade das betrachtete Objekt enthält – das ist genau die entscheidende Herausforderung für den Bau von Quantencomputern. Makroskopische Objekte schließlich hinterlassen praktisch immer Spuren, wechselwirken also z.B. über Wärmestrahlung mit ihrer Umgebung.
Umgekehrt: Wenn wir wissen wollen, welcher Spalt vom einzelnen Teilchen genommen wurde, so muss das Teilchen beim Spaltdurchgang eine entsprechende Information in seiner physikalischen Umwelt hinterlassen. Es muss am Spalt mit einem makroskopischen System wechselwirken, z.B. einem Messinstrument.
Dieses makroskopische System wird dabei (ganz im Sinne Weinbergs) gemeinsam mit dem durchfliegenden Teilchen quantenmechanisch betrachtet, beispielsweise durch eine gemeinsame Wellenfunktion. Dabei kommt es zu Wechselbeziehungen (Verschränkungen) zwischen der Teilchen-Wahrscheinlichkeitsamplitude und den unzähligen Wahrscheinlichkeitsamplituden des makroskopischen Systems.
Man kann sich vorstellen, dass dadurch der Teilchen-Wahrscheinlichkeitspfeil sehr oft einen kleinen Schubs nach rechts oder links erhält und seine Ausrichtung (seine Phase) in unkontrollierbarer Weise geändert wird. Die Kohärenz zwischen den beiden Quantenwellen geht verloren; sie werden dekohärent.
Damit geht die Information über die relative Ausrichtung der beiden Wahrscheinlichkeitspfeile verloren – sie verliert sich im Dickicht der Quantenfreiheitsgrade des makroskopischen Systems, mit dem das Teilchen an den Spalten wechselwirkt. Im statistischen Mittel ist dann das Betragsquadrat der Pfeilsumme gleich der Summe der Betragsquadrate der beiden Pfeile, d.h. die Wahrscheinlichkeiten summieren sich.
Begründung:
Bei zwei Amplituden \[ a = |a| \, e^{i \alpha} \] \[ b = |b| \, e^{i \beta} \] gilt für das Betragsquadrat ihrer Summe (also z.B. für die Trefferwahrscheinlichkeit nach Interferenz der Amplituden am Leuchtschirm) \[ |a + b|^{2} = \] \[ = (a + b) \cdot (a + b)^{*} = \] \[ = a a^{*} + b b^{*} + a b^{*} + a^{*} b = \] \[ = |a|^{2} + |b|^{2} + |a| \cdot |b| \cdot \left( e^{i (\alpha - \beta)} + e^{i (\beta - \alpha)} \right) = \] \[ = |a|^{2} + |b|^{2} + |a| \cdot |b| \cdot 2 \, \cos {(\alpha - \beta)} \] Bei zufällig verteilten Phasen \(\alpha\) und \(\beta\) mittelt sich hier der cos-Interferenzterm weg und es bleibt das klassische Addieren von Wahrscheinlichkeiten (gegeben durch die Betragsquadrate der beiden Amplituden): \[ |a|^{2} + |b|^{2} \]
Dekohärenz erklärt also, wie die Interferenz ununterscheidbarer Möglichkeiten verloren geht, sobald eine Wechselwirkung mit einem makroskopischen System die beiden Möglichkeiten unterscheidbar macht. Aus der Summe quantenmechanischer Wahrscheinlichkeitsamplituden wird dabei die Summe klassischer Wahrscheinlichkeiten. Dagegen erklärt Dekohärenz nicht, warum mal der eine und mal der andere Spalt gewählt wird. Der grundsätzliche Wahrscheinlichkeitscharakter der Quantenmechanik bleibt also bestehen.
Darüber hinaus kann Dekohärenz erklären, warum sich in bestimmten Situationen nur bestimmte Messgrößen einstellen können. Warum z.B. bildet sich im Doppelspaltexperiment ein Lichtblitz an einer bestimmten Stelle auf dem Leuchtschirm und signalisiert damit einen Teilchenort?
Analysen zeigen, dass es sogenannte robuste Quantenzustände gibt, die durch Dekohärenz nicht zerstört werden. Dazu gehören bei elektrischer Wechselwirkung zwischen Teilchen die sogenannten lokalisierten Zustände, bei denen der Teilchenort recht genau festliegt – kein Wunder also, dass in unserer makroskopischen Welt die Dinge immer an einem definierten Ort zu finden sind. Die Quantenwelle, die im Doppelspaltexperiment auf dem Leuchtschirm auftrifft, ist zunächst eine quantenmechanische Überlagerung solcher lokalisierter Zustände. Die Wechselwirkung mit dem makroskopischen Leuchtschirm führt zur Dekohärenz zwischen den lokalisierten Zuständen, so dass klassische Wahrscheinlichkeiten für das Auftreten der einzelnen lokalisierten Zustände und damit Teilchenorte übrig bleiben. Welcher Teilchenort allerdings tatsächlich gemessen wird, bleibt offen.
Aus einer quantenmechanischen Welle entsteht also bei Kontakt mit einem makroskopischen System durch Dekohärenz eine klassische Überlagerung von robusten Quantenzuständen, die mit unterschiedlichen Wahrscheinlichkeiten auftreten und die zu klassischen Messwerten passen, z.B. zu einem Teilchenort. Die robusten Quantenzustände sind dabei dekohärent zueinander, da die ursprüngliche Phaseninformation zwischen ihnen, wie sie vor dem Kontakt noch vorhanden war, sich in den vielen Freiheitsgraden des makroskopischen Systems verliert.
Unbefriedigend bleibt aber nach wie vor, dass es keine Erklärung dafür gibt, warum nun ein bestimmter Messwert und damit ein bestimmter robuster Quantenzustand in der Realität tatsächlich auftritt. Die Kopenhagener Interpretation würde hier einfach nur sagen: "So ist es nun einmal, ob es Dir gefällt oder nicht." Dahinter steht der Gedanke, dass Wellenfunktionen auch bei Berücksichtigung der Dekohärenz immer noch lediglich Hilfsmittel sind, um unser Wissen über das physikalische System zu repräsentieren und entsprechende Wahrscheinlichkeiten berechenbar zu machen.
Man kann aber auch einen anderen Standpunkt einnehmen und Wellenfunktionen als physikalisch reale Objekte ansehen (letztlich steckt also eine andere Definition des Begriffs Realität dahinter). Dieser Weg wurde von Hugh Everett im Jahr 1957 eingeschlagen und u.a. von Bryce Seligman DeWitt weiter fortgeführt; er führt letztlich zur Viele-Welten-Interpretation der Quantenmechanik (siehe z.B. Peter Byrne: Die Parallelwelten des Hugh Everett, Spektrum der Wissenschaft, April 2008, S.24, oder auch Kapitel 4 in meinem Buch Grenzen der Wirklichkeit: Kosmologie, Quantenwelten und die Suche nach der Unendlichkeit).
Früher wurde die Viele-Welten-Interpretation meistens als bizarres Hirngespinst abgetan, doch mittlerweile mausert sie sich zu einer durchaus ernst zu nehmenden und von vielen Physikern akzeptierten Sichtweise, da sie sich logisch aus den Regeln der Quantenmechanik ergibt – vorausgesetzt, man akzeptiert, dass Quantenmechanik und Wellenfunktionen tatsächlich die physikalische Realität widerspiegeln und nicht nur mathematische Hilfsmittel zur Beschreibung der Welt sind. Schauen wir uns also diese Interpretation etwas genauer an:
Grundvoraussetzung ist, dass man die Trennung zwischen beobachtetem Quantensystem und makroskopischem Beobachter aufgibt und die ganze Welt quantenmechanisch beschreibt. Es gibt also so etwas wie eine universelle Wellenfunktion, die das gesamte Universum umfasst.
Nun tritt bei einer Messung Dekohärenz auf, d.h. die Wellenfunktion spaltet sich auf in mehrere Anteile, die dekohärent zueinander sind und deren gegenseitige Beeinflussung (Interferenz) makroskopisch nicht messbar ist. Wenn man beim Doppelspaltexperiment also im Prinzip weiß, welchen Spalt das Teilchen genommen hat, so gibt es fortan zwei Wellenfunktionsanteile in der universellen Wellenfunktion: einen, bei dem die Information "Spalt 1 wurde genommen" makroskopisch vorliegt, und einen, bei dem die Information "Spalt 2 wurde genommen" makroskopisch vorliegt.
Jeder dieser Anteile umfasst auch die makroskopische Welt inklusive Messinstrument und ggf. dem Physiker, der das Instrument abliest. Da sich fortan beide Wellenfunktionsanteile unabhängig voneinander dekohärent weiterentwickeln, merken beide Welten nichts voneinander. Der Physiker, der durch Wellenfunktionsanteil 1 beschrieben wird, hat gemessen, dass Spalt 1 genommen wurde, und analog für Spalt 2.
Man kann dies so verstehen, als ob sich die makroskopische Welt durch die Messung des Spaltdurchgangs in zwei unabhängige Anteile aufgespalten hat, die zwei verschiedenen makroskopischen Realitäten entspricht. Die Dekohärenz erschafft gleichsam verschiedene makroskopische Realitäten. In jeder dieser Realitäten wird das Messergebnis für den gewählten Spalt als zufällig interpretiert. Es gibt jedoch weiterhin so etwas wie eine übergreifende Quanten-Realität, die durch die universelle Wellenfunktion beschrieben wird und die beide makroskopische Realitätszweige gleichermaßen umfasst.
Nun finden in unserer Umwelt ständig solche Mess-Ereignisse statt, nämlich jedesmal, wenn eine quantenmechanische Überlagerung ihre Kohärenz verliert und eines der möglichen Messergebnisse sich in der makroskopischen Umwelt manifestiert. Die universelle Wellenfunktion der Welt spaltet sich gleichsam ständig in einzelne dekohärente Anteile auf, die verschiedenen makroskopischen Realitäten entsprechen.
Die von uns erlebte Realität formt sich durch diesen Prozess also ständig neu, wobei zugleich auch jede andere mögliche erlebbare Realität mit entsteht. Die Frage, warum unsere Welt so ist wie sie ist, erhält damit eine vollkommen neue Bedeutung: Sie ist einfach nur eine von fast unendlich vielen möglichen Welten (makroskopischen Realitäten) und spiegelt nur einen winzigen Ausschnitt der allumfassenden Realität wider, die durch die universelle Wellenfunktion beschrieben wird. Wir sehen einfach zufällig einen bestimmten Zweig der Wellenfunktion, während alle anderen Zweige aus unserem Blickfeld verschwinden, wobei sich diese Verzweigung ununterbrochen fortsetzt und jeder Zweig sich selbst als einzige Realität begreift.
Kein Wunder, dass eine solch bizarre Weltsicht kaum Anhänger fand, als Hugh Everett sie im Jahr 1957 in seiner Doktorarbeit vorschlug. Everett war vermutlich ziemlich enttäuscht über die fehlende Akzeptanz seiner Arbeit und verließ die theoretische Physik – er arbeitete seitdem lieber für das Pentagon. Seine Viele-Welten-Interpretation ruft tatsächlich zumindest bei mir ein mulmiges Gefühl hervor: Sollte unsere Realität tatsächlich so aussehen? Entstehen tatsächlich ständig Kopien von mir selbst, die dann andere Wege gehen und die genauso real sind wie ich selbst? Was bedeutet der Begriff "ICH" in so einer Welt überhaupt noch?
Ein Gefühl der Verlorenheit und Bedeutungslosigkeit macht sich breit, wenn man diese Welt für möglich hält. Tatsächlich scheint diese Weltsicht durchaus zur Persönlichkeit von Hugh Everett zu passen. In Peter Byrnes Artikel Die Parallelwelten des Hugh Everett (Spektrum der Wissenschaft, April 2008, S.24) findet man beispielsweise das folgende Zitat von Donald Reisler (einem engen Kollegen von Hugh Everett): "Everett war nicht sympatisch. Er analysierte die Dinge mit kalter, brutaler Logik." Aus diesem Artikel geht hervor, dass Everett offenbar ein sehr intelligenter, aber kein besonders warmherziger und glücklicher Mensch war. Zudem rauchte und trank er wie es ihm beliebte und so starb er bereits im Jahr 1982 mit nur 51 Jahren an einem Herzinfarkt.
Wenn man in der Zeit zurückblickt, so passt Everetts Interpretation durchaus zu der Erkenntnis über unserer eigene Winzigkeit, die uns die Naturwissenschaft im Lauf der Zeit immer stärker nahegelegt hat. So hat Kopernikus um das Jahr 1509 die Erde aus dem Mittelpunkt der Welt gerückt und die Sonne an ihre Stelle gesetzt. Später wurde klar, dass auch die Sonne nur einer von Milliarden Sternen der Milchstraße ist, und auch die Milchstraße stellte sich als nur eine von Milliarden Galaxien heraus. Unsere Erde ist ein absolut winziges Stäubchen im Universum!
Und dann zeigte Charles Darwin im Jahr 1858 auch noch, dass wir sogar auf dieser winzigen Erde nur einen Zweig der Evolution darstellen, so wie alle anderen Lebewesen auch. Sehr viele Zufälle waren notwendig, damit dieser menschliche Evolutionszweig überhaupt entstehen konnte – man denke an das Ende der Dinosaurier aufgrund eines kosmischen Asteroiden-Zufallstreffers sowie die zufällige Änderung des Klimas in Ostafrika, die den aufrechten Gang hervorbrachte. Die durchaus hochentwickelten Dinosaurier haben es mehr als 100 Millionen Jahre lang nicht geschafft, eine ähnlich intelligente Art wie uns hervorzubringen, und auch die Säugetiere haben da wohl einfach nur Glück gehabt.
Nun soll also die Erde nicht nur ein winziges Staubkorn im Universum sein, auf dem wir nur ein Zufallszweig der Evolution sind, sondern die Realität selbst soll ein Zufallszweig einer umfassenderen universellen Quanten-Realität sein. Das ist für uns Menschen einfach zuviel – kein Wunder, dass sich beispielsweise manche Religionsgemeinschaften immer wieder dieser Weltsicht entgegenzustemmen versuchen.
Die Naturwissenschaft liefert nun einmal leider nicht immer die Antworten, die man sich als Mensch wünschen würde. Vielleicht muss man diese ganze Angelegenheit einfach mit einem gewissen Abstand und einer Portion Humor betrachten, so wie dies beispielsweise in Douglas Adams Vierteiler The Hitchhiker's Guide to the Galaxy vielfach geschieht (man denke an die Zahl 42 als ernüchternde Antwort auf die Frage nach dem Leben, dem Universum und einfach allem). Sehr nett finde ich angesichts der Mühen bei der Interpretation der Quantenmechanik auch folgende letzte Botschaft Gottes an seine Schöpfung:
We apologise for the inconvenience.
(God's Final Message to His Creation, written in letters of fire on the side of the Quentulus Quazgar Mountains, from Douglas Adams: "The Hitchhiker's Guide to the Galaxy") Übersetzt:
Wir bitten die Unannehmlichkeiten zu entschuldigen.
(Gottes letzte Botschaft an seine Schöpfung, geschrieben in brennenden Buchstaben am Rande der Quentulus-Quazgar-Berge, aus Douglas Adams: "The Hitchhiker's Guide to the Galaxy")
Also: Nicht zu verbissen an die Sache herangehen. Feynman würde wohl sagen: "If you don't like it: go to another Universe!" (siehe Richard Feynman: the QED Lecture at University of Auckland ).
Die neueren Forschungen im Rahmen der String- und M-Theorie (siehe Buchkapitel 8.1) legen tatsächlich nahe, dass die Viele-Welten-Interpretation gar nicht so bizarr ist, wie sie zunächst anmutet. In der Kopenhagener Interpretation macht es beispielsweise keinen Sinn, über das Universum als Ganzes im Rahmen der Quantenmechanik nachzudenken, da dort immer ein äußerer klassisch beschriebener Beobachter benötigt wird, der Messungen am Quantensystem vornimmt. Den gibt es aber nicht, wenn man die gesamte Welt als Quantensystem auffasst.
In der Viele-Welten-Interpretation braucht man diesen äußeren Beobachter nicht, und eine universelle Wellenfunktion für das gesamte Universum ist zumindest prinzipiell denkbar. Edward Witten vermutet, dass genau hier ein entscheidender Aspekt für das Verständnis der Quantenmechanik liegen könnte. In Does God play dice? schreibt er:
... it is hard to see what it means to apply quantum mechanics to the whole universe. ... If we had a good understanding of what quantum mechanics means when applied to the whole universe, we might ultimately say that the notion that "God plays dice" results from trying to describe a quantum reality in classical terms.
Eigene Übersetzung:
... es ist schwer zu sehen, was es bedeutet, die Quantenmechanik auf das gesamte Universum anzuwenden. ... Wenn wir ein gutes Verständnis darüber hätten, was Quantenmechanik bedeutet, wenn man sie auf das gesamte Universum anwendet, so würden wir letztlich vielleicht sagen: Die Auffassung "Gott würfelt" ergibt sich daraus, dass wir die Quantenrealität mit klassischen Begriffen zu beschreiben versuchen."
Im Rahmen der String- und M-Theorie eröffnet sich noch eine weitere Möglichkeit für verschiedene existierende Realitäten oder Universen – man spricht auch vom Multiversum (siehe z.B. das Buch von Stephen Hawking und Leonard Mlodinow: Der große Entwurf: Eine neue Erklärung des Universums).
Hintergrund:
Es gibt vermutlich sehr viele verschiedene Variationen, die unsichtbaren sechs Raumdimensionen einzurollen, die die M-Theorie benötigt. Dadurch entsteht eine Art Landschaft möglicher Theorien, wobei jedes Energieminimum zu einem anderen Vakuumzustand in einem stabilen oder metastabilen Universum gehört (Zahlen wie \(10^{500}\) mögliche verschiedene Vakua kursieren hier).
Die physikalischen Gesetze und die physikalischen Parameter in den nicht-eingerollten Dimensionen sind in jedem dieser Vakua unterschiedlich, und man spekuliert, dass unser Universum nur deswegen die beobachteten Parameter und Gesetze aufweist, weil dies so für das Entstehen von Leben notwendig ist (anthropisches Prinzip).
Es wäre dann unmöglich, beispielsweise den Wert der elektrischen Elementarladung oder den Wert der dunklen Energie aus anderen Prinzipien heraus zu berechnen. Diese Werte hätten vielmehr die Bedeutung von Umgebungsparametern analog zum Abstand der Erde von der Sonne – auch dieser Abstand lässt sich nicht aus anderen Prinzipien ableiten, sondern er muss notwendigerweise in einem engen Wertebereich liegen, der flüssiges Wasser und damit die Entstehung von Leben auf der Erde ermöglicht.
Aus heutiger Sicht gibt es mindestens die folgenden Möglichkeiten, wie es zur Koexistenz vieler Universen im Rahmen eines Multiversums kommen kann (siehe Steven Weinberg: Living in the Multiverse, arXiv:hep-th/0511037v1 sowie Alejandro Jenkins, Gilad Perez: Leben im Multiversum, Spektrum der Wissenschaft, Mai 2010, S. 24):
Es gibt also mehrere Denkmöglichkeiten, wobei auch Kombinationen dieser Ideen denkbar sind. In Steven Weinbergs "Living in the Multiverse" findet man dazu die folgende nette Anekdote: Auf die Frage "Wieviel Vertrauen haben Sie in die Idee des Multiversums" soll Weinbergs Kollege Martin Rees (ein britischer Astronom) gesagt haben, er würde das Leben seines Hundes darauf verwetten. Andrei Linde (russischer Kosmologe und Mitbegründer der Inflationstheorie des Universums) würde sogar sein eigenes Leben darauf verwetten. Steven Weinberg selbst würde dagegen lediglich das Leben der Hunde dieser beiden Physiker setzen. Arme Hunde, aber Schrödingers Katze ergeht es auch nicht viel besser.
Die Diskussion über die Interpretation der Quantenmechanik ist selbst 100 Jahre nach ihrer Formulierung keineswegs abgeschlossen. Es ist durchaus möglich, dass die Quantenmechanik erst im Rahmen einer fundamentalen Theorie der Naturgesetze wirklich verstanden werden kann, beispielsweise zusammen mit der M-Theorie.
Sowohl für die Quantenmechanik als auch für die M-Theorie gibt es bisher keine einfachen Grundprinzipien, aus denen sich beide ableiten lassen. Im Rahmen der M-Theorie müssen Quanten- und Stringunschärfe konsistent zusammenkommen, um unsere Welt zu erklären, auch wenn noch niemand genau weiß, wie das gehen soll. Daher könnte in dieser Synthese der beiden Unschärfen vielleicht auch das Geheimnis der Quantenmechanik selbst verborgen sein (siehe auch die Zusatzinfos zur M-Theorie in Kapitel 8.1 ). Edward Witten schreibt dazu in Reflections on the fate of spacetime (Physics Today, April 1996):
The existence of such symmetries (gemeint sind Dualitäten in der M-Theorie) ... gives one the feeling that the natural formulation of the theorie (gemeint ist die M-Theorie) may eventually prove to be inherently quantum mechanical and thus, in a sense, may entail an explanation of quantum mechanics.
Frei übersetzt:
Die Existenz der Dualitäten in der M-Theorie ... geben einem das Gefühl, dass eine natürliche Formulierung der M-Theorie sich letztlich als inhärent quantenmechanisch erweisen könnte, so dass sie in gewissem Sinne eine Erklärung der Quantenmechanik mit sich bringen könnte.
Vielleicht ergibt sich der richtige Blickwinkel auf die Quantenmechanik also erst im Rahmen einer umfassenden fundamentalen Theorie der Natur, die uns zwingt, sowohl die Grundlagen der Quantentheorie als auch der allgemeinen Relativitätstheorie neu zu überdenken und zu vereinen (siehe z.B. auch Gerard 't Hooft in Does God play dice?). Ich bin gespannt, wie sich dieses Thema noch entwickeln wird.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 21 December 2023