Wir haben oben die Zustandsgrößen \(S, E, V, N\) sowie die davon abgeleiteten Größen \(T, p, \mu\) kennengelernt. Dabei sind \(S, E, V, N\) sogenannte extensive Größen, d.h. die Größen zweier Teilsysteme addieren sich, wenn man sie zu einem Gesamtsystem zusammensetzt.
Dagegen sind \(T, p, \mu\) intensive Größen – sie addieren sich nicht, denn sie sind die Ableitung einer intensiven Größe (z.B. \(S\)) nach einer anderen intensiven Größe (z.B. \(E\)).
Im thermischen Gleichgewicht nehmen diese intensiven Größen teilweise oder alle (je nach Randbedingungen) identische Werte in den beteiligten Teilsystemen an. Die intensiven Größen sind teilweise sehr nützlich, um die Wechselwirkung von makroskopischen Systemen zu studieren, besonders wenn ein System sehr viel größer als das andere System ist und beispielsweise seine Temperatur deshalb nahezu konstant bleibt. Außerdem lassen sich die intensiven Größen meist sehr gut messen, im Gegensatz beispielsweise zur Entropie S oder der Energie E.
Wenn man ein System durch die extensiven Größen \(E, V, N\) sowie \(S(E,V,N)\) beschreibt, so kann man diese Größen beispielsweise fest vorgeben (abgeschlossenes System) oder sie quasistatisch variieren und sich für Änderungen \(dE, dV, dN, dS\) interessieren – genau das haben wir oben ständig gemacht.
Die Funktion \(S(E,V,N)\) können wir für normale Systeme (bei denen \(S\) mit \(E\) anwächst) invertieren und \(E\) als Funktion \(E(S,V,N)\) schreiben. Für den Zusammenhang zwischen den totalen Differentialen \(dE, dV, dN, dS\) bedeutet das: \[ dE(S,V,N) = \] \[ = \frac{\partial E}{\partial S} \, dS + \frac{\partial E}{\partial V} \, dV + \frac{\partial E}{\partial N} \, dN = \] \[ = T \, dS - p \, dV + \mu \, dN \] mit \[ \frac{\partial E}{\partial S} =: T \] \[ \frac{\partial E}{\partial V} =: - p \] \[ \frac{\partial E}{\partial N} =: \mu \] für die drei partiellen Ableitungen.
Betrachtet man ein System im Kontakt mit einem anderen System, so gleichen sich die intensiven Variablen wie beispielsweise die Temperaturen aneinander an. Es ist daher oft nützlich, beispielsweise statt der Entropie \(S\) oder der Energie \(E\) die entsprechende partielle Ableitung \( \frac{\partial E}{\partial S} =: T \) zur Beschreibung des Systems zu verwenden. Statt eines abgeschlossenen Systems mit vorgegebener Energie \(E\) könnte man dann ein System im Kontakt mit einem anderen sehr großen System (Wärmebad) betrachten (beispielsweise die großräumige Umgebung), das die Temperatur \(T\) vorgibt (z.B. Zimmertemperatur) oder den üblichen Atmosphärendruck.
Den Übergang von der Variable \(S\) zur Variable \(T\) könnte man im Prinzip so machen:
Die Gleichung \[ \frac{\partial E}{\partial S} =: T \] definiert die neue Variable \(T\) als Funktion von \(S, V, N\), denn \(E\) hängt ja von diesen Variablen ab. Wir haben also \[ T(S,V,N) \] Normalerweise kann man diese Beziehung umdrehen und \(S\) als Funktion von \(T, V, N\) schreiben: \( S(T,V,N) \). Das kann man nun einsetzen und \(E\) als Funktion von \(T, V, N\) schreiben: \[ E( S(T,V,N), V, N) \] Bildet man nun \(dE\), so führt der Term \(T \, dS \) zu Produkten wie \[ \frac{\partial E}{\partial S} \, \frac{\partial S}{\partial T} \, dT \] denn \(S\) ist ja nun keine Variable mehr und muss durch Änderungen in \(T\) usw. ausgedrückt werden, eben als \(S(T,V,N)\).
Es gibt aber einen Trick, um den unangenehmen Term \(T \, dS \) loszuwerden: Statt \(E\) betrachten wir die neue Funktion \[ F := E - T \, S \] d.h. wir ziehen einfach noch das Produkt von alter und neuer Variable ab.
Man bezeichnet \(F\) auch als freie (Helmholtz-) Energie. In der Chemie ist übrigens der Buchstabe \(A\) statt \(F\) gebräuchlich.
Das Abziehen von \(T \, S \) bewirkt, dass der Term \(T \, dS \) in \(dF\) wegfällt und durch \( - S dT \) ersetzt wird – wir haben also die Änderung \(dS\) nach der alten Variable \(S\) durch die Änderung \(dT\) nach der neuen Variablen \(T\) ersetzt: \[ dF = dE - T \, dS - S \, dT = \] \[ = T \, dS - p \, dV + \mu \, dN - T \, dS - S \, dT = \] \[ = - p \, dV + \mu \, dN - S \, dT = \] \[ = - S \, dT - p \, dV + \mu \, dN \] Da hier nur noch die Änderungen \(dT, dV, dN\) stehen bleiben, ist es natürlich sinnvoll, \(F\) als Funktion von \(T, V, N\) anzusehen, also \( F := E - T \, S \) als Funktionsdefinition \[ F(T,V,N) := \] \[ = E( S(T,V,N), V, N) - T \, S(T,V,N) \] zu verstehen – das nennt man eine Legendre-Transformation.
Analog geht man in der klassischen Mechanik von der Lagrangefunktion \(L(v,x)\) über \[ p := \frac{\partial L}{\partial v} \] zur Hamiltonfunktion \[ H(p,x) = p \, v - L \] über – mit etwas anderen Vorzeichen, siehe Quantenfeldtheorie und Eichfelder, Kapitel 3).
Das totale Differential \[ dF(T,V,N) = \frac{\partial F}{\partial T} \, dT + \frac{\partial F}{\partial V} \, dV + \frac{\partial F}{\partial N} \, dN \] führt dann durch Vergleich mit \[ dF = - S \, dT - p \, dV + \mu \, dN \] von oben zu \[ \frac{\partial F}{\partial T} = - S \] \[ \frac{\partial F}{\partial V} = - p \] \[ \frac{\partial F}{\partial N} = \mu \] Wozu können wir das nun gebrauchen?
Besonders nützlich ist die freie Energie, wenn die Temperatur \(T\) konstant ist, d.h. wenn es sich um einen isothermen Prozess handelt – dann ist nämlich die neue Variable \(T\) fix und demnach \(dT = 0\).
Ein Beispiel für einen solchen Prozess liefert ein kleines Teilsystem, das mit einem viel größeren System (einem Wärmebad oder Wärmereservoir) thermisch so eng gekoppelt ist, dass sich seine Temperatur schnell der Temperatur des Wärmebades anpasst. Das Wärmebad soll dabei so groß sein, dass wir dessen Temperatur als konstant ansehen können (es könnte z.B. die Umgebung des Systems sein). Zusätzlich wollen wir davon ausgehen, dass sich die Teilchenzahl nicht ändert: \(dN = 0\). Dann ist bei einer isothermen Volumenänderung \[ dF = - p \, dV \] d.h. die Änderung der freien Energie ist bei einem isothermen Prozess mit konstanter Teilchenzahl gleich der Arbeit, die am System verrichtet wird. Die freie Energie merkt also bei diesem Prozess nichts von der Wärmemenge, die man braucht, um die Temperatur konstant zu halten.
Schauen wir uns nun den Fall an, dass sich das System noch nicht im thermischen Gleichgewicht befindet. Allerdings müssen wir annehmen, dass bereits ein Temperatur- und Druckausgleich im System stattgefunden hat, damit wir mit einem Wert für \(T\) und \(p\) auskommen und keine Temperatur- und Druckverteilung brauchen.
Das chemische Potential \(\mu\) könnte dagegen noch vom Ort abhängen, d.h. wir können das System noch nicht durch ein einheitliches \(\mu\) kennzeichnen. Es könnte also noch Teilchenströme innerhalb des Systems geben, die die Entropie erhöhen können. Die Teilchenzahl soll wieder konstant sein: \(dN = 0\). Von oben wissen wir, dass in diesem Fall \[ dS \gt \frac{\delta Q}{T} \] gilt (Gleichheit gilt bei quasistatischen Vorgängen im thermischen Gleichgewicht).
Nun gilt die Gleichung \[ dE = \delta Q + \delta W \] ganz allgemein (für \(dN = 0\)), also auch hier. Da der Druck überall gleich ist, können wir außerdem \( \delta W = - p \, dV \) einsetzen. Freigestellt nach \(\delta Q\) ergibt das \[ \delta Q = dE + p \, dV \] und somit \[ dS \gt \frac{\delta Q}{T} = \frac{dE + p \, dV}{T} \] Hier können wir \(dE\) durch \(dF\) ausdrücken: \[ dF = dE - T \, dS - S \, dT \] ergibt \[ dE = dF + T \, dS + S \, dT \] Oben eingesetzt ergibt das \[ dS \gt \frac{dE + p \, dV}{T} = \] \[ = \frac{dF + T \, dS + S \, dT + p \, dV}{T} \] Hier können wir mit \(T\) multiplizieren und auf beiden Seiten den Term \( T \, dS \) wegnehmen: \[ 0 \gt dF + S \, dT + p \, dV \] oder umgestellt \[ dF \lt - S \, dT - p \, dV \] Bei einer quasistatischen Änderung (sowie \(dN = 0\)) haben wir hier ein Gleichheitszeichen, was die Formel von weiter oben ergibt.
Was bedeutet diese Gleichung? Sie macht besonders Sinn, wenn wir den Fall \(dT = 0\) sowie \(dV = 0\) betrachten. Die Temperatur soll also durch Kontakt mit dem Wärmebad festliegen, und außerdem halten wir das Volumen fest. Dann gilt nach der Gleichung \( dF \lt 0 \) und im Gleichgewicht schließlich \( dF = 0 \). Das System strebt also ein Minimum der freien Energie an.
Da Druck und Temperatur bereits ausgeglichen sind, kann dieses Absinken der freien Energie nur noch durch interne Teilchenflüsse (Konzentrationsausgleich) und chemische Reaktionen geliefert werden. Das macht die freie Energie für die Chemie so interessant! Die chemische Reaktion läuft bei konstanter Temperatur und festem Volumen so ab, dass die freie Energie minimal wird. Dabei freiwerdende (oder verbrauchte) Energie wird an das Wärmebad abgegeben bzw. aus diesem entnommen.
Man kann die Voraussetzung, dass die Temperatur die ganze Zeit über durch das Wärmebad festliegen soll, sogar fallenlassen (der Prozess muss also nicht ständig isotherm sein). Wichtig ist nur, dass die Temperatur zu Beginn denselben Wert wie am Schluss hat, d.h. \(\Delta T = 0\). Das System beginnt also in einem Nicht-Gleichgewichtszustand (aber bei überall gleicher Temperatur \(T\) des Wärmebades) und steuert dann irgendwie auf das Gleichgewicht zu, bei dem es dann schließlich wieder überall dieselbe Temperatur wie das Wärmebad annimmt.
Zwischendurch darf es sich vorübergehend aber durchaus erhitzen oder abkühlen. Dass das geht, sieht man so:
Zu Beginn und am Schluss ist \(F\) jeweils gleich \(E - T \, S\) (mit unterschiedlichem \(E\) und \(S\), aber gleichem \(T\), wobei \(T\) zugleich die Temperatur des Wärmebades (z.B. des Labors) ist). Die (nicht unbedingt kleine) Änderung von \(F\) ist also \[ \Delta F = \Delta E - T \, \Delta S \] Nun ist die Summe der Entropieänderungen von System und Wärmebad positiv, denn sie geben die Gesamtentropie an: \[ \Delta S + \Delta S' \gt 0 \] oder umgestellt \[ \Delta S \gt - \Delta S' \] wobei \(\Delta S'\) die Entropieänderung des Wärmebades ist. Also ist \[ \Delta F = \Delta E - T \, \Delta S \lt \Delta E + T \, \Delta S' \] Aus Sicht des Wärmebades verläuft der Prozess quasistatisch (das wollen wir so annehmen, da es hinreichend groß sein soll, so dass es sich ständig annähernd im thermischen Gleichgewicht befindet). Es ist also \[ \Delta S' = \frac{\Delta Q'}{T} \] (\(T\) ist ja im großen Wärmebad annähernd konstant). Damit haben wir \[ \Delta F \lt \Delta E + \Delta Q' \] Da Volumen und Teilchenzahl konstant sind und demnach die Energieübertragung nur durch Wärme erfolgt, ist \[ \Delta E = -\Delta E' = - \Delta Q' \] und somit \[ \Delta E + \Delta Q' = 0 \] Also haben wir als Endergebnis \[ \Delta F \lt 0 \]
Fassen wir zusammen:
|
Die freie (Helmholtz-) Energie \(F\): Die freie (Helmholtz-) Energie \(F\) kann man aus der Energie durch Subtraktion von \(T \, S\) erhalten: \[ F := E - T \, S \] Für eine (nicht unbedingt quasistatische) Änderung von \(F(T,V,N)\) gilt: \[ dF \le - S \, dT - p \, dV + \mu \, dN \] Im thermischen Gleichgewicht ist \(F\) eine Funktion von \(T, V, N\) (d.h. \(S\) wurde durch \(T\) ersetzt), und in der obigen Formel gilt das Gleichheitszeichen für quasistatische Änderungen. Bei einem isothermen quasistatischen Prozess ohne Teilchenaustausch (also \(dT = 0\) wegen Wärmebad sowie \(dN = 0\)) gibt also \[ dF = - p \, dV \] die am System verrichtete Arbeit aufgrund der Volumenänderung an. Ist das System dagegen noch nicht im thermischen Gleichgewicht, aber zusätzlich \(dV = 0\), so ist \[ dF \le 0 \] Die freie Energie strebt also bei einem isothermen Prozess mit konstantem Volumen und Teilchenzahl ein Minimum an. Beispielsweise können Konzentrationsausgleiche oder chemische Reaktionen stattfinden, bis das Gleichgewicht und damit das Minimum von \(F\) erreicht sind. Dabei kann man die Voraussetzung, dass die Temperatur die ganze Zeit über durch das Wärmebad festliegen soll, sogar fallenlassen (der Prozess muss also nicht ständig isotherm sein). Wichtig ist nur, dass die Temperatur zu Beginn überall denselben Wert wie am Schluss hat, festgelegt durch das Wärmebad. Die freie Energie \(F\) wird dann am Schluss (im Gleichgewicht) kleiner sein als zu Beginn.
|
Vollkommen analog kann man auch bei den anderen Variablen vorgehen.
So kann man von \(V\) zu \(- p\) übergehen und die
sogenannte Enthalpie
\[
H(S,p,N) = E + p \, V
\]
definieren.
Nützlich ist sie besonders für
isobare Prozesse, bei denen also der Druck konstant bleibt.
Das kann man z.B. durch einen beweglichen Gaskolben erreichen, der eine konstante Kraft
ausübt.
Oder man macht beides: \(S\) durch \(T\) ersetzen sowie \(V\) durch \(- p\). Hier definiert man die freie Enthalpie \[ G(T,p,N) = E - T \, S + p \, V \] Ein System mit konstanter Temperatur, Druck und Teilchenzahl, das sich noch nicht im thermischen Gleichgewicht befindet, strebt ein Minimum der freien Enthalpie an, d.h. Konzentrationsausgleiche, chemische Reaktionen und Volumenänderungen laufen in die entsprechende Richtung. Dieser Fall kommt in der Chemie sehr häufig vor: die Umgebung gibt den Luftdruck vor und liefert auch das Wärmebad. Wie bei der freien Energie können wir auch hier die Bedingung fallenlassen, dass Druck und Temperatur ständig konstant sein müssen – sie müssen nur zu Beginn und am Ende des Prozesses gleich dem Außendruck und der Außentemperatur sein. Das weist man ganz analog zur freien Energie nach: \[ \Delta G = \] \[ = \Delta \, E - T \, \Delta S + p \, \Delta V \lt \] \[ \lt \Delta \, E + T \, \Delta S' + p \, \Delta V = \] \[ = \Delta E + T \, \Delta S' - p \, \Delta V' = \] \[ = \Delta E + \Delta Q' + \Delta W' = \] \[ = \Delta E + \Delta E' = 0 \] Wieder haben wir verwendet, dass aus Sicht des Wärmebades der Prozess quasistatisch abläuft, also das thermische Gleichgewicht des Wärmebades nicht sonderlich stört.
Eine weitere nützliche Möglichkeit besteht darin, \(S\) durch \(T\) sowie \(N\) durch \(\mu\) zu ersetzen
und das großkanonische Potential
\[
J(T,V,\mu) = F - \mu \, N =
\]
\[ = E - T \, S - \mu \, N
\]
einzuführen (hier werden auch oft die
Buchstaben \(\Omega\) oder \(\phi\) statt \(J\) verwendet, aber die haben wir oben bereits
für andere Dinge benutzt).
Dann wäre bei quasistatischen Änderungen
\[
dJ =
dF - \mu \, dN - N \, d\mu =
\]
\[ = - S \, dT - p \, dV + \mu \, dN - \mu \, dN - N \, d\mu =
\]
\[
= - S \, dT - p \, dV - N \, d\mu
\]
Daraus liest man für die partiellen Ableitungen ab:
\[
\frac{\partial J}{\partial T} = - S
\]
\[
\frac{\partial J}{\partial V} = - p
\]
\[
\frac{\partial J}{\partial \mu} = - N
\]
Zusammenfassung:
Wie wir gesehen haben,
können wir ganz flexibel extensive Variablen (also \(S, V, N\)) teilweise oder ganz durch
intensiven Variablen (also \(T, p, \mu\)) ersetzen, die wir beispielsweise durch ein
großes Wärmebad vorgeben können. Dazu können wir
passende thermodynamische Potentiale definieren.
Alle diese Beschreibungen des thermischen Gleichgewichtes sind
dabei gleichwertig zueinander und wir können
uns die jeweils günstigste aussuchen.
Mikroskopisch macht es einen Unterschied, ob wir beispielsweise \(E\) vorgeben oder lieber \(T\). Vorgabe von \(E\) führt zum mikrokanonischen Ensemble, Vorgabe von \(T\) zum kanonischen Ensemble. Letztlich können wir jedem Dreier-Satz von Variablen ein thermodynamisches Potential und ein statistisches Ensemble zuordnen. Makroskopisch sind aber alle diese Potentiale und statistischen Ensembles gleichwertig. Die Details zu den verschiedenen statistischen Ensembles werden wir uns gleich noch ansehen.
Im Prinzip bezeichnet man alle Gleichungen, bei denen man ein thermodynamisches Potential nach einer Größe partiell ableitet und diese Ableitung in Bezug zu einer anderen Größe setzt, auch als Zustandsgleichungen. So ist die Gleichung \[ \frac{1}{T} = \frac{\partial S(E,V,N)}{\partial E} \] eine Zustandsgleichung, die einen Zusammenhang zwischen den Größen \(T, E, V\) und \(N\) herstellt. Da normalerweise \(E\) mit zunehmendem \(T\) anwächst, kann man diesen Zusammenhang nach \(E\) freistellen und \(E\) als Funktion von \(T, V, N\) schreiben. Das bezeichnet man auch als kalorische Zustandsgleichung.
Genau diese Rechnung haben wir übrigens oben kurz nach der Einführung der Temperatur bereits gemacht: Wir haben die Gleichung \[ \epsilon = \frac{E}{N} = b \, k \, T \] hergeleitet. Bei einem idealen Gas wäre dann \( b = 3/2 \) und wir hätten \[ E = 3/2 \, N \, k \, T \] als kalorische Zustandsgleichung des idealen Gases.
Statt für die Energie interessiert man sich häufig für den Druck, den man ebenfalls als Funktion von \(T, V, N\) schreiben möchte. Der Druck war definiert als die partielle Ableitung \[ \frac{p}{T} = - \frac{\partial S(E,V,N)}{\partial dV} \] Diese partielle Ableitung wertet man aus und setzt danach die kalorische Zustandsgleichung für \(E\) ein, schreibt also \(E(T,V,N)\). Den entstehenden Zusammenhang zwischen \(p, T, V, N\) bezeichnet man als thermische Zustandsgleichung.
Man kann diese Gleichung auch mit Hilfe der freien Energie \(F\) herleiten, sofern diese bekannt ist: \[ - p = \frac{\partial F(T,V,N)}{\partial V} \] Schauen wir uns als Beispiel wieder das ideale Gas an, wobei wir von oben die Formel \[ \phi = B^{N} \, V^{N} \, \epsilon^{b N} \] für die Zahl der Mikrozustände bis zur Energie \(E\) verwenden: \[ \frac{p}{T} = - \frac{\partial S}{\partial V} = \] \[ = k \, \frac{\partial \ln{\Omega}}{\partial V} = \] \[ k \, \frac{\partial \ln{\phi}}{\partial V} = \] \[ k \, \frac{1}{\phi} \, \frac{\partial \phi}{\partial V} = \] \[ = k \, \frac{1}{V^{N}} \, N \, V^{N - 1} = \] \[ = k \, \frac{N}{V} \] Etwas umgestellt lautet die Formel dann \[ p \, V = N \, k \, T \] Das ist die wohlbekannte Zustandsgleichung des idealen Gases.
Das mikrokanonische Ensemble, das wir bisher verwendet haben, setzt streng genommen ein makroskopisch isoliertes System voraus, dessen Energie bis auf eine minimale Unschärfe \( \delta E \) (makroskopisch klein, mikroskopisch groß) fest vorgegeben ist.
Wir haben aber dieses Ensemble auch dann verwendet, wenn das System nicht makroskopisch isoliert ist, sondern in (schwachem) Kontakt mit anderen System steht. Dabei haben wir Energiefluktuationen, die außerhalb der vorgegebenen Unschärfe \(\delta E\) liegen, einfach weggelassen. Das ist gerechtfertigt, wenn solche Fluktuationen extrem selten sind. Das ist bei makroskopischen Systemen der Fall, wie wir noch sehen werden. Bei mikroskopischen Systemen stimmt es dagegen nur, falls diese sehr gut von der Außenwelt abgeschirmt sind. Die mikrokanonische Verteilung mit ihrer festen Unschärfe \( \delta E \) taugt also nichts für Systeme aus nur wenigen Teilchen, wenn diese in Wechselwirkung mit ihrer Umgebung stehen.
Versuchen wir, eine Alternative zum mikrokanonischen Ensemble zu finden, die makroskopisch dasselbe leistet, die aber dennoch beliebige Energiefluktuationen prinzipiell zulässt. Dabei können wir nun auf die Begriffe zurückgreifen, die wir am Anfang dieses Kapitels noch nicht hatten, insbesondere auf die Temperatur.
Wir haben ja bei der Diskussion der thermodynamischen Potentiale oben gesehen: Statt durch \(E, V, N\) können wir einen makroskopischen Gleichgewichtszustand auch durch \(T, V, N\) kennzeichnen.
Wir geben also nicht mehr die Energie (mit ihrem kleinen Intervall) vor, sondern die Temperatur.
Man kann sich überlegen, dass man dadurch automatisch den Mittelwert der Energie festlegt. Im Prinzip sind aber beliebige Energiefluktuationen möglich. Bei makroskopischen Systemen sind größere Energiefluktuationen nun extrem selten, wie wir noch sehen werden. Die Energie liegt also fast immer in einem kleinen Energieintervall \(\delta E\) bei ihrem Mittelwert – eine nachträgliche Rechtfertigung für das mikrokanonische Ensemble.
Wenn wir die Temperatur \(T\) statt der Energie \(E\) verwenden, so müssen wir nicht mehr fordern, dass unser System makroskopisch abgeschlossen ist. Es kann (und soll) in thermischem Gleichgewicht mit einem großen Wärmebad sein, das dieselbe Temperatur aufweist. Man kann auch sagen: Das Wärmebad gibt die Temperatur vor.
Durch die identische Temperatur ist sichergestellt, dass bei konstantem Volumen und fester Teilchenzahl keine makroskopischen Energiemengen übertragen werden können. Mikroskopische Energiefluktuationen zwischen unserem System und dem Wärmebad sind aber möglich.
Dieses Bild ist sehr realistisch, denn da man kein makroskopisches System absolut isolieren kann, befindet es sich immer im Kontakt mit der Außenwelt – selbst wenn es der leere Weltraum mit seiner Wärmestrahlung ist. Diese Außenwelt stellen wir hier als Wärmebad dar.

Die beiden Systeme A und A' sollen also
zusammen ein makroskopisch abgeschlossenes System Ag im thermischen
Gleichgewicht mit Energie \(E_{g}\) bilden, das im Ganzen durch ein mikrokanonisches Ensemble
mit einem entsprechendem sehr kleinen Energieintervall \(\delta E\)
beschrieben wird.
Wir brauchen also das mikrokanonische Ensemble als Ausgangspunkt für unser Gesamtsystem!
So ganz nutzlos waren unsere Überlegungen dazu also nicht! Dabei soll A' ein makroskopisches Wärmebad mit Temperatur \(T\) sein, das sehr viel größer als System A ist, so dass ein Energieaustausch die Temperatur von A' nicht ändert. Ein Volumen- oder Teilchenaustausch soll nicht stattfinden.
Wie wir noch sehen werden, muss unser System A dabei nicht unbedingt makroskopisch sein.
Es kann auch ein einzelnes Teilchen sein, das im thermischen Gleichgewicht ständig Energie mit dem Wärmebad A' austauscht. Die Temperatur ist dann über das Wärmebad definiert. So kann beispielsweise Ag auch ein Gas in einem Behälter sein, A ist ein einzelnes Gasteilchen in diesem Behälter und A' sind alle übrigen Gasteilchen in demselben Behälter (A und A' müssen also nicht unbedingt räumlich getrennt sein).
Die Wahrscheinlichkeiten \(P_{n}\), mit der die einzelnen Mikrozustände im Teilsystem A auftreten, ergeben nun wieder eine statistische Gesamtheit, die man als kanonisches Ensemble bezeichnet.
Mikroskopisch wird sich dieses Ensemble von dem bisherigen mikrokanonischen Ensemble unterscheiden, aber für ein makroskopisches System A muss es zu identischen makroskopisch Ergebnissen führen, denn wir haben oben ja gesehen, dass man Gleichgewichts-Makrozustände wahlweise durch \((E,V,N)\) bzw. \((S,V,N)\) oder durch \((T,V,N)\) kennzeichnen kann. Versuchen wir, die Wahrscheinlichkeiten \(P_{n}\) für das kanonische Ensemble auszurechnen. Das ist glücklicherweise recht einfach:
Jeder Zustand \( |n_{g}\rangle \) des Gesamtsystems Ag setzt sich zusammen aus einem Zustand \( |n\rangle \) unseres Teilsystems A und einem Zustand \( |n'\rangle \) des Wärmebades A'. Wir schreiben auch \[ |n_{g}\rangle = |n,n'\rangle \] (das kann man als Tensorprodukt lesen). Dabei haben wir die Wechselwirkung zwischen A und A' weitgehend vernachlässigt, so dass wir die Zustände der beiden Teilsysteme einfach auf diese Weise zum Gesamtzustand zusammensetzen dürfen. Entsprechend addieren sich auch die Energien der beiden Zustände einfach zur Energie des Gesamtzustandes: \[ E_{g}(n,n') = E_{n} + E'_{n'} \] Die Wechselwirkung soll nur soweit eine Rolle spielen, dass sie Energiefluktuationen zwischen A und A' ermöglicht, ohne dabei die Quantenzustände der beiden Teilsysteme zu verändern. A und A' dürfen also nicht zu stark miteinander wechselwirken.
Da unser Gesamtsystem durch ein mikrokanonisches Ensemble beschrieben wird, muss die Gesamtenergie \( E_{g}(n,n') = E_{n} + E'_{n'} \) in einem Energieintervall zwischen \( E_{g} \) und \( E_{g} + \delta E \) liegen, d.h. es ist \[ E_{g} \lt E_{n} + E'_{n'} \lt E_{g} + \delta E \] Wir können \(E_{n}\) subtrahieren und erhalten \[ E_{g} - E_{n} \lt E'_{n'} \lt E_{g} + \delta E - E_{n} \] In diesem Bereich muss die Energie \(E'_{n'}\) des Wärmebades liegen, wenn wir eine bestimmte Energie \(E_{n}\) für unser System A sowie das Gesamtenergie-Intervall vorgeben.
Die Wahrscheinlichkeit, dass sich System A im Zustand \( |n\rangle \) und Wärmebad A' im Zustand \( |n'\rangle \) befindet, nennen wir \(P_{n,n'}\). Wenn wir nun \(n\) festhalten und über alle \(n'\) summieren, die energetisch erlaubt sind, dann erhalten wir die Wahrscheinlichkeit, dass sich System A im vorgegebenem Zustand \( |n\rangle \) und Wärmebad A' in irgendeinem energetisch dazu passenden Zustand \( |n'\rangle \) befindet: \[ P_{n} = \sum_{n'}' P_{n,n'} \] Energetisch passend sind alle Wärmebad-Zustände \( |n'\rangle \), deren Energie \(E'_{n'}\) die Beziehung \[ E_{g} - E_{n} \lt E'_{n'} \lt E_{g} + \delta E - E_{n} \] erfüllen. Über diese \(n'\) geht die Summe (daher der Strich am Summenzeichen, der die Energiebedingung symbolisieren soll). Man kann auch sagen: Bei gegebenem \(n\) ist für alle anderen \(n'\) (die die Energiebedingung nicht erfüllen) die Wahrscheinlichkeit \( P_{n,n'} = 0 \).
Die Summe können wir leicht ausrechnen:
Da das Gesamtsystem ein mikrokanonisches Ensemble sein soll,
ist
\[
P_{n,n'} = \frac{1}{\Omega_{g}(E_{g})}
\]
und zwar
unabhängig von \(n\) und \(n'\) –
alle Mikrozustände im Energieintervall sind ja im mikrokanonischen Ensemble
gleich wahrscheinlich, und \( \Omega_{g}(E_{g}) \) ist die Zahl der
Mikrozustände des Gesamtsystems im Energieintervall.
Insgesamt haben wir also \[ P_{n} = \sum_{n'}' \, \frac{1}{\Omega_{g}(E_{g})} \] Diese Summe enthält \( \Omega'(E_{g} - E_{n}) \) identische Summanden, denn \( \Omega'(E_{g} - E_{n}) \) ist die Zahl der Wärmebad-Zustände im Energieintervall von \( E_{g} - E_{n} \) bis \( E_{g} + \delta E - E_{n} \), und über diese Zustände wird ja summiert. Also lautet unser Ergebnis: \[ P_{n} = \frac{\Omega'(E_{g} - E_{n})}{\Omega_{g}(E_{g})} \] Wir ermitteln also unter den vielen Zuständen \( |n,n'\rangle \) im Gesamtenergie-Intervall (das sind \( \Omega_{g}(E_{g}) \) Stück) den Anteil derjenigen Zustände, bei denen unser System A im vorgegebenem Zustand \( |n\rangle \) mit Energie \(E_{n}\) ist und das Wärmebad sich in irgendeinem Zustand \( |n'\rangle \) im dazu passenden Energieintervall von \( E_{g} - E_{n} \) bis \( E_{g} + \delta E - E_{n} \) befindet (das sind \( \Omega'(E_{g} - E_{n}) \) Stück).
Wichtig ist: Die obige Formel gilt auch für ein nicht-makroskopisches System A, denn die Terme rechts setzen nur voraus, dass das Wärmebad A' und das Gesamtsystem Ag makroskopisch sind.
Bei der mikrokanonischen Verteilung für ein makroskopisches System A hätten wir nun gesagt: Wir nehmen an, dass alle \(P_{n}\) im schmalen Energieintervall gleich groß sind, also unabhängig von \(n\) sind. Rechts hätten wir dann \(E_{n}\) durch \(E\) ersetzt, denn das Energieintervall soll ja sehr schmal sein, so dass \(E_{n}\) sehr nahe bei \(E\) liegt. Damit hätten wir \[ P_{n} = \frac{\Omega'(E_{g} - E)}{\Omega_{g}(E_{g})} \] gehabt. Nun gilt mikrokanonisch (siehe weiter oben) \[ \Omega_{g}(E_{g}) = \Omega(E) \cdot \Omega'(E_{g} - E) \] und somit \[ P_{n} = \frac{\Omega'(E_{g} - E)}{\Omega_{g}(E_{g})} = \frac{1}{\Omega(E)} \] für \(E_{n}\) im Energieintervall bei \(E\). Das wäre genau unsere mikrokanonische Verteilung.
Bei der kanonischen Verteilung wollen wir dagegen alle Energiewerte \(E_{n}\) zulassen, auch außerhalb des Energieintervalls, dafür aber die Temperatur festlegen. Dabei wollen wir ausnutzen, dass das Wärmebad A' viel größer als unser System A ist.
Schauen wir uns dazu den Zähler \( \Omega'(E_{g} - E_{n}) \) in unserer Formel \[ P_{n} = \frac{\Omega'(E_{g} - E_{n})}{\Omega_{g}(E_{g})} \] an. Das ist die Zustandanzahl des Wärmebades im Energieintervall bei der Energie \( E_{g} - E_{n} \). Aus den \(E_{n}\) können wir später mit Hilfe der \(P_{n}\) eine mittlere Energie \(E\) für unser System A ausrechnen, und diese Energie wollen wir verwenden, um \[ \Omega'(E_{g} - E_{n}) = \] \[ = \Omega'(E_{g} - E + E - E_{n}) = \] \[ = \Omega'(E' + E - E_{n}) \] zu schreiben, wobei \( E' := E_{g} - E \) dann eine mittlere Energie für das Wärmebad ist und \( E - E_{n} \) die Abweichung der Mikrozustands-Energie vom Energie-Mittelwert unseres Teilsystems ist (also eine Art Energiefluktuation).
Diese Energiefluktuation des kleinen Teilsystems A wird viel kleiner sein als die mittlere Energie \(E'\) unseres Wärmebades, das wir uns ja unendlich groß vorstellen können. Wir könnten daher auf die Idee kommen, \( \Omega'(E' + E - E_{n}) \) um \(E'\) herum in eine Taylorreihe zu entwickeln und nur die lineare oder quadratische Näherung mitzunehmen.
Das wäre jedoch ungünstig, denn wir wissen ja von oben, dass die Zustandszahl sehr empfindlich von der Energie abhängt, so dass eine solche Näherung vermutlich nicht ausreichend ist. Viel besser ist es, den Logarithmus dieser Zahl (also die Entropie) um \(E'\) zu entwickeln, denn der Logarithmus ist selbst nur relativ wenig energieabhängig. Außerdem wollen wir ja die Temperatur des Wärmebades A' vorgeben, und die ergibt sich automatisch als erste Ableitung des Logarithmus nach der Energie. Also: \[ k \, \ln{\Omega'(E' + E - E_{n})} = \] \[ = S'(E' + E - E_{n}) = \] \[ = S'(E') + \frac{\partial S'(E')}{\partial E'} \, (E - E_{n}) + \, ... = \] \[ = k \, \ln{\Omega'(E')} + \frac{E - E_{n}}{T} + \, ... \] Dabei haben wir \[ \frac{1}{T} = \frac{1}{T'} = \frac{\partial S'(E')}{\partial E'} \] verwendet. Höhere Terme lassen wir nun in sehr guter Näherung weg und teilen durch \(k\): \[ \ln{\Omega'(E' + E - E_{n})} = \] \[ = \ln{\Omega'(E')} + \frac{E - E_{n}}{kT} = \] \[ = \ln{\Omega'(E')} + \ln{\left( e^{\frac{E - E_{n}}{kT} } \right)} = \] \[ = \ln{ \left( \Omega'(E') \, e^{\frac{E - E_{n}}{kT} } \right) } \] Anwenden der Exponentialfunktion ergibt dann \[ \Omega'(E' + E - E_{n}) = \Omega'(E') \, e^{\frac{E - E_{n}}{kT} } \] Das können wir nun im Zähler von \(P_{n}\) einsetzen: \[ P_{n} = \frac{\Omega'(E_{g} - E_{n})}{\Omega_{g}(E_{g})} = \] \[ = \frac{ \Omega'(E') \, e^{(E - E_{n}) / (kT)} }{\Omega_{g}(E_{g})} =: \frac{1}{Z} \, e^{- \frac{E_{n}}{kT}} \] mit \[ \frac{1}{Z} := \frac{\Omega'(E')}{\Omega_{g}(E_{g})} \, e^{\frac{E}{kT}} \] Wichtig: \(Z\) hängt nicht von \(E_{n}\) ab, d.h. die \(E_{n}\)-Abhängigkeit steckt alleine in der Exponentialfunktion. \(Z\) ist also im Grunde ein Normierungsfaktor.
Um \(Z\) auszurechnen, brauchen wir die obige Formel für \(1/Z\) glücklicherweise nicht, denn \(Z\) ist als Normierungsfaktor bereits durch die Tatsache festgelegt, dass \(P_{n}\) eine Wahrscheinlichkeit ist, so dass die Summe über alle \(P_{n}\) gleich 1 sein muss: \[ 1 = \sum_{n} P_{n} = \frac{1}{Z} \, \sum_{n} e^{- \frac{E_{n}}{kT}} \] und somit \[ Z = \sum_{n} \, e^{- \frac{E_{n}}{kT}} \] Diese Summe bezeichnet man als kanonische Zustandssumme. Damit haben wir unser Ziel erreicht:
|
kanonisches Ensemble: Wir betrachten ein (nicht unbedingt makroskopisches) System A mit vorgegebener Temperatur \(T\) (d.h. der Energiemittelwert \(E\) wird im System A vorgegeben). Konkret realisiert man diese Vorgabe dadurch, dass sich A im thermischen Gleichgewicht mit einem sehr großen Wärmebad A' der Temperatur \(T\) befindet. A und A' bilden dabei zusammen ein makroskopisch abgeschlossenes System Ag mit der Energie \(E_{g}\), das durch ein mikrokanonisches Ensemble beschrieben wird. Teilchenzahl und Volumen von A und A' sollen konstant sein. Die Wahrscheinlichkeit für einen Mikrozustand mit Energie \(E_{n}\) im System A ist dann gegeben durch: \[ P_{n} = \frac{1}{Z} \, e^{- \frac{E_{n}}{kT}} \] mit der kanonischen Zustandssumme \[ Z = \sum_{n} \, e^{- \frac{E_{n}}{kT}} \] |
Der wesentliche Unterschied zum mikrokanonischen Ensemble ist, dass
unser System A nicht unbedingt makroskopisch sein muss, und dass
die Wahrscheinlichkeiten \(P_{n}\) nicht mehr nur in einem winzigen Energieintervall
ungleich Null sind (und dort konstant), sondern dass
sie generell ungleich Null sind und exponentiell abnehmen.
Für Energien deutlich oberhalb der Energie \( kT \) werden die
Wahrscheinlichkeiten dann schnell sehr klein. Wir erinnern uns: \( kT \)
entsprach oben einer typischen Einteilchen-Energie.

Woher kommt diese exponentielle Abnahme der Wahrscheinlichkeit mit wachsender Zustandsenergie \(E_n\)?
Wenn wir uns die Rechnung oben ansehen, so finden wir den Grund:
Die Zustandsanzahl \( \Omega'(E_{g} - E_{n}) \)
im Wärmebad nimmt exponentiell ab, wenn wir ihm eine kleine Energiemenge \( E_{n} \)
entziehen (denn die Entropie des Wärmebades nimmt in erster Näherung linear ab,
wobei \(1/T\) die Steigung bestimmt).
Das Gesamtsystem hat entsprechend weniger Möglichkeiten, dem Teilsystem A
diese Energie \(E_{n}\) zur Verfügung zu stellen.
Die kanonische und die mikrokanonische Verteilung sind also sehr unterschiedlich, was die Wahrscheinlichkeiten \( P_{n} \) für die Mikrozustände betrifft. Dennoch sollen sie makroskopisch (also bei makroskopischen Systemen A) zu identischen Beschreibungen führen. Wie kann das sein?
Der Hauptgrund ist: Wenn wir uns ansehen, mit welcher Wahrscheinlichkeit die Energie \(E_{n}\) in einem bestimmten Energieintervall liegt, so sind bei einem makroskopischen System A die kanonische und die mikrokanonische Energieverteilung fast identisch: Beide haben ein extrem scharfes Maximum am Energiemittelwert und sind ansonsten Null oder fast Null.
Bei der mikrokanonischen Verteilung hatten wir dies über das erlaubte kleine Energieintervall \(\delta E\) von Hand extra eingebaut. Bei der kanonischen Verteilung ergibt es sich dagegen von selbst:
Die Zustände werden bei großer Teilchenzahl \(N\) mit zunehmender Energie sehr schnell immer dichter, und zwar ungefähr mit \( E_{n}^{N} \) (wir setzen wieder vereinfacht \(b = 1\)), wobei die Teilchenzahl \(N\) typischerweise bei \(10^{20}\) liegt.
Obwohl die Wahrscheinlichkeit \( P_{n} \) bei größeren Energien exponentiell abnimmt, nimmt die Zustandsdichte so schnell zu, dass die Wahrscheinlichkeit, einen Zustand in einem höher liegenden Energiebereich zu erwischen, zunächst stark wächst. Irgendwann besiegt eine abfallende Exponentialfunktion aber jedes Polynom, selbst ein so stark wachsendes wie \( E_{n}^{N} \). Daher fällt die Wahrscheinlichkeit ab einer bestimmten Energie plötzlich stark ab, denn die Wahrscheinlichkeit \(P_{n}\) wird dann so gering, dass dies durch die wachsende Zustandsdichte nicht mehr kompensiert werden kann.
Mathematisch kann man das so präzisieren: Die Wahrscheinlichkeit, einen Zustand in einem makroskopisch kleinen Energieintervall zwischen \(E\) und \(E + \delta E\) zu finden, ist bei kleinem \(\delta E\) ungefähr gleich der mittleren Wahrscheinlichkeit \[ P(E) = \frac{1}{Z} \, e^{- \frac{E}{kT}} \] für die einzelnen Zustände in diesem Intervall mal der Zustandsanzahl für dieses Intervall, also insgesamt ungefähr proportional zu \[ E^{N} \, e^{- \frac{E}{kT}} \] Für große \(N\) hat diese Funktion ein sehr scharfes Maximum. Bereits bei nur 100 Teilchen ist dieses Maximum schon gut ausgeprägt, wie die folgende Grafik der Funktion \[ x^{100} \, e^{- x} \] mit \( x = E/(kT) \) zeigt:
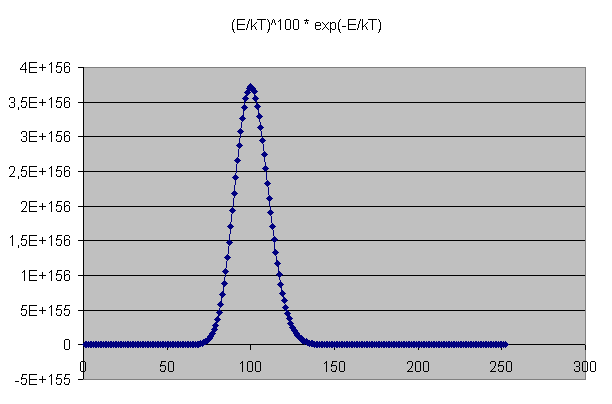
Die Wahrscheinlichkeitdichte, dass ein makroskopisches System mit gegebener Temperatur
eine mittlere Energie \(E\) besitzt, weist ein
starkes Maximum auf, wie die hier dargestellte Funktion
\(
x^{100} \, e^{- x}
\)
mit \( x = E/(kT) \)
bereits bei \(N = 100\) Teilchen zeigt.
Der in der Grafik dargestellte Energie-Peak der kanonischen Verteilung wird
bei der mikrokanonischen Verteilung letztlich durch ein schmales hohes Rechteck
mit Breite \(\delta E\) angenähert, was bei großen \(N\)
(hoher sehr schmaler Peak) eine sehr gute Näherung ergibt.
Es ist oft viel einfacher, mit der kanonischen anstatt mit der mikrokanonischen Verteilung zu rechnen, da es hier kein Hantieren mit dem Energieintervall gibt: Man summiert immer über alle Mikrozustände. Außerdem gilt die kanonische Verteilung auch für mikroskopische Systeme, solange diese im Gleichgewicht mit einem Wärmebad stehen. Man kann also bei der kanonischen Verteilung sehr schön das Entstehen makroskopischen Verhaltens bei wachsender Teilchenzahl untersuchen.
Dazu muss man allerdings beispielsweise wissen, wie man die Entropie für eine kanonische Verteilung berechnen soll. Das können wir aber noch nicht, denn die Entropie hatten wir bisher nur für ein mikrokanonisches Ensemble definiert, also für ein makroskopisch abgeschlossenes System mit vorgegebener Energie \(E\) (bis auf die kleine Unschärfe \(\delta E\)). Wir müssen also diese Definition erweitern, so dass sie auch für ein kanonisches Ensemble anwendbar ist und makroskopisch dieselben Resultate liefert.
Für ein mikrokanonisches Ensemble war die Entropie definiert als \[ S = k \, \ln{\Omega(E)} \] wobei \( \Omega(E) \) die Zahl der Zustände im Energieintervall zwischen \(E\) und \(E + \delta E\) ist. Die Wahrscheinlichkeit \(P_{n}\) für einen Mikrozustand war außerhalb dieses Intervalls gleich Null und innerhalb des Intervalls gleich \[ P_{n} = \frac{1}{\Omega(E)} =: P(E) \] Dabei haben wir jetzt für die konstante Wahrscheinlichkeit im Energieintervall die Bezeichnung \(P(E)\) eingeführt, so dass wir die Entropie auch schreiben können als \[ S = k \, \ln{\Omega(E)} = \] \[ = k \, \ln{\left(\frac{1}{P(E)}\right)} = \] \[ = - k \, \ln{P(E)} \] Je unwahrscheinlicher jeder einzelne erreichbare Mikrozustände im erreichbaren Energieintervall ist (je mehr es also von ihnen gibt), umso größer ist die Entropie.
Vorsicht: \(S\) ist positiv, denn \(P(E)\) ist kleiner als 1, so dass \(\ln{P(E)}\) negativ ist.
Beim Übergang zum kanonischen Ensemble wollen wir \(P(E)\) nun anders interpretieren (denn nun sind ja die einzelnen Mikrozustände nicht mehr gleich wahrscheinlich):
\(E\) soll die mittlere Energie des Systems sein, ist also in dem obigen Bild die Position des Peaks. \(P(E)\) ist dann die Wahrscheinlichkeit für die Mikrozustände bei dieser mittleren Energie, also bei dem Peak. Das macht Sinn, denn die Energie \(E_{n}\) eines makroskopischen Systems liegt mit hoher Wahrscheinlichkeit sehr nahe bei der mittleren Energie \(E\), so dass nur die Wahrscheinlichkeit für die Mikrozustände bei dieser Energie für die makroskopische Entropie relevant ist.
Umgekehrt ist diese Interpretation von \(P(E)\) auch noch für die mikrokanonische Verteilung korrekt, denn die mittlere Energie liegt dort im Energieintervall \(\delta E\), und dort ist \( P(E) \) die konstante Wahrscheinlichkeit der Zustände, so dass wir unsere ursprüngliche Definition der Entropie zurückgewinnen.
Diese erweiterte Definition der Entropie können wir noch etwas umschreiben. Dazu verwenden wir eine besondere Eigenschaft der Wahrscheinlichkeiten \(P_{n}\). Man kann zeigen (siehe z.B. Landau, Lifschitz: Lehrbuch der theoretischen Physik, Statistische Physik), dass man bei konstanter Teilchenzahl die Energieabhängigkeit der Wahrscheinlichkeiten \(P_{n}\) im thermischen Gleichgewicht immer in der Form \[ P_{n} = \alpha \, e^{\beta E_{n}} \] mit energieunabhängigen Koeffizienten \(\alpha\) und \(\beta\) schreiben kann. (dasselbe gilt dann für \(P(E)\), denn \(P(E)\) ist ja das \(P_{n}\) bei dem \(E_{n}\), das bei der mittleren Energie \(E\) liegt). Für den Logarithmus folgt dann nämlich \[ \ln{P_{n}} = \ln{\alpha} + \beta \, E_{n} \] so dass die Additivität der Entropie gewährleistet ist – sowohl Entropie als auch Energie sind ja additive (extensive) Größen, wenn man Systeme zusammensetzt.
Bei der mikrokanonischen Verteilung wäre dann im Energieintervall \(\delta E\) \[ \alpha = \frac{1}{\Omega(E)} \] \[ \beta = 0 \] Bei der kanonischen Verteilung dagegen haben wir \[ \alpha = \frac{1}{Z} \] \[ \beta = - \frac{1}{kT} \] Unsere beiden bisher bekannten Verteilungen haben also die behauptete Energieabhängigkeit. Schreiben wir damit die Entropie nun um, wobei wir \[ E = \sum_{n} P_{n} \, E_{n} \] für den Mittelwert der Energie sowie \[ 1 = \sum_{n} P_{n} \] verwenden: \[ S = - k \, \ln{P(E)} = \] \[ = - k \, \ln{\left( \alpha \, e^{\beta E} \right)} = \] \[ = - k \, \left( \ln{\alpha} + \beta \, E \right) = \] \[ = - k \, \left( \ln{\alpha} + \beta \, \sum_{n} P_{n} \, E_{n} \right) = \] \[ = - k \, \sum_{n} P_{n} \, \left( \ln{\alpha} + \beta \, E_{n} \right) = \] \[ = - k \, \sum_{n} P_{n} \, \ln{P_{n}} = \] \[ = - k \, \langle \ln{P} \rangle \] wobei \[ \langle \ln{P} \rangle = \sum_{n} P_{n} \, \ln{P_{n}} \] der Mittelwert des Logarithmus der Wahrscheinlichkeit ist.
Mit \[ E = \langle E \rangle = \sum_{n} P_{n} \, E_{n} \] könnte man auch kurz schreiben: \[ S = - k \, \ln{P( \langle E \rangle )} = - k \, \langle \ln{P} \rangle \] Fassen wir zusammen:
|
Entropie (verallgemeinerte Definition): Treten die Mikrozustände eines Makrozustandes mit der Wahrscheinlichkeit \(P_{n}\) auf, so ist die Entropie \(S\) dieses Makrozustandes definiert als \[ S = - k \, \sum_{n} P_{n} \, \ln{P_{n}} =: - k \, \langle \ln{P} \rangle \] Im thermischen Gleichgewicht bei konstanter Teilchenzahl ist die Energieabhängigkeit der Wahrscheinlichkeiten allgemein durch \[ P_{n} = \alpha \, e^{\beta E_{n}} \] mit energieunabhängigen Koeffizienten \(\alpha\) und \(\beta\) gegeben. So ist bei der mikrokanonischen Verteilung \( \alpha = 1/\Omega(E) \) und \( \beta = 0 \), bei der kanonischen Verteilung dagegen \( \alpha = 1/Z \) und \( \beta = - 1/(kT) \). Damit kann man die Entropie auch als \[ S = - k \, \ln{P(E)} \] schreiben. Dabei ist \[ E = \langle E \rangle = \sum_{n} P_{n} \, E_{n} \] die mittlere Energie, und \(P(E)\) ist die Wahrscheinlichkeit \(P_{n}\) für einen Mikrozustand bei der mittleren Energie \(E_{n} = E\). Im mikrokanonischen Ensemble ist \( P(E) = 1/\Omega(E) \) im Energieintervall, so dass \( S = - k \, \ln{P(E)} = k \, \ln{\Omega(E)} \) unsere ursprüngliche Definition von oben ergibt.
|
In Kapitel 2 werden wir diese Definition noch einmal
aus Sicht der Informationstheorie näher begründen.
Man kann zeigen, dass bei vorgegebener mittlerer Energie \( E = \langle E \rangle \) die kanonische Verteilung diejenige mit der größten Entropie ist, während bei vorgegebenem sehr kleinen Energieintervall die mikrokanonische Verteilung die Entropie maximiert.
Das ist sogar ein alternativer Weg, um beispielsweise die kanonische Verteilung herzuleiten: Man startet mit der obigen verallgemeinerten Entropiedefinition und maximiert diese Entropie unter der Nebenbedingung, dass die mittlere Energie vorgegeben ist. Die Temperatur spielt dann die Rolle eines Lagrange-Multiplikators. Allerdings muss man dann noch begründen, warum die obige verallgemeinerte Entropie im thermischen Gleichgewicht überhaupt maximal werden soll. Mehr dazu im nächsten Kapitel 2 ).
Wenn man also die Mikrozustände und die Temperatur kennt, so kann man mit der kanonischen Verteilung die Entropie berechnen und damit alle anderen thermodynamischen Größen bestimmen.
Einfacher ist es aber, statt der Entropie die freie Energie \(F\) zu verwenden, denn oben haben wir gesehen, dass die freie Energie \(F(T,V,N)\) das geeignete thermodynamische Potential ist, wenn man die Temperatur als Variable verwenden möchte. Um \(F\) zu berechnen, können wir die oben bereits verwendete Formel \[ S = - k \, ( \ln{\alpha} + \beta \, E ) \] nutzen und die Werte für die kanonische Verteilung einsetzen, also \( \alpha = 1/Z \) und \( \beta = - 1/(kT) \). Damit ist \[ S = - k \, \left( \ln{\left(\frac{1}{Z}\right)} - \frac{E}{kT} \right) = \] \[ = k \, \ln{Z} + \frac{E}{T} \] Diese Gleichung multiplizieren wir mit \(T\) und stellen sie nach \( - kT \, \ln{Z} \) frei: \[ - kT \, \ln{Z} = E - T \, S \] Das ist aber gerade die freie Energie \(F\), d.h. wir haben:
|
Die freie Energie im kanonischen Ensemble: Im kanonischen Ensemble ist die freie Energie \(F(T,V,N)\) durch den Logarithmus der Zustandssumme \[ Z = \sum_{n} \, e^{- \frac{E_{n}}{kT}} \] gegeben. Im Detail gilt: \[ F = - k T \, \ln{Z} \] |
Von oben wissen wir, dass wir andere thermodynamische Größen dann als
partielle Ableitungen von F berechnen können:
\[
\frac{\partial F}{\partial T} = - S
\]
\[
\frac{\partial F}{\partial V} = - p
\]
\[
\frac{\partial F}{\partial N} = \mu
\]
Man berechnet also die Zustandssumme als Funktion von \(T, V, N\) und
kann dann über die obigen Formeln leicht \(F, S, p, \mu\) als Funktionen
von \(T, V, N\) ausrechnen. Über \( F = E - T \, S \) kann man
dann auch \(E\) berechnen. Natürlich kann man alternativ \(S\) auch direkt
über \( S = - k \, \sum_{n} P_{n} \, \ln{P_{n}} \)
und \(E\) über \( E = \sum_{n} P_{n} \, E_{n}\)
berechnen.
In manchen Fällen ist es günstig, nicht nur Energiefluktuationen zwischen dem Wärmebad A' und unserem System A bei identischer Temperatur \(T\) zuzulassen, sondern auch Teilchenzahlfluktuationen bei gleichem chemischen Potential \(\mu\).
Die Rechnung geht dann komplett analog zum vorherigen Abschnitt. Diesmal müssen wir allerdings für einen Mikrozustand \( |n\rangle \) unseres A-Systems nicht mehr nur durch die Energie \(E_{n}\) angeben, sondern auch die Teilchenzahl \(N_{n}\). Die Wahrscheinlichkeit, einen Mikrozustand mit Energie \(E_{n}\) und Teilchenzahl \(N_{n}\) im System A vorzufinden, ist dann gleich \[ P_{n} = \frac{\Omega'(E_{g} - E_{n}, N_{g} - N_{n})} {\Omega_{g}(E_{g}, N_{g})} \] Den Logarithmus des Zählers entwickeln wir wieder um \(E'\) und \(N'\) (wobei \(N\) und \(N'\) analog zu \(E\) und \(E'\) die Mittelwerte in den Systemen A und A' angeben): \[ S'(E' + E - E_{n}, N' + N - N_{n}) = \] \[ = S'(E',N') + \] \[ + \frac{\partial S'(E',N')}{\partial E'} \, (E - E_{n}) + \] \[ + \frac{\partial S'(E',N')}{\partial N'} \, (N - N_{n}) + \] \[ + \, ... = \] \[ = k \, \ln{\Omega'(E',N')} + \] \[ + \frac{E - E_{n}}{T} - \frac{(N - N_{n}) \, \mu}{T} + \, ... \] Dabei haben wir \[ \frac{1}{T} = \frac{1}{T'} = \frac{\partial S'}{\partial E'} \] \[ - \frac{\mu}{T} = - \frac{\mu'}{T'} = \frac{\partial S'}{\partial N'} \] verwendet. Anwenden der Exponentialfunktion und Einsetzen im Zähler von \(P_{n}\) ergibt \[ P_{n} = \] \[ = \frac{\Omega'(E',N')}{\Omega_{g}(E_{g})} \, e^{ \frac{(E - E_{n}) - (N - N_{n}) \mu}{kT} } = \] \[ =: \frac{1}{Z_{G}} \, e^{ \frac{\mu N_{n} - E_{n}}{kT} } \] mit der großkanonischen Zustandssumme \[ \frac{1}{Z_{G}} := \frac{\Omega'(E',N')}{\Omega_{g}(E_{g})} \, e^{\frac{E - \mu N}{kT}} \] Aus der Normierung der \(P_{n}\) (also Summe über alle \(n\) muss 1 sein) folgt hier \[ Z_{G} = \sum_{n} \, e^{\frac{\mu N_{n} - E_{n}}{kT}} \] Zusammengefasst haben wir also:
|
großkanonisches Ensemble: Wir betrachten ein (nicht unbedingt makroskopisches) System A mit vorgegebener Temperatur \(T\) und vorgegebenem chemischen Potential \(\mu\) (d.h. der Energiemittelwert \(E\) und die mittlere Teilchenzahl \(N\) werden vorgegeben). Konkret realisiert man diese Vorgabe dadurch, dass sich A im thermischen Gleichgewicht mit einem sehr großen Wärmebad A' mit Temperatur \(T\) und chemischen Potential \(\mu\) befindet, wobei Teilchenaustausch erlaubt ist. A und A' bilden dabei zusammen ein makroskopisch abgeschlossenes System Ag mit der Energie \(E_{g}\) und der Teilchenzahl \(N_{g}\), das durch ein mikrokanonisches Ensemble beschrieben wird. Das Volumen von A und A' soll konstant sein. Energie und Teilchenzahl von A und A' dürfen aber um ihre Mittelwerte schwanken. Die Wahrscheinlichkeit für einen Mikrozustand mit Energie \(E_{n}\) und Teilchenzahl \(N_{n}\) im System A ist dann gegeben durch: \[ P_{n} = \] \[ =: \frac{1}{Z_{G}} \, e^{ \frac{\mu N_{n} - E_{n}}{kT} } \] mit der großkanonischen Zustandssumme \[ Z_{G} = \sum_{n} \, e^{\frac{\mu N_{n} - E_{n}}{kT}} \] |
Man kann nun wieder zeigen, dass für makroskopische Körper die Teilchenzahl \(N_{n}\)
mit hoher Wahrscheinlichkeit sehr nahe an ihrem Mittelwert \(N\) liegt, analog zur Energie.
Für makroskopische Körper ergibt daher das großkanonische Ensemble wieder dieselben
thermodynamischen Größen wie das kanonische oder das mikrokanonische Ensemble zuvor.
Die mikroskopischen Teilchenzahl-Fluktuationen spielen makroskopisch keine Rolle.
Oben haben wir gesehen, dass das großkanonische Potential \(J(T,V,\mu)\) das geeignete thermodynamische Potential ist, wenn man die Temperatur und das chemische Potential als Variable verwenden möchte. Um \(J\) zu berechnen, können wir wie bei der kanonischen Verteilung vorgehen. Dabei muss \(\alpha\) allerdings durch \[ \alpha \, e^{\frac{\mu N_{n}}{kT}} \] ersetzt werden, was in der Entropie zu einem Zusatzterm führt, d.h. \[ S = \] \[ = - k \, \sum_{n} P_{n} \left( \frac{\mu N_{n}}{kT} + \ln{\alpha + \beta E_{n}} \right) = \] \[ = - k \, \left( \frac{\mu N}{kT} + \ln{\alpha + \beta E} \right) = \] \[ = - \frac{\mu}{T} \, N + k \ln{Z_{G}} + \frac{E}{T} \] wobei hier die großkanonische Zustandssumme \(Z_{G}\) verwendet wird. Diese Gleichung multiplizieren wir wieder mit \(T\) und stellen sie nach \( - kT \, \ln{Z_{G}} \) frei: \[ - kT \, \ln{Z_{G}} = E - T \, S - \mu \, N \] Das ist aber gerade das großkanonische Potential \(J\) , d.h. wir haben:
|
Das großkanonische Potential im großkanonischen Ensemble: Im großkanonischen Ensemble ist das großkanonische Potential \(J(T,V,\mu)\) durch den Logarithmus der großkanonischen Zustandssumme \[ Z_{G} = \sum_{n} e^{\frac{\mu N_{n} - E_{n}}{kT}} \] gegeben. Im Detail gilt: \[ J = - k T \, \ln{Z_{G}} \] |
Von oben wissen wir, dass wir andere Thermodynamische Größen dann als
partielle Ableitungen von \(J\) berechnen können:
\[
\frac{\partial J}{\partial T} = - S
\]
\[
\frac{\partial J}{\partial V} = - p
\]
\[
\frac{\partial J}{\partial \mu} = - N
\]
Besonders die letzte Gleichung ist interessant, denn sie erlaubt es, die
mittlere Teilchenzahl \(N\) zu berechnen, was wir gleich auch nutzen werden!
Da diese Gleichung so wichtig ist, möchte ich hier noch einmal ihre
Gültigkeit direkt nachweisen:
\[
N = - \frac{\partial J}{\partial \mu} =
\]
\[
k T \, \frac{\partial}{\partial \mu} \ln{Z_{G}}
=
\]
\[ =
k T \, \frac{1}{Z_{G}} \, \frac{\partial Z_{G}}{\partial \mu}
=
\]
\[
=
k T \, \frac{1}{Z_{G}} \, \sum_{n}
\frac{N_{n}}{kT} \, e^{\frac{\mu N_{n} - E_{n}}{kT}}
=
\]
\[ =
\sum_{n} N_{n} \, P_{n}
\]
Wir haben nun bereits mehrere thermodynamische Potentiale und einige damit zusammenhängende statistische Ensembles kennengelernt. Vermutlich ist Ihnen, lieber Leser, dabei ein allgemeines Prinzip aufgefallen:
Wir haben mit drei extensiven Größen begonnen, um einen Gleichgewichtszustand zu charakterisieren: \(E, V, N\). Dazu haben wir ein passendes statistisches Ensemble definiert, bei dem diese drei Größen fest vorgegeben waren: das mikrokanonische Ensemble. Die kleine Energieunschärfe \(\delta E\) diente dabei nur dazu, sicherzustellen, dass genügend viele Mikrozustände zu diesem Makrozustand gehören, denn ein makroskopisches System lässt sich prinzipiell niemals so gut von seiner Umgebung isolieren, als dass es in einem einzigen scharfen Energie-Mikrozustand \(E_n\) existieren könnte.
Man kann nun kleine Fluktuationen in einer oder mehrerer dieser Größen zulassen, wobei der Mittelwert aber vorgegeben bleibt. Das erreicht man durch entsprechenden Kontakt mit einem großen Wärmebad. Damit der Mittelwert der extensiven Größe weiterhin konstant bleibt, muss man eine zugehörige intensive Größe definieren, die man im Wesentlichen als Ableitung der Entropie nach der extensiven Größe festlegt. Diese intensive Größe muss im betrachteten System denselben Wert wie im Wärmebad besitzen, damit das System mit dem Wärmebad im thermischen Gleichgewicht ist und die Mittelwerte konstant bleiben.
Zu den extensiven Größen \(E, V, N\) gehören dabei die intensiven Größen \(T, p, \mu\).
Lässt man beispielsweise durch Kontakt mit einem Wärmebad Fluktuationen in \(E\) zu, so müssen Wärmebad und System dasselbe \(T\) aufweisen.
Ein solches System mit Fluktuationen in \(E\) wird durch eine neue statistische Gesamtheit beschrieben: das kanonische Ensemble. Der Logarithmus der entsprechenden Zustandssumme ergibt das zugehörige thermodynamische Potential, das man über eine Legendre-Transformation beim Wechsel von der extensiven Größe \(E\) zur intensiven Größe \(T\) erhält.
Analog kann man auch bei \(E\) und \(N\) ( → großkanonisches Ensemble) oder bei \(V\) und \(N\) vorgehen. So kann man auch leicht ein Ensemble konstruieren, bei dem \(E\) und \(V\) fluktuieren dürfen – entsprechend werden \(T\) und \(p\) durch das Wärmebad vorgegeben.
Für makroskopische Systeme sind alle diese statistischen Gesamtheiten und die entsprechenden thermodynamischen Potentiale gleichwertig, d.h. man kann sich die jeweils günstigste aussuschen. Das liegt daran, dass die Fluktuationen mit sehr hoher Wahrscheinlichkeit winzig sind, so dass es makroskopisch keinen Unterschied macht, ob die extensive Größe fest vorgegeben wird oder im Kontakt mit dem Wärmebad fluktuieren darf, wobei das Wärmebad die entsprechende intensive Größe vorgibt. Lediglich in den mikroskopischen Eigenschaften unterscheiden sich die einzelnen Ensembles – das mikrokanonische Ensemble kennt keine wirklichen Energiefluktuationen, das kanonische Ensemble schon.
Man kann das großkanonische Ensemble sehr gut verwenden, um ideale Quantengase zu untersuchen, also ein Gas aus vielen gleichartigen identischen Quantenteilchen ohne direkte Wechselwirkung in einem großen Volumen \(V\).
Zu Beginn haben wir ein solches Gas bereits betrachtet, als wir die Zahl der Mikrozustände in einem Volumen \(V\) abgeschätzt haben. Dabei haben wir uns zunächst angesehen, welche Zustände (stehende Wellen) ein einzelnes Teilchen in dem Volumen \(V\) einnehmen kann. Die N-Teilchenzustände haben wir dann einfach gebildet, indem wir die \(N\) Teilchen auf die verschiedenen Einteilchenzustände zufällig verteilt haben. Quantenmechanisch wäre ein solcher N-Teilchenzustand das Produkt von \(N\) Einteilchenzuständen. Bei zwei Teilchen wäre beispielsweise \[ \psi_{g}(\boldsymbol{x}_1, \boldsymbol{x}_2) = \psi_{1}(\boldsymbol{x}_1) \, \psi_{2}(\boldsymbol{x}_2) \] wobei \( \psi_{g} \) die Gesamtwellenfunktion und \(\psi_{1}\) bzw. \(\psi_{2}\) die Wellenfunktionen von Teilchen 1 und 2 sind, die sich an den Orten \(\boldsymbol{x}_1\) und \(\boldsymbol{x}_2\) aufhalten.
Wir haben dabei allerdings etwas vernachlässigt:
Auch wenn die Teilchen kaum Wechselwirkung miteinander haben, so gibt es dennoch quantenmechanische (Anti-) Symmetriebedingungen an den N-Teilchenzustand der identischen Teilchen (siehe Die Symmetrie der Naturgesetze, Kapitel 4.4 ).
Diese Bedingungen hängen damit zusammen, dass die \(N\) Teilchen ununterscheidbar sind, d.h. es muss \[ |\psi_{g}(\boldsymbol{x}_1, \boldsymbol{x}_2)|^2 = |\psi_{g}(\boldsymbol{x}_2, \boldsymbol{x}_1)|^2 \] sein. Die Wahrscheinlichkeit, dass sich Teilchen 1 am Ort \(\boldsymbol{x}_1\) und Teilchen 2 am Ort \(\boldsymbol{x}_2\) aufhält, muss also genauso groß sein wie umgekehrt.
Diese Bedingung ist wegen dem Betragsquadrat sowohl für symmetrische als auch für antisymmetrische Zustandsfunktionen erfüllt, also wenn \[ \psi_{g}(\boldsymbol{x}_1, \boldsymbol{x}_2) = \pm \psi_{g}(\boldsymbol{x}_2, \boldsymbol{x}_1) \] ist.
Bei Fermionen (Teilchen mit Spin 1/2, z.B. Elektronen, Protonen oder Neutronen) trifft der antisymmetrische Fall zu: \[ \psi_{g}(\boldsymbol{x}_1, \boldsymbol{x}_2) = \] \[ = \psi_{1}(\boldsymbol{x}_1) \, \psi_{2}(\boldsymbol{x}_2) - \psi_{2}(\boldsymbol{x}_1) \, \psi_{1}(\boldsymbol{x}_2) \] Wäre hier \(\psi_{1} = \psi_{2} = \psi\), so wäre \(\psi_{g} = 0\). Das ist kein erlaubter 2-Teilchen-Zustand Daher ist es nicht erlaubt, dass zwei Fermionen beide denselben Einteilchenzustand einnehmen, d.h. \(\psi_{1}\) und \(\psi_{2}\) müssen verschiedene Einteilchen-Wellen sein. Jede mögliche Einteilchen-Quantenwelle darf also maximal mit einem Fermion besetzt sein.
Bosonen (Teilchen mit Spin 0 oder 1, beispielsweise entsprechende Atome) sind dagegen sehr gerne im selben Einteilchenzustand, denn ihre N-Teilchen-Wellenfunktion muss symmetrisch sein: \[ \psi_{g}(\boldsymbol{x}_1, \boldsymbol{x}_2) = \] \[ = \psi_{1}(\boldsymbol{x}_1) \, \psi_{2}(\boldsymbol{x}_2) + \psi_{2}(\boldsymbol{x}_1) \, \psi_{1}(\boldsymbol{x}_2) \] Diese Symmetrieeffekte sind unwichtig, solange die mittlere Teilchenzahl in einem Einteilchenzustand deutlich kleiner als Eins ist, denn dann kommt es nur sehr selten vor, dass zwei Teilchen denselben Einteilchenzustand beanspruchen. Das ist bei üblichen Gasen bei Raumtemperatur der Fall, nicht aber beispielsweise bei den dicht gepackten Neutronen in einem Neutronenstern oder den Elektronen in einem weißen Zwerg.
Entscheidend ist also die mittlere Teilchenzahl in einem Einteilchenzustand, also die mittlere Zahl der Teilchen, die im Volumen \(V\) dieselbe stehende Welle mit demselben Teilchenspin ausbilden wollen.
Diese Teilchenzahl können wir mit dem großkanonischen Ensemble leicht ausrechnen! Wir können nämlich einen Einteilchenzustand mit den darin enthaltenen Teilchen als ein kleines Subsystem A ansehen, das sich in einem großen Wärmebad A' befindet. Dieses Wärmebad besteht aus den anderen Einteilchenzuständen mit den darin enthaltenen Teilchen. Dabei wollen wir voraussetzen, dass sich nur ein kleiner Teil aller Teilchen in dem betrachteten Einteilchenzustand befindet, so dass sich sehr viel mehr Teilchen im Wärmebad A' aufhalten (diese Bedingung muss man bei der sogenannten Bose-Einstein-Kondensation im Auge behalten). Die Wechselwirkung zwischen A und A' ist nur schwach, denn die Teilchen sollen nur wenig miteinander wechselwirken und Symmetrieeffekte gibt es nur innerhalb eines Einteilchenzustandes, also nicht zwischen A und A'.
Unser Subsystem A kann nun Teilchen und damit auch Energie mit dem Wärmebad A' austauschen,
d.h. Teilchen können unseren Einteilchenzustand betreten und wieder verlassen.
Das Subsystem A wird also durch ein großkanonisches Ensemble beschrieben und wir können
seine mittlere Teilchenzahl ausrechnen.
Schauen wir uns dazu seine Mikrozustände an, die wir bisher mit \( |n\rangle \) bezeichnet haben. Dazu passend war \(E_{n}\) die Energie und \(N_{n}\) die Teilchenzahl dieses Mikrozustandes. Es bietet sich nun an, die Bezeichnungsweise etwas anzupassen, denn ein Mikrozustand von A ist vollständig gekennzeichnet durch den Einteilchenzustand und die Zahl der Teilchen in diesem Einteilchenzustand (die sogenannte Besetzungszahl).
Den Einteilchenzustand können wir hier mit \[ |\boldsymbol{p},\sigma\rangle \] bezeichnen. Dabei ist \( \boldsymbol{p} \) der Teilchenimpuls, der aufgrund der Randbedingungen im Volumen nur diskrete Werte annehmen kann, und \( \sigma \) ist der Teilchenspin in z-Richtung bzw. bei masselosen Teilchen die Helizität.
Hinzu kommt die Besetzungszahl dieses Einteilchenzustandes, die wir mit \( n(\boldsymbol{p},\sigma) \) bezeichnen wollen – es ist also \[ N_{n} = n(\boldsymbol{p},\sigma) \] in unserem Einzustands-Subsystem A.
Die Energie eines Teilchens im Einteilchenzustand nennen wir \( \epsilon(\boldsymbol{p},\sigma) \), d.h. die Energie des Mikrozustandes mit \( n(\boldsymbol{p},\sigma) \) Teilchen ist \[ E_{n} = n(\boldsymbol{p},\sigma) \, \epsilon(\boldsymbol{p},\sigma) \] Damit können wir die großkanonische Zustandssumme für A ausrechnen, die wir hier mit \( Z_{G}(\boldsymbol{p},\sigma) \) bezeichnen: \[ Z_{G}(\boldsymbol{p},\sigma) = \sum_{n} \, e^{\frac{\mu N_{n} - E_{n}}{kT}} = \] \[ = \sum_{n(\boldsymbol{p},\sigma)} \, e^{ \frac{\mu \, n(\boldsymbol{p},\sigma) - n(\boldsymbol{p},\sigma) \, \epsilon(\boldsymbol{p},\sigma)} {kT}} = \] \[ = \sum_{n(\boldsymbol{p},\sigma)} \, \left( e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} \right)^{n(\boldsymbol{p},\sigma)} \] Für Bosonen sind alle Besetzungszahlen erlaubt und die Summe bildet eine geometrische Reihe, die wir komplett aufsummieren können. Bei Fermionen kann ein Einteilchenzustand dagegen maximal mit einem Teilchen besetzt sein, d.h. in der Summe treten nur die beiden Summanden mit n(\boldsymbol{p},\sigma) gleich Null und Eins auf:
Bosonen:
\[
Z_{G}(\boldsymbol{p},\sigma)
=
\frac{1}{ 1 - e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} }
\]
Fermionen:
\[
Z_{G}(\boldsymbol{p},\sigma)
=
1 + e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}}
\]
Für die mittlere Teilchenzahl hatten wir oben die Formel
\[
N = - \frac{\partial J}{\partial \mu} =
\]
\[ =
k T \, \frac{\partial}{\partial \mu} \ln{Z_{G}}
=
\]
\[ =
k T \, \frac{1}{Z_{G}} \, \frac{\partial Z_{G}}{\partial \mu}
\]
gefunden.
Für unseren Fall ist
\[
N = \langle n(\boldsymbol{p},\sigma) \rangle
\]
d.h.
die mittlere Besetzungszahl ist folgende:
Bosonen (Boseverteilung):
Mit \[ Z_{G}(\boldsymbol{p},\sigma) = \frac{1}{ 1 - e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } \] erhalten wir \[ \langle n(\boldsymbol{p},\sigma) \rangle = k T \, \frac{1}{Z_{G}} \, \frac{\partial Z_{G}}{\partial \mu} = \] \[ = k T \, \left( 1 - e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} \right) \cdot \] \[ \cdot \frac{- 1} { \left( 1 - e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} \right)^2} \, \frac{- e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } {k T} = \] \[ = \frac{ e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma) }{kT} } } { 1 - e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT} } } = \] \[ = \frac{1}{ e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} } - 1 } \]
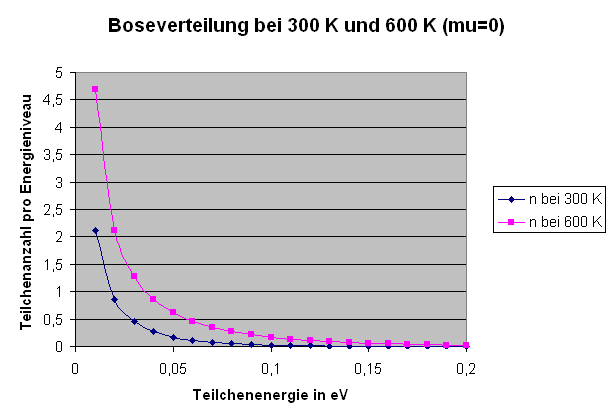
Die Grafik zeigt die Boseverteilung bei \( \mu = 0 \)
(siehe Anmerkungen weiter unten) für Zimmertemperatur
(300 K) und doppelter Zimmertemperatur (600 K).
Auf der x-Achse ist die Teilchenenergie \( \epsilon(\boldsymbol{p},\sigma) \) aufgetragen
und auf der y-Achse die mittlere Besetzungszahl \( \langle n(\boldsymbol{p},\sigma) \rangle \).
Fermionen (Fermiverteilung):
Mit \[ Z_{G}(\boldsymbol{p},\sigma) = 1 + e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} \] erhalten wir \[ \langle n(\boldsymbol{p},\sigma) \rangle = k T \, \frac{1}{Z_{G}} \, \frac{\partial Z_{G}}{\partial \mu} = \] \[ = k T \, \frac{1}{1 + e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } \, \frac{ e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } {k T} = \] \[ = \frac{ e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } { 1 + e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} } = \] \[ = \frac{1} { e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT}} + 1 } \]
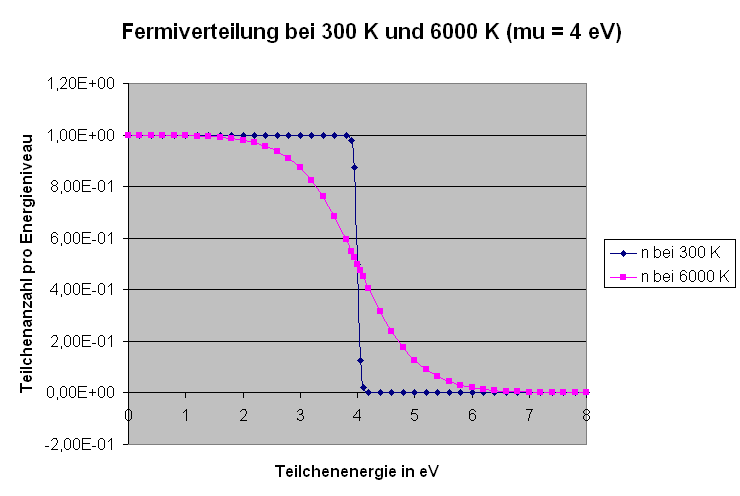
Die Grafik zeigt analog zu oben die sogenannte Fermiverteilung bei \( \mu = 4 \, \mathrm{eV} \)
(das sind typische Werte für Festkörper) für
Zimmertemperatur (300 K) und für die Oberflächentemperatur der Sonne (6000 K):
Man sieht, dass bei Zimmertemperatur praktisch jedes Energieniveau
unterhalb von 4 eV mit einem Teilchen besetzt ist, darüber aber
die Nivaus nur sehr dünn besetzt sind. Bei 6000 K wird diese recht
scharfe Stufenfunktion deutlich aufgeweicht,
d.h. viele Teilchen springen von den Niveaus unter 4 eV in Niveaus über 4 eV.
Die mittleren Besetzungszahlen für Fermionen und Bosonen unterscheiden sich insgesamt nur durch ein
kleines, aber entscheidendes Vorzeichen vor der Eins im Nenner:
\[
\langle n(\boldsymbol{p},\sigma) \rangle =
\frac{1}{ e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} } \pm 1 }
\]
(\(- 1\) bei Bosonen, \(+ 1\) bei Fermionen).
Den klassischen Grenzfall erreicht man, wenn der Exponent
\[
\frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT}
\]
und mit ihm die e-Funktion im Nenner deutlich größer als Eins wird,
so dass der Term \( \pm 1 \) im Nenner unwichtig gegenüber der Exponentialfunktion wird.
Der Unterschied zwischen Fermionen und Bosonen verschwindet dann und wir erhalten:
klassischer Grenzfall:
\[ \langle n(\boldsymbol{p},\sigma) \rangle = \frac{1}{ e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} } } = e^{ \frac{\mu - \epsilon(\boldsymbol{p},\sigma)} {kT}} \] mit \[ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} \gg 1 \]
Statt nur die Teilchen eines einzigen
Einteilchenniveaus durch ein großkanonisches Ensemble zu beschreiben,
kann man auch die Teilchen des gesamten Quantengases durch ein solches Ensemble beschreiben.
Dabei stellt man sich das Quantengas wieder in Kontakt mit einem äußeren Wärme- und Teilchenreservoir vor, welches \(T\) und \(\mu\) vorgibt. Das großkanonische Potential \(J\) des Gases ergibt sich dann einfach als Summe der großkanonischen Potentiale der Einteilchenniveaus, die wir bereits berechnet haben – das großkanonische Potential ist ja bei gleichem \(T\) und \(\mu\) eine extensive Größe analog zu \(E, N, S\), wie die Formel \[ J = E - T \, S - \mu \, N \] zeigt.
Man kann sich das aber auch explizit anhand der Wahrscheinlichkeiten überlegen, denn ein Mikrozustand des Gesamtsystems ist eindeutig durch die Besetzungszahlen der Einteilchenniveaus festgelegt – es spielt in der Quantentheorie bei identischen Teilchen nämlich keine Rolle, welches Teilchen sich in welchem Einteilchenzustand befindet. Die Teilchen sind ununterscheidbar.
Der Symmetrieaspekt wird dabei durch die Bedingung an die Besetzungszahlen vollständig berücksichtigt: Bei Fermionen ist jede Besetzungszahl maximal 1, bei Bosonen dagegen unbegrenzt.
Die Wahrscheinlichkeit für einen Mikrozustand des Gesamtsystems ist nun gleich dem Produkt der Wahrscheinlichkeiten für die einzelnen Besetzungszahlen der Einteilchenniveaus, und der Logarithmus macht aus dem Produkt eine Summe. Dabei ist nützlich, dass es beim großkanonischen Ensemble keine Nebenbedingung für die Gesamtzahl der Teilchen gibt. \[ J = \sum_{\boldsymbol{p}, \sigma} \, J(\boldsymbol{p},\sigma) = \] \[ = - k T \, \sum_{\boldsymbol{p}, \sigma} \, \ln{Z_{G}(\boldsymbol{p},\sigma)} \] Aus diesem großkanonischen Potential kann man dann alles Weitere berechnen, wie wir bereits wissen. Da die Impulse fast kontinuierlich sind, kann man die Impulssumme durch ein Impulsintegral mit dem Volumen als Normierungsfaktor ersetzen – bis auf eine Ausnahme: den Grundzustand mit \(\boldsymbol{p} = 0\) muss man beim Bosegas gesondert behandeln, da sich in ihm eine makroskopische Teilchenzahl ansamme\ln{kann. Schauen wir uns diese sogenannte Bose-Einstein-Kondensation etwas genauer an:
Betrachten wir bei Bosonen die Summe aller mittleren Besetzungszahlen oberhalb des Grundzustandes, so stellen wir fest, dass bei gegebener Temperatur \(T\) und Volumen \(V\) sich im Mittel nur eine bestimmte maximale Anzahl Teilchen in diesen Niveaus befinden kann. Es gibt eine maximale Teilchendichte für Teilchen mit Energie größer Null, die im Mittel nicht überschritten werden kann, wobei diese maximale Teilchendichte mit steigendem \(T\) anwächst.
Steigt bei festem \(T\) die Dichte oder sinkt bei fester Dichte die Temperatur, so haben ab einer bestimmten Grenze nicht mehr alle Teilchen in den Energieniveaus oberhalb von Null Platz – die mittleren Besetzungszahlen für diese Niveaus, so wie sie das thermische Gleichgewicht vorgibt, sind dann einfach zu gering, um alle Teilchen aufzunehmen.
Eine makroskopische Teilchenzahl muss sich in diesem Fall in den Grundzustand mit Energie Null begeben, so dass ein makroskopisch besetzter kohärenter Quantenzustand entsteht – das nennt man Bose-Einstein-Kondensation.
Sie findet allerdings erst bei sehr niedrigen Temperaturen im Mikro-Kelvin-Bereich statt, ist also experimentell nicht einfach zu realisieren. Bei Temperatur Null sind schließlich alle Bosonen im Grundzustand. Die Teilchen im Grundzustand tragen dabei weder zur Gesamtenergie noch zum Druck bei – das Kondensat hat keinen Druck und keine innere Energie.
Ganz allgemein findet man beim Bosegas eine Druckverminderung im Vergleich zum klassischen Grenzfall – die Symmetrie der Wellenfunktionen wirkt ähnlich wie eine anziehende Kraft zwischen den Teilchen.
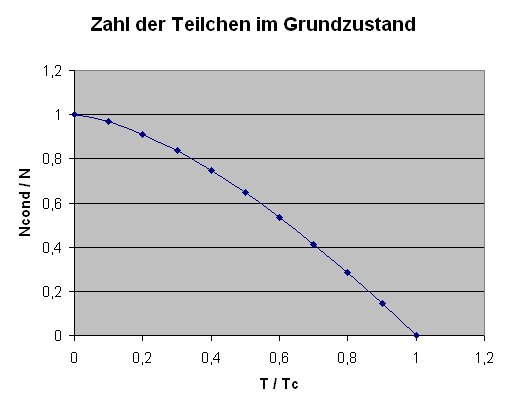
Bose-Einstein-Kondensation:
Bei gegebener Teilchendichte \(N/V\) wächst
unterhalb einer kritischen Temperatur \(T_{c}\)
die Zahl der Teilchen \(N_{\mathrm{cond}}\) im Grundzustand
plötzlich sprunghaft an,
bis bei \(T=0\) schließlich alle Teilchen im Grundzustand sind.
Die genaue Formel lautet:
\[
\frac{N_{\mathrm{cond}}}{N}
= 1 - \left( \frac{T}{T_{c}} \right)^{3/2}
\]
Siehe auch
M.Stingl:
Statistische Mechanik,
Seiten 176 und 177, u.a. Formel (12.11).
Bei Fermionen ist eine Ansammlung im Grundzustand
aufgrund des Pauli-Prinzips nicht erlaubt, so dass Fermionen
bei tiefen Temperaturen die Energieniveaus schrittweise von unten nach oben auffüllen.
Man spricht auch von einem entarteten Fermigas.
Da die Teilchen dabei auch einen immer größeren Impuls haben,
übt ein Fermigas selbst bei Temperatur Null noch einen Druck aus.
Ganz allgemein findet man beim Fermigas eine Druckerhöhung im Vergleich zum klassischen Grenzfall – die Antisymmetrie der Wellenfunktionen wirkt ähnlich wie eine abstoßende Kraft zwischen den Teilchen. Dieser Druck hält beispielsweise einen weißen Zwerg oder einen Neutronenstern gegen die Kraft der Gravitation stabil – zumindest bis zu einer bestimmten Grenze für die Sternmasse (siehe Zeitpfad, Kapitel 2.3: Sterne entstehen und vergehen ).
Erhöht man die Temperatur, so findet man immer mehr Teilchen auch in höheren Energieniveaus, wie die obigen Formeln für \( \langle n(\boldsymbol{p},\sigma) \rangle \) zeigen. Schließlich nimmt das Gas die Eigenschaften eines klassischen idealen Gases an.
Noch einige Worte zum chemischen Potential \(\mu\):
Allgemein hängt \(\mu\) im Quantengas von \(T, V, N\) ab, wobei \(N\) die mittlere Gesamt-Teilchenzahl ist (genau genommen hängt \(\mu\) von \(T\) und der Dichte \(N/V\) ab). Diesen Zusammenhang kann man beispielsweise aus der Bedingung \[ \sum_{\boldsymbol{p},\sigma} \, \langle n(\boldsymbol{p},\sigma) \rangle = N \] ableiten.
Will man bei gegebenem \(T\) und \(V\) im Kontakt mit dem Wärmebad (mit dem auch Teilchen ausgetauscht werden dürfen) eine bestimmte mittlere Gesamtteilchenzahl \(N\) realisieren, so muss man \(\mu\) entsprechend einstellen (so wie man analog \(T\) entsprechend einstellen muss, um ein bestimmtes mittleres \(E\) zu realisieren). An den mittleren Besetzungszahlen kann man aber immerhin ablesen, welche Werte für \(\mu\) überhaupt möglich sind, denn alle \( \langle n(\boldsymbol{p},\sigma) \rangle \) müssen positiv oder Null sein, und zwar für jedes Energieniveau \( \epsilon(\boldsymbol{p},\sigma) \), wobei diese Energien alle größer-gleich Null sind.
Bei Bosonen ist \[ \langle n(\boldsymbol{p},\sigma) \rangle = \frac{1}{ e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} } - 1 } \] d.h. \(\mu\) muss kleiner-gleich Null sein, so dass \( \epsilon(\boldsymbol{p},\sigma) - \mu \) immer größer-gleich Null ist – der Nenner ist dann positiv.
Bei Fermionen ist dagegen \[ \langle n(\boldsymbol{p},\sigma) \rangle = = \frac{1} { e^{ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT}} + 1 } \] d.h. der Nenner ist immer positiv und es gibt keine Einschränkungen für \(\mu\).
Oben hatten wir gesehen, dass \[ \frac{\epsilon(\boldsymbol{p},\sigma) - \mu} {kT} \gg 1 \] zum klassischen Grenzfall führt. Diese Bedingung können wir auch als \[ - \mu \gg kT - \epsilon(\boldsymbol{p},\sigma) \] schreiben. Da diese Bedingung für alle \(\epsilon(\boldsymbol{p},\sigma)\) gelten muss, auch für \( \epsilon(\boldsymbol{p},\sigma) = 0 \), muss das chemische Potential im klassischen Grenzfall betragsmäßig große negative Werte im Vergleich zu \(kT\) haben: \[ - \mu \gg kT \] Man kann sich deshalb vorstellen, dass man immer weiter weg vom klassischen Grenzfall kommt, je größere Werte \(\mu\) hat. Bei \(\mu = 0\) oder gar positiven \(\mu\) ist man garantiert nicht mehr im klassischen Grenzfall und kann nicht mehr davon ausgehen, dass die mittleren Besetzungszahlen klein gegen Eins sind.
Bei Bosonen ist der größte erlaubte Wert \(\mu = 0\). Je näher \(\mu\) an Null heranrückt, umso größer wird die mittlere Besetzungszahl für den Grundzustand mit \( \epsilon(\boldsymbol{p},\sigma) = 0 \), bis sie sogar divergiert.
Die Grafik zur Bose-Verteilung oben zeigt diese Divergenz sehr schön. Immer mehr Teilchen befinden sich dann im Grundzustand – wir kennen das schon als Bose-Einstein-Kondensation. Der Wert \(\mu = 0\) wird allerdings nur im Grenzfall mit unendlich großem Volumen erreicht, denn nur dann sind auch unendlich viele Teilchen vorhanden, so dass die Besetzungszahl des Grundzustandes divergieren kann. Bei endlichem Volumen bleibt \(\mu\) immer etwas kleiner als Null und justiert sich gerade so, dass der Grundzustand entsprechend gefüllt ist, bis sich bei \(T = 0\) sogar alle \(N\) Teilchen in ihm befinden.
Bei masselosen Bosonen wie den Photonen ist die Lage etwas anders,
denn Photonen mit
Energie Null gibt es nicht – es gibt also keine Bose-Einstein-Kondensation
bei Photonen. Wir werden uns gleich überlegen, dass für Photonen generell \(\mu = 0\) gilt – es ist
also
\[
\langle n(\boldsymbol{p},\sigma) \rangle =
\frac{1}{ e^{ \frac{\epsilon(\boldsymbol{p},\sigma)} {kT} } - 1 }
\]
mit der Helizität \( \sigma = \pm 1 \) und \( \epsilon(\boldsymbol{p},\sigma) \gt 0 \).
Das bedeutet, dass die mittlere Photonenzahl nicht über ein chemisches Potential gesteuert werden kann, sondern sich alleine aufgrund des thermischen Gleichgewichts ergibt. Die Anzahl der Photonen in einem Hohlraum ist nicht festgelegt – es können ständig neue Photonen entstehen oder wieder verschwinden, wozu allerdings eine Wechselwirkung mit anderer Materie notwendig ist, beispielsweise mit den Wänden des Behälters, denn Photonen wechselwirken untereinander praktisch gar nicht.
Mathematisch kann man \(\mu = 0\) für Photonen beispielsweise an der obigen Herleitung des großkanonischen Ensembles ablesen: Die Wahrscheinlichkeit, einen Mikrozustand mit Energie \(E_{n}\) und Photonenzahl \(N_{n}\) im System A vorzufinden, ist bei Photonen gleich \[ P_{n} = \frac{\Omega'(E_{g} - E_{n})}{\Omega_{g}(E_{g})} \] also analog zum kanonischen Ensemble, denn man braucht keinen Photonenaustausch zwischen dem System A und dem Wärmebad. Entsprechend fällt die Ableitung nach der Teilchenzahl und damit \(\mu\) weg.
Dennoch werden die Mikrozustände von A auch durch die Teilchenzahl gekennzeichnet, anders als beim kanonischen Ensemble. Das wirkt sich in den Summen über die Mikrozustände wie beim großkanonischen Ensemble aus.
Dass bei Photonen \(\mu = 0\) ist, kann man auch direkt an der Entropie ablesen: \(S(E,V,N)\) strebt bei vorgegebenem \(E, V\) ein Maximum an, indem sich die mittlere Photonenzahl \(N\) entsprechend einstellt. Im Entropie-Maximum gilt dann \[ \frac{\partial S}{\partial N} = - \frac{\mu}{T} = 0 \] d.h. \(\mu\) muss Null sein.
Auch die Energie zeigt, dass bei Photonen \(\mu = 0\) ist: Im thermischen Gleichgewicht (d.h. \(S\) ist konstant im Maximum) gilt bei konstantem \(V\) die Gleichung \[ dE = \mu \, dN \] Wenn man das System nun isoliert, also \(E\) konstant hält, kann ein Photonenzahlzuwachs \(dN\) keine Energieerhöhung \(dE\) erzeugen, sondern die Energie \(E\) verteilt sich nur auf mehr Photonen. Es ist also \(dE = 0\), so dass \( \mu = 0 \) sein muss. Zur Erinnerung: \(\mu\) ist der Energiezuwachs \(dE\), den ein neues Teilchen bewirkt (dazu einfach \(dN = 1\) setzen).
Bei Fermionen kann dagegen \(\mu\) im Prinzip beliebig positiv werden.
Je größer \(\mu\) im Vergleich zu \(kT\) wird, umso stufenförmiger wird die
Fermiverteilung, wie die Grafik oben zeigt.
Dabei gibt \(\mu\) die Position der Stufe an, d.h. bei kleinen \(T\) sind die Einteilchenniveaus ungefähr bis zur Energie \[ \epsilon(\boldsymbol{p},\sigma) = \mu \] besetzt und ein neues Teilchen muss mit der Energie \(\mu\) an der Stufenkante einsteigen (\(\mu\) war ja der Energiezuwachs pro neuem Teilchen).
Damit ist auch klar: Je größer \(\mu\) bei festem \(V\) wird, umso mehr Teilchen braucht man, um diese Niveaus zu besetzen, d.h. umso größer ist die mittlere Gesamtteilchenzahl \(N\) und damit die mittlere Dichte \(N/V\). Bei großen Dichten hat man also auch ein großes \(\mu\) und damit (bei nicht zu großem \(T\)) eine ziemlich stufenförmige Fermiverteilung, also ein weitgehend entartetes Fermigas. Das ist beispielsweise für Elektronen in einem Festkörper bei Zimmertemperatur der Fall.
Bei großen Temperaturen wird die Stufenform der Fermiverteilung immer mehr aufgeweicht und \(\mu\) wird immer kleiner. Sobald \(kT\) den Wert überschreitet, den \(\mu\) bei \(T = 0\) hatte, wird \(\mu\) schließlich sogar negativ. Das muss auch so sein, denn im klassischen Grenzfall muss \(\mu\) ja betragsmäßig große negative Werte annehmen (siehe oben).
Natürlich kann man noch viel mehr zu idealen Quantengasen sagen. Es würde jedoch zu weit führen, hier weiter ins Detail zu gehen. Mehr dazu findet man in jedem guten Buch der statistischen Physik.
Damit sind wir bei unserem Exkurs durch die statistische Physik am Ende angekommen. Ich hoffe, Sie konnten einen Eindruck davon gewinnen, was Entropie eigentlich ist und wie sich mit ihr die thermodynamischen Eigenschaften makroskopischer Körper berechnen lassen. Im nächsten Kapitel werden wir die Entropie noch einmal von einer anderen Seite beleuchten, die ihre wahre Natur noch deutlicher macht: Wir werden sehen, was Entropie mit Information zu tun hat.
Wir haben oben ein makroskopisches quantenmechanisches System immer durch ein Gemisch von Quantenzuständen \( |n\rangle \) beschrieben, wobei \(P_{n}\) die klassische Wahrscheinlichkeit bezeichnet, mit der ein Zustand \( |n\rangle \) zum Gesamt-Messergebnis beiträgt. So etwas kann man formal durch eine Dichtematrix beschreiben, und zwar so:
Nehmen wir an, wir wollten den Erwartungswert der Observablen \(\hat{A}\) bei unserem System bestimmen, wobei \(\hat{A}\) wie immer einem hermiteschen Operator mit reellen Eigenwerten \( a_{\alpha} \) und zugehörigen Eigenzuständen \( |\alpha\rangle \) entspricht, d.h. \[ \hat{A} \, |\alpha\rangle = a_{\alpha} \, |\alpha\rangle \] Die Eigenwerte \( a_{\alpha} \) sind dabei die Messwerte, die bei der Observablen \(\hat{A}\) möglich sind.
Wenn unser System im Mikrozustand \( |n\rangle \) ist, so ist die Wahrscheinlichkeit für den Messwert \( a_{\alpha} \) gleich \[ |\langle \alpha | n \rangle|^{2} \] Unser System ist aber nur mit der Wahrscheinlichkeit \(P_{n}\) im Zustand \( |n\rangle \), d.h. die Wahrscheinlichkeit, dass das System in diesem Zustand ist und dass dann der Messwert \( a_{\alpha} \) gemessen wird, ist gleich dem Produkt der Wahrscheinlichkeiten, also gleich \[ P_{n} \, |\langle\alpha|n\rangle|^{2} \] Die Summe dieser Produkte über alle Zustände \( |n\rangle \) gibt dann die Wahrscheinlichkeit an, dass der Messwert \( a_{\alpha} \) bei unserem Sysrem gemessen wird, wobei uns egal ist, in welchem Mikrozustand \( |n\rangle \) sich das System zufällig befindet. Die Wahrscheinlichkeit \(P_{\alpha}\) für den Messwert \( a_{\alpha} \) ist also gleich \[ P_{\alpha} = \] \[ = \sum_{n} \, P_{n} \, |\langle\alpha|n\rangle|^{2} = \] \[ = \sum_{n} \, \langle\alpha|n\rangle \, P_{n} \, \langle n|\alpha\rangle =: \] \[ =: \langle\alpha| \, \hat{\rho} \, |\alpha\rangle \] Im letzten Schritt sehen wir, wie die Dichtematrix \( \hat{\rho} \) entsteht (genauer Dichteoperator oder statistischer Operator; die Dichtematrix besteht dann eigentlich aus den Matrixelementen \( \langle m | \, \hat{\rho} \, | n \rangle \), siehe auch Die Symmetrie der Naturgesetze, Kapitel 4.2 und Kapitel 4.5 ): \[ \hat{\rho} := \sum_{n} \, |n\rangle \, P_{n} \, \langle n| \] Die Dichtematrix dient lediglich dazu, die klassischen Mittelungen in kompakter Form zu schreiben. Mehr steckt nicht dahinter! Man kann auch ganz ohne Dichtematrix arbeiten und die klassische Mittelung über die Wahrscheinlichkeiten \(P_{n}\) einfach immer ausschreiben. Das haben wir oben auch getan, denn die Formeln mit der Dichtematrix sind zwar schön kurz, aber man muss sie oft erst entschlüssen, um zu sehen, was dahinter steckt.
Den Erwartungswert \( \langle \hat{A} \rangle \) für den Messwert von \( \hat{A} \) bei unserem System kann man nun mit Hilfe der Dichtematrix kompakt so schreiben: \[ \langle \hat{A} \rangle = \] \[ = \sum_{\alpha} \, P_{\alpha} \, a_{\alpha} = \] \[ = \sum_{\alpha} \, \langle \alpha | \, \hat{\rho} \, | \alpha \rangle \, a_{\alpha} = \] \[ \sum_{\alpha} \, \langle \alpha| \, \hat{\rho} \, \hat{A} \, |\alpha \rangle =: \] \[ =: \mathrm{Spur} (\hat{\rho} \hat{A}) \] Wenn man die Wahrscheinlichkeiten \(P_{n}\) für ein statistisches Ensemble kennt, so kann man die Dichtematrix für dieses Ensemble sofort hinschreiben. Die Dichtematrix \( \hat{\rho} \) für das mikrokanonische Ensemble (also feste Teilchenzahl \(N\), festes Volumen \(V\) und Energie im Intervall zwischen \(E\) und \(E + \delta E\)) ist beispielsweise gleich \[ \hat{\rho} = \sum_{n}' \, \frac{ |n \rangle \, \langle n| }{\omega(E) \, \delta E} \] mit der Zustandsdichte \(\omega(E)\), wobei der Strich über der Summe wieder andeutet, dass nur über Zustände mit \(E_{n}\) zwischen \(E\) und \(E + \delta E\) summiert werden darf. Manchmal findet man hierfür auch eine verkürzte Schreibweise mit einer Delta-Funktion in der physikalischen Literatur.
Die Formel \[ \rho := \sum_{n} \, | n \rangle \, P_{n} \, \langle n| \] ist nicht die allgemeinste Form der Dichtematrix, denn sie erfasst insbesondere nicht den Fall, bei dem sich das System in einem reinen Zustand \( |\psi\rangle \) befindet. In diesem Fall ist nämlich \[ P_{\alpha} = | \langle \alpha | \psi \rangle |^{2} = \] \[ = \langle \alpha |\psi \rangle \, \langle \psi | \alpha \rangle = \] \[ =: \langle \alpha | \, \hat{\rho} \, | \alpha \rangle \] so dass die Dichtematrix hier durch \[ \hat{\rho} = | \psi \rangle \, \langle \psi | \] gegeben ist.
Ganz allgemein können wir die Dichtematrix immer in der Form \[ \hat{\rho} = \sum_{n m} \, | n \rangle \, \langle n| \, \hat{\rho} \, | m \rangle \, \langle m| = \] \[ =: \sum_{n m} \, | n \rangle \, \rho_{nm} \, \langle m | \] schreiben, wobei wir zweimal die vollständige Basis \( |n\rangle \) bzw. \( |m\rangle \) eingeschoben haben.
Ist das System in einem reinen Zustand |\psi\rangle , so ist \[ \rho_{nm} = \langle n| \psi \rangle \, \langle \psi |m \rangle \] d.h. \(\rho_{nm}\) ist nicht diagonal und zerfällt in zwei Faktoren.
Liegt dagegen ein statistisches Gemisch der Basiszustände vor, so reproduziert \[ \rho_{nm} = P_{n} \, \delta_{nm} \] unsere Formel von oben, d.h. \(\rho_{nm}\) ist diagonal, wobei die Diagonalelemente die Wahrscheinlichkeiten der Zustände im statistischen Gemisch angeben.
Zwischen diesen beiden Extremfällen sind natürlich auch andere Zwischenformen für \(\rho_{nm}\) möglich. Dabei kann man sich merken:
Je diagonaler \(\rho_{nm}\) ist, umso mehr liegt ein statistisches Gemisch vor, d.h. umso weniger befindet sich das System in einem reinen Quantenzustand.
Dabei muss die Orthonormalbasis \( |n\rangle \) natürlich so gewählt sein, dass \(\rho_{nm}\) so diagonal wie möglich ist.
Es erscheint oft ungewohnt, dass man ein quantenmechanisches System durch eine Dichtematrix beschreiben soll – ist man doch gewohnt, mit reinen Quantenzuständen zu arbeiten. Deshalb ist es sehr nützlich, sich im Detail einmal anzusehen, wie eine klassische Mittelung für ein quantenmechanisches System entsteht, d.h. wie aus einem reinen Zustand eine Dichtematrix wird. Die folgende Darstellung orientiert sich an Franz Embacher: Grundidee der Dekohärenz und an Franz Embacher: Zur Bedeutung der Zahl der Umgebungsfreiheitsgrade.
Entscheidend ist, dass unser System A nicht alleine auf der Welt ist, sondern unvermeidlich in Kontakt mit seiner Umgebung steht, die wir wieder mit A' bezeichnen (analog zum Wärmebad oben). Das Gesamtsystem Ag aus A und Umgebung A' wollen wir durch einen reinen Zustand \[ |\psi_{g}(t)\rangle \] beschreiben, wobei \(t\) die Zeitabhängigkeit dieses Gesamtzustandes darstellt. Warum ein reiner Zustand? Nun, wir wollen ja sehen, wie eine Dichtematrix für unser Teilsystem A entsteht, also macht es Sinn, für diesen Zweck von einem reinen Zustand für das Gesamtsystem auszugehen.
Nehmen wir weiter an, dass sich zur Anfangszeit \(t = 0\) auch unser System A und seine Umgebung A' jeweils einzeln in einem reinen Zustand befinden. Dann ist der Gesamtzustand das Tensorprodukt dieser beiden Zustände: \[ |\psi_{g}(0)\rangle = |\psi(0)\rangle \, |\psi'(0)\rangle \] (das ergibt ein Produkt von Wellenfunktionswerten, wenn man Argumente in die Funktionen einsetzt).
Zur Zeit \(t = 0\) sind daher System A und Umgebung A' unabhängig voneinander. Für spätere Zeiten gilt diese Produktdarstellung nicht mehr, denn es soll eine (schwache) Wechselwirkung zwischen A und seiner Umgebung A' geben. Im Gesamtzustand \( |\psi_{g}(t)\rangle \) sind dann später die Anteile von A und Umgebung A' quantenmechanisch miteinander verschränkt, also nicht mehr unabhängig voneinander.
Wir interessieren uns nun ausschließlich für die Eigenschaften von System A, nicht aber für seine Umgebung A'. Eine entsprechende Observable (die wir analog zu oben ebenfalls \( \hat{A} \) nennen – sorry für die Doppelverwendung des Buchstabens A für das System und die Observable) wirkt dann als Operator nur auf den Teil der Quantenzustände, die zu System A gehören. Die Wahrscheinlichkeit \( P_{\alpha} \) für einen Messwert \( \alpha \) der Observable darf also nicht von der Umgebung abhängen, egal wie sie aussieht.
Mathematisch können wir das so ausdrücken: Eine Orthonormalbasis des Gesamtsystems Ag ist durch Produktzustände \[ |n n'\rangle = |n\rangle \, |n'\rangle \] gegeben, wobei die Zustände \( |n\rangle \) eine Orthonormalbasis für das System A und die Zustände \( |n'\rangle \) eine Orthonormalbasis für die Umgebung A' bilden. Dabei gilt \[ \langle n n' | m m' \rangle = \delta_{n m} \, \delta_{n' m'} \] Man kann das Zahlenpaar \( (n, n') \) gleichsam als Doppelindex ansehen, der die Basiszustände des Gesamtsystems durchnummeriert. Die Matrixelemente der Observable \( \hat{A} \) sehen dann so aus: \[ \langle n n' | \, \hat{A} \, | m m' \rangle = \langle n | \, \hat{A} \, | m \rangle \, \delta_{n' m'} \] oder kurz \[ A_{n n', m m'} = A_{nm} \, \delta_{n'm'} \] Die Matrixelemente sind also diagonal im zweiten Indexteil und ansonsten unabhängig von ihm.
Wenn wir für \( |n\rangle \) als Basis die Eigenvektoren \( |\alpha\rangle \) (zu den Eigenwerten \(a_{\alpha}\)) von \(\hat{A}\) wählen, dann ist \[ \langle \alpha n' | \, \hat{A} \, | \beta m' \rangle = a_{\alpha} \, \delta_{\alpha \beta} \, \delta_{n' m'} \] Rechnen wir den Erwartungswert für \(\hat{A}\) im Gesamtsystem zur Zeit \(t\) aus: \[ \langle \psi_{g}(t) | \, \hat{A} \, | \psi_{g}(t) \rangle = \] \[ = \sum_{\alpha \beta n' m'} \, \langle \psi_{g}(t) | \alpha n' \rangle \, \langle \alpha n' | \, \hat{A} \, | \beta m' \rangle \, \langle \beta m' | \psi_{g}(t) \rangle = \] \[ = \sum_{\alpha \beta n' m'} \, \langle \psi_{g}(t) | \alpha n' \rangle \, a_{\alpha} \, \delta_{\alpha\beta} \, \delta_{n'm'} \, \langle \beta m' | \psi_{g}(t) \rangle = \] \[ = \sum_{\alpha n'} \, \langle \psi_{g}(t) | \alpha n' \rangle \, a_{\alpha} \, \langle \alpha n' | \psi_{g}(t) \rangle = \] \[ = \sum_{\alpha} \, a_{\alpha} \, \left( \sum_{n'} \, \left|\langle \alpha n' | \psi_{g}(t) \rangle \right|^{2} \right) \] Da \[ \langle \psi_{g}(t) | \, \hat{A} \, | \psi_{g}(t) \rangle \] der Erwartungswert für die Messwerte der Observablen \( \hat{A} \) ist, gilt zugleich \[ \langle \psi_{g}(t) | \, \hat{A} \, | \psi_{g}(t) \rangle = \sum_{\alpha} \, a_{\alpha} \, P_{\alpha}(t) \] Vergleichen wir dies mit unserem Rechenergebnis, so lesen wir ab: Die Wahrscheinlichkeit \( P_{\alpha}(t) \), im Gesamtsystem für die Observable \( \hat{A} \) zur Zeit \(t\) den Messwert \(a_{\alpha}\) zu finden, ist gegeben durch \[ P_{\alpha}(t) = \sum_{n'} \, \left|\langle \alpha n' | \psi_{g}(t) \rangle \right|^{2} \] Es wird hierbei über alle Basiszustände \( |n'\rangle \) der Umgebung summiert. Das ist auch anschaulich klar, denn \[ \left|\langle \alpha n' | \psi_{g}(t) \rangle \right|^{2} \] ist ja die Wahrscheinlichkeit dafür, im Gesamtsystem zur Zeit \(t\) für das Teilsystem A den Messwert \(a_{\alpha}\) und zugleich in der Umgebung den Basiszustand mit Quantenzahl \(n'\) zu finden. Wenn wir uns nicht für \(n'\) interessieren, dann muss man die Wahrscheinlichkeiten für alle \(n'\) summieren, denn \(n'\) darf dann irgendeinen beliebigen Wert annehmen.
Versuchen wir, eine Dichtematrix für das System A aufzustellen, die das obige \( P_{\alpha}(t) \) reproduziert. Diese Dichtematrix soll ein Operator sein, der nur im Zustandsraum von System A wirkt, analog zu unserer Observablen.
Zum Vergleich: Die Dichtematrix \(\rho_{g}\) im Gesamtsystem Ag hat die Form \[ (\rho_{g})_{nn'mm'}(t) = \langle n n' | \psi_{g}(t) \rangle \, \langle \psi_{g}(t) | m m' \rangle \] denn das Gesamtsystem befindet sich ja nach Voraussetzung im reinen Zustand \( |\psi_{g}(t) \rangle \).
Da wir uns nicht für die Umgebung A' interessieren, wollen wir es mit der Idee versuchen, dass wir einfach über \(n'\) summieren müssen, d.h. wir bilden die Spur über die Zustände der Umgebung (wir verifizieren gleich, dass wir richtig geraten haben):
|
Dichtematrix für ein System A im Kontakt mit seiner Umgebung A': \[ \rho_{nm}(t) := \sum_{n'} \, \langle n n' | \psi_{g}(t) \rangle \, \langle \psi_{g}(t) | m n' \rangle \] Dabei sind \( | n n' \rangle \) Basiszustände des Gesamtsystems (System A plus Umgebung A'), wobei sich die gestichenen Indices auf die Umgebung beziehen. Es wird also die Spur über die Umgebungs-Indices gebildet. Der Zustand \( |\psi_{g}(t)\rangle \) beschreibt den Zustand des Gesamtsystems. Alle Observablen, die sich nur auf das System A beziehen, lassen sich mit der obigen Dichtematrix berechnen, die das System A quantenmechanisch beschreibt.
|
Diese Dichtematrix wirkt nur auf den Zuständen des Systems A.
Überprüfen wir, dass sie
die obige Wahrscheinlichkeit \( P_{\alpha}(t) \) reproduziert:
\[
P_{\alpha}(t)
=
\langle \alpha| \, \hat{\rho} \, |\alpha \rangle
=
\]
\[
\sum_{nm} \,
\langle \alpha | n \rangle
\, \rho_{nm}(t) \,
\langle m | \alpha \rangle
=
\]
\[
=
\sum_{nm} \,
\langle \alpha |n \rangle
\,
\sum_{n'} \,
\langle n n' | \psi_{g}(t) \rangle \,
\langle \psi_{g}(t) | m n' \rangle
\,
\langle m| \alpha \rangle
=
\]
\[
=
\sum_{n'} \,
\langle \alpha n' | \psi_{g}(t) \rangle \,
\langle \psi_{g}(t) | \alpha n' \rangle =
\]
\[
=
\sum_{n'} \,
\left|\langle \alpha n' | \psi_{g}(t) \rangle \right|^{2}
\]
Halten wir fest:
Wenn das Gesamtsystem aus System A und Umgebung A' sich zur Zeit \(t\) in einem reinen Zustand \( |\psi_{g}(t)\rangle \) befindet, dann wird das System A durch obige Dichtematrix \( \rho_{nm}(t) \) beschrieben.
Dabei ist noch nicht festgelegt, ob diese Dichtematrix für System A eher einem reinen Zustand oder eher einem statistischen Gemisch entspricht. Wenn beispielsweise zur Anfangszeit \(t = 0\) sich System A und Umgebung A' beide einzeln in einem reinen Zustand befinden, dann ist ja der Gesamtzustand gleich \[ |\psi_{g}(0)\rangle = |\psi(0)\rangle \, |\psi'(0)\rangle \] und die obige Dichtematrix hat die Form \[ \rho_{nm}(0) = \] \[ = \sum_{n'} \, \langle n n' | \psi_{g}(0) \rangle \, \langle \psi_{g}(0) | m n' \rangle = \] \[ = \sum_{n'} \, \langle n|\psi(0)\rangle \, \langle n'|\psi'(0)\rangle \, \langle \psi(0) |m \rangle \, \langle \psi'(0) |n'\rangle = \] \[ = \langle n| \psi(0) \rangle \, \langle \psi(0) |m \rangle \, \, \sum_{n'} \, \langle \psi'(0) | n' \rangle \, \langle n' | \psi'(0) \rangle = \] \[ = \langle n|\psi(0) \rangle \, \langle \psi(0) |m \rangle \] so wie wir das bei einer Dichtematrix auch erwarten, die zu einem reinen Zustand gehört.
Um die Dichtematrix genau berechnen zu können, müsste man im Prinzip den Gesamtzustand \( |\psi_{g}(t)\rangle \) für jede Zeit \(t\) kennen.
So genau wollen wir die Dichtematrix aber gar nicht ermitteln, denn wir interessieren uns eher für zeitliche Mittelwerte, wobei die Beobachtungszeit sehr viel länger ist als die typischen mikroskopischen Veränderungszeiten. Das gilt besonders für das thermische Gleichgewicht, bei dem wir uns für kurzzeitige Fluktuationen überhaupt nicht mehr interessieren, sondern die Dichtematrix als zeitlich konstant annehmen.
Machen wir es konkret und verwenden wir für \( |n\rangle \) und \( |n'\rangle \) die Energie-Eigenzustände von System A und Umgebung A' mit den Energien \(E_{n}\) und \(E'_{n'}\). Für das Gesamtsystem Ag haben wir dann die Basis \[ |n n'\rangle \] die aber streng genommen keine Eigenvektoren des Gesamt-Hamiltonoperators \[ \hat{H}_{g} = \hat{H} + \hat{H}' + \hat{H}_{int} \] sind, denn der Wechselwirkungs-Hamiltonoperator \(\hat{H}_{int}\) zwischen System A und Umgebung A' muss nicht diagonal in dieser Basis sein. Da diese Wechselwirkung aber hier als klein angenommen wird, sind \( |n n'\rangle \) fast Eigenvektoren von \(\hat{H}\) (man kann dann beispielsweise Störungstheorie anwenden).
Geben wir nun die Energie des Gesamtsystems (bis auf eine kleine Energieunschärfe) vor. Dann sind alle jene Energiezustände \( |n n'\rangle \) erreichbar, die bei dieser Energie liegen. Es kann auch Energie zwischen dem System A und der Umgebung A' ausgetauscht werden. Letztlich wird der Gesamtzustand \( |\psi_{g}(t)\rangle \) zu jedem Zeitpunkt \(t\) irgendeinen ziemlich zufälligen Überlapp mit jedem der energetisch erreichbaren Zustände \( |n n'\rangle \) haben, zumindest bei einem makroskopischen Gesamtsystem mit sehr vielen Mikrozuständen.
Die Amplitude (also dieser Überlapp) \[ \langle n n' |\psi_{g}(t) \rangle \] erscheint also wie gwürfelt. Ob das wirklich so ist, hängt von den Details der Wechselwirkung \( \hat{H}_{int} \) und von der gewählten Basis \( |n n'\rangle \) ab – man spricht auch von der bevorzugten Basis. Wir können uns gut vorstellen, dass unserer Energiebasis eine solche bevorzugte Basis ist, denn in realen Systemen im thermischen Gleichgewicht kommt es wirklich zu gleichsam zufälligen Energiefluktuationen zwischen System und Umgebung.
Wenn man die Amplitude \( \langle n n' |\psi_{g}(t)\rangle \) würfelt, so gibt es zwei Aspekte: ihren Betrag und ihre Phase, denn die Amplitude ist ja eine komplexe Zahl (bildlich gesprochen ein Pfeil in der zweidimensionalen Ebene).
Bei der Phase ist es einfach: sie wird irgendeinen zufälligen Wert zwischen \(0\) und \(2\pi\) haben. Wie sieht es aber mit dem Betrag aus?
Die Summe der Betragsquadrate dieser Amplituden über alle \(n\) und \(n'\) muss Eins sein, denn wir haben es mit einem auf Eins normierten Zustand und mit einer Orthonormalbasis zu tun.
Nehmen wir an, es gibt \(\Omega\) verschiedene n-Werte und \(\Omega'\) verschiedene n'-Werte. \(\Omega\) ist also die Dimension des Zustandsraums für das System A und \(\Omega'\) die entsprechende Dimension für die Umgebung A'.
Da zumindest die Umgebung makroskopisch sein soll, ist \(\Omega'\) eine unvorstellbar große Zahl, wie wir von oben wissen, beispielsweise \(10^{(10^{20})}\). Da es \(\Omega \cdot \Omega'\) Amplituden gibt, deren Betragsquadrate zusammen Eins ergeben müssen, wird jede einzelne Amplitude im Mittel den Betrag \[ \frac{1}{\sqrt{\Omega \cdot \Omega'}} \] haben, außer in dem sehr seltenen Fall, dass der Gesamtzustand zufällig einen großen Überlapp mit nur einem Mikrozustand hat (da \(\Omega'\) riesig ist, sind die Energie-Mikrozustände quasikontinuierlich, so dass dieser Fall äußerst unwahrscheinlich ist).
Was bedeutet das für die Dichtematrix \[ \rho_{nm}(t) = \] \[ = \sum_{n'} \, \langle n n' | \psi_{g}(t) \rangle \, \langle \psi_{g}(t) | m n' \rangle \] Für die Diagonalelemente \(n = m\), also \[ \rho_{nn}(t) = \] \[ = \sum_{n'} \, \langle n n' | \psi_{g}(t) \rangle \, \langle \psi_{g}(t) | n n' \rangle = \] \[ = \sum_{n'} \, \left| \langle n n' | \psi_{g}(t) \rangle \right|^2 \] spielt die Phase der Amplituden keine Rolle, d.h. ihre Größenordung kann folgendermaßen grob abgeschätzt werden: \[ \rho_{nn}(t) = \] \[ = \sum_{n'} \, \left| \langle n n' |\psi_{g}(t) \rangle \right|^{2} = \] \[ = \Omega' \cdot \frac{1}{\Omega \cdot \Omega'} = \frac{1}{\Omega} \] Bei den Nichtdiagonal-Elementen \( \rho_{nm}(t) \) mit \(n \ne m\) sind die Phasen dagegen wichtig und wir haben näherungsweise für \(n \ne m\) mit der Schreibweise \[ \langle n n' |\psi_{g}(t) \rangle =: \left| \langle n n' |\psi_{g}(t)\rangle \right| \, e^{i \theta_{nn'}} \] die folgende Formel: \[ \rho_{nm}(t) = \] \[ = \sum_{n'} \, \langle n n' |\psi_{g}(t)\rangle \, \langle \psi_{g}(t) | m n' \rangle = \] \[ = \sum_{n'} \, \left| \langle n n' |\psi_{g}(t)\rangle \right| \, \left| \langle m n' |\psi_{g}(t)\rangle \right| \, e^{i \, (\theta_{nn'} - \theta_{mn'} )} \] Diese Summe macht ungefähr folgendes: Sie addiert sehr viele komplexe Zahlen mit Betrag von etwa \(1/(\Omega \cdot \Omega')\) und zufälliger Phase. Man kann sich vorstellen, dass man sehr viele sehr kleine, zufällig ausgerichtete Pfeile aneinanderfügt und sich damit zufällig durch die komplexe Ebene bewegt, so wie bei einer Brownschen Bewegung (random walk).
Aus der Statistik weiß man: Macht man \(N\)-mal einen Schritt der Länge \(L\) in eine zufällige Richtung, so entfernt man sich im Mittel um \[ L \cdot \sqrt{N} \] von seinem Ausgangspunkt.
In unserem Fall machen wir \(\Omega'\) Schritte der mittleren Länge \(1/(\Omega \cdot \Omega')\), entfernen uns also typischerweise um \[ \frac{1}{\Omega \cdot \Omega'} \cdot \sqrt{\Omega'} \] vom Nullpunkt. Die komplexe Zahl, die dabei herauskommt, wird also einen mittleren Betrag von \[ \frac{1}{\Omega \cdot \Omega'} \cdot \sqrt{\Omega'} = \frac{1}{\Omega \cdot \sqrt{\Omega'} } \] haben sowie eine zufällige Phase.
Damit können wir die beiden Fälle zusammenfassen: Bei zufälligen Phasen der Amplituden und einer statistischen Verteilung der Amplitudenbeträge erwarten wir für die Elemente der Dichtematrix von System A ungefähr die folgende Größenordnung:
| \[ \rho_{nm}(t) = \frac{1}{\Omega} \cdot \left( \delta_{nm} + O_{nm}\left(\frac{1}{\sqrt{\Omega'}} \right) \right) \] |
Dabei ist
\[
O_{nm}\left(\frac{1}{\sqrt{\Omega'}} \right)
\]
eine komplexe Zahl mit irgendeiner zufälligen Phase
und einem mittleren Betrag von
\( 1/\sqrt{\Omega'}\).
Da die Umgebung unvorstellbar viele Mikrozustände \(n'\) hat, ist \(\Omega'\) extrem groß und es bleiben praktisch nur noch die Diagonalelemente übrig. Das ist dann die Dichtematrix eines statistischen Ensembles ohne jede Interferenz zwischen den Mikrozuständen.
Da \(\Omega\) gerade die Zahl der erreichbaren Mikrozustände im System \(A\) ist, ergibt sich bei unserer Näherung sogar das mikrokanonische Ensemble. Entscheiden ist also, dass das System A in Kontakt mit einer makroskopischen Umgebung A' mit sehr vielen Mikrozuständen ist, und dass die Wechselwirkung mit der Umgebung die Phasenbeziehungen im System A durcheinanderwirbelt (→ zufällige Phasen, random walk).
Die obige Argumentation kann nicht für jede Orthonormalbasis richtig sein, denn man kann ja jederzeit einen Basiswechsel durchführen und damit die diagonale Dichtematrix in eine nichtdiagonale Dichtematrix umrechnen. Daher hatten wir oben von einer bevorzugten Basis gesprochen. Will man herausfinden, welches die bevorzugte Basis ist, so muss man in eine genauere Analyse einsteigen, was aber den Rahmen hier sprengen würde, denn die Details der Wechselwirkung kommen hier ins Spiel.
Um zu sehen, was bei der obigen Argumentation schief gehen kann, schauen wir uns noch einmal den Zeitpunkt \(t = 0\) an, bei dem unser System A und seine Umgebung A' noch jeweils unabhängig voneinander sind und einzeln in einem reinen Zustand sind: \[ |\psi_{g}(0)\rangle = |\psi(0)\rangle \, |\psi'(0)\rangle \] Dann ist \[ \langle n n' |\psi_{g}(0) \rangle = \] \[ = |\langle n n' |\psi_{g}(0)\rangle| \, e^{i \theta_{nn'}} = \] \[ = \langle n |\psi(0)\rangle \, \langle n' |\psi'(0)\rangle = \] \[ = |\langle n |\psi(0)\rangle| \, e^{i \theta_{n}} \, |\langle n' |\psi'(0)\rangle| \, e^{i \theta_{n'}} \] d.h. die Phase zerfällt in eine Summe: \[ \theta_{nn'} = \theta_{n} + \theta_{n'} \] Die Phase in \( \rho_{nm}(0) \) ist wegen der Formel (siehe oben) \[ \rho_{nm}(t) = \] \[ = \sum_{n'} \, \left| \langle n n' |\psi_{g}(t)\rangle \right| \, \left| \langle m n' |\psi_{g}(t)\rangle \right| \, e^{i \, (\theta_{nn'} - \theta_{mn'} )} \] gegeben durch \[ \theta_{nn'} - \theta_{mn'} = \] \[ = \theta_{n} + \theta_{n'} - \theta_{m} - \theta_{n'} = \] \[ = \theta_{n} - \theta_{m} \] Hier sehen wir es: Die Phasendifferenz hängt nicht mehr von \(n'\) ab, wird also von der Umgebung nicht beeinflusst. Daher laufen wir bei der Summe über \(n'\) auch nicht mehr in zufällige Richtungen, sondern immer in dieselbe Richtung, so dass die Nicht-Diagonalelemente der Dichtematrix von derselben Größenordnung sind wie die Diagonalelemente. Halten wir fest:
|
Bedingung für Dekohärenz: Die Dichtematrix von System A wird dann diagonal, wenn die Phasendifferenz \[ \theta_{nn'} - \theta_{mn'} \] zweier Amplituden \[ \langle n n' |\psi_{g}(t) \rangle =: \left| \langle n n' |\psi_{g}(t)\rangle \right| \, e^{i \theta_{nn'}} \] \[ \langle m n' |\psi_{g}(t)\rangle =: \left| \langle m n' |\psi_{g}(t)\rangle \right| \, e^{i \theta_{mn'}} \] in zufälliger Weise vom Umgebungsindex \(n'\) abhängt.
|
Ein anschauliches Bild dazu:
Die Amplituden \[ \langle n n' |\psi_{g}(t)\rangle \] können wir uns als Pfeile oder Uhrzeiger in der Ebene vorstellen, wobei die Phase \( \theta_{nn'} \) der Drehwinkel des Pfeils ist. Die Gesamtheit der Pfeile für alle Werte von \(n\) und \(n'\) definiert den Mikrozustand des Gesamtsystems. Diese Pfeile können wir in eine Tabelle eintragen, wobei wir die Zeilen mit \(n\) und die Spalten mit dem Umgebungsindex \(n'\) durchnummerieren. Wir haben also sehr viele Spalten, denn die Umgebung ist makroskopisch.
Zur Zeit \( t = 0 \) ist \[ \theta_{nn'} = \theta_{n} + \theta_{n'} \] d.h. wenn wir in der Tabelle eine Spalte nach rechts gehen, so drehen sich alle Pfeile um denselben Winkel weiter (und strecken sich um denselben Faktor). Die Drehung und Streckung der Pfeile erfolgt in den verschiedenen Zeilen synchron im Gleichschritt, wenn wir in der Tabelle nach rechts laufen. Wenn wir die Drehrichtung zweier Pfeile in derselben Spalte vergleichen, so ändert sich dieser Dreh-Unterschied nicht, wenn wir zu einer anderen Spalte übergehen. Es herrscht Kohärenz zwischen den einzelnen Zeilen und damit zwischen den Zuständen von System A.
Nur ein Gesamtzustand, bei dem System A und Umgebung A' unabhängig voneinander sind, verhält sich so speziell. Ein allgemeiner Gesamtzustand wird diese spezielle Eigenschaft nicht aufweisen. Im Lauf der Zeit bewirkt die Wechselwirkung zwischen System A und Umgebung A', dass die Pfeile der Tabelle aus dem Takt geraten. Wenn wir jetzt nach rechts laufen, so werden sich die Pfeile verschiedener Zeilen nicht mehr in gleicher Weise drehen. Wenn wir jetzt die Drehrichtung zweier Pfeile in derselben Spalte vergleichen, so ändert sich dieser Dreh-Unterschied, wenn wir zu einer anderen Spalte übergehen. Es herrscht Dekohärenz zwischen den einzelnen Zeilen.
Die Zeit, bis die Pfeile der verschiedenen Spalten aus dem Takt geraten sind,
nennt man Dekohärenzzeit.
Eine Bowlingkugel hat an der Luft bei Zimmertemperatur eine Deköhärenzzeit von etwa \(10^{- 26}\) Sekunden. Ein Lichtstrahl kann in dieser Zeit noch nicht einmal einen Atomkern durchqueren, d.h. die Pfeile geraten praktisch sofort aus dem Takt.
Sogar im leeren Weltraum weit weg zwischen allen Galaxien wäre die Deköhärenzzeit der Bowlingkugel aufgrund der kosmischen Hintergrundstrahlung immer noch bei \(10^{- 18}\) Sekunden, entsprechend einem Lichtweg von einem Atomdurchmesser.
Ein Staubteilchen von 10 Mikrometern hält dagegen im leeren Weltraum immerhin schon 0,1 Mikrosekunden kohärent durch.
Man sieht: Makroskopische Körper sind praktisch immer dekohärent, also nicht durch einen reinen Quantenzustand zu beschreiben.
Ein freies Elektron bleibt bei Zimmertemperatur im Ultrahochvakuum dagegen immerhin etwa 10 Sekunden kohärent. Nur deshalb sind Quanten-Interferenz-Experimente mit Elektronen überhaupt möglich – bei Bowlingkugeln wird man dagegen vergeblich nach Interferenzen suchen. Zu den Dekohärenzzeiten siehe Wikipedia: Dekohärenz.
Um das Dichtematrix-Element \( \rho_{nm}(t) \) auszurechnen, müssen wir uns die Zeilen \(n\) und \(m\) herausgreifen und in jeder Spalte die beiden entsprechenden Pfeile zu einem neuen Pfeil zusammenfassen, indem wir die Pfeillängen multiplizieren und den Dreh-Unterschied der beiden Pfeile als Drehausrichtung des neuen Pfeils verwenden. Diese neuen Pfeile müssen wir nun alle aneinanderhängen, was bei zufälligen Dreh-Unterschieden den Zufallsweg in der komplexen Ebene ergibt und zu einem recht kleinen Gesamtpfeil führt. Für \(n = m\) gibt es dagegen keine Drehunterschiede und es kommt ein vergleichsweise viel größerer Gesamtpfeil ohne Drehwinkel zustande. Die Länge dieses Pfeils ist die Wahrscheinlichkeit, im System A den Zustand \(n\) vorzufinden.
⟸ Zurück zu Kapitel 1a: Was ist Entropie? (Teil 1)
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 28 November 2023