Zusammenfassung des Buchkapitels:
In der QCD kann die Wechselwirkung zwischen den Quarks innerhalb eines Hadrons nicht mit Hilfe von Feynmangraphen berechnet werden, da die starke Farbladung bei diesen Abständen zu groß ist und die Störungsrechnung deshalb nicht funktioniert (siehe vorhergehendes Kapitel).
Es gibt aber glücklicherweise eine alternative Formulierung, die statt Feynmangraphen den Begriff der sogenannten Pfadintegrale verwendet. Im Wesentlichen beinhalten diese Pfadintegrale die Aufsummation von Wahrscheinlichkeitspfeilen zu jeder denkbaren Konfigurationen der Quarks und starken Kraftfelder in einem Hadron. Dabei müssen diese Felder keine Lösungen der klassischen Feldgleichungen sein.
Solche Aufsummierungen können heute mit Hilfe geeigneter Methoden auf modernen Computern recht zuverlässig durchgeführt werden. Das dazu verbreitete Verfahren trägt den Namen Gitterrechnung oder auch Gittereichtheorie. Es geht auf eine Idee von Kenneth G. Wilson aus dem Jahre 1974 zurück.
Die Grundidee dieses Verfahrens ist einfach: Man überzieht das Volumen des Hadrons mit einem möglichst feinen Gitter (realistisch sind beispielsweise 32 mal 32 mal 32 Gitterpunkte), und betrachtet das starke Kraftfeld an diesen Gitterpunkten zu festen Zeitpunkten (z.B 96 Zeitpunkte). Je feiner das Raum-Zeit-Gitter gewählt werden kann, umso besser wird die Rechengenauigkeit, umso größer wird aber auch der Rechenaufwand.
Bei den Gitter-QCD-Rechnungen müssen an jedem Gitterpunkt die Werte des Quarkfeldes und des starken Kraftfeldes betrachtet werden. Dabei kann man sich jedoch nicht auf ein bestimmtes Quark beschränken, da jedes beliebige Quark virtuell auftreten kann, ebenso wie jede beliebige starke Gluon-Feldkonfiguration. Quarks kommen als Teilchen und Antiteilchen vor und treten darüber hinaus in 6 verschiedenen Flavorn (u,d,s,c,b,t) und mit 3 verschiedenen Farbladungen (rot, gelb, blau) auf. Somit müssen an jedem Gitterpunkt 2 ×6 ×3 = 32 Quarkfelder betrachtet werden. Das starke Kraftfeld steuert 32 weitere reelle Zahlen je Gitterpunkt bei (8 Farbladungspaarungen mal 4 Komponenten, die ihren Ursprung in Einsteins Relativitätstheorie haben).
Die Berechnung erfordert daher im Prinzip die Aufsummation einer gigantischen Anzahl von Summanden, denn jede denkbare Wertekombination all dieser Felder an den einzelnen Gitterpunkten ergibt einen Summanden. Eine solche astronomische Zahl von Termen aufzusummieren ist nicht möglich. Man kann aber mit Hilfe statistischer Verfahren das Endergebnis mittlerweile zuverlässig abschätzen. Damit gelingt es, die Massen vieler Hadronen auf wenige Prozent genau zu berechnen. Je größer die Computerleistung dabei ist, umso genauer stimmen auch die Ergebnisse. Die QCD ist damit als die korrekte Theorie der starken Wechselwirkung bestätigt!
(für Leser mit mathematisch-physikalischem Hintergrundwissen)
In den bisherigen Buchkapiteln wurde Quantenfeldtheorie meist in ihrer störungstheoretischen Version dargestellt, wie sie durch Feynmangraphen repräsentiert wird. Das funktioniert, solange die Ladung der entsprechenden Wechselwirkung deutlich kleiner als 1 ist, also beispielsweise in der QED und in der QCD bei hohen Impulsen, bei denen die gleitende starke Ladung relativ klein wird (siehe Kapitel 5.4).
Bei den Energien und Impulsen, wie sie die Quarks und Gluonen innerhalb von Hadronen normalerweise aufweisen, ist die starke Ladung dagegen nicht mehr deutlich kleiner als 1, d.h. Feynmangraphen funktionieren hier nicht mehr. Es gibt aber glücklicherweise eine alternative Formulierung der QCD, die nicht auf der Störungstheorie basiert, sondern deren Grundlage sogenannte Pfadintegrale sind. Die im Buchkapitel angesprochenen Berechnungen basieren auf dieser Methode und tragen den Namen Gittereichtheorie oder auch Gitter-QCD, da man zur Berechnung der Pfadintegrale Raum und Zeit diskretisieren muss, also mit einem möglichst feinmaschigen Gitter überzieht.
Es würde den Rahmen des Kapitels sprengen, hier im Detail auf die Gitter-QCD eingehen zu wollen. Die wesentlichen Kernideen lassen sich aber auch ohne Details plausibel machen:
Die Idee zu Pfadintegralen geht im Wesentlichen auf Richard P. Feynman zurück. Bereits in Kapitel 5.3 ist uns diese Idee begegnet, als wir uns die Frage gestellt hatten, wie sich ein elektromagnetisches Feld auf Wahrscheinlichkeitsamplituden auswirkt. Dort wird zunächst jedem möglichen Pfad (Weg) \( \gamma \), den ein Teilchen zurücklegen kann, eine entsprechende Wahrscheinlichkeitsamplitude (komplexe Zahl) zugordnet.
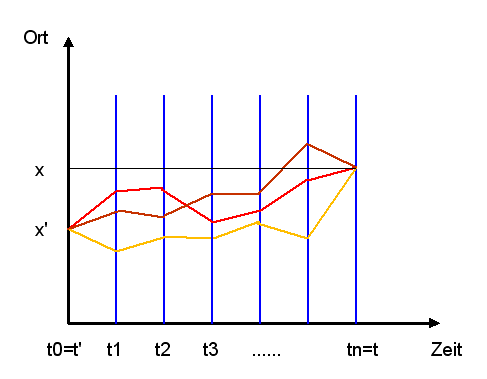
Ist ein elekromagnetisches Potential \(A^{\mu}\) vorhanden, so ändert sich die Phase dieser Amplitude um den Betrag \[ \alpha = - \frac{q}{\hbar} \, \int_{\gamma} A_{\mu} \, dx^{\mu} \] Erst die Summe aller Amplituden über alle möglichen Wege zwischen zwei Punkten \(x'\) und \(x\) ergibt die Gesamtamplitude \( C(t,x;t',x') \) dafür, dass ein Teilchen am Endpunkt \(x\) zur Zeit \(t\) gefunden wird, wenn es zu einer früheren Zeit \(t'\) am Startpunkt \(x'\) losläuft – man spricht vom Propagator. Formal wird diese Summe im räumlich eindimensionalen Fall durch folgendes Integral über alle Wege (Pfade) \(\gamma\) ausgedrückt, welche die beiden Raum-Zeit-Punkte miteinander verbinden: \[ C(t,x;t',x') = \int_{\gamma} D[\gamma] \, e^{\frac{i}{\hbar} S[\gamma]} \] Dabei ist \( S[\gamma] \) die sogenannte Wirkung, die zum Weg \(\gamma\) gehört, und \( D[\gamma] \) ist ein Integrationsmaß im Funktionenraum der Wege.
Letztlich definiert man das obige Integral, indem man das Zeitintervall zwischen \(t'\) und \(t\) in \(n\) gleich große Teilintervalle zerlegt und jeden Weg \(\gamma\) näherungsweise als Polygonzug zwischen den Punkten \[ x' = \gamma(0) \] \[ x_{1} = \gamma(t_{1}) \] \[ x_{2} = \gamma(t_{2}) \] \[ ... \] \[ x = \gamma(t) \] auffasst. Das Integral läuft dann über alle Polygonzüge, oder gleichwertig dazu über alle möglichen Zwischenwerte für \(x_{1}, x_{2}, \, ... \), d.h. aus dem Integral \[ \int_{\gamma} D[\gamma] \, ... \] wird ein Intergal \[ \int dx_{1} \, dx_{2} \, ... \, dx_{n - 1} \, ... \] Die Zeit wird also diskretisiert, es wird über die möglichen Wegpunkte auf dem Zeitgitter integriert, und dieses Zeitgitter wird dann beliebig fein gemacht. Mehr dazu siehe in Quantenfeldtheorie und Eichfelder, Kapitel 3.

Man kann diese Idee auf Quantenfeldtheorien übertragen.
Dort sind allerdings nicht mehr die Orte \(\gamma(t)\) eines Teilchens
zu verschiedenen Zeiten \(t\) die relevanten Freiheitsgrade,
sondern die Werte der betrachteten Felder an den einzelnen Raumpunkten zu den verschiedenen Zeiten.
Statt der Wege \( \gamma \) werden in der QCD also die Quarkfelder \( \psi \) und die Gluon-Eichpotentiale \( A^{\mu} \) betrachtet. Ein Pfadintegral in der QCD sieht dann analog zu oben folgendermaßen aus:
| Pfadintegral in der Quantenfeldtheorie mit Fermionen und Eichpotentialen: \[ \langle O \rangle = \frac{1}{Z} \, \int D[\psi,A] \, e^{\frac{i}{\hbar} S[\psi,A]} \, O[\psi,A] \] |
Dabei wird über alle Feldkonfigurationen integriert, die die Quarkfelder \( \psi \) und die
Gluon-Eichpotentiale \( A^{\mu} \) in Raum und Zeit aufweisen können, wobei diese Felder
keine Lösungen der klassischen Feldgleichungen zu sein brauchen.
Der Ausdruck \( D[\psi,A] \) ist ein entsprechendes Integrationsmaß im Raum dieser Felder, auf das wir gleich noch zurückkommen. Weiter ist \( \langle O \rangle \) der Erwartungswert der beobachtbaren Größe \( O \), d.h. \( O[\psi,A] \) ordnet jeder Feldkonfiguration eine Zahl zu, die diese beobachtbare Größe charakterisiert.
\( \frac{1}{Z} \) eine Normierungskonstante (in Analogie zur statistischen Physik aus Zustandssumme genannt), die durch \[ Z = \int D[\psi,A] \, e^{\frac{i}{\hbar} S[\psi,A]} \] gegeben ist, und \( S[\psi,A] \) ordnet jeder Feldkonfiguration eine reelle Zahl zu, die man wie oben als Wirkung dieser Feldkonfiguration bezeichnet und die dieselbe physikalische Einheit wie das Planck'sche Wirkungsquantum \( \hbar \) besitzt.
Man kann das obige Pfadintegral \[ \langle O \rangle = \frac{1}{Z} \, \int D[\psi,A] \, e^{\frac{i}{\hbar} S[\psi,A]} \, O[\psi,A] \] also so verstehen: Jede mögliche Feldkonfiguration (gegeben durch Funktionen \(\psi\) und \(A\)) trägt bei einer Messgröße \(O\) mit der Wahrscheinlichkeitsamplitude \( e^{\frac{i}{\hbar} S[\psi,A]} \, O[\psi,A] \) zum Gesamtresultat bei, wobei alle diese Amplituden mit geeignetem Integrationsmaß \( D[\psi,A] \) und Normierung \(1/Z\) im Pfadintegral aufsummiert werden. Dabei wird die Phase jeder Amplitude wesentlich durch die Wirkung \( S[\psi,A] \) (gemessen in der Einheit \(\hbar\)) bestimmt.
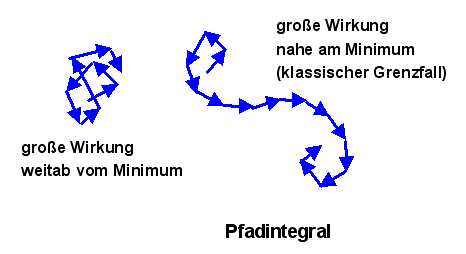
Für große Werte der Wirkung \( S[\psi,A] \) im Vergleich zu \(\hbar\) ändert sich die Phase bereits bei kleinen Änderungen der Felder zumeist sehr rasch, so dass sich unterschiedliche Feldbeiträge im Pfadintegral gegenseitig auslöschen (destruktive Interferenz).
Nur bei den Feldbereichen, für die die Wirkung vorübergehend konstant wird (z.B. bei einem Minimum der Wirkung) können sich verschiedene Beiträge im Integral verstärken und einen relevanten Beitrag liefern (konstruktive Interferenz).
Daher kommt es, dass im klassischen Grenzfall (also bei großen Wirkungen) nur die Felder wichtig sind, bei denen die Wirkung \( S[\psi,A] \) ein Minimum aufweist (Maxima sind meist nicht relevant bzw. werden durch passende Definition der Wirkung in Minima verwandelt). Man spricht auch klassisch vom Prinzip der kleinsten Wirkung. Aus diesem Prinzip lassen sich die klassischen Feldgleichungen für \( \psi \) und \( A^{\mu} \) herleiten, sowie analog weiter oben die klassische Bewegungsgleichung für die Bahnkurve \(\gamma\) eines Teilchens.
Besitzt die Wirkung \( S[\psi,A] \) dagegen Werte in derselben Größenordnung wie \(\hbar\),
so sind alle Feldkonfigurationen relevant, nicht nur diejenigen, bei denen die Wirkung ein Minimum aufweist
und die damit Lösungen der klassischen Feldgleichungen sind.
Das ist der Quantenfall, wie er beispielsweise für die Beschreibung von Hadronen wichtig ist.
Man sagt auch anschaulich, die Felder fluktuieren um ihre klassischen Werte.
Das bedeutet: Auch Felder, die nicht Lösungen des klassischen Feldgleichungen sind, führen zu
Wahrscheinlichkeitsamplituden, die berücksichtigt werden müssen.
Die Quantenfeldtheorie lässt sich komplett auf dieser Idee der Pfadintegrale aufbauen, und bei Eichtheorien ist dieser Weg auch der erfolgreichste. Dabei kann man nicht nur die Regeln für Feynmangraphen aus diesen Pfadintegralen ableiten, sondern auch von den Pfadintegralen ausgehend einen anderen, nicht-störungstheoretischen Weg einschlagen: den Weg der Gittereichtheorie.
In der Gittereichtheorie werden die benötigten Pfadintegrale direkt numerisch berechnet, indem man Raum und Zeit mit einem möglichst feinmaschigen Gitter überzieht, die Felder nur an den Gitterpunkten und an den Verbindungslinien auswertet und schließlich zu unendlich kleinem Gitterabstand hin extrapoliert. Letztlich sind die obigen Pfadintegrale durch eine solche Grenzwertbildung überhaupt erst definiert.
Schauen wir uns zum Vergleich noch einmal das ursprüngliche Pfadintegral über alle Wege \(\gamma\) an: Dort wurde die Zeit diskretisiert und das Integral über alle möglichen Wegpunkte zu diesen Zwischenzeiten gebildet: \[ \int dx_{1} \, dx_{2} \, ... \, dx_{n - 1} \, ... \] Da in der Quantenfeldtheorie nicht mehr der Weg der relevante Freiheitsgrad ist, sondern die Felder, muss man die Wegpunkte auf dem Zeitgitter durch die Feldwerte auf dem Raum-Zeit-Gitter ersetzen: \[ x_{i} := \gamma(t_{i}) \] wird ersetzt durch \[ \psi_{i} := \psi(t_{i},\boldsymbol{x}_{i}) \] für die Quarkfelder und \[ A_{i} := A(t_{i},\boldsymbol{x}_{i}) \] für die Eichpotentiale, wobei \( (t_{i},\boldsymbol{x}_{i}) \) die Punkte auf dem Raumzeitgitter sind. Entsprechend entsteht ein Integral der Form \[ \int d\psi_{1} \, dA_{1} \, d\psi_{2} \, dA_{2} \, ... \, d\psi_{n - 1} \, dA_{n - 1} \, ... \] bei dem über alle Feldwerte an allen Gitterpunkten integriert wird. Pro Raum-Zeit-Gitterpunkt entstehen so mehrere Integrationsvariablen, nämlich eine für jedes Feld an diesem Gitterpunkt. Verwendet man beispielsweise ein Gitter von \(10 \cdot 10 \cdot 10 \cdot 10 = 10 \, 000\) Gitterpunkten, so entstehen mindestens \(10 \, 000\) Integrationsvariablen, über die zu integrieren ist. Da dabei der Integrand \( e^{\frac{i}{\hbar} S[\psi,A]} \) sehr unterschiedliche Phasen aufweisen kann, entsteht oft ein Integral, bei dem wild kreisende Zeiger aufsummiert werden müssen, was den Grenzwert für immer feinere Gitter sehr schwierig gestaltet.
Man wendet daher meist den folgenden Trick an (auch Wick-Rotation genannt):
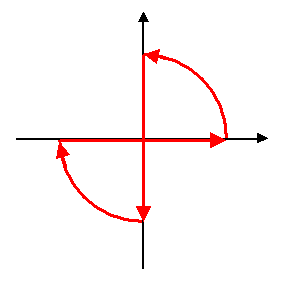
Die Wirkung \(S\) kann als Zeitintegral über die sogenannte Lagrangefunktion \(L\) geschrieben werden, die wiederum von den Feldern abhängt: \[ S = \int dt \, L \] Man verwendet nun, dass die Lagrangefunktion \(L\) über die Felder analytisch von der Zeit \(t\) abhängt, d.h. dass man die reelle Variable \(t\) durch eine komplexe Variable \(z\) ersetzen kann und dass jedes Wegintegral von \(L\) über einen geschlossenen Weg \(\Gamma\) in der komplexen Zeitebene den Wert Null hat: \[ \int_{\Gamma} dz \, L(z) = 0 \] Nun wählen wir folgenden speziellen Weg für \(\Gamma\): Wir gehen auf der reellen Zeitachse von minus nach plus Unendlich, also \[ z = \Gamma(t) = t \] mit reellem \(t\) dort, gehen auf einem Kreisbogen im Unendlichen auf die imaginäre Achse über, laufen die imaginäre Zeitachse von plus nach minus Unendlich, also \[ z = \Gamma(t) = - i t \] mit reellem \(t\) dort, und dann auf einem Kreisbogen wieder zu unserem Startpunkt auf die reelle Zeitachse bei minus Unendlich. Weiter fordern wir Randbedingungen für die Felder im Unendlichen, so dass diese und damit auch \(L\) auf den Kreisbögen im Unendlichen der komplexen Zeitebene so klein werden, dass die Kreisbögen keinen Beitrag zum Gesamtintegral liefern.
Damit haben wir
\[
0 = \int_{\Gamma} dz \, L(z) =
\int dt \, L(t) - \int i \, dt \, L(i t)
\]
wobei \( i \) die imaginäre Einheit ist, oder kurz
\[
\int dt \, L(t) = \int i \, dt \, L(i t)
\]
wobei \( L(i t) \) bedeutet, dass die Zeitvariablen in den Feldern, die in
L eingehen, analytisch fortgesetzt werden und dann
auf der imaginären Achse auszuwerten sind.
Damit erhalten wir für den Integranden des Pfadintegrals:
\[
e^{\frac{i}{\hbar} S} = e^{\frac{i}{\hbar} \int dt \, L(t)} =
\]
\[ =
e^{\frac{i}{\hbar} \int i \, dt \, L(i t)} =
e^{- \frac{1}{\hbar} \int dt \, L(i t) } =
\]
\[
=:
e^{- \frac{1}{\hbar} S_{E} }
\]
wobei man
\[
S_{E} = \int dt \, L(i t)
\]
auch als euklidische Wirkung bezeichnet, da die Ersetzung von \(t\) durch \( i t \)
für die Minkowskimetrik
\[
g(x,x) = (ct)^{2} - \boldsymbol{x}^{2}
\]
bedeutet,
dass daraus der Term
\[
(i ct)^{2} - \boldsymbol{x}^{2} =
- [(ct)^{2} + \boldsymbol{x}^{2}]
\]
wird, was (bis auf das Gesamtvorzeichen) der euklidischen Metrik
im vierdimensionalen Raum entspricht.
Der Integrand \[ e^{- \frac{1}{\hbar} S_{E} } \] ist nun keine oszillierende komplexwertige Funktion mehr, denn es steht kein imaginäres \(i\) mehr im Exponenten, sondern eine reelle \(- 1\), so dass die entsprechenden Pfadintegrale viel besser konvergieren und berechnet werden können.
Fassen wir zusammen: Das Pfadintegral berechnen wir auf einem Raum-Zeit-Gitter durch die Formel
| Pfadintegral in der Gittereichtheorie: \[ \langle O \rangle = \frac{1}{Z} \int d\psi_{1} \, dA_{1} \, d\psi_{2} \, dA_{2} \, ... \] \[ ... \, d\psi_{n - 1} \, dA_{n - 1} \, e^{- \frac{1}{\hbar} S_{E}[\psi,A] } \, O[\psi,A] \] |
wobei in \( S_{E}[\psi,A] \) die Felder analytisch in der Zeit fortgesetzt werden
und auf dem Raumgitter sowie den Gitterpunkten auf der imaginären Zeitachse
ausgewertet werden müssen,
um \( S_{E}[\psi,A] \) zu berechnen ( \( S_{E}[\psi,A] \) hängt dabei zugleich von allen
Feldwerten einer Feldkonfiguration an allen Gitterpunkten ab).
Um das hochdimensionale Pfadintegral auszurechnen, bedient man sich statistischer Methoden: Man erzeugt per Zufallsgenerator möglichst umfangreiche Stichproben für die Feldwerte an den Gitterpunkten mit einer Wahrscheinlichkeitsverteilung proportional zu \( e^{- \frac{1}{\hbar} S_{E}[\psi,A] } \) und kann dann \( \langle O \rangle \) als Mittelwert von \( O[\psi,A] \) über diese Feldwerte näherungsweise berechnen. Das macht man für immer feinere Gitter und versucht so, den Grenzfall für unendlich feine Gitter abzuschätzen.
Dabei muss man eine ganze Reihe von Feinheiten beachten, d.h. die konkret zu verwendenden Formeln werden i.A. komplizierter sein. So muss man berücksichtigen, dass im Integral jede Eichklasse (also alle Eichpotentiale, die sich ineinander umeichen lassen und daher physikalisch gleichwertig sind) nur einmal berücksichtigt wird (siehe Quantenfeldtheorie und Eichfelder, Kapitel 5).
Außerdem muss man beachten, dass nur die Quarkfelder auf den Gitterpunkten definiert sind, also gleichsam auf den Gitterpunkten leben. Die Eichpotentiale leben dagegen auf den Verbindungslinien zwischen den Gitterpunkten, da sie zur kovarianten Ableitung gehören, die eichunabhängig die Änderung der Quarkfelder zwischen benachbarten Gitterpunkten angibt (siehe Kapitel 5.3).
In Kapitel 6.3 werden wir das Verfahren der Renormierung kennenlernen. Dabei beseitigt man die auftretenden Divergenzen der Quantenfeldtheorie dadurch, dass man zunächst alle divergenten Ausdrücke durch einen Impuls-Cutoff \( M \) regularisiert und somit endlich macht, dann alle Größen durch physikalisch messbare Parameter (Masse, Ladung) an Stelle der nackten Parameter ausdrückt und schließlich Terme erhält, bei denen sich der Grenzwert \( M \) gegen Unendlich durchführen lässt.
Die Einführung eines Raum-Zeit-Gitters zur Auswertung von Pfadintegralen stellt nun ebenfalls eine Regularisierung dar, wirkt also ähnlich wie ein Impuls-Cutoff \( M \), indem kleinere Raum-Zeit-Abstände ausgeschlossen werden. Der Übergang zu immer feineren Gittern entspricht dabei dem Übergang zu immer größeren Werten für den Impuls-Cutoff \( M \), wobei die nackten Parameter der Theorie (Quarkmassen und die starke Farbladung) für jeden Gitterabstand anhand physikalischer Messgrößen (z.B. ausgewählten Hadronenmassen) immer wieder neu justiert (renormiert) werden müssen. Insofern lässt sich das Renormierungsverfahren auch sehr schön mit Hilfe von Raum-Zeit-Gittern verstehen.
Wie man nun die Pfadintegrale konkret verwendet, um Hadronenmassen auszurechnen, ist eine komplexe Angelegenheit, insbesondere wenn es um die Massen von Hadronen geht, die über die starke Wechselwirkung in andere Hadronen zerfallen können. Etwas einfacher ist es bei den Hadronen, die nicht über die starke Wechselwirkung zerfallen können, die also im Sinne der QCD stabil wären, wenn es nur die starke Wechselwirkung gäbe. Wir wollen hier allerdings nicht näher auf die technischen Details dazu eingehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 01 February 2024