Quelle: Wikimedia Commons File:ECClines-3.svg, CC BY-SA 3.0.
Ursprünglich hatte ich vor, auch die drei noch nicht besprochenen Millenium Problems des Clay Mathematics Institutes jeweils in einem eigenen Kapitel zu besprechen. Das wären die Vermutung von Birch und Swinnerton-Dyer, die Vermutung von Hodge und die Existenz und Glattheit der Lösungen der Navier-Stokes-Gleichungen. Leider sind aber die beiden ersten Vermutungen mathematisch recht anspruchsvoll, so dass man nur mit einiger Vorarbeit die Chance hat, sie wirklich zu verstehen. Das erschien mir nun doch zu aufwändig, zumal diese beiden Vermutungen nicht wirklich so relevant sind wie beispielsweise das P=NP?-Problem oder die Riemannsche Vermutung. Die Navier-Stokes-Gleichungen kann man dagegen recht gut anschaulich verstehen, denn sie beschreiben das Verhalten von strömenden Stoffen (beispielsweise Wasser). Ein ganzes Kapitel erschien mir jedoch zu umfangreich dafür.
Es gibt neben den sieben Millenium-Problemen noch viele weitere interessante mathematische Probleme, die teilweise sogar sehr einfach zu verstehen und dennoch bis heute ungelöst sind, beispielsweise die Goldbach'sche Vermutung. Andere Vermutungen wurden aufwändig bewiesen, und wieder andere wurden sogar widerlegt! Und schließlich gibt es auch Vermutungen, deren Unentscheidbarkeit gezeigt werden konnte. Ich möchte den Leser in diesem Kapitel einfach einmal auf einen lockeren Streifzug durch viele dieser mathematischen Probleme mitnehmen, die wir bisher noch nicht betrachtet haben, ohne dabei überall ins Detail zu gehen. Mal sehen, was uns da so alles begegnen wird.
Dies ist eines der sieben Millenium Problems des Clay Mathematics Institutes. Wenn man sich die Kurzbeschreibung ansieht, so lernt man, dass es um rationale Lösungen algebraischer Gleichungen geht, und dass man bei bestimmten algebraischen Gleichungen (den elliptischen Gleichungen) eine Methode zu haben glaubt, mit der man bestimmen kann, ob es endlich oder unendlich viele rationale Lösungen der Gleichung gibt – das ist zumindest die Vermutung, die es zu beweisen gilt. Genauer kann man zu der betrachteten Gleichung eine analytische Funktion \(L(s)\) analog zur Riemannschen Zetafunktion \(\zeta(s)\) definieren, deren Verhalten bei \(s=1\) darüber Auskunft gibt: Ist \(L(1) = 0\) , so gibt es unendlich viele rationale Lösungen, ansonsten gibt es nur endlich viele rationale Lösungen.
Algebraische Gleichungen haben große Ähnlichkeit mit den diophantischen Gleichungen aus Kapitel 3.5 – das waren Gleichungen der Form \( P(x,y,...) = 0 \) , wobei \(P\) ein Polynom in den reellen Variablen \(x, y, ... \) ist mit ganzen Zahlen als Koeffizienten. Gesucht waren Lösungen für die Variablen in den natürlichen Zahlen. Algebraische Gleichungen sehen genauso aus, aber man sucht Lösungen in den rationalen Zahlen (also den Brüchen). Manchmal lässt man auch rationale Zahlen als Koeffizienten zu, was aber gleichwertig ist, denn man kann durch Multiplikation der Gleichung mit genügend großen Zahlen (dem Produkt der Nenner aller Koeffizienten) rationale Koeffizienten immer in ganzzahlige Koeffizienten umwandeln. Jede Lösung einer diophantischen Gleichung in den natürlichen Zahlen ist damit automatisch eine Lösung der identischen algebraischen Gleichung. Wie der genaue Zusammenhang zwischen rationalen und natürlichen Lösungen ist, müsste man sich noch genauer ansehen – wir lassen das hier weg. Für die diophantischen Gleichungen wissen wir aus Kapitel 3.5 jedenfalls:
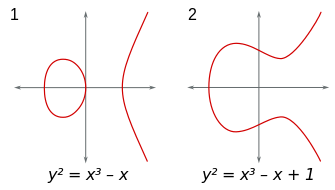
Das wird bei allgemeinen algebraischen Gleichungen wohl ähnlich sein. Und es wird vermutlich auch für die Frage gelten, ob es endlich viele oder unendlich viele rationale Lösungen gibt. Daher macht es keinen Sinn, eine Methode zu suchen, die diese Frage für alle algebraischen Gleichungen beantworten kann. Es gibt keine solche Universal-Methode. Deshalb die Einschränkung auf eine bestimmte Sorte algebraischer Gleichungen. Diese bestimmte Sorte sind Gleichungen sogenannter elliptischer Kurven in der Ebene, d.h. es gibt nur zwei Variablen \(x\) und \(y\) und die Gleichung lässt sich generell (ggf. nach geeigneten Umformungen) in der Form \[ y^2 = x^3 + a x^2 + b x + c \] schreiben (man kann wohl sogar noch weiter vereinfachen, so dass man ohne den \(x^2\)-Term auskommt). Die Gleichung ist also vom Grad 3, d.h. die höchste Potenz einer Variable ist 3. Gesucht werden Punkte \( (x,y) \) mit rationalen Werten (Brüche) für \(x\) und \(y\), die auf der Kurve liegen, die von der Gleichung beschrieben wird, die also die Gleichung erfüllen.
Warum sind gerade diese Gleichungen so interessant? Nun, zumindest in zwei Variablen sind alle anderen Fälle bereits gelöst:
Bleibt also in 2 Variablen nur noch der Fall mit Grad 3 zu klären, also unsere elliptische Gleichung oben.
Wie sieht so eine elliptische Kurve aus?
Nun, für große positive oder negative \(x\) dominiert der \(x^3\)-Term, d.h.
für große positive \(x\) wächst \(|y|\) etwa wie \(x^{3/2}\) an,
während für große
negative \(x\) der \(x^3\)-Term negativ ist und es entsprechend keine Lösungen
für reelle \(y\) gibt. Dazwischen macht das \(x\)-Polynom 3-ten Grades auf der rechten Seite
typischerweise eine Rechts- und eine Linkskurve,
und es kommt nun darauf an, ob diese Kurve in die negativen Zahlen reicht oder nicht.
Einen guten Überblick dazu findet man beispielsweise bei
Jürg Kramer:
Die Vermutung von Birch und Swinnerton-Dyer,
Elem. Math. 57 (2002), 115 - 120.

Quelle:
Wikimedia Commons File:ECClines-3.svg,
CC BY-SA 3.0.
Kann man irgendetwas über die Punkte mit rationalen Koordinaten auf einer solchen Elliptischen Kurve sagen?
Wenn man bereits solche Punkte kennt, kann man dann neue solche Punkte auf der Kurve konstruieren?
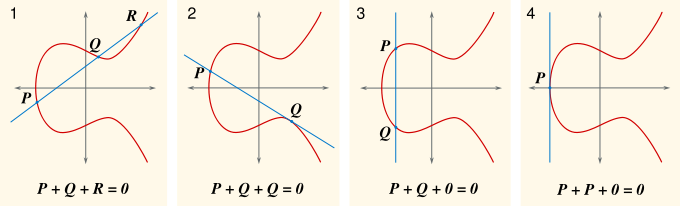
Man kann! Aus zwei solchen Punkten \(P\) und \(Q\) kann man einen neuen Punkt \(R\) konstruieren,
indem man \(P\) und \(Q\) durch eine Gerade verbindet – dann ist \(R\) der Schnittpunkt
dieser Geraden mit der elliptischen Kurve, und er hat rationale Koordinaten, wie man zeigen kann.
Es ist nützlich, diesen Punkt noch an der \(x\)-Achse zu spiegeln
und dann diesen Punkt mit \( P + Q \) zu bezeichnen. Hier ist die Darstellung
dieser Konstruktion:
Quelle: Wikimedia Commons File:ECClines.svg,
von Emmanuel Boutet, CC BY-SA 3.0
Tatsächlich kann man diese Konstruktion als eine Art Addition von Punkten ansehen, denn sie ist kommutativ (sieht man sofort) und assoziativ (muss man erst noch zeigen). Mehr dazu siehe unter Wikipedia: Vermutung von Birch und Swinnerton-Dyer . Auf diese Weise hat man die Menge der rationalen Punkte auf einer elliptischen Kurve zu einer abelschen Gruppe gemacht. Man kann nun die Struktur dieser Gruppe genauer untersuchen. Letztlich bestimmt diese Gruppenstruktur, ob es endlich oder unendlich viele rationale Punkte auf der Kurve gibt. Dreht sich die Addition im Kreis, d.h. kann man nur eine endliche Zahl rationaler Kurvenpunkte erreichen? Oder kann man durch diese Addition immer neue rationale Punkte auf der Kurve konstruieren?
Die Vermutung besagt nun, dass man diese Gruppenstruktur mit Hilfe des Verhaltens einer gewissen analytischen Funktion \(L(s)\) analog zur Riemannschen Zetafunktion untersuchen kann: Ist \(L(1) = 0\) , so gibt es unendlich viele rationale Lösungen, ansonsten gibt es nur endlich viele rationale Lösungen. Genau das gilt es zu beweisen.
Hier ist noch eines der sieben Millenium Problems des Clay Mathematics Institutes: die Vermutung von Hodge. Leider ist diese Vermutung nicht ganz einfach zu verstehen, so dass wir hier nur leicht an der Oberfläche kratzen können. Also versuchen wir es:
Es geht um sogenannte nichtsinguläre algebraische Varietäten der Dimension \(n\) über den komplexen Zahlen. Uff – hilfreich ist der Hinweis, dass es sich dabei um spezielle gutartige reelle Mannigfaltigkeiten der Dimension \(2n\) handelt, also um spezielle gekrümmte \(2n\)-dimensionale Räume. Solche Räume hatten wir in Kapitel 5.3 bereits kennengelernt. Je zwei reelle Koordinaten kann man dabei zu einer komplexen Zahl (Koordinate) zusammenfassen, so dass man einen \(n\)-dimensionalen Raum mit komplexen Koordinaten erhält. Die Bezeichnung algebraisch kommt daher, dass man die Räume über Polynomgleichungen definieren kann.
Die Vermutung von Hodge beschäftigt sich mit der topologischen Klassifikation dieser Räume, also mit der Frage, welche verschiedenen großräumigen Gestalttypen diese Räume aufweisen können. Die Topologie interessiert sich allgemein für die großräumige Struktur des Raumes, beispielsweise für das Loch in einem Ring, nicht aber für die genaue Form des Rings. Mehr dazu siehe Kapitel 5.3. Um die Topologie eines Raumes zu untersuchen, kann man ein mächtiges Werkzeug benutzen: sogenannte Kohomologiegruppen. Einige Details dazu kann man in Die Symmetrie der Naturgesetze, Kapitel 5.1.13 Topologie und Differentialformen: de-Rham-Kohomologie und harmonische Formen finden.
Man kann nun Unterräume niedrigerer Dimension dieser Räume betrachten, so wie der Äquator ein Unterraum der Erdoberfläche ist. Auf diesen Unterräumen kann man ebenfalls Kohomologiegruppen definieren, also sich die Topologie ansehen. Die Vermutung von Hodge besagt nun grob, dass man aus den Kohomologiegruppen der Unterräume alles Wesentliche über die Kohomologiegruppen des Gesamtraumes lernt.
Vielleicht ist die folgende Beschreibung von John Baez für mathematisch versierte Leser hilfreich (siehe John Baez's Description of the Millenium Prize Problems – dort sind also auch die übrigen Millenium Prize Problems kurz beschrieben; die Hervorhebungen stammen von mir):
So – das muss hier reichen. Mehr Information ist nur mit mehr Aufwand zu haben, und das würde den Rahmen hier sprengen.
Kommen wir zum letzten der sieben Millenium Problems des Clay Mathematics Institutes: den Navier-Stokes-Gleichungen. Diese Differenzialgleichungen beschreiben das Strömungsverhalten einer inkompressiblen Flüssigkeit mit innerer Reibung (Viskosität). Die Flüssigkeit wird dabei als Kontinuum angesehen, d.h. das Verhalten einzelner Moleküle wird nicht berücksichtigt. Wasser ist normalerweise in guter Näherung so eine Flüssigkeit.
Es gibt eine vektorielle und eine skalare Navier-Stokes-Gleichung.
Die vektorielle Navier-Stokes-Gleichung ist einfach nur
Newtons Grundgesetz Kraft gleich Masse mal Beschleunigung
für ein sehr kleines (infinitesimales)
Volumenelement der Flüssigkeit. Die Kraft entsteht dabei durch
Druckunterschiede, die Reibung mit benachbarten Volumenelementen
und ggf. durch eine äußere Komponente, beispielsweise die Schwerkraft.
Die skalare Navier-Stokes-Gleichung sagt zusätzlich, dass die Flüssigkeit
inkompressibel – also nicht zusammendrückbar – sein soll.
Es gibt keinen Raumbereich, in den mehr Flüssigkeit hinein- als hinausströmt oder umgekehrt.
Und das ist es auch schon!
Angenommen, wir starten mit einer glatt und gleichförmig fließenden Strömung.
Dann kann es passieren, dass diese Strömung nicht so glatt bleibt, sondern
dass sich komplizierte Wirbel und Turbulenzen entwickeln.
Die Frage ist: Bleibt die Strömung, wie sie die Navier-Stokes-Gleichungen beschreiben,
trotzdem für alle Zeiten gutartig, oder schaukeln sich die Turbulenzen mit der Zeit auf,
so dass sich Singularitäten entwickeln und die Lösung der Gleichungen nicht mehr definiert ist?
Solche Singularitäten könnten beispielsweise Stellen mit unendlicher Strömungsenergie sein,
möglicherweise zum Zentrum von turbulenten Wirbeln hin. Bei einer echten Flüssigkeit kann so etwas natürlich
nicht passieren. Wenn dies dagegen bei den Lösungen der Navier-Stokes-Gleichungen geschieht,
so bedeutet das, dass diese Gleichungen bei extremen Turbulenzen
keine realistische Beschreibung der Wirklichkeit
mehr liefern, d.h. die Beschreibung einer Flüssigkeit als ein viskoses inkompressibles Kontinuum
würde hier an seine Grenzen stoßen.

Quelle:
Wikimedia Commons File:Jupiter 3rd spot.jpg, Public Domain
In zwei Dimensionen ist das Problem bereits gelöst: Es entwickeln sich keine bösartigen Singularitäten und die Lösungen bleiben für alle Zeit physikalisch sinnvoll. In drei Dimensionen fehlt ein solcher Beweis. Immerhin weiß man, dass die Strömung für alle Zeiten gutartig bleibt, wenn sie am Anfang relativ langsam und gleichmäßig fließt. Fließt sie zu schnell, so weiß man immerhin, dass sie noch für eine gewisse Zeitspanne \(T\) gutartig bleibt, wobei \(T\) davon abhängt, wie wild und schnell die Strömung anfangs bereits ist. Die maximal mögliche Zeitspanne \(T\), bis zu der die Strömungslösung gutartig bleibt, nennt man auch blow-up-time. Nun gilt es herauszufinden, ob die blow-up-time endlich oder unendlich ist.
Computerberechnungen von Strömungen deuten darauf hin, dass keine Singularitäten auftreten und die Strömung für alle Zeiten definiert und gutartig bleibt. Die blow-up-time wäre demnach unendlich und die Navier-Stokes-Gleichungen wären ein realistisches Modell von Flüssigkeiten auch bei starker Turbulenz und langen Zeiträumen. Das würde man gerne beweisen – notfalls auch dadurch, dass man Bedingungen formuliert, die das gewährleisten. Mehr dazu siehe auch John Baez's Description of the Millenium Prize Problems und in der Original-Beschreibung des Millenium Problems von Charles L. Fefferman.

Quelle:
Wikimedia Commons File:Leonhard Euler by Handmann .png, gemeinfrei
Die Eulersche Vermutung aus dem Jahr 1769 besagt: Die diophantische Gleichung \[ x^4 + y^4 + z^4 = t^4 \] hat keine Lösungen in den natürlichen Zahlen. Man fand auch mehr als 200 Jahre lang kein Gegenbeispiel, bis Noam Elkies im Jahr 1988 dann doch eines fand (siehe auch Andrew Wiles: The Birch and Swinnerton-Dyer Conjecture ): \[ 2.682.440^4 + 15.365.639^4 + 18.796.760^4 \] \[ = 20.615.673^4 \] Und Elkies bewies außerdem, dass es unendlich viele weitere Gegenbeispiele geben muss. Das kleinste Gegenbeispiel wurde von Roger Frye gefunden: \[ 95.800^4 + 217.519^4 + 414.560^4 = 422.481^4 \] Hier sieht man ein schönes Beispiel dafür, dass die vergebliche Suche nach Gegenbeispielen noch lange kein Beweis dafür ist, dass es keine gibt. Irgendwann findet vielleicht jemand in den unendlichen Tiefen des Zahlenuniversum dann doch eines, so wie hier. Bei drei Variablen zur dritten Potenz (also \( x^3 + y^3 = z^3 \) ) konnte Euler übrigens beweisen, dass es keine Lösungen in den natürlichen Zahlen gibt. Bei 5 Variablen zur 5-ten Potenz fanden 1966 L. J. Lander und T. R. Parkin das Gegenbeispiel \[ 27^5 + 84^5 + 110^5 + 133^5 = 144^5 \] Mehr dazu siehe Wikipedia: Eulersche Vermutung.

Quelle:
Wikipemia Commons File:Pierre de Fermat.jpg, gemeinfrei
Ähnlich zur obigen Eulerschen Vermutung sieht die berühmte Fermatsche Vermutung aus. Sie lautet: Die diophantische Gleichung \[ x^n + y^n = z^n \] hat keine Lösung in den natürlichen Zahlen, wenn der natürliche Exponent \(n\) größer als 2 ist. Dabei sind \(x, y\) und \(z\) die Variablen, die die Gleichung lösen sollen, und \(n\) ist eine vorgegebene natürliche Zahl. Für \(n = 2\) gibt es dagegen unendlich viele Lösungen, beispielsweise \[ 3^2 + 4^2 = 5^2 \] Die Vermutung stammt aus dem Jahr 1637 und konnte erst mehr als 350 Jahre später (im Jahr 1994) von Andrew Wiles aufwendig bewiesen werden, wobei elliptische Kurven (siehe oben) eine wichtige Rolle spielen. Simon Singh beschreibt in seinem bekannten Buch Fermats letzter Satz – Die abenteuerliche Geschichte eines mathematischen Rätsels (ISBN 342333052X) sehr schön die Hintergründe und die Entstehungsgeschichte dieses Jahrhundert-Beweises. Schon interessant: die Vermutung von Euler ist falsch, die recht ähnliche Vermutung von Fermat ist dagegen richtig. Offenbar liegen WAHR und FALSCH im Reich der natürlichen Zahlen bisweilen recht nahe beieinander.
Einfacher geht es nicht: Die Goldbachsche Vermutung behauptet, dass man jede gerade Zahl ab 4 als Summe zweier Primzahlen schreiben kann: \begin{align} 4 &= 2 + 2 \\ 6 &= 3 + 3 \\ 8 &= 3 + 5 \\ 10 &= 3 + 7 = 5 + 5 \\ 12 &= 5 + 7 \\ 14 &= 3 + 11 = 7 + 7 \\ \end{align} Bis \(10^{18}\) (also eine Milliarde-Milliarde) ist die Vermutung mittlerweile per Computer nachgeprüft und bestätigt worden, aber ein Beweis fehlt bis heute. Die Summe zweier Primzahlen muss übrigens immer gerade sein, denn Primzahlen sind ungerade Zahlen (sonst wäre ja 2 ein Teiler der Zahl und die Zahl damit keine Primzahl mehr).
Wie die obige Liste zeigt,
gibt es oft mehr als eine Möglichkeit, zwei geeignete Primzahlen zu finden.
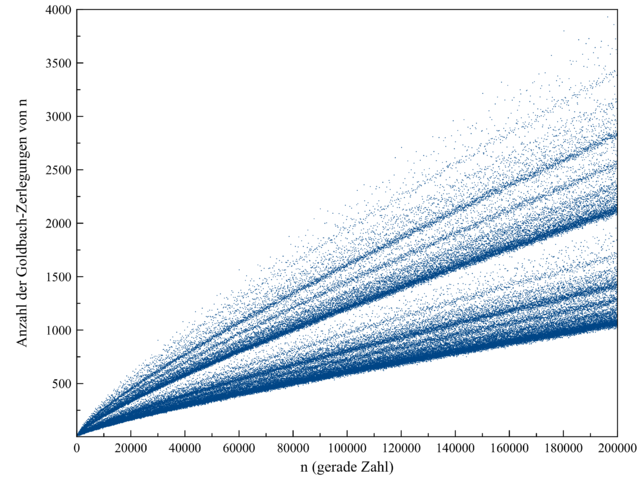
Je größer die gerade Zahl ist, umso mehr Möglichkeiten gibt es im Mittel,
wie die folgende Abbildung zeigt:
Quelle:
Wikimedia Commons File:Goldbach200000.png, dort gemeinfrei
Für jede gerade Zahl \(n\) gibt es einen blauen Datenpunkt in dieser Grafik. Offenbar variiert die Zahl der Möglichkeiten von Zahl zu Zahl, denn es ergibt sich keine glatte Kurve. Dennoch scheint es so etwas wie eine statistische Verteilung zu geben, die es zunehmend unwahrscheinlicher macht, dass bei großen Zahlen ein blauer Datenpunkt genau auf der \(x\)-Achse zu liegen kommt, so dass es Null Möglichkeiten gibt. Daher ist heute praktisch jeder von der Gültigkeit der Goldbachschen Vermutung überzeugt.
Ein Beweis ist das aber nicht, denn das Zahlenuniversum ist unendlich groß und ist daher immer für Überaschungen gut, wie die Eulersche Vermutung oben gezeigt hat. In Kapitel 4.6 konnten wir bei den Goodsteinfolgen sehen, wie sich tief im Zahlengebirge das Verhalten einer Zahlenfolge grundlegend ändert. Die Goodsteinfolge zu \(n = 4\) wächst beispielsweise fast eine Ewigkeit lang an, um dann doch in den fernen Tiefen der Unendlichkeit schließlich einzuknicken und gegen Null zu schrumpfen. Hätte man diese Goodsteinfolge mit dem Computer Zahl für Zahl berechnet, so hätte man dieses Einknicken auch nach Monaten nicht beobachtet und wäre wohl zu dem falschen Schluss gelangt, dass die Folge ewig weiterwächst. Analog kann also heute niemand mit Sicherheit wissen, dass nicht doch irgendwo sehr weit rechts in der obigen Grafik ein blauer Datenpunkt genau auf der \(x\)-Achse liegt und damit ein Gegenbeispiel zur Goldbachschen Vermutung liefert.
Übrigens gibt es einen sehr schönen Roman von A. Doxiadis zu diesem Thema: Onkel Petros und die Goldbach'sche Vermutung (Lübbe 2000, ISBN 3-7857-0951-X ). Sehr spannend und lesenswert!
Noch eine sehr einfache Vermutung aus dem Reich der Primzahlen: Die Vermutung über Primzahlzwillinge behauptet, dass es unendlich viele Primzahlzwillinge gibt. Dabei bezeichnet man zwei Primzahlen, die direkt hintereinander kommen (also mit Abstand 2), als Primzahlzwilling. Die ersten Primzahlzwillinge sind (3 und 5), (5 und 7), (11 und 13), (17 und 19) usw..
Nun gibt es unendlich viele Primzahlen, wie schon Euklid im vierten Jahrhundert vor Christus wusste
(siehe Wikipedia: Satz von Euklid ).
Allerdings werden die Primzahlen bei größeren Zahlen immer seltener und liegen im Mittel
immer weiter auseinander, so dass Primzahlzwillinge ebenfalls seltener werden.
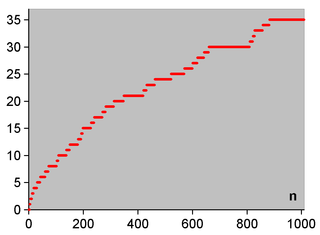
Die folgende Grafik zeigt, wieviele Primzahlzwillinge (\(n\) und \(n+2\)) es bis zur Zahl \(n\) gibt:
Quelle:
Wikimedia Commons File:Anzahl Primzahl-Zwillingspaare.png, gemeinfrei
Geht man zu noch größeren \(n\) über, so sieht man, dass die Kurve immer weiter ansteigt, d.h. es kommen ständig neue Primzahlzwillinge hinzu. Allerdings wird der Anstieg langsam immer schwächer. Im Prinzip könnte es einen letzten Primzahlzwilling geben, so dass die Kurve ab dieser Zahl horizontal verläuft. Dennoch geht man heute aufgrund verschiedener Indizien meist davon aus, dass es unendlich viele solcher Zwillinge gibt – beweisen kann man das bis heute allerdings nicht. Es scheint aber immerhin gewisse Fortschritte in diese Richtung zu geben, siehe Wikipedia: Primzahlzwilling. Vielleicht gibt es ja bald einen Beweis?!
Jede natürliche Zahl lässt sich eindeutig in Primfaktoren zerlegen. Zählen wir mal nach, wie viele Primfaktoren das typischerweise sind: \begin{align} 3 = 3 \; &\Rightarrow \; 1 \; \mathrm{Primfaktor} \\ 4 = 2 \cdot 2 \; &\Rightarrow \; 2 \; \mathrm{Primfaktoren} \\ 5 = 5 \; &\Rightarrow \; 1 \; \mathrm{Primfaktor} \\ 6 = 3 \cdot 2 \; &\Rightarrow \; 2 \; \mathrm{Primfaktoren} \\ 7 = 7 \; &\Rightarrow \; 1 \; \mathrm{Primfaktor} \\ 8 = 2 \cdot 2 \cdot 2 \; &\Rightarrow \; 3 \; \mathrm{Primfaktoren} \\ & ... \end{align} So könnten wir immer weiter machen und dann an einem beliebigen Punkt aufhören. Insgesamt scheint eine ungerade Anzahl Primfaktoren häufiger aufzutreten als eine gerade Anzahl Primfaktoren, oder wir haben zumindest Gleichstand. Die Vermutung von George Pólya aus dem Jahr 1919 sagt nun, dass das immer so ist, egal bis zu welcher natürlichen Zahl wir uns die Primfaktorzerlegung ansehen. Präzise formuliert lautet die Vermutung:
Dabei zählen wir die 1 und 2 nicht mit. Die folgende Grafik zeigt,
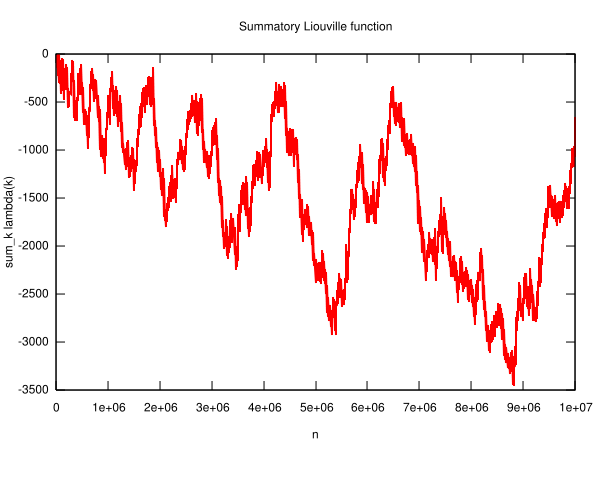
dass diese Vermutung bis \(n\) gleich 10 Millionen
zutrifft:
Quelle:
Wikimedia Commons File:Liouville-big.svg, von Wikimedia-User Linas (Linas Vepstas),
CC BY-SA 3.0.
Für die Zahlen bis 10 Millionen gilt die Vermutung von Pólya demnach, denn die Kurve liegt immer im negativen Bereich oder maximal bei Null, so dass die Zahlen mit ungerader Primfaktorzahl immer in der Mehrheit (mindestens 50%) sind. Allerdings gibt es durchaus Schwankungen, d.h. zwischendurch erreichen die Zahlen mit gerader Primfaktorzahl mehrfach immerhin Gleichstand, und zwar bei \(n\) = 4, 6, 10, 16, 26, 40, 96, 586 (siehe Wolfram MathWorld: Pólya Conjecture ). Nach \(n = 586\) bleibt die Kurve dann aber für lange Zeit im negativen Bereich, wie wir oben sehen.
Bleibt die Kurve für immer im negativen Bereich oder maximal bei Null, wie Pólya vermutete? Im Jahr 1958, zeigte C. B. Haselgrove, dass es ein Gegenbeispiel zu Pólyas Vermutung geben muss – die Kurve muss also irgendwo in den positiven Bereich wechseln. Ein erstes explizites Gegenbeispiel wurde dann 1960 von R. S. Lehman gefunden. Es lautet \( n = 906.180.359 \). Bei den Zahlen bis zu diesem \(n\) gibt es eine Zahl mehr mit gerader Primfaktoranzahl und die Kurve \(L(n)\) liegt bei 1.
Das kleinste Gegenbeispiel wurde dann 1980 von Minoru Tanaka ermittelt:
\( n = 906.150.257 \) . Für die ersten gut 900 Millionen Zahlen stimmt
die Vermutung also: Die Kurve \(L(n)\) wird bis hierher nicht positiv
und die Mehrheit (mindestens 50%) dieser Zahlen hat eine ungerade Anzahl Primfaktoren!
Doch offenbar ist diese Mehrheit nicht zuverlässig. Die Zahlen mit
einer gerade Anzahl Primfaktoren holen irgendwann auf und können zwischendurch
die Mehrheit gewinnen, so dass die Differenzkurve \(L(n)\) doch noch in den positiven Bereich
hineinläuft.
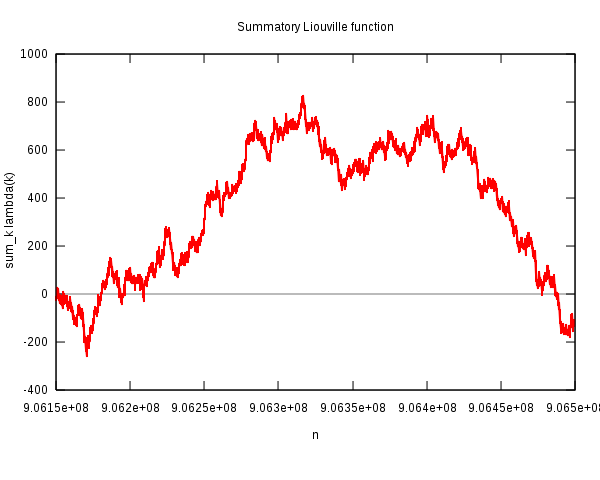
Die folgende Grafik zeigt stark vergrößert genau den kleinen Zahlenbereich, in dem das geschieht:
Quelle: Wikipedia File:Liouville-polya.svg,
von Wikimedia-User Linas (Linas Vepstas),
CC BY-SA 3.0.
Dieser Bereich mit Gegenbeispielen (also positiver Funktion \(L(n)\) ) ist insgesamt recht klein.
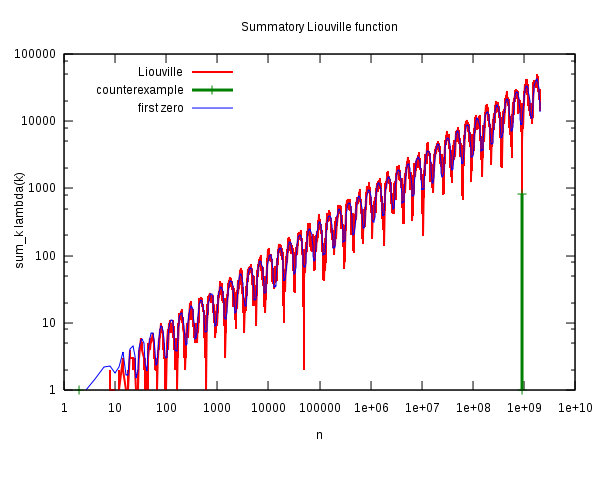
Einen Gesamtüberblick in doppelt-logarithmischer Darstellung gibt die folgende Grafik:
Quelle: Wikipedia File:Liouville-log.svg,
von Wikimedia-User Linas (Linas Vepstas),
CC BY-SA 3.0.
Erklärung dazu:
Die rote Kurve ist hier die Differenzfunktion \(L(n)\) (ohne negatives Vorzeichen),
und der Bereich, in dem sie positiv wird und die Pólya-Vermutung entsprechend verletzt ist,
ist grün dargestellt. Fast wirkt es, als hätten wir hier einen zufälligen Ausreißer.
Auch vorher gibt es mehrere solche Ausreißer, die aber rechtzeitig stoppen, so dass
die Vermutung gerade noch hält. Die unterlagerte gleichförmige Oszillation der Kurve
kann man übrigens durch den Beitrag der ersten nichttrivialen Nullstelle der Riemannschen
Zetafunktion zur Primzahlverteilung erklären, also gleichsam durch die erste Oberwelle
der Primzahl-Verteilung (siehe am Schluss von
Kapitel 5.2: Die Riemannsche Vermutung ).
Wenn man die Primzahlverteilung so annähert,
so ergibt sich die blau dargestellte Kurve.
Die weiteren Nullstellen führen dann zu weiteren Oberschwingungen, die die blaue erste Oberwelle
überlagern und schließlich die rote Kurve ergeben. Offenbar verstärken sich diese Oberschwingungen
im grünen Bereich gleichsam zufällig so stark,
dass \(L(n)\) positiv wird – es wäre sicher interessant,
herauszufinden, wie viele Oberschwingungen (Nullstellen) man dazu braucht; es dürften
sehr viele sein.
Irgendwie hat man das Gefühl, es hätte auch genauso gut anders kommen können, so dass Pólya recht behalten hätte. Mathematische Wahrheit hat hier einen fast zufälligen Charakter, und die numerische Untersuchung der Funktion \(L(n)\) ähnelt einem physikalischen Experiment. Übrigens weiß bis heute niemand, ob die Kurve \(L(n)\) unendlich oft ihr Vorzeichen wechselt, ob also die Mehrheiten immer wieder hin- und herschwanken, oder ob der obige grüne Bereich der einzige Ausrutscher ist. Um Forrest Gump leicht abgewandelt zu zitieren: "Die Funktion \(L(n)\) ist wie eine Schachtel Pralinen. Man weiß nie, was man bei sehr großen Zahlen kriegt."
Hier ist noch eine Vermutung, die sich mit Primzahlen und Primfaktorzerlegung beschäftigt und die daher eng mit der Verteilung der Primzahlen (genauer: der Riemannschen Vermutung) zusammenhängt.
In Kapitel 5.2: Die Riemannsche Vermutung haben wir die Möbiusfunktion \(\mu(n)\) kennengelernt, die folgendermaßen für alle natürlichen Zahlen n definiert ist:
Für natürliche Zahlen \(n\) ohne doppelte Primfaktoren ist also \( \mu(n) = 1 \) für eine gerade Anzahl verschiedener Primfaktoren und \( \mu(n) = -1 \) für eine ungerade Anzahl verschiedener Primfaktoren.
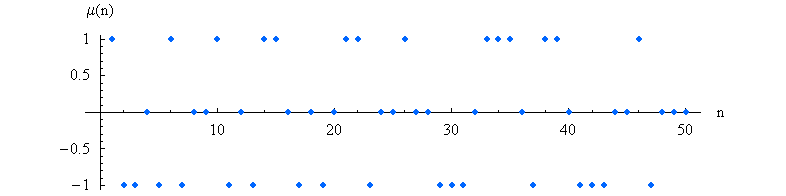
Die Möbius-Funktion oszilliert wie zufällig zwischen den Werten 1, 0 und -1 hin und her.
Die ersten Werte dieser Funktion lauten
1,-1, -1, 0, -1, 1, -1, 0, 0, 1, -1, 0, ... .
Die folgende Grafik zeigt die
ersten 50 Werte der Möbius-Funktion:
Quelle:
Wikimedia Commons File:MoebiusMu.PNG, Public Domain.
Was geschieht, wenn wir diese Funktionswerte immer weiter aufsummieren,
also die sogenannte Mertens-Funktion
\[
M(n) = \mu(1) + \mu(2) + \, ... \, + \mu(n)
\]
bilden?
Diese Summe wird bei wachsendem \(n\) mal größer, mal kleiner,
je nachdem, ob eine 1 oder eine −1
hinzukommt (bei Null verändert sich natürlich nichts).
Fast wie bei einer Zufallsbewegung (Random Walk) scheint die Kurve mal nach oben
und mal nach unten zu wandern:
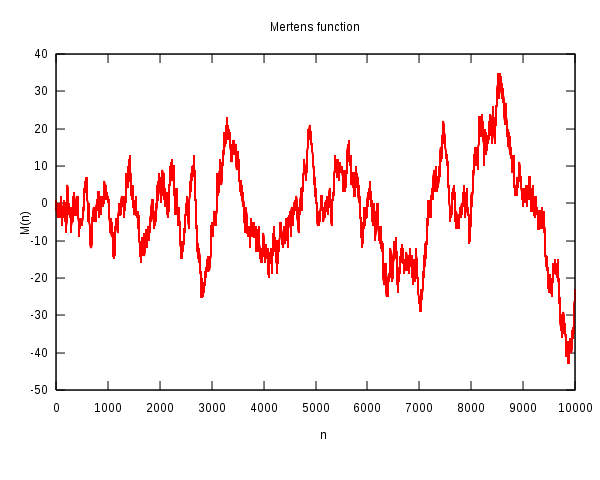
Quelle: Wikipedia File:Mertens.svg
von Wikipedia-User Linas (Linas Vepstas),
CC BY-SA 3.0
Die Vermutung von Mertens besagt nun, dass man sich bei dieser Irrfahrt nach \(n\) Schritten immer näher als \( \sqrt{n} \) an der \(x\)-Achse befindet: \[ |M(n)| < \sqrt{n} \] Physiker kennen etwas Ähnliches von einer Zufallsbewegung: Geht man \(n\) Schritte zufällig mal nach oben oder mal nach unten, so wächst der Erwartungswert für den Abstand zur \(x\)-Achse proportional zu \( \sqrt{n} \) an. Niemand verbietet allerdings, dass man bei einer solchen Irrfahrt in jedem Schritt immer nach oben läuft – es ist nur sehr unwahrscheinlich. Mehr zum Vergleich mit Zufallsbewegungen siehe weiter unten.
Könnte man die Vermutung von Mertens beweisen, so würde daraus die Gültigkeit der Riemannschen Vermutung folgen (nicht aber umgekehrt, siehe unten). Die Vermutung von Mertens ist also sogar etwas stärker als die Riemannsche Vermutung.
Mertens rechnete seine Vermutung im Jahr 1897 bis \(n = 10.000\) nach. Später wurde die Gültigkeit bis \(n = 500.000\) und dann sogar bis \(n = 10^{14}\) per Computer nachgewiesen.
Und dennoch ist die Vermutung in dieser Form falsch, wie te Riele und Odlyzko im Jahr 1985 beweisen konnten. Sie fanden jedoch keineswegs ein konkretes Gegenbeispiel, sondern sie zeigten in einem indirekten Beweis, dass die Kurve \(M(n)\) für irgendwelche \(n\) ziemlich genau den Wert \( 1,06 \cdot \sqrt{n} \) erreicht (und ggf. überschreitet) und analog für irgendwelche \(n\) ziemlich genau den Wert \( - 1,009 \cdot \sqrt{n} \) erreicht (und ggf. überschreitet).
Auch heute (2008) ist noch kein konkretes Gegenbeispiel zu Mertens' Vermutung bekannt, und bis \(10^{14}\) gibt es auch keines. Allerdings muss bis etwa \(10^{156}\) irgendwo mindestens eines sein. Diese Obergrenze ist allerdings so irrwitzig groß, dass nicht die geringste Chance besteht, alle Zahlen bis dahin einzeln zu überprüfen – sie ist weit größer als die Zahl der Atome im sichtbaren Universum (diese beträgt weniger als \(10^{100}\), siehe Wikipedia: Universum). Mit brutaler Rechenpower kommt man hier also nicht weiter. Das ist schon eine bemerkenwerte Situation: Man weiß, dass es Gegenbeispiele geben muss, aber sie könnten so tief in den Weiten des Zahlenuniversums liegen, dass wir sie vielleicht nie finden!
Man kann die Mertens-Vermutung etwas abschwächen – und schon wird sie vermutlich richtig, oder genauer: Sie wird äquivalent zur Riemannschen Vermutung, von der man heute glaubt, dass sie stimmt (auch wenn man das noch nicht beweisen konnte, siehe Kapitel 5.2: Die Riemannsche Vermutung ). Dazu wandelt man die Obergrenze etwas ab: nicht mehr \( \sqrt{n} = n^{1/2} \), sondern \( C_\epsilon \cdot n^{1/2 + \epsilon} \) ist die Obergrenze, wobei \( \epsilon \) eine beliebig (kleine) positive Zahl sein darf (aber nicht Null), und \( C_\epsilon \) ein dazu passender reeller Vorfaktor ist. Man sagt also, dass es zu jeder (beliebig kleinen) positiven reellen Zahl \( \epsilon \) eine reelle positive Zahl \( C_\epsilon \) gibt, so dass \[ |M(n)| < C_\epsilon \cdot n^{1/2 + \epsilon} \] für alle \(n\) gilt. Wenn man also beispielsweise \( \epsilon = 0,00001 \) wählt, so ist \( n^{1/2 + \epsilon} = n^{0,50001} \) fast wie \( \sqrt{n} = n^{1/2} \) , und man kann durch Wahl eines genügend großen Vorfaktors \( C_\epsilon \) alle Gegenbeispiele verhindern, sofern die Riemannsche Vermutung stimmt (wovon wir ausgehen). Wenn Sie die obige Vermutung beweisen können, so haben Sie die Riemannsche Vermutung bewiesen, eine Millionen Dollar gewonnen und gehen unsterblich in die Geschichte der Mathematik ein – das wäre doch mal etwas!
Man kann nun diese abgeschwächte Behauptung mit den Eigenschaften unserer oben erwähnten Zufallsbewegung (Random Walk) vergleichen, bei der man in jedem Schritt zufällig entweder um 1 hoch oder runter springt. Und tatsächlich kann man zeigen, dass eine solche Zufallsbewegung die obige Ungleichung erfüllt. In diesem Sinn ist also die obige Ungleichung eine recht starke Zufallseigenschaft, die auch die Mertens-Funktion aufweist, sofern die Riemannsche Vermutung gilt. Man sagt auch manchmal etwas vereinfacht, dass die Riemannsche Vermutung gleichwertig ist zu der Aussage, dass natürliche Zahlen ohne doppelte Primfaktoren dieselbe Wahrscheinlichkeit haben, eine gerade oder ungerade Anzahl verschiedener Primfaktoren aufzuweisen.
Man kann sogar mit Hilfe von Kolmogorovs Law of the iterated logarithm eine noch stärkere Ungleichung für Zufallsbewegungen herleiten, die dann auch stärker als die Riemannsche Vermutung wäre. Kein Mensch weiß heute, ob die Mertens-Funktion \(M(n)\) auch diese stärkere Ungleichung noch erfüllen kann und damit auch in diesem Sinn eine starke Zufalls-Eigenschaft erfüllt. Doch das ist Zukunftsmusik – heute reicht uns schon die Frage, ob die Möbius-Funktion und damit die Primzahlen zufällig genug sind, so dass die Riemannsche Vermutung gilt. Weitere Details dazu findet man beispielsweise in dem sehr lesenswerten Artikel von Pete L. Clark: The Prime Number Theorem and the Riemann Hypothesis (ich finde ihn leider nicht mehr frei im Internet). Aus diesem Artikel stammen auch viele der hier dargestellten Informationen. Einen umfassenden Überblick zur Riemannschen Vermutung findet man auch in Borwein, Choi, Rooney, Weirathmueller: The Riemann Hypothesis.
Hier geht es um eine spezielle Zahlenfolge: Wir starten mit irgendeiner natürlichen Zahl \(a_0\) und bilden mit dieser Startzahl eine Zahlenfolge nach der folgenden Regel:
Gerade Zahlen werden also halbiert und die Folge schrumpft, während ungerade Zahlen verdreifacht werden und durch Addition von 1 in eine gerade Zahl verwandelt werden. Die Frage lautet nun: Endet diese Zahlenfolge für jeden Startwert schließlich bei Eins und bricht dann ab? Man weiß es nicht, obwohl man allgemein davon ausgeht, dass es so ist! Weder ein Beweis noch ein Gegenbeispiel konnte bisher gefunden werden. Bis mindestens \( 2,95 \cdot 10^{20} \) (Stand: Juli 2020) gibt es jedenfalls kein Beispiel, bei dem die Folge nicht bei 1 endet, und falls es später eines gibt, und falls dabei die Folge in einen Zyklus gerät (also nicht unbegrenzt wächst), so muss dieser Zyklus mindestens 10.439.860.591 Zahlen umfassen (siehe Wikipedia: Collatz-Problem und Wikipedia: Collatz conjecture ).
Hier ist als Beispiel die entsprechende Zahlenfolge für den Startwert 27 (siehe Wikipedia: Collatz conjecture ). Sie lautet
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
Als Grafik sieht das dann so aus:
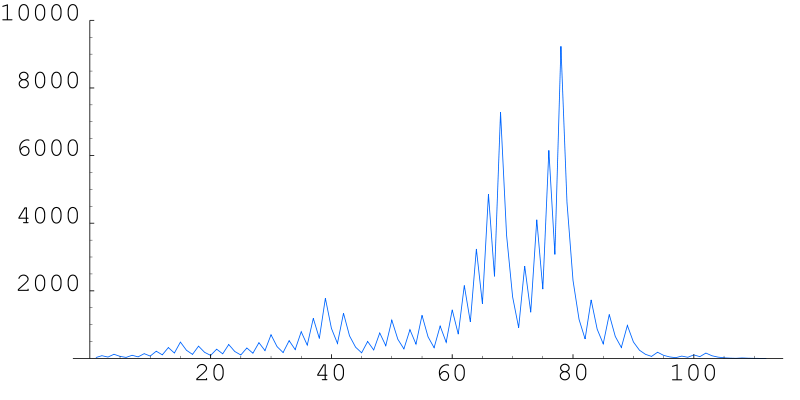
Quelle:
Wikimedia Commons File:Collatz5.svg, dort Public Domain
Man sieht sehr schön, wie die Folge bei jeder ungeraden Zahl nach oben springt, um dann nach unten zu fallen, solange die Zahlen beim Halbieren gerade bleiben.
Die harmonische Reihe \[ H_n = 1 + \frac{1}{2} + \frac{1}{3} + \, ... \, + \frac{1}{n} \] divergiert logarithmisch, wenn wir unendlich viele Terme aufsummieren (also \(n\) gegen Unendlich laufen lassen). Diese Divergenz können wir beseitigen, wenn wir den natürlichen Logarithmus \( \ln (n) \) abziehen. Den Grenzwert von \( H_n - \ln (n) \) für \(n\) gegen Unendlich nennt man Euler-Mascheroni-Konstante (Abkürzung: \( \gamma \)). Diese Zahl gibt also gleichsam an, um welchen Wert die harmonische Reihe mehr divergiert als der natürliche Logarithmus. \[ \gamma := \lim_{n \rightarrow \infty} \left( 1 + \frac{1}{2} + \frac{1}{3} + \, ... \, + \frac{1}{n} - \ln (n) \right) \] Der numerische Wert lautet auf 100 Dezimalstellen genau \begin{align} \gamma = 0,&57721 \, 56649 \, 01532 \, 86060 \, 65120 \\ &90082 \, 40243 \, 10421 \, 59335 \, 93992 \\ &35988 \, 05767 \, 23488 \, 48677 \, 26777 \\ &66467 \, 09369 \, 47063 \, 29174 \, 67495 \\ & \, ... \end{align} Ist diese Zahl eine rationale Zahl, also als Bruch darstellbar, so dass die Dezimaldarstellung oben entweder abbricht oder periodisch ist? Falls ja, so muss der Nenner größer als \( 10^{244.663} \) sein, also weit größer als die Zahl der Atome im sichtbaren Universum. Die Periode wäre also sehr lang.
Und falls \( \gamma \) nicht rational ist (wovon die Meisten ausgehen), ist sie dann algebraisch (also Nullstelle eines Polynoms) oder transzendent wie beispielsweise die Kreiszahl \(\pi\) (also keine Nullstelle eines Polynoms)? Keiner weiß es bis heute! Übrigens: Wer sehen möchte, warum \(e\) und \(\pi\) transzendent sind, findet unter Wikipedia-Beweisarchiv: Beweis der Transzendenz von e und π den Beweis dazu.
Vereinfacht gesagt geht es hier um die Frage, ob zwei verschieden aussehende
Produkte von Gruppenelementen identisch sind oder nicht.
Sind beispielsweise zwei verschiedene Zugfolgen bei
Rubiks Zauberwürfel
gleichwertig zueinander? Gibt es einen gruppenspezifischen Algorithmus, der das für beliebig
vorgegebene Produkte von Gruppenelementen (Zugfolgen) allgemein nach endlicher Laufzeit entscheiden kann?

Quelle:
Wikimedia Commons File:Rubik's cube v3.svg,
CC BY-SA 3.0.
Machen wir es konkret (siehe Wikipedia: Word problem for groups ): Unsere Gruppe soll rekursiv darstellbar sein, d.h. man kann eine endliche oder unendliche Liste von Generatoren (Grudnelementen) aufschreiben, so dass sich jedes Gruppenelement als endliches Produkt dieser Generatoren und ihrer Inversen schreiben lässt (siehe Wikipedia: Presentation of a group – die Unterscheidung zwischen der Gruppe und ihrer Darstellung lasse ich hier zur Vereinfachung weg). Für die Generatoren schreiben wir Großbuchstaben
und für die inversen Generatoren entsprechend \( A^{-1}\) usw.. Jedes Gruppenelement kann man dann als ein Produkt dieser Generatoren wie beispielsweise \( CDADEEA \) schreiben. Beim Zauberwürfel wären die Generatoren beispielsweise durch das Verdrehen der sechs äußeren Würfelebenen in eine bestimmte Drehrichtung um 90 Grad gegeben (die drei mittleren Ebenen kann man sich als starr vorstellen, entsprechend einer festen räumlichen Orientierung der sechs Mittelstücke). Der inverse Generator ist dann die Drehung in der entgegengesetzten Richtung. Jede Veränderung des Würfels lässt sich als eine Abfolge (Produkt) dieser sechs Grunddrehungen und ihrer Inversen darstellen. In Wikipedia: Zauberwürfel findet man als entsprechende Notation die sechs Buchstaben \( V, H, R, L, O, U \).
Man kann sich die Generatoren auch als Alphabet und Produkte (Abfolgen) der Generatoren als Strings (Wörter) in diesem Alphabet vorstellen. Genauso haben wir es ja bei unserem Beispiel \( CDADEEA \) schon gemacht. Das neutrale Element würden wir dann durch den leeren String " " darstellen. Beim Zauberwürfel wäre das dann überhaupt keine Veränderung des Würfels.
Um die Gruppenstruktur zu definieren, braucht man noch eine Reihe von Multiplikationsregeln. Wir müssen wissen, wie sich Produkte der Generatoren verhalten. So könnte eine Multiplikationsregel beispielsweise \( AB = C \) für die drei Generatoren \(A, B\) und \(C\) lauten, was wir auch als \( ABC^{-1} = " " \) schreiben können. Jede Multiplikationsregel definiert auf diese Weise ein Produkt von Generatoren (einen String), das gleich dem neutralen Element (dem leerem String) ist. Beim Zauberwürfel wäre eine dieser Regeln, dass das vierfache Ausführen derselben Grunddrehung das neutrale Element ergibt, denn dann man hat dann eine der Ebenen einmal im Kreis gedreht. Für jeden Generator \(A\) würde dann beim Zauberwürfel die Regel \(AAAA = " " \) gelten.
Die Multiplikationsregeln bewirken, dass verschiedene Generator-Produkte dasselbe Gruppenelement darstellen können – wir hatten gerade das Zauberwürfel-Beispiel \(AAAA = " " \). In diesem Beispiel können wir in jeder Zugfolge an jeder Stelle ein vierfaches Generatorprodukt so wie \(AAAA \) einfügen, ohne das Ergebnis der Zugfolge (das Gruppenelement) zu ändern. Analog können wir aus Zugfolgen solche Viererprodukte auch herausstreichen. Dasselbe haben wir für Produkte der Form \( AA^{-1}\). Ganz allgemein geben die Multiplikationsregeln eine Liste von Produkten an, die gleichwertig zum neutralen Element sind und die man entsprechend überall einfügen und herausnehmen kann. Je nach Komplexität der Regeln entstehen so vielfältige Möglichkeiten, gegebene Produkte (Strings) umzuformen und auf unterschiedlichste Weise zu verlängern und ggf. wieder zu verkürzen.
Und nun kommt die spannende Frage bei einer gegebenen Gruppe mit gegebenen Generatoren und Multiplikationsregeln:
Es gibt sehr viele Gruppen, bei denen das geht. Ein Beispiel sind die endliche Gruppen (es gibt also nur endlich viele Gruppenelemente), bei denen die Multiplikationsregeln durch eine Gruppen-Multiplikationstabelle gegeben sind. Ein anderes Beispiel sind alle abelschen Gruppen (d.h. die Gruppenelemente sind vertauschbar). Die Regeln sind dann einfach genug, so dass der Algorithmus je zwei gegebene Produkte in eine Art Normalform bringen kann. So könnte er schrittweise die Gruppenelemente geeignet vertauschen und dann geeignete Teilprodukte herauskürzen, die identisch zum neutralen Element sind.
Es gibt aber auch Gruppen, deren Multiplikationsregeln zu kompliziert sind, um so eine einfache Strategie zu erlauben – es gibt hier keine Normalform. Daher muss man notfalls viele Stringpaare separat betrachten und sich eine geeignete Strategie für deren Umformung überlegen, ohne Garantie, eine zu finden. Eine allgemeine Strategie, die für jedes beliebige Stringpaar der Gruppe funktioniert, gibt es nicht. Das kann sogar bei Gruppen mit nur endlich vielen Generatoren der Fall sein, wie Pyotr Sergeyevich Novikov und William Boone im Jahr 1955 bewiesen (endlich viele Generatoren können dabei unendlich viele Gruppenelemente als Produkte erzeugen).
Es gibt also Gruppen, bei denen die Gleichheit zweier Generatorprodukte unentscheidbar ist. Es gibt keinen allgemeinen Algorithmus, der die Gleichheit zweier beliebiger Generatorprodukte dieser Gruppe nach endlich vielen Schritten allgemein entscheiden kann. Er mag bei bestimmten Produkten Erfolg haben, aber nicht bei allen.
Gibt es Beispiele für solche Gruppen mit unentscheidbarem Wortproblem, also ohne ein allgemeines Entscheidungsverfahren für die Gleichheit von beliebigen Generatorprodukten? Solche Beispiele kann man konstruieren, indem man Multiplikationsregeln aufstellt, die zum Verhalten von universellen Turingmaschinen passen (siehe wolframscience.com - Word problems ). So gibt es offenbar ein Beispiel mit 14 Generatoren und 52 Multiplikationsregeln, und man vermutet, dass es noch einfachere Beispiele geben sollte. Man sieht also, dass diese Beispiele nicht zufällig entstehen, sondern dass sich die Gruppe wie ein Computer verhält. Daher treten auch dieselben Probleme auf wie bei Computern (Stichwort: Halteproblem).
Man kann statt Gruppen auch Semigruppen betrachten – bei diesen fehlt das inverse Element, so dass die Multiplikationsregeln, die die Gleichheit gewisser Generatorprodukte (Strings) angeben, nicht einfach in eine Gleichheit mit dem leeren String umgeschrieben werden können. Auch bei Semigruppen kann man einen Bezug zu Turingmaschinen herstellen und zeigen, dass die Gleichheit von zwei Strings nicht allgemein entscheidbar ist (mehr dazu siehe z.B. Albert Meyer: The Word Problem for Semigroups, MIT 2005). Hier ist ein konkretes Beispiel von Gennadií Makanin aus dem Jahr 1966 für eine Semigruppe mit nur drei Generatoren \(A, B, C\), deren Wortproblem unentscheidbar ist (siehe wolframscience.com - Word problems ). Die Multiplikationsregeln dieser Semigruppe lauten:
Diese Regeln sind recht komplex und man ahnt, dass sie speziell designed sind, so dass ein komplexes Verhalten auftritt und das Wortproblem unentscheidbar wird.
Spielen wir ein kleines Spiel mit speziellen Dominosteinen: So ein Dominostein hat eine obere und eine untere Hälfte, auf der jeweils ein String (eine Zeichenfolge) steht. Hier ein Beispiel mit drei solchen nummerierten Dominosteinensorten (siehe Wikipedia: Postsches Korrespondenzproblem ):
Nr.1 Nr.2 Nr.3 |A | |AB | |BAA| |ABA| |BB | |AA |
Kann man endlich viele Dominosteine dieser drei Sorten so nebeneinanderlegen, dass die obere und die untere Zeile gleich sind (Lücken sind egal)? Im obigen Beispiel geht das so:
Nr: 1 3 2 3 |A |BAA|AB |BAA| |ABA|AA |BB |AA |
Wenn man vier Dominosteine der Sorte 1, 3, 2, 3 hintereinanderlegt, so steht in beiden Zeilen die Buchstabenfolge
ABAAABBAA
Gesucht wird nun eine Methode (ein Algorithmus), der man irgendeinen endlichen Satz aus solchen oder ähnlichen Dominosteinen geben kann und die immer nach endlich vielen Schritten die Frage beantworten kann, ob man endlich viele Dominosteine aus diesem vorgegebenen Satz wie oben so hintereinanderlegen kann, dass obere und untere Zeile identisch sind. Die Methode muss dabei universell sein, muss also mit jedem beliebigen endlichen Dominostein-Sortiment zurechtkommen. Das nennt man das Postsche Korrespondenzproblem. Dieses Problem ist unentscheidbar, d.h. es gibt keinen solchen universellen Algorithmus. Die Schwierigkeit besteht einfach darin, dass man mit immer längeren Dominoketten versuchen kann, zum Erfolg zu kommen – man kann immer versuchen, hier und da noch einige Steinchen einzuschieben und das Problem damit zu lösen.
Hier ist noch so ein Puzzle, für das es keinen universellen Lösungsalgorithmus gibt
(Details siehe Wikipedia: Wang-Parkettierung ).
Wieder geht es um spezielle Dominosteine, oder hier vielleicht besser: um Kacheln
wie beispielsweise die Folgenden
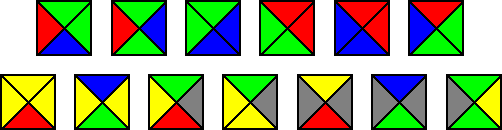
Quelle:
Wikimedia Commons File:Wang tiles.png,
dort gemeinfrei):
Alle Kacheln sind gleich groß und jeder Außenkante ist eine Farbe zugeordnet. Kann man mit einem solchen Kachel-Sortiment die unendliche Ebene lückenlos so kacheln, dass immer nur Kanten gleicher Farbe aneinanderstoßen? Dabei darf man die Kacheln nicht drehen oder spiegeln. Natürlich stehen unendlich viele Kacheln jeder Sorte aus dem vorgegebenen Sortiment zur Verfügung.
Schwer zu sagen! Aber die Aufgabe ist noch schwerer: Gesucht wird wieder eine universelle Methode (ein Algorithmus), die mit jedem endlichen Kachelsortiment zurechtkommt und nach endlich vielen Schritten die obige Frage beantwortet. Wang dachte 1961 noch, einen solchen Algorithmus gefunden zu haben, wobei dieser die Ebene periodisch kachelt – das Kachelmuster wiederholt sich also immer wieder.
Fünf Jahre später zeigte Robert Berger jedoch, dass es auch nicht-periodische Kachelungen gibt, die Wangs Algorithmus übersehen musste (ein Beispiel ist Wikimedia Commons File:Wang tesselation.svg). Auch das oben dargestellte Kachelsortiment von Karel Culik kann für eine solche nicht-periodische Kachelung verwendet werden, nicht aber für eine periodische. Heute weiß man, dass es einen universellen Algorithmus nicht gibt, der auch alle möglichen nichtperiodischen Kachelungen für beliebige Kachelsortimente korrekt erkennen kann. Das Problem ist unentscheidbar. Wieder einmal kann man nämlich zeigen, dass Kachelungen dieselbe Leistungskraft wie Turingmaschinen besitzen. Man kann jede Turingmaschine derart in ein Kachelsortiment übersetzen, dass man damit die Ebene genau dann kacheln kann, wenn die Turingmaschine nicht hält. Turings Halteproblem schlägt damit auf die Kachelungen durch.
Damit wollen wir unsere kleine Reise beenden. Natürlich gäbe es noch viel mehr zu sehen. So kann man in Wikipedia: List of statements undecidable in ZFC eine ganze Liste von Problemen finden, die im Rahmen der üblichen mathematischen Fundamente (Mengenlehre mit Auswahlaxiom, oft als ZFC abgekürzt, siehe Kapitel 4.2 ) unentscheidbar sind. Wenn man sich diese Probleme ansieht, so erkennt man, dass sie sich mit komplizierten Unendlichkeiten befassen, die durch die Standardaxiome der Mengenlehre nicht ausreichend festgelegt sind. Es würde zu weit führen, hier ins Detail zu gehen. Wer aber möchte, kann im nächsten Kapitel die Reise zu diesen Unendlichkeiten ein wenig fortsetzen.
© Jörg Resag, www.joerg-resag.de
last modified on 12 April 2023