Zusammenfassung des Buchkapitels:
Das Elektron besitzt neben Masse und Ladung eine weitere sehr wichtige Eigenschaft: den Spin. Dieser ist ein typisches Quantenphänomen ohne klassisches Gegenstück. Am ehesten lässt sich der Spin mit einem inneren Drehimpuls vergleichen, d.h. das Elektron verhält sich in bestimmten Situationen annhähernd so, als würde es rotieren.
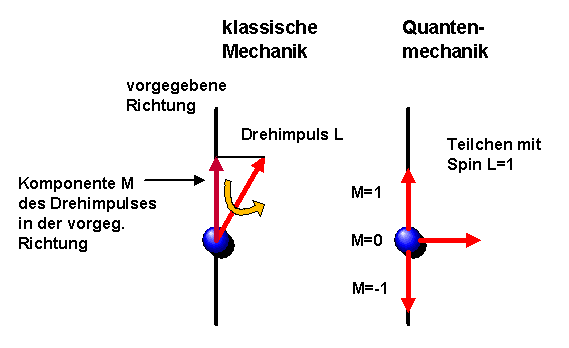
Bei einer Messung des Spins gibt man zunächst eine beliebige Richtung im Raum vor, typischerweise durch Anlegen eines Magnetfeldes. Man misst auf diese Weise die sogenannte Spinkomponente parallel zur vorgegebenen Achse. Das folgende Bild stellt den Unterschied zwischen klassischem Drehimpuls und quantenmechanischem Spin beispielhaft dar:

Für ein Elektron gilt:
Die Spinkomponente \(M\) kann nur zwei Werte annehmen,
nämlich die Werte \(+1/2\) und \(-1/2\), d.h. \(L = 1/2\)
(die Spin-Maßeinheit \(\hbar\) haben wir hier weggelassen).
Man sagt, das Elektron besitzt den Spin \(1/2\).
In der Deutung des Spins durch eine
klassische Rotation würde das bedeuten, dass das Elektron immer
mit der gleichen Drehgeschwindigkeit um die vorgegebene
Achse rotiert, und zwar entweder rechts oder links herum.
Der Spin des Elektrons beeinflusst dessen Verhalten in Magnetfeldern. Lässt man einen Strahl elektrisch neutraler Teilchen mit Spin 1/2 durch ein inhomogenes Magnetfeld laufen, so teilt sich dieser Strahl in zwei Teilstrahlen auf, einen mit \(M = 1/2\) und einen mit \(M = -1/2\).
Für Teilchen mit Spin \(1/2\) gilt das sogenannte Pauliprinzip, das eine entscheidende Rolle für den Aufbau der Atome spielt.
Quelle:
Wikimedia Commons File:Wolfgang Pauli young.jpg, dort gemeinfrei in den USA.
In einer vereinfachten Formulierung besagt das Pauliprinzip:
Das führt zur Schalenstruktur der Atomhülle.
Die präzise Formulierung des Pauliprinzips besagt, dass eine Vielteilchenwellenfunktion für Elektronen antisymmetrisch bezüglich der Vertauschung von Elektronmesswerten ist, wie das folgende Bild zeigt:

Eine Folge davon ist, dass die Elektronen ununterscheidbar werden,
und dass sie es vermeiden, bei gleichem Spin am selben Ort zu sein.
Das Pauliprinzip ist eines der seltenen Beispiele, wo eine einfache Regel keine einfache Begründung hat (so hat es Richard Feynman einmal ausgedrückt). Die Erklärung steckt tief inmitten der Synthese aus spezieller Relativitätstheorie und Quantentheorie.
a) Die Wahrscheinlichkeitsamplituden des Spins
Zum Thema Ununterscheidbarkeit und Pauliprinzip finden Sie ausführliche Infos in Die Symmetrie der Naturgesetze, Kapitel 4.4: Identische Teilchen.
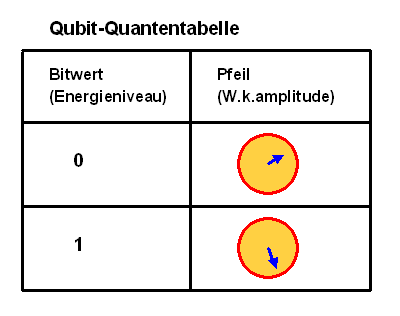
Die quantenmechanische Beschreibung eines Teilchens mit Spin L = 1/2 (z.B. ein Elektron) kann man sich gut veranschaulichen, wobei wir nur den Spin betrachten und den Ort etc. weglassen. Man braucht einfach nur eine Tabelle mit zwei Pfeilen, einen für M = 1/2 (Spin oben) und einen für M = - 1/2 (Spin unten). Das folgende Bild aus Die Grenzen der Berechenbarkeit, Kapitel 5.8: Quantencomputer stellt diese Tabelle dar, wobei der Bitwert 1 dem Spinwert M = 1/2 entspricht und der Bitwert 0 dem Spinwert M = - 1/2 . Spin in der vorgegebenen Richtung (nennen wir sie z-Richtung) bedeutet also Bit gesetzt, Spin entgegen der z-Richtung bedeutet Bit nicht gesetzt. Hintergrund: So kann man Quanten-Bit (Qubit) durch einen Spin realisieren:
Man kann einen solchen Quantenzustand auch als Punkt auf einer Kugeloberfläche darstellen (Bloch-Kugel):
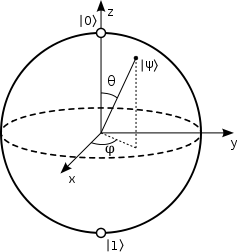
Quelle:
Wikimedia Commons File:Bloch sphere.svg, von WSmite-Meister,
CC BY-SA 3.0 DEED
Man kann sich vorstellen, dass die Punkte auf der Kugel der Spinrichtung entsprechen,
d.h. im klassischen Bild geht die Rotationsachse durch den Mittelpunkt und diesen Punkt.
Würde man den Spin in der Richtung messen, die der Spinrichtung auf der Bloch-Kugel entspricht,
so würde man immer die Spinkomponente M = 1/2 messen.
Das passt zu unserer Anschauung, dass der Spin in diese Richtung zeigt.
Für die Spinmessung in z-Richtung ergeben die Kugelkoordinaten-Winkel \(\theta\) und \(\varphi\) des Punktes die beiden Pfeile in der obigen Tabelle und bestimmen damit die Wahrscheinlichkeiten, den Spin in oder entgegen der z-Richtung ausgerichtet zu messen. Die Formeln für diese beiden Pfeile lauten: \[ c_{-1/2} = \sin{ \left( \frac{\theta}{2} \right) } \, e^{- i \frac{\varphi}{2}} \] \[ c_{+1/2} = \cos{ \left( \frac{\theta}{2} \right) } \, e^{ i \frac{\varphi}{2}} \] Diese beiden Pfeile sehen so aus:
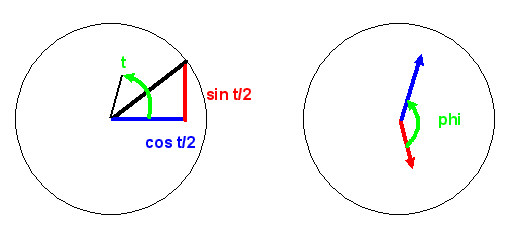
Rechts: Darstellung der Pfeilrichtungen.
Der Winkel \(\varphi\) (phi) ist dann der Winkel zwischen \(c_{-1/2}\) und \(c_{+1/2}\)
und legt damit die relative Orientierung der beiden Pfeile zueinander fest.
Die absolute Orientierung spielt keine Rolle, d.h. man kann das Bild rechts insgesamt um einen
beliebigen Winkel drehen, ohne den Informationsgehalt des Quantenzustands zu ändern.
Im Bild links sieht man, dass die Längenquadrate dieser Pfeile sich zu Eins aufaddieren, so wie
es bei Wahrscheinlichkeiten sein muss.
Mehr dazu in Die Grenzen der Berechenbarkeit, Kapitel 5.8: Quantencomputer.
Einen Spin in \(\theta - \varphi\)-Richtung erhält man, wenn man einen in z-Richtung ausgerichteten Spin entsprechend dreht bzw. kippt. Das ergibt die obigen Formeln. Diese Formeln machen auch klar, was geschieht, wenn man einen einen solchen allgemein ausgerichteten Spin weiter dreht und kippt: Beim Drehen um die z-Achse wächst einfach der Drehwinkel \(\varphi\) entsprechend an, und beim Kippen weg von der z-Achse wächst der Kippwinkel \(\theta\) an.
Bei \( \theta=0 \) (zur Vereinfachung setzen wir auch \( \varphi = 0 \), was aber hier unerheblich ist) ist \[ c_{-1/2} = 0 \] \[ c_{+1/2} = 1 \] d.h. der Spin zeigt in z-Richtung und es wird immer der Wert \( M = 1/2 \) für die Spinkomponente in z-Richtung gemessen. Kippt man den Spin gegen die z-Achse (d.h. vergrößert man \(\theta\)), so wird \(c_{-1/2}\) langsam größer und \(c_{+1/2}\) kleiner, so dass die Wahrscheinlichkeit für den Wert \( M = 1/2 \) (Spin oben) sinkt und die Wahrscheinlichkeit für den Wert \( M = - 1/2 \) (Spin unten) steigt.
Kippt man den Spin ganz nach unten (\(\theta = 180\) Grad), so wird schließlich \[ c_{-1/2} = 1 \] \[ c_{+1/2} = 0 \] d.h. der Spin zeigt gegen die z-Richtung und es wird immer der Wert \( M = - 1/2 \) für die Spinkomponente in z-Richtung gemessen.
Das funktioniert nur, weil die Formeln immer den halben Winkel enthalten (für \(\theta\), aber aus Konsistenzgründen bei allgemeinen Drehungen analog für \(\varphi\)) – das ist typisch für Spin 1/2.
Interessant ist, dass deswegen eine 360-Grad-Drehung um die z-Achse (also \(\varphi = 360\) Grad) gerade zu einem Vorzeichenwechel führt, d.h. die Pfeile werden invertiert. Die Quantentabelle hat aber immer noch denselben Informationsgehalt wie vor der 360-Grad-Drehung, denn nur die relative Orientierung der Pfeile zueinander ist wichtig! Man darf also alle Pfeile zugleich drehen, ohne dass sich der Informationsgehalt des Quantenzustandes ändert.
Man kann allgemein untersuchen, wie sich Quantenzustände bei Drehungen verhalten müssen. Dazu kann man sehr kleine (infinitesimale) Änderungen untersuchen und diese dann zu endlichen Drehungen aufsummieren. Wichtig ist, dass die Gruppenstruktur der Drehungen erhalten bleibt, denn zwei nacheinander ausgeführte Drehungen entsprechen zusammen ebenfalls einer Drehung. Also müssen auch die beiden Dreh-Umrechnungen des Quantenzustandes zusammen die Dreh-Umrechnung ergeben, die der zusammengesetzten Drehung entspricht – allerdings nicht ganz, denn wir haben eine Freiheit bei der Festlegung des Quantenzustandes: Nur die relative Orientierung der Pfeile in der Tabelle zueinander ist wichtig!
Wenn sie sich für die Details interessieren, finden Sie diese in Die Symmetrie der Naturgesetze, Kapitel 4.6: Darstellung von Symmetrien in der Quantentheorie und Kapitel 4.8: Drehungen, Spin und Drehimpuls (nur für Leser mit entsprechender mathematischer und physikalischer Vorbildung geeignet).
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 29 December 2023