
Quelle: Wikipemia Commons File:Steven-weinberg-2.jpg, dort gemeinfrei.
Zusammenfassung des Buchkapitels:
Die schwache Wechselwirkung (siehe Kapitel 4.1) fügt sich sehr gut in das Schema der Eichtheorie ein, das bei der elektromagnetischen und der starken Wechselwirkung bisher so erfolgreich war. Um die schwache Wechselwirkung als Eichtheorie zu beschreiben, darf man sie allerdings nicht isoliert betrachten. Durch viele Arbeiten aus den Jahren 1962 bis 1968, insbesondere von Salam und Weinberg, wurde klar, dass man sie zusammen mit der elektromagnetischen Wechselwirkung betrachten muss! Es gelang, eine einzige Eichtheorie zu formulieren, die beide Wechselwirkungen umfasst und die den Namen Theorie der elektroschwachen Wechselwirkung trägt.

Quelle:
Wikipemia Commons File:Steven-weinberg-2.jpg, dort gemeinfrei.
Nun sind elektromagnetische und schwache Wechselwirkung zunächst sehr unterschiedlich.
Wie lassen sie sich also vereinigen?
Man behandelt sie dazu zunächst im Rahmen einer Eichtheorie als praktisch gleichwertig und bricht dann diese Gleichwertigkeit erst anschließend auf. Der entsprechende Mechanismus nennt sich spontane Symmetriebrechung.
Bei der elektroschwachen Wechselwirkung ist die zu brechende Symmetrie
eine U(2)-Eichsymmetrie. Dabei fasst man zunächst beispielsweise Elektron und Elektron-Neutrino
als zwei gleichwertige Ausprägungen eines einzigen Fermions auf, die sich nur durch eine
spezielle Ladung unterscheiden, welche man schwachen Isospin nennt.
Das Elektron-Neutrino bekommt den schwachen Isospin +1/2, das Elektron −1/2
zugeordnet (analog machen wir es auch mit den anderen Lepton- und Quarkfamilien).
Dieser Isospin ist das Analogon zur Farbladung bei Quarks (die allerdings
3 Werte aufweisen kann, entsprechend der Eichgruppe SU(3) ).
So wie die Gluonen Farbladungen zwischen Quarks austauschen können, so können auch die
Feldquanten der U(2)-Eichtheorie schwache Isospinwerte austauschen und ein Elektron
in ein Elektron-Neutrino umwandeln (und umgekehrt). Genau das tut die schwache Wechselwirkung auch!
Allerdings ist die Theorie so nicht zu gebrauchen, denn sie enthält vier masselose Feldquanten, analog zu den acht Gluonen der QCD. Um die kurze Reichweite der schwachen Wechselwirkung zu beschreiben, brauchen wir aber drei Feldquanten mit recht großer Masse sowie ein masseloses Feldquant, das das Photon der elektromagnetischen Wechselwirkung beschreiben soll und das nur auf geladene Teilchen (z.B. das Elektron) wirkt, nicht aber auf die elektrisch neutralen Neutrinos.
Das Photon können wir konstruieren, indem wir die beiden Feldquanten, die den schwachen Isospin nicht ändern, quantenmechanisch überlagern (mischen, also ineinander verdrehen). Den entsprechenden Mischungswinkel (Drehwinkel) nennt man Weinbergwinkel oder schwachen Mischungswinkel \( \theta_W \). Bei dieser Mischung entsteht neben dem Photon ein zweites Feldquant, das wir der schwachen Wechselwirkung zuordnen können – wir nennen es Z-Boson. Es wechselwirkt im Gegensatz zum Photon auch mit den Neutrinos. Die beiden anderen Feldquanten, die den schwachen Isospin ändern können, bleiben unverändert – wir nennen sie W^{+}- und W^{−}-Boson (entsprechend ihrer elektrischen Ladung) und ordnen sie der schwachen Wechselwirkung zu. Weitere Details dazu im Buchkapitel.
Nun müssen wir den drei Feldquanten der schwachen Wechselwirkung (W^{+}-, W^{−}- und Z-Boson) noch eine Masse verleihen. Das erreichen wir durch die spontane Brechung der U(2)-Eichsymmetrie. Diese Symmetriebrechung entsteht dadurch, dass man den leeren Raum (das Vakuum) mit einem bestimmten Feld gleichmäßig anfüllt: dem Higgs-Feld. Man kann sich dazu das Vakuum mit einer Ansammlung unendlich vieler kleiner Kompassnadeln angefüllt vorstellen. Aufgrund der gegenseitigen magnetischen Kräfte richten sich die Magnetnadeln spontan alle in einer bestimmten Richtung aus, was die Symmetriebrechung ergibt.

Eine Störung dieses Feldes (rote Nadel oben) wäre dann
das berühmte Higgs-Teilchen.
Mehr zu diesem Thema siehe auch in Zeitpfad, Kapitel 2.2.
Die W- und Z-Bosonen wechselwirken nun mit diesem überall vorhandenen Higgs-Feld. Man kann sich vorstellen, dass sie eine Hülle aus Magnetnadeln um sich herum ansammeln und dadurch eine Masse von fast 100 GeV gewinnen. Die genaue Rechnung zeigt, dass ihre Massen über den experimentell ebenfalls messbaren Weinbergwinkel miteinander zusammenhängen: \[ \frac{M_{W}}{M_{Z}} = \cos{\theta_{W}} \] Diese Vorhersage lässt sich experimentell überprüfen – sie stimmt (mehr dazu im Buchkapitel)! Das Photon wechselwirkt dagegen nicht mit den Higgs-Magnetnadeln und bleibt masselos.
Insgesamt ergeben sich die folgenden zusätzlichen Bausteine für die Feynmangraphen der schwachen Wechselwirkung (das Higgs-Boson lassen wir hier weg):
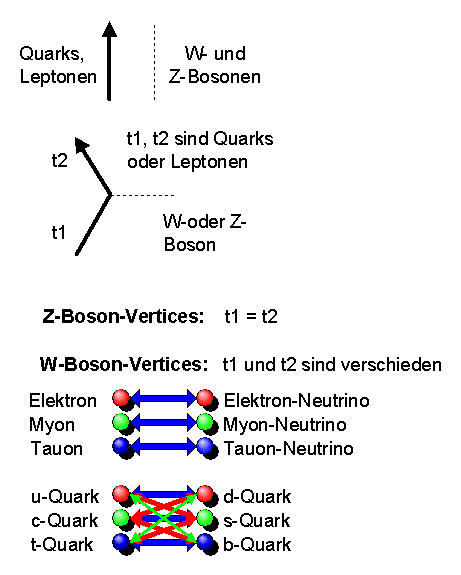
Die W-Boson-Vertices ermöglichen Zerfälle, die ansonsten nicht möglich wären:


Ohne die schwache Wechselwirkung wären beispielsweise Myonen, Neutronen oder geladene Pionen stabile Teilchen.
Ohne die schwache Wechselwirkung wäre auch die Kernfusion im Inneren unserer Sonne nicht möglich,
da sie dort für die notwendige Umwandlung von Protonen in Neutronen sorgt.
Wir sehen, dass die Existenz der schwachen Wechselwirkung durchaus von Bedeutung
für unsere Welt ist, denn ohne sie würde unsere Sonne nicht leuchten.

Die schwache Wechselwirkung weist noch eine Besonderheit auf: Sie wirkt nur auf linkshändige Fermionfelder.
Für die fast masselosen Neutrinos bedeutet das, dass ihr Teilchenspin immer gegen die Flugrichtung orientiert ist
(bei Antineutrinos ist es umgekehrt). In Flugrichtung gesehen rotieren Neutrinos im klassischen Bild also links herum
(gegen den Uhrzeigersinn).
Bei Teilchen mit größerer Masse ist es so, dass die schwache Wechselwirkung umso mehr einen Spin gegen
die Flugrichtung bevorzugt, je schneller das Teilchen ist (genauer: je größer dessen Energie relativ zur Ruhemasse ist).
Die schwache Wechselwirkung bricht damit die sogenannte Spiegelsymmetrie (Parität). Unsere Welt
ist nicht gleichwertig zu ihrem Spiegelbild.
Tauscht man zusätzlich zur Spiegelung noch alle Teilchen gegen ihre Antiteilchen aus, so könnte man vermuten, dass die Welt sich analog zu vorher verhält (CP-Symmetrie). Aber: sie tut es nur annähernd, nicht aber exakt! Man spricht von der CP-Verletzung. Erst wenn man den Vorgang auch noch in umgekehrter Zeitrichtung betrachtet, passt es wieder (CPT-Symmetrie).
Errata:
S. 182 unten: Das negativ geladene Pion besteht natürlich nicht aus einem up-Quark und einem down-Antiquark, sondern aus einem up-Antiquark und einem down-Quark, so wie in Abb. 6.8 dargestellt.
a) Verletzung der Spiegelsymmetrie und Pionzerfall
b) Wozu brauchen wir die spontane Symmetriebrechung in der elektroschwachen Wechselwirkung?
c) Supraleitung als Analogon zur spontanen Symmetriebrechung
d) Mathematische Details zur elektroschwachen Wechselwirkung
Anmerkung: Ausführliche Informationen zu den im Buchkapitel angesprochenen Neutrino-Oszillationen
und zur CP-Verletzung gibt es in den Zusatzinformationen zu Kapitel 4.2.
Warum zerfällt ein negatives Pion viel lieber in ein Myon plus Myon-Antineutrino als in ein Elektron plus Elektron-Antineutrino (siehe auch Kapitel 4.1)? Normalerweise sind Zerfälle, bei denen mehr Energie frei wird, bevorzugt, so dass eigentlich der Zerfall in das viel leichtere Elektron häufiger sein müsste.
Der Grund dafür liegt in der Verletzung der Spiegelsymmetrie durch die schwache Wechselwirkung. Das Pion hat Spin Null, dreht sich also selbst nicht. Wenn ein ruhendes negatives Pion in zwei Teilchen zerfällt, so fliegen diese in entgegengesetzte Richtungen auseinander. Dabei müssen sie entgegengesetzt zueinander rotieren, so dass sich ihre Spins zu Null addieren. Da das Antineutrino seinen Spin immer parallel zu seiner Flugrichtung ausgerichtet hat, muss das Elektron oder Myon seinen Spin ebenfalls parallel zu seiner Flugrichtung ausgerichtet haben, so dass dieser entgegengesetzt zum Neutrinospin orientiert ist:
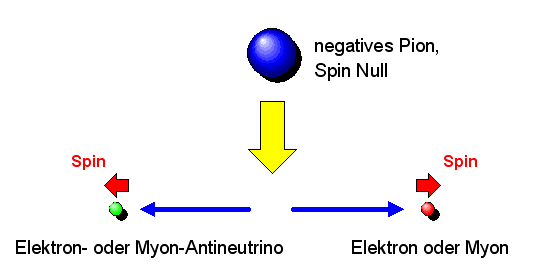
Nun bevorzugt die schwache Wechselwirkung bei einem Teilchen mit Masse
umso mehr einen Spin gegen die Flugrichtung, je schneller das Teilchen ist (genauer: je größer \(E/m\) ist),
und unterdrückt entsprechend umso mehr einen Spin in Flugrichtung.
Das beim Pionzerfall entstandene Elektron oder Myon hat nun seinen Spin zwangsläufig in Flugrichtung ausgerichtet,
d.h. die schwache Wechselwirkung unterdrückt hier die Entstehung des leichteren und damit schnelleren Elektrons
zu Gunsten des etwa 200 mal schwereren Myons. Der Pionzerfall liefert damit einen direkten Nachweis für
die Verletzung der Spiegelsymmetrie durch die schwache Wechselwirkung. Beim Zerfall des
positiven Pions ist es übrigens analog – man muss nur jedes Teilchen durch dessen Antiteilchen ersetzen
und die Spins umdrehen.
Siehe dazu auch
Wikipedia: Paritätsverletzung.
Zu den Begriffen Helizität und Chiralität siehe auch
Die Symmetrie der Naturgesetze 4.13 b) Spin 1/2, Helizität versus Chiralität.
Wieso ist man sich so sicher, dass man den Mechanismus der spontanen Symmetriebrechung für die elektroschwache Wechselwirkung benötigt? Wäre es nicht einfacher gewesen, direkt eine Quantenfeldtheorie mit massiven Quarks, Leptonen und insbesondere massiven W- und Z-Bosonen aufzustellen?
Es hat tatsächlich viele Versuche in diese Richtung gegeben, und sie sind alle gescheitert. Das Hauptproblem entsteht durch die massiven W- und Z-Bosonen. Diese Teilchen haben Spin 1, so wie das Photon. Bei massiven Spin-1-Teilchen kann die Spinkomponente in irgendeiner vorgegebenen Raumrichtung die drei Werte +1, 0, −1 annehmen. In der klassischen Analogie bedeuten diese drei Werte, dass die Rotationsachse des Teilchens parallel, senkrecht oder antiparallel zur gewählten Raumrichtung liegt (siehe Kapitel 2.7 ). Bewegt sich das Teilchen, so kann man die Bewegungsrichtung als Referenz-Raumrichtung verwenden und die Spinkomponente in dieser Bewegungsrichtung angeben – man nennt dies auch die Helizität des Teilchens. Helizität + 1 und -1 bedeuten dabei, dass die zugehörige quantenmechanische Welle senkrecht zur Bewegungsrichtung schwingt (transversal polarisiert ist), während sie bei Helizität 0 parallel zur Bewegungsrichtung schwingt (longitudinal polarisiert ist).
Bei sehr großen Energien führt nun die Helizität 0 (longitudinale Polarisation) zu Problemen. Die W- und Z-Bosonen wechselwirken viel zu stark miteinander und es kommt zu unsinnigen Resultaten, beispielsweise zu Wahrscheinlichkeiten über 100 Prozent. Man sagt auch, die Theorie ist nicht renormierbar.
Wären die W- und Z-Bosonen so wie das Photon masselos, so gäbe es dieses Problem nicht, denn masselose Teilchen mit Spin 1 haben immer Helizität +1 oder −1, aber nie Null. Sie rotieren im klassischen Analogon immer rechts oder links herum um die Bewegungsrichtung und die zugehörige quantenmechanische Welle ist immer transversal polarisiert, so wie wir das von Licht her kennen. Die störende Helizität Null fällt hier weg und die Theorie wird renormierbar, so wie wir das vom Photon in der QED her kennen.
Aus den Zusatzinfos zu Kapitel 5.3 wissen wir, dass man eine solche Theorie mit masselosen Spin-1-Teilchen als Eichtheorie formulieren muss. Hier noch einmal kurzgefasst die Kernidee:
Aus den Wellenfunktionen dieser Teilchen muss man passende Vierer-Vektorfelder \( A^{\mu}(x) \) (Eichpotentiale) konstruieren, die ein einfaches Raum-Zeit-Transformationsverhalten besitzen, wenn man das Bezugssystem wechselt. Problem: solche Vektorfelder haben zu viele Freiheitsgrade – sie erlauben beispielsweise longitudinale Polarisationen, die es bei masselosen Spin-1-Teilchen nicht gibt. Daher muss man diese longitudinalen Polarisationen jederzeit aus \( A^{\mu}(x) \) eliminieren können. Das geht mit Hilfe einer Eichtransformation von \( A^{\mu}(x) \) und führt automatisch auch zu einer Eichtransformation der Fermionfelder \( \psi(x) \). Eine kleine Rechnung zum Thema Eichpotentiale und Polarisation befindet sich etwas weiter unten.
Die Lage sieht also so aus: Eine Theorie mit massiven W- und Z-Bosonen liefert bei hohen Energien sinnlose Resultate, hervorgerufen durch die mögliche Helizität Null dieser Teilchen. Wären W- und Z-Bosonen dagegen masselos, so könnten wir eine konsistente Eichtheorie aufbauen, die renormierbar ist und die auch bei hohen Energien noch sinnvolle Resultate liefert, denn hier eliminieren Eichtransformationen die störende Helizität Null. Allerdings haben W- und Z-Bosonen nun einmal eine relativ große Masse um die 90 GeV. Was also ist zu tun?
Die Lösung lautet: Wir brauchen eine Theorie, die bei den üblicherweise zugänglichen Energien massive W- und Z-Bosonen besitzt, die aber bei höheren Energien in eine Eichtheorie masseloser W- und Z-Bosonen übergeht. Die Übergangsenergie liegt dabei bei etwa 250 GeV, wie genauere Analysen zeigen. Der einzige bekannte Weg zu einer solchen Theorie besteht darin, mit einer Eichtheorie masseloser W- und Z-Bosonen zu beginnen, aber bei Energien unterhalb von etwa 250 GeV diese Eichsymmetrie spontan zu brechen, was tatsächlich den W- und Z-Bosonen bei diesen Energien eine Masse und damit die mögliche Helizität Null verleiht (massive W- und Z-Bosonen vertragen sich nicht mit der Eichsymmetrie, weshalb diese spontan gebrochen sein muss). Bei höheren Energien verschwindet diese Eichsymmetrie-Brechung und mit ihr die Masse der W- und Z-Bosonen, so dass die restaurierte Eichsymmetrie die störende Helizität wieder eliminieren kann und eine renormierbare Eichtheorie entsteht.
Mehr zu diesem Thema findet man auch in Lisa Randell's Buch Verborgene Universen in Kapitel Kap. III.10 .
Eichpotentiale und Polarisation (kleine Rechnung für Fortgeschrittene):
In der Quantenfeldtheorie gehören zu massiven Teilchen mit Spin 1 die sogenannten Vektorpotentiale \(A^{\mu}(x)\). Diese erfüllen Gleichungen der Form
|
Proca-Gleichung: \[ (\partial_{\mu} \, \partial^{\mu} + m^{2}) A^{\nu}(x) = j^{\nu}(x) \] sowie \[ \partial_{\mu} A^{\mu}(x) = 0 \] |
siehe z.B. Itzykson, Zuber: Quantum Field Theory, Kap. 3-2-3 Massive Vector Fields – wir lassen hier die Faktoren \(c\) und \(\hbar\) konsequent weg, d.h. wir arbeiten mit natürlichen Einheiten, in denen alle Größen in Energieeinheiten angegeben werden; außerdem gilt ab sofort Einsteins Summenkonvention, d.h. über doppelt vorkommende Indices wird summiert.
Die erste Gleichung ist die bekannte Klein-Gordon-Gleichung zur Teilchenmasse \(m\), allerdings mit einem Quellterm \( j^{\nu}(x) \) (siehe auch die Zusatzinfos zum Thema Propagator in Kapitel 5.2 ).
Die zweite Gleichung \( \partial_{\mu} A^{\mu}(x) = 0 \) ergibt sich laut Weinberg als Nebenbedingung an die vier Potentiale \(A^{\mu}(x)\), da man zu ihrer Konstruktion nur drei Wellenfunktionen zu den drei Helizitäten +1, 0, −1 zur Verfügung hat.
Bei Masse \( m = 0 \) kennen wir die obigen Gleichungen aus der Elektrodynamik. Dabei ist \( A^{\mu}(x) \) das Vierer-Eichpotential des elektromagnetischen Feldes in der Lorentz-Eichung, wobei die zweite Gleichung genau diese Lorentz-Eichbedingung darstellt, und \( j^{\nu}(x) \) ist die Viererstromdichte. Aus den beiden Gleichungen ergibt sich automatisch die Stromerhaltung \[ \partial_{\mu} j^{\mu}(x) = 0 \] (einfach \(\partial_{\nu}\) auf die erste Gleichung anwenden, nach rechts durchtauschen und \( \partial_{\nu} A^{\nu}(x) = 0 \) verwenden).
Im Quell-freien leeren Raum (also \( j^{\nu}(x) = 0 \) ) kann man jede Lösung als Überlagerung ebener Wellen \[ a^{\mu}(k) \, e^{i k x} \] schreiben mit \[ k x = g(k,x) = k_{\mu} x^{\mu} = \omega t - \boldsymbol{k x} \] Dabei ist \( a^{\mu}(k) \) die Amplitude der ebenen Welle mit Vierer-Wellenzahl \(k\). Die beiden Gleichungen ergeben dann die Bedingungen \[ k^{2} = m^{2} \] sowie \[ k_{\mu} a^{\mu}(k) = 0 \] mit \[ k^{2} = k_{\mu} k^{\mu} = \omega^{2} -\boldsymbol{k}^{2} \] Ausgeschrieben ergeben beide Gleichungen:
| \[ \omega^{2} -\boldsymbol{k}^{2} = m^{2} \] \[ \omega a^{0} = \boldsymbol{a k} \] |
Wenn also \( a^{0} \) ungleich Null ist, so ist auch das Skalarprodukt \( \boldsymbol{a k} \) ungleich Null, d.h. die ebene \(\boldsymbol{A}\) -Welle besitzt dann auch eine longitudinale Komponente. Die ebene \(A^{0}\) -Welle besitzt dagegen sowieso keine Polarisation, da hier nur eine Zahl und kein Vektor an jedem Raumpunkt schwingt.
Um den Zusammenhang der Polarisation mit der Masse \(m\) herzustellen, kann man analog zur Elektrodynamik auch bei \(m > 0\) einen Feldstärketensor \[ F^{\mu\nu} := \partial^{\mu} A^{\nu} -\partial^{\nu} A^{\mu} \] einführen, was mit \[ A = \begin{pmatrix} A^0 \\ \boldsymbol{A} \end{pmatrix} = \begin{pmatrix} \phi \\ \boldsymbol{A} \end{pmatrix} \] ausgeschrieben die beiden Gleichungen \begin{align} \boldsymbol{E} &= -\mathrm{grad} \, \phi - \frac{d\boldsymbol{A}}{dt} \\ \boldsymbol{B} &= \mathrm{rot} \, \boldsymbol{A} \end{align} ergibt. In diese Gleichungen setzen wir nun die ebenen Wellen \[ A^{\mu}(x) = a^{\mu}(k) e^{i k x} \] ein, also \begin{align} \phi(x) &= a^{0}(k) \, e^{i (\omega t -\boldsymbol{kx})} \\ \boldsymbol{A}(x) &= \boldsymbol{a}(k) \, e^{i (\omega t -\boldsymbol{kx})} \end{align} Die Rechnung ergibt dann: \[ \boldsymbol{E} = i \boldsymbol{k} a^{0} e^{i (\omega t -\boldsymbol{kx})} - i \omega \boldsymbol{a} e^{i (\omega t -\boldsymbol{kx})} = \] \[ = i (\boldsymbol{k} a^{0} - \omega \boldsymbol{a}) \, e^{i (\omega t -\boldsymbol{kx})} \] \[ \boldsymbol{B} = rot \boldsymbol{A} = -i \boldsymbol{k} \times \boldsymbol{a} \, e^{i (\omega t -\boldsymbol{kx})} \] Die zweite Gleichung zeigt, dass das \(\boldsymbol{B}\) -Feld immer tangential polarisiert ist, denn \( \boldsymbol{k} \times \boldsymbol{a} \) steht immer senkrecht auf der Wellen-Bewegungsrichtung \(\boldsymbol{k}\).
Die Amplitude \[ (\boldsymbol{k} a^{0} - \omega \boldsymbol{a}) \] des \(\boldsymbol{E}\) -Feldes (erste Gleichung) ergibt multipliziert mit \(\boldsymbol{k}\) das Skalarprodukt \[ \boldsymbol{k}^{2} a^{0} - \omega \boldsymbol{ak} \] Für \(\boldsymbol{ak}\) können wir hier aufgrund der Nebenbedingung oben \( \omega a^{0} \) einsetzen, so dass sich für das Skalarprodukt der Term \[ \boldsymbol{k}^{2} a^{0} -\omega \omega a^{0} = a^{0} (\boldsymbol{k}^{2} -\omega^{2}) = -a^{0} m^{2} \] ergibt. Das \(\boldsymbol{E}\) -Feld hat also eine longitudinale Komponente (parallel zu \(\boldsymbol{k}\)), die mit der Teilchenmasse \(m\) anwächst (sofern \(a^{0}\) ungleich Null ist, denn wenn \(a^{0} = 0\) ist, so folgt bereits aus der Nebenbedingung \( \omega a^{0} = \boldsymbol{a k} \), dass dann \( \boldsymbol{a k} = 0 \) gilt, so dass das \(\boldsymbol{E}\) -Feld und sogar das \(\boldsymbol{A}\) -Feld transversal polarisiert ist).
Halten wir fest:
| Während das \(\boldsymbol{B}\) -Feld immer transversal polarisiert ist, besitzt das \(\boldsymbol{E}\) -Feld bei \(m > 0 \) und \(a^{0} \ne 0 \) auch eine longitudinale Komponente. Diese verschwindet im masselosen Grenzfall \( m = 0 \), also insbesondere bei elektromagnetischen ebenen Wellen. |
Das ist letztlich damit gemeint, wenn oben von Polarisationen die Rede ist. Im masselosen Fall kann man sogar die Potentiale \(A^{\mu}\) selbst so eichen, dass eine ebene \(A^{\mu}\) -Welle transversal polarisiert ist, denn man kann durch Umeichung erreichen, dass \( A^{0} = \phi = 0 \) und damit \(a^{0} = 0 \) ist. Die Nebenbedingung ergibt dann unmittelbar \( \boldsymbol{a k} = 0 \). Im Fall mit Masse gibt es dagegen keine allgemeine Eichfreiheit für die Potentiale \(A^{\mu}\).
Supraleiter spielen im LHC eine entscheidende Rolle, um mit starken Strömen die notwendigen Magnetfelder erzeugen zu können, die die hochrelativistischen Protonen auf ihrer Kreisbahn halten. Dabei werden die Spezialkabel in den Dipol-Elektromagneten mit flüssigem Helium soweit heruntergekühlt, dass sie supraleitend werden und elektrische Ströme ohne jeden Widerstand leiten (mehr dazu siehe Kapitel 8.2 ).
Neben diesem eher praktischen Aspekt ist Supraleitung aber auch aus Sicht der theoretischen Physik sehr interessant, denn Supraleitung liefert ein konkretes Beispiel für eine spontane Symmetriebrechung, die viele Analogien zur spontanen Symmetriebrechung in der elektroschwachen Wechselwirkung aufweist:
In der elektroschwachen Wechselwirkung erfolgt die Symmetriebrechung in der einfachsten Version durch das gleichsam von Hand hinzugefügte elementare Higgs-Feld. Auch komplexere Szenarien sind theoretisch denkbar, bei denen die Symmetriebrechung stattdessen dynamisch über neue sehr starke Kräfte (Technicolor-Kräfte genannt) zwischen neuartigen Elementarteilchen erfolgt, aus denen sich das Higgs-Teilchen zusammensetzt. Das wäre dann analog zur Supraleitung, in der die Wechselwirkung zwischen Elektronen und Gitterschwingungen zu einer (relativ schwachen) Anziehungskraft zwischen je zwei Elektronen führt, die zusammen ein Spin-Null-Quasiteilchen (Cooper-Paar) bilden. Unterhalb der kritischen Temperatur sammeln sich makroskopische Mengen dieser bosonischen Cooper-Paare in nur einem einzigen Quantenzustand (dem Grundzustand) – man spricht auch von Bose-Einstein-Kondensation.
Die vielen Cooper-Paare in diesem Grundzustand verhalten sich dabei vollkommen synchron, d.h. sie werden durch eine einzige makroskopische Wellenfunktion \(\psi\) beschrieben. Dabei ist es schwierig, einen signifikanten Anteil Cooper-Paare aus diesem Grundzustand herauszuheben – sie bewegen sich gewissermaßen gerne im Gleichklang. Wenn aber keine Cooper-Paare bzw. Elektronen aus der Herde ausbrechen, so entsteht auch kein elektrischer Widerstand, denn ein solcher Widerstand kommt gerade dadurch zu Stande, dass Elektronen durch Gitterschwingungen aus ihrem Kurs abgelenkt werden. Das Bose-Einstein-Kondensat aus Cooper-Paaren bewegt sich mit Widerstand Null durch den Supraleiter, d.h. Supraleitung ist ein makroskopisches Quantenphänomen. Analog kann man sich vorstellen, dass eine Art Higgs-Quanten-Kondensat das Vakuum durchdringt und die elektroschwache Symmetriebrechung gewirkt. Im Buchkapitel hatte ich dieses Higgs-Kondensat durch parallel ausgerichtete Pfeile dargestellt.
Wenn nun ein Magnetfeld versucht, in einen Supraleiter einzudringen, so entstehen in diesem sofort elektrische Gegenströme, die dieses Eindringen unterbinden (Lenz'sche Regel). Analog muss sich auch das Higgs-Kondensat im Vakuum verhalten, wenn von einem Teilchen schwache Kraftfelder ausgehen und versuchen, in das Vakuum einzudringen. Das Higgs-Kondensat reagiert und schwächt dieses Eindringen exponentiell ab. Das ist der Grund dafür, warum die schwache Wechselwirkung weit unterhalb von 250 GeV so schwach wirkt.
Da die Formeln bei Supraleitern nicht allzu kompliziert sind, wollen wir sie uns etwas genauer ansehen (nur für daran interessierte Leser mit entsprechendem Hintergrundwissen gedacht):
Die Cooper-Paare im Grundzustand können durch eine einzige makroskopische Wellenfunktion \( \psi(t,\boldsymbol{x}) \) beschrieben werden, analog zu den im Gleichtakt schwingenden Photonen in einem LASER. Dabei ist \( |\psi(t,\boldsymbol{x})|^{2} \) die Wahrscheinlichkeitsdichte dafür, ein Cooper-Paar zur Zeit \(t\) am Ort \(\boldsymbol{x}\) anzutreffen. Wenn wir die Ladung des Cooper-Paares in die Wellenfunktion mit aufnehmen, so können wir in guter Näherung \[ |\psi(t,\boldsymbol{x})|^{2} =: \rho(t,\boldsymbol{x}) \] auch als Ladungsdichte der Cooper-Paare interpretieren, sofern wir so große Teilvolumina betrachten, dass sich immer sehr viele Cooper-Paare darin befinden. Umgekehrt können wir die Wellenfunktion also schreiben als \[ \psi(t,\boldsymbol{x}) = \sqrt{\rho(t,\boldsymbol{x})} \, e^{i \theta(t,\boldsymbol{x})} \] Dabei ist \( \theta(t,\boldsymbol{x}) \) die Phase der Wellenfunktion zur Zeit \(t\) am Ort \(\boldsymbol{x}\) (wird oft auch als \( S(t,\boldsymbol{x}) \) bezeichnet).
Aufgrund der Supraleitung können wir davon ausgehen, dass die Ladungsdichte \( \rho(t,\boldsymbol{x}) \) der Cooper-Paare im Supraleiter räumlich und zeitlich praktisch konstant ist, da jeder lokale Überschuss ein elektrisches Feld hervorrufen würde, welcher die Cooper-Paare sofort wieder gleichmäßig verteilen würde. Wir setzen daher in guter Näherung \[ \rho(t,\boldsymbol{x}) = \rho_{0} \] Die Dynamik von \(\psi\) steckt also alleine in der Phase \( \theta \). Um diese Dynamik zu beschreiben, benötigen wir eine entsprechende Gleichung für \(\psi\) im Gitter des Supraleiters.
Es stellt sich heraus, dass dies in guter Näherung die Schrödingergleichung in einem äußeren elektromagnetischen Potential ist, wie wir sie in den Zusatzinfos zu Kapitel 5.3 kennengelernt haben. Dabei wird \( m \) irgendeine effektive Masse für das Cooper-Paar im Gitter des Supraleiters sein, und \(q\) ist die Ladung des Cooper-Paars, also die doppelte Elementarladung.
Mit Hilfe dieser Schrödingergleichung kann man leicht nachrechnen, dass die Ladungsdichte \[ |\psi(t,\boldsymbol{x})|^{2} =: \rho(t,\boldsymbol{x}) \] zusammen mit der Stromdichte \[ \boldsymbol{j}(t,\boldsymbol{x}) = \frac{1}{m} \, \mathrm{Re} \, [ \psi^{*} (\hat{\boldsymbol{P}} -q \boldsymbol{A}) \psi ] \] (siehe Wikipedia: Wahrscheinlichkeitsstromdichte; Re bezeichnet den Realteil) die Kontinuitätsgleichung \[ \frac{d\rho}{dt} + \mathrm{div} \, \boldsymbol{j} = 0 \] erfüllt, d.h. wir können im Fall der Supraleitung das obige \( \boldsymbol{j} \) als elektrische Stromdichte der Cooper-Paare interpretieren.
Dabei bedeutet Re in der Formel für \( \boldsymbol{j} \), dass der Realteil des Ausdrucks zu nehmen ist, \[ \hat{\boldsymbol{P}} = \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \] ist der Impulsoperator mit \( \frac{d}{d\boldsymbol{x}} = \mathrm{grad} \) (Gradient) und \( \boldsymbol{A} \) ist das Vektorpotential. Aus Kapitel 5.3 wissen wir, dass wir den Operator \[ \hat{\boldsymbol{v}} := (\hat{\boldsymbol{P}} -q \boldsymbol{A}) / m \] als Geschwindigkeitsoperator interpretieren können, so dass wir die intuitive Formel \[ \boldsymbol{j} = Re \, [ \psi^{*} \hat{\boldsymbol{v}} \psi ] \] erhalten. Da \( \rho = |\psi|^{2} = \psi^{*} \psi \) ist, haben wir hier schon fast die klassische Formel \( \boldsymbol{j} = \rho \boldsymbol{v} \) mit der klassischen Stromgeschwindigkeit \( \boldsymbol{v} \) vor uns. Mit \( \psi(t,\boldsymbol{x}) = \sqrt{\rho_{0}} \, e^{i \theta(t,\boldsymbol{x})} \) folgt \[ \hat{\boldsymbol{v}} \psi = \left( \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} - q \boldsymbol{A} \right) \, \sqrt{\rho_{0}} \, e^{i \theta} \, \frac{1}{m} = \] \[ = \left( \hbar \frac{d\theta}{d\boldsymbol{x}} - q \boldsymbol{A} \right) \,\sqrt{\rho_{0}} \, e^{i \theta} \, \frac{1}{m} \] und wir erhalten die sogenannte London-Gleichung (benannt nach den Brüdern Fritz und Heinz London, siehe Wikipedia: London-Gleichung)
| London-Gleichung: \[ \boldsymbol{j} = \left( \hbar \frac{d\theta}{d\boldsymbol{x}} -q \boldsymbol{A} \right) \, \rho_{0} \, \frac{1}{m} \] |
Diese Gleichung ersetzt die klassische Gleichung \[ \boldsymbol{j} = \sigma \boldsymbol{E} \] nach der ein elektrisches Feld \(\boldsymbol{E}\) die Ladungen gegen den Widerstand \(\sigma\) vorantreibt und so eine elektrische Stromdichte \(\boldsymbol{j}\) erzeugt. Diese Gleichung wäre bei Supraleitung sinnlos, da \( \sigma = 0 \) ist.
Übrigens verletzt die London-Gleichung noch nicht die Eichsymmetrie, denn wenn wir die Eichtransformation \[ \boldsymbol{A}' = \boldsymbol{A} + \frac{d\chi}{d\boldsymbol{x}} \] und die zugehörige Phasenänderung \[ \theta' := \theta + \frac{q}{\hbar} \chi \] einsetzen, so heben sich beide Änderungen gegenseitig auf.
Da wir außerdem eine raumzeitlich konstante Ladungsdichte \( \rho(t,\boldsymbol{x}) = \rho_{0} \) angenommen hatten, folgt aus der Kontinuitätsgleichung direkt \( \mathrm{div} \, \boldsymbol{j} = 0 \) und somit \[ 0 = \mathrm{div} \, \boldsymbol{j} = \left( \hbar \frac{d^2 \theta}{d\boldsymbol{x}^2} - q \, \mathrm{div} \boldsymbol{A} \right) \, \rho_{0} \, \frac{1}{m} \] Wir verwenden für das Vektorpotential \(\boldsymbol{A}\) die Coulombeichung \( \mathrm{div} \boldsymbol{A} = 0 \) und erhalten \[ \left( \frac{d}{d\boldsymbol{x}} \right)^{2} \theta(t,\boldsymbol{x}) = 0 \] In einem Supraleiter hängt die Lösung dieser Gleichung von Randbedingungen ab und davon, ob der Supraleiter beispielsweise Löcher hat (z.B. wie ein Ring geformt ist). Die einfachste Lösung (insbesondere im Fall ohne Loch) ist \[ \theta(t,\boldsymbol{x}) = \mathrm{const} \] d.h. in der London-Gleichung ist dann \[ \frac{d\theta}{d\boldsymbol{x}} = 0 \] Wikipedia: London equations zitiert dazu ein Theorem von Bloch, nach dem der Impulsoperator \[ \hat{\boldsymbol{P}} = \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \] auf \(\psi\) angewendet Null ergeben muss, da \(\psi\) der Grundzustand ist. Das wäre jedenfalls eine Brechung der Eichsymmetrie.
Richard Feynman verwendet in seinen Feynman Lectures: Quantenmechanik in Kap. 21 die konstante Lösung für \(\theta\) für einen Supraleiter ohne Löcher ohne weitere Begründung.
Mein Eindruck ist: In einem einfach zusammenhängenden Gebiet (also ohne Loch) kann man ein konstantes \(\theta\) durch eine entsprechende Umeichung erreichen, d.h. ein konstantes \(\theta\) entspricht einer Eichfixierung von \(\psi\) und \(\boldsymbol{A}\). Etwas weiter unten werden wir ohne spezielle Annahmen für \(\theta\) zeigen, dass ein Supraleiter Magnetfelder aus seinem Inneren verdrängt. Für ein konstantes \(\theta\) ergibt sich jedenfalls: \[ \boldsymbol{j} = -q \boldsymbol{A} \rho_{0} \frac{1}{m} \] Wendet man den Rotationsoperator \( \mathrm{rot} \) auf diese Gleichung an, so ergibt sich daraus \[ \mathrm{rot} \boldsymbol{j} = -q \boldsymbol{B} \, \rho_{0} \frac{1}{m} \] Diese Gleichung erhalten wir weiter unten auch ohne spezielle Annahmen für \(\theta\).
Im statischen Fall sind \(\boldsymbol{j}\) und \(\boldsymbol{A}\) zeitunabhängig und hängen über die Maxwellgleichung wie folgt zusammen: \[ \frac{d^2 \boldsymbol{A}}{d\boldsymbol{x}^2} = -\mu_{0} \boldsymbol{j} \] (siehe z.B. Wikipedia: Vektorpotential ). Setzen wir hier die obige Gleichung \( \boldsymbol{j} = -q \boldsymbol{A} \, \rho_{0} / m \) ein, so erhalten wir
| \[ \frac{d^2 \boldsymbol{A}}{d\boldsymbol{x}^2} = \mu_{0} q \boldsymbol{A} \, \rho_{0} \frac{1}{m} =: \lambda^{2} \boldsymbol{A} \] |
mit einer positiven reellen Konstante \(\lambda^{2}\) (nicht zu verwechseln mit einer Wellenlänge).
Wir betrachten nun ein kleines Gebiet an der Oberfläche des Supraleiters und bezeichnen die Koordinate senkrecht zur Oberfläche mit \(x\), wobei positive \(x\) innerhalb des Supraleiters liegen sollen und die Grenze bei \(x = 0\) liegt.
Dann hat die obige Gleichung dort (für \(x > 0\) ) die Lösungen \[ e^{+ \lambda x} \] \[ e^{-\lambda x} \] wobei die allgemeine Lösung eine reelle Linearkombination dieser beiden Lösungen ist. Da die Lösung \( e^{+ \lambda x} \) aber im Inneren exponentiell anwächst und beim Zusammenführen aller Teilgebiete keine sinnvolle Gesamtlösung ergibt, bleibt nur die zweite Lösung \[ \boldsymbol{A}(x) = \boldsymbol{A}(0) \, e^{-\lambda x} \] übrig, d.h. das Vektorpotential und mit ihm das Magnetfeld wird zum Inneren des Supraleiters hin exponentiell abgeschirmt (Meissner-Effekt). Die Abschirmung wird durch Oberflächenströme \[ \boldsymbol{j} = -q \boldsymbol{A} \, \rho_{0} \frac{1}{m} = \boldsymbol{j}(0) \, e^{-\lambda x} \] bewirkt, die ebenfalls nach innen hin exponentiell schwächer werden. Die exponentielle Abschirmung ist dabei sehr effektiv: die Eindringtiefe \(1/\lambda\) liegt typischerweise bei etwa 0,1 μm.

Quelle:
Wikimedia Commons File:EfektMeisnera.svg, dort gemeinfrei.
In Wikipedia: London-Gleichung
wird alternativ direkt die exponentielle Abschirmung
für das Magnetfeld \( \boldsymbol{B} \) hergeleitet. Dazu wird auf die London-Gleichung
\[
\boldsymbol{j} = \left( \hbar \frac{d\theta}{d\boldsymbol{x}} -q \boldsymbol{A} \right) \,
\rho_{0} \, \frac{1}{m}
\]
der Rotationsoperator \( \mathrm{rot} \)
angewendet und
\[
\mathrm{rot} \frac{d\theta}{d\boldsymbol{x}} = \mathrm{rot} \, \mathrm{grad} \, \theta = 0
\]
sowie
\[
\mathrm{rot} \boldsymbol{A} = \boldsymbol{B}
\]
verwendet. Ergebnis:
\[
\mathrm{rot} \boldsymbol{j} = -q \boldsymbol{B} \,\rho_{0} \frac{1}{m}
\]
Nun gilt im statischen Fall die Maxwellgleichung
\[
\mu_{0} \boldsymbol{j} = \mathrm{rot} \boldsymbol{B}
\]
die wir hier einsetzen können:
\[
\mathrm{rot} \, (\mathrm{rot} \boldsymbol{B}) \frac{1}{\mu_{0}} = -q \boldsymbol{B} \,\rho_{0} \frac{1}{m}
\]
Mit
\[
\mathrm{rot} \, (\mathrm{rot} \boldsymbol{B}) =
\]
\[ =
\mathrm{grad} \, (\mathrm{div} \boldsymbol{B}) - \left(\frac{d}{d\boldsymbol{x}}\right)^{2} \boldsymbol{B} =
\]
\[
= - \left(\frac{d}{d\boldsymbol{x}}\right)^{2} \boldsymbol{B}
\]
(wegen der Maxwellgleichung \( \mathrm{div} \boldsymbol{B} = 0 \) fällt der erste Term weg) folgt:
\[
\left(\frac{d}{d\boldsymbol{x}}\right)^{2} \boldsymbol{B} = \mu_{0} q \boldsymbol{B} \,\rho_{0} \frac{1}{m}
=: \lambda^{2} \boldsymbol{B}
\]
und analog zu oben folgt aus dieser Gleichung das exponentielle Abfallen von
\(\boldsymbol{B}\) von der Oberfläche des Supraleiters nach innen.
Diese Herleitung läuft praktisch analog zur vorherigen Herleitung, hat aber den Vorteil, dass wir keine Lösung für \(\theta\) brauchen, da \(\theta\) im statischen Fall für \(\boldsymbol{B}\) irrelevant ist.
Daher gilt diese Herleitung auch für einen supraleitenden Ring, d.h. auch hier wird das Magnetfeld aus dem Supraleiter herausgedrängt. Wegen der Maxwellgleichung \[ \mu_{0} \boldsymbol{j} = \mathrm{rot} \boldsymbol{B} \] bedeutet das auch hier, dass die Ströme nur an der Oberfläche des Supraleiters fließen, nicht aber in seinem Inneren. Das werden wir etwas weiter unten noch brauchen (Stichwort Flussquantisierung).
Die obige Gleichung \[ \left(\frac{d}{d\boldsymbol{x}}\right)^{2} \boldsymbol{A} = \lambda^{2} \boldsymbol{A} \] können wir noch etwas umstellen: \[ - \left(\frac{d}{d\boldsymbol{x}}\right)^{2} \boldsymbol{A} + \lambda^{2} \boldsymbol{A} = 0 \] Um den Zusammenhang zur elektroschwachen Wechselwirkung herzustellen, muss man diese Gleichung als statische (also zeitunabhängige) Version der Proca-Gleichung \[ (\partial_{\mu} \, \partial^{\mu} + m^{2}) A^{\nu}(x) = j^{\nu}(x) \] von oben ansehen, denn \[ \partial_{\mu} \partial^{\mu} = \left(\frac{d}{c \, dt}\right)^{2} - \left(\frac{d}{d\boldsymbol{x}}\right)^{2} \] Dabei übernimmt \(\lambda\) die Rolle der Masse des A-Feldes. Bei der statischen Proca-Gleichung nimmt das Potential exponentiell mit dem Abstand zur Quelle \(j\) ab, so wie bei der Supraleitung das Potential exponentiell mit dem Abstand zur Oberfläche abnimmt (Stichwort Yukawa-Potential, siehe auch die Zusatzinfos zu Kapitel 5.2). Das Innere des Supraleiters entspricht dabei dem physikalischen Vakuum der elektroschwachen Wechselwirkung. Die Analogie zum Supraleiter kann damit das exponentielle Abfallen der schwachen Wechselwirkung bei zunehmendem Abstand erklären.
Noch ein Hinweis am Rande: Bei einem ringförmigen Supraleiter mit einem Loch in der Mitte kann man wieder das Phänomen der Flussquantisierung herleiten auf das wir bereits in den Zusatzinfos zu Kapitel 5.3 gestoßen sind: Der Magnetfluss durch den supraleitenden Ring kann keine beliebigen Werte annehmen, sondern er muss ein ganzzahliges Vielfaches des sogenannten Flussquants \( h/q \) sein. Hier die Herleitung dazu:
Bei einem supraleitenden Ring ist die Lösung mit konstanter Phase \(\theta\) nicht korrekt – das passt dazu, dass man hier \(\theta\) nicht generell wegeichen kann, analog zum Aharanov-Bohm-Effekt (siehe Zusatzinfos zu Kapitel 5.3 ).
Es gilt aber immer noch, dass das Magnetfeld aus ihm herausgedrängt wird und dass deshalb Ströme nur an seiner Oberfläche fließen. In seinem Inneren ist also \( \boldsymbol{j} = 0 \). Nach der London-Gleichung gilt dort also: \[ 0 = \left( \hbar \frac{d\theta}{d\boldsymbol{x}} -q \boldsymbol{A} \right) \rho_{0} \frac{1}{m} \] oder umgestellt \[ \frac{d\theta}{d\boldsymbol{x}} = \frac{q}{\hbar} \boldsymbol{A} \] Wir bilden nun das Wegintegral entlang eines geschlossenen Weges \(\gamma\), der im Inneren des Ringes verläuft und dabei das Loch in der Ringmitte einmal umschließt: \[ \int_{\gamma} d\boldsymbol{x} \, \frac{d\theta}{d\boldsymbol{x}} = \frac{q}{\hbar} \int_{\gamma} d\boldsymbol{x} \, \boldsymbol{A} \] Links steht die Änderung der Phase \(\theta\), wenn man das Ringloch einmal umläuft. Da die Wellenfunktion aber an jeder Stelle eindeutig sein muss, kann sich die Phase \(\theta\) nur um ein ganzzahliges Vielfaches \(n\) von \(2 \pi\) ändern, d.h. links steht \( n \, 2 \pi \).
Das Intergral rechts ergibt den magnetischen Fluss durch den Ring, also durch die von \gamma begrenzte Kreisfläche \(F(\gamma)\): \[ \int_{\gamma} d\boldsymbol{x} \, \boldsymbol{A} = \int_{F(\gamma)} d\boldsymbol{f} \, \mathrm{rot} \boldsymbol{A} = \] \[ = \int_{F(\gamma)} d\boldsymbol{f} \, \boldsymbol{B} \] Also erhalten wir \[ n \, 2\pi = \frac{q}{\hbar} \, \int_{F(\gamma)} d\boldsymbol{f} \, \boldsymbol{B} \] und schließlich
|
Flussquantisierung: \[ \int_{F(\gamma)} d\boldsymbol{f} \, \boldsymbol{B} = n \, \frac{h}{q} \] |
Letztlich ist der Grund genau derselbe wie in Kapitel 5.3, nämlich dass eine Wellenfunktion ringförmig einen magnetischen Fluss umgibt. Bei der Supraleitung handelt es sich allerdings um eine makroskopische Wellenfunktion, die nicht leicht zu stören ist, so dass sich der Effekt hier tatsächlich experimentell nachweisen lässt. Soviel zur Flussquantisierung.
Zurück zum Hauptthema:
Wie wir oben gesehen haben, kann
die Analogie zum Supraleiter das exponentielle Abfallen der schwachen Wechselwirkung bei zunehmendem Abstand erklären.
Um den Zusammenhang zur Masse der W- und Z-Bosonen herzustellen, müssen wir auch die zeitabhängige Procagleichung
betrachten – das geht streng genommen über unsere bisherige Analogie hinaus, in der wir nur den statischen Fall der Supraleitung betrachtet haben.
Insofern liefert die Analogie noch keine direkte Erklärung für die Massen, wohl aber für das exponentielle Abfallen der schwachen Kräfte.
Um zur Masse zu gelangen, müssen wir sehen, dass die zeitabhängige Procagleichung auch ebene Wellen als Lösungen erlaubt, so wie die Maxwellgleichungen
neben statischen Feldern auch Lichtwellen ermöglichen. Bei ebenen Wellen können wir nun wieder den Zusammenhang zwischen Impuls und Wellenzahl
dazu verwenden, um \(\lambda\) (in natürlichen Einheiten) als Masse der Teilchen zu interpretieren, die zu diesen ebenen Wellen gehören.
Man kann tatsächlich in Analogie zur Supraleitung durch Symmetriebrechung einen Massenterm in der Proca-Gleichung erzeugen. Dazu starten wir mit der masselosen Proca-Gleichung (siehe oben; wir verwenden ab hier wieder natürliche Einheiten)
| Proca-Gleichung bei Masse Null: \[ \partial_{\mu} \partial^{\mu} A^{\nu}(x) = j^{\nu}(x) \] sowie \[ \partial_{\mu} A^{\mu}(x) = 0 \] |
Diese Gleichung gilt beispielsweise in der Elektrodynamik für das elektromagnetische Viererpotential. Nun brauchen wir noch passende Ströme \( j^{\nu}(x) \). In Analogie zur Supraleitung wollen wir annehmen, dass diese Ströme durch ein skalares komplexes Feld \(\phi(x)\) entstehen. Dieses Feld soll der Wellenfunktion \(\psi\) der Cooper-Paare von oben entsprechen, d.h. mit \(\phi\) ist irgendeine Ladungsdichte verbunden, über die \(\phi\) mit \(A^{\mu}(x)\) wechselwirkt. In der elektroschwachen Wechselwirkung entspricht später \(\phi\) dem Higgs-Feld.
Um aus \(\phi\) eine passende Viererstromdichte \( j^{\nu}(x) \)zu konstruieren, müssen wir beachten, dass dieser Strom erhalten sein muss, also wie bei der Supraleitung die Kontinuitätsgleichung \( \partial_{\nu} j^{\nu}(x) = 0 \) erfüllen muss – nur dann kann man \(j^{0}(x)\) als Ladungsdichte und \(\boldsymbol{j}(x)\) als räumliche Stromdichte dieser Ladungsdichte interpretieren.
Dass die Kontinuitätsgleichung für die Stromdichte erfüllt sein muss, kann man aus der masselosen Proca-Gleichung ablesen, indem man \(\partial_{\nu}\) auf sie anwendet und \( \partial_{\nu} A^{\nu}(x) = 0 \) beachtet.
Für \(\phi(x)\) brauchen wir dazu zunächst eine dynamische Gleichung, die die zeitliche Entwicklung von \(\phi\) beschreibt. Da \(\phi(x)\) ein skalares Feld der Masse \(m\) sein soll, wäre dies bei einem freien \(\phi\)-Feld die Klein-Gordon-Gleichung \[ \left( \partial_{\mu} \partial^{\mu} + m^{2} \right) \phi(x) = 0 \] Da sich \(\phi\) aber unter dem Einfluss des Viererpotentials \(A^{\nu}(x)\) bewegen soll, ändert sich diese Bewegungsgleichung nach dem Prinzip der minimalen Kopplung (siehe Kapitel 5.3 ):
|
Klein-Gordon-Gleichung im Vektorpotential: \[ \left[ (\partial_{\mu} + i q A_{\mu}) \, (\partial^{\mu} + i q A^{\mu}) + m^{2} \right] \, \phi(x) = 0 \] |
was wir wegen \( \partial_{\mu} A^{\mu} = 0 \) auch schreiben können als
\[ \left[ \partial_{\mu} \partial^{\mu} + 2 i q A_{\mu} \partial^{\mu} -q^{2} A_{\mu} A^{\mu} + m^{2} \right] \, \phi(x) = 0 \] In Analogie zur Supraleitung oben bilden wir nun eine Viererstromdichte \( j^{\nu}(x) \), welche die Kontinuitätsgleichung \( \partial_{\nu} j^{\nu} = 0 \) erfüllt. Dazu verwenden wir die obige Bewegungsgleichung und multiplizieren sie von links mit dem komplex konjugiertsen Feld \( \phi^{*}(x) \). Analog verwenden wir das komplex konjugierte der obigen Bewegungsgleichung und multiplizieren sie von links mit \(\phi(x)\). Wir erhalten die folgenden beiden Gleichungen: \[ \phi^{*}(x) \, \big[ \partial_{\mu} \partial^{\mu} + 2 i q A_{\mu} \partial^{\mu} + \] \[ - q^{2} A_{\mu} A^{\mu} + m^{2} \big] \, \phi(x) = 0 \] \[ \phi(x) \, \big[ \partial_{\mu} \partial^{\mu} -2 i q A_{\mu} \partial^{\mu} + \] \[ - q^{2} A_{\mu} A^{\mu} + m^{2} \big] \, \phi^{*}(x) = 0 \] Nun ziehen wir die untere Gleichung von der oberen Gleichung ab, so dass die Terme mit \( A_{\mu} A^{\mu} \) und \( m^{2} \) wegfallen: \[ \phi^{*}(x) \partial_{\mu} \partial^{\mu} \phi(x) - \phi(x) \partial_{\mu} \partial^{\mu} \phi^{*}(x) + \] \[ + 2 i q A_{\mu} \, \left[ \phi^{*}(x) \partial^{\mu} \phi(x) + \phi(x) \partial^{\mu} \phi^{*}(x) \right] = 0 \] Diesen Ausdruck können wir wegen \( \partial_{\mu} A^{\mu} = 0 \) auch folgendermaßen schreiben: \[ \partial_{\mu} \, [ \phi^{*}(x) \partial^{\mu} \phi(x) - \phi(x) \partial^{\mu} \phi^{*}(x) + \] \[ + 2 i q A_{\mu} \phi^{*}(x) \phi(x) ] = 0 \] Der Ausdruck in der Eckigen Klammer erfüllt also die Kontinuitätsgleichung. Um einen reellen Ausdruck zu erhalten und um einen Ausdruck analog zur Stromdichte in der Supraleitung oben zu erhalten, multiplizieren wir noch mit \( i / 2 \) (auf den Massenfaktor \( 1/m \) verzichten wir hier) und definieren die skalare Klein-Gordon-Stromdichte als
| Klein-Gordon-Stromdichte im Vektorpotential: \[ j^{\mu} := \] \[ = \frac{i}{2} \, [ \phi^{*} (\partial^{\mu} \phi) -\phi (\partial^{\mu} \phi)^{*} ] - q A^{\mu} |\phi|^{2} = \] \[ = \frac{1}{2} \, [ \phi^{*} (i \partial^{\mu} \phi) + \phi (i \partial^{\mu} \phi)^{*} ] - q A^{\mu} |\phi|^{2} = \] \[ = \mathrm{Re} \, [ \phi^{*} (i \partial^{\mu} \phi) ] - q A^{\mu} \, |\phi|^{2} = \] \[ = \mathrm{Re} \, [ \phi^{*} (i \partial^{\mu} -q A^{\mu}) \, \phi ] = \] \[ = \mathrm{Re} \, [ \phi^{*} (\hat{P}^{\mu} -q A^{\mu}) \, \phi ] \] |
Diese Viererstromdichte erfüllt wie gezeigt die Kontinuitätsgleichung \( \partial_{\mu} j^{\mu} = 0 \).
Nun gehen wir analog zur Supraleitung vor: Wir nehmen an, dass bei niedrigen Energien im gesamten leeren Raum \[ \phi(x) = \mathrm{const} \] ist, wobei die Konstante größer als Null sein soll. Damit ist die Phase von \(\phi\) festgelegt, was einer bestimmten Eichfixierung entspricht. Das \(\phi\)-Feld im Vakuum entspricht dem Quantenkondensat aus Cooper-Paaren, die sich im Supraleiter im Grundzustand befinden. Analog zur London-Gleichung mit konstanter Phase ergibt sich: \[ j^{\mu} = -q A^{\mu} |\phi|^{2} \] Setzen wir dies in die masselose Proca-Gleichung oben ein, so erhalten wir \[ \partial_{\mu} \partial^{\mu} A^{\nu} = j^{\nu} = \] \[ = - q A^{\nu} |\phi|^{2} =: -\lambda^{2} A^{\nu} \] d.h. wir erhalten die Proca-Gleichung mit Masse \[ \lambda^{2} = q \, |\phi|^{2} \] Die zunächst masselosen Feldquanten der Vektorpotentiale erhalten durch die spontane Symmetriebrechung eine Masse!
Um weitere Teilchen (z.B. Quarks) zu berücksichtigen, die ebenfalls Quelle eines Vektorpotentials sein können, können wir in der masselosen Proca-Gleichung oben auch noch weitere Ströme \( J^{\mu} \) hinzufügen. Insgesamt ergibt sich so die Proca-Gleichung mit Masse und äußeren Quellen
|
Proca-Gleichung nach spontaner Symmetriebrechung mit zusätzlichen äußeren Quellen: \[ (\partial_{\mu} \partial^{\mu} + \lambda^{2}) A^{\nu}(x) = J^{\nu}(x) \] sowie \[ \partial_{\mu} A^{\mu}(x) = 0 \] und \[ \lambda^{2} = q \, |\phi|^{2} \] |
Wie bei der Supraleitung schirmen also aufgrund der spontanen Symmetriebrechung die \(\phi\)-Viererströme \[ j^{\mu} = -q A^{\mu} |\phi|^{2} \] das \(A\)-Feld ab, das durch andere Quellen (z.B. Quarks, Viererstrom \(J^{\nu}\) ) erzeugt wird (statischer Fall der obigen Gleichung).
Wenn das \(A\)-Feld versucht, in das Vakuum einzudringen, so entstehen in diesem sofort \(\phi\)-Gegenströme, die dieses Eindringen weitgehend unterbinden.
Dabei entspricht der Anteil mit \(\mu = 1, 2, 3\) des \(\phi\)-Viererstroms dem Stromdichtevektor \[ \boldsymbol{j} = -q \boldsymbol{A} |\phi|^{2} \] während der Anteil mit \(\mu = 0\) einer \(\phi\)-Ladungsdichte \[ j^{0} = \rho = -q A^{0} |\phi|^{2} \] entspricht, die das eindringende Potential \(A^{0}\) am Eindringen in das Vakuum hindert (so wie klassisch das statische elektrische Potential in einem guten Leiter konstant ist).
Die obige Gleichung hat aber auch ohne zusätzliche Quellen \(J^{\nu}\) dynamische Lösungen, nämlich ebene \(A\)-Wellen. Diese Wellen entsprechen beim Übergang zur Quantentheorie massiven \(A\)-Teilchen (bzw. in der elektroschwachen Wechselwirkung dann W- und Z-Bosonen).
Diese Masse wird dabei ebenfalls durch die Ströme \[ j^{\mu} = -q A^{\mu} |\phi|^{2} \] erzeugt. Die vordringende masselose \(A\)-Welle induziert dabei einen Gegenstrom \( j^{\mu} \) im Vakuum, der ein \(A\)-Gegenfeld erzeugt und so das Vordringen der \(A\)-Welle verzögert. Das wirkt sich dann analog zu einer Masse der \(A\)-Welle aus.
(für Leser mit mathematisch-physikalischem Hintergrundwissen gedacht)
Wir haben oben gesehen, wie masselose \(A\)-Felder (Eichpotentiale, also gleichsam Photonen) durch die spontane Symmetriebrechung eine Masse erhalten können. Dabei durchdringt ein skalares \(\phi\)-Feld das gesamte Vakuum, so wie das Quark-Kondensat aus Cooper-Paaren einen Supraleiter durchdringt. Will ein \(A\)-Feld nun in dieses Vakuum eindringen, so erzeugt es darin \(\phi\)-Gegenströme, die ein \(A\)-Gegenfeld erzeugen. Ein statisches \(A\)-Feld wird dadurch exponentiell abgeschwächt, und eine ebene \(A\)-Welle wird so modifiziert, als ob die entsprechenden \(A\)-Feldquanten eine Masse hätten.
Was wir bisher nicht betrachtet haben, ist die Dynamik weiterer Teilchen (Quarks und Leptonen), die an das \(A\)-Feld ankoppeln (Ströme \(J^{\nu}\) oben). Das wollen wir nun teilweise nachholen, wobei wir direkt die korrekten Formeln des Standardmodells ableiten wollen. Um den Rahmen nicht zu sprengen, beschränken wir uns auf eine einzige zusätzliche Fermionfamilie, nämlich auf das Elektron und sein Neutrino. Weitere Familien werden weitgehend ähnlich behandelt.
Da Elektronen und Neutrinos Spin 1/2 tragen (also Fermionen sind), kann man ihnen ein Diracfeld \(\psi(x)\) (auch Diracspinor genannt) zuordnen, dessen Dynamik durch die Dirac-Gleichung beschrieben wird (siehe Zusatzinfos zu Kapitel 5.1 ).
Dabei gibt es einen klar definierten Zusammenhang zwischen Diracfeld und Wellenfunktion (siehe z.B. Die Symmetrie der Naturgesetze, Kap. 4.13: Spin 1/2, Dirac- und Weyl-Gleichung ). Das Diracfeld ist ein 4-komponentiger komplexwertiger Vektor, wobei die Zahl 4 dadurch zustande kommt, dass es die beiden Spinwerte +1/2 und −1/2 bezogen auf eine gegebene Raumachse gibt, und zusätzlich positive und negative Energien, wobei wir die negativen Energien mit Antiteilchen in Verbindung bringen können. Man kann nun jedes Diracfeld \(\psi\) eindeutig in einen linkshändigen und einen rechtshändigen Anteil zerlegen: \[ \psi(x) = \psi_{L}(x) + \psi_{R}(x) \] Übrigens kann man die Basis sogar so wählen, dass die oberen beiden Komponenten des Diracfeldes zum linkshändigen und die unteren beiden Komponenten zum rechtshändigen Feld gehören – wir brauchen das aber hier nicht explizit. Die Diracgleichung stellt wiederum einen Zusammenhang zwischen links- und rechtshändigem Feld her.
Bei masselosen Teilchen gehören linkshändige Felder zur Helizität -1/2 und rechtshändige Felder zur Helizität + 1/2, d.h. die Teilchen rotieren in Flugrichtung gesehen anschaulich links oder rechts herum (siehe auch Abschnitt a: Verletzung der Spiegelsymmetrie und Pionzerfall oben; bei Antiteilchen ist es umgekehrt).
Allgemein beschreibt bei beliebiger Teilchenmasse der Begriff der Händigkeit, wie sich das Diracfeld bei Geschwindigkeitstransformationen (Boosts) verändert. Linkshändige und rechtshändige Felder verhalten sich dabei entgegengesetzt zueinander: Wenn man ein linkshändiges massives Diracfeld mit definiertem Impuls durch einen Boost auf immer höhere Impulse bringt, so wird der Wellenfunktionsanteil mit Teilchen-Helizität -1/2 immer größer und der mit Helizität + 1/2 immer kleiner. Bei einem rechtshändigen Diracfeld ist es umgekehrt. Wenn man umgekehrt ein massives Teilchen mit gegebener Helizität immer langsamer macht, so werden linkshändiges und rechtshändiges Diracfeld im Ruhesystem schließlich gleich groß. Details dazu siehe Die Symmetrie der Naturgesetze, Kap. 4.13 b: Spin 1/2, Helizität versus Chiralität.
Nun treten in der schwachen Wechselwirkung nur Neutrinos mit Helizität -1/2 auf. Da Neutrinos nahezu masselos sind, werden sie also in sehr guter Näherung durch ein linkshändiges Diracfeld beschrieben. Rechtshändige Neutrino-Diracfelder werden in der schwachen Wechselwirkung gar nicht gebraucht. Anders bei den Elektronen, die eine positive Masse besitzen, so dass links- und rechtshändige Diracfelder gebraucht werden.
In der schwachen Wechselwirkung gibt es nun Umwandlungen von Elektronen in Elektron-Neutrinos und umgekehrt. Aus einem linkshändigen Neutrino-Diracfeld kann also ein Elektronen-Diracfeld werden. Dieses muss ebenfalls linkshändig sein, wie eine genauere Analyse zeigt. Sehr hochenergetischen Elektronen können sich also praktisch nur mit Helizität -1/2 in Neutrinos umwandeln, die dann ebenfalls Helizität -1/2 besitzen.
Um diese Umwandlungen im Rahmen einer Eichtheorie zu beschreiben, fassen wir das linkshändige Neutrino-Diracfeld \( \nu_{L}(x) \) und das linkshändige Elektron-Diracfeld \( e_{L}(x) \) formal als zwei Komponenten eines einzigen Feldes auf:
|
linkshändiges Isospin-Dublett aus Elektron- und Elektron-Neutrino-Diracfeld: \[ \psi_{L}(x) := \begin{pmatrix} \nu_{L}(x) \\ e_{L}(x) \end{pmatrix} \] |
Die Komponenten von \(\psi_{L}(x)\) tragen also nun zwei Indices: einen Diracindex (mit Werten von 1 bis 4) und einen sogenannten schwachen Isospin-Index, der zwei Werte aufweisen soll: einen für das Elektron-Neutrino-Feld (z.B. den Wert +1/2 oder alternativ auch den Wert 1) und einen für das Elektron-Feld (z.B. den Wert −1/2 oder alternativ auch den Wert 2).
Dieser schwache Isospin ist das Analogon zur Farbladung (rot, gelb, blau) in der starken Wechselwirkung. Streng genommen wissen wir momentan auch noch gar nicht, welcher Isospin-Index zu welcher Leptonsorte gehört, denn wir werden gleich zunächst davon ausgehen, dass alle Isospin-Indices gleichwertig sind, analog zu den drei Farbladungswerten der QCD. Erst die spontane Symmetriebrechung wird diese Gleichwertigkeit später aufheben.
Wir betrachten nun Eichtransformationen \(U\), die verschiedene schwache Isospin-Komponenten miteinander mischen, so wie in der QCD die drei Farbladungen gemischt werden. Auf diese Weise werden wir später Übergänge zwischen den schwachen Isospin-Komponenten erhalten, so wie Gluonen in der QCD Farbladungen verändern können. Wir ermöglichen so später die physikalischen Umwandlungen zwischen Elektronen und ihren Neutrinos.
Diese Übergänge darf es allerdings nur bei linkshändigen Feldern geben, d.h. \(U\) soll nur bei linkshändigen Feldern auf den schwachen Isospin-Index wirken – die rechtshändigen Felder haben sowieso keinen Isospin-Index. Wir bilden also eine Eichtheorie, die eine Symmetrie zwischen linkshändigem Elektron- und Neutrinofeld ausdrückt: beide sind zunächst vollkommen gleichwertig.
In der QCD hatten wir drei Farbladungen und entsprechend Eichtransformationen \(U\) aus SU(3) betrachtet. Nun haben wir zwei schwache Isospin-Werte, so dass man \(U\) aus SU(2) vermuten könnte. Man braucht aber später \(U\) aus U(2), da man nur so zugleich ein Z-Boson und ein Photon konstruieren kann, die den schwachen Isospin beide nicht ändern (siehe Buchkapitel).
Per Konvention wollen wir bei Eichtransformationen von \(\psi_{L}\) zusätzlich einen Faktor \[ \mathrm{det} U =: e^{i \varphi} \] herausziehen, d.h. wir definieren die lokale Eichtransformation von \psi_{L} als
| lokale Eichtransformation des linkshändigen Dubletts (Elektron und Neutrino-Feld): \[ \psi_{L}'(x) := \frac{U(x)}{\mathrm{det} \, U(x)} \, \psi_{L}(x) = \] \[ = U(x) \, e^{-i \varphi(x)} \, \psi_{L}(x) \] |
Dabei wirkt die komplexe 2-mal-2-Matrix \(U\) ausschließlich auf den schwachen Isospin-Index, verändert also nicht den Diracindex.
Letztlich bewirkt das Herausziehen des Faktors \( \mathrm{det} U \), dass die Matrix \( U(x) / \mathrm{det} U(x) \) aus SU(2) ist, denn \[ \mathrm{det} \left( \frac{U(x)}{\mathrm{det} \, U(x)} \right) = \frac{\mathrm{det} U(x)}{\mathrm{det} U(x)} = 1 \] Hätte man sich also gleich auf SU(2) beschränken können? Nein, denn sowohl \(U\) als auch \( \mathrm{det} U \) werden für die rechtshändigen Felder bzw. für die Higgs-Felder noch gebraucht.
Bei dem rechtshändigem Elektronenfeld \( e_{R}(x) \) gibt es keinen schwachen Isospin-Index, denn es gibt auch kein dazu passendes Neutrinofeld. Wir werden später sehen, dass eine Eichtransformation von \( e_{R} \) wie folgt aussehen muss:
| lokale Eichtransformation des rechtshändigen Elektron-Diracfeldes: \[ e_{R}'(x) := \frac{1}{\mathrm{det} \, U(x)} \, e_{R}(x) = \] \[ = e^{-i \varphi(x)} \, e_{R}(x) \] |
Im Vergleich zu \(\psi_{L}\) fällt also die Matrix \(U\) hier weg. Entsprechend gibt es später bei rechtshändigen Feldern auch keine Teilchenumwandlungen (Übergänge in ein Neutrinofeld).
Für die spontane Symmetriebrechung brauchen wir noch das Higgs-Feld. Um zusammen mit \(\psi_{L}\) eichinvariante Terme damit konstruieren zu können, brauchen wir analog zu \(\psi_{L}\) ein schwaches Isospin-Dublett aus zwei komplexwertigen Higgs-Feldern (da diese Felder skalar sind, also Spin Null aufweisen, gibt es bei ihnen auch keine Händigkeit oder Helizität). Das sind genau die beiden Higgs-Zeigerfelder, die im Buchkapitel erwähnt werden:
| Isospin-Dublett aus zwei skalaren (komplexwertigen) Higgs-Feldern: \[ \phi(x) := \begin{pmatrix} \phi_{1}(x) \\ \phi_{2}(x) \end{pmatrix} \] |
Die beiden Werte für den schwachen Isospin-Index haben wir hier mit 1 und 2 bezeichnet. Es stellt sich heraus, dass die passende Eichtransformation von \(\phi\) einfach die Multiplikation mit der Matrix \(U\) ist:
| lokale Eichtransformation des Higgs-Dubletts: \[ \phi'(x) := U(x) \, \phi(x) \] |
Anmerkung: In vielen Büchern sind die Eichtransformationen anders definiert, wobei es zum Teil Konventionssache ist, wo man den Faktor \( \mathrm{det} U \) unterbringt. Oft bringt man dort auch die Ladungen frühzeitig ins Spiel. Wir wollen die Ladungen aber zunächst in den Eichpotentialen verstecken und sie erst dann ins Spiel bringen, wenn wir die Identifikation mit den physikalischen Teilchen vornehmen.
Diese Vorgehensweise hat den Vorteil, dass wir uns zunächst über Ladungen noch keine Gedanken zu machen brauchen und dass es in den Formeln keinen Unterschied zwischen linkshändigem Elektron- und Neutrinofeld gibt – Eichsymmetrie bedeutet ja, dass linkshändiges Elektron und Neutrino zunächst vollkommen gleichwertige Teilchen sind, so wie die drei Farbladungen bei Quarks vollkommen gleichwertig sind. Erst die Brechung der Symmetrie hebt diese Gleichwertigkeit später auf, und dann kommen auch die Ladungen ins Spiel.
Um die Feldgleichungen und Stromdichten aufzustellen, benötigen wir nach dem Prinzip der minimalen Kopplung (siehe Zusatzinfos zu Kapitel 5.3 ) Vektorpotentiale \( A^{\mu}(x) \) sowie zugehörige kovarianten Ableitungen. Für das Higgsfeld \(\phi\) hatten wir diese bereits in dem genannten Kapitel angegeben:
| Kovariante Ableitung für \( \phi(x) \): \[ D_\mu^{(\phi)} := \partial_\mu -i A_\mu \] Dabei transformieren sich die Eichpotentiale bei einer lokalen Eichtransformation \[ \phi' := U \,\phi \] folgendermaßen: \[ i A_\mu' = i U A_\mu U^{ -1} + (\partial_\mu U) U^{ -1} \] denn dann erfüllt die kovariante Ableitung die Beziehung \[ (\partial_{\mu} − i A'_{\mu}) U \phi = U (\partial_{\mu} − i A_{\mu}) \phi \] |
Die mit dem imaginären \( i \) multiplizierten Vektorpotentiale \( i A^{\mu}(x) \) sind dabei Elemente aus dem Tangentialraum der Gruppe U(2) am Einselement, d.h. jedes \( A^{\mu}(x) \) ist eine hermitesche komplexwertige 2-mal-2-Matrix, die wie \(U\) auf den schwachen Isospin-Index wirkt, also beispielsweise ein Elektronenfeld in ein Neutrinofeld umwandeln kann.
Wie sieht die kovariante Ableitung für das rechtshändige Elektronfeld \( e_{R}(x) \) aus? Die zugehörige Eichtransformation war \[ e_{R}'(x) := \frac{1}{\mathrm{det} \, U(x)} \, e_{R}(x) = e^{-i \varphi(x)} \, e_{R}(x) \] d.h. e_{R}(x) transformiert sich wie in der Elektrodynamik mit einem U(1)-Gruppenelement \[ \frac{1}{\mathrm{det} U} = e^{-i \varphi} \] Nun können wir jedes Gruppenelement \(U\) aus U(2) immer in der Form \[ U = e^{i K} \] mit einer hermiteschen Matrix \(K\) schreiben.
Anwendung der Determinante ergibt \[ \mathrm{det} U = e^{i \, \mathrm{tr} K} \] mit der Spur \( \mathrm{tr} \, K \) des Exponenten. Es ist also \[ \varphi = \mathrm{tr} \, K \] Daraus können wir entnehmen, dass die zu dieser Eichtransformation gehörenden Vektorpotentiale einfach durch Spurbildung aus den bereits vorhandenen Vektorpotentialen \(A^{\mu}\) gewonnen werden können, denn es gilt: \[ i \, \mathrm{tr} \, A_\mu' = \] \[ = i \, \mathrm{tr} \, (U A_\mu U^{ -1}) + \mathrm{tr} \, ((\partial_\mu U) U^{ -1}) = \] \[ = i \, \mathrm{tr} \, A_\mu + i \partial_\mu \, \mathrm{tr} \, K = \] \[ = i \, \mathrm{tr} \, A_\mu + i \, \partial_\mu \varphi \] Das ist genau die Transformation, die zur Eichtransformation \[ e_{R}'(x) = e^{-i \varphi(x)} e_{R}(x) \] und zur kovarianten Ableitung \[ D_\mu^{(e_{R})} := \partial_\mu + i \, \mathrm{tr} \, A_{\mu} \] passt, wie wir aus der Elektrodynamik wissen.
| Kovariante Ableitung für e_{R}(x) : \[ D_\mu^{(e_{R})} := \partial_\mu + i \, \mathrm{tr} \, A_{\mu} \] Dabei transformieren sich die Eichpotentiale bei einer lokalen Eichtransformation \[ e_{R}'(x) := \frac{1}{\mathrm{det} U(x)} \, e_{R}(x) = e^{-i \varphi(x)} \, e_{R}(x) \] folgendermaßen: \[ \mathrm{tr} \, A_\mu' = \mathrm{tr} \, A_\mu + \partial_\mu \varphi \] |
Kombinieren wir die Formeln für \(\phi\) und \(e_{R}\), so erhalten wir die Formeln für \(\psi_{L}\):
| Kovariante Ableitung für \(\psi_{L}(x)\): \[ D_\mu^{(\psi_{L})} := \partial_\mu - i A_{\mu} + i \, \mathrm{tr} \, A_{\mu} \] |
wobei wir die 2-mal-2-Einheitsmatrix \( 1 \) für den ersten und dritten Term nicht explizit hinschreiben.
Nun sind wir gerüstet, um uns die Dynamik dieser Felder anzusehen. Beginnen wir mit der Dynamik des linkshändigen Dubletts (Elektron und Neutrino) im äußeren \(A\)-Feld, die durch die Diracgleichung beschrieben wird, wobei wir nach dem Prinzip der minimalen Kopplung die entsprechenden kovarianten Ableitungen verwenden müssen.
Außerdem müssen wir die Fermionmassen zunächst gleich Null setzen, denn sonst würde die Diracgleichung links- und rechtshändige Felder miteinander mischen, und dann wäre unklar, welche kovariante Ableitung verwendet werden muss (die Gleichung wäre nicht mehr eichinvariant). Zudem wüssten wir gar nicht, ob nun die Elektronenmasse oder die verschwindend kleine Neutrinomasse einzusetzen ist. Die Fermionmassen werden erst später durch die spontane Symmetriebrechung erzeugt.
Die masselose Diracgleichung lautet: \[ i \gamma^{\mu} D_\mu^{(\psi_{L})} \psi_{L} = 0 \] oder ausgeschrieben: \[ i \gamma^{\mu} (\partial_\mu -i A_{\mu} + i \, \mathrm{tr} \, A_{\mu}) \, \psi_{L} = 0 \] Um die Verbindung zu den physikalischen Teilchen (Photon sowie W- und Z-Boson) zu erhalten, führen wir zunächst reellwertige elektroschwache Felder \( B_{\mu} \) und \( W_{\mu}^{k} \) und zugehörige elektroschwache Ladungen \(g'\) und \(g\) ein, d.h. wir definieren
| Definition der W- und B-Felder und der elektroschwachen Ladungen \(g'\) und \(g\): \[ -A_{\mu}(x) =: \frac{g'}{2} B_{\mu}(x) \, 1 + \frac{g}{2} W_{\mu}^{k}(x) \sigma^{k} \] |
(mit Summe über \(k\) von 1 bis 3; das Vorzeichen wurde so gewählt, dass nachher \(g\) und \(g'\) dasselbe Vorzeichen wie die positive Elementarladung \(e\) erhalten, also ebenfalls positiv sind; der Faktor \(1/2\) erweist sich ebenfalls später als nützlich).
Die obige Formel bedeutet lediglich, dass wir die hermiteschen 2-mal-2-Isospinmatrizen \( A_{\mu} \) als reelle Linearkombination der 4 Basismatrizen \(1\) (2-mal-2-Einheitsmatrix) und \(\sigma^{k}\) (Paulimatrizen) schreiben und aus den reellwertigen Koeffizientenfunktionen noch die reellen Faktoren \(\frac{g}{2}\) und \(\frac{g'}{2}\) herausziehen. Hier noch einmal die bekannten Paulimatrizen:

Die Funktionen \( B_{\mu}(x) \) und \( W_{\mu}^{k}(x) \) sind also für jedes \(\mu\) einfache reellwertige Funktionen (also keine Matrizen). Dabei ziehen wir den Faktor \(\frac{g'}{2}\) aus dem Einheitsmatrix-Anteil und \(\frac{g}{2}\) aus dem Rest-Anteil heraus, da sich beide Anteile bei Eichtransformationen nicht miteinander vermischen und wir so getrennte Transformationsregeln für \(B_{\mu}\) und \(W_{\mu}^{k}\) erhalten (die Rechnung dazu lassen wir hier weg).
Wenn wir den \(A\)-Anteil in der obigen Diracgleichung für \( \psi_{L} \) durch die neuen Felder ausdrücken, so ergibt sich wegen \( \mathrm{tr} \, \sigma^{k} = 0 \) und \( \mathrm{tr} \, 1 = 2 \) der Term \[ -A_{\mu} + \mathrm{tr} \, A_{\mu} = \] \[ = \frac{g'}{2} B_{\mu} \, 1 + \frac{g}{2} W_{\mu}^{k} \sigma^{k} -g' B_{\mu} \, 1 = \] \[ = \frac{g}{2} W_{\mu}^{k} \sigma^{k} -\frac{g'}{2} B_{\mu} \, 1 \] d.h. wir haben \[ i \gamma^{\mu} \left[ \partial_\mu + \frac{i}{2} \left( g W_{\mu}^{k} \sigma^{k} - g' B_{\mu} \, 1 \right) \right] \psi_{L} = 0 \] Ausgeschrieben mit Hilfe der Pauli-Matrizen bedeutet diese Gleichung:
| Diracgleichungen für das linkshändige Neutrino- und Elektronfeld: \[ i \gamma^{\mu} \bigg\{ \partial_\mu \nu_{L}(x) + \frac{i}{2} \big[ g ( W_{\mu}^{1} -i W_{\mu}^{2} ) \, e_{L}(x) + \] \[ + (g W_{\mu}^{3} -g' B_{\mu} ) \, \nu_{L}(x) \big] \bigg\} = 0 \] \[ i \gamma^{\mu} \bigg\{ \partial_\mu e_{L}(x) + \frac{i}{2} \big[ g ( W_{\mu}^{1} + i W_{\mu}^{2} ) \, \nu_{L}(x) + \] \[ + (-g W_{\mu}^{3} -g' B_{\mu} ) \, e_{L}(x) \big] \bigg\} = 0 \] |
Es gibt also in jeder Gleichung einen Term, der das jeweils andere Feld hinzumischt, z.B. in der ersten Gleichung den Term \[ g ( W_{\mu}^{1} -i W_{\mu}^{2} ) \, e_{L}(x) \] Diese Terme bewirken letztlich die Umwandlungen von Neutrinos in Elektronen und umgekehrt. Die Feldkombinationen \[ W_{\mu}^{1} -i W_{\mu}^{2} \] \[ W_{\mu}^{1} + i W_{\mu}^{2} \] entsprechen daher den beiden geladenen W-Bosonen, und \( g \) ist die entsprechende schwache Kopplungskonstante (Ladung) für die Ankopplung der W-Bosonen. Meist schreibt man daher auch \[ W_{\mu}^{+} := \frac{1}{\sqrt{2}} \left( W_{\mu}^{1} - i W_{\mu}^{2} \right) \] \[ W_{\mu}^{-} := \frac{1}{\sqrt{2}} \left( W_{\mu}^{1} + i W_{\mu}^{2} \right) \] Es gibt aber auch in jeder Gleichung einen Term, der das Feld nicht zwischen Elektron und Neutrino wechselt und dennoch eine Ankopplung an das Eichpotential bewirkt. In der ersten Gleichung ist das der Term \[ ( g W_{\mu}^{3} - g' B_{\mu} ) \, \nu_{L}(x) \] und in der zweiten Gleichung der Term \[ (-g W_{\mu}^{3} -g' B_{\mu} ) \, e_{L}(x) \] Da diese Terme keine Veränderung des Teilchenflavors bewirken, können sie in der elektroschwachen Wechselwirkung als Überlagerung der elektromagnetischen und der Z-Boson-Wechselwirkung verstanden werden. Wir fassen entsprechend die Felder \(W_{\mu}^{3}\) und \(B_{\mu}\) als Überlagerung (Verdrehung) des elektromagnetischen Vektorpotentials \( A_{\mu}^{(\gamma)} \) und des Z-Boson-Vektorpotentials \( Z_{\mu} \) auf:
| Photon- (\gamma) und Z-Boson-Vektorpotential: \[ W_{\mu}^{3} =: Z_{\mu} \cos{\theta_{W}} + A_{\mu}^{(\gamma)} \sin{\theta_{W}} \] \[ B_{\mu} =: -Z_{\mu} \sin{\theta_{W}} + A_{\mu}^{(\gamma)} \cos{\theta_{W}} \] |
Dabei ist \( \theta_{W} \) der Weinbergwinkel (elektroschwacher Mischungswinkel), der experimentell bestimmt werden muss.
Im Buchkapitel hatte ich das \( W_{\mu}^{3} \)-Feld als Amplitude \( a \) und das \( B_{\mu} \) -Feld als Amplitude \( b \) bezeichnet (und den Raumzeit-Index \(\mu\) ignoriert) sowie den Term \( W_{\mu}^{3} \sigma^{3} \) mit einem A-Quant und den Term \( B_{\mu} \, 1 \) mit einem B-Quant in Verbindung gebracht. Weiter wird im Buchkapitel das elektromagnetische Potential \( A_{\mu}^{(\gamma)} \) als \( \gamma \) und das Z-Boson-Vektorpotential \( Z_{\mu} \) als \(Z\) bezeichnet.
Setzen wir die obigen Gleichungen ein, so ergibt sich in der Diracgleichung für das Neutrinofeld der Term (siehe auch die analoge Ableitung im Buchkapitel): \[ g W_{\mu}^{3} -g' B_{\mu} = \] \[ = g \, ( Z_{\mu} \cos{\theta_{W}} + A_{\mu}^{(\gamma)} \sin{\theta_{W}} ) + \] \[ - g' \, ( -Z_{\mu} \sin{\theta_{W}} + A_{\mu}^{(\gamma)} \cos{\theta_{W}} ) = \] \[ = Z_{\mu} \, ( g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ + A_{\mu}^{(\gamma)} \, ( g \sin{\theta_{W}} -g' \cos{\theta_{W}} ) \] Da das Neutrino elektrisch neutral ist, darf es keine Kopplung an das elektromagnetische \(A_{\mu}^{(\gamma)}\) -Potential geben, d.h. die zweite Klammer muss Null sein: \[ g \sin{\theta_{W}} = g' \cos{\theta_{W}} \] In der Diracgleichung für das Elektronenfeld ergibt sich wiederum der Term (siehe auch die analoge Ableitung im Buchkapitel; ersetze einfach in der obigen Rechnung \(g\) durch \(-g\) ): \[ -g W_{\mu}^{3} -g' B_{\mu} = \] \[ = Z_{\mu} \, ( -g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ + A_{\mu}^{(\gamma)} \, ( -g \sin{\theta_{W}} -g' \cos{\theta_{W}} ) \] In der Diracgleichung für \( e_{L}(x) \) ergibt sich also insgesamt der Term \[ \partial_\mu + \frac{i}{2} (-g W_{\mu}^{3} -g' B_{\mu} ) = \] \[ = \partial_\mu + \frac{i}{2} [ Z_{\mu} ( -g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ + A_{\mu}^{(\gamma)} ( -g \sin{\theta_{W}} -g' \cos{\theta_{W}} ) ] = \] \[ = \partial_\mu + \frac{i}{2} Z_{\mu} ( -g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ - \frac{i}{2} A_{\mu}^{(\gamma)} ( g \sin{\theta_{W}} + g' \cos{\theta_{W}} ) \] Betrachten wir darin den Term mit dem elektromagnetischen Viererpotential \(A_{\mu}^{(\gamma)}\). Aus Kapitel 5.3 wissen wir, dass bei der elektromagnetischen Wechselwirkung die kovarianten Ableitungen (in natürlichen Einheiten) die Form \[ \partial_\mu + i q A_\mu^{(\gamma)} \] haben. Setzen wir für das Elektron die elektrische Ladung \( q = -e \) mit der positiven Elementarladung \(e\) ein, so wird daraus \[ \partial_\mu - i e A_\mu^{(\gamma)} \] Vergleich mit dem Ausdruck oben ergibt, dass \[ \frac{i}{2} A_{\mu}^{(\gamma)} ( g \sin{\theta_{W}} + g' \cos{\theta_{W}} ) = i e A_\mu^{(\gamma)} \] sein muss, also \[ \frac{1}{2} ( g \sin{\theta_{W}} + g' \cos{\theta_{W}} ) = e \] Zusammen mit der Beziehung \[ g \sin{\theta_{W}} = g' \cos{\theta_{W}} \] von oben ergibt das
| Zusammenhang zwischen elektrischer Elementarladung \(e\) und den schwachen Ladungen \(g\) und \(g'\): \[ e = g \, \sin{\theta_{W}} = g' \, \cos{\theta_{W}} \] |
Die Diracgleichungen für das linkshändige Neutrino- und Elektronfeld sehen also jetzt so aus: \[ i \gamma^{\mu} \, \bigg\{ \partial_\mu \nu_{L}(x) + i \, \big[ g/\sqrt{2} W_{\mu}^{+} e_{L}(x) + \] \[ + \frac{1}{2} Z_{\mu} \, ( g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) \, \nu_{L}(x) \big] \bigg\} = 0 \] \[ i \gamma^{\mu} \, \bigg\{ \partial_\mu e_{L}(x) + i \, \big[ g/\sqrt{2} W_{\mu}^{-} \nu_{L}(x) + \] \[ + \frac{1}{2} Z_{\mu} \, ( -g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) \, e_{L}(x) + \] \[ - e A_{\mu}^{(\gamma)} e_{L}(x) \big] \bigg\} = 0 \] Man kann die Ladungsfaktoren der \(Z_{\mu}\) -Terme noch etwas umschreiben, indem man \( \sin{\theta_{W}} \) und \( \cos{\theta_{W}} \) durch \(g\) und \(g'\) ausdrückt.
Aus \[ g \sin{\theta_{W}} = g' \cos{\theta_{W}} \] folgt nämlich, dass wir \[ \tilde{g} \sin{\theta_{W}} = g' \] \[ \tilde{g} \cos{\theta_{W}} = g \] schreiben können mit einem neuen reellen Parameter \(\tilde{g}\), denn multiplizieren wir die erste Gleichung mit \(g\) und die zweite Gleichung mit \(g'\), so erhalten wir \[ g \tilde{g} \, \sin{\theta_{W}} = g g' = g' \tilde{g} \, \cos{\theta_{W}} \] und somit wieder \( g \sin{\theta_{W}} = g' \cos{\theta_{W}} \).
Den Parameter \(\tilde{g}\) können wir ebenfalls ausrechnen, indem wir die beiden Gleichungen quadrieren und addieren: \[ (\tilde{g} \sin{\theta_{W}})^{2} + (\tilde{g} \cos{\theta_{W}})^{2} = g'^{2} + g^{2} \] Links klammern wir \( \tilde{g}^{2} \) aus und verwenden \( (\sin{\theta_{W}})^{2} + (\cos{\theta_{W}})^{2} = 1 \). Ergebnis: \[ \tilde{g} = \sqrt{g^{2} + g'^{2}} \] Für die Ladung \(e\) erhalten wir außerdem \[ e = g \sin{\theta_{W}} = g' \cos{\theta_{W}} = \frac{g g'}{\tilde{g}} \] Fassen wir zusammen:
|
Wie man den Weinbergwinkel durch die schwachen Ladungen g und g' ausdrückt: \[ \sin{\theta_{W}} = \frac{g'}{\tilde{g}} \] \[ \cos{\theta_{W}} = \frac{g}{\tilde{g}} \] \[ \tilde{g} = \sqrt{g^{2} + g'^{2}} \] \[ e = \frac{g g'}{\tilde{g}} \] |
Im Buchkapitel werden diese Zusammenhänge auch grafisch anhand eines Dreiecks demonstriert. Für die Ladungsfaktoren der \(Z_{\mu}\) -Terme ergibt sich damit: \[ g \cos{\theta_{W}} + g' \sin{\theta_{W}} = \] \[ =\frac{g^{2} + g'^{2}}{\tilde{g}} = \tilde{g} \] \[ -g \cos{\theta_{W}} + g' \sin{\theta_{W}} = \] \[ = \frac{ -g^{2} + g'^{2} }{\tilde{g}} \] Ergebnis:
|
Diracgleichungen für das linkshändige Neutrino- und Elektronfeld:
\[
i \gamma^{\mu} \bigg\{ \partial_\mu \nu_{L}(x) +
\]
\[
+ i \left[ \frac{g}{\sqrt{2}} W_{\mu}^{+} e_{L}(x)
+ \frac{\tilde{g}}{2} Z_{\mu} \nu_{L}(x) \right] \bigg\}
= 0
\]
|
Die Ladung \( g \) gehört also zur Ankopplung an das W-Boson-Potential, das zur Umwandlung des Teilchenflavors (schwachen Isospins) führt. Die Ankopplung an das elektromagnetische Potential erfolgt nur für das Elektronenfeld, und zwar mit der elektrischen Elementarladung \( e \). Das Neutrinofeld ist dagegen elektrisch neutral (war ja gerade so gemacht). Die Ankopplung an das Z-Boson-Potential erfolgt für Neutrino und Elektron mit jeweils unterschiedlichen Kombinationen von \(g\) und \(g'\).
Zur Kontrolle rechnen wir noch die Diracgleichung für das rechtshändige Elektronfeld aus. Die masselose Diracgleichung lautet: \[ i \gamma^{\mu} D_\mu^{(e_{R})} e_{R} = 0 \] oder ausgeschrieben: \[ i \gamma^{\mu} (\partial_\mu + i \, \mathrm{tr} A_{\mu}) e_{R} = 0 \] Dabei ist \[ \mathrm{tr} A_{\mu} = -g' B_{\mu} \, 1 = \] \[ = g' Z_{\mu} \sin{\theta_{W}} - g' A_{\mu}^{(\gamma)} \cos{\theta_{W}} = \] \[ = \frac{g'^{2}}{\tilde{g}} Z_{\mu} - e A_{\mu}^{(\gamma)} \] Die Diracgleichung lautet also:
| Diracgleichungen für das rechtshändige Elektronfeld: \[ i \gamma^{\mu} \bigg\{ \partial_\mu + i \left( \frac{g'^{2}}{\tilde{g}} Z_{\mu} -e A_{\mu}^{(\gamma)} \right) \bigg\} e_{R} = 0 \] |
Die Ankopplung an das elektromagnetische Vektorpotential erfolgt also wie beim linkshändigen Elektron mit der Elementarladung \(e\), während das Z-Boson mit einem anderen Ladungsfaktor ankoppelt. Das Photon macht also beim Elektron keinen Unterschied zwischen rechtshändigem und linkshändigem Feld, das Z-Boson dagegen schon, wenn auch nicht so extrem wie das W-Boson, das ausschließlich an linkshändige Felder ankoppelt.
Bleibt als letzte Gleichung noch die masselose Klein-Gordon-Gleichung für die beiden Higgsfelder, wobei wir nur die kovariante Ableitung betrachten wollen, da später noch ein Term hinzukommt, der die spontane Symmetriebrechung bewirkt: \[ D_{\mu}^{(\phi)} = \partial_{\mu} -i A_{\mu} = \] \[ = \partial_{\mu} + i \left[ \frac{g'}{2} B_{\mu} \, 1 + \frac{g}{2} W_{\mu}^{k} \sigma^{k} \right] \] Die Terme mit \(k = 1, 2\) ergeben wieder W-Boson-Terme, die den Isospin-Index ändern. Die Terme in der Diagonalen (die den Isospin-Index nicht ändern) lauten \[ \frac{g'}{2} B_{\mu} + \frac{g}{2} W_{\mu}^{3} \] sowie \[ \frac{g'}{2} B_{\mu} -\frac{g}{2} W_{\mu}^{3} \] Diese Terme hatten wir oben bereits (bis auf Vorzeichen) ausgerechnet:
Oberer Diagonalterm: \[ \frac{g'}{2} B_{\mu} + \frac{g}{2} W_{\mu}^{3} = \] \[ = - \frac{1}{2} ( -g W_{\mu}^{3} -g' B_{\mu} ) = \] \[ = - \frac{1}{2} [ Z_{\mu} ( -g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ + A_{\mu}^{(\gamma)} ( -g \sin{\theta_{W}} -g' \cos{\theta_{W}} ) ] = \] \[ = \left[ \frac{1}{2} \frac{ g^{2} -g'^{2} }{\tilde{g}} Z_{\mu} + e A_{\mu}^{(\gamma)} \right] \] Unterer Diagonalterm: \[ \frac{g'}{2} B_{\mu} - \frac{g}{2} W_{\mu}^{3} = \] \[ = - \frac{1}{2} ( g W_{\mu}^{3} -g' B_{\mu} ) = \] \[ = - \frac{1}{2} [ Z_{\mu} ( g \cos{\theta_{W}} + g' \sin{\theta_{W}} ) + \] \[ + A_{\mu}^{(\gamma)} ( g \sin{\theta_{W}} -g' \cos{\theta_{W}} ) ] = \] \[ = - \frac{\tilde{g}}{2} Z_{\mu} \] Das \(\phi_{1}\) -Higgsfeld ist also elektrisch geladen, das \(\phi_{2}\) -Higgsfeld ist dagegen elektrisch neutral, und beide koppeln auch an das Z-Boson.
Nun zur spontanen Symmetriebrechung (die wir bisher noch gar nicht gebraucht haben): Wir wollen wieder davon ausgehen, dass es einen Mechanismus gibt, der bei niedriger Energie (so wie im heutigen Universum) das \(\phi\) -Feld im gesamten Raum auf einen Wert ungleich Null einstellt, analog zum Quantenkondensat der Cooper-Paare in der Supraleitung. Ein Beispiel für einen solchen Mechanismus liefert das Potential \[ V(\phi) = \frac{\lambda^{2}}{2} \left( |\phi|^{2} - \frac{\eta^{2}}{2} \right)^{2} \] (mit reellen Parametern \(\lambda\) und \(\eta\)) das sein Minumum bei \[ |\phi| = \frac{\eta}{\sqrt{2}} \] hat. Dabei ist \[ |\phi|^{2} = |\phi_{1}|^{2} + |\phi_{2}|^{2} \] Die Summe der beiden quadrierten Higgs-Zeigerlängen muss also im Energie-Minimum gleich \(\eta^{2}/2\) sein.

Quelle:
Wikimedia Commons File:Mexican hat potential polar.svg, dort Public Domain.
Man kann nun durch eine geeignete Eichtransformation \(U(x)\) alle Felder so redefinieren, dass
\( \phi_{1} = 0 \) und \( \phi_{2} \) reell wird.
Das bezeichnet man auch als unitäre Eichung. Erst nach
Festlegung dieser Eichung darf man letztlich oben die entsprechenden Felder
mit dem Elektron oder dem Neutrino bzw. den verschiedenen Eichpotentialen (W, Z, γ)
identifizieren, denn vorher könnte eine Umeichung Elektron- und Neutrinofeld miteinander mischen
und so wieder alles durcheinanderbringen.
Das übrig gebliebene Higgs-Feld \( \phi_{2} \) ist dabei elektrisch neutral, wie wir gesehen haben.
Das Energie-Minimum liegt bei unitärer Eichung dann bei \( \phi_{2} = \eta / \sqrt{2} \).
Dieses Higgs-Feld \[ \phi = \begin{pmatrix} 0 \\ \frac{\eta}{\sqrt{2}} \end{pmatrix} \] wirkt nun wie das Quantenkondensat der Cooper-Paare in der Supraleitung und schirmt das Vakuum gegen das Eindringen von \(A\)-Feldern ab. Dadurch entstehen Massen für die W- und Z-Bosonen, so wie wir das am Beispiel der Supraleitung bereits gesehen haben. Um die Formeln herzuleiten, müsste man sich Gedanken über die korrekte Verallgemeinerung der Gleichung \( \partial_{\mu} \partial^{\mu} A^{\nu} = j^{\nu} \) auf die Eichgruppe U(2) machen. In der Literatur arbeitet man statt dessen meist mit der sogenannten Lagrangedichte, an der sich die Massenterme ebenfalls ablesen lassen. Wir wollen das hier nicht weiter verfolgen, um den Rahmen des Kapitels nicht zu sprengen.
Noch ein Hinweis zum sogenannten Goldstone-Boson:
Ohne die unitäre Eichung, die nach der spontanen Symmetriebrechung \(\phi_{2}\) reell macht,
wären auch Abweichungen vom \(\phi\)-Minimum in imaginärer \(\phi_{2}\) -Richtung möglich, d.h.
man hätte
\[
\phi_{2} = \frac{\eta}{\sqrt{2}} + \chi + i \xi
\]
Die entsprechenden Formeln (die wir hier nicht zeigen) legen nun auf den ersten Blick nahe,
dass man \(\chi\) als Higgs-Feld mit Masse und \(\xi\) als weiteres Higgs-Feld
ohne Masse (d.h. als sogenanntes Goldstone-Boson) interpretieren sollte.
Für \(\chi\) ist die Interpretation korrekt – das ist das massive Higgs-Feld. Das Goldstone-Bosonfeld \(\xi\), das letztlich durch die spontane Symmetriebrechung entsteht, kann jedoch nicht mit einem physikalischen Teilchen in Verbindung gebracht werden.
Vielmehr ist es ein spurioser (d.h. scheinbarer) Freiheitsgrad, der einer Eichfreiheit entspricht (dieser Punkt hatte bei der Entwicklung der Theorie durchaus für Verwirrung gesorgt). Es muss zusammen mit den Vektorpotentialen \(A_{\mu}\) betrachtet werden und mit diesen zu physikalisch interpretierbaren Feldern kombiniert werden.
Dabei kommt beispielsweise der Term \( \partial_{\mu}\xi \) zu \(A_{\mu}\) hinzu und generiert dort die longitudinale Polarisation der neuen \(A_{\mu}\) -Felder. Genau diese longitudinale Polarisation brauchen sie auch, denn bei der spontanen Symmetriebrechung werden die \(A_{\mu}\) -Felder ja massiv. Man sagt auch, dass die longitudinale Polarisation der \(A_{\mu}\) -Felder das Goldstone-Boson auffrisst.
Die unitäre Eichung erledigt diese Probleme mit einem Schlag, da sie das \(\xi\)-Feld direkt eliminiert und so dafür sorgt, dass die anderen Felder problemlos mit physikalischen Teilchen in Verbindung gebracht werden können. In der Quantentheorie der elektroschwachen Wechselwirkung darf man allerdings die unitäre Eichung nicht anwenden, wenn man die Renormierbarkeit der Theorie zeigen möchte – man muss da sehr viel vorsichtiger zu Werke gehen, da die Renormierbarkeit auf der Existenz der Eichsymmetrie beruht, die man daher nicht einfach durch eine Eichung komplett ausschalten darf.
Die unitäre Eichung fixiert die Eichfreiheit der Felder noch nicht vollständig. Es bleibt eine Rest-Eichfreiheit übrig, nämlich die Eichtransformation \[ U(\alpha(x)) := \begin{pmatrix} e^{i \alpha(x)} & 0 \\ 0 & 1 \end{pmatrix} \] Das ist genau die Eichtransformation, die zur elektromagnetischen Wechselwirkung gehört. Sie verändert das eichfixierte \(\phi\)-Feld nicht, da sie nur auf das geladene \(\phi_{1}\)-Feld wirkt, das aber auf Null eichfixiert ist. Für die anderen Felder gilt: \[ \psi_{L}' = \frac{U(\alpha)}{\mathrm{det} U(\alpha)} \, \psi_{L} = \] \[ = \begin{pmatrix} e^{i \alpha(x)} & 0 \\ 0 & 1 \end{pmatrix} \, \frac{1}{e^{i \alpha}} \, \psi_{L} = \] \[ = \begin{pmatrix} 1 & 0 \\ 0 & e^{-i \alpha} \end{pmatrix} \, \psi_{L} \] also \[ \nu_{L}' = \nu_{L} \] und \[ e_{L}' = e^{-i \alpha} \, e_{L} \] sowie \[ e_{R}' = \frac{1}{\mathrm{det} U(\alpha)} \, e_{R} = e^{-i \alpha} \, e_{R} \] d.h. nur die beiden geladenen Elektronenfelder unterliegen in gleicher Weise der Rest-Eichfreiheit. Analog kann man nachrechnen, dass sich bezüglich der Rest-Eichfreiheit \(U(\alpha)\) die \(W^{+}\) und \(W^{-}\) -Felder wie geladene Felder mit dem passenden Phasenfaktor verändern und dass sich \(A_{\mu}^{(\gamma)}\) wie ein elektromagnetisches Viererpotential eichtransformiert.
Hier sieht man auch sehr schön, warum man bei manchen Eichtransformationen oben den Faktor \( 1 / \mathrm{det} U \) hinzugefügt hat: Nur so passt bzgl. der elektromagnetischen Wechselwirkung und der zugehörigen Rest-Eichfreiheit nachher alles zusammen (wobei man die Konventionen auch anders treffen kann, solange die Eichtransformationen sich relativ zueinander korrekt verhalten).
Das soll an dieser Stelle genügen, um einen ersten Eindruck von der Theorie der elektroschwachen Wechselwirkung zu gewinnen. Natürlich fehlen noch viele weitere Details, aber das würde den Rahmen des Kapitels sprengen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 24 January 2025