Zusammenfassung des Buchkapitels:
Warum ist die schwache Wechselwirkung schwach? Der Betrag der schwachen Ladung ist von der gleichen Größenordnung wie der Betrag der elektrischen Elementarladung. An der Ladung kann es also nicht liegen.
Bei schwachen Zerfällen tritt ein W- oder Z-Boson als innere Linie zwischen dem zerfallenden Teilchen und den Zerfallsprodukten auf. Jede innere Linie eines Feynmangraphens führt zu einem Faktor der Form \[ \frac{1}{E^2-(pc)^2-(mc^2)^2} \] wie wir aus Kapitel 5.2 wissen. Dabei ist \(E\) die Energie, \(p\) der Impuls und \(m\) die Masse des virtuellen Teilchens (hier W- oder Z-Boson).
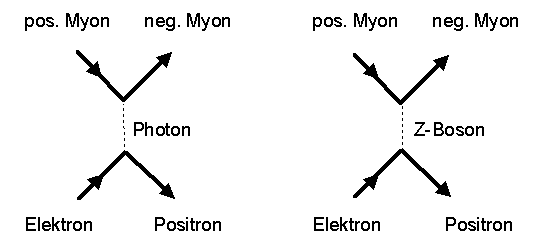
Der Grund für die geringe Stärke der schwachen Wechselwirkung bei den meisten Teilchenzerfällen liegt darin begründet, dass die virtuell auftretenden W- und Z-Bosonen eine sehr große Masse von um die 90 GeV aufweisen, weit oberhalb der bei den Zerfällen typischerweise auftretenden Energien und Impulse der inneren W- und Z-Bosonlinien. Daher ist der Nenner im obigen Term relativ groß und der Bruch relativ klein. Bei genügend hohen Energien kann der Nenner aber auch klein, der Bruch groß und die schwache Wechselwirkung damit stärker werden. Das kann man beispielsweise bei der folgenden Reaktion erreichen:

Die elektroschwache Theorie sagt nun eine Z-Bosonmasse von etwa 90 GeV voraus.
Solange die Energie des Elektrons und Positrons noch weit unterhalb
von 50 GeV liegt, spielt der Feynmangraph mit dem virtuellen Z-Boson
keine Rolle.
Die Situation ändert sich, sobald die Elektron- und Positronenergie in
den Bereich von 40 bis 50 GeV kommt, so dass deren Summe im Bereich der
Z-Bosonmasse \(m_Z\) liegt.
Nun wird der Faktor der inneren Z-Bosonlinie sehr groß, so dass die
Wahrscheinlichkeit stark ansteigt, dass sich ein Myon-Antimyon-Paar bildet.
Im Experiment sollten wir daher eine starke Zunahme der Erzeugung
von Myon-Antimyon-Paaren bei Elektron- und Positronenergien von etwa
40 bis 50 GeV beobachten:
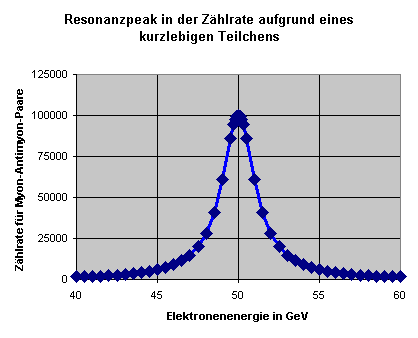
Aus dem gemessenen Maximum des Peaks lässt sich
umgekehrt die Masse des zwischenzeitlich erzeugten
virtuellen Z-Bosons ermitteln.
Die Rechnung zeigt darüber hinaus, dass sich die Breite
des Resonanzpeaks mit der mittleren
Lebensdauer des Z-Bosons in Zusammenhang bringen lässt.
Je breiter der Peak ist, umso kürzer ist die Lebensdauer des Z-Bosons.
Mehr dazu im Buchkapitel und unten in den Zusatzinfos.
Im Jahre 1983 gelang es tatsächlich, die W- und Z-Bosonen am damaligen CERN-Proton-Antiproton-Collider erstmals nachzuweisen. In den darauf folgenden Jahren wurden diese Teilchen am LEP-Beschleuniger des CERN in Elektron-Positron-Kollisionen sehr genau vermessen mit folgendem Ergebnis:
Die Z-Masse konnte zu 91,190 GeV bestimmt werden, mit einer Breite des Resonanzpeaks von 2500 MeV. Aus der Breite kann man die Zahl der existierenden leichten Neutrinosorten bestimmen: Es gibt nur die bekannten Elektron-, Myon- und Tau-Neutrinos und vermutlich insgesamt auch nur die drei bekannten Quark- und Leptonfamilien (Details dazu siehe unten). Die W- und Z-Bosonmassen erfüllen zusammen mit dem separat gemessenen Weinbergwinkel sehr gut die im vorherigen Kapitel vorhergesagte Beziehung \[ \frac{M_{W}}{M_{Z}} = \cos{\theta_{W}} \] Im Jahr 1995 wurde am Tevatron dann auch das schwerste Quark nachgewiesen, das Top-Quark:
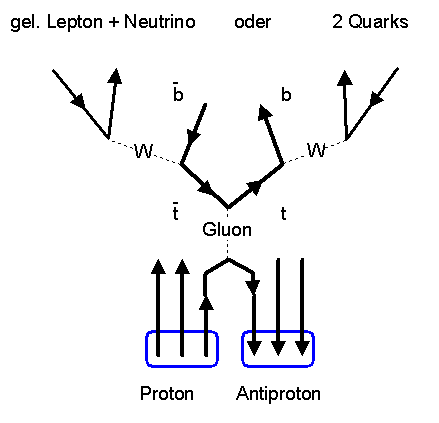
Die Masse des top-Quarks liegt bei 170 GeV (also ca. 170 mal schwerer als das Proton und damit ungefähr so schwer
wie ein Goldatom).
Wegen seiner großen Masse zerfällt es extrem schnell typischerweise in ein W-Boson
und ein Bottom-Quark. Es zerfällt sogar so schnell, dass es noch nicht einmal genügend Zeit hat,
zuvor ein Hadron zu bilden.
Auch das Higgs-Boson konnte im Jahr 2012 am LHC-Beschleuniger schließlich nachgewiesen werden. Damit sind alle vom Standardmodell vorhergesagten Teilchen in den Experimenten gefunden worden. Es gibt heute keine experimentellen Resultate, die ihm widersprechen.
So schön dieses Ergebnis zunächst ist, so wenig hilfreich ist es andererseits. Das Standardmodell weist nämlich neben seinen eleganten Zügen auch einige Mängel auf, die nahelegen, dass es nicht die fundamentale Theorie der Naturgesetze und der Struktur der Materie sein kann. Insbesondere enthält es eine große Zahl freier Parameter, die nicht im Rahmen dieser Theorie berechnet werden können: die 12 Quark- und Leptonmassen, die starken, schwachen und elektrischen Elementarladungen, die relativen Stärken der schwachen W-Boson-Vertices sowie einige weitere Parameter (Details im Buchkapitel). Zudem gibt es eine Reihe von ästhetischen Schönheitsfehlern: Der Mechanismus der spontanen Symmetriebrechung durch das Higgs-Boson sieht etwas künstlich aus, die starke Wechselwirkung bleibt von der elektroschwachen Wechselwirkung völlig getrennt, und die Gravitation ist nicht einbezogen.
Alle diese Punkte zeigen uns, dass wir mit dem Standardmodell trotz seines Erfolges noch nicht am Ziel angekommen sein können. Die Erwartungen sind daher hoch, dass wir mit modernen Hochleistungsbeschleunigern irgendwann neue Phänomene offenlegen, die über das Standardmodell hinausgehen.
Errata:
Seite 193: Der Satz
"... Es wird dabei besonders effektiv
die Kollisionsenergie in die Z-Bosonwelle übertragen,
die diese Energie dann wieder abgibt, indem besonders
viele andere Teilchen entstehen, beispielsweise Hadronen."
ist ein wenig irreführend, da Z-Bosonen häufig in nur zwei Teilchen zerfallen.
Gemeint ist, dass bei der Resonanzenergie die Erzeugungsrate (der Wirkungsquerschnitt) für
neue Teilchen groß wird, wenn Elektron und Positron auf Kollisionskurs sind.
a) Z-Resonanz und die Anzahl Neutrinosorten
b) Resonanz und Breit-Wigner-Formel; Vergleich mit der klassischen Mechanik
c) das Hierarchieproblem
d) Quark-Jets (Hadronen-Jets)
Eines der wichtigsten Ergebnisse des LEP ist die Bestimmung der Anzahl Neutrinofamilien aus der Breite der Z-Resonanz (siehe Buchkapitel). Schauen wir uns an, wie man das konkret macht:
Das Z-Boson zerfällt praktisch auschließlich in Lepton-Antilepton-Paare (Elektron, Myon, Tauon oder Neutrinos plus entsprechendes Antiteilchen) sowie in Quark-Antiquark-Paare, aus denen verschiedene Hadronen entstehen. Man spricht auch von verschiedenen Zerfallskanälen.
Leider lassen sich die Neutrinos, die beim Z-Zerfall entstehen, nicht direkt beobachten, denn Neutrinos wechselwirken kaum mit Materie und entkommen daher unerkannt den Teilchendetektoren. Wir können also nicht direkt erkennen, ob beim Z-Zerfall nur die drei bekannten Neutrinosorten (Elektron-, Myon, Tau-Neutrino) entstehen, oder ob vielleicht noch weitere bisher unbekannte Neutrinotypen erzeugt werden.
Es gibt jedoch einen indirekten Weg, solche Neutrinos aufzuspüren. Dazu verwendet man, dass sich die Zerfallsraten für die einzelnen Kanäle (einschließlich der Neutrino-Kanäle) zur Gesamt-Zerfallsrate des Z-Bosons aufsummieren müssen. Das bedeutet genauer:
Würde man zur Zeit Null eine Anzahl \( N(0) \) Z-Bosonen erzeugen, und könnten diese nur über den i-ten Kanal zerfallen (z.B. in Elektron-Positron-Paare), so wären nach der Zeit t noch \[ N_{i}(t) = N(0) \, e^{- t/\tau_{i}} \] übrig. Dabei ist \( \tau_{i} \) die mittlere Lebensdauer des Z-Bosons, wenn es nur den i-ten Zerfallskanal gäbe. Die Zerfallsrate (Anzahl Z-Boson-Zerfälle pro Zeiteinheit) über den i-ten Zerfallskanal ist also \[ \frac{d}{dt} N_{i}(t) = - \frac{1}{\tau_{i}} N(0) \, e^{- t/\tau_{i}} = - \frac{1}{\tau_{i}} \, N(t) \] Nun müssen die Zerfallsraten aller Kanäle zusammen die Gesamt-Zerfallsrate \[ \frac{d}{dt} N(t) = - \frac{1}{\tau} \, N(t) \] ergeben, wobei \(\tau\) die tatsächliche mittlere Lebensdauer des Z-Bosons ist: \[ \sum_{i} \frac{d}{dt} N_{i}(t) = - \sum_{i} \frac{1}{\tau_{i}} \, N(t) = \] \[ = \frac{d}{dt} N(t) = - \frac{1}{\tau} \, N(t) \] Es muss daher \[ \sum_{i} \frac{1}{\tau_{i}} = \frac{1}{\tau} \] gelten. Durch Multiplikation mit \(\hbar\) erhalten wir die Gesamtbreite der Resonanz \[ \Gamma = \frac{\hbar}{\tau} \] (siehe auch unten). Deshalb definieren wir analog auch für jeden einzelnen Zerfallskanal die Partial-Zerfallsbreite \[ \Gamma_{i} := \frac{\hbar}{\tau_{i}} \] Die Zerfallsbreite \( \Gamma_{i} \) wäre also die Breite der Z-Resonanz, wenn es nur den i-ten Zerfallskanal gäbe. Aus \[ \sum_{i} \frac{1}{\tau_{i}} = \frac{1}{\tau} \] folgt damit \[ \sum_{i} \Gamma_{i} = \Gamma \] d.h. die Partial-Zerfallsbreiten für die einzelnen Kanäle addieren sich zur Gesamtbreite der Z-Resonanz.
Direkt messen können wir nur die Zerfälle in geladene Leptonen oder Hadronen (Quarks), nicht aber in Neutrinos, denn diese entkommen unerkannt den Detektoren. Wenn wir nun die Z-Zerfallsbreiten in geladene Leptonen und Hadronen bestimmen und addieren würden, so müsste es eine Lücke zur Gesamt-Zerfallsbreite des Z-Bosons geben, die den unsichtbaren Zerfallskanälen entspricht, also insbesondere den Zerfällen in Neutrinos. Die Breite dieser Lücke wollen wir als \( \Gamma_{inv} \) bezeichnen, wobei inv für invisible (unsichtbar) steht. Es gilt also
| \[ \Gamma = \Gamma_{e} + \Gamma_{\mu} + \Gamma_{\tau} + \Gamma_{had} + \Gamma_{inv} \] |
wobei \( \Gamma_{had} \) für die Zerfallsbreite in Quark-Antiquark-Paare (Hadronen) steht usw..
Allerdings können wir die partiellen Zerfallsbreiten in geladene Leptonen und Hadronen nicht direkt messen, denn wir beobachten ja nicht den Zerfall einer bekannten Anzahl Z-Bosonen, sondern wir lassen am LEP Elektronen und Positronen kollidieren und schauen nach, wie oft dabei beispielsweise ein Quark-Antiquark-Paar (also Hadronen) entsteht. Man kann die Rate für diesen Prozess durch den sogenannten Wirkungsquerschnitt \( \sigma^{had} \) ausdrücken: \[ N_{had} = \sigma_{had} \, N_{e+} \, N_{e-} \frac{1}{F} \] Dabei ist \(N_{e+}\) die Zahl der eintreffenden Positronen, \(N_{e-}\) die Zahl der eintreffenden Elektronen, \(N_{had}\) ist die Zahl der Kollisionen, bei denen ein Quark-Antiquark-Paar (und damit Hadronen) entsteht, und \(F\) ist die Fläche, auf der Elektron- und Positron-Strahl miteinander kollidieren (siehe Wikipedia: Wirkungsquerschnitt).
Anschaulich bedeutet die obige Formel: Wenn wir ein Elektron-Positron-Paar kollidieren lassen (also \( N_{e+} = N_{e-} = 1 \)) und die Fläche \(F\) theoretisch so klein machen, dass die gleich \(\sigma_{had}\) wird, so ist \(N_{had} = 1\), d.h. Elektron und Positron reagieren dann garantiert miteinander zu Hadronen. Man kann sich daher \(\sigma_{had}\) als die Fläche vorstellen, die ein Elektron einem Positron entgegenstellt, wenn es um die Bildung von Hadronen geht.
Analoge Formeln gelten auch für die anderen Kanäle. Wir können also die Wirkungsquerschnitte für die einzelnen Kanäle messen, wobei der Wirkungsquerschnitt von der Energie abhängt, die Elektron und Positron gemeinsam zur Verfügung stellen.
Tragen wir den Wirkungsquerschnitt eines beliebigen Kanals gegen diese Energie auf, so ergibt sich genau unsere Breit-Wigner-Resonanzkurve, aus der wir direkt die Z-Boson-Masse m und die Z-Boson-Gesamtbreite \(\Gamma\) (nicht aber die Partialbreite \(\Gamma_{i}\) des Kanals) ablesen können. Die Breite der Resonanzkurve ist in jedem Kanal immer die Gesamtbreite \(\Gamma\), denn die Summe aller Kanal-Wirkungsquerschnitte muss ja bei jeder Energie den Gesamt-Wirkungsquerschnitt ergeben, und der bildet ebenfalls eine Resonanzkurve mit Breite \(\Gamma\).
Glücklicherweise gibt es einen Zusammenhang zwischen Wirkungsquerschnitt und Zerfallsbreite. Im hadronischen Kanal werden beispielsweise beide umso stärker, je höher die Wahrscheinlichkeit dafür ist, dass ein Z-Boson in ein Quark-Antiquark-Paar zerfällt. Der Wirkungsquerschnitt hängt zusätzlich davon ab, wie groß die Wahrscheinlichkeit dafür ist, dass aus Elektron und Positron überhaupt ein Z-Boson gebildet wird, und diese Wahrscheinlichkeit hängt umgekehrt auch mit der Zerfallswahrscheinlichkeit des Z-Bosons in ein Elektron-Positron-Paar zusammen. Die Formel lautet (wir geben alle Energien, Zerfallsbreiten, Massen und Längen in MeV an, so dass wir uns Faktoren wie \(c^2\) und \(\hbar\) hier schenken): \[ \sigma_{i}(E) = 12 \pi \frac{\Gamma_{e} \, \Gamma_{i} }{ (E^2 - m^2)^2 + m^2 \Gamma^2 } \approx \] \[ \approx \frac{3 \pi}{ m^2 } \frac{ \Gamma_{e} \, \Gamma_{i} }{ (E - m)^2 + (\Gamma/2)^2 } \] Dabei ist \(E\) die Energie von Elektron plus Positron im Schwerpunktsystem (in dem beide Teilchen frontal mit entgegengesetztem Impuls kollidieren), \(m\) ist die Z-Bosonmasse und \(\Gamma\) die Z-Boson-Gesamtbreite, \(\sigma_{i}(E)\) ist der Wirkungsquerschnitt für den i-ten Kanal bei der Energie \(E\), \(\Gamma_{i}\) ist die partielle Z-Zerfallsbreite für diesen Kanal und \(\Gamma_{e}\) ist die Zerfallsbreite für den Zerfall in Elektron + Positron.
Manchmal findet man leicht abweichende Formeln, die aber in der Nähe der Resonanz alle sehr gut übereinstimmen. Die erste Formel ist die gängige Formel in der Teilchenphysik, während die zweite Formel unsere Standard-Breit-Wigner-Resonanzformel ist. Man gelangt von der ersten zur zweiten Formel über die Näherung \[ (E^2 - m^2)^2 = \] \[ = [(E + m) \, (E - m)]^2 \approx \] \[ \approx [2m \, (E - m)]^2 \] für Energien \(E\) im Bereich der Resonanz \(m\).
Die Breite der Resonanz ist also in jedem Kanal durch die Gesamtbreite \(\Gamma\) gegeben. Die Partialbreite \(\Gamma_{i}\) jedes Kanals tritt nur als Faktor im Zähler auf, d.h. die Partialbreiten sind nicht an der Breite irgendeiner Resonanzkurve ablesbar (das wäre nur dann möglich, wenn es nur einen Kanal gäbe, so dass \(\Gamma_{i} = \Gamma\) ist). Insofern ist der Ausdruck Partialbreite etwas verwirrend.
Wenn wir den Wirkungsquerschnitt genau auf der Resonanzenergie \( E = m \) messen, so vereinfacht sich die Formel zu
| \[ \sigma_{i}(m) = 12 \pi \, \frac{\Gamma_{e} \, \Gamma_{i} }{ m^2 \Gamma^2 } \] |
Der Wirkungsquerschnitt im i-ten Kanal ist also proportional zur i-ten Partial-Zerfallsbreite \(\Gamma_{i}\), d.h. die relativen Verhältnisse der Partialbreiten untereinander entsprechen den relativen Verhältnissen der Wirkungsquerschnitte.
Anders gesagt: Wenn bei der Elektron-Positron-Kollision auf der Z-Resonanz ein Kanal i doppelt so häufig vorkommt wie ein Kanal j, so zerfällt das Z-Boson auch doppelt so häufig in Kanal i wie in Kanal j (eigentlich unmittelbar einleuchtend). Wir können also auf der Z-Resonanz direkt die relativen Verhältnisse der Partialbreiten zueinander bestimmen, einfach indem wir die Prozent-Anteile (Verzweigungsverhältnisse) der einzelnen Streuprodukte messen.
Was noch fehlt ist eine absolute Skala für die partiellen Zerfallsbreiten. Dazu können wir beispielsweise den gemessenen Wirkungsquerschnitt für den Elektron-Positron-Kanal herausgreifen (also \(i = e\)), aus der Resonanzkurve \(m\) und \(\Gamma\) ablesen und dann aus dem Wirkungsquerschnitt im Maximum (\(E = m\)) mit der obigen Formel \(\Gamma_{e}\) bestimmen.
Damit hätten wir eine absolute Skala für die partiellen Zerfallsbreiten gefunden und müssten die anderen Zerfallskanäle nur noch mit dem Elektron-Positron-Kanal vergleichen. So finden wir beispielsweise, dass Myon-Antimyon-Paare und Tauon-Antitauon-Paare genauso oft entstehen wie Elektron-Positron-Paare, so dass die entsprechenden Zerfallsbreiten genauso groß sein müssen wie \(\Gamma_{e}\) (von kleinen Abweichungen aufgrund der Tauon-Masse einmal abgesehen). Quark-Antiquark-Paare (Hadronen) sind dagegen etwa 20,8 -Mal häufiger als Elektron-Positron-Paare, so dass ungefähr \( \Gamma_{had} = 20,8 \, \Gamma_{e} \) sein muss.
In der Praxis verwendet man lieber den hadronischen Kanal zur Festlegung der Skala, da die Wahrscheinlichkeit für den Z-Zerfall in Hadronen am größten ist. Durch Vergleich mit dem Elektron-Positron-Kanal weiß man, dass ungefähr \( \Gamma_{had} = 20,8 \, \Gamma_{e} \) ist, was wir für \( \Gamma_{e} \) in der obigen Formel einsetzen können und so einen Zusammenhang zwischen dem gemessenen \( \sigma_{had}(m) \) und \( \Gamma_{had} \) erhalten.
Die absolute Skala der partiellen Zerfallsbreiten wird also über den hadronischen Kanal festgelegt. Die anderen Zerfallsbreiten sind dann über ihre Verhältnisse zur hadronischen Zerfallsbreite festgelegt. In der realen Analyse muss man den gemessenen hadronischen Wirkungsquerschnitt übrigens noch mit einem Strahlungs-Korrekturterm versehen – die Sache ist also noch etwas komplexer als hier dargestellt.
Insgesamt ergeben sich aus dem Experiment die folgenden partiellen Zerfallsbreiten für das Z-Boson (die dabei entstehenden relativ glatten Zahlen sind eher zufällig):
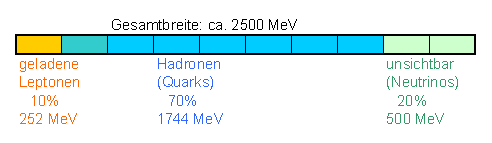
Die einzelnen Zerfallsbreiten stimmen dabei sehr gut mit den im Standardmodell berechneten Zerfallsbreiten überein (siehe z.B. Wikipedia: W and Z bosons). Addiert man die Zerfallsbreiten der geladenen Leptonen und Hadronen, so bleibt im Vergleich zur Z-Gesamtbreite eine Lücke \( \Gamma_{inv} \) von etwa 500 MeV. Diese Lücke entspricht Zerfällen in andere Teilchen, die den Detektoren entgehen, also typischerweise Neutrinos. Man kann im Rahmen des Standardmodells ausrechnen, wie groß die Zerfallsbreite in Neutrinos ist. Für jeden Neutrino-Kanal beträgt diese theoretische Zerfallsbreite ungefähr \[ \Gamma_{\nu} = 167 \, \mathrm{MeV} \] Wenn wir also von drei Neutrinosorten ausgehen, in die das Z-Boson zerfallen kann, so ergibt sich aus dem Standardmodell \[ 3 \, \Gamma_{\nu} = 501 \, \mathrm{MeV} \] Das entspricht im Rahmen der Genauigkeit gerade der gemessenen unsichtbaren Zerfallsbreite. Es gibt also beim Zerfall des Z-Bosons keinerlei unbekannte Zerfallsprodukte, die uns entgangen sein können. Das Z-Boson zerfällt nur in die bekannten Quarks, geladenen Leptonen und Neutrinos. Es gibt neben den drei bekannten Neutrinosorten keine weiteren unbekannten Neutrinos im Z-Zerfall.
Natürlich ist nicht streng auszuschließen, dass es Neutrinos mit einer Masse oberhalb der halben Z-Masse geben könnte (denn diese können beim Z-Zerfall nicht erzeugt werden). Da aber alle bekannten Neutrinos nahezu masselos sind, gilt dies als sehr unwahrscheinlich. Man geht daher davon aus, dass es keine weiteren Neutrinos gibt.
Dann aber kann es im Rahmen des Standardmodells auch kein weiteres geladenes Lepton geben, denn geladenes Lepton und zugehöriges Neutrino müssen dort immer in Paaren vorkommen, sonst funktioniert die Eichsymmetrie nicht.
Im Standardmodell gibt es nun eine Eich-Anomalie, auf die wir auch im Buchkapitel 6.1 kurz eingehen. Sie besagt, dass die Summe der elektrischen Ladungen aller Quarks und Leptonen gleich Null sein muss (wobei man die elektrischen Quarkladungen dreifach zählen muss, da Quarks in drei Farbladungs-Varianten vorkommen).
Eine weitere Quarkfamilie (neben den bekannten drei Familien) ist deshalb ebenfalls ausgeschlossen, denn sonst müsste es auch eine entsprechende Leptonfamilie geben, um die Ladungen zu kompensieren. Wenn es nur drei Neutrinos gibt, so gibt es also auch nur drei geladene Leptonen und dann auch nur drei Quarkfamilien. Man geht daher heute davon aus, dass es nur die drei bekannten Quark- und Leptonfamilien gibt. Das Standardmodell ist insofern komplett.
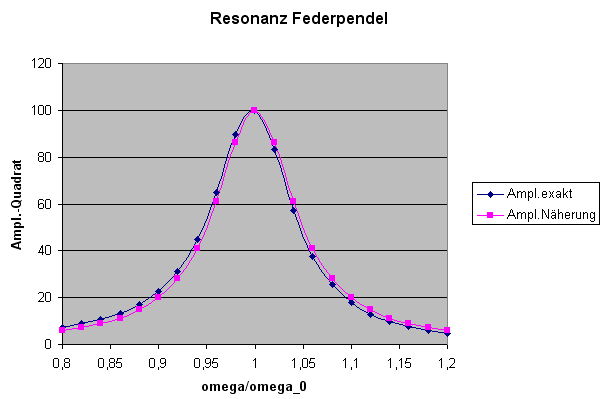
Der oben dargestellte Resonanzpeak wurde mit der Breit-Wigner-Formel berechnet (siehe Wikipedia: Breit-Wigner-Formel). Diese Formel hatten wir in Kapitel 2.5 in den Zusatzinformationen bereits hergeleitet und in Zusammenhang mit der mittleren Lebensdauer des instabilen Zwischenteilchens gebracht.
Das Phänomen der Resonanz tritt nicht nur bei Quantensystemen auf, sondern auch bereits in der klassischen Mechanik bei der sogenannten erzwungenen Schwingung. Da sich hierbei eine starke Analogie zur Quanten-Resonanz ergibt (siehe Buchkapitel) und die Sache recht übersichtlich bleibt, wollen wir sie uns hier näher ansehen:
Wir betrachten einen kleinen Körper der Masse \(m\), der sich am Ende einer elastischen Feder befindet (also ein Federpendel). Die Auslenkung des Körpers aus seiner Ruhelage bezeichnen wir mit \(x\). Die Rückstellkraft der Feder beträgt also gerade \[ - D x \] wobei \(D\) die Federkonstante ist (das negative Vorzeichen besagt, dass die Rückstellkraft entgegen der Auslenkungsrichtung wirkt).
Außerdem wollen wir Reibungskräfte berücksichtigen, die sich proportional zur Geschwindigkeit \[ x' = dx/dt \] des Körpers verhalten, d.h. die Reibungskraft beträgt \[ - R x' \] wobei \(R\) der Reibungskoeffizient ist (das negative Vorzeichen besagt, dass die Reibungskraft entgegen der Geschwindigkeit wirkt, also abbremst).
Um Resonanz zu erzeugen, brauchen wir noch eine periodische äußere Kraft, die zusätzlich auf den Körper einwirkt. Wir schreiben diese Kraft als \[ A \, e^{i \omega t} \] Dabei ist \(A\) die maximale Stärke der Kraft und \[ \omega = 2 \pi f \] ist die feste Kreisfrequenz (d.h. \(f\) ist die Frequenz), mit der die äußere Kraft wirkt (\(t\) ist wie immer die Zeit). Wie üblich verwenden wir aus Bequemlichkeit die komplexe e-Funktion \[ e^{i \omega t} = \cos{\omega t} + i \, \sin{\omega t} \] welche die einzelnen Rechenschritte erheblich vereinfacht. Man kann in jedem Rechenschritt jederzeit den Realteil separat betrachten und so die Rechnung auch ohne komplexe Zahlen nachvollziehen.
Nach dem Newtonschen Bewegungsgesetz (Kraft = Masse mal Beschleunigung) ist demnach \[ m x'' = - D x - R x' + A e^{i \omega t} \] wobei \[ x'' = \frac{d^2x}{dt^2} \] die Beschleunigung ist.
Etwas umgestellt lautet diese Bewegungsgleichung:
| Bewegungsgleichung der erzwungenen Schwingung: \[ m x'' + R x' + D x = A e^{i \omega t} \] |
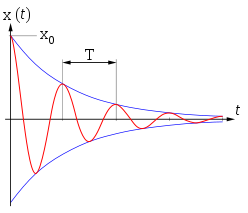
Wenn keine äußere Kraft wirkt (also \(A = 0\)), so haben wir eine gedämpfte Schwingung vor uns. Die entsprechende Bewegungsgleichung \[ m x'' + R x' + D x = 0 \] lässt sich dann leicht durch den Ansatz \[ x = a e^{i \alpha t} \] lösen, denn Einsetzen in die Bewegungsgleichung und Ausführen der Ableitungen nach der Zeit \(t\) ergibt: \[ - m a \, \alpha^2 \, e^{i \alpha t} + i R a \, \alpha \, e^{i \alpha t} + D a \, e^{i \alpha t} = 0 \] Division durch \( a \, e^{i \alpha t} \) sowie durch \( - m \) ergibt die quadratische Gleichung \[ \alpha^2 - i \frac{R}{m} \alpha - \frac{D}{m} = 0 \] die die folgenden Lösungen hat: \[ \alpha = i \frac{R}{2m} \pm \sqrt{- \left( \frac{R}{2m} \right)^2 + \frac{D}{m}} \] Wir wollen uns im Folgenden auf den Fall beschränken, bei dem die Dämpfung \(D\) so gering ist, dass der Term rechts unter der Wurzel positiv bleibt, denn nur so ergibt sich eine gedämpfte Schwingung (ist die Dämpfung zu hoch, so wird jede Schwingung erstickt und das System kriecht langsam in die Ruhelage). In diesem Fall setzen wir \[ \frac{1}{\tau} := \frac{R}{m} \] \[ \omega_0 := \sqrt{\frac{D}{m}} \] \[ \omega := \sqrt{- \left( \frac{R}{2m} \right)^2 + \frac{D}{m}} = \] \[ = \sqrt{\omega_0^2 - \frac{1}{(2 \tau)^2}} \] so dass die beiden Lösungen als \[ \alpha = \frac{i}{2 \tau} \pm \omega \] geschrieben werden können. Die Bedeutung dieser Größen wird klar, wenn wir sie in den Ansatz einsetzen: \[ x = a \, e^{i \alpha t} = \] \[ = a \, e^{i \, \left( \frac{i}{2 \tau} \pm \omega \right) \, t} = \] \[ = a \, e^{- \frac{t}{2\tau}} \,e^{\pm i \omega t} \] Die allgemeine Lösung der gedämpften Schwingung ist eine beliebige Linearkombination dieser beiden Lösungen, wobei man sich auf den Realteil beschränken kann. Halten wir fest:
|
gedämpfte Schwingung: Die allgemeine Lösung der Bewegungsgleichung \[ m x'' + R x' + D x = 0 \] einer gedämpften Schwingung (mit hinreichend kleiner Dämpfung) lautet: \[ x = e^{- \frac{t}{2\tau}} \, \left( a e^{+ i \omega t} + b e^{- i \omega t} \right) \] mit der Relaxationszeit \[ \tau := \frac{m}{R} \] und der Kreisfrequenz \[ \omega := \sqrt{- \left( \frac{R}{2m} \right)^2 + \frac{D}{m}} = \] \[ = \sqrt{\omega_0^2 - \frac{1}{(2 \tau)^2}} \] Dabei ist \[ \omega_0 := \sqrt{\frac{D}{m}} \] die Kreisfrequenz der ungedämpften Schwingung und \(a\) und \(b\) sind durch die Anfangsbedingungen festgelegt. |
Wikimedia Commons File:Damped oscillation graph2.svg, User:Jahobr, dort Public Domain.
Wikimedia Commons File:Damped spring.gif, von Oleg Alexandrov, dort Public Domain.
Die Relaxationszeit \( \tau \) wurde hier analog zum zerfallenden Quantenzustand (siehe
Kapitel 2.5) so gewählt, dass
das Quadrat der maximalen Amplitude nach der Zeitdauer \(\tau\) auf \(1/e\) abfällt.
Bei der klassischen Schwingung ist die Energie der Schwingung im Moment maximaler Auslenkung gerade gleich der potentielle Energie und damit gleich dem halben Amplitudenquadrat. Die Relaxationszeit gibt daher an, wie die Energie der Schwingung abnimmt.
In der Quantentheorie steht das Amplitudenquadrat dagegen für die Wahrscheinlichkeit, den entsprechenden Zustand vorzufinden, während die Energie in der Frequenz steckt. Die Analogie lautet also (bei kleiner Dämpfung):
| Quantenwelle: | Amplitudenquadrat ⇔ Wahrscheinlichkeit | Frequenz ⇔ Energie |
| klassische Schwingung: | Amplitudenquadrat ⇔ Schwingungsenergie | Frequenz ⇔ Federstärke |
Die Dämpfung bedeutet also bei der klassischen Schwingung, dass Energie durch Reibung verloren geht,
während sie bei einem instabilen Quantenzustand bedeutet, dass die Wahrscheinlichkeit für diesen
Quantenzustand abnimmt, da es eine (relativ kleine) Wechselwirkung mit anderen Quantenzuständen gibt,
in die er übergehen (zerfallen) kann.
Man kann dies aber auch so interpretieren, dass der Erwartungswert für die im instabilen Quantenzustand lokalisierte Energie abnimmt (da der Zustand immer unwahrscheinlicher wird) und der Energie-Erwartungswert in anderen Quantenzuständen zunimmt.
Damit wird die Analogie wieder enger. In beiden Fällen geht in diesem Sinn Energie an die Umgebung verloren, da es eine kleine Wechselwirkung mit dieser Umgebung gibt. Wichtig ist auch, dass diese Energie sich in der Umgebung irgendwie verteilt, also nicht wieder an die Schwingung zurückgegeben wird – genau diese Bedingungen braucht man, um die exponentielle Abnahme der Amplitude zu erreichen.
Was geschieht nun, wenn wir die periodische äußere Kraft \( A \, e^{i \omega t} \) wirken lassen, wobei hier die Kreisfrequenz \( \omega \) von außen vorgegeben wird?
Die entsprechende Bewegungsgleichung \[ m x'' + R x' + D x = A \, e^{i \omega t} \] lässt sich wieder wie zuvor durch den Ansatz \[ x = a \, e^{i \alpha t} \] lösen. Einsetzen in die Bewegungsgleichung und Ausführen der Ableitungen nach der Zeit \(t\) ergibt: \[ - m a \, \alpha^2 e^{i \alpha t} + i R a \, \alpha e^{i \alpha t} + D a \, e^{i \alpha t} = A e^{i \omega t} \] Wir interessieren uns hier nur für Lösungen \( x = a e^{i \alpha t} \) mit einer zeitunabhängigen Amplitude \(a\) und einer zeitunabhängigen Kreisfrequenz \(\alpha\). Man spricht auch vom eingeschwungenen Zustand, bei dem anfängliche Zusatzschwingungen bereits aufgrund der Dämpfung abgeklungen sind.
In diesem Fall muss \[ \alpha = \omega \] sein, um die Zeit \(t\) aus der Gleichung eliminieren zu können. Die Schwingung erfolgt also mit der von außen vorgegebenen Frequenz.
Division durch \( a e^{i \omega t} \) sowie durch \( - m \) ergibt mit \( \tau = m/R \) und \( \omega_0 := \sqrt{D/m} \) die Gleichung \[ a \, \omega^2 - i a \frac{\omega}{\tau} - a \, \omega_0^2 = - \frac{A}{m} \] Hier können wir links \(a\) ausklammern und nach \(a\) freistellen:
| Amplitude der erzwungenen Schwingung: \[ a = - \frac{A}{m} \, \frac{1}{\omega^2 - \omega_0^2 - i \frac{\omega}{\tau}} \] |
Die Amplitude \(a\) hängt also diesmal davon ab, mit welcher Kreisfrequenz \(\omega\) die äußere Kraft wirkt und damit die gleichfrequente Schwingung des Federpendels erzwingt.
Die Amplitude besitzt dabei auch einen Imaginäranteil, der zu einer Phasenverschiebung der Federpendelschwingung gegenüber der äußeren Anregungskraft führt – mehr dazu gleich.
Schauen wir uns zunächst an, wie das Betragsquadrat der Amplitude \(a\) von der Kreisfrequenz \(\omega\) abhängt: \[ |a|^2 = a a_{*} = \] \[ = \left( \frac{A}{m} \right)^2 \, \frac{1}{(\omega^2 - \omega_0^2)^2 + \left( \frac{\omega}{\tau} \right)^2} = \] \[ = \left( \frac{A}{m} \right)^2 \, \frac{1}{ \left( (\omega + \omega_0) \, (\omega - \omega_0) \right)^2 + \left( \frac{\omega}{\tau} \right)^2} \] Große Amplitudenwerte entstehen hier, wenn die von außen vorgegebene Kreisfrequenz \(\omega\) ungefähr der Kreisfrequenz \(\omega_0\) entspricht, mit der das ungedämpfte Federpendel schwingt (was bei schwacher Dämpfung auch ungefähr die Kreisfrequenz des gedämpften Federpendels ist). Genau das bezeichnet man als Resonanz.
Im Bereich der Resonanz können wir in guter Näherung \( \omega + \omega_0 \) durch \( 2\omega_0 \) und \( \omega/\tau \) durch \( \omega_0/\tau \) ersetzen: \[ |a|^2 \approx \left( \frac{A}{m} \right)^2 \, \frac{1}{ ((2\omega_0) (\omega - \omega_0))^2 + \left( \frac{\omega}{\tau} \right)^2 } = \] \[ = \left( \frac{A}{2\omega_0 m} \right)^2 \, \frac{1}{(\omega - \omega_0)^2 + \left( \frac{1}{2\tau} \right)^2} \]
Den Zusammenhang mit der Breit-Wigner-Formel aus Kapitel 2.5
erhalten wir, wenn wir
\[
E = \hbar \omega
\]
und
\[
\Gamma = \frac{\hbar}{\tau}
\]
verwenden, denn dann erhalten wir
im Bereich der Resonanz
\[
|a|^2 \sim
\frac{1}{ (E - E_{0})^2 + \left( \frac{\Gamma}{2} \right)^2 }
\]
Wie wir sehen, ist die Analogie nicht perfekt, denn wir haben oben beim Federpendel
ja eine Näherung eingesetzt,
die allerdings im Bereich der Resonanz gut erfüllt ist.
Ähnlich gehen auch in der Quantentheorie einige Annahmen und Näherungen ein, um die Breit-Wigner-Formel abzuleiten.
Der grundlegende Mechanismus ist jedoch in beiden Fällen sehr ähnlich: Es gibt ein System, das gedämpfte Schwingungen mit einer bestimmten Frequenz ausführen kann (Federpendel oder quantenmechanische Amplitude eines instabilen Zustandes), es gibt eine schwache Wechselwirkung mit der Umgebung, die die Dämpfung bzw. den Zerfall bewirkt, und es gibt eine äußere Schwingung (äußere Kraft oder äußere Quantenwelle), die über einen Mechanismus oder eine Wechselwirkung Energie bzw. Wahrscheinlichkeit auf das System übertragen kann.
Die Formeln mögen im Detail unterschiedlich sein, führen jedoch im Bereich der Resonanz zu sehr ähnlichen Resultaten und können daher dort durch die Breit-Wigner-Formel gut beschrieben werden.
Das gilt auch für den Phasenunterschied zwischen äußerer Anregungsschwingung und der Schwingung des betrachteten Systems, der im Bereich der Resonanz 90 Grad beträgt. Man kennt das auch aus der Erfahrung, wenn man manuell eine Feder oder eine Schaukel zum Schwingen bringen will: Einerseits sollte man möglichst die Eigenfrequenz des Systems verwenden, andererseits aber auch immer im richtigen Moment ziehen oder drücken – im Idealfall genau um 90 Grad (1/4 Schwingungsperiode) versetzt.
Beim Federpendel können wir die Phasenverschiebung der Lösung \[ x = a \, e^{i \alpha t} \] gegenüber der äußeren Kraft \[ A \, e^{i \omega t} \] an der Amplitude \[ a = - \frac{A}{m} \, \frac{1}{ \omega^2 - \omega_0^2 - i \frac{\omega}{\tau} } \] ablesen: Bei \( \omega = \omega_0 \) ist \[ a = - \frac{A}{m} \, \frac{1}{- i \frac{\omega}{\tau} } = - i \, \frac{A}{m} \, \frac{\tau}{\omega} \] Die Amplitude \(a\) läuft also bei Resonanz um 90 Grad (wegen dem Faktor \(-i\)) hinter der äußeren Kraftamplitude \(A\) her, oder umgekehrt liegt die äußere Anregungsschwingung bei Resonanz um 1/4 -Schwingungsperiode vor der Federpendel-Schwingung und zieht diese damit gleichsam hinter sich her. Durch dieses Hinterherziehen kann ein Maximum an Energie auf das Federpendel übertragen werden. Das entspricht genau unserer Alltagserfahrung mit Pendeln, Schaukeln oder Federn.
Wir können die Resonanz-Analogie zwischen klassischer Mechanik und Quantenmechanik noch etwas weiter treiben, indem wir die Näherung, die oben zur Breit-Wigner-Formel geführt hat, direkt in die Bewegungsgleichung des Federpendels einbauen. Die neue Bewegungsgleichung wird dann zumindest im Bereich der Resonanz ein ähnliches Verhalten ergeben wie die ursprüngliche Bewegungsgleichung, und sie wird die Breit-Wigner-Formel reproduzieren.
Wie müssen wir die ursprüngliche Bewegungsgleichung \[ x'' + \frac{x'}{\tau} + \omega_0^2 x = \frac{A}{m} e^{i \omega t} \] abändern? Für \( x = a e^{i \omega t} \) ergibt die Gleichung das Ergebnis \[ - a \, \omega^2 + i a \frac{\omega}{\tau} + a \, \omega_0^2 = \frac{A}{m} \] und hier hatten wir links letztlich die Näherung \[ - a \, \omega^2 + i a \frac{\omega}{\tau} + a \, \omega_0^2 = \] \[ = a \, (\omega_0^2 - \omega^2) + i a \frac{\omega}{\tau} = \] \[ = a \, (\omega_0 + \omega) \, (\omega_0 - \omega) + i a \frac{\omega}{\tau} \approx \] \[ \approx a \, 2 \omega_0 \, (\omega_0 - \omega) + i a \frac{\omega_0}{\tau} = \] \[ = a \, 2 \omega_0^2 - a \, 2\omega_0 \, \omega + i a \frac{\omega_0}{\tau} \] verwendet. Dieses Ergebnis wird von der neuen Bewegungsgleichung \[ 2\omega_0^2 x - 2\omega_0 \, (-i) \, x' + i \frac{\omega_0}{\tau} x = \frac{A}{m} e^{i \omega t} \] reproduziert, wenn wir dort unseren Ansatz \( x = a e^{i \omega t} \) einsetzen. Division durch \(2\omega_0\) ergibt \[ \omega_0 x + i x' + \frac{i}{2\tau} x = \frac{A}{m} \, \frac{1}{2\omega_0} \, e^{i \omega t} \] Freistellen nach \( - i x' \) liefert dann \[ - i x' = \omega_0 x + \frac{i}{2\tau} x - \frac{A}{m} \, \frac{1}{2\omega_0} \, e^{i \omega t} \] Diese Gleichung hat große Ähnlichkeit mit der zeitabhängigen Schrödingergleichung aus der Quantenmechanik (siehe Kapitel 2.3). Noch besser wird das sichtbar, wenn wir die Gleichung komplex konjugieren, mit \(\hbar\) multiplizieren und \(x^{*} =\psi \) schreiben:
| \[ i \hbar \frac{d \psi}{dt} = E_{0} \psi - \frac{i}{2\tau} \psi - f \, e^{- i \omega t} \] |
mit \[ E_{0} = \hbar \omega_0 \] \[ f = \frac{A}{m} \, \frac{\hbar}{2\omega_0} \] Man kann diese Gleichung quantenmechanisch so interpretieren, dass \(\psi\) die Amplitude eines fast-stabilen Zustandes ist, der näherungsweise eine Gleichung \[ H_{0} \psi = E_{0} \psi \] erfüllt und der zwei Störungen ausgesetzt ist: einer Wechselwirkung mit seiner Umgebung, die ihn langsam zerfallen lässt, was durch den Term \[ - \frac{i}{2\tau} \psi \] näherungsweise dargestellt wird, sowie einer periodischen Störung \[ - f \, e^{- i \omega t} \] beispielsweise aufgrund einer Lichtwelle oder einer Elektron + Positron -Welle.
Eine solche Schrödingergleichung sollte sich näherungsweise in der Quantentheorie aus der jeweils exakten Schrödingergleichung ableiten lassen, um die Anregung von Resonanzen zu beschreiben.
Anmerkung: Die Herleitung des Terms \( - \frac{i}{2\tau} \psi \) im Rahmen der sogenannten Wigner-Weisskopf-Näherung findet man beispielsweise in Otto Nachtmann: Phänomene und Konzepte der Elementarteilchenphysik, Anhang I.
Im Buchkapitel werden mehrere Hinweise angesprochen, die darauf hindeuten, dass es eine Physik jenseits des Standardmodells geben sollte, z.B.
Es gibt nun einen weiteren Hinweis, der darauf hindeutet, dass die Physik jenseits des Standardmodells nicht erst in weiter Ferne liegt, sondern sich in Reichweite des LHC-Beschleunigers befinden könnte. Man bezeichnet diesen Hinweis als Hierarchieproblem. Es besagt kurz folgendes:
Es gab schon vor dem Nachweis dess Higgs-Teilchens viele Indizien dafür, dass es leichter als 1 TeV sein muss (das hat sich bestätigt, denn es wiegt 0,125 TeV = 125 GeV). So bleibt die elektroschwache Wechselwirkung zwischen W-, Z- und Higgs-Boson bei hohen Energien nur dann schwach, wenn das Higgs-Teilchen leichter als etwa 1 TeV ist.
Zugleich deuten die gleitenden Kopplungskonstanten im Standardmodell auf eine mögliche übergreifende Theorie bei 1013 TeV (das sind 1016 GeV) hin – mit entsprechend schweren weiteren Teilchen.
Falls das Standardmodell bis zu diesen hohen Energien gültig ist und erst dort in eine übergreifende Theorie übergeht, so beeinflussen die sehr schweren Teilchen der übergreifenden Theorie als virtuelle Teilchen wiederum die Higgs-Masse. Diese kann nur dann kleiner als 1 TeV bleiben, wenn es zu einer extremen Feinabstimmung der Parameter in der übergreifenden Theorie kommt. Das gilt als sehr unwahrscheinlich, d.h. eine solche übergreifende Theorie mit schweren Teilchen sollte die Higgs-Masse weit über 1 TeV treiben.
Dieser Widerspruch deutet darauf hin, dass eine oder mehrere der genannten Voraussetzungen nicht zutreffen. Dies führt fast immer zu Phänomenen, die sich am LHC beobachten lassen sollten. Hier einige Möglichkeiten:
Wenn am LEP oder LHC aus einem erzeugten Z-Boson ein hohenergetisches Quark-Antiquark-Paar entsteht, so wissen wir aus Kapitel 4.3, dass sich durch das Zerreißen des starken Kraftfeldschlauchs zwischen ihnen viele Hadronen bilden, die meist in Form zweier Hadronen-Jets in die Richtung der beiden Quarks auseinanderfliegen. Dadurch entstehen sogenannte 2-Jet-Ereignisse. Hier ist ein solches Ereignis vom LEP:
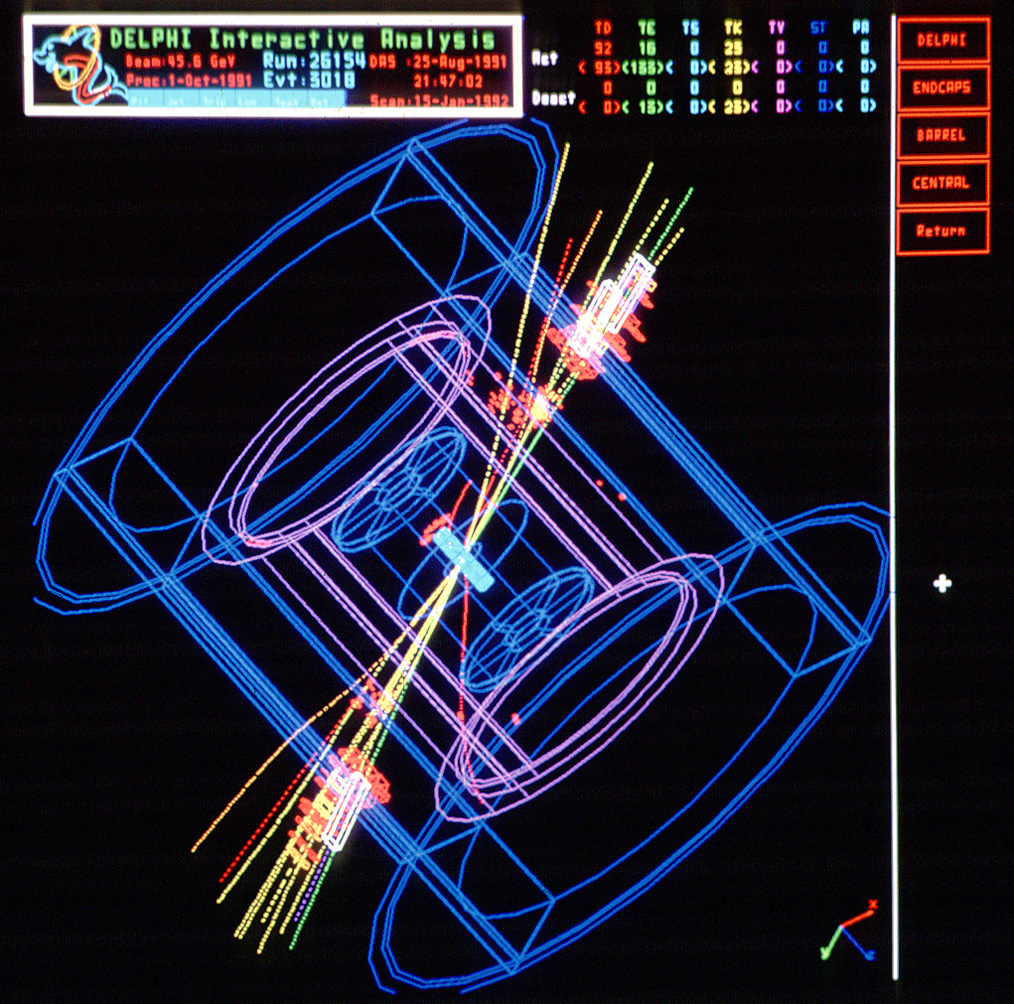
Quelle: Cern Document Server, http://cdsweb.cern.ch/record/39449,
verwendet gemäß der Bedingungen unter
Accessing CERN copyrighted material: The CERN Document Server contains multimedia material
under CERN copyright. You can freely download and use the high-resolution version of these files,
provided you agree and respect the conditions of use.
Solche Hadronen-Jets entstehen auch beispielsweise, wenn man sehr hochenergetische Elektronen beispielsweise auf Protonen schießt,
um deren Inneres auszuleuchten (analog zu Rutherfords Streuexperiment bei Atomen aus Buchkapitel 1.3,
siehe dazu auch Buchkapitel 4.3 ).
Damit sind Hadronen-Jets ein indirekter Nachweis dafür, dass Hadronen aus Quarks bestehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 05 February 2025